
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | John Onimisi Obidi | -- | 2762 | 2025-07-04 14:33:55 | | | |
| 2 | John Onimisi Obidi | -308 word(s) | 2454 | 2025-07-04 15:04:54 | | | | |
| 3 | John Onimisi Obidi | -10 word(s) | 2444 | 2025-07-04 15:09:01 | | | | |
| 4 | John Onimisi Obidi | Meta information modification | 2444 | 2025-07-04 15:11:21 | | | | |
| 5 | John Onimisi Obidi | -161 word(s) | 2283 | 2025-07-04 15:19:40 | | | | |
| 6 | John Onimisi Obidi | + 4 word(s) | 2287 | 2025-07-04 15:34:56 | | | | |
| 7 | John Onimisi Obidi | -107 word(s) | 2180 | 2025-07-04 15:46:55 | | | | |
| 8 | John Onimisi Obidi | Meta information modification | 2180 | 2025-07-04 15:53:56 | | | | |
| 9 | Catherine Yang | -1 word(s) | 2179 | 2025-07-07 04:03:08 | | | | |
| 10 | John Onimisi Obidi | -151 word(s) | 2028 | 2025-07-09 21:51:34 | | | | |
| 11 | John Onimisi Obidi | -9 word(s) | 2019 | 2025-07-09 21:55:15 | | | | |
| 12 | John Onimisi Obidi | Meta information modification | 2019 | 2025-07-09 21:56:25 | | | | |
| 13 | John Onimisi Obidi | Meta information modification | 2019 | 2025-07-09 21:57:18 | | |
Video Upload Options
This is an introductory material on the Master Entropic Equation of the Theory of Entropicity (ToE).
1. A Concise Introduction to the Master Entropic Equation (MEE) of the Evolving Theory of Entropicity (ToE)
Following from the axioms and principes of the Theory of Entropicity(ToE), first formulated by John Onimisi Obidi, [1][2][3][4] we present a single master action for the entropic scalar field ''S(x)'' that unifies all known entropy formulations—thermodynamic, statistical, information-theoretic, and quantum—and naturally incorporates Fisher information corrections. Starting from

we show how each classical entropy expression (Clausius, Boltzmann, Gibbs, Shannon, Rényi, Tsallis, and von Neumann) emerges by appropriate identifications of ''S(x)''. We then derive the local entropy current and demonstrate the second law as a Noether theorem. Finally, we extend the action to include a Fisher information term derived variationally, yielding the complete effective action
This framework lays the groundwork for exploring entropy as a fundamental field underlying all interactions.
Here, we discuss the motivation for treating entropy as a fundamental field and review prior work (in particular, Jacobson, Verlinde, Padmanabhan, Frieden). The notion of entropy has traditionally been that of a ''derived'' quantity—an accounting tool measuring disorder or information—but not as a ''fundamental field'' in its own right. In this work, we argue that we must promote entropy to a dynamical scalar field ''S(x)'' with its own kinetic term and potential, from which all classical entropy laws emerge. Below we review the key prior developments:
2. A Brief Review of Some of the Key Prior Developments of Entropic Approaches
Jacobson's Thermodynamics of Spacetime
Jacobson[5] showed that demanding the Clausius relation
for all local Rindler horizons, with ''S'' proportional to horizon area and ''T'' the Unruh temperature, leads directly to Einstein's field equations. Here, entropy constrains geometry but does not propagate as an independent field.
Verlinde's Entropic Gravity
Verlinde[6] proposed that gravity arises as an entropic force,
where `$\nabla S$` is the gradient of the entropy associated with a holographic screen. Again, ''S'' guides dynamics but lacks its own action principle.
Padmanabhan's Entropy Functionals
Padmanabhan[7] introduced entropy functionals on null surfaces whose extremization reproduces the Einstein–Hilbert action. Schematically, with `$P^{abcd}$` related to the gravitational Lagrangian, yet no independent bulk entropy field is identified.
with `$P^{abcd}$` related to the gravitational Lagrangian, yet no independent bulk entropy field is identified.
=== Frieden's Extreme Physical Information ===
Frieden<ref>Frieden, B.R. (2004). ''Science from Fisher Information: A Unification.'' Cambridge University Press.</ref> formulated the Extreme Physical Information (EPI) principle by extremizing a combination of Shannon entropy and Fisher information:
where  is the Fisher information and
is the Fisher information and  the physical information. This yields field equations (e.g. Schrödinger's equation) from inference, but does not treat entropy as a propagating field.
the physical information. This yields field equations (e.g. Schrödinger's equation) from inference, but does not treat entropy as a propagating field.
=== Position of the Theory of Entropicity ===
In contrast to these approaches, the Theory of Entropicity posits the master action above, in which ''S(x)'' is a genuine scalar field:
* A canonical kinetic term <math>-\tfrac12(\nabla S)^2</math> enables propagation of entropy.
* A potential <math>V(S)</math> encodes self-interaction, e.g. <math>V(S)=-2k_B\ln|\psi|</math>.
* A universal coupling <math>\eta\,S\,T^{\mu}{}_{\mu}</math> introduces back-reaction on matter and geometry.
As shown in Sections 3 and 4, this single variational principle yields all classical entropy laws (Eqs. eq:claudia–eq:epi) and their associated currents and second-law statements via Noether's theorem.
== '''How ToE Subsumes and Extends These Approaches''' ==
{| class="wikitable" style="width:100%;"
! style="width:20%;" | ''Prior Work''
! style="width:30%;" | ''Key Insight''
! style="width:50%;" | ''ToE Extension''
|-
| '''Jacobson (1995)'''
| ''δQ = T dS'' on local horizons
| Promotes ''S'' from horizon bookkeeping to a bulk field ''S(x)'' with its own dynamics.
|-
| '''Verlinde (2011)'''
| ''F = T ∇S'' entropic force
| Embeds ∇S in a Lagrangian with kinetic term <math>\tfrac12(\partial S)^2</math>.
|-
| '''Padmanabhan (2003–10)'''
| Entropy functionals ↔ Einstein–Hilbert action (surface terms)
| Replaces multiple surface functionals with one bulk master action for ''S(x)''.
|-
| '''Frieden’s EPI (1989–)'''
| Extremize Shannon + Fisher over ''p(x)''
| Derives both Shannon and Fisher pieces from a single ToE variational principle, producing the master action plus subleading corrections.
|}
== '''The ToE Master Action''' ==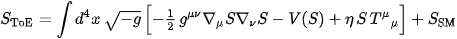
This action is the first proposal to:
* Identify local entropy (Boltzmann, Gibbs, Shannon, von Neumann) with the field value ''S(x)''.
* Endow ''S(x)'' with a canonical kinetic term and potential ''V(S)''.
* Couple ''S'' universally to matter and geometry via <math>\eta\,S\,T^\mu{}_\mu</math>.
* Derive all classical entropy laws and information measures—and their thermodynamic second law—by standard field‐theoretic procedures (Euler–Lagrange, Noether) from one unified action.
Thus ToE not only unifies but generalizes earlier entropic‐gravity and information-based approaches by making entropy itself the fundamental mediator of forces and geometry.
= '''Master Action of the Theory of Entropicity''' =
The master action of the Theory of Entropicity is defined by:

'''Explanation of terms'''
* ''g<sub>μν</sub>'' – the spacetime metric, signature −+++.
* ''φ<sub>i</sub>'' – all Standard Model matter fields (scalars, fermions, gauge fields).
* ''T<sup>μ</sup><sub>μ</sub>'' – the trace of the matter stress–energy tensor, ''T<sup>μν</sup> = -(2/√−g) δS<sub>SM</sub>/δg<sub>μν</sub>''.
* ''η'' – a dimensionful coupling constant controlling back‐reaction of entropy on matter and geometry.
* ''V(S)'' – self‐interaction potential for the entropy field (e.g.\ mass term, logarithmic potential, or other).
= '''Derivation of Classical Entropy Expressions''' =
Starting from the above ToE Master Equation<math name="eq:master_action"/>, one can derive the following well known entropy equations or expressions:
1. '''Clausius relation'''
<math>
dS = \frac{\delta Q_{\rm rev}}{T}
</math>.
2. '''Boltzmann entropy'''
<math>
S = k_B \ln \Omega
</math>.
3. '''Gibbs entropy'''
<math>
S = -\,k_B \sum_i p_i\ln p_i
</math>.
4. '''Shannon entropy'''
<math>
H = - \sum_i p_i\log_2 p_i
</math>.
5. '''Rényi entropy'''
<math>
H_{\alpha} = \frac{1}{1-\alpha}\ln\sum_i p_i^{\alpha}
</math>.
6. '''Tsallis entropy'''
<math>
S_q = \frac{1}{q-1}\bigl(1 - \sum_i p_i^q\bigr)
</math>.
7. '''von Neumann entropy'''
<math>
S_{\rm vN} = -\,k_B\,\mathrm{Tr}\bigl[\rho\ln\rho\bigr]
</math>.
Each case emerges by identifying boundary terms or stationary configurations of ''S(x)'' with the appropriate statistical ensemble or density operator.
= '''Entropy Current and Second Law''' =
Under the global shift symmetry
<math>S \to S + \mathrm{const}</math>,
Noether’s theorem yields a conserved current:
<math>
J_S^\mu = -\,\sqrt{-g}\;g^{\mu\nu}\,\nabla_{\nu}S.
</math>
On shell, the Euler–Lagrange equation for ''S(x)'' implies

realizing the local second‐law inequality.
3. Derivation of the Master Entropic Equation (MEE) of the Theory of Entropicity (ToE)
We now show how to derive both Shannon–entropy and Fisher–information terms from one unified variational principle.
== 1. Define the Total Information Functional ==
 The first piece is Shannon entropy density; the second is Fisher information weighted by ''λ''.
The first piece is Shannon entropy density; the second is Fisher information weighted by ''λ''.
== 2. Impose the Entropy–Probability Relation ==
Enforce

<math>
S(x) + k_B \ln p(x) = 0
\quad\Longleftrightarrow\quad
p = e^{-S/k_B}
</math>
via a Lagrange multiplier ''Λ(x)''. Define the augmented functional:

== 3. Extremize in ''p'', ''S'', and ''Λ'' ==
<math>
\delta_{p,S,Λ}\;J[p,S,Λ] \;=\; 0.
</math>
* Variation w.r.t.\ ''Λ'' enforces <math>S + k_B\ln p = 0</math>.
* Variation w.r.t.\ ''p'' yields an equation mixing <math>\ln p</math> and <math>\nabla\ln p</math>.
* Variation w.r.t.\ ''S'' returns the master entropic action with both Shannon and Fisher pieces.
4. Eliminate ''p'' and ''Λ''
Substitute <math>p = e^{-S/k_B}</math> into ''J'' and eliminate ''Λ''. The resulting effective action is: * The first two terms reproduce the ToE kinetic + potential structure.
* The first two terms reproduce the ToE kinetic + potential structure.
* ''η S T<sup>μ</sup><sub>μ</sub>'' is the universal matter–geometry coupling.
* The final term is the derived Fisher‐information correction.
5. The Master Entropic Equation (MEE)
Including the Standard Model (SM) terms into the above expression, the action then generalizes to:

where '''<math>\Phi</math>''' denotes all '''Standard Model (SM)''' fields and ''g<sub>μν</sub>'' is the spacetime metric tensor.
This expression is the Master Entropic Equation (MEE) of the Theory of Entropicity (ToE).
6. Recovering Special Cases & Identities
From <math>S_{\rm eff}[S]</math>, one can:
# Identify <math>S</math> with Gibbs, Shannon, von Neumann, or wavefunction‐surprisal densities.
# Derive the entropy current via Noether’s theorem under <math>S\to S+\mathrm{const}</math>, yielding <math>\nabla_\mu J^\mu \ge 0</math>.
# Read off the entropic field action (kinetic + potential).
# Vary <math>S</math> to obtain the Euler–Lagrange field equation.
# Inspect the <math>\eta\,S\,T^\mu{}_\mu</math> term for the matter coupling.
Thus all seven entropy identities and the full master dynamics emerge from one unified action principle of the Theory of Entropicity(ToE).
''Further directions you might explore:''
* Explicit form and interpretation of the <math>p</math>‐variation.
* Stability analysis of fluctuations around a vacuum entropy configuration.
* Extensions to include quantum corrections or higher‐derivative Fisher terms.
* Connections with information‐geometry and Frieden’s EPI program in curved space.
= '''Theory of Entropicity (ToE) Effective‐Field‐Theory Hierarchy with Fisher‐Type Correction''' =
== 1. Effective‐Field‐Theory Hierarchy ==
We decompose the total ToE action into a leading entropic piece <math>S^{(0)}</math> and a subleading Fisher gradient correction <math>S^{(1)}</math>:

;'''Leading ToE Action (''S<sup>(0)</sup>''):'''
:Generates geometry and interactions purely from the entropy field.
;'''Subleading Gradient Correction (''S<sup>(1)</sup>''):'''
:A Fisher‐inspired <math>(\nabla S)^2</math> term, controlled by <math>\lambda\ll1</math>.
== 2. Quantum/Statistical Origin ==
Such gradient corrections naturally arise when integrating out high‐frequency modes or incorporating 1‐loop fluctuations of <math>S</math>. They enrich the effective propagation of <math>S</math> without invalidating the tree‐level postulate that entropy drives dynamics.
== 3. Preservation of Shift Symmetry ==
Both <math>S^{(0)}</math> and <math>S^{(1)}</math> respect the global shift symmetry
<math>
S(x)\;\to\;S(x)+\mathrm{const},
</math>
ensuring the existence of a conserved entropy current and the second‐law condition <math>\nabla_\mu J^\mu\ge0</math>.
== 4. Information‐Geometric Embedding ==
Interpreting <math>S^{(1)}\propto(\nabla S)^2</math> as an information‐geometric “stiffness” of the entropy manifold does not contradict the ToE claim that entropy underlies geometry. It simply acknowledges that the curvature of the entropy configuration space feeds back as an effective rigidity.
== 5. Bottom Line ==
By treating Fisher‐type terms as controlled, higher‐order effective corrections rather than replacements of the core action, one preserves the primacy of the entropy‐driven ToE master action. Fisher information then appears naturally as a fine‐tuning of the entropy field’s propagation.
= '''Fisher Information Extension''' =
We present the variational derivation of the Fisher term via a Lagrange multiplier method. The complete effective action becomes:

= '''References''' =
<references/>
References
- Obidi, John Onimisi (2025-03-29). ''Review and Analysis of the Theory of Entropicity ...''. Cambridge University. doi:10.33774/coe-2025-7lvwh. https://doi.org/10.33774/coe-2025-7lvwh
- Obidi, John Onimisi (2025-04-14). ''Einstein and Bohr Finally Reconciled ...''. Cambridge University. doi:10.33774/coe-2025-vrfrx. https://doi.org/10.33774/coe-2025-vrfrx
- Obidi, John Onimisi (2025-06-14). ''On the Discovery of New Laws of Conservation ...''. Cambridge University. doi:10.33774/coe-2025-n4n45. https://doi.org/10.33774/coe-2025-n4n45
- HandWiki contributors (2025). ''Physics: A Concise Introduction to the Evolving Theory of Entropicity (ToE)''. HandWiki. Last revision 4 July 2025 12:21 UTC. Retrieved 4 July 2025 13:47 UTC. [https://handwiki.org/wiki/index.php?title=Physics:A_Concise_Introduction_to_the_Evolving_Theory_of_Entropicity_(ToE)&oldid=3740897 Permanent link]
- Jacobson, T. (1995). "Thermodynamics of spacetime: the Einstein equation of state." ''Physical Review Letters'' 75 (7): 1260–1263.
- Verlinde, E. (2011). "On the origin of gravity and the laws of Newton." ''Journal of High Energy Physics'' 2011:29.
- Padmanabhan, T. (2010). "Thermodynamical aspects of gravity: new insights." ''Reports on Progress in Physics'' 73:046901.
- Padmanabhan, T. (2010). "Thermodynamical aspects of gravity: new insights." ''Reports on Progress in Physics'' 73:046901.
- HandWiki contributors (2025). ''Physics: A Concise Introduction to the Evolving Theory of Entropicity (ToE)''. HandWiki. Last revision 4 July 2025 12:21 UTC. Retrieved 4 July 2025 13:47 UTC. [https://handwiki.org/wiki/index.php?title=Physics:A_Concise_Introduction_to_the_Evolving_Theory_of_Entropicity_(ToE)&oldid=3740897 Permanent link]




