Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Gabriele Bocchetta
 -- 2641 2023-07-05 16:42:20 |
2 references update
Fanny Huang
 -3 word(s) 2638 2023-07-07 07:46:15 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Bocchetta, G.; Fiori, G.; Sciuto, S.A.; Scorza, A. Smart Materials. Encyclopedia. Available online: https://encyclopedia.pub/entry/46471 (accessed on 29 June 2024).
Bocchetta G, Fiori G, Sciuto SA, Scorza A. Smart Materials. Encyclopedia. Available at: https://encyclopedia.pub/entry/46471. Accessed June 29, 2024.
Bocchetta, Gabriele, Giorgia Fiori, Salvatore Andrea Sciuto, Andrea Scorza. "Smart Materials" Encyclopedia, https://encyclopedia.pub/entry/46471 (accessed June 29, 2024).
Bocchetta, G., Fiori, G., Sciuto, S.A., & Scorza, A. (2023, July 05). Smart Materials. In Encyclopedia. https://encyclopedia.pub/entry/46471
Bocchetta, Gabriele, et al. "Smart Materials." Encyclopedia. Web. 05 July, 2023.
Smart Materials
Edit
This entry is adapted from the peer-reviewed paper 10.3390/act12070261

The introduction of smart materials (SMs) will become increasingly relevant as biomedical technologies progress. Smart materials sense and respond to external stimuli (e.g., chemical, electrical, mechanical, or magnetic signals) or environmental circumstances (e.g., temperature, illuminance, acidity, or humidity), and provide versatile platforms for studying various biological processes because of the numerous analogies between smart materials and biological systems. 

smart materials force measurement biomedical

1. Classification of Smart Materials

SMs can be divided into two main classes, i.e., passive and active [1][2][3][4][5][6][7]. Figure 1 depicts a schematic diagram of their classification, which is based mainly on their characteristics and how they react to external stimuli. In the scientific literature, passive SMs are defined as being capable of transferring energy without transducing it [2][3][4][5]. The term “passive” also suggests that this category of materials needs a power supply and does not change their characteristics considerably when exposed to environmental changes. Although technically not SMs [6], optical fibers are considered passive SMs by many authors in the literature [1][2][4][5][8], therefore they were included. Active SMs, on the other hand, can transduce energy [9], and they are further classified into two types. The first type of active SMs can change their properties when exposed to external stimuli, e.g., chromic materials can change their color when exposed to different types of outside stimuli [10], whereas the second type of active SMs can convert one form of energy, e.g., thermal, electrical, mechanical, or chemical, into another. Photovoltaic solar cells, which can convert solar energy into electricity [11], or piezoelectric and pyroelectric materials, which generate electricity when subjected to mechanical or thermal loads, are examples of this type of active SM. Furthermore, in the presence of an electric field, piezoelectric materials can produce mechanical strain and vice versa [12]. Shape memory alloys can be modified in shape, and their original shape restored by heating or cooling [13].
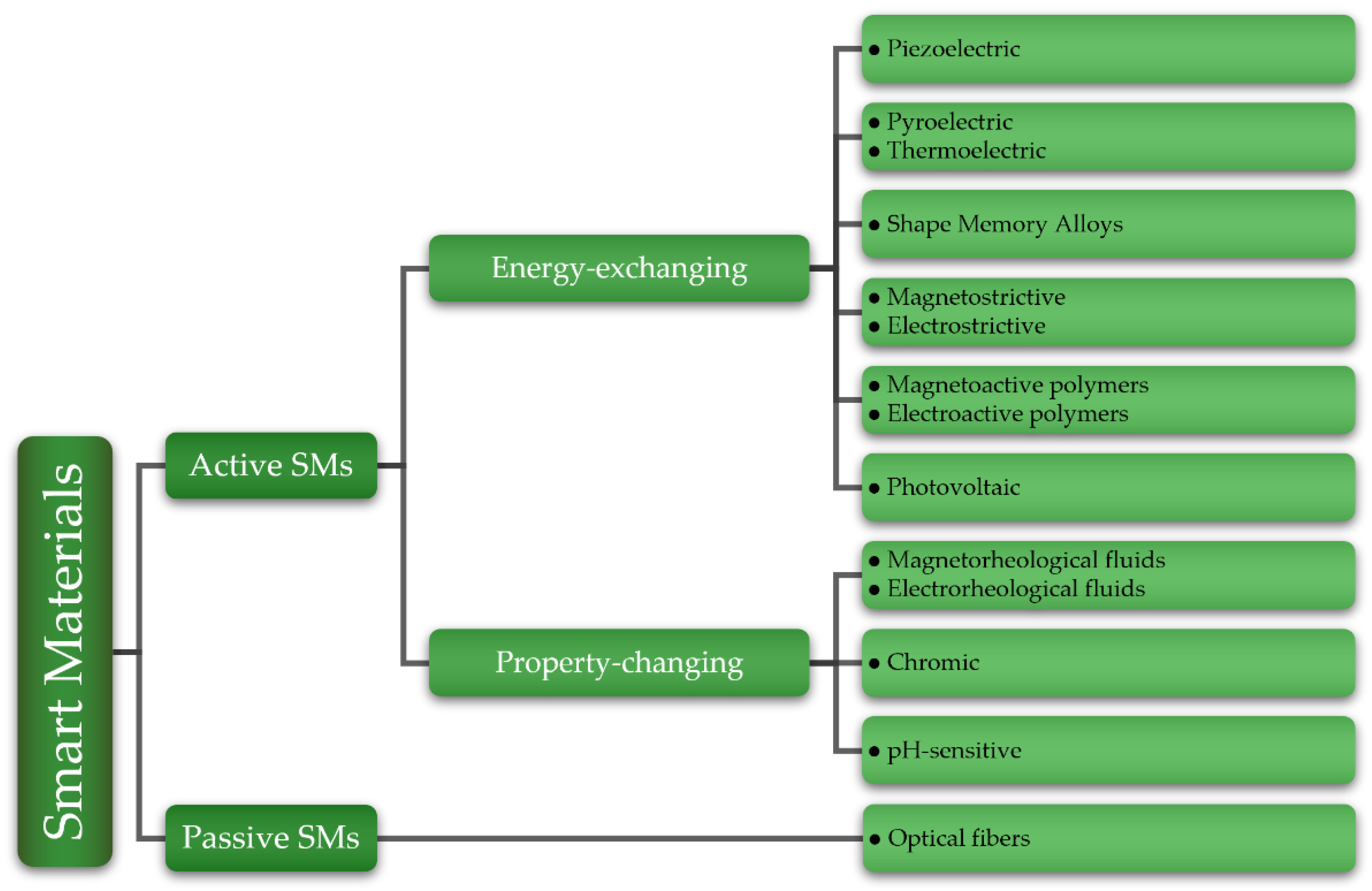
Figure 1. Smart Materials classification: examples of active and passive SMs.
Another classification method for SMs is based on their reversibility and bidirectionality [6][14]. Some active SMs exhibit the ability to switch between input and output energy types. Many materials that deal with electricity conversion have this property, e.g., piezoelectric, pyroelectric, and thermoelectric materials, which can convert and reverse electricity into mechanical strain and temperature difference, respectively. Moreover, bidirectional materials can be used in a variety of other applications, such as the two-way shape memory effect, which allows shape memory alloys to be used to provide multiple or switchable outcomes, enabling the replacement of multi-part components with a single piece of material, or piezoelectric materials in self-sensing actuators, which combine their dual effects as a sensor and actuator simultaneously [15][16].

2. Types of Smart Materials

There are many different types of SMs, which can be divided by compound, e.g., organic or inorganic [17]; by material, e.g., metallic or polymeric [18][19]; or by state, e.g., solids, gels, or fluids [20]. Whether organic, metallic, or gel, generally all SMs are classified into types based on their behavior, depending on how they react to different external conditions, and the main properties that SMs exhibit which distinguish them from other materials are:
  • Transiency—SMs are capable of responding to multiple stimuli and existing in a variety of states;
  • Immediacy—SMs’ response time is usually quick, and they can respond in real-time;
  • Self-actuation—SMs’ inherent property and refers to the ability to change appearance and shape;
  • Selectivity—SMs reaction is distinct and predictable;
  • Directness—SMs action and reaction take place in the same place.
In the following section, the types of SMs used in biomedical force measurement systems are briefly discussed, while Table 1 lists an example of how several types of active SMs react to external stimuli of different origins.
Table 1. Examples of active SMs behavior depending on different stimuli.
Material Input Output
Piezoelectric Electric field Mechanical strain
Mechanical load Electric potential
Pyroelectric Thermal load Electric potential
Electric field Temperature change
Thermoelectric Thermal load Electric potential
Electric field Temperature change
Shape memory alloys Thermal load Mechanical strain
Magnetic field
Magneto- Actuators 12 00261 i001 strictive Magnetic field Mechanical strain
Mechanical load Magnetization
Electro- Electric field Mechanical strain
Mechanical load Electric potential
Magneto- Actuators 12 00261 i002 active polymers Magnetic field Mechanical strain
Electro- Electric field
Photovoltaic Incident light Electric potential
Magneto- Actuators 12 00261 i003 rheological fluids Magnetic field Viscosity change
Electro- Electric field
Photo- Actuators 12 00261 i004 chromic Incident light Color change
Thermo- Thermal load
Magneto- Magnetic field
Electro- Electric field
Piezo- Mechanical load
pH-sensitive pH change Color change

2.1. Piezoelectric Materials

Piezoelectric materials are among the most common of all SMs. Piezoelectricity is a property of materials that can be seen as an electric charge or voltage generated by the application of mechanical loads or, in the opposite case, as a mechanical deformation brought on by the application of an electric field. These piezoelectric effects, discovered by Pierre and Jacques Curie between 1880 and 1881, were classified as “direct piezoelectric effect” and “converse piezoelectric effect”, respectively. The Curie brothers investigated the effect of mechanical pressure on electricity induction in some specific crystals, such as quartz, Rochelle salt, tourmaline, and cane sugar [21][22][23][24]. The direction of the applied mechanical load determines the polarization of the piezoelectric material; on the contrary, when an electric field is applied, the material has the ability to change its shape, allowing the energy to be released as a mechanical strain. Piezoelectricity is a property of many organic and inorganic materials, including ceramic and polymeric materials [23]. Among the most common piezoelectric materials, lead zirconate titanate (PZT), lead titanate, polyvinylidene fluoride (PVDF), lead magnesium niobate–lead titanate (PMN-PT), and barium titanate (BTO) can be found [25]. The piezoelectric material’s constitutive equations are expressed in many forms, but the two most used are [26]:
ε i j = C i j k l σ k l + d k i j E k ,
D i = d i k l σ k l + e i j E k ,
where the indexes represent various directions in the material coordinate system, εij denotes the strain tensor, Cijkl the elastic compliance matrix, σkl the stress tensor, dkij the matrix of piezoelectric coefficients, and Ek the electric field. The first term in Equation (1) indicates Hooke’s law, while the second one is the converse piezoelectric effect. Likewise, Di and eij indicate the electric flux density and the dielectric permittivity matrix, respectively. Generally, the electromechanical properties of an anisotropic piezoelectric continuum can be defined by 18 independent coefficients because of its symmetry. Furthermore, the linear piezoelectricity theory is based on hypotheses such as infinitesimal deformations, linear stress-strain relations, and stationary electric fields. Equations (1) and (2) can be expressed in alternate forms by considering the boundary conditions and including other variables, e.g., temperature effect [26]. Moreover, to this day, there are ongoing attempts to define more accurate analytical models that consider the nonlinearities of piezoelectric materials [27], since at low levels of applied electric field and stress, the linear model provides a reasonable approximation of the functional characteristics of piezoelectric materials, but it becomes progressively inaccurate as the electric field and stress levels increase.

2.2. Shape Memory Alloys

Shape Memory Alloys (SMAs) are a class of metallic alloys that can be classified into two categories based on the type of stimuli they respond to, i.e., thermo-responsive and magneto-responsive [28]. The first type can be activated thermally by heating, and the second type reacts to static and oscillating magnetic fields. The underlying driving mechanism in both cases is the reversible martensitic transformation. In particular, thermo-responsive SMAs can be plastically deformed when subjected to a mechanical load below a certain temperature, and can revert to the original shape between two transformation phases (austenitic and martensitic) when heated above a certain temperature. The increase in temperature can be also induced by Joule effect when SMAs are powered electrically. In this case, they can be classified as three stage smart actuators (i.e., Joule effect to temperature variation to mechanical deformation). SMAs can exist in three different crystal structures, i.e., austenite, twinned martensite, and detwinned martensite (Figure 2a) [13]. At lower temperatures, the martensite phase is stable, while austenite is stable at higher temperatures. The thermoelastic transformation of martensite depends on two effects: the shape memory effect (SME) and superelasticity. Figure 2b shows the difference in transformation temperature from the martensitic to the austenitic phase. During cooling, Ms is the martensite starting temperature, and Mf represents the martensite final temperature. In the same way, As and Af indicate the austenite starting and final temperature, respectively [3]. The SME phenomenon occurs when the structure is heated or cooled to specific characteristic transition temperatures, and afterward, SMAs recover their original size and shape.
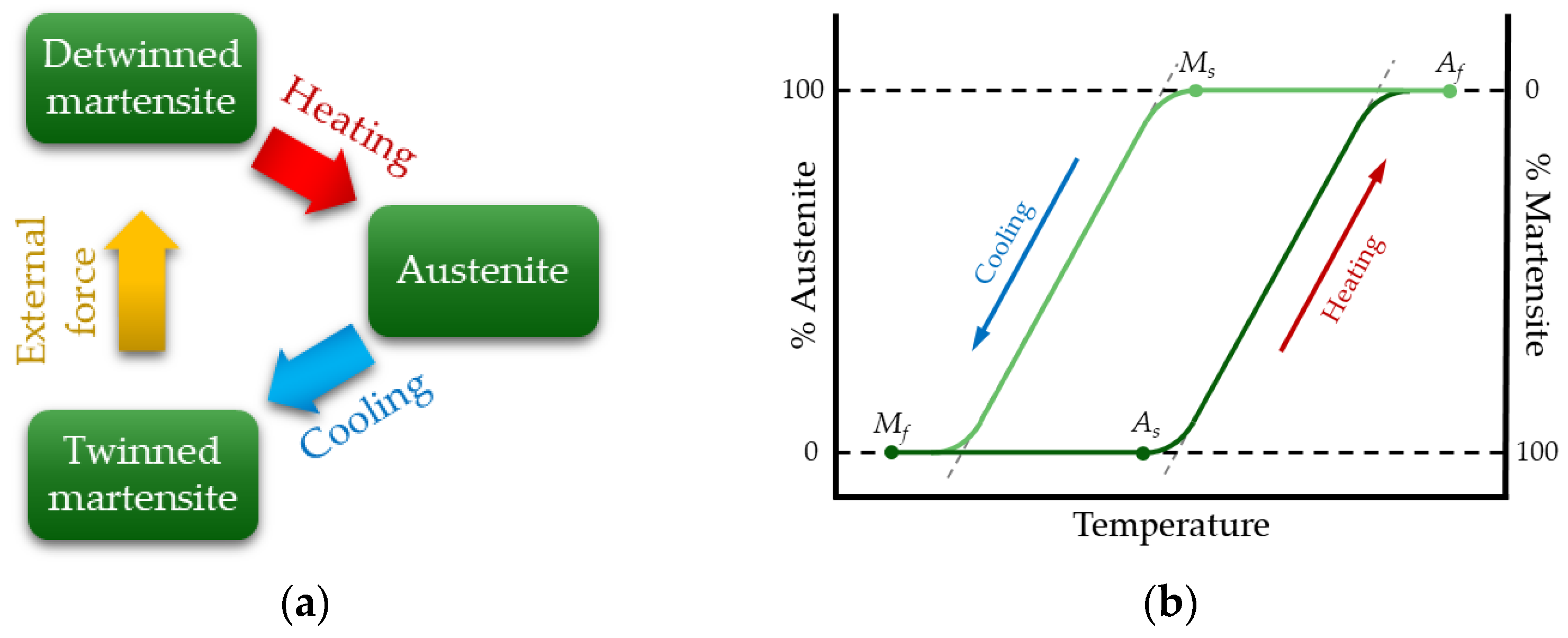
Figure 2. SMAs undergo phase transformation: (a) between the three different crystals and (b) temperature hysteresis.
This effect is observed when the SMA temperature is below Mf and, when the alloy is in deformed martensite, it will regain its original shape by heating it above the Af temperature [13][29]. At higher temperatures, one-way SMAs only have one original shape, whereas two-way SMAs can have two recoverable shapes: one in the austenite phase and the other in the martensite phase. Regarding superelasticity, this property of SMAs allows the materials to resist large cyclic deformations without residual deformation and cover large elastic deformations (up to 8%) [4][29]. Superelasticity occurs at very high temperatures when there is a stable austenite structure. Historically, Ölander discovered shape recovery while researching Cadmium-Gold alloys in 1932 [30], and this phenomenon has since been observed in many other alloys. Among the most widespread, nickel-titanium alloys are one of the most effective and they are commercially available under the name Nitinol.

2.3. Magnetostrictive and Electrostrictive Materials

Magnetostrictive materials are able to convert energy between the magnetic and elastic states [1]. This phenomenon, known as magnetostriction, describes the alteration in physical dimensions that many magnetic materials show when their magnetization changes. The magnetostriction energy transformation process is bidirectional: from mechanical deformation to magnetization, and vice versa. These materials have complex behavior because of their frequency-dependent hysteresis and nonlinear properties. The material’s molecular dipoles and magnetic field boundaries rotate to align with the field as a magnetic field is applied. The material elongates or contracts as a result. Figure 3 shows a schematic representation of the deformation of a magnetostrictive material when a magnetic field is applied, and by way of illustration, four points along the curve are described:
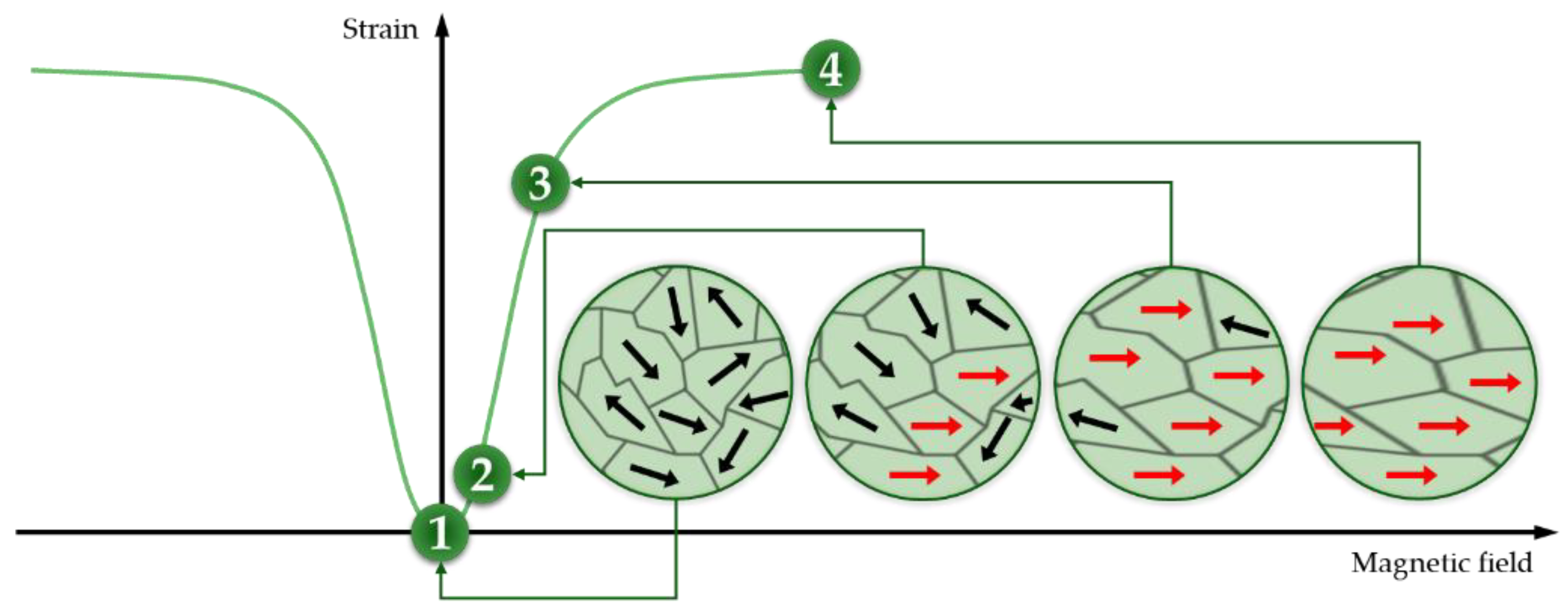
Figure 3. Strain trend of a magnetostrictive material due to changes in the magnetic field.
  • Magnetic domains have a random orientation when no magnetic field is applied. Therefore, no change in size occurs;
  • By magnetizing, a small region of the magnetic domain is reoriented in the same direction as the magnetic field, and the strain starts to occur;
  • As the magnetization increases, the number of magnetic domains that align increases. Moreover, a linear relationship between the applied magnetic field and strain can be found (points 2 to 3);
  • When all magnetic domains align to the magnetic field, there is no further strain.
When subjected to magnetic fields or stresses, the behavior of a magnetostrictive material depends on different effects [31]. The strain in magnetostrictive materials obtained by applying a magnetic field is known as the Joule effect. James Prescott Joule performed the first measurements of magnetostriction by quantifying the change in length of magnetized iron samples. The Joule effect can be described by the following equation [32]:
ε = C H σ + λ H ,
where CH is the elastic compliance coefficient matrix under constant field H, and λ indicates the magnetostrictive coefficient. In addition, that strain can produce a stress due to the material’s elasticity, which in turn can produce magnetization. The latter phenomenon is called the Villari effect, and it can be expressed as follows [33]:
B = λ σ + μ σ H ,
where B is the magnetic induction, and μσ is the pure linear magnetic permeability matrix at constant applied stress [34]. Finally, magnetized materials can produce magnetic fields because of their magnetic permeability. Iron alloys exhibiting cubic Laves phase and containing rare earth elements, such as samarium (SmFe2), terbium (TbFe2), or dysprosium (DyFe2), have the highest known magnetostriction. In particular, Terfenol-D (TbxDy1−xFe2) is one of the most commonly used engineering magnetostrictive material because of its large deformation at room temperature [31][35]. Terfenol-D is an alloy of terbium (Ter), iron (Fe), and dysprosium (-D), and its formulation was developed at the Naval Ordnance Laboratory (NOL) by a research group led by Arthur E. Clark [36]. Due to their high saturation magnetostriction, materials based on cobalt ferrite (CoFe2O4) are widely used in magnetostrictive applications, and they are an effective Terfenol-D substitution if rare-earth elements are not available [37].
Moving on to electrostrictive materials, the phenomenon that takes its name occurs when a material changes its size in response to an electric field. The ions are displaced from their initial positions when they are exposed to an electric field, increasing or decreasing their size. The principle behind electrostriction is similar to that seen in magnetostriction, with the difference being the nature of the applied external field, i.e., electric or magnetic. Moreover, electrostrictive materials are often grouped with piezoelectric ones; in fact, piezoelectric materials also have this property, and the electrostrictive effect can be classified as a linear piezoelectric effect contribution that is dependent on electric fields. As with piezoelectric materials and Equation (1), one of the fundamental equations for electrostrictive materials is:
ε i j = C i j k l σ k l + d k i j E k + M k l i j E k E l ,
Equation (5) is composed of three terms: firstly, Hooke’s law; then the converse piezoelectric effect; and finally, the electrostrictive effect. The latter depends on the components Mklij of the fourth rank tensor; those components indicate the electrostrictive coefficients [38][39]. However, since the piezoelectric effect occurs only in non-centrosymmetric materials, the two phenomena are theoretically independent. Conversely, the electrostrictive effect, which is characterized by an even rank tensor, is not symmetry-restricted and occurs in all materials, including amorphous ones. Thus, the strain on the applied electric field described by the electrostrictive effect has a nonlinear dependence [40]. While all dielectrics present electrostriction, relaxor ferroelectrics [41][42] are a class of ceramics that have extremely high electrostrictive coefficients, and among them the most common are lead lanthanum zirconate titanate (PLZT) [43][44], lead magnesium niobate (PMN) [39][45], and lead magnesium niobate-lead titanate (PMN-PT) [46].

2.4. Optical Fibers

Optical fibers are transparent and flexible fibers, usually made of plastic or glass, characterized by an inner diameter (core) in the order of micrometers [4][6][8]. They are commonly used to convey light between two ends and are widely employed in fiber-optic communications, where they allow transmission over larger distances and at higher bandwidths than electrical connections. Optical fibers are preferred to metal wires because they are able to carry signals with minimal loss and, in addition, they are immune to electromagnetic interference. The concept behind optical fibers, based on the guiding of light by the phenomenon of refraction, was discovered in the early 1840s by Babinet and Colladon. The light transmission in an optical fiber occurs by complete internal reflection if the transmitting fiber, also known as the core, is clad with a material that has a lower refractive index. Moreover, the transmission of light throughout a fiber via total internal reflection allows only specific modes of propagation, which are dependent on the diameter of the fiber and the wavelength of light utilized [47]. Optical fibers are used for several applications and, in addition to communication, lighting, and imaging, they are used as sensors. The principle of optical fiber gratings, in particular, is based on periodic changes in the refractive index along the core of optical fibers. Fiber gratings are classified into two main types: short and long-period gratings, e.g., short period gratings, also known as Fiber Bragg Gratings (FBGs), reflect specific wavelengths while transmitting all others. As a result, FBG can be used as an inline optical fiber to block specific wavelengths, making it suitable for sensing applications [48][49]. Optical fiber systems can also be based on interferometric techniques, which use the interference between two beams propagating through different optical paths of a single fiber or two different fibers. Optical fiber interferometers can be dived into four main categories: Sagnac, Mach-Zhnder, Michelson, and Fabry-Pérot interferometers [50].

References

  1. Schwartz, M.M. Encyclopedia of Smart Materials, 1st ed.; Wiley-Interscience: New York, NY, USA, 2002; ISBN 978-0471177807.
  2. Kamila, S. Introduction, Classification and Applications of Smart Materials: An Overview. Am. J. Appl. Sci. 2013, 10, 876–880.
  3. Qader, I.N.; Kok, M.; Dagdelen, F.; Aydogdu, Y.; Qader, I.N. A Review of Smart Materials: Researches and Applications. El-Cezerî J. Sci. Eng. 2019, 6, 755–788.
  4. Bahl, S.; Nagar, H.; Singh, I.; Sehgal, S. Smart Materials Types, Properties and Applications: A Review. Mater. Today Proc. 2020, 28, 1302–1306.
  5. Damodharan, J.; Sreedharan, A.; Ramalingam, T. A Review on Smart Materials, Types and Applications. Int. J. Eng. Technol. Sci. Res. 2018, 5, 649–653.
  6. Addington, M.; Schodek, D.L. Smart Materials and Technologies: For the Architecture and Design Professions, 1st ed.; Architectural Press: Oxford, UK, 2004; ISBN 978-0750662253.
  7. Olabi, A.-G. (Ed.) Encyclopedia of Smart Materials, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2021; ISBN 978-0128157336.
  8. Correia, R.; James, S.; Lee, S.W.; Morgan, S.P.; Korposh, S. Biomedical Application of Optical Fibre Sensors. J. Opt. 2018, 20, 073003.
  9. Fairweather, J.A. Designing with Active Materials: An Impedance Based Approach; Rensselaer Polytechnic Institute: New York, NY, USA, 1998.
  10. Ferrara, M.; Bengisu, M. Materials That Change Color—Smart Materials Intelligent Design; SpringerBriefs in Applied Sciences and Technology; Springer International Publishing: Cham, Switzerland, 2014; ISBN 978-3-319-00289-7.
  11. Parida, B.; Iniyan, S.; Goic, R. A Review of Solar Photovoltaic Technologies. Renew. Sustain. Energy Rev. 2011, 15, 1625–1636.
  12. Bai, Y.; Siponkoski, T.; Peräntie, J. Ferroelectric, Pyroelectric, and Piezoelectric Properties of a Photovoltaic Perovskite Oxide. Appl. Phys. Lett 2017, 110, 63903.
  13. Mohd Jani, J.; Leary, M.; Subic, A.; Gibson, M.A. A Review of Shape Memory Alloy Research, Applications and Opportunities. Mater. Des. 2014, 56, 1078–1113.
  14. Mohamed, A.S.Y. Smart Materials Innovative Technologies in Architecture; Towards Innovative Design Paradigm. Energy Procedia 2017, 115, 139–154.
  15. Liseli, J.B.; Agnus, J.; Lutz, P.; Rakotondrabe, M. An Overview of Piezoelectric Self-Sensing Actuation for Nanopositioning Applications: Electrical Circuits, Displacement, and Force Estimation. IEEE Trans. Instrum. Meas. 2020, 69, 2–14.
  16. Ivan, I.A.; Aljanaideh, O.; Agnus, J.; Lutz, P.; Rakotondrabe, M. Quasi-Static Displacement Self-Sensing Measurement for a 2-DOF Piezoelectric Cantilevered Actuator. IEEE Trans. Ind. Electron. 2017, 64, 6330–6337.
  17. Mir, S.H.; Nagahara, L.A.; Thundat, T.; Mokarian-Tabari, P.; Furukawa, H.; Khosla, A. Review—Organic-Inorganic Hybrid Functional Materials: An Integrated Platform for Applied Technologies. J. Electrochem. Soc. 2018, 165, B3137–B3156.
  18. Roy, I.; Gupta, M.N. Smart Polymeric Materials: Emerging Biochemical Applications. Chem. Biol. 2003, 10, 1161–1171.
  19. Kim, J. Multifunctional Smart Biopolymer Composites as Actuators. In Biopolymer Composites in Electronics; Sadasivuni, K.K., Cabibihan, J.-J., Ponnamma, D., Al-Maadeed, M.A.S.A., Kim, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 311–331. ISBN 978-0081009741.
  20. Hajalilou, A.; Amri Mazlan, S.; Lavvafi, H.; Shameli, K. Field Responsive Fluids as Smart Materials, 1st ed.; Engineering Materials; Springer: Singapore, 2016; ISBN 978-9811024948.
  21. Curie, J.; Curie, P. Développement Par Compression de l’électricité Polaire Dans Les Cristaux Hémièdres à Faces Inclinées. Bull. Minéralogie 1880, 3, 90–93.
  22. Heywang, W.; Lubitz, K.; Wersing, W. Piezoelectricity, 1st ed.; Springer Series in Materials Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 114, ISBN 978-3-540-68680-4.
  23. Cady, W.G. Piezoelectricity: An Introduction to the Theory and Applications of Electromechanical Phenomena in Crystals, 2nd ed.; Dover Publications: New York, NY, USA, 1964; Volume 2.
  24. Gupta, S. Introduction to Ferroelectrics and Related Materials. In Ferroelectric Materials for Energy Harvesting and Storage; Woodhead Publishing: Cambridge, UK, 2020; pp. 1–41. ISBN 978-0081028025.
  25. Wu, Y.; Ma, Y.; Zheng, H.; Ramakrishna, S. Piezoelectric Materials for Flexible and Wearable Electronics: A Review. Mater. Des. 2021, 211, 110164.
  26. ANSI/IEEE Std 176-1987; Institute of Electrical and Electronics Engineers IEEE Standard on Piezoelectricity: An American National Standard. American National Standards Institute: Washington, DC, USA; IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society (UFFC-S) Seattle Chapter: Piscataway, NJ, USA, 1988; pp. 8–10.
  27. Cheng, L.; Liu, W.; Hou, Z.G.; Yu, J.; Tan, M. Neural-Network-Based Nonlinear Model Predictive Control for Piezoelectric Actuators. IEEE Trans. Ind. Electron. 2015, 62, 7717–7727.
  28. Sun, L.; Huang, W.M.; Ding, Z.; Zhao, Y.; Wang, C.C.; Purnawali, H.; Tang, C. Stimulus-Responsive Shape Memory Materials: A Review. Mater. Des. 2012, 33, 577–640.
  29. Naresh, C.; Bose, P.S.C.; Rao, C.S.P. Shape Memory Alloys: A State of Art Review. IOP Conf. Ser. Mater. Sci. Eng. 2016, 149, 012054.
  30. Ölander, A. An Electrochemical Investigation of Solid Cadmium-Gold Alloys. J. Am. Chem. Soc. 1932, 54, 3819–3833.
  31. Olabi, A.G.; Grunwald, A. Design and Application of Magnetostrictive Materials. Mater. Des. 2008, 29, 469–483.
  32. Wahi, S.K.; Kumar, M.; Santapuri, S.; Dapino, M.J. Computationally Efficient Locally Linearized Constitutive Model for Magnetostrictive Materials. J. Appl. Phys. 2019, 125, 215108.
  33. Dapino, M.J.; Smith, R.C.; Calkins, F.T.; Flatau, A.B. A Magnetoelastic Model for Villari-Effect Magnetostrictive Sensors; Center for Research in Scientific Computation, North Carolina State University: Raleigh, NC, USA, 2002.
  34. Apicella, V.; Clemente, C.S.; Davino, D.; Leone, D.; Visone, C. Review of Modeling and Control of Magnetostrictive Actuators. Actuators 2019, 8, 45.
  35. Keswani, B.C.; Patil, S.I.; Kolekar, Y.D.; Ramana, C.V. Improved Magnetostrictive Properties of Cobalt Ferrite (CoFe2O4) by Mn and Dy Co-Substitution for Magneto-Mechanical Sensors. J. Appl. Phys. 2019, 126, 174503.
  36. Clark, A.E.; Savage, H.T. Magnetostriction of Rare Earth-Fe2 Compounds under Compressive Stress. J. Magn. Magn. Mater. 1983, 31–34, 849–851.
  37. Turtelli, R.S.; Kriegisch, M.; Atif, M.; Grössinger, R. Co-Ferrite—A Material with Interesting Magnetic Properties. IOP Conf. Ser. Mater. Sci. Eng. 2014, 60, 012020.
  38. Hom, C.L.; Shankar, N. Fully Coupled Constitutive Model for Electrostrictive Ceramic Materials. J. Intell. Mater. Syst. Struct. 1994, 5, 795–801.
  39. Uchino, K. Electrostrictive Actuators: Materials and Applications. Am. Ceram. Soc. Bull. 1986, 65, 647–652.
  40. Newnham, R.E.; Sundar, V.; Yimnirun, R.; Su, J.; Zhang, Q.M. Electrostriction: Nonlinear Electromechanical Coupling in Solid Dielectrics. J. Phys. Chem. B 1997, 101, 10141–10150.
  41. Park, S.E. Relaxor Based Ferroelectric Single Crystals for Electro-Mechanical Actuators. Mater. Res. Innov. 1997, 1, 20–25.
  42. Eric Cross, L. Relaxor Ferroelecirics. Ferroelectrics 1987, 76, 241–267.
  43. Somwan, S.; Ngamjarurojana, A.; Limpichaipanit, A. Dielectric, Ferroelectric and Induced Strain Behavior of PLZT 9/65/35 Ceramics Modified by Bi2O3 and CuO Co-Doping. Ceram. Int. 2016, 42, 10690–10696.
  44. Zhang, Q.; Pan, W.; Bhalla, A.; Cross, L.E. Electrostrictive and Dielectric Response in Lead Magnesium Niobate–Lead Titanate (0.9PMN·0.1PT) and Lead Lanthanum Zirconate Titanate (PLZT 9.5/65/35) under Variation of Temperature and Electric Field. J. Am. Ceram. Soc. 1989, 72, 599–604.
  45. Damjanovic, D.; Newnham, R.E. Electrostrictive and Piezoelectric Materials for Actuator Applications. J. Intell. Mater. Syst. Struct. 1992, 3, 190–208.
  46. Coutte, J.; Dubus, B.; Debus, J.C.; Granger, C.; Jones, D. Design, Production and Testing of PMN–PT Electrostrictive Transducers. Ultrasonics 2002, 40, 883–888.
  47. Shah, R.Y.; Agrawal, Y.K. Introduction to Fiber Optics: Sensors for Biomedical Applications. Indian J. Pharm. Sci. 2011, 73, 17.
  48. Fang, Z. Fundamentals of Optical Fiber Sensors, 1st ed.; Wiley: Hoboken, NJ, USA, 2012; ISBN 9780470575406.
  49. Barrias, A.; Casas, J.R.; Villalba, S. A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors 2016, 16, 748.
  50. Lee, B.H.; Kim, Y.H.; Park, K.S.; Eom, J.B.; Kim, M.J.; Rho, B.S.; Choi, H.Y. Interferometric Fiber Optic Sensors. Sensors 2012, 12, 2467–2486.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Biomedical
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Gabriele Bocchetta
,
Giorgia Fiori
,
Salvatore Andrea Sciuto
,
Andrea Scorza
View Times: 718
Revisions: 2 times (View History)
Update Date: 07 Jul 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback