Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Engineering, Biomedical
The introduction of smart materials (SMs) will become increasingly relevant as biomedical technologies progress. Smart materials sense and respond to external stimuli (e.g., chemical, electrical, mechanical, or magnetic signals) or environmental circumstances (e.g., temperature, illuminance, acidity, or humidity), and provide versatile platforms for studying various biological processes because of the numerous analogies between smart materials and biological systems.
- smart materials
- force measurement
- biomedical
1. Classification of Smart Materials
SMs can be divided into two main classes, i.e., passive and active [1,3,5,6,8,11,17]. Figure 1 depicts a schematic diagram of their classification, which is based mainly on their characteristics and how they react to external stimuli. In the scientific literature, passive SMs are defined as being capable of transferring energy without transducing it [3,5,6,8]. The term “passive” also suggests that this category of materials needs a power supply and does not change their characteristics considerably when exposed to environmental changes. Although technically not SMs [11], optical fibers are considered passive SMs by many authors in the literature [1,3,6,8,18], therefore they were included in this review. Active SMs, on the other hand, can transduce energy [19], and they are further classified into two types. The first type of active SMs can change their properties when exposed to external stimuli, e.g., chromic materials can change their color when exposed to different types of outside stimuli [20], whereas the second type of active SMs can convert one form of energy, e.g., thermal, electrical, mechanical, or chemical, into another. Photovoltaic solar cells, which can convert solar energy into electricity [21], or piezoelectric and pyroelectric materials, which generate electricity when subjected to mechanical or thermal loads, are examples of this type of active SM. Furthermore, in the presence of an electric field, piezoelectric materials can produce mechanical strain and vice versa [22]. Shape memory alloys can be modified in shape, and their original shape restored by heating or cooling [23].
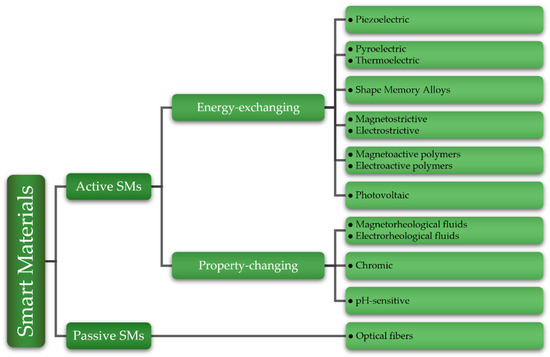
Figure 1. Smart Materials classification: examples of active and passive SMs.
Another classification method for SMs is based on their reversibility and bidirectionality [11,24]. Some active SMs exhibit the ability to switch between input and output energy types. Many materials that deal with electricity conversion have this property, e.g., piezoelectric, pyroelectric, and thermoelectric materials, which can convert and reverse electricity into mechanical strain and temperature difference, respectively. Moreover, bidirectional materials can be used in a variety of other applications, such as the two-way shape memory effect, which allows shape memory alloys to be used to provide multiple or switchable outcomes, enabling the replacement of multi-part components with a single piece of material, or piezoelectric materials in self-sensing actuators, which combine their dual effects as a sensor and actuator simultaneously [25,26].
2. Types of Smart Materials
There are many different types of SMs, which can be divided by compound, e.g., organic or inorganic [27]; by material, e.g., metallic or polymeric [28,29]; or by state, e.g., solids, gels, or fluids [30]. Whether organic, metallic, or gel, generally all SMs are classified into types based on their behavior, depending on how they react to different external conditions, and the main properties that SMs exhibit which distinguish them from other materials are:
-
Transiency—SMs are capable of responding to multiple stimuli and existing in a variety of states;
-
Immediacy—SMs’ response time is usually quick, and they can respond in real-time;
-
Self-actuation—SMs’ inherent property and refers to the ability to change appearance and shape;
-
Selectivity—SMs reaction is distinct and predictable;
-
Directness—SMs action and reaction take place in the same place.
In the following section, the types of SMs used in biomedical force measurement systems are briefly discussed, while Table 1 lists an example of how several types of active SMs react to external stimuli of different origins.
Table 1. Examples of active SMs behavior depending on different stimuli.
| Material | Input | Output | ||
|---|---|---|---|---|
| Piezoelectric | Electric field | Mechanical strain | ||
| Mechanical load | Electric potential | |||
| Pyroelectric | Thermal load | Electric potential | ||
| Electric field | Temperature change | |||
| Thermoelectric | Thermal load | Electric potential | ||
| Electric field | Temperature change | |||
| Shape memory alloys | Thermal load | Mechanical strain | ||
| Magnetic field | ||||
| Magneto- |  |
strictive | Magnetic field | Mechanical strain |
| Mechanical load | Magnetization | |||
| Electro- | Electric field | Mechanical strain | ||
| Mechanical load | Electric potential | |||
| Magneto- |  |
active polymers | Magnetic field | Mechanical strain |
| Electro- | Electric field | |||
| Photovoltaic | Incident light | Electric potential | ||
| Magneto- |  |
rheological fluids | Magnetic field | Viscosity change |
| Electro- | Electric field | |||
| Photo- |  |
chromic | Incident light | Color change |
| Thermo- | Thermal load | |||
| Magneto- | Magnetic field | |||
| Electro- | Electric field | |||
| Piezo- | Mechanical load | |||
| pH-sensitive | pH change | Color change | ||
2.1. Piezoelectric Materials
Piezoelectric materials are among the most common of all SMs. Piezoelectricity is a property of materials that can be seen as an electric charge or voltage generated by the application of mechanical loads or, in the opposite case, as a mechanical deformation brought on by the application of an electric field. These piezoelectric effects, discovered by Pierre and Jacques Curie between 1880 and 1881, were classified as “direct piezoelectric effect” and “converse piezoelectric effect”, respectively. The Curie brothers investigated the effect of mechanical pressure on electricity induction in some specific crystals, such as quartz, Rochelle salt, tourmaline, and cane sugar [32,33,34,35]. The direction of the applied mechanical load determines the polarization of the piezoelectric material; on the contrary, when an electric field is applied, the material has the ability to change its shape, allowing the energy to be released as a mechanical strain. Piezoelectricity is a property of many organic and inorganic materials, including ceramic and polymeric materials [34]. Among the most common piezoelectric materials, lead zirconate titanate (PZT), lead titanate, polyvinylidene fluoride (PVDF), lead magnesium niobate–lead titanate (PMN-PT), and barium titanate (BTO) can be found [36]. The piezoelectric material’s constitutive equations are expressed in many forms, but the two most used are [37]:
where the indexes represent various directions in the material coordinate system, εij denotes the strain tensor, Cijkl the elastic compliance matrix, σkl the stress tensor, dkij the matrix of piezoelectric coefficients, and Ek the electric field. The first term in Equation (1) indicates Hooke’s law, while the second one is the converse piezoelectric effect. Likewise, Di and eij indicate the electric flux density and the dielectric permittivity matrix, respectively. Generally, the electromechanical properties of an anisotropic piezoelectric continuum can be defined by 18 independent coefficients because of its symmetry. Furthermore, the linear piezoelectricity theory is based on hypotheses such as infinitesimal deformations, linear stress-strain relations, and stationary electric fields. Equations (1) and (2) can be expressed in alternate forms by considering the boundary conditions and including other variables, e.g., temperature effect [37]. Moreover, to this day, there are ongoing attempts to define more accurate analytical models that consider the nonlinearities of piezoelectric materials [38], since at low levels of applied electric field and stress, the linear model provides a reasonable approximation of the functional characteristics of piezoelectric materials, but it becomes progressively inaccurate as the electric field and stress levels increase.
2.2. Shape Memory Alloys
Shape Memory Alloys (SMAs) are a class of metallic alloys that can be classified into two categories based on the type of stimuli they respond to, i.e., thermo-responsive and magneto-responsive [39]. The first type can be activated thermally by heating, and the second type reacts to static and oscillating magnetic fields. The underlying driving mechanism in both cases is the reversible martensitic transformation. In particular, thermo-responsive SMAs can be plastically deformed when subjected to a mechanical load below a certain temperature, and can revert to the original shape between two transformation phases (austenitic and martensitic) when heated above a certain temperature. The increase in temperature can be also induced by Joule effect when SMAs are powered electrically. In this case, they can be classified as three stage smart actuators (i.e., Joule effect to temperature variation to mechanical deformation). SMAs can exist in three different crystal structures, i.e., austenite, twinned martensite, and detwinned martensite (Figure 2a) [23]. At lower temperatures, the martensite phase is stable, while austenite is stable at higher temperatures. The thermoelastic transformation of martensite depends on two effects: the shape memory effect (SME) and superelasticity. Figure 2b shows the difference in transformation temperature from the martensitic to the austenitic phase. During cooling, Ms is the martensite starting temperature, and Mf represents the martensite final temperature. In the same way, As and Af indicate the austenite starting and final temperature, respectively [5]. The SME phenomenon occurs when the structure is heated or cooled to specific characteristic transition temperatures, and afterward, SMAs recover their original size and shape.
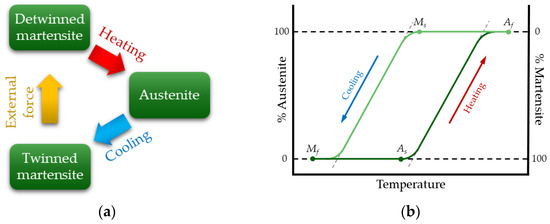
Figure 2. SMAs undergo phase transformation: (a) between the three different crystals and (b) temperature hysteresis.
This effect is observed when the SMA temperature is below Mf and, when the alloy is in deformed martensite, it will regain its original shape by heating it above the Af temperature [23,40]. At higher temperatures, one-way SMAs only have one original shape, whereas two-way SMAs can have two recoverable shapes: one in the austenite phase and the other in the martensite phase. Regarding superelasticity, this property of SMAs allows the materials to resist large cyclic deformations without residual deformation and cover large elastic deformations (up to 8%) [6,40]. Superelasticity occurs at very high temperatures when there is a stable austenite structure. Historically, Ölander discovered shape recovery while researching Cadmium-Gold alloys in 1932 [15], and this phenomenon has since been observed in many other alloys. Among the most widespread, nickel-titanium alloys are one of the most effective and they are commercially available under the name Nitinol.
2.3. Magnetostrictive and Electrostrictive Materials
Magnetostrictive materials are able to convert energy between the magnetic and elastic states [1]. This phenomenon, known as magnetostriction, describes the alteration in physical dimensions that many magnetic materials show when their magnetization changes. The magnetostriction energy transformation process is bidirectional: from mechanical deformation to magnetization, and vice versa. These materials have complex behavior because of their frequency-dependent hysteresis and nonlinear properties. The material’s molecular dipoles and magnetic field boundaries rotate to align with the field as a magnetic field is applied. The material elongates or contracts as a result. Figure 3 shows a schematic representation of the deformation of a magnetostrictive material when a magnetic field is applied, and by way of illustration, four points along the curve are described:
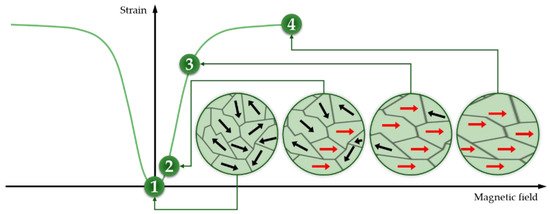
Figure 3. Strain trend of a magnetostrictive material due to changes in the magnetic field.
-
Magnetic domains have a random orientation when no magnetic field is applied. Therefore, no change in size occurs;
-
By magnetizing, a small region of the magnetic domain is reoriented in the same direction as the magnetic field, and the strain starts to occur;
-
As the magnetization increases, the number of magnetic domains that align increases. Moreover, a linear relationship between the applied magnetic field and strain can be found (points 2 to 3);
-
When all magnetic domains align to the magnetic field, there is no further strain.
When subjected to magnetic fields or stresses, the behavior of a magnetostrictive material depends on different effects [41]. The strain in magnetostrictive materials obtained by applying a magnetic field is known as the Joule effect. James Prescott Joule performed the first measurements of magnetostriction by quantifying the change in length of magnetized iron samples. The Joule effect can be described by the following equation [42]:
where CH is the elastic compliance coefficient matrix under constant field H, and λ indicates the magnetostrictive coefficient. In addition, that strain can produce a stress due to the material’s elasticity, which in turn can produce magnetization. The latter phenomenon is called the Villari effect, and it can be expressed as follows [43]:
where B is the magnetic induction, and μσ is the pure linear magnetic permeability matrix at constant applied stress [44]. Finally, magnetized materials can produce magnetic fields because of their magnetic permeability. Iron alloys exhibiting cubic Laves phase and containing rare earth elements, such as samarium (SmFe2), terbium (TbFe2), or dysprosium (DyFe2), have the highest known magnetostriction. In particular, Terfenol-D (TbxDy1−xFe2) is one of the most commonly used engineering magnetostrictive material because of its large deformation at room temperature [41,45]. Terfenol-D is an alloy of terbium (Ter), iron (Fe), and dysprosium (-D), and its formulation was developed at the Naval Ordnance Laboratory (NOL) by a research group led by Arthur E. Clark [46]. Due to their high saturation magnetostriction, materials based on cobalt ferrite (CoFe2O4) are widely used in magnetostrictive applications, and they are an effective Terfenol-D substitution if rare-earth elements are not available [47].
Moving on to electrostrictive materials, the phenomenon that takes its name occurs when a material changes its size in response to an electric field. The ions are displaced from their initial positions when they are exposed to an electric field, increasing or decreasing their size. The principle behind electrostriction is similar to that seen in magnetostriction, with the difference being the nature of the applied external field, i.e., electric or magnetic. Moreover, electrostrictive materials are often grouped with piezoelectric ones; in fact, piezoelectric materials also have this property, and the electrostrictive effect can be classified as a linear piezoelectric effect contribution that is dependent on electric fields. As with piezoelectric materials and Equation (1), one of the fundamental equations for electrostrictive materials is:
Equation (5) is composed of three terms: firstly, Hooke’s law; then the converse piezoelectric effect; and finally, the electrostrictive effect. The latter depends on the components Mklij of the fourth rank tensor; those components indicate the electrostrictive coefficients [49,50]. However, since the piezoelectric effect occurs only in non-centrosymmetric materials, the two phenomena are theoretically independent. Conversely, the electrostrictive effect, which is characterized by an even rank tensor, is not symmetry-restricted and occurs in all materials, including amorphous ones. Thus, the strain on the applied electric field described by the electrostrictive effect has a nonlinear dependence [51]. While all dielectrics present electrostriction, relaxor ferroelectrics [52,53] are a class of ceramics that have extremely high electrostrictive coefficients, and among them the most common are lead lanthanum zirconate titanate (PLZT) [54,55], lead magnesium niobate (PMN) [50,56], and lead magnesium niobate-lead titanate (PMN-PT) [57].
2.4. Optical Fibers
Optical fibers are transparent and flexible fibers, usually made of plastic or glass, characterized by an inner diameter (core) in the order of micrometers [6,11,18]. They are commonly used to convey light between two ends and are widely employed in fiber-optic communications, where they allow transmission over larger distances and at higher bandwidths than electrical connections. Optical fibers are preferred to metal wires because they are able to carry signals with minimal loss and, in addition, they are immune to electromagnetic interference. The concept behind optical fibers, based on the guiding of light by the phenomenon of refraction, was discovered in the early 1840s by Babinet and Colladon. The light transmission in an optical fiber occurs by complete internal reflection if the transmitting fiber, also known as the core, is clad with a material that has a lower refractive index. Moreover, the transmission of light throughout a fiber via total internal reflection allows only specific modes of propagation, which are dependent on the diameter of the fiber and the wavelength of light utilized [58]. Optical fibers are used for several applications and, in addition to communication, lighting, and imaging, they are used as sensors. The principle of optical fiber gratings, in particular, is based on periodic changes in the refractive index along the core of optical fibers. Fiber gratings are classified into two main types: short and long-period gratings, e.g., short period gratings, also known as Fiber Bragg Gratings (FBGs), reflect specific wavelengths while transmitting all others. As a result, FBG can be used as an inline optical fiber to block specific wavelengths, making it suitable for sensing applications [59,60]. Optical fiber systems can also be based on interferometric techniques, which use the interference between two beams propagating through different optical paths of a single fiber or two different fibers. Optical fiber interferometers can be dived into four main categories: Sagnac, Mach-Zhnder, Michelson, and Fabry-Pérot interferometers [61].
This entry is adapted from the peer-reviewed paper 10.3390/act12070261
This entry is offline, you can click here to edit this entry!
