Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Jinfa Liao
 -- 2216 2024-03-16 03:29:52 |
2 format correct
Catherine Yang
Meta information modification 2216 2024-03-18 03:01:17 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Zhou, Q.; Liao, J.; Liao, C.; Zhao, B. Phase Equilibrium Studies in the RE2O3-REF3-LiF System. Encyclopedia. Available online: https://encyclopedia.pub/entry/56352 (accessed on 29 April 2024).
Zhou Q, Liao J, Liao C, Zhao B. Phase Equilibrium Studies in the RE2O3-REF3-LiF System. Encyclopedia. Available at: https://encyclopedia.pub/entry/56352. Accessed April 29, 2024.
Zhou, Quan, Jinfa Liao, Chunfa Liao, Baojun Zhao. "Phase Equilibrium Studies in the RE2O3-REF3-LiF System" Encyclopedia, https://encyclopedia.pub/entry/56352 (accessed April 29, 2024).
Zhou, Q., Liao, J., Liao, C., & Zhao, B. (2024, March 16). Phase Equilibrium Studies in the RE2O3-REF3-LiF System. In Encyclopedia. https://encyclopedia.pub/entry/56352
Zhou, Quan, et al. "Phase Equilibrium Studies in the RE2O3-REF3-LiF System." Encyclopedia. Web. 16 March, 2024.
Phase Equilibrium Studies in the RE2O3-REF3-LiF System
Edit
This entry is adapted from the peer-reviewed paper 10.3390/met14030314

The solubility of rare earth oxides in molten salt directly affects the selection of operational parameters in the electrolysis process. When the added amount of RE2O3 is less than its solubility, it leads to a decreased electrolytic efficiency. Conversely, an excessive amount of oxide is prone to settle at the bottom of the electrolytic cell, impeding smooth production. The RE2O3 solubility in the fluoride salt can be represented by the phase equilibrium of the RE2O3-REF3-LiF system. The isothermal lines in the primary phase field of rare earth oxide represent the solubility of the oxide in the fluoride salt at the corresponding temperature.

rare earth molten salt electrolysis phase equilibrium solubility

1. Introduction

Rare earth metals and alloys are increasingly used in the field of new materials, and there is a strong market demand. Rare earth elements have unique physical and chemical properties due to their special electronic structures, such as excellent optical and electrical properties, magnetic properties, and active chemical properties. With the development of modern science and technology, REEs have become indispensable key materials for high-tech and novel functional materials [1][2].

In the process of producing rare earth metals through oxide–fluoride melt system electrolysis, REF3 and LiF form an electrolyte with a low melting point, low density, and high electrical conductivity. Under the action of electrical current, the dissolved RE2O3 is converted to rare earth metals and oxygen at the cathode and anode, respectively. As the electrolysis process progresses, the dissolved RE2O3 in the molten salt is continuously consumed, requiring continuous addition of RE2O3 to maintain a high concentration in the electrolyte [3][4][5]. When the amount of RE2O3 added to the molten salt is lower than its solubility, the electrolysis efficiency and productivity are low. Conversely, if the amount of RE2O3 added to the molten salt exceeds its solubility, the excess RE2O3, being denser than the REF3-LiF melt, tends to form deposits at the bottom of the electrolytic cell, increasing the cell resistance, affecting the metal purity, and even seriously impeding the smooth progress of production [6][7]. Therefore, the solubility of RE2O3 in the REF3-LiF-RE2O3 system provides the essential data for establishing a suitable feeding system in electrolytic production, playing an important role in improving electrolysis efficiency and maintaining the effective volume of the electrolytic cell. However, there have been significant differences in the solubility data of RE2O3 in the fluoride system, and the semi-empirical models developed based on these data have difficulty in accurately predicting the solubility of rare earth oxides [8][9].

2. Nd2O3-NdF-LiF System

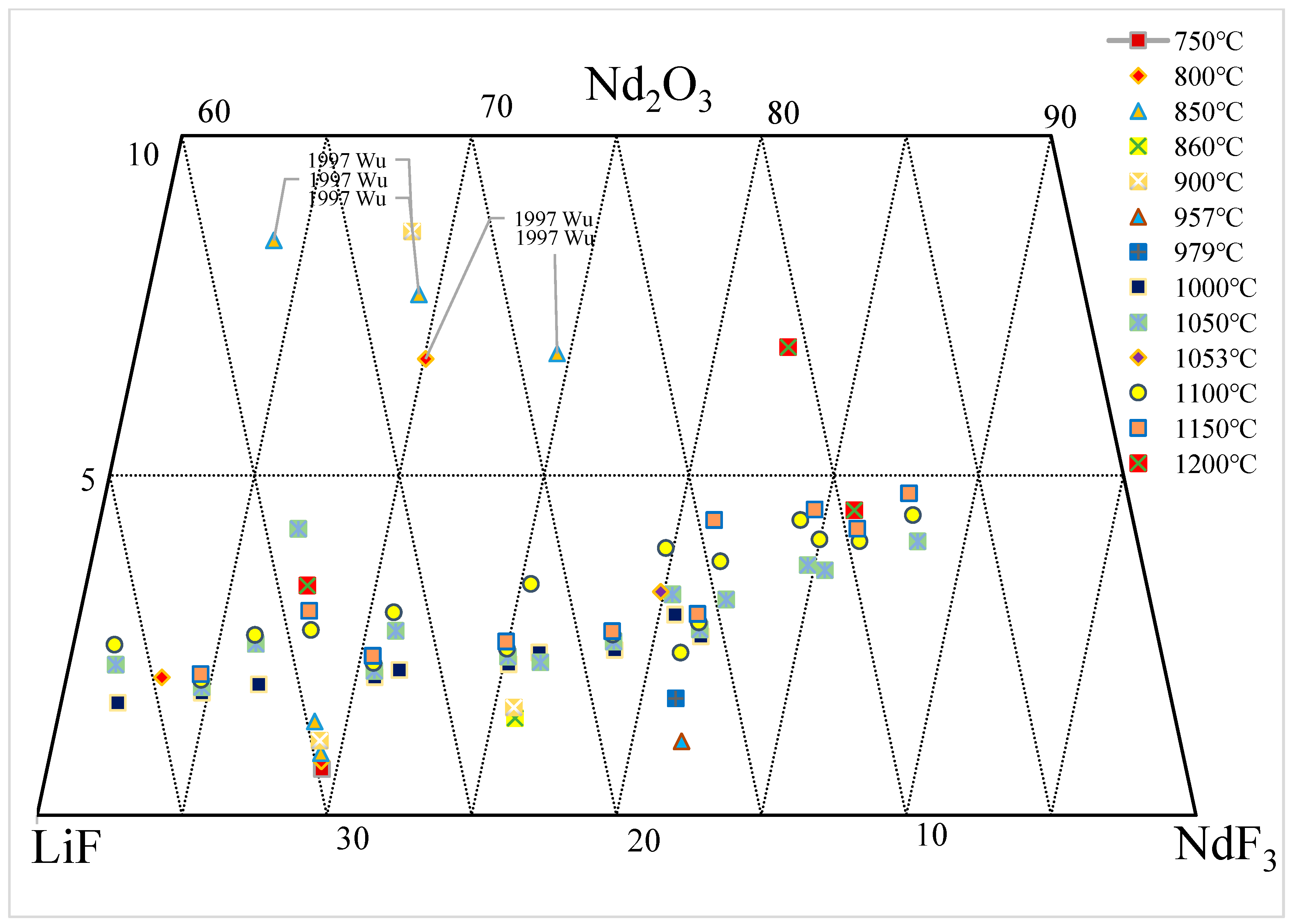
Due to the importance of neodymium–iron–boron magnetic materials, there has been an increasing amount of research on the phase equilibrium of the Nd2O3-NdF-LiF system, which is relevant to the production of neodymium through molten salt electrolysis [10][11]. Solubility data of Nd2O3 in the NdF3-LiF system reported in the literature are summarized in Table 1. Figure 1 summarizes the solubility data of Nd2O3 in the NdF3-LiF system and annotates these data in the Nd2O3-NdF-LiF ternary phase diagram. It can be observed that large amounts of experimental data have been published in the range of 750–1200 °C and 60–90 wt.% NdF3. In the liquid phase, the concentration of Nd2O3 mostly remains below 5 wt.% and increases with the temperature and percentage of NdF3. However, the solubility data published by Wu et al. [12] significantly deviate from other data, with a decrease in Nd2O3 concentration as NdF3 increases, indicating the unreliability of these data. The abundance of experimental data shown in Figure 1 indicates the importance of phase equilibrium research in the Nd2O3-NdF-LiF system, both in terms of theoretical significance and practical applications, which has attracted numerous researchers to invest substantial efforts into studying this area. However, there are significant differences and even contradictions among these experimental data [12][13][14][15][16][17][18][19][20][21][22][23], as detailed in the following two figures.
Figure 1. Liquidus points on the phase diagram of the NdF3-LiF-Nd2O3 system in the NdF3-rich corner (experimental data from [12][13][14][15][16][17][18][19][20][21][22][23]).
Table 1. Solubility of Nd2O3 in NdF3-LiF fluoride melts.
wt.% mol% Normalization (wt.%) T.  
NdF3 LiF Nd2O3 NdF3 LiF Nd2O3 NdF3 LiF Nd2O3 (°C) Ref.
58 42 0.54 15 85 0.08 57 42 0.54 800 [13]
58 42 0.75 15 85 0.12 57 42 0.74 850 [13]
58 42 0.82 15 85 0.13 57 42 0.81 860 [13]
58 42 0.96 15 85 0.15 57 42 0.95 900 [13]
63 37 1.68 18 82 0.29 62 36 1.65 1000 [16]
63 37 2.27 18 82 0.40 62 36 2.21 1050 [16]
63 37 2.57 18 82 0.45 61 36 2.51 1100 [16]
65 35 2.07 19 81 0.37 63 35 2.03 800 [21]
66 34 1.83 20 80 0.34 65 33 1.8 1000 [14]
66 34 1.92 20 80 0.35 65 33 1.88 1050 [14]
66 34 2.03 20 80 0.37 65 33 1.99 1100 [14]
66 34 2.12 20 80 0.39 65 33 2.08 1150 [14]
68 32 1.96 22 78 0.38 67 31 1.92 1000 [13]
68 32 2.59 22 78 0.50 66 31 2.52 1050 [13]
68 32 2.73 22 78 0.53 66 31 2.65 1100 [13]
70 30 9.24 23 77 1.96 64 28 8.46 850 [12]
70 30 1.4 23 77 0.28 69 30 1.38 850 [22]
70 30 4.4 23 77 0.90 67 29 4.21 1050 [22]
70 30 0.68 23 77 0.14 69 30 0.68 750 [16]
70 30 0.8 23 77 0.16 69 30 0.79 800 [16]
70 30 0.92 23 77 0.18 69 30 0.91 850 [16]
70 30 1.11 23 77 0.22 69 30 1.1 900 [16]
70 30 2.8 23 77 0.57 68 29 2.72 1100 [20]
70 30 3.1 23 77 0.63 68 29 3.01 1150 [20]
70 30 3.5 23 77 0.71 68 29 3.38 1200 [20]
72 28 2.07 25 75 0.44 71 27 2.03 1000 [14]
72 28 2.17 25 75 0.46 71 27 2.12 1050 [14]
72 28 2.29 25 75 0.48 70 27 2.24 1100 [14]
72 28 2.4 25 75 0.51 70 27 2.34 1150 [14]
73 27 2.18 26 74 0.47 71 26 2.14 1000 [16]
73 27 2.79 26 74 0.60 71 26 2.71 1050 [16]
73 27 3.08 26 74 0.67 71 26 2.99 1100 [16]
75 25 7.2 28 72 1.69 70 23 6.72 800 [12]
75 25 8.3 28 72 1.96 69 23 7.66 850 [12]
75 25 9.4 28 72 2.24 69 23 8.59 900 [12]
77 23 1.45 30 70 0.34 76 23 1.43 860 [13]
77 23 1.61 30 70 0.38 76 23 1.58 900 [13]
77 23 2.27 30 70 0.54 75 23 2.22 1000 [14]
77 23 2.39 30 70 0.57 75 23 2.33 1050 [14]
77 23 2.51 30 70 0.60 75 23 2.45 1100 [14]
77 23 2.62 30 70 0.63 75 23 2.55 1150 [14]
78 22 2.45 31 69 0.60 76 21 2.39 1000 [16]
78 22 2.3 31 69 0.56 76 22 2.25 1050 [16]
78 22 3.52 31 69 0.87 75 21 3.4 1100 [16]
80 20 7.29 34 66 1.95 75 19 6.79 850 [12]
81 19 2.49 35 65 0.66 79 19 2.43 1000 [14]
81 19 2.62 35 65 0.70 79 19 2.55 1050 [14]
81 19 2.73 35 65 0.73 79 19 2.66 1100 [14]
81 19 2.78 35 65 0.74 79 19 2.7 1150 [14]
83 17 1.1 39 61 0.31 82 17 1.09 957 [18]
83 17 1.75 39 61 0.49 81 17 1.72 979 [18]
83 17 3.4 39 61 0.97 80 17 3.29 1053 [18]
83 17 3.04 39 61 0.86 81 16 2.95 1000 [16]
83 17 3.36 39 61 0.96 80 16 3.25 1050 [16]
83 17 2.45 39 61 0.69 81 17 2.39 1100 [15]
83 17 4.09 39 61 1.17 80 16 3.93 1100 [16]
84 16 2.7 40 60 0.79 82 16 2.63 1000 [14]
84 16 2.81 40 60 0.82 82 16 2.73 1050 [14]
84 16 2.92 40 60 0.86 81 16 2.84 1100 [14]
84 16 3.05 40 60 0.90 81 16 2.96 1150 [14]
85 15 3.28 42 58 1.00 82 15 3.18 1050 [17]
85 15 3.88 42 58 1.18 82 15 3.74 1100 [17]
85 15 4.54 42 58 1.39 81 14 4.34 1150 [17]
88 12 3.82 49 51 1.29 85 12 3.68 1050 [16]
88 12 4.54 49 51 1.54 84 11 4.34 1100 [16]
88.5 11.5 3.74 50 50 1.29 85 11 3.61 1050 [17]
88.5 11.5 4.23 50 50 1.46 85 11 4.06 1100 [17]
88.5 11.5 4.71 50 50 1.63 85 11 4.5 1150 [17]
88.5 11.5 7.4 51 49 2.66 82 11 6.89 1200 [23]
90 10 4.2 54 46 1.54 86 10 4.03 1100 [20]
90 10 4.4 54 46 1.61 86 10 4.21 1150 [20]
90 10 4.7 54 46 1.73 86 10 4.49 1200 [20]
92 8 4.2 60 40 1.67 88 8 4.03 1050 [17]
92 8 4.62 60 40 1.84 88 8 4.42 1100 [17]
92 8 4.97 60 40 1.99 88 8 4.73 1150 [17]
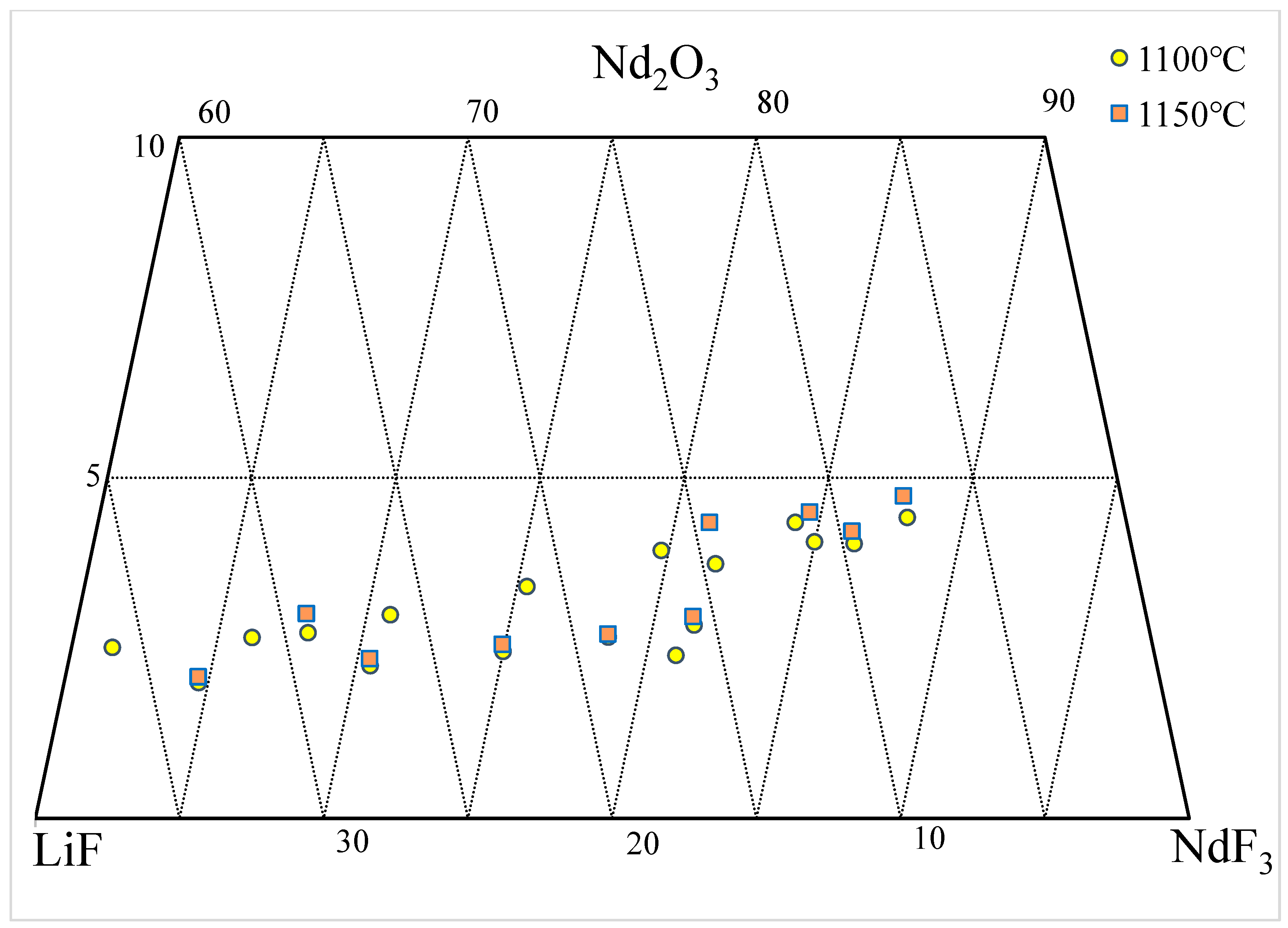
Figure 2 represents the solubility data of Nd2O3 in the NdF3-LiF molten salt at 1100 and 1150 °C, plotted on the ternary phase diagram. According to all the available literature, at the same NdF3/LiF ratio, the solubility of Nd2O3 increases with increasing temperatures, and connecting the solubility data at the same temperature should obtain a smooth liquidus line (isotherm). However, it is difficult to determine a consistent liquidus line at 1100 and 1150 °C, based on the data shown in the figure. Some data points indicate a higher solubility of Nd2O3 at 1100 °C compared with 1150 °C. The estimated 1100 and 1150 °C isotherms are shown in the figure. These contradictory data not only pose challenges for production technicians but also cannot be used for developing thermodynamic databases.
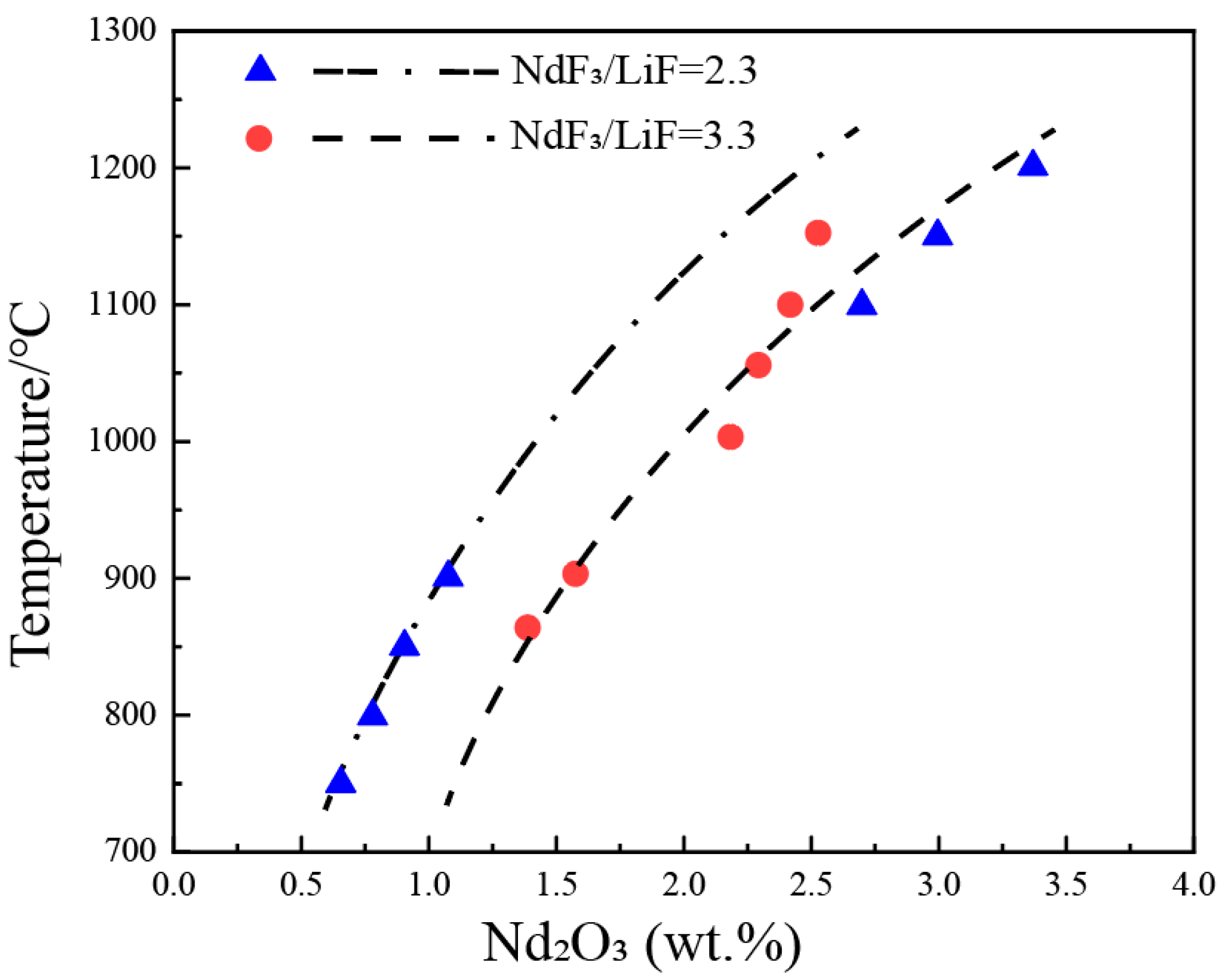
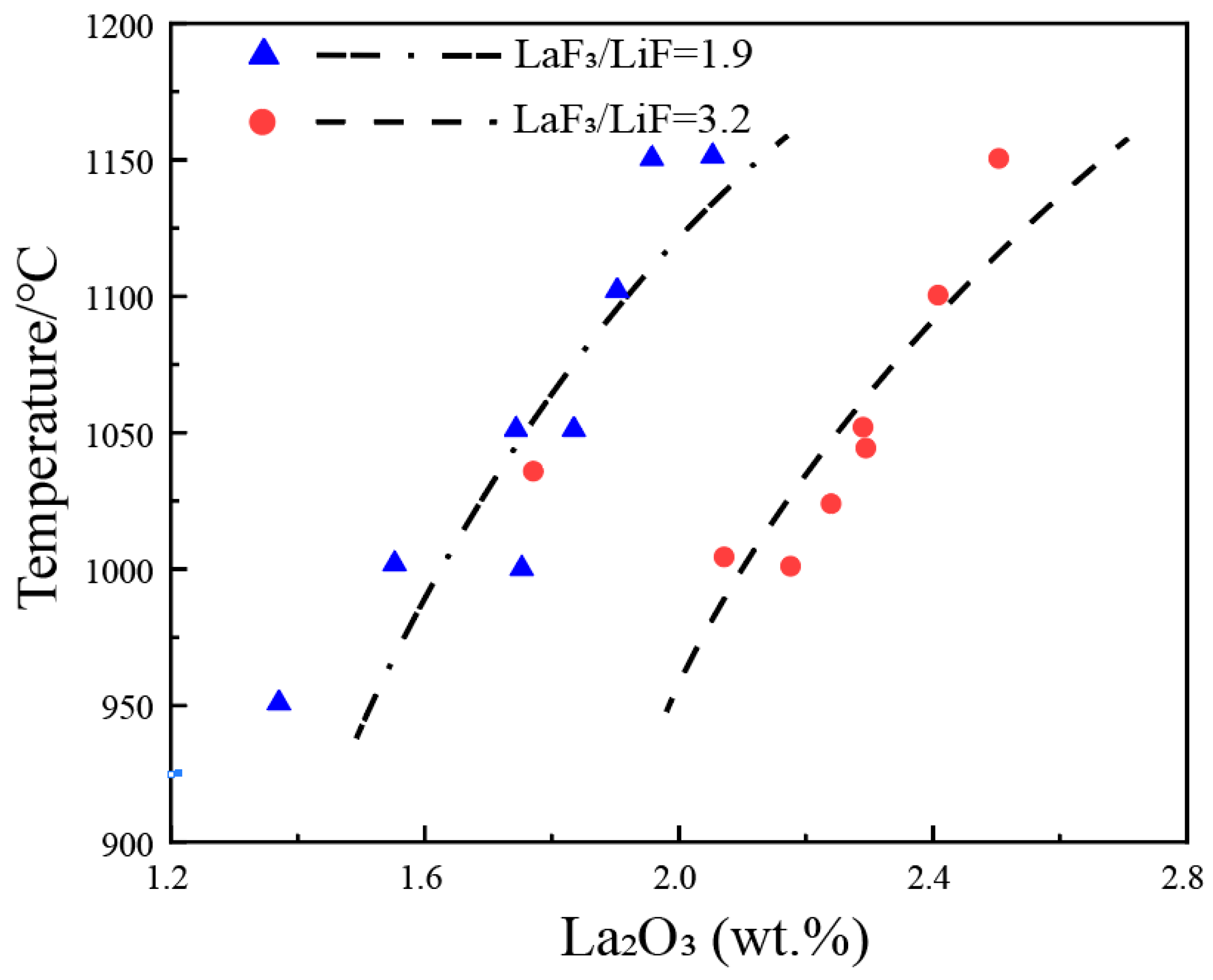
Figure 2. Liquidus points and estimated 1100 and 1150 °C isotherms on the phase diagram of NdF3-LiF-Nd2O3 system (experimental data from [14][15][16][17][20]).
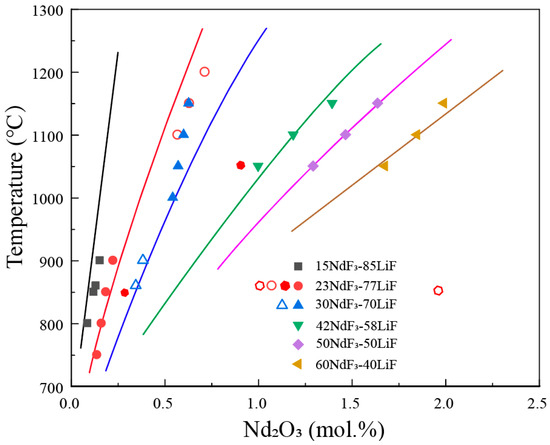
Figure 3 shows the solubility data of Nd2O3 in the NdF3-LiF system on a pseudo-binary phase diagram of Nd2O3-(NdF3 + LiF), with NdF3/LiF ratios of 2.3 and 3.3. It can be observed that the liquidus temperatures increase sharply with an increase in the concentration of Nd2O3. For every 1 wt.% increase in Nd2O3, the liquidus temperature rises by approximately 150 °C. In other words, the solubility of Nd2O3 is not sensitive to temperature, as increasing the temperature by 150 °C only results in a 1 wt.% increment in Nd2O3 solubility. The current consensus in the research is that, at the same temperature, a higher NdF3/LiF ratio leads to a greater solubility of Nd2O3. From the figure, it can be observed that at lower temperatures (800–900 °C), the solubility of Nd2O3 in NdF3/LiF = 3.3 is higher than that in NdF3/LiF = 2.3. However, at higher temperatures (1100–1150 °C), the solubility of Nd2O3 in NdF3/LiF = 3.3 is lower than that in NdF3/LiF = 2.3, indicating a significant discrepancy in the experimental data among different researchers. The dashed lines in the figure represent the estimated liquidus lines corresponding to NdF3/LiF ratios of 2.3 and 3.3, based on the experimental data.
Figure 3. Pseudo-binary phase diagram of NdF3-(LiF + Nd2O3) at fixed NdF3/LiF of 2.3 and 3.3 [13][14][20].

3. La2O3-LaF-LiF System

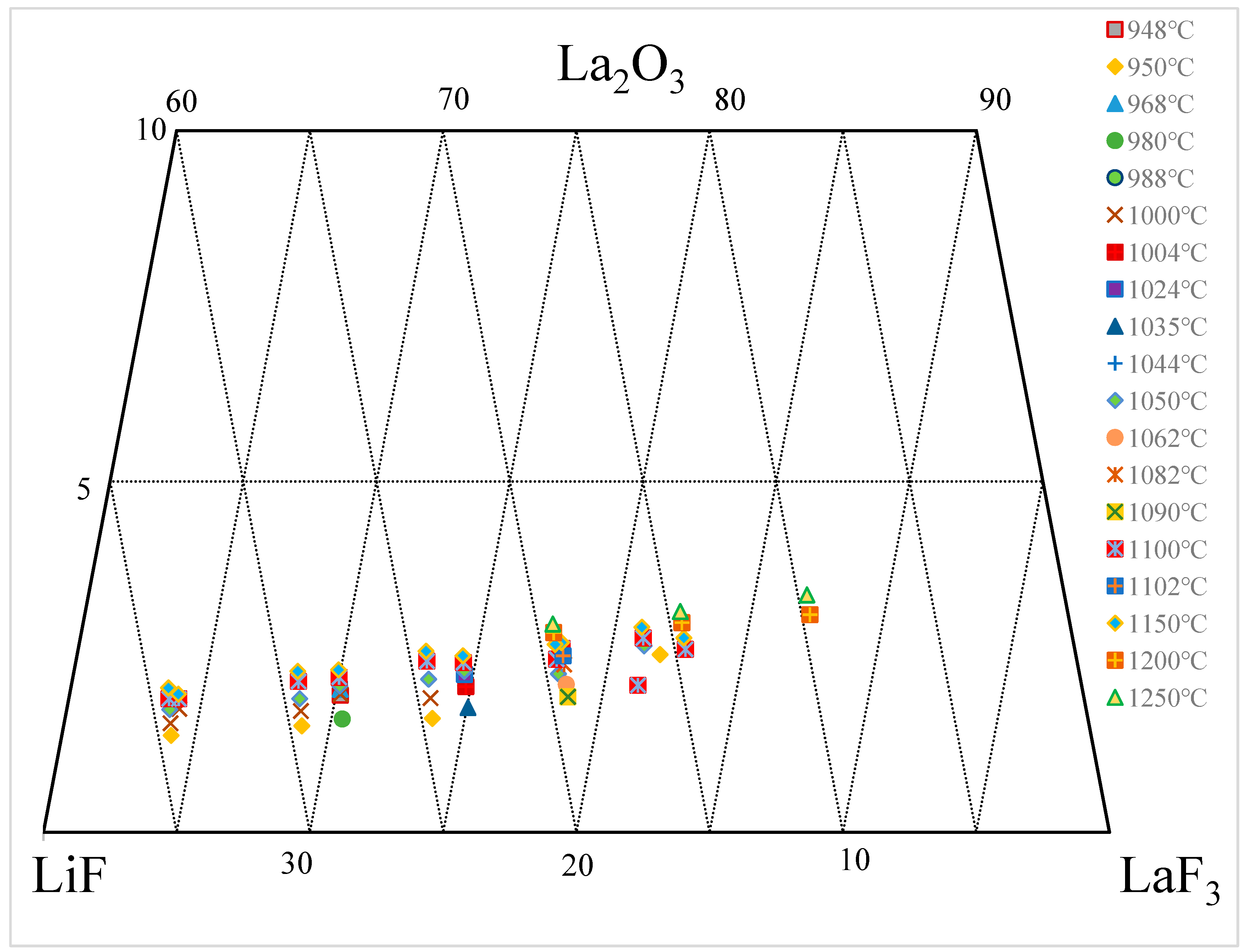
Figure 4 presents the solubility data of La2O3 in the LaF3-LiF system annotated on a ternary phase diagram based on the summary of the literature data shown in Table 2. Within the range of 948–1250 °C and 60–90 wt.% LaF3, the solubility of La2O3 in the LaF3-LiF system ranges from 1.3 to 3.4 wt.%. With an increase in temperature and LaF3, there is a tendency for the solubility of La2O3 to increase, but the change is not significant [14][24][25][26].
Figure 4. Liquidus points shown on the phase diagram of LaF3-LiF-La2O3 system in LaF3-rich corner (experimental data from [14][24][25][26]).
Table 2. Solubility of La2O3 in LaF3-LiF fluoride melts.
wt.% mol% Normalization (wt.%) T.  
LaF3 LiF La2O3 LaF3 LiF La2O3 LaF3 LiF La2O3 (°C) Ref.
65 35 1.4 20 80 0.26 64 35 1.38 950 [24]
65 35 1.58 20 80 0.29 64 34 S 1000 [24]
65 35 1.78 20 80 0.33 64 34 1.75 1050 [24]
65 35 1.94 20 80 0.36 64 34 1.9 1100 [24]
65 35 2.1 20 80 0.39 64 34 2.06 1150 [24]
65 35 1.79 20 80 0.33 64 34 1.76 1000 [14]
65 35 1.87 20 80 0.35 64 34 1.84 1050 [14]
65 35 1.94 20 80 0.36 64 34 1.9 1100 [14]
65 35 2.01 20 80 0.37 64 34 1.97 1150 [14]
70 30 1.54 24 76 0.32 69 30 1.52 950 [24]
70 30 1.76 24 76 0.36 69 29 1.73 1000 [24]
70 30 1.94 24 76 0.40 69 29 1.9 1050 [24]
70 30 2.2 24 76 0.45 68 29 2.15 1100 [24]
70 30 2.35 24 76 0.49 68 29 2.3 1150 [24]
72 28 1.99 25 75 0.43 70 28 1.95 948 [25]
72 28 2.08 25 75 0.45 70 28 2.04 968 [25]
72 28 1.64 25 75 0.35 70 28 1.61 980 [26]
72 28 2.17 25 75 0.47 70 28 2.12 988 [25]
72 28 2.01 25 75 0.43 70 28 1.97 1000 [14]
72 28 2.13 25 75 0.46 70 28 2.09 1050 [14]
72 28 2.26 25 75 0.49 70 28 2.21 1100 [14]
72 28 2.37 25 75 0.51 70 28 2.32 1150 [14]
75 25 1.65 28 72 0.38 74 25 1.62 950 [24]
75 25 1.95 28 72 0.45 74 25 1.91 1000 [24]
75 25 2.23 28 72 0.52 73 24 2.18 1050 [24]
75 25 2.5 28 72 0.58 73 24 2.44 1100 [24]
75 25 2.65 28 72 0.62 73 24 2.58 1150 [24]
76 24 2.23 30 70 0.53 75 23 2.18 1000 [14]
76 24 2.12 30 70 0.50 75 23 2.08 1004 [25]
76 24 2.3 30 70 0.55 75 23 2.25 1024 [25]
76 24 1.81 30 70 0.43 75 23 1.78 1035 [26]
76 24 2.36 30 70 0.56 75 23 2.31 1044 [25]
76 24 2.35 30 70 0.56 75 23 2.3 1050 [14]
76 24 2.48 30 70 0.59 75 23 2.42 1100 [14]
76 24 2.58 30 70 0.62 74 23 2.52 1150 [14]
80 20 2.31 35 65 0.61 78 20 2.26 1050 [24]
80 20 2.53 35 65 0.67 78 20 2.47 1100 [24]
80 20 2.75 35 65 0.73 78 19 2.68 1150 [24]
80 20 2.93 35 65 0.78 78 19 2.85 1200 [24]
80 20 3.06 35 65 0.82 78 19 2.97 1250 [24]
80 20 2.56 35 65 0.68 78 19 2.5 1050 [14]
80 20 2.15 35 65 0.57 79 19 2.1 1062 [25]
80 20 2.45 35 65 0.65 78 19 2.39 1082 [25]
80 20 1.97 35 65 0.52 79 19 1.93 1090 [14]
80 20 2.69 35 65 0.71 78 19 2.62 1100 [14]
80 20 2.58 35 65 0.69 78 19 2.52 1102 [25]
80 20 2.78 35 65 0.74 78 19 2.7 1150 [14]
83 17 2.14 39 61 0.62 81 17 2.1 1100 [15]
83 17 2.73 39 61 0.79 81 16 2.66 1050 [14]
83 17 2.85 39 61 0.83 81 16 2.77 1100 [14]
83 17 3.01 39 61 0.88 81 16 2.92 1150 [14]
85 15 2.68 43 57 0.83 83 15 2.61 1100 [24]
85 15 2.85 43 57 0.88 83 15 2.77 1150 [24]
85 15 3.08 43 57 0.96 82 15 2.99 1200 [24]
85 15 3.25 43 57 1.01 82 15 3.15 1250 [24]
90 10 3.2 54 46 1.19 87 10 3.1 1200 [24]
90 10 3.5 54 46 1.30 87 10 3.38 1250 [24]
Figure 5 annotates the solubility data of La2O3 on a pseudo-binary phase diagram of La2O3-(LaF3 + LiF), with the LaF3/LiF weight ratios of 1.9 and 3.2. It can be observed that the liquidus temperature increases sharply with an increase in the concentration of La2O3. For every 1 wt.% increase in La2O3 in the melt, the liquidus temperature rises by approximately 300 °C. In other words, the solubility of La2O3 is not sensitive to temperature, as increasing the temperature by 300 °C only results in a 1 wt.% increment in La2O3 solubility. At the same temperature, a higher LaF3/LiF weight ratio leads to a greater solubility of La2O3, but scattered data make it difficult to obtain precise liquidus lines. The dashed lines in the figure represent the estimated liquidus lines corresponding to LaF3/LiF weight ratios of 1.9 and 3.2, based on the experimental data.
Figure 5. Pseudo-binary phase diagram of (LaF3 + LiF)-La2O3 at fixed LaF3/LiF of 1.9 and 3.2 [14][24][25].

4. Y2O3-YF3-LiF System

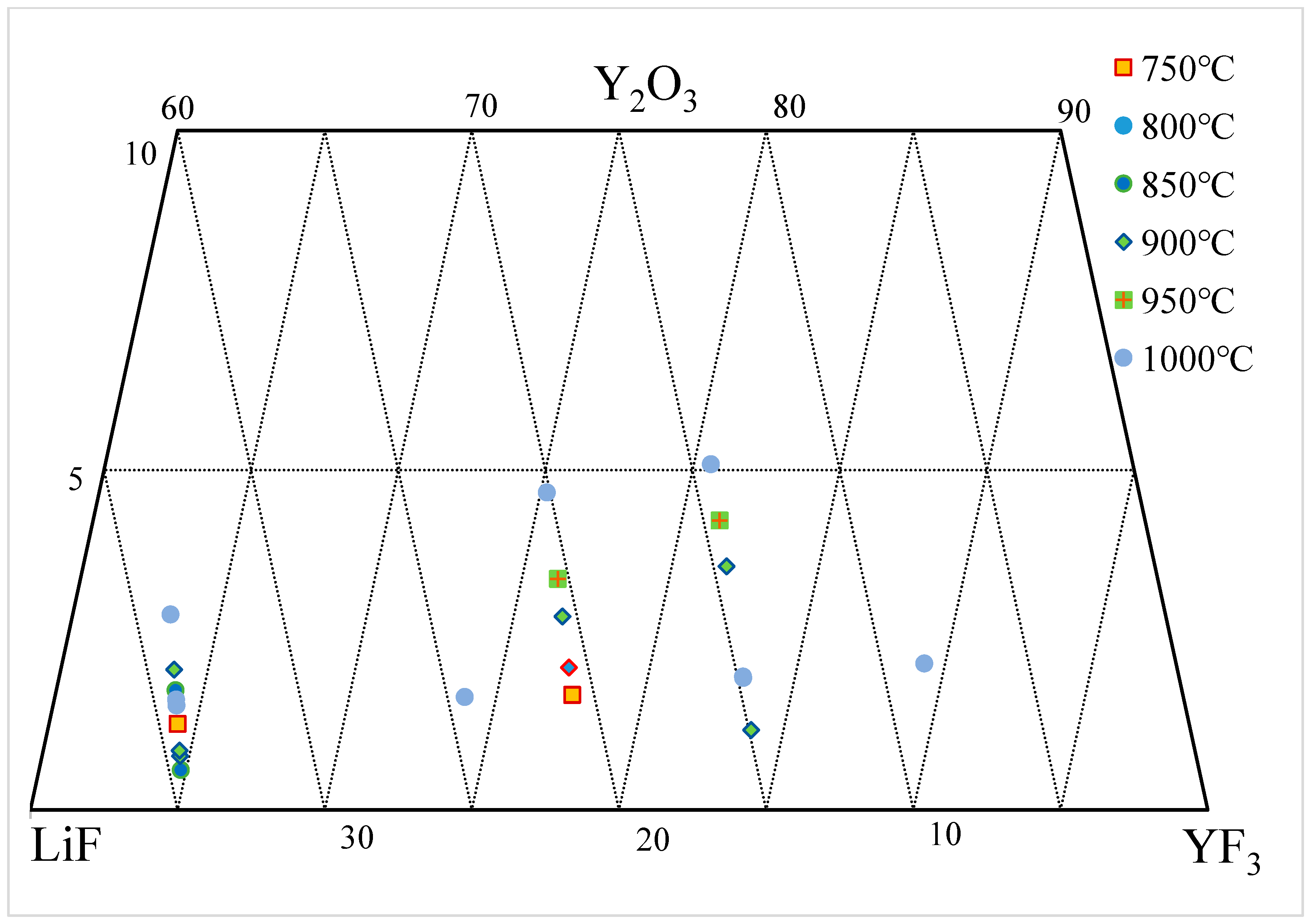
Figure 6 presents the solubility data of Y2O3 in the YF3-LiF system annotated on a ternary phase diagram, and the data from the literature are summarized in Table 3 [27][28]. Within the range of 725–1009 °C and 60–90 wt.% YF3, the solubility of Y2O3 in the YF3-LiF system ranges from 0.45 to 5.09 wt.%. Data published by the same group of researchers indicate that the solubility of Y2O3 in YF3-LiF increases with temperature and YF3. However, as can be seen from the figure, there are significant differences in the data from different researchers. 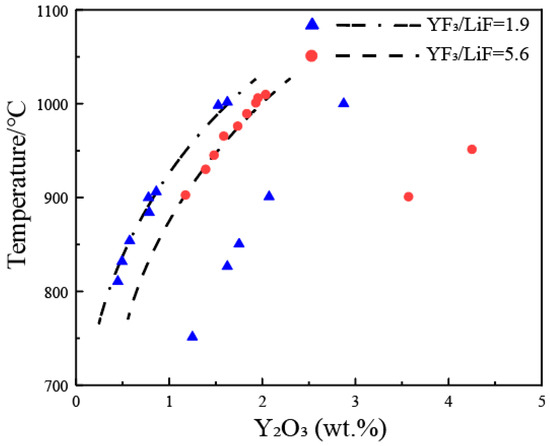Figure 7 annotates partial solubility data of Y2O3 on a pseudo-binary phase diagram of Y2O3-(YF3 + LiF), with YF3/LiF weight ratios of 1.9 and 5.6. From the figure, it can be observed that the liquidus temperature increases with an increase in the concentration of Y2O3, but the extent of increase is not as significant as in the La2O3-LaF3-LiF and Nd2O3-NdF3-LiF systems. Therefore, the solubility of Y2O3 in the YF3-LiF system increases rapidly with increasing temperature. In principle, at the same temperature, a higher YF3/LiF ratio leads to a greater solubility of Y2O3, but there are significant differences in the data from the two groups of researchers in the figure. The dashed lines in the figure represent the estimated liquidus lines corresponding to the YF3/LiF weight ratios of 1.9 and 5.6, based on the experimental data.
Figure 6. Liquidus points shown on the phase diagram of YF3-LiF-Y2O3 system in YF3-rich corner.
Metals 14 00314 g014
Figure 7. Pseudo-binary phase diagram of (YF3 + LiF)-Y2O3 at fixed YF3/LiF of 1.9 and 5.6 [28][29].
Table 3. Solubility of Y2O3 in YF3-LiF fluoride melts.
wt.% mol% Normalization (wt.%) T.  
YF3 LiF Y2O3 YF3 LiF Y2O3 YF3 LiF Y2O3 (°C) Ref.
58 42 1.17 20 80 0.26 58 41 1.16 725 [29]
58 42 1.25 20 80 0.28 58 41 1.23 750 [29]
58 42 1.48 20 80 0.33 58 41 1.46 800 [29]
58 42 1.87 20 80 0.42 57 41 1.84 875 [29]
58 42 2.09 20 80 0.47 57 41 2.05 920 [29]
58 42 2.35 20 80 0.53 57 41 2.3 950 [29]
58 42 2.87 20 80 0.65 57 40 2.79 1000 [29]
65 35 1.28 25 75 0.32 64 34 1.26 750 [29]
65 35 0.45 25 75 0.11 65 35 0.45 810 [28]
65 35 1.63 25 75 0.41 64 34 1.6 825 [29]
65 35 0.5 25 75 0.12 65 35 0.5 831 [28]
65 35 1.79 25 75 0.45 64 34 1.76 850 [29]
65 35 0.59 25 75 0.15 65 35 0.59 850 [28]
65 35 0.8 25 75 0.20 65 35 0.79 882 [28]
65 35 0.8 25 75 0.20 65 35 0.79 900 [28]
65 35 2.11 25 75 0.53 64 34 2.07 900 [29]
65 35 0.88 25 75 0.22 65 34 0.87 900 [28]
65 35 1.65 25 75 0.41 64 34 1.62 1000 [28]
65 35 2.96 25 75 0.75 63 34 2.87 1000 [29]
65 35 1.65 25 75 0.41 64 34 1.62 1000 [28]
75 25 1.69 35 65 0.51 74 24 1.66 1000 [28]
79 21 1.72 40 60 0.57 78 21 1.69 750 [29]
79 21 2.14 40 60 0.71 77 21 2.1 800 [29]
79 21 2.26 40 60 0.75 77 21 2.21 825 [29]
79 21 2.93 40 60 0.98 77 20 2.85 900 [29]
79 21 3.52 40 60 1.18 76 20 3.4 950 [29]
79 21 4.9 40 60 1.66 75 20 4.67 1000 [29]
85 15 3.72 50 50 1.45 82 15 3.59 900 [29]
85 15 1.19 50 50 0.46 84 15 1.18 900 [28]
85 15 1.41 50 50 0.54 84 15 1.39 929 [28]
85 15 1.51 50 50 0.58 84 15 1.49 943 [28]
85 15 4.45 50 50 1.75 81 14 4.26 950 [29]
85 15 1.61 50 50 0.62 84 15 1.58 964 [28]
85 15 1.78 50 50 0.69 83 15 1.75 974 [28]
85 15 1.88 50 50 0.73 83 15 1.85 988 [28]
85 15 5.36 50 50 2.11 81 14 5.09 1000 [29]
85 15 1.98 50 50 0.77 83 15 1.94 1000 [28]
85 15 2 50 50 0.77 83 15 1.96 1000 [28]
85 15 2.09 50 50 0.81 83 15 2.05 1009 [28]
91 9 2.2 64 36 1.02 89 9 2.15 1000 [28]

5. Solubility Model of RE2O3-REF3-LiF System

High-temperature phase equilibrium experiments not only consume a significant amount of time and funding, as mentioned above, they also yield substantial variations in the data among different researchers and experimental methods, which brings confusion to the applications of these data. Various thermodynamic models, such as FactSage [30][31], MTDATA [32], and Thermo-Calc [33], have been developed to predict the thermodynamic properties of slags, molten salts, and alloys. The solubility of rare earth oxides in molten salts can theoretically be predicted using thermodynamic models. However, the construction of the core database for these thermodynamic models relies heavily on a large amount of experimental data. The lack of accurate thermodynamic data for rare earth oxide–molten salt systems currently hinders the ability of existing thermodynamic models to predict their properties, including solubility. Researchers have attempted to establish semi-empirical models [8][9] to predict the solubility of rare earth oxides in molten salts based on available experimental data. 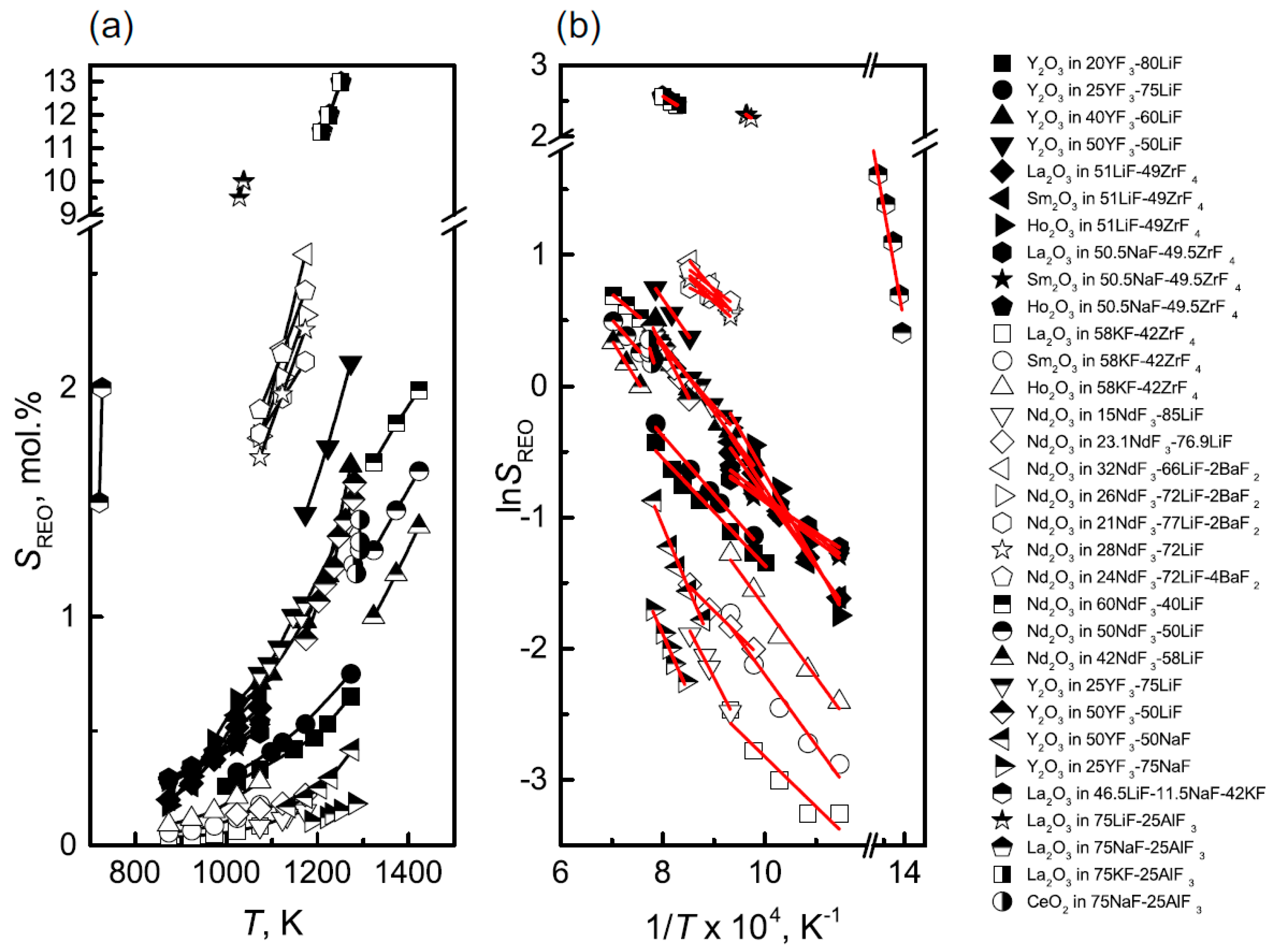Figure 8 summarizes the solubility of various rare earth oxides in fluoride salts, where Figure 8a shows the relationship between solubility and temperature, and Figure 8b demonstrates the relationship between the logarithm of solubility and the reciprocal of temperature [9]. It can be observed that the solubility of rare earth oxides in molten salts generally increases with temperature but with significant variations among different systems. For most systems, the logarithm of solubility exhibits a linear relationship with the reciprocal of temperature.
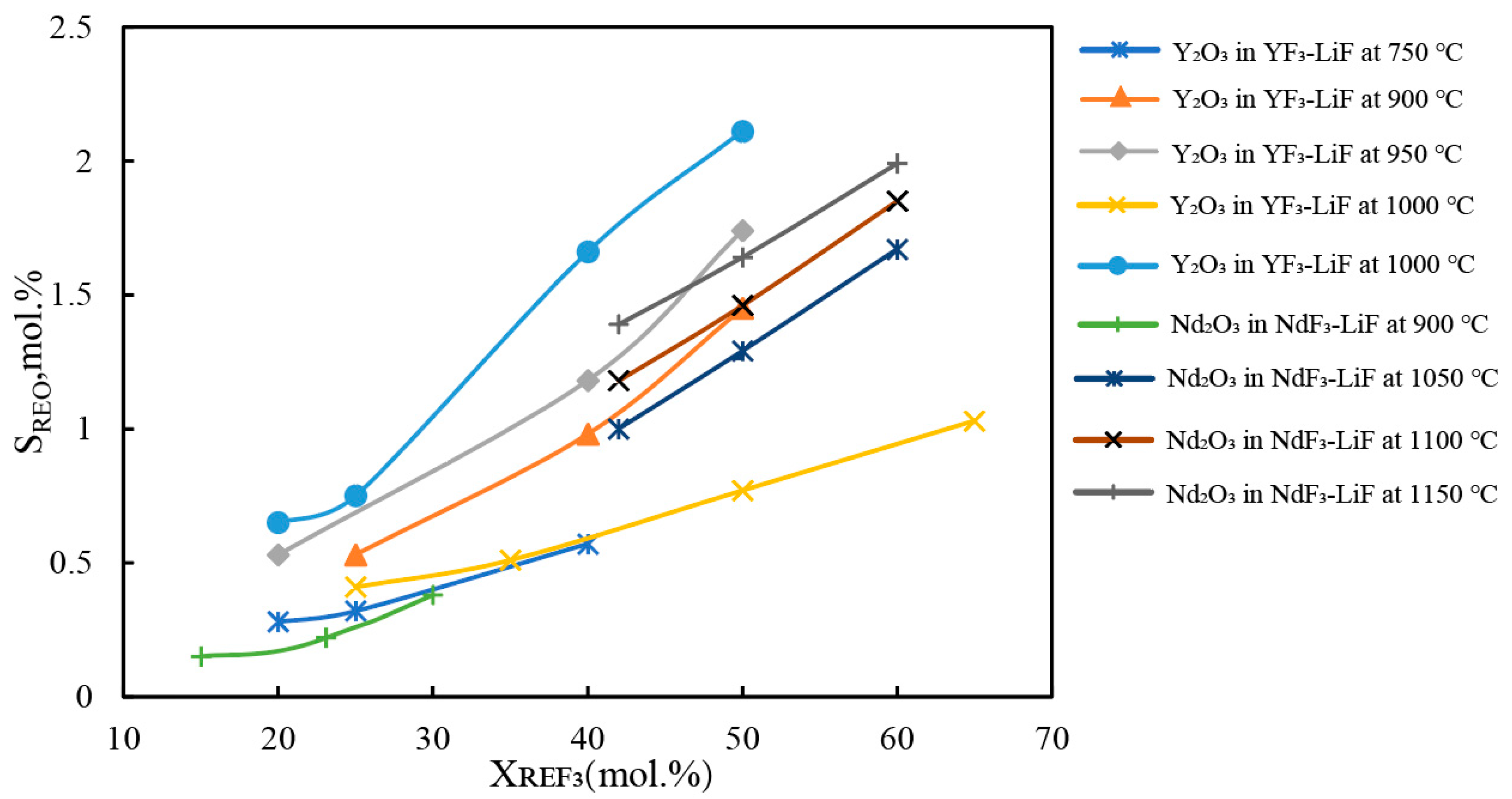
Figure 8. Solubility of rare earth oxides (sREO) in fluoride melts as a function of temperature: (a) solubility vs. temperature and (b) logarithm of solubility vs. reciprocal of the temperature [9].
Figure 9 illustrates the relationship between the solubility of Nd2O3 and Y2O3 and the concentration of rare earth fluoride (REF3). Within the studied concentration and temperature ranges, the solubility of the oxides increases with an increase in the concentration of REF3 in the molten salt. At higher temperatures, the solubility of rare earth oxides is more sensitive to the concentration of REF3 in the molten salt. As shown in Figure 9, the solubility data for different rare earth oxides in fluoride salts exhibit considerable variability, making it difficult to be expressed by a unified model. Guo et al. [9] proposed semi-empirical prediction models for each rare earth oxide with available solubility experimental data. For example, they developed a solubility prediction model for Nd2O3 in the NdF3-LiF-(MgF2/CaF2) system using the data from three articles [12][13][17]. 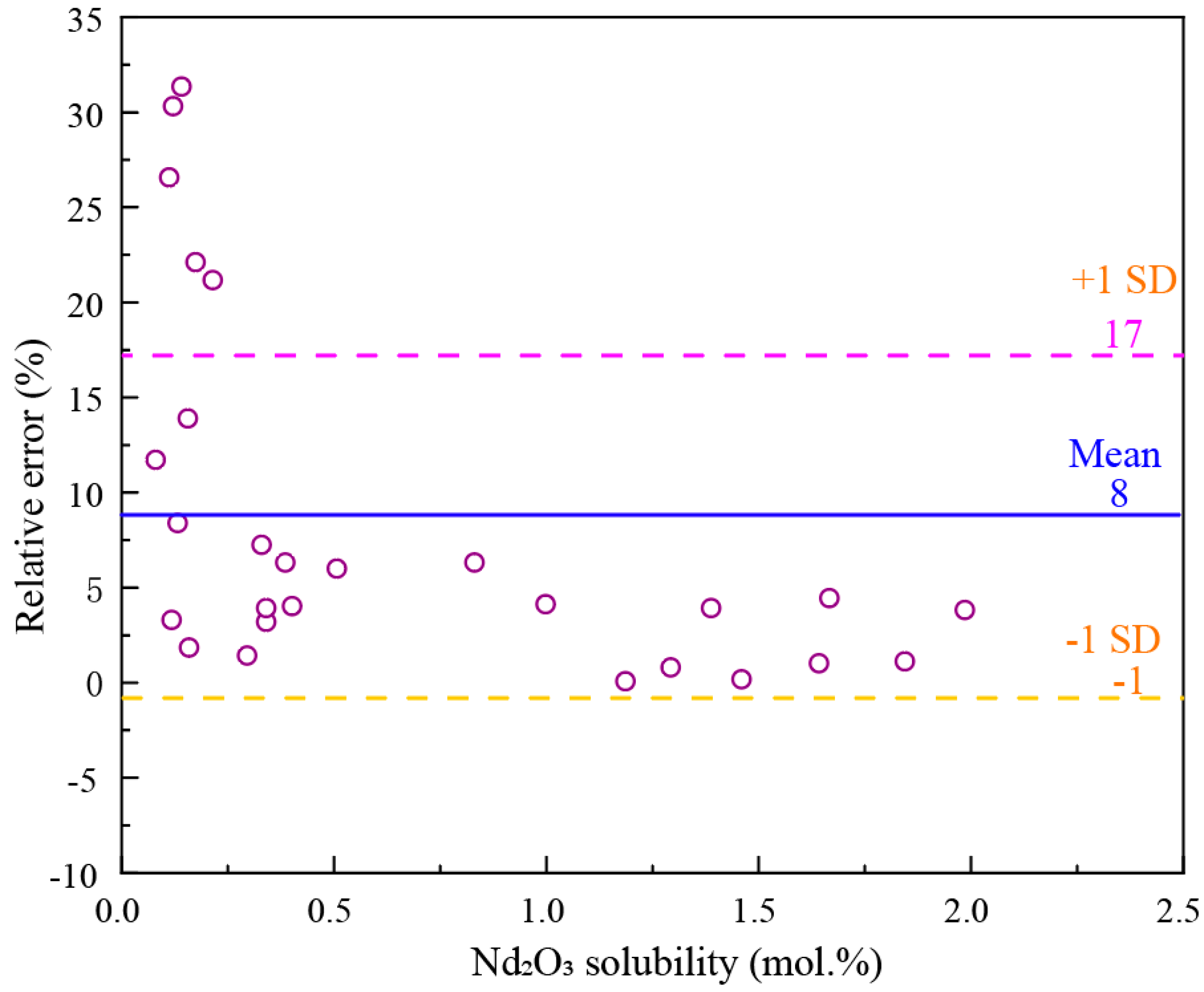The comparison between the predicted and experimental results is shown in Figure 10, with an average error of 8%. However, the error can reach 30% for low solubility cases.
Figure 9. Solubility of rare earth oxides in fluoride melts as a function of REF3 content (data from Refs. [13][17][28][29]).
Figure 10. Relative error between the experimental data and the data calculated with the current model for Nd2O3 solubility [9].
As shown in Figure 1, the solubility data of Nd2O3 in the NdF3-LiF system reported in the literature are much more extensive than those used by Guo et al. [9]. Figure 11 compares the solubility calculated by Guo et al.’s model [9] with all the experimental solubility data of Nd2O3 in the NdF3-LiF system. It can be seen that the solubilities calculated by Guo et al.’s model show a big difference compared with the experimental data in low NdF3 fluoride salt.
Metals 14 00314 g018
Figure 11. Nd2O3 solubility in melts with different NdF3 concentration and at different temperatures (data from references [12][13][14][16][17][20][22]).

References

  1. Balaram, V. Rare earth elements: A review of applications, occurrence, exploration, analysis, recycling, and environmental impact. Geosci. Front. 2019, 10, 1285.
  2. Huang, X.W.; Li, H.W.; Wang, C.F.; Wang, G.Z.; Xue, X.X.; Zhang, G.C. Development Status and Research Progress in Rare Earth Industry in China. Chin. J. Rare Met. 2007, 31, 279–288.
  3. Liu, H.; Zhang, Y.; Luan, Y.; Yu, H.; Li, D. Research Progress on Preparation of Rare Earth Metals by Molten Salt Electrolysis. Chin. Rare Earths 2021, 42, 133–143.
  4. Liu, Y.B.; Chen, G.H.; Yu, B.; Chen, X. Research Progress of Tapping Technology for Molten Salt Electrolytic Preparation of Rare Earth Metals. Chin. Rare Earths 2018, 39, 134–140.
  5. Wu, Y.F.; Ma, S.Y.; Wang, Z.F.; Bian, X.; Liu, Z.X.; Liu, Y.L. Formation Mechanism and countermeasures of nodules at furnace bottom of 15kA rare earth molten salt electrilysis cell. China Nonferrous Metall. 2023, 52, 81–87.
  6. Ji, Y.Z.; Xiao, F.X.; Sun, S.C.; Chen, J.Q.; Tu, G.F. Research Progress on Model Cell of High Current Rare Earth Reduction Cell. J. Chin. Soc. Rare Earth 2022, 40, 38–45.
  7. Guo, X.L.; Sun, Z.; Sietsma, J.; Blanpain, B.; Guo, M.X.; Yang, Y. Quantitative Study on Dissolution Behavior of Nd2O3 in Fluoride Melts. Ind. Eng. Chem. Res. 2018, 57, 1380–1388.
  8. Guo, X.L.; Sietsma, J.; Yang, Y.X. Chapter 15-A Critical Evaluation of Solubility of Rare Earth Oxides in Molten Fluorides. In Rare Earths Industry; Elsevier: Amsterdam, The Netherlands, 2015; pp. 223–234.
  9. Guo, X.L.; Sun, Z.; Sietsma, J.; Yang, Y.X. Semiempirical Model for the Solubility of Rare Earth Oxides in Molten Fluorides. Ind. Eng. Chem. Res. 2016, 55, 4773–4781.
  10. Abbasalizadeh, A.; Teng, L.; Seetharaman, S.; Sietsma, J.; Yang, Y. Rare Earth Extraction from NdFeB Magnets and Rare Earth Oxides Using Aluminum Chloride/Fluoride Molten Salts. Rare Earths Ind. Technol. Econ. Environ. Implic. 2016, 357–373.
  11. Yang, Y.; Walton, A.; Sheridan, R.; Güth, K.; Gauß, R.; Gutfleisch, O.; Buchert, M.; Steenari, B.M.; Gerven, V.T.; Jones, P.T.; et al. REE Recovery from End-of-Life NdFeB Permanent Magnet Scrap: A Critical Review. J. Sustain. Metall. 2017, 3, 122–149.
  12. Wu, W.Y.; Sun, J.Z.; Hai, L.; Gao, H.J. Solubility of Nd2O3 in Fluorine Salt System. Chin. Rare Rare Earths 1991, 3, 34–37.
  13. Stefanidaki, E.; Photiadis, G.M.; Kontoyannis, C.G.; Vik, A.F.; Østvold, T. Oxide solubility and Raman spectra of NdF3-LiF-KF-MgF2-Nd2O3 melts. J. Chem. Soc. Dalton Trans. 2002, 11, 2302–2307.
  14. Zhu, X.P.; Sun, S.C.; Liu, C.; Tu, G.F. Solubility of RE2O3 (RE = La and Nd) in light rare earth fluoride molten salts. J. Rare Earths 2018, 36, 765–771.
  15. Zhang, L.J. Study on Determination Method of Rare Earth Oxide Solubility in Rare Earth Molten Salt. Ph.D. Thesis, Northeastern University, Shenyang, China, 2018.
  16. Liu, K.R. Study on Molten Salt Properties and Electrode Process of Neodymium Electrolysis. Ph.D. Thesis, Northeastern University, Shenyang, China, 2001.
  17. Hu, X.W. Research and Application of Molten Salt Structure of NdF3-LiF-Nd2O3 Series. Ph.D. Thesis, Northeastern University, Shenyang, China, 2009.
  18. Liu, F.Y. Fundamental Electrochemical Study on Neodymium Molten Salt Electrolysis in Fluoride Bath. Ph.D. Thesis, The Faculty and the Board of Trustees of the Colorado School of Mines, St. Golden, CO, USA, 2019.
  19. Zhu, X.P. The study on Physicochemical Properties of REF3-LiF-RE2O3 Molten Salt. Ph.D. Thesis, Northeastern University, Shenyang, China, 2012.
  20. Chen, L.Y.; Liu, S.Z.; Li, B. Study on Solubility and Dissolution Rate of Nd2O3 in NdF3-LiF Molten Salt by Square Wave Voltammetry. Chin. J. Rare Met. 2016, 40, 225–243.
  21. Keller, R.; Larimer, K.T. Electrolysis of Neodymium Oxide. Final Report for the Period August 19, 1991 through February 28, 1997; EMEC Consultants: Export, PA, USA, 1997.
  22. Remazeilles, C.; Gibilaro, M.; Massot, L.; Chiron, C.; Martinez, A.M.; Chamelot, P. In-situ electrochemical oxide monitoring in LiF-NdF3-Nd2O3: Application to Nd2O3 solubility determination. J. Electroanal. Chem. 2021, 893, 115334.
  23. Takeda, O.; Nakano, K.; Kobayashi, F.; Lu, X.; Sato, Y.; Zhu, H. Solubilities of RE2O3 in REF3-LiF (RE = Nd, Dy) at 1473 K. J. Sustain. Metall. 2022, 8, 1498–1508.
  24. Liang, X.; Chen, S.; Hong, K.; Chen, D.; Li, Z.; Lai, Y.; Xu, J. Solubility of La2O3 in LaF3-LiF molten salt system. J. Chin. Soc. Rare Earths 2021, 39, 594–600.
  25. Xu, M.X. Study on Physicochemical Properties of Molten Salts of LaF3-LiF-La2O3 Series. Ph.D. Thesis, Northeastern University, Boston, MA, USA, 2014.
  26. Zhu, X.P. Research of Physical and Chemical Properties of LaF3-LiF-La2O3 Molten Salt System. Master’s Thesis, Northeastern University, Shenyang, China, 2012.
  27. Wang, X.; Zeng, J.Y.; Cai, B.Q. Solubility of Y2O3 in NaF-AlF3-LiF molten salt system. Rare Met. Cem. Carbides 2020, 48, 29–32.
  28. Bratland, D. On the Possible Electrowinning of Yt-Al Alloys. The Solubility of Yttria and of Alumina in Molten Mixtures of Yttrium Fluoride and Lithium Fluoride. Light Met. 1976, 1, 183–201.
  29. Reddy, R.G.; Kumar, S.G. Solubility and thermodynamic properties of Y2O3 in LiF-YF3 melts. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 1994, 25, 91–96.
  30. Jung, I.V.; Ende, M. Computational thermodynamic calculations: FactSage from CALPHAD thermodynamic database to virtual process simulation. Metall. Mater. Trans. B 2020, 51, 1851–1874.
  31. Bale, C.W.; Bélisle, E.; Chartrand, P.; Decterov, S.; Eriksson, G.; Gheribi, A.; Hack, K.; Jung, I.H.; Kang, Y.B.; Melançon, J.; et al. Reprint of: FactSage thermochemical software and databases, 2010–2016. Calphad 2016, 55, 1–19.
  32. Davies, R.; Dinsdale, A.; Gisby, J.; Robinson, J.; Martin, S. MTDATA-thermodynamic and phase equilibrium software from the national physical laboratory. Calphad 2002, 26, 229–271.
  33. Andersson, J.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Chemistry, Physical
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Quan Zhou
,
Jinfa Liao
,
Chunfa Liao
,
Baojun Zhao
View Times: 73
Revisions: 2 times (View History)
Update Date: 18 Mar 2024
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback