Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Boris B Straumal
 -- 2361 2022-10-25 08:04:12 |
2 format correct
Vivi Li
 -5 word(s) 2356 2022-10-26 03:29:50 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Straumal, B.;  Korneva, A.;  Kuzmin, A.;  Klinger, L.;  Lopez, G.A.;  Vershinin, N.;  Straumal, A.;  Gornakova, A. High Entropy Alloys for Energy Conversion and Storage. Encyclopedia. Available online: https://encyclopedia.pub/entry/31072 (accessed on 16 December 2024).
Straumal B,  Korneva A,  Kuzmin A,  Klinger L,  Lopez GA,  Vershinin N, et al. High Entropy Alloys for Energy Conversion and Storage. Encyclopedia. Available at: https://encyclopedia.pub/entry/31072. Accessed December 16, 2024.
Straumal, Boris, Anna Korneva, Alexei Kuzmin, Leonid Klinger, Gabriel A. Lopez, Nikolai Vershinin, Alexander Straumal, Alena Gornakova. "High Entropy Alloys for Energy Conversion and Storage" Encyclopedia, https://encyclopedia.pub/entry/31072 (accessed December 16, 2024).
Straumal, B.,  Korneva, A.,  Kuzmin, A.,  Klinger, L.,  Lopez, G.A.,  Vershinin, N.,  Straumal, A., & Gornakova, A. (2022, October 25). High Entropy Alloys for Energy Conversion and Storage. In Encyclopedia. https://encyclopedia.pub/entry/31072
Straumal, Boris, et al. "High Entropy Alloys for Energy Conversion and Storage." Encyclopedia. Web. 25 October, 2022.
High Entropy Alloys for Energy Conversion and Storage
Edit
This entry is adapted from the peer-reviewed paper 10.3390/en15197130

The multicomponent alloys with nearly equal concentration of components are known as high entropy alloys (HEAs). The HEAs quickly became very important in materials science due to their unique properties. Nowadays, the HEAs are frequently used in energy conversion and storage applications. HEAs can consist of five, six or more components. Plasma cladding permits coating of the large surfaces of cheap substrates with (often expensive) HEAs and to enlarge, in such a way, their application area. The large-area coatings deposited by plasma cladding possess multiple advantages such as low thermal distortion, very high energy density, as well as low dilution of the substrate material. Plasma cladding ensures good metallurgical bonding between coating and substrate. The costs of operation and equipment are also very attractive. During plasma cladding, the mixed powders are blown by carrier gas into a plasma torch or are positioned on a substrate. 

plasma cladding coatings wetting phase transitions high-entropy alloys phase diagrams grain boundary

1. Introduction

In recent years, high entropy alloys (HEAs) have become a research hotspot in materials science. Nowadays, HEAs are frequently used for the energy conversion and storage applications [1][2][3][4]. HEAs are also called multi-principal alloys, baseless alloys, or alloys without main component. They were first proposed by Brian Cantor and coworkers [5] and Jien-Wei Yeh and his team [6]. The first HEAs were alloys with six or more components in equiatomic proportions. It was unexpected that such alloys may form a uniform disordered solid solution. This is because their unique combination of atoms with different atomic radii can strongly prevent the nucleation of second phases and their subsequent growth [5][6][7][8][9][10][11][12]. Such alloys can exhibit better properties than traditional alloys. In particular, they possess high hardness [7][8], good strength at high temperatures [9], and excellent wear, oxidation, and corrosion resistance [10][11][12]. The most used approaches to manufacturing HEAs are casting or arc melting technologies [5][6][7][8][9][10][11][12]. In these methods, the elemental powders are mixed first and then remelted several times in order to ensure the homogeneity of HEAs. However, the size of HEA parts produced by casting or arc melting is limited. This fact impedes the application of HEAs. One of the ways to overcome this restriction is to produce the part from other regular or ordinary (possibly even cheaper) material and to deposit the HEA coating on the surface. Due to this fact, various methods were used to produce the HEA coatings, such as plasma cladding [1][2][13][14], plasma spray [15][16][17][18][19][20][21][22], thermal spray [23], laser cladding [24][25][26][27], magnetron sputtering [28][29][30][31][32][33][34][35][36][37], vacuum arc deposition [38][39][40][41], electric arc deposition [42], and electron beam deposition [43]. All these deposition methods have their advantages and disadvantages. For example, thermal spraying can take place in low vacuum. On the other hand, the increased oxidation of the components can proceed. The magnetron sputtering or vacuum arc deposition ensure high density and uniformity of coatings, they also do not include melting of HEA during manufacturing. However, the maximal thickness does not exceed a few μm. In the case of plasma cladding, the coatings can be a hundred times thicker. Also, the small droplets of a melt can form during the vacuum arc deposition; in most cases, they need to be filtered with magnetic loops, decreasing the deposition rate. The magnetron sputter-deposited films have columnar grain structure, and the coatings after vacuum arc deposition have uniform equiaxed grains. Researchers listed here only several differences of HEA synthesis methods. Each of them has, therefore, its own niche (which frequently partly overlaps with those of other synthesis methods). This entry discusses the plasma cladding, which started to be developed quite recently, just few years ago, and, nevertheless, has already taken its own place among other technologies.
Plasma cladding is an effective way to manufacture the coatings with large area, with advantages such as low thermal distortion, very high energy density, as well as small dilution of the substrate material [40][41]. Plasma cladding assures good metallurgical bonding between coating and substrate, it also has a low cost in equipment and operation [42][43]. The powder of a material to be clad melts rapidly under the plasma torch, and then solidifies. The whole process takes place with a high temperature gradient. As a result, the fine-grained and tough coating forms on the substrate. The coaxial and preplaced powder schemes are the two most popular plasma cladding systems. In the first scheme, the surface of the substrate is irradiated by the plasma torch forming the liquid melt pool. The carrier (or working) gas ejects the powder under pressure from the nozzle. The powder then melts in the plasma torch, forming a cladding layer. The working gas (usually argon) feeds the powder from this nozzle into the melted pool. Argon also acts as a shielding gas to avoid oxidization. Thus, the powder feeding nozzle moves simultaneously with the plasma torch. They scan the substrate “line-by-line”. In the case of preplaced powder systems, the substrate is covered by the powder mixture as cladding material before melting. Frequently, glue is used to fix the pre-placed mixed powders to the surface and form the few mm thick powder bed. Before cladding, the samples are usually preheated at ~100 °C for few hours to remove the glue. Then, the plasma torch scans the preplaced powder mixture. As a result, the powder mixture melts and, afterwards, rapidly cools down. The cladding layer is formed in such a way.
Researchers have to underline that recently the focus in HEA investigations has begun to move from homogeneous HEAs to heterogeneous ones [13][14][15][16][17][25][26][27]. Such HEAs contain more that one phase, high specific area of grain boundaries (GB), and interphase boundaries (IBs), as well as other elements of inhomogeneity. The concept of GB phase transitions can be very useful in the development of inhomogeneous HEAs. The GB phase transformations include GB wetting by a second phase (liquid or solid), including formation of thin films of various GB phases [44][45][46][47]. For example, complete or incomplete GB wetting can strongly affect the microstructure, after solidification, of the melted pool during the plasma cladding. 

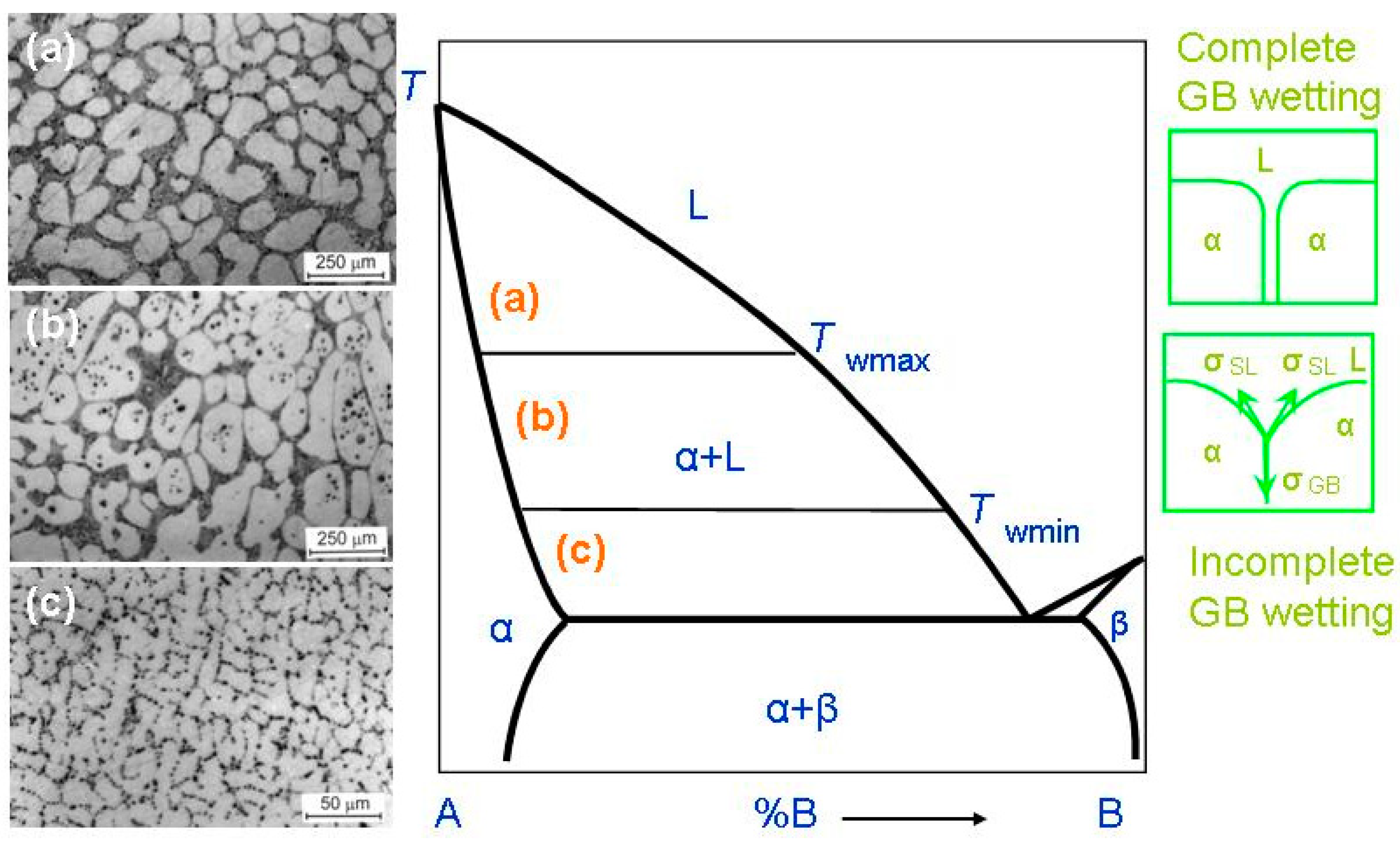
2. Grain Boundary Wetting Phase Transitions

In most cases, HEAs contain numerous components. Therefore, the equilibrium phase diagrams for such complicated systems must be constructed in 5–6 or more dimensions. Due to this trouble, researchers are forced to use a simplified approach. Fortunately, the most important features of GB wetting phase transitions [48] can be described using the simple two-dimensional phase diagram for binary alloys like that shown in Figure 1. Bold lines in this scheme (e.g., solidus, liquidus, solvus, and eutectic lines) depict the bulk phase transitions. The thin lines (like tie-lines at Twmin and Twmax) depict the GB phase transformations. When the solidification of HEAs starts, the composition of an alloy can be found in the phase diagram in the liquid area L. Afterwards, by cooling, it crosses the liquidus line and moves into the two-phase area L + α. In this L + α area the melt is in equilibrium with solid solution α. The solid solution α is based on component A. By following cooling, the amount of solid solution α in this L + α mixture increases and the portion of melt L decreases. The composition of remaining melt L follows the liquidus line. Thus, the melt becomes more and more enriched by component B. Similarly, the composition of solidifying phase α changes along the solidus line. If the concentration of component B in α-phase is low, the solidification finishes at the solidus line. Afterwards, the solidified alloy has only phase, namely the solid solution α. However, the portions of α-phase solidified at the end of the process are enriched by the component B. If researchers discuss the multicomponent HEAs instead of this simple example of binary alloy, the GB wetting transitions would be more complicated. This is because, for example, an HEA with five components is described by the 5D phase diagram. Therefore, when the liquid alloy L with five components starts to crystallize, it can intersect with not only one binary-phase region, α + L, such as in Figure 1, but numerous multiphase areas. Only afterwards can HEA be completely solid and contain only one α-phase. These multiphase regions can contain more than one liquid phase and one solid phase.
Figure 1. Binary A–B diagram of 3D phases for the discussion of the GB wetting phenomena. Thick lines (solidus, solvus, liquidus, eutectic lines) mark the bulk transitions between 3D phases. Thin lines at Twmin and Twmax mark the tie-lines for the wetting of α/α GBs by the liquid phase, L. On the left-hand side of the figure the micrographs are shown for the L + (Al) polycrystals containing liquid and solid phases. Case (a) shows the alloy structure above Twmax. Here, all (Al)/(Al) GBs are fully wetted. The scheme (b) shows the alloy structure between Twmax and Twmin. Here, some (Al)/(Al) GBs are completely wetted, and other (Al)/(Al) GBs are partially wetted. The scheme (c) shows the alloy structure below Twmin. This sample contains only partially wetted (Al)/(Al) GBs. The respective thermodynamic schemes for complete and incomplete GB wetting are shown right. Here, σGB is the GB energy, σSL is the IB energy, θ is the contact angle. The micrographs are reprinted with permission from ref. [49]. Copyright 2021 MDPI.
When a polycrystal crosses the α + L area of the phase diagram, it contains, first, the interphase boundaries (IBs) between liquid phase, L, and solid phase, α-phase. It also contains the α/α grain boundaries (GBs). The melt, L, contacts the solid phase, α, in the triple junctions (TJs) between GBs and, respectively, two solid/liquid IBs, (see green schemes on the right-hand side of Figure 1). The GB has the energy σGB and each solid/liquid IB has energy 2σSL. If σGB < 2σSL, (see lower scheme in right-hand side of Figure 1), the GB has a non-zero contact angle, θ > 0, with the melt. The GB wetting in this case is partial (or incomplete). The micrograph (c) on the left-hand side of the phase diagram shows an example of how the microstructure of the two-phase α + L polycrystal of the Al–Mg alloy can appear below Twmin. This sample contains only (Al)/(Al) GBs partially wetted by the Mg-rich melt. If the energy of two solid/liquid IBs, 2σSL, is lower than the GB energy, σGB > 2σSL (see upper scheme in Figure 1), then the contact angle becomes equal to zero, θ = 0. In this case, the thick melted layer should separate the solid α-grains, and the GB wetting is complete. The transition between complete and partial GB wetting is described for numerous binary alloys. In these alloys the θ value decreases with growing temperature and becomes zero at a certain temperature, Tw (called the temperature of GB wetting phase transition) [50][51][52]. Above Tw, the GB is completely wetted. The GB wetting phase-transition is in principle two-dimensional one. Nevertheless, it can be of first or second order, similar to phase transformations in the bulk [53][54][55]. In the case of a first-order GB wetting transition, the first temperature derivative of θ, dθ/dT, has a discontinuity at Tw. The dθ/dT suddenly descends at Tw from a certain finite value to zero [50][53][54]. In case of the continuous (second-order) wetting transition in GBs, the dθ/dT value continuously changes with growing T and smoothly reaches zero dθ/dT = 0 at Tw [54][55]. One must take into consideration that the σGB value can strongly depend both on the grain boundary misorientation angle, χ, and on the grain boundary inclination angle, ψ [56]. The dependences of GB energy on χ and ψ, σGB(χ) and σGB (ψ), possess the sharp cusps at certain χ and ψ values [57]. These special misorientation and inclination angles, χ and ψ, are determined by the coincidence site lattices. Due to this fact, the σGB can vary in a rather broad interval of values. Obviously, the lower σGB, the higher GB contact with the liquid phase would be at θ. This means that contact angles in a polycrystal can vary in a very broad interval. Moreover, these contact angles for different GBs should decrease with growing temperature with a different rate. Also, the low-angle GBs have lower σGB than high-angle GBs, and, therefore, the higher Tw values [58]. Actually, the low-angle GBs are not continuous two-dimensional (2D) defects, but consist of arrows of 1D defects, namely dislocations. The GB triple junctions are also 1D defects, and for them, it is lower than for high-angle GBs [59]. Due to these reasons, the spectrum of Tw temperatures in a polycrystal can be quite broad.
Such microstructures of two-phase polycrystals can be seen in Figure 1 (micrographs in the left-hand side). These are the microstructures of the binary Al–Mg alloys. As a result, a conventional phase diagram for 3D-phases gets the additional tie-lines at Twmin and Twmax for 2D GB wetting transformations. At T > Twmax all GBs in a polycrystal are fully wetted and contain, therefore, the melted layer between solid grains. The micrograph (a) on the left-hand side of the phase diagram shows an example of how the microstructure of the two-phase α + L polycrystal of the Al–Mg alloy can appear above Twmax. The micrograph (a) is reprinted with permission from ref. [49]. In this sample, all (Al)/(Al) GBs are completely wetted by the Mg-rich melt. The liquid phase surrounded all solid (Al) grains. The Twmax tie-line describes the GB wetting transformation for GBs with the lowest σGB in a polycrystal. By cooling, the first partially wetted GBs appear below Twmax. Between Twmax and Twmin, the amount of completely wetted GBs decreases with decreasing T. The micrograph (b) on the left-hand side of the phase diagram shows an example of how the microstructure of the two-phase α + L polycrystal of the Al–Mg alloy can appear between Twmin and Twmax. The micrograph (b) is reprinted with permission from ref. [49]. In this sample, some (Al)/(Al) GBs are completely wetted by the Mg-rich melt and other (Al)/(Al) GBs are partially wetted by the liquid phase. At Twmin, the completely wetted GBs disappear. The Twmin tie-line describes the GBs with the highest energy σGB. Below Twmin there are no completely wetted GBs in an alloy, and the polycrystal has only partially wetted GB with θ > 0. The respective example of the Al–Mg alloy is shown in the micrograph (c) on the left-hand side of the phase diagram.
Above Twmax, the liquid phase completely surrounds each solid grain (or crystallite). Thus, solid grains cannot contact each other. It is because the “dry” GBs are thermodynamically forbidden above Twmax. Researchers can see, therefore, how the new GB tie-lines appear in the α + L area of a conventional binary diagram for bulk or 3D phases.
Researchers must underline here that GB wetting phenomena can be observed not only in HEA coatings, but also in the bulk HEAs manufactured by the arc or induction melting in argon or vacuum [60][61][62][63][64][65][66][67][68][69][70][71][72][73][74][75][76][77][78][79][80], electric-current-assisted sintering (ECAS) [81], or additive manufacturing [82].

References

  1. Zhou, H.; He, J. Synthesis of the new high entropy alloy and its application in energy conversion and storage. Front. Energy Res. 2020, 8, 73.
  2. Amiri, A.; Shahbazian-Yassar, R. Recent progress of high-entropy materials for energy storage and conversion. J. Mater. Chem. A 2021, 9, 782–823.
  3. Liu, H.; Syama, L.; Zhang, L.; Lee, C.; Liu, C.; Dai, Z.; Yan, Q. High-entropy alloys and compounds for electrocatalytic energy conversion applications. SusMat 2021, 1, 482–505.
  4. Fu, M.; Ma, X.; Zhao, K.; Li, X.; Su, D. High-entropy materials for energy-related applications. iScience 2021, 24, 102177.
  5. Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218.
  6. Yeh, J.-W.; Chen, S.-K.; Lin, S.-J.; Gan, J.-Y.; Chin, T.-S.; Shun, T.-T.; Tsau, C.-H.; Chang, S.-Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303.
  7. Zhu, J.M.; Fu, H.M.; Zhang, H.F.; Wang, A.M.; Li, H.; Hu, Z.Q. Synthesis and properties of multiprincipal component AlCoCrFeNiSix alloys. Mater. Sci. Eng. A 2010, 527, 7210–7214.
  8. Zhou, Y.J.; Zhang, Y.; Wang, Y.L.; Chen, G.L. Solid solution alloys of AlCoCrFeNiTix with excellent room-temperature mechanical properties. Appl. Phys. Lett. 2007, 90, 181904.
  9. Hsu, C.Y.; Juan, C.C.; Wang, W.R.; Sheu, T.S.; Yeh, J.W.; Chen, S.K. On the superior hot hardness and softening resistance of AlCoCrxFeMo0.5Ni high-entropy alloys. Mater. Sci. Eng. A 2011, 528, 3581–3588.
  10. Chuang, M.H.; Tsai, M.H.; Wang, W.R.; Lin, S.J.; Yeh, J.W. Microstructure and wear behavior of AlxCo1.5CrFeNi1.5Tiy high-entropy alloys. Acta Mater. 2011, 59, 6308–6317.
  11. Liu, C.; Wang, H.; Zhang, S.; Tang, H.; Zhang, A. Microstructure and oxidation behavior of new refractory high entropy alloys. J. Alloys Compd. 2014, 583, 162–169.
  12. Lee, C.P.; Chen, Y.Y.; Hsu, C.Y.; Yeh, J.W.; Shih, H.C. The effect of boron on the corrosion resistance of the high entropy alloys Al0.5CoCrCuFeNiBx. J. Electrochem. Soc. 2007, 154, C424.
  13. Gao, P.-H.; Fu, R.-T.; Chen, B.-Y.; Zeng, S.-C.; Zhang, B.; Yang, Z.; Guo, Y.-C.; Liang, M.-X.; Li, J.-P.; Lu, Y.-Q.; et al. Corrosion resistance of CoCrFeNiMn high entropy alloy coating prepared through plasma transfer arc claddings. Metals 2021, 11, 1876.
  14. Wang, M.; Lu, Y.; Zhang, G.; Cui, H.; Xu, D.; Wei, N.; Li, T. A novel high-entropy alloy composite coating with core-shell structures prepared by plasma cladding. Vacuum 2021, 184, 109905.
  15. Zhang, D.; Yu, Y.; Feng, X.; Tian, Z.; Song, R. Thermal barrier coatings with high-entropy oxide as a top coat. Ceram. Int. 2022, 48, 1349–1359.
  16. Wang, L.; Zhang, F.; Yan, S.; Yu, G.; Chen, J.; He, J.; Yin, F. Microstructure evolution and mechanical properties of atmosphere plasma sprayed AlCoCrFeNi high-entropy alloy coatings under post-annealing. J. Alloys Compd. 2021, 872, 159607.
  17. Xue, M.; Mao, X.; Lv, Y.; Chi, Y.; Yang, Y.; He, J.; Dong, Y. Comparison of micro-nano FeCoNiCrAl and FeCoNiCrMn coatings prepared from mechanical alloyed high-entropy alloy powders. J. Therm. Spray Technol. 2021, 30, 1666–1678.
  18. Zhang, Z.; Zhang, B.; Zhu, S.; Yu, Y.; Wang, Z.; Zhang, X.; Lu, B. Microstructural characteristics and enhanced wear resistance of nanoscale Al2O3/13 wt. % TiO2-reinforced CoCrFeMnNi high entropy coatings. Surf. Coat. Technol. 2021, 412, 127019.
  19. Xiao, J.-K.; Li, T.-T.; Wu, Y.-Q.; Chen, J.; Zhang, C. Microstructure and tribological properties of plasma-sprayed CoCrFeNi-based high-entropy alloy coatings under dry and oil-lubricated sliding conditions. J. Therm. Spray Technol. 2021, 30, 926–936.
  20. Meghwal, A.; Anupam, A.; Luzin, V.; Schulz, C.; Hall, C.; Murty, B.S.; Kottada, R.S.; Berndt, C.C.; Ang, A.S.M. Multiscale mechanical performance and corrosion behaviour of plasma sprayed AlCoCrFeNi high-entropy alloy coatings. J. Alloys Compd. 2021, 854, 157140.
  21. Zhu, S.; Zhang, Z.; Zhang, B.; Yu, Y.; Wang, Z.; Zhang, X.; Lu, B. Microstructure and properties of Al2O3-13 wt.% TiO2-reinforced CoCrFeMnNi high-entropy alloy composite coatings prepared by plasma spraying. J. Therm. Spray Technol. 2021, 30, 772–786.
  22. Liang, J.-T.; Cheng, K.-C.; Chen, Y.-C.; Chiu, S.-M.; Chiu, C.; Lee, J.-W.; Chen, S.-H. Comparisons of plasma-sprayed and sputtering Al0.5CoCrFeNi2 high-entropy alloy coatings. Surf. Coat. Technol. 2020, 403, 126411.
  23. Ma, X.; Ruggiero, P.; Bhattacharya, R.; Senkov, O.N.; Rai, A.K. Evaluation of new high entropy alloy as thermal sprayed bondcoat in thermal barrier coatings. J. Therm. Spray Technol. 2021, 30, 2951–2960.
  24. Straumal, B.; Klinger, L.; Kuzmin, A.; Lopez, G.A.; Korneva, A.; Straumal, A.; Vershinin, N.F.; Gornakova, A.S. High entropy alloys coatings deposited by laser cladding: A review of grain boundary wetting phenomena. Coatings 2022, 12, 343.
  25. Sun, Z.; Zhang, M.; Wang, G.; Yang, X.; Wang, S. Wear and corrosion resistance analysis of FeCoNiTiAlx high-entropy alloy coatings prepared by laser cladding. Coatings 2021, 11, 155.
  26. Wen, X.; Cui, X.; Jin, G.; Liu, Y.; Zhang, Y.; Fang, Y. In-situ synthesis of nano-lamellar Ni1.5CrCoFe0.5Mo0.1Nbx eutectic high-entropy alloy coatings by laser cladding: Alloy design and microstructure evolution. Surf. Coat. Technol. 2021, 405, 126728.
  27. Qiua, X. Microstructure and corrosion properties of Al2CrFeCoxCuNiTi high entropy alloys prepared by additive manufacturing. J. Alloys Compd. 2021, 887, 161422.
  28. Hussien, M.; Walton, K.; Vishnyakov, V. Synthesis and corrosion resistance of FeMnNiAlC10 multi-principal element compound. Materials 2021, 14, 6356.
  29. Rao, S.G.; Shu, R.; Boyd, R.; le Febvrier, A.; Eklund, P. The effects of copper addition on phase composition in (CrFeCo)1−yNy multicomponent thin films. Appl. Surf. Sci. 2022, 572, 151315.
  30. Cai, Z.; Wang, Z.; Yang, W.; Zhang, P.; Lu, Y.; Pu, J. Microstructure and corrosion behavior of AlCrTiV-X (X = Cu, Mo, CuMo) high-entropy alloy films in 3.5 wt.% NaCl solution. Surf. Interf. 2021, 27, 101558.
  31. Peighambardoust, N.S.; Alamdari, A.A.; Unal, U.; Motallebzadeh, A. In vitro biocompatibility evaluation of Ti1.5ZrTa0.5Nb0.5Hf0.5 refractory high-entropy alloy film for orthopedic implants: Microstructural, mechanical properties and corrosion behaviour. J. Alloys Compd. 2021, 883, 160786.
  32. Huang, T.-C.; Hsu, S.-Y.; Lai, Y.-T.; Tsai, S.-Y.; Duh, J.-G. Effect of NiTi metallic layer thickness on scratch resistance and wear behavior of high entropy alloy (CrAlNbSiV) nitride coating. Surf. Coat. Technol. 2021, 425, 127713.
  33. Yang, J.; Zhang, F.; Chen, Q.; Zhang, W.; Zhu, C.; Deng, J.; Zhong, Y.; Liao, J.; Yang, Y.; Liu, N.; et al. Effect of Au-ions irradiation on mechanical and LBE corrosion properties of amorphous AlCrFeMoTi HEA coating: Enhanced or deteriorated? Corros. Sci. 2021, 192, 109862.
  34. Chang, Y.-Y.; Chung, C.-H. Tribological and mechanical properties of multicomponent CrVTiNbZr(N) coatings. Coatings 2021, 11, 41.
  35. Pogrebnjak, A.D.; Bagdasaryan, A.A.; Horodek, P.; Tarelnyk, V.; Buranich, V.V.; Amekura, H.; Okubo, N.; Ishikawa, N.; Beresnev, V.M. Positron annihilation studies of defect structure of (TiZrHfNbV)N nitride coatings under Xe14+ 200 MeV ion irradiation. Mater. Lett. 2021, 303, 130548.
  36. Chen, S.N.; Zhang, Y.F.; Zhao, Y.M.; Yan, W.Q.; Wu, S.; Chen, L.; Pang, P.; Liao, B.; Wu, X.Y.; Ouyang, X.P. Preparation and regulation of AlCrNiTiSi high entropy alloy coating by a multi-arc magnetic filter cathode vacuum arc system. Surf. Interf. 2021, 26, 101400.
  37. Xu, W.; Liao, M.; Liu, X.; Ji, L.; Ju, P.; Li, H.; Zhou, H.; Chen, J. Microstructures and properties of (TiCrZrVAl)N high entropy ceramics films by multi-arc ion plating. Ceram. Int. 2021, 47, 24752–24759.
  38. Voiculescu, I.; Geantă, V.; Vasile, I.M.; Ştefănoiu, R.; Tonoiu, M. Characterisation of weld deposits using as filler metal a high entropy alloy. J. Optoel. Adv. Mater. 2013, 15, 650–654.
  39. Ustinova, A.I.; Demchenkova, S.A.; Melnychenko, T.V.; Skorodzievskii, V.S.; Polishchuk, S.S. Effect of structure of high entropy CrFeCoNiCu alloys produced by EB PVD on their strength and dissipative properties. J. Alloys Compd. 2021, 887, 161408.
  40. Cheng, J.B.; Liang, X.B.; Wang, Z.H.; Xu, B.S. Formation and mechanical properties of CoNiCuFeCr high-entropy alloys coatings prepared by plasma transferred arc cladding process. Plasma Chem. Plasma Process. 2013, 33, 979.
  41. Cheng, J.; Liu, D.; Liang, X.; Xu, B. Microstructure and electrochemical properties of CoCrCuFeNiNb high-entropy alloys coatings. Acta Metall. Sin. 2014, 27, 1031.
  42. Cheng, J.B.; Liu, D.; Liang, X.B.; Chen, Y.X. Evolution of microstructure and mechanical properties of in situ synthesized TiC-TiB2/CoCrCuFeNi high entropy alloy coatings, Surf. Coat. Technol. 2015, 281, 109.
  43. Sudha, C.; Shankar, P.; Rao, R.V.S.; Thirumurugesan, R.; Vijayalakshmi, M.; Raj, B. Microchemical and microstructural studies in a PTA weld overlay of Ni–Cr–Si–B alloy on AISI 304L stainless steel. Surf. Coat. Technol. 2008, 202, 2103.
  44. Chang, L.-S.; Straumal, B.B.; Rabkin, E.; Gust, W.; Sommer, F. The solidus line of the Cu–Bi phase diagram. J. Phase Equil. 1997, 18, 128–135.
  45. Molodov, D.A.; Czubayko, U.; Gottstein, G.; Shvindlerman, L.S.; Straumal, B.B.; Gust, W. Acceleration of grain boundary motion in Al by small additions of Ga. Philos. Mag. Lett. 1995, 72, 361–368.
  46. Chang, L.-S.; Rabkin, E.; Straumal, B.B.; Hoffmann, S.; Baretzky, B.; Gust, W. Grain boundary segregation in the Cu–Bi system. Defect Diffus. Forum 1998, 156, 135–146.
  47. Schölhammer, J.; Baretzky, B.; Gust, W.; Mittemeijer, E.; Straumal, B. Grain boundary grooving as an indicator of grain boundary phase transformations. Interf. Sci. 2001, 9, 43–53.
  48. Rabkin, E.I.; Shvindlerman, L.S.; Straumal, B.B. Grain boundaries: Phase transitions and critical phenomena. Int. J. Mod. Phys. B 1991, 5, 2989–3028.
  49. Straumal, B.B.; Kogtenkova, O.; Zięba, P. Wetting transition of grain boundary triple junctions. Acta Mater. 2008, 56, 925–933.
  50. Straumal, B.; Gust, W.; Molodov, D. Wetting transition on the grain boundaries in Al contacting with Sn-rich melt. Interface Sci. 1995, 3, 127–132.
  51. Straumal, B.B.; Gust, W.; Watanabe, T. Tie lines of the grain boundary wetting phase transition in the Zn-rich part of the Zn–Sn phase diagram. Mater. Sci. Forum 1999, 294–296, 411–414.
  52. Straumal, A.B.; Yardley, V.A.; Straumal, B.B.; Rodin, A.O. Influence of the grain boundary character on the temperature of transition to complete wetting in Cu–In system. J. Mater. Sci. 2015, 50, 4762–4771.
  53. Straumal, B.B.; Gornakova, A.S.; Kogtenkova, O.A.; Protasova, S.G.; Sursaeva, V.G.; Baretzky, B. Continuous and discontinuous grain boundary wetting in the Zn–Al system. Phys. Rev. B 2008, 78, 054202.
  54. Gornakova, A.S.; Straumal, B.B.; Tsurekawa, S.; Chang, L.-S.; Nekrasov, A.N. Grain boundary wetting phase transformations in the Zn–Sn and Zn–In systems. Rev. Adv. Mater. Sci. 2009, 21, 18–26.
  55. Straumal, B.; Muschik, T.; Gust, W.; Predel, B. The wetting transition in high and low energy grain boundaries in the Cu(In) system. Acta Metall. Mater. 1992, 40, 939–945.
  56. Maksimova, E.L.; Shvindlerman, L.S.; Straumal, B.B. Transformation of Σ17 special tilt boundaries to general boundaries in tin. Acta Metall. 1988, 36, 1573–1583.
  57. Ernst, F.; Finnis, M.W.; Koch, A.; Schmidt, C.; Straumal, B.; Gust, W. Structure and energy of twin boundaries in copper. Z. Metallk. 1996, 87, 911–922.
  58. Straumal, B.B.; Kogtenkova, O.A.; Gornakova, A.S.; Sursaeva, V.G.; Baretzky, B. Review: Grain boundary faceting-roughening phenomena. J. Mater. Sci. 2016, 51, 382–404.
  59. Straumal, B.B.; Bokstein, B.S.; Straumal, A.B.; Petelin, A.L. First observation of a wetting transition in low-angle grain boundaries. JETP Lett. 2008, 88, 537–542.
  60. Yasuda, H.Y.; Yamada, Y.; Cho, K.; Nagase, T. Deformation behavior of HfNbTaTiZr high entropy alloy singe crystals and polycrystals. Mater. Sci. Eng. A 2021, 809, 140983.
  61. Nagase, T.; Iijima, Y.; Matsugaki, A.; Ameyama, K.; Nakano, T. Design and fabrication of Ti–Zr-Hf-Cr-Mo and Ti–Zr-Hf-Co-Cr-Mo high entropy alloys as metallic biomaterials. Mater. Sci. Eng. C 2020, 107, 110322.
  62. Eleti, R.R.; Chokshi, A.H.; Shibata, A.; Tsuji, N. Unique high-Temperature deformation dominated by grain boundary sliding in heterogeneous necklace structure formed by dynamic recrystallization in HfNbTaTiZr BCC refractory high entropy alloy. Acta Mater. 2020, 183, 64–77.
  63. Yao, H.; Liu, Y.; Sun, X.; Lu, Y.; Wang, T.; Li, T. Microstructure and mechanical properties of Ti3V2NbAlxNiy low-Density refractory multielement alloys. Intermetallics 2021, 133, 107187.
  64. Yi, J.; Wang, L.; Tang, S.; Yang, L.; Xu, M.; Liu, L. Microstructure and mechanical properties of Al0.5CoCuNiTi high entropy alloy. Philos. Mag. 2021, 101, 1176–1187.
  65. Yi, J.; Tang, S.; Zhang, C.; Xu, M.; Yang, L.; Wang, L.; Zeng, L. Microstructure and mechanical properties of a new refractory equiatomic CrHfNbTaTi high-Entropy alloy. JOM 2021, 73, 934–940.
  66. Nong, Z.; Wang, H.; Wang, D.; Zhu, J. Investigation on structural stability of as-Cast Al0.5CrCuFeMnTi high entropy alloy. Vacuum 2020, 182, 109686.
  67. Du, X.H.; Huo, X.F.; Chang, H.T.; Li, W.P.; Duan, G.S.; Huang, J.C.; Wu, B.L.; Zou, N.F.; Zhang, L. Superior strength-Ductility combination of a Co-Rich CoCrNiAlTi high entropy alloy at room and cryogenic temperatures. Mater. Res. Express 2020, 7, 034001.
  68. Hernández-Negrete, O.; Tsakiropoulos, P. On the microstructure and isothermal oxidation at 800 and 1200 °C of the Nb–24Ti–18Si–5Al–5Cr–5Ge–5Sn (at.%) silicide-Dased alloy. Materials 2020, 13, 722.
  69. Jung, Y.; Lee, K.; Hong, S.J.; Lee, J.K.; Han, J.; Kim, K.B.; Liaw, P.K.; Lee, C.; Song, G. Investigation of phase-transformation path in TiZrHf(VNbTa)x refractory high-Entropy alloys and its effect on mechanical property. J. Alloys Compd. 2021, 886, 161187.
  70. Sun, F.; Zhang, J.Y.; Marteleur, M.; Brozek, C.; Rauch, E.F.; Veron, M.; Vermaut, P.; Jacques, P.J.; Prima, F. A new titanium alloy with a combination of high strength, high strain hardening and improved ductility. Scr. Mater. 2015, 94, 17–20.
  71. Yi, J.; Wang, L.; Xu, M.; Yang, L. Two new 3d transition metals AlCrCuFeTi and AlCrCuFeV high-Entropy alloys: Phase components, microstructures, and compressive properties. Appl. Phys. A 2021, 127, 74.
  72. Mukarram, M.; Mujahid, M.; Yaqoob, K. Design and development of CoCrFeNiTa eutectic high entropy alloys. J. Mater. Res. Technol. 2021, 10, 1243–1249.
  73. Guo, Z.; Liu, R.; Wang, C.T.; He, Y.; He, Y.; Ma, Y.; Hu, X. Compressive Mechanical properties and shock-Induced reaction behavior of a Ti–29Nb–13Ta–4.6Zr alloy. Met. Mater. Int. 2020, 26, 1498–1505.
  74. Jia, Y.; Zhang, L.; Li, P.; Ma, X.; Xu, L.; Wu, S.; Jia, Y.; Wang, G. Microstructure and mechanical properties of Nb–Ti–V–Zr refractory medium-entropy alloys. Front. Mater. 2020, 7, 172.
  75. Petroglou, D.; Poulia, A.; Mathiou, C.; Georgatis, E.; Karantzalis, A.E. A further examination of MoTaxNbVTi (x = 0.25, 0.50, 0.75 and 1.00 at.%) high-Entropy alloy system: Microstructure, mechanical behavior and surface degradation phenomena. Appl. Phys. A 2020, 126, 364.
  76. Zhao, J.; Utton, C.; Tsakiropoulos, P. On the microstructure and properties of Nb-12Ti-18Si-6Ta-2.5W-1Hf (at %) silicide-Based alloys with Ge and Sn additions. Materials 2020, 13, 1778.
  77. Wei, Q.; Luo, G.; Zhang, J.; Jiang, S.; Chen, P.; Shen, Q.; Zhang, L. Designing high entropy alloy-Ceramic eutectic composites of MoNbRe0.5TaW(TiC)x with high compressive strength. J. Alloys Compd. 2020, 818, 152846.
  78. Xiang, C.; Fu, H.M.; Zhang, Z.M.; Han, E.-H.; Zhang, H.F.; Wang, J.Q.; Hu, G.D. Effect of Cr content on microstructure and properties of Mo0.5VNbTiCrx high-Entropy alloys. J. Alloys Compd. 2020, 818, 153352.
  79. Edalati, P.; Floriano, R.; Mohammadi, A.; Li, Y.; Zepon, G.; Li, H.-W.; Edalati, K. Reversible room temperature hydrogen storage in high-Entropy alloy TiZrCrMnFeNi. Scr. Mater. 2020, 178, 387–390.
  80. Xiao, D.H.; Zhou, P.F.; Wu, W.Q.; Diao, H.Y.; Gao, M.C.; Song, M.; Liaw, P.K. Microstructure, mechanical and corrosion behaviors of AlCoCuFeNi-(Cr,Ti) high entropy alloys. Mater. Des. 2017, 116, 438–447.
  81. Döleker, K.M.; Erdogan, A.; Zeytin, S. Laser re-Melting influence on isothermal oxidation behavior of electric current assisted sintered CoCrFeNi, CoCrFeNiAl0.5 and CoCrFeNiTi0.5Al0.5 high entropy alloys. Surf. Coat. Technol. 2021, 407, 126775.
  82. Cui, W.; Li, W.; Chen, W.-T.; Liou, F. Laser Metal Deposition of an AlCoCrFeNiTi0.5 High-entropy alloy coating on a Ti6Al4V substrate: Microstructure and oxidation behavior. Crystals 2020, 10, 638.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Mechanical
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Boris Straumal
,
Anna Korneva
,
Alexei Kuzmin
,
Leonid Klinger
,
Gabriel A. Lopez
,
Nikolai Vershinin
,
Alexander Straumal
,
Alena Gornakova
View Times: 515
Revisions: 2 times (View History)
Update Date: 26 Oct 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback