Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Savino Longo
 + 4975 word(s) 4975 2022-03-10 09:15:10 |
2 format correct
Vivi Li
 + 65 word(s) 5040 2022-03-17 02:29:20 | |
3 format correct
Vivi Li
 -12 word(s) 5028 2022-03-18 05:13:44 | |
4 format correct
Vivi Li
 Meta information modification 5028 2022-03-18 06:54:14 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Longo, S. Plasma Modeling and Prebiotic Chemistry. Encyclopedia. Available online: https://encyclopedia.pub/entry/20658 (accessed on 15 November 2024).
Longo S. Plasma Modeling and Prebiotic Chemistry. Encyclopedia. Available at: https://encyclopedia.pub/entry/20658. Accessed November 15, 2024.
Longo, Savino. "Plasma Modeling and Prebiotic Chemistry" Encyclopedia, https://encyclopedia.pub/entry/20658 (accessed November 15, 2024).
Longo, S. (2022, March 16). Plasma Modeling and Prebiotic Chemistry. In Encyclopedia. https://encyclopedia.pub/entry/20658
Longo, Savino. "Plasma Modeling and Prebiotic Chemistry." Encyclopedia. Web. 16 March, 2022.
Plasma Modeling and Prebiotic Chemistry
Edit
This entry is adapted from the peer-reviewed paper 10.3390/molecules26123663

The plasma kinetics involves elementary processes by which free electrons ultimately activate weakly reactive molecules, such as carbon dioxide or methane, thereby potentially starting prebiotic reaction chains. These processes include electron–molecule reactions and energy exchanges between molecules. They are basic processes, for example, in the famous Miller-Urey experiment, and become relevant in any prebiotic scenario where the primordial atmosphere is significantly ionized by electrical activity, photoionization or meteor phenomena. The kinetics of plasma displays remarkable complexity due to the non-equilibrium features of the energy distributions involved.

Miller-Urey experiment prebiotic chemistry plasma kinetics electrons prebiotic molecules

1. Introduction

Earth’s chemical history and the origin of life are two of the most crucial topics in astrochemistry and astrobiology [1][2][3][4]. Two main theories [5][6] have been proposed regarding the emergence of life on Earth: (i) exogeneous delivery and (ii) endogenous synthesis. According to the first theory, prebiotic molecules have reached the Earth’s surface by means of comets, meteors and asteroids. The so-called delivery, that is, the actual transport of molecules from space to Earth, represents the key point of the Panspermia theory [7][8][9][10][11]. It was demonstrated that carbonate and sulfate micrometeoroids (especially calcite and anhydrite) may act as good prebiotic molecule carriers [12][13][14], in view of the well-known association between carbonates/sulfates and organic matter presence [15][16][17][18]. Recently, the role of the chemical composition of the primordial atmosphere was pointed out, in the context of the atmospheric entry of the aforementioned carbonate and sulfate micrometeoroids [19].
On the other hand, the endogenous synthesis approach, developed in the 1950s and 1960s, speculates that primordial atmospheres of terrestrial planets were filled up with methane, ammonia and hydrogen, and it theorizes that the primordial clouds provide the necessary chemical and energetic conditions to activate small molecules and link them into bigger molecules, in order to synthesize the building blocks of life. The topic of early Earth’s atmosphere as a source of prebiotic matter comes from the Miller-Urey experiments [20][21][22], partially modeled on Oparin’s hypothesis of reducing primordial atmosphere [23]. So, the endogenous theory states that the synthesis of organic molecules occurred directly on Earth starting from simple parent molecules. Actually, a third theory concerning the origins of life has been proposed, related to the production of organic molecules and even amino acids in hydrothermal vents [24].
Miller-Urey’s experimental apparatus (left side of Figure 1) consisted of two glass flasks: the lower one was partially filled with liquid water—to mimic the primordial ocean—, and a gas mixture composed of methane, ammonia and hydrogen—reproducing the primordial atmosphere—filled the other balloon. In this primordial gas, Miller placed two electrodes to simulate a lightning-like electric discharge. Therefore, Miller and Urey recreated the disequilibrium chemistry conditions by applying an electrical discharge to the gases, which probably formed a highly reducing primordial atmosphere. The two flasks in the apparatus were connected in a hydrological cycle, which allowed it to mimic rain after the electrical discharge. The analyses demonstrated that, after the experiment, the primordial ocean was rich in carbon compounds, which contained significant amounts of amino acids. Miller and Urey demonstrated that organic molecules can form spontaneously from inorganic components, in such primordial reducing environments. It can be stated that the Miller-Urey experiment is the first abiotic synthesis of organic compounds, under simulated primordial Earth conditions, in the context of the studies on the origin of life.
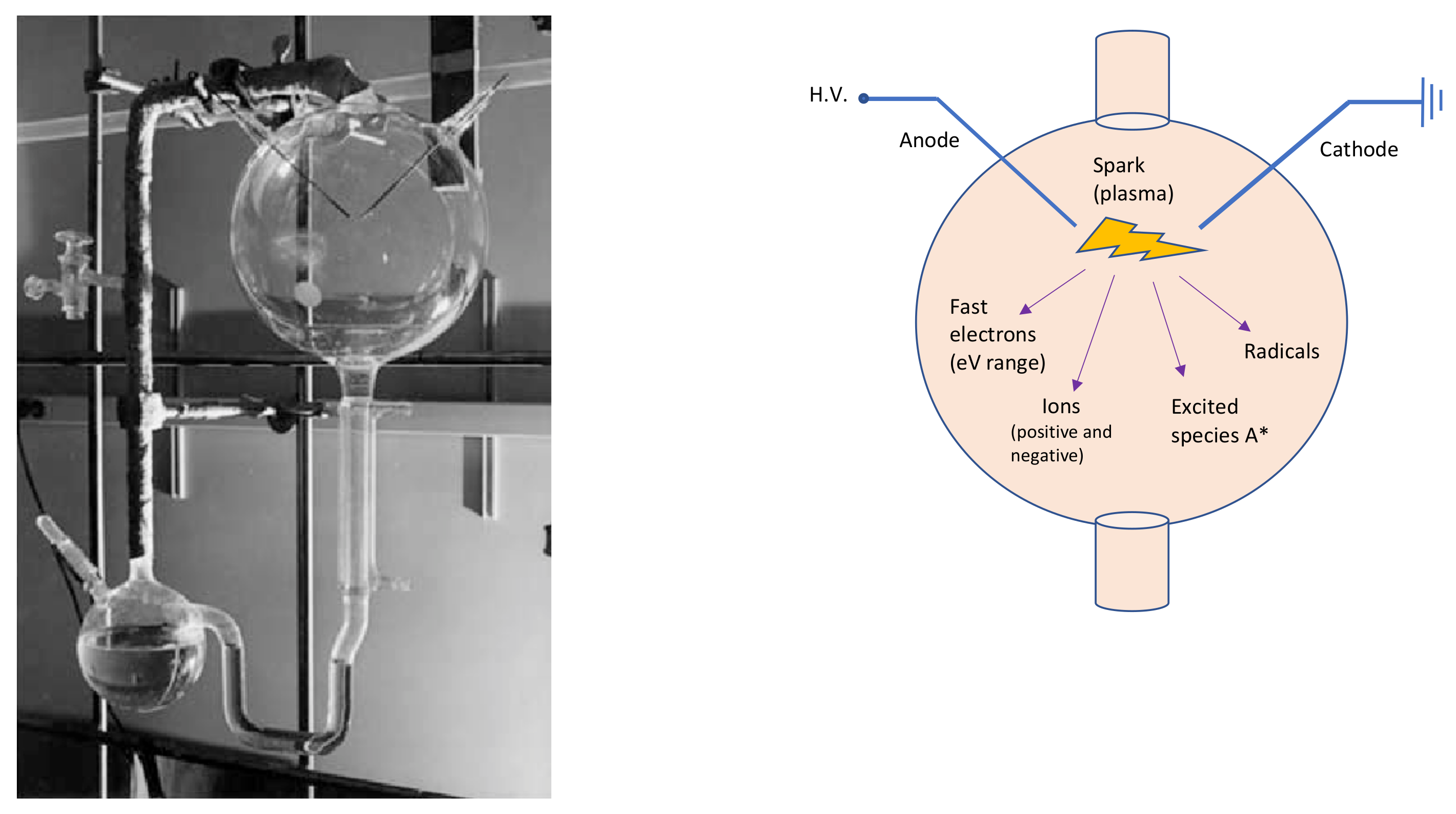
Figure 1. On the left, the Miller-Urey experimental apparatus. The lower flask contains the primordial ocean model, while, through the gas inlet/outlet on the right, the rest of the apparatus is filled with the strongly reducing primordial atmosphere, based on the knowledges of Miller’s times. The third neck of the lower flask is used to sample the liquid for analysis. The higher balloon displays the spark gap. Photo adapted from [25]. On the right, a schematic sketch of the upper glass flask. A* symbolizes the excited species.
Although recent progress in astrochemistry and astrobiology suggests a role of increasing importance of the activation process by UV radiation and shock waves [26][27], the following considerations must be taken into account: (i) The Miller-Urey experiment represents a milestone in prebiotic chemistry, from the conceptual, historical and pedagogical point of view; therefore, a better understanding of the experiment can add new interesting results in prebiotic studies; (ii) The chemical activation by shock waves, like that produced by meteors, proceeds, in the case of high Mach numbers, through the ionization of the gas. Fast energy electrons are still responsible for the chemical activation of the neutral gas. A better understanding of the Miller-Urey experience phenomenology can also help, therefore, in the scenarios of chemical activation by shock waves; (iii) The activation mechanism by electric discharge needs to be better understood in light of the growing knowledge of electrical phenomena in planetary atmospheres, such as those of Venus and Titan.
With respect to the studies carried out in the few years following Miller experiment, considerable progress has been made in terms of theoretical and methodological understanding (see [28][29] and references therein). Moreover, hypotheses regarding the composition of the primordial terrestrial atmosphere have changed considerably.
The composition and depth of the primordial atmosphere are the subject of a lively debate in the planetology community. Dating back to Oparin [23] and Haldane [30], most scientists believe that, at the very least, the primordial atmosphere was enriched in reducing low-molar-mass components (methane, ammonia and even hydrogen). Additionally, there is no reason to assume that an early Earth atmosphere (a mixture of components with very different molar mass, like nitrogen and hydrogen) should have uniform composition in its lower and upper regions: probably, the early atmosphere was enriched in low mass components at high altitudes.
Hypotheses regarding the chemical composition of the Earth’s earliest atmosphere are numerous. Moreover, it is believed that there were many atmospheres over the vastness of Earth’s geological time [31]. Geologically based argumentations, that treat the atmosphere as outgassed from solid Earth, indicate that the Earth’s primitive atmosphere was composed mostly of H2O, CO2 and N2, with traces of CO and H2 [32][33][34].
Since the 1980s, geoscientists have been disputing Miller’s hypothesis of highly reducing primordial atmosphere [35]. Many experiments were carried out using CO and CO2 atmospheres [36][37], showing that a CO-dominant atmosphere might have produced organic compounds; however, the synthesis of organic compounds by the action of electric discharges in neutral gas mixtures is much less efficient, in this case. Results presented by Cleaves et al. [38] demonstrated that neutral atmospheres can produce amino acids in much higher amount than previously thought. A complete and exhaustive review about the origin and conditions of the Earth’s earliest atmospheres can be found in the work by Zahnle et al. [39], with particular attention to the issue concerning the origin of life (∼4.6–4 Gys ago).
Under the hypotheses that the primordial Earth’s atmosphere consisted predominantly of CO and CO2, the chemical channels previously considered for a reducing atmosphere (based on the preliminary production of the highly reactive HCN molecule) must be reformulated and subjected to new studies, bearing in mind that other components, even minority ones, can play a role in subsequent chemical reactions. Although theoretical studies on the CO and CO2 system in the context of the Miller-Urey experiment are advanced [40][41][42], one aspect of these studies is still rather primitive, namely the role of electrons in the plasma (a word indicating an ionized gas introduced by I. Langmuir [43]) in producing the first excited and radical species and ions, which later enter several chemical channels to form prebiotic molecules. Studies of chemical kinetics performed in the case of gas discharges with chemical composition enormously simpler than the one used in Miller-type experiences have shown that ionization and excitation processes have an extremely complex and interesting kinetics. These studies show that the efficiency of radical formation can be much greater than the one observed in the much more phenomenological studies devoted to Miller’s experience so far.
Several studies actually considered the chemical activation via plasma electron of planetary atmospheric compositions with a prebiotic perspective. For example, plasma chemistry has been studied in electric discharges fed with chemical compositions compatible with the present atmosphere of Titan [44][45][46][47][48] and for Venus and Jupiter atmospheres [49].
Titan resembles the terrestrial planets, and particularly Earth, as it is the only other body in our solar neighbourhood with liquid reservoirs on its surface. The familiar role of water in our atmosphere is replaced by methane, which survives as a liquid at the extremely low temperature conditions at the surface (−180 ∘C). The scheme in Figure 2 reports the chain of reactions of prebiotic chemistry in Titan atmosphere.
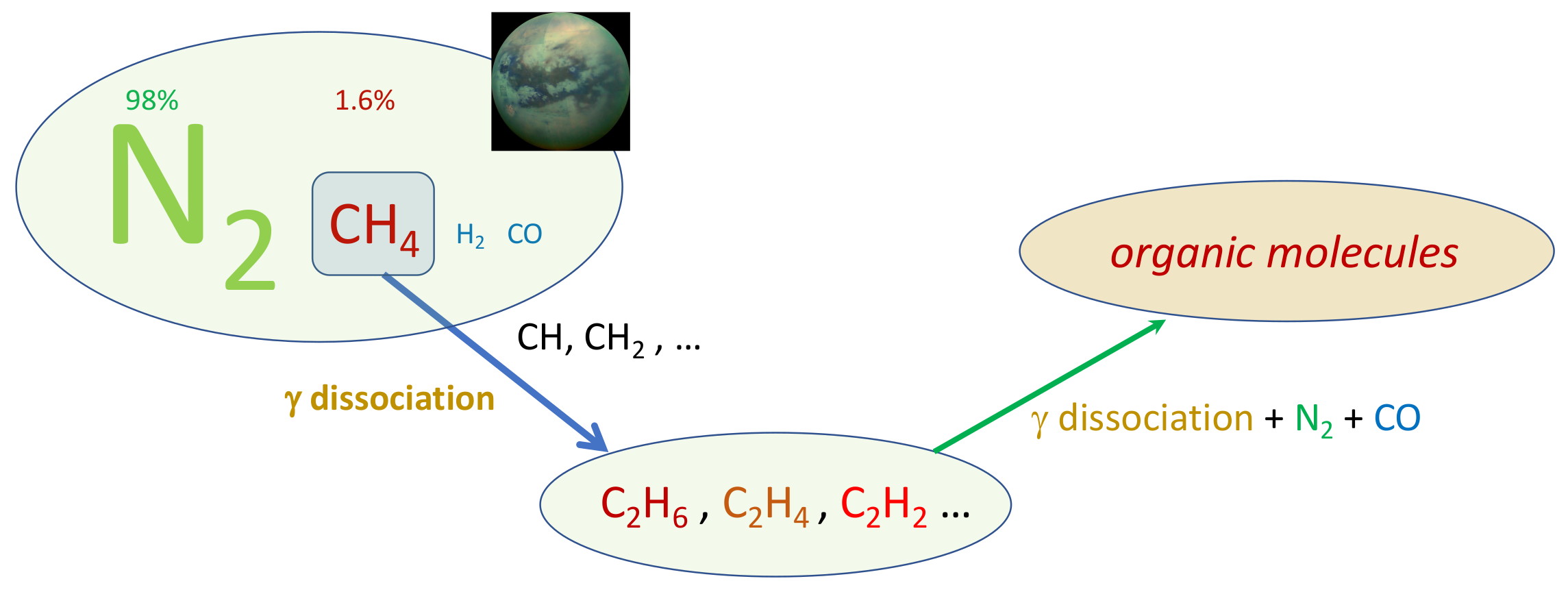
Figure 2. Prebiotic chemistry in Titan atmosphere.
The fact that plasma chemistry might be relevant to the interpretation of the Miller-Urey experience was mentioned in the 1978 Libby review [50]: in particular, this review discusses the capacity of the methyl cation CH+3, formed by the ionization of methane, to produce higher organic species by ion-neutral reactions. At that time, however, there was no possibility to model the kinetics of complex molecular plasma like ionized methane. This was developed more recently, mostly for the study of material science processes where CH4 is ionized in order to ultimately fix carbon into diamonds [51][52], or carbon nanotubes [53].
All these considerations lead to the the idea of exploring prebiotic molecular mechanisms in the early stages of the production of new chemical species from a plasma kinetics point of view, highlighting therefore the importance of electrons and excited molecules in chemical channels.

2. Tools from Plasma Kinetics

Plasma kinetics is the study of chemical reaction rates in ionized gases [54]. It is a very active field of study with many applications in microelectronics, aerospace, medicine and astrochemistry, just to name a few. Thanks to many previous studies [55][56][57], researchers have knowledge of the physical conditions of a plasma associated with natural phenomena, such as for example lightning discharges.
Plasma kinetics was born with the intent to understand more quantitatively the physics of systems with a considerable degree of non-equilibrium, in particular ionosphere chemistry. Over time, it has developed its own calculation and prediction methods, principally coming from statistical mechanics, which are very specialized with respect to those used in chemical kinetics of gases and in chemical kinetics in general.
In such non-equilibrium (sometimes called “low-temperature”, or “cold”) plasmas, electrons have a much greater kinetic energy (from few eV to few tens of eV) than that of atomic and molecular neutral species, and distributions of speed and energy are not trivial. These peculiarities are produced by energy flows and energy exchanges within the system, whose main origin is the acceleration of electrons (and, to a lesser extent, of ions) by the electric field; the electric field is applied to the plasma by means of two electrodes at different electrical potential. Electrons maintain a high average energy because of the slow processes of dissipation of electronic kinetic energy, due to the unfavorable mass-ratio between electrons and other species (which slows down energy transfer in elastic collisions), and the small cross sections for inelastic processes (compared to the corresponding elastic ones). The energy distribution of free electrons is therefore a complex function that cannot be reduced to the Maxwell-Boltzmann distribution, as normally assumed in the chemical kinetics of gases. This is of paramount importance, because the violation of the Maxwell-Boltzmann distribution rules out the renowned Arrhenius law, used in kinetic studies of prebiotic processes.
In view of the knowledge produced in plasma science, there is little doubt that the earlier studies on the kinetics of the Miller-Urey experience must be reconsidered. The primary chemical activation of the gas is associated with chemical dissociation and ionization of small monomers molecules present in the original Miller-Urey mixture and modern variants: these molecules are CO2, CO, H2, NH3, CH4, H2O, NO, and a few others. While a huge number of studies has been produced concerning chemical reactions of activated monomers to produce amino acids, aldehydes and sugars, very little has been studied in the direction of a better understanding of the primary chemical activation. In this process, the presence of high energy free electrons (whose share is to be determined), fast ions, quantum mechanics and statistical mechanics of activation are new fields where progress occurs on a month-by-month basis.
Very effective deterministic, stochastic and hybrid methods have been developed over the years to determine the electron energy distribution, typically as a function of the reduced electric field Ɛ/N (Ɛ is the magnitude of the electric field, N is the gas number density) and the neutral gas composition [58][59][60][61][62][63][64][65][66]. The strong gap between the average energy of the electronic component and that of the neutral component leads in turn to a chemical kinetics that requires adequate models, so far not very much used outside plasma electronics, aerospace and a few studies on the chemistry of the interstellar medium. These models root in the determination of reaction channels following the flow of energy provided by free electrons, which constantly produces reactive species such as ions, free radicals and excited states of atoms and molecules. Such a state-of-the-art entails concrete possibilities that the know-how implemented and validated in the field of plasma kinetics can lead to remarkable results if applied to the study of those systems in astrobiology where similar circumstances are met. Taking into account specifically the chemical peculiarities of Miller-Urey’s experience, particularly in the new formulations that are emerging, these aspects will be illustrated in the following sections by means of two case studies, which, however, only aim to represent a small example of the great variety of useful research that can be performed on the same basis.

3. Kinetics of Molecular Activation by Plasma Electrons

The theoretical study of reaction rates involving molecules has progressed remarkably since the first formulation of Miller-Urey’s experience. A particularly important technique, developed in parallel in plasma kinetics and in astrophysics, is the so-called state-to-state (STS) approach. In this formulation of chemical kinetics, the individual excited levels of molecules are treated as individual species, with their own characteristic reaction data. The STS is able to comply with the fact that the specific reaction rates of the different excited states of most molecules may differ by orders of magnitude. Furthermore, the distribution of populations of the different levels in a system far from equilibrium, such as a cold plasma, can differ considerably from the results obtained in statistical mechanics applied to equilibrium systems, that is, the Boltzmann distribution.
As a result, the mole fraction of tens or hundreds, sometimes thousands, of individual “components”, χi, must be calculated by solving extended systems of ordinary differential equations (ODE’s) of the form
d d t χ i = R i ( χ j ) ,
(1)
addressed in this context by the term Master Equation (ME). Ri is the reaction rate for the i-th STS component, which is a function potentially of all of the χ’s: it includes many terms describing elementary reactions between STS components. The ME is tricky to solve accurately, since the different contributions to its r.h.s. may differ by orders of magnitude, making the system of ODEs so-called “stiff” in computational terms. Nevertheless, many fruitful and concrete applications of this approach have been demonstrated for reactive fluids, lasers and electric discharges [67][68][69][70][71][72].
An example is provided by the chemical activation of CO2, which is a very stable molecule, often abundant in the atmospheres of rocky planets. It appears that some processes, under the conditions of a primordial atmosphere, can activate chemically this molecule with the help of physical energy in the form of, for example, kinetic energy of the free electrons. In this respect and in recent years, great progress has been made in the theoretical understanding of the chemical plasma activation of CO2, due to the importance that this process plays in the CO2 recycling study for the mitigation of the climatic consequences of CO2 accumulation in the atmosphere [73][74].
Since the most effective dissociation path of CO2 is through the asymmetric stretching vibrational mode, it is necessary to distinguish the 22 vibrational levels of this mode [73]. Electron-impact vibrational excitation processes, the so-called “eV-processes”, however, can only pump energy into the lowest vibrational levels, say the first 4 or 5, because cross sections of the direct excitation of higher levels are very low:
e + CO 2 ( v ) → e + CO 2 ( v + 1 ) .
(2)
Subsequently, CO2 molecules reach the dissociation limit with the help of a different process, named VV1, where a vibrationally excited CO2 molecule interacts with a more excited one pushing it to higher excitation:
CO 2 ( v = 1 ) + CO 2 ( w ) → CO 2 ( v = 0 ) + CO 2 ( w + 1 ) . (3)
The mechanism in Equation (3), proposed by Russian scientists about 40 years ago [75], pushes molecules up the internal energy ladder until they reach the dissociation threshold, i.e.:
CO 2 ( v = 1 ) + CO 2 ( w = 21 ) → CO 2 ( v = 0 ) + CO + O . (4)
The process described by the reactions in Equations (2)–(4) is extremely effective in increasing the efficiency of activation, since the direct dissociation channel with electronic states as intermediates has an energetic cost in the order of 10 eV, whereas the energy cost for vibrational excitation is less than 1 eV.
In the last few years, many researchers, including two authors of the present entry, aimed to achieve a better understanding of this mechanism using computer simulations. For example, a recent scheme is based on the characterization of the upwards flux in energy space, J [76][77][78]. J is a functional of the function f(ϵ), which is the distribution of molecules according to their internal energy ϵ. The theoretical basis of this approach is the relative smallness of energy difference between consecutive vibrational quantum states compared with the binding energy for the majority of molecules; that is, in many molecules the vibrational levels for a given electronic curve are numerous. For example, in the case of the nitrogen molecule, they are around 50 for the electronic ground state, depending on the potential energy curve assumed; a lower number, 15, holds for the hydrogen molecule. Most of the chemical processes between excited vibrational levels involve the exchange of no more than one quantum. Researchers are therefore in the transition/continuum regime as schematically represented in Figure 3. Consequently, it is possible to formulate the problem by means of a diffusion equation, or more generally of a drift and diffusion equation, that is the Fokker-Planck equation:
∂ f ∂ t = − ∂ a 1 ( ϵ ) f ∂ ϵ + 1 2 ∂ 2 a 2 ( ϵ ) f ∂ ϵ 2 . (5)
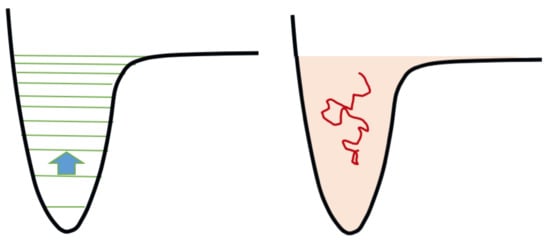
Molecules 26 03663 g003 550
Figure 3. Symbolic representation of the state-to-state chemical kinetics and its equivalent in the continuum. On the left, the arrow represents a one-quantum collisional transition between two consecutive levels. On the right: the level manifold is approximated by a continuum of energy, the kinetics is sampled by Brownian motions, the energy transport is drift-diffusive. Drawing adapted from [76].
It has been shown [76][77][78] that the two transport coefficients in Equation (5), namely the two jump moments a1(ϵ) and a2(ϵ), can be calculated starting from the rate coefficients of the chemical reactions involving the different vibrational states. The calculation is not simple and the use of formulas requires the evaluation of numerous data; nevertheless the calculation is possible and produces results that are reliable and comparable with those based on the explicit discretization of the internal energy. However, discretization requires very long computational times and can hardly be applied to future theoretical formulations of Miller’s experience, especially considering that in this experience complex species formed starting from monomers with numerous levels of internal energy are also involved.
The mathematics of diffusion, namely the continuity equation of the flux through the internal energy space, demonstrates that, at steady-state, the aforementioned flux functional J, whose expression is:
J = b ( ϵ ) f ( ϵ ) − D ( ϵ ) ∂ f ∂ ϵ , (6)
where the internal energy drift b(ϵ) and diffusion D(ϵ) coefficients are:
b ( ϵ ) = a 1 − 1 2 ∂ a 2 ∂ ϵ , D ( ϵ ) = 1 2 a 2 ( ϵ ) , (7)
is a constant, that is, it does not depend on the internal energy ϵ. Furthermore, it can be shown that J[f] is the dissociation rate. f(ϵ) can be easily calculated by solving the Fokker-Planck equation based on rate coefficients of vibrational processes and the known value of J [78]. But, since J needs f to be calculated, the process is iterated until J is self-consistency attained, and the problem is solved. The behavior of f as a function of J can provide additional insight into the process of molecular dissociation. This is shown in the plots in Figure 4, which are based on calculations of the described type: in all cases, on the x-axis researchers set the internal energy, which goes from the value 0, corresponding to the zero-point energy of the quantum oscillator that describes the asymmetric stretching motion, to the dissociation energy. The plotted functions are precisely the internal energy distributions. The two plots differ in the value of Tv, the excitation temperature of the 0→1 transition.
Figure 4. Calculated vibrational distribution function of CO2 molecules based on the functional method J[f] described in the text, in the case of a lower vibrational temperature Tv=0.19 eV (a) and an higher one Tv=0.25 eV (b). In the low Tv case, the vibrational distribution has strong impact on the dissociation rate J. In the higher Tv case, J becomes rather insensitive to the vibrational distribution. Figure adapted from [77].
Comparing the plot on the left in Figure 4 (lower temperature) with the one on the right (higher temperature) and observing the values of J corresponding to the different curves shown in each of the two figures, two completely different behaviors can be observed. While in the case of the lower temperature, the function can only be modified with considerable variations of the functional J, in the case of high temperature, completely different energy distributions are obtained for very small variations of the functional J. On the one hand, the low-temperature case exemplifies that the energy distribution determines the dissociation rate, especially in the high-energy region, which is closer to where the dissociation takes place. On the other hand, in the high temperature case, a regime is realized in which the functional J, and therefore the dissociation rate of the molecules, changes very little even in the hypothesis of large variations of the high energy part of the distribution.
This last result is very important in a reconsideration of the Miller-Urey experiment with an atmosphere rich in CO2. In such an atmosphere, locally produced plasmas may produce radicals from CO2 with a very high energetic efficiency, which was unforeseeable at Miller’s times.
A similar synergistic mechanism could speed up considerably the dissociation of other molecules relevant to modern studies of planetary atmospheres in a prebiotic perspective: one of those is methane (CH4). A continuum model for the internal energy flux in methane is completely lacking at present, but it is within reach of the present knowledge and methods and could advance the understanding of prebiotic chemistry, again, with the help of methods from plasma kinetics.
As regards electron kinetics, the characterization of the distribution of free electrons is fundamental to describe the thermodynamic state and its departure from equilibrium [65]. From the distribution function, it is also possible to calculate macroscopic quantities, such as electron swarm parameters [79], and electron impact rate coefficients. To calculate the electron distribution function, it is necessary to solve the Electron Boltzmann Equation (EBE). Several codes are available as open-source for calculation of the Electron Velocity Distribution Function (EVDF). Most of them are based on the two-term expansion of the EVDF in Legendre polynomials, such as BOLSIG+ [64] and LoKI-B [80]. At the expenses of computational time, other codes employ different numerical methods based on multi-term expansion of the EVDF in Legendre polynomials (e.g., the MultiBolt code [81]) and Monte Carlo (MC) simulations (e.g., the METHES code [82]), in order to obtain more accurate calculations.
Recently, a code based on the Monte Carlo Flux (MCF) method [59] has been implemented and benchmarked by some of the present authors against two-term and multi-term Boltzmann solvers [66][83]. The MCF method provides detailed calculations of the EVDF through a variance reduction technique, that provides a highly computationally efficient solution of the electron transport problem, compared with conventional MC simulations. In MCF, the phase space of electrons is partitioned into cells, and the problem of electron transport is reformulated in the following form [65]:
n i t + Δ t = ∑ j q j i ( Δ t ) n j ( t ) − n i ( t ) ∑ j q i j ( Δ t ) , (8)
where ni(t) is the number of electrons in the i-th cell at time t, Δt is the MC time step for calculation of the transition probabilities qij(Δt). Hence, a set of MC simulations is performed to calculate the coefficients qij by placing systematically sample electrons in the i-th cell and collecting the number of electrons in any j-cell after a time Δt [65] (Figure 5).
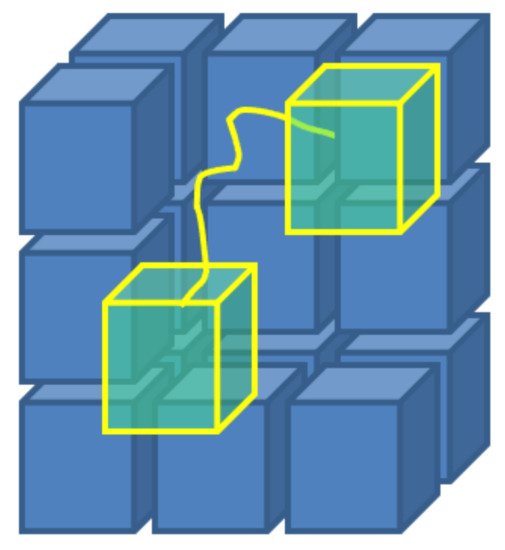
Molecules 26 03663 g005 550
Figure 5. A scheme of the concept behind the Monte Carlo Flux method: stochastic simulations, that take place in the phase space, allow to calculate the transition frequencies qij between sub-regions of the same phase space, obtained by arbitrary partition.
Then, the time evolution of the electron distribution is obtained by an iterative solution of Equation (8). As an alternative, the steady-state solution can also be calculated by means of an eigenvalue method [59]. The advantage of MCF is that it can calculate EVDFs with uniform statistical accuracy in low density regions that cannot be treated by the MC method. Moreover, in [83], the MCF method has also been extended to take into account the thermal velocity distribution function of gas molecules, together with an accurate description of rotational and vibrational excited states for a pure CO2 gas.
In the present entry, MCF has been employed for simulations of electrons in mixtures of gases representative of the composition of the primordial Earth atmosphere [84]. In particular, two different compositions have been analyzed:
  • A highly reduced mixture of gases including CH4, NH3 and H2O, with molar fractions of 0.7, 0.2 and 0.1, respectively. This composition is taken as representative of Miller-Urey-type experiments and it has also been considered in recent experimental investigation by Scherer and co-authors [85].
  • A mildly reduced mixture of gases dominated by N2 and CO2, with traces of CO, H2O and H2. The molar fractions of the gases are 0.7 for N2, 0.2 for CO2, 0.05 for H2O, 0.025 for CO and for H2. This composition is representative of a prebiotic Earth atmosphere (around 3.8 Gy) at sea level, as suggested in the pioneering study by Kasting [35]. At higher altitudes, traces of O2 and O are also formed from photo-dissociation of CO2 [35]. 
Here, the cross sections sets that are used as input for the simulations are illustrated for each gas. In this work, researchers include also superelastic collisions from vibrational states, i.e., collisions of electrons with excited states leading to de-excitation. The cross sections for these processes have been calculated with the formula of Klein-Rosseland [86].
  • Methane: Cross sections for CH4 are taken from the Magboltz code version 11.9 developed by Biagi [87].
  • Ammonia: Cross sections for NH3 are taken from the Hayashi database of the LXCat database [88].
  • Water vapour: Cross sections for H2O are taken from Biagi’s code Magboltz version 11.9 [87].
  • Carbon dioxide: Electron impact cross sections for CO2 are taken from the Biagi database of LXCat [89]. The elastic momentum transfer cross sections from the Biagi database is corrected to take into account the population of vibrational bending mode levels and quadrupole rotational collisions, according to Vialetto and co-authors [83].
  • Carbon monoxide: Electron impact cross sections for CO are the ones from the Magboltz source code v 11.9 [87]. In [90], this set has been used for calculations of electron transport parameters in CO, with particular focus on the treatment of dipole rotational collisions. A Morse anharmonic oscillator is used for calculations of the energy of vibrational states, whereas a rigid rotator model is assumed for rotational levels [91].
  • Hydrogen: Electron impact cross sections for H2 are taken from the IST-Lisbon database of LXCat [92].
  • Nitrogen: Electron impact cross sections for N2 are taken from the IST-Lisbon database of LXCat [92].
MCF simulations have been performed for different values of the reduced electric field, namely 0.1, 10, 20 and 50 Td (1 Td = 10−21 V m2). The population of rotational and vibrational levels is calculated according to a Boltzmann distribution at 300 K. Zeroth (f0) and first order (f1) Legendre polynomials coefficients calculated from MCF are shown in Figure 6 for the highly reduced and mildly reduced mixture of gases.
Figure 6. Zeroth (solid line) and first order (dashed line) Legendre polynomials coefficients calculated from MCF at different reduced electric fields for (a) a highly reduced composition of gases, including CH4, NH3 and H2O in a ratio of 0.7:0.2:0.1 and (b) a mildly reduced composition of gases, including N2, CO2, CO, H2O and H2 in the ratio of 0.7:0.2 for N2/CO2 with traces of CO, H2O and H2 in fractions of 0.05, 0.025 and 0.025, respectively.
In both conditions, the simulated EEDFs show strong deviations from a Boltzmann equilibrium distribution, due to the several electron–molecules interactions that are taken into account. In particular, in Figure 6a, an energetic tail of the EEDF is obtained for energies above 1 eV. This is due to the presence of a deep Ramsauer-Townsend minimum in the elastic momentum transfer cross section of CH4, that is the dominant gas of this mixture. For energies lower than 1 eV, electron impact rotational collisions with water molecules are dominant and lead to a peak in the body of the EEDFs. In Figure 6b, a more structured EEDF is obtained with the presence of plateaux and drops in the distributions. This feature is typical of molecular gases, such as N2 and CO2, that present resonant vibrational processes. In fact, those inelastic processes act as a sharp barrier that electrons have to overcome to reach higher energies [91]. Moreover, in this case, the magnitude of the first Legendre polynomial coefficient of the EVDF expansion (f1) is comparable with the zeroth order one (f0). This indicates that the popular two-term approximation that is employed in many codes (e.g., in [64][80]) would not be accurate for calculations of steady-state EVDFs.
In both cases, the calculated distribution of kinetic energy differs by orders of magnitude, in specific regions, from the Maxwell Boltzmann distribution. Researchers therefore already have the certainty, in extreme cases of composition, that the calculation of the specific reaction rates performed with traditional methods of the primary processes of Miller experience is totally inadequate.
To summarize, calculations show that: (i) a strong deviation from the equilibrium distributions is obtained considering both a Miller-Urey-type composition of gases and a more realistic primordial Earth atmosphere; (ii) computationally efficient calculations can be performed using MCF, where great details are included in the molecular physics of vibrational and rotational states; (iii) consistent and complete sets of cross sections can be gathered from the literature to study the electron kinetics in gas mixtures relevant for the interpretation of Miller-Urey’s experiment as well as its modern variants.
Future work should be focused on coupling the MCF method with other codes that calculate the non-equilibrium vibrational distribution function of the molecules, such as the Fokker-Planck method that has been introduced before.

References

  1. Chang, S.; DesMarais, D.; Mack, R.; Miller, S.; Strathearn, G. Prebiotic Organic Syntheses and the Origin of Life, in Earth’s Earliest Atmospheres; Princeton University Press: Princeton, NJ, USA, 1983; pp. 53–92.
  2. Lazcano, A.; Miller, S.L. The origin and early evolution of life: Prebiotic chemistry, the pre-RNA world, and time. Cell 1996, 85, 793–798.
  3. Miller, S.L.; Cleaves, H.J. Prebiotic chemistry on the primitive Earth. Syst. Biol. 2006, 1, 1.
  4. Ehrenfreund, P.; Rasmussen, S.; Cleaves, J.; Chen, L. Experimentally tracing the key steps in the origin of life: The aromatic world. Astrobiology 2006, 6, 490–520.
  5. Chyba, C.; Sagan, C. Endogenous production, exogenous delivery and impact-shock synthesis of organic molecules: An inventory for the origins of life. Nature 1992, 355, 125–132.
  6. Bernstein, M. Prebiotic materials from on and off the early Earth. Philos. Trans. R. Soc. B Biol. Sci. 2006, 361, 1689–1702.
  7. Maurette, M.; Brack, A.; Kurat, G.; Perreau, M.; Engrand, C. Were micrometeorites a source of prebiotic molecules on the early Earth? Adv. Space Res. 1995, 15, 113–126.
  8. Ehrenfreund, P.; Irvine, W.; Becker, L.; Blank, J.; Brucato, J.; Colangeli, L.; Derenne, S.; Despois, D.; Dutrey, A.; Fraaije, H.; et al. Astrophysical and astrochemical insights into the origin of life. Rep. Prog. Phys. 2002, 65, 1427.
  9. Burchell, M.J. Panspermia today. Int. J. Astrobiol. 2004, 3, 73–80.
  10. Coulson, S. On panspermia and the survivability of micrometre-sized meteoroids within the Earth’s atmosphere. Int. J. Astrobiol. 2004, 3, 151–156.
  11. Flynn, G.; Keller, L.; Jacobsen, C.; Wirick, S. An assessment of the amount and types of organic matter contributed to the Earth by interplanetary dust. Adv. Space Res. 2004, 33, 57–66.
  12. Micca Longo, G.; Longo, S. Theoretical analysis of the atmospheric entry of sub-mm meteoroids of MgxCa1-xCO3 composition. Icarus 2018, 310, 194–202.
  13. Micca Longo, G.; Piccinni, V.; Longo, S. Evaluation of CaSO4 micrograins in the context of organic matter delivery: Thermochemistry and atmospheric entry. Int. J. Astrobiol. 2019, 18, 345–352.
  14. Micca Longo, G.; D’Elia, M.; Fonti, S.; Longo, S.; Mancarella, F.; Orofino, V. Kinetics of White Soft Minerals (WSMs) Decomposition under Conditions of Interest for Astrobiology: A Theoretical and Experimental Study. Geosciences 2019, 9, 101.
  15. Matrajt, G.; Messenger, S.; Brownlee, D.; Joswiak, D. Diverse forms of primordial organic matter identified in interplanetary dust particles. Meteorit. Planet. Sci. 2012, 47, 525–549.
  16. Yabuta, H.; Uesugi, M.; Naraoka, H.; Ito, M.; Kilcoyne, A.L.D.; Sandford, S.A.; Kitajima, F.; Mita, H.; Takano, Y.; Yada, T.; et al. X-ray absorption near edge structure spectroscopic study of Hayabusa category 3 carbonaceous particles. Earth Planets Space 2014, 66, 156.
  17. Dong, H.; Rech, J.A.; Jiang, H.; Sun, H.; Buck, B.J. Endolithic cyanobacteria in soil gypsum: Occurrences in Atacama (Chile), Mojave (United States), and Al-Jafr Basin (Jordan) Deserts. J. Geophys. Res. Biogeosci. 2007, 112.
  18. Gooding, J.L.; Wentworth, S.J.; Zolensky, M.E. Calcium carbonate and sulfate of possible extraterrestrial origin in the EETA 79001 meteorite. Geochim. Cosmochim. Acta 1988, 52, 909–915.
  19. Micca Longo, G.; Longo, S. The role of primordial atmosphere composition in organic matter delivery to early Earth. Rend. Lincei. Sci. Fis. E Nat. 2020, 31, 53–64.
  20. Miller, S.L. A Production of Amino Acids Under Possible Primitive Earth Conditions. Science 1953, 117, 528–529.
  21. Miller, S.L. Production of Some Organic Compounds under Possible Primitive Earth Conditions1. J. Am. Chem. Soc. 1955, 77, 2351–2361.
  22. Miller, S.L.; Urey, H.C. Organic Compound Synthes on the Primitive Eart. Science 1959, 130, 245–251.
  23. Oparin, A. Proischogdenie Zhizni; Moscovsky Robotchii: Moscow, Russia, 1924.
  24. Marshall, W.L. Hydrothermal synthesis of amino acids. Geochim. Cosmochim. Acta 1994, 58, 2099–2106.
  25. Lazcano, A.; Bada, J.L. The 1953 Stanley L. Miller Experiment: Fifty Years of Prebiotic Organic Chemistry. Orig. Life Evol. Biosph. 2003, 33, 235–242.
  26. Trainer, M.G.; Pavlov, A.A.; Curtis, D.B.; Mckay, C.P.; Worsnop, D.R.; Delia, A.E.; Toohey, D.W.; Toon, O.B.; Tolbert, M.A. Haze aerosols in the atmosphere of early Earth: Manna from heaven. Astrobiology 2004, 4, 409–419.
  27. Hasenkopf, C.A.; Freedman, M.A.; Beaver, M.R.; Toon, O.B.; Tolbert, M.A. Potential climatic impact of organic haze on early Earth. Astrobiology 2011, 11, 135–149.
  28. Balucani, N. Elementary reactions and their role in gas-phase prebiotic chemistry. Int. J. Mol. Sci. 2009, 10, 2304–2335.
  29. Bada, J.L. New insights into prebiotic chemistry from Stanley Miller’s spark discharge experiments. Chem. Soc. Rev. 2013, 42, 2186–2196.
  30. Haldane, J.B.S. Sciende and Human Life; Harper and Brothers: New York, NY, USA, 1933.
  31. Hart, M.H. The evolution of the atmosphere of the earth. Icarus 1978, 33, 23–39.
  32. Holland, H.D. Petrologic Studies: A Volume to Honor A.F. Buddington; Geological Society of America: New York, NY, USA, 1962; p. 447.
  33. Abelson, P.H. Chemical Events on the Primitive Earth. Proc. Natl. Acad. Sci. USA 1966, 55, 1365.
  34. Holland, H. The Chemical Evolution of the Atmosphere and Oceans; Princeton University Press: Princeton, NJ, USA, 1984.
  35. Kasting, J.F. Earth’s early atmosphere. Science 1993, 259, 920–926.
  36. Schlesinger, G.; Miller, S.L. Prebiotic synthesis in atmospheres containing CH4, CO, and CO2. J. Mol. Evol. 1983, 19, 376–382.
  37. Miyakawa, S.; Yamanashi, H.; Kobayashi, K.; Cleaves, H.J.; Miller, S.L. Prebiotic synthesis from CO atmospheres: Implications for the origins of life. Proc. Natl. Acad. Sci. USA 2002, 99, 14628.
  38. Cleaves, H.J.; Chalmers, J.H.; Lazcano, A.; Miller, S.L.; Bada, J.L. A Reassessment of Prebiotic Organic Synthesis in Neutral Planetary Atmospheres. Orig. Life Evol. Biosph. 2008, 38, 105–115.
  39. Zahnle, K.; Schaefer, L.; Fegley, B. Earth’s Earliest Atmospheres. Cold Spring Harb. Perspect. Biol. 2010, 2, a004895.
  40. Saitta, A.M.; Saija, F. Miller experiments in atomistic computer simulations. Proc. Natl. Acad. Sci. USA 2014, 111, 13768.
  41. Pietrucci, F.; Saitta, A.M. Formamide reaction network in gas phase and solution via a unified theoretical approach: Toward a reconciliation of different prebiotic scenarios. Proc. Natl. Acad. Sci. USA 2015, 112, 15030.
  42. Ferus, M.; Pietrucci, F.; Saitta, A.M.; Knížek, A.; Kubelík, P.; Ivanek, O.; Shestivska, V.; Civiš, S. Formation of nucleobases in a Miller–Urey reducing atmosphere. Proc. Natl. Acad. Sci. USA 2017, 114, 4306.
  43. Langmuir, I. Oscillations in ionized gases. Proc. Natl. Acad. Sci. USA 1928, 14, 627.
  44. Reid Thompson, W.; Henry, T.J.; Schwartz, J.M.; Khare, B.; Sagan, C. Plasma discharge in N2 + CH4 at low pressures: Experimental results and applications to Titan. Icarus 1991, 90, 57–73.
  45. Alcouffe, G.; Cavarroc, M.; Cernogora, G.; Ouni, F.; Jolly, A.; Boufendi, L.; Szopa, C. Capacitively coupled plasma used to simulate Titan’s atmospheric chemistry. Plasma Sources Sci. Technol. 2009, 19, 015008.
  46. Sciamma-O’Brien, E.; Ricketts, C.L.; Salama, F. The Titan Haze Simulation experiment on COSmIC: Probing Titan’s atmospheric chemistry at low temperature. Icarus 2014, 243, 325–336.
  47. Dubois, D.; Carrasco, N.; Jovanovic, L.; Vettier, L.; Gautier, T.; Westlake, J. Positive ion chemistry in an N2-CH4 plasma discharge: Key precursors to the growth of Titan tholins. Icarus 2020, 338, 113437.
  48. Köhn, C.; Dujko, S.; Chanrion, O.; Neubert, T. Streamer propagation in the atmosphere of Titan and other N2:CH4 mixtures compared to N2:O2 mixtures. Icarus 2019, 333, 294–305.
  49. Dubrovin, D.; Nijdam, S.; van Veldhuizen, E.M.; Ebert, U.; Yair, Y.; Price, C. Sprite discharges on Venus and Jupiter-like planets: A laboratory investigation. J. Geophys. Res. Space Phys. 2010, 115.
  50. Libby, W.F. Plasma chemistry. J. Vac. Sci. Technol. 1979, 16, 414–417.
  51. Gicquel, A.; Silva, F.; Hassouni, K. Diamond Growth Mechanisms in Various Environments. J. Electrochem. Soc. 2000, 147, 2218.
  52. Herrebout, D.; Bogaerts, A.; Yan, M.; Gijbels, R.; Goedheer, W.; Dekempeneer, E. One-dimensional fluid model for an rf methane plasma of interest in deposition of diamond-like carbon layers. J. Appl. Phys. 2001, 90, 570–579.
  53. Okita, A.; Suda, Y.; Oda, A.; Nakamura, J.; Ozeki, A.; Bhattacharyya, K.; Sugawara, H.; Sakai, Y. Effects of hydrogen on carbon nanotube formation in CH4/H2 plasmas. Carbon 2007, 45, 1518–1526.
  54. Physical Kinetics of Ionized Gases. In Fundamentals of Ionized Gases; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; Chapter 3; pp. 133–193.
  55. Meek, J.M.; Craggs, J.D. Electrical Breakdown of Gases; Oxford at The Clarendon Press: Oxford, UK, 1953.
  56. Von Engel, A. Electric Plasmas-Their Nature and Uses; Taylor and Francis, Ltd.: London, UK, 1983; 254p.
  57. Williams, E.R.; Geotis, S.G.; Bhattacharya, A. A radar study of the plasma and geometry of lightning. J. Atmos. Sci. 1989, 46, 1173–1185.
  58. Braglia, G. The diffusion and drift of electrons in gases a Monte-Carlo simulation. Phys. B+ C 1977, 92, 91–112.
  59. Schaefer, G.; Hui, P. The Monte Carlo flux method. J. Comput. Phys. 1990, 89, 1–30.
  60. Bogaerts, A.; Gijbels, R. Mathematical description of a direct current glow discharge in argon. Fresenius’ J. Anal. Chem. 1996, 355, 853–857.
  61. Biagi, S.F. Monte Carlo simulation of electron drift and diffusion in counting gases under the influence of electric and magnetic fields. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 421, 234–240.
  62. Longo, S. Monte Carlo models of electron and ion transport in non-equilibrium plasmas. Plasma Sources Sci. Technol. 2000, 9, 468–476.
  63. Loffhagen, D.; Winkler, R.; Donkó, Z. Boltzmann equation and Monte Carlo analysis of the spatiotemporal electron relaxation in nonisothermal plasmas. Eur. Phys. J. Appl. Phys. 2002, 18, 189–200.
  64. Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722–733.
  65. Capitelli, M.; Celiberto, R.; Colonna, G.; Esposito, F.; Gorse, C.; Hassouni, K.; Laricchiuta, A.; Longo, S. Fundamental Aspects of Plasma Chemical Physics: Kinetics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2015; Volume 85.
  66. Vialetto, L.; Longo, S.; Diomede, P. Benchmark calculations for electron velocity distribution function obtained with Monte Carlo Flux simulations. Plasma Sources Sci. Technol. 2019, 28, 115015.
  67. Gordiets, B.F.; Osipov, A.I.; Stupochenko, E.V.; Shelepin, L.A. Vibrational Relaxation in Gases and Molecular Lasers. Sov. Phys. Uspekhi 1973, 15, 759–785.
  68. Capitelli, M.; Armenise, I.; Bruno, D.; Cacciatore, M.; Celiberto, R.; Colonna, G.; Pascale, O.D.; Diomede, P.; Esposito, F.; Gorse, C.; et al. Non-equilibrium plasma kinetics: A state-to-state approach. Plasma Sources Sci. Technol. 2007, 16, S30–S44.
  69. Laux, C.O.; Pierrot, L.; Gessman, R.J. State-to-state modeling of a recombining nitrogen plasma experiment. Chem. Phys. 2012, 398, 46–55.
  70. Kim, J.G.; Boyd, I.D. State-resolved master equation analysis of thermochemical nonequilibrium of nitrogen. Chem. Phys. 2013, 415, 237–246.
  71. Armenise, I.; Kustova, E. State-to-state models for CO2 molecules: From the theory to an application to hypersonic boundary layers. Chem. Phys. 2013, 415, 269–281.
  72. Kadochnikov, I.N.; Arsentiev, I.V. Kinetics of nonequilibrium processes in air plasma formed behind shock waves: State-to-state consideration. J. Phys. D: Appl. Phys. 2018, 51, 374001.
  73. Guerra, V.; Silva, T.; Ogloblina, P.; Grofulović, M.; Terraz, L.; da Silva, M.L.; Pintassilgo, C.D.; Alves, L.L.; Guaitella, O. The case for in situ resource utilisation for oxygen production on Mars by non-equilibrium plasmas. Plasma Sources Sci. Technol. 2017, 26, 11LT01.
  74. Pietanza, L.D.; Colonna, G.; D’Ammando, G.; Laricchiuta, A.; Capitelli, M. Vibrational excitation and dissociation mechanisms of CO2 under non-equilibrium discharge and post-discharge conditions. Plasma Sources Sci. Technol. 2015, 24, 042002.
  75. Rusanov, V.D.; Fridman, A.A.; Sholin, G.V. The physics of a chemically active plasma with nonequilibrium vibrational excitation of molecules. Sov. Phys. Uspekhi 1981, 24, 447–474.
  76. Viegas, P.; van de Sanden, M.C.M.; Longo, S.; Diomede, P. Validation of the Fokker–Planck Approach to Vibrational Kinetics in CO2 Plasma. J. Phys. Chem. C 2019, 123, 22823–22831.
  77. Longo, S.; van de Sanden, M.C.M.; Diomede, P. Fokker–Planck equation for chemical reactions in plasmas. Rend. Lincei. Sci. Fis. E Nat. 2019, 30, 25–30.
  78. Diomede, P.; van de Sanden, M.C.M.; Longo, S. Vibrational Kinetics in Plasma as a Functional Problem: A Flux-Matching Approach. J. Phys. Chem. A 2018, 122, 7918–7923.
  79. Petrović, Z.L.; Dujko, S.; Marić, D.; Malović, G.; Nikitović, Ž.; Šašić, O.; Jovanović, J.; Stojanović, V.; Radmilović-Radjenović, M. Measurement and interpretation of swarm parameters and their application in plasma modelling. J. Phys. D Appl. Phys. 2009, 42.
  80. Tejero-del-Caz, A.; Guerra, V.; Gonçalves, D.; da Silva, M.L.; Marques, L.; Pinhão, N.; Pintassilgo, C.D.; Alves, L.L. The LisbOn KInetics Boltzmann solver. Plasma Sources Sci. Technol. 2019, 28, 043001.
  81. Stephens, J. A multi-term Boltzmann equation benchmark of electron-argon cross-sections for use in low temperature plasma models. J. Phys. D Appl. Phys. 2018, 51, 125203.
  82. Rabie, M.; Franck, C.M. METHES: A Monte Carlo collision code for the simulation of electron transport in low temperature plasmas. Comput. Phys. Comm. 2016, 203, 268–277.
  83. Vialetto, L.; Viegas, P.; Longo, S.; Diomede, P. Benchmarking of Monte Carlo Flux simulations of electrons in CO2. Plasma Sources Sci. Technol. 2020.
  84. McCollom, T.M. Miller-Urey and beyond: What have we learned about prebiotic organic synthesis reactions in the past 60 years? Annu. Rev. Earth Planet. Sci. 2013, 41, 207–229.
  85. Scherer, S.; Wollrab, E.; Codutti, L.; Carlomagno, T.; da Costa, S.G.; Volkmer, A.; Bronja, A.; Schmitz, O.J.; Ott, A. Chemical analysis of a “Miller-type” complex prebiotic broth. Orig. Life Evol. Biosph. 2017, 47, 381–403.
  86. Fowler, R.H. XXIII. Statistical equilibrium with special reference to the mechanism of ionization by electronic impacts. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1924, 47, 257–277.
  87. Magboltz - Transport of Electrons in Gas Mixtures. Available online: http://magboltz.web.cern.ch/magboltz/ (accessed on 2 August 2019).
  88. Hayashi Database. Available online: www.lxcat.net (accessed on 18 December 2020).
  89. Biagi Database. Available online: www.lxcat.net (accessed on 18 December 2020).
  90. Vialetto, L.; Guerra, V.; Diomede, P.; Longo, S.; Ben Moussa, A.; van Dijk, J.; Alves, L.L. Effect of anisotropic scattering on electron transport parameters in CO. Plasma Sources Sci. Technol. 2021. in preparation.
  91. Capitelli, M.; Ferreira, C.M.; Gordiets, B.F.; Osipov, A.I. Plasma Kinetics in Atmospheric Gases; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 31.
  92. IST-Lisbon Database. Available online: www.lxcat.net (accessed on 18 December 2020).
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Physics, Fluids & Plasmas
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Savino Longo
View Times: 753
Revisions: 4 times (View History)
Update Date: 18 Mar 2022
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback