Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Olesja Starkova
 + 9282 word(s) 9282 2022-03-01 04:11:47 |
2 format correct
Conner Chen
-8061 word(s) 1221 2022-03-15 03:46:09 | |
3 format correct
Conner Chen
-8059 word(s) 1223 2022-03-15 03:48:09 | |
4 format correct
Conner Chen
-8059 word(s) 1223 2022-03-15 03:54:21 | |
5 format correct
Conner Chen
Meta information modification 1223 2022-03-25 03:48:52 | |
6 format correct
Conner Chen
Meta information modification 1223 2022-03-25 03:50:27 | |
7 format correct
Conner Chen
-2 word(s) 1221 2022-03-25 03:54:05 | |
8 format correct
Conner Chen
Meta information modification 1221 2022-03-25 03:54:41 | |
9 format correct
Conner Chen
Meta information modification 1221 2022-03-25 03:56:25 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Starkova, O. Models for Predicting Material Durability and Service Lifetime. Encyclopedia. Available online: https://encyclopedia.pub/entry/20557 (accessed on 27 July 2024).
Starkova O. Models for Predicting Material Durability and Service Lifetime. Encyclopedia. Available at: https://encyclopedia.pub/entry/20557. Accessed July 27, 2024.
Starkova, Olesja. "Models for Predicting Material Durability and Service Lifetime" Encyclopedia, https://encyclopedia.pub/entry/20557 (accessed July 27, 2024).
Starkova, O. (2022, March 14). Models for Predicting Material Durability and Service Lifetime. In Encyclopedia. https://encyclopedia.pub/entry/20557
Starkova, Olesja. "Models for Predicting Material Durability and Service Lifetime." Encyclopedia. Web. 14 March, 2022.
Models for Predicting Material Durability and Service Lifetime
Edit
This entry is adapted from the peer-reviewed paper 10.3390/polym14050907

Substantial gains and savings of resources of time and money can be gained through the use of modelling and simulation to understand material system performance. Since for development of the new materials validation is expensive and time-consuming, the bottleneck is time and funding—modelling might be the way to replace testing programs, which would be beneficial for providing new innovative materials faster to the market.

modelling lifetime prediction accelerated testing methods durability mechanical properties creep fatigue

1. Arrhenius Model

The Arrhenius model is widely used when temperature is the dominant accelerating factor in ageing. It is assumed that a single dominant degradation mechanism does not change during the exposure period, while the degradation rate is accelerated with an increase of exposure temperature [1]. The Arrhenius relation is given by
K ( T ) = A   exp ( − E a R T )   o r     ln K ( T ) = − E a R T + ln A
where K is a reaction rate or degradation rate, A is a constant related to material and degradation process, Ea is the process activation energy, R is the universal gas constant, and T is the absolute temperature. The degradation rate is proportional to the inverse time for degradation of a mechanical property for a given value set by the lifetime criterion, and log(t) vs. 1/T is a linear function with the slope Ea/R (Figure 1). The Arrhenius relationship is widely used for lifetime predictions of polymers and composites through monitoring ultimate mechanical properties and their retention, e.g., tensile strength, interfacial shear strength, creep strength, and fatigue strength [2][3].
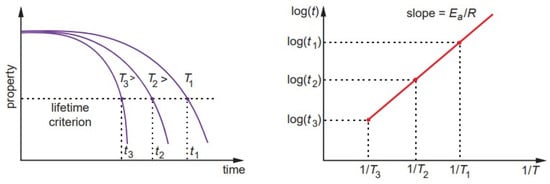
Polymers 14 00907 g002 550
Figure 1. Lifetime prediction according to the Arrhenius model.
The durability prediction methodology in most studies is based on the time shift concept [4][3][5][6][7][8][9][10]. According to Equation (1), the time shift factor (TSF) for two different exposure temperatures T1 and (T1< T2) can be calculated as
T S F = t 1 t 2 = A   exp ( − E a / R T 2 ) A   exp ( − E a / R T 1 ) = exp [ E a R ( 1 T 1 − 1 T 2 ) ]
Equation (2) has been further used in the predictive methods based on superposition principles and assessment of the temperature shift factors. The activation energy in Equations (1) and (2) is commonly evaluated by thermal analysis methods, e.g., differential scanning calorimetry or thermogravimetric analysis by measuring heat capacity changes or mass losses under different heating rates. Alternatively, Ea can be determined by dynamic thermal mechanical analysis (DMTA) assessing Tg dependence on the test frequenc [11][12].
Some recent studies considering the Arrhenius model and TSF approach for predicting the long-term strength of various FRP are listed in Table 1. Note that this methodology can be applied for assessment of tensile strength [5][13], interlaminar shear strength [6][9][10] or bond strength [8], under both static and fatigue loadings [9]. The accelerating temperature effect can also be coupled with other factors, e.g., absorbed water. For instance, Gagani et al. [9] applied the time shift concept to assess interlaminar shear fatigue lifetime of GFRP considering the effects of temperature and water immersion. The glass transition temperature of the material, and its decrease due to absorbed water, was used in Equation (2), enabling representation of both dry and water saturated samples in the same Arrhenius-based master curve. 
Table 1. A condensed list of recent works on methods for predicting long-term mechanical properties of polymers and polymer composites.
Prediction Method Material Property Ref.
Rate models      
Arrhenius model GFRP Tensile strength [5][13]
  GFRP ILSS [10]
  GFRP Fatigue ILSS [9]
  GFRP bars Tensile strength [4]
  CFRP/GFRP rods ILSS [6]
  BFRP bars Residual tensile strength [7]
  GFRP rods Bond strength [8]
Eyring’s model PA6,6, PC, CFRP Creep failure time [14]
Zhurkov’ model PP Fatigue strength [15]
Superposition principles      
Time–temperature (TTSP) Epoxy Creep compliance [11][16]
  Epoxy Stress relaxation [17]
  Filled epoxy Stiffness/Relaxation modulus [18]
  PMMA Creep compliance [19]
  Polyvinyl chloride, epoxy Stress threshold of LVE [20][21]
  Flax/vinylester Creep compliance [22]
  CFRP Creep compliance [23][24]
  CFRP, GFRP Static/creep/fatigue strength [25][26]
Time–moisture (TMSP) Epoxy Creep compliance [11][16]
  Epoxy Relaxation/storage modulus [27][28][29][30][31]
  Epoxy-based compounds Relaxation modulus [32]
  Vinylester Creep strain [33]
  Polyester Creep strain [34]
  PA6, PA6,6 Storage modulus [30][35]
  CFRP, GFRP Fatigue strength [36]
Time–stress (TSSP) PA6 Creep strain [37]
  PMMA Creep compliance [19][38][39]
  HDPE Creep strain/lifetime [40]
  Polycarbonate Creep compliance [41]
  PA6,6 fibres Creep strain [42]
  Glass/PA, PP, HDPE Creep compliance [43]
  HDPE/wood flour Creep strain [44]
  Graphite/epoxy FRP Creep strain [45]
  Kevlar yarns, PA6, epoxy Creep strain (stepped isostress test) [46][47][48]
Coupled      
TTSP + TMSP Epoxy Creep compliance [11]
TTSP + TMSP PA6,6 Storage modulus [35]
TTSP + TMSP Acrylate-based polymers Storage modulus [49]
TTSP + TMSP CFRP, GFRP Static/creep/fatigue strength [36][50]
TTSP + TSSP HDPE/wood flour Creep strain [44]
TASP+TMSP Epoxy, polyester Creep compliance, stress relaxation [27][28]
TTSP+TASP Epoxy Relaxation modulus [17][51]
TTSP+TASP+TSSP PMMA Creep strain [38]
Plasticity-controlled failure PP, PP/CNT, glass/PP, carbon/PEEK, PC/GF, PA6 Lifetime (tensile, creep, fatigue) [52][53][54][55][56][57]
  PA6,6, PC, CFRP Creep lifetime [14]
Parametric methods HDPE Creep lifetime (Larson–Miller, Monkman–Grant) [40]
  GFRP Creep lifetime (Monkman–Grant) [58]
  Rubber-bonded composite Creep lifetime (Larson–Miller) [59]
  Adhesive anchor in concrete Creep lifetime (Monkman–Grant) [60]
  Short fibre thermoplastics Fatigue lifetime (Larson–Miller) [61][62]

2. Eyring’s Model

The reaction rate of a process can rely on several stressors. For example, nonthermal stresses such as humidity, voltage and mechanical stress may also play a significant role in accelerating degradation [1]. The Eyring model is based on chemical reaction-rate theory and describes how the rate of degradation of a material varies with stress. It is assumed that the contribution of each stressor to the reaction rate is independent; thus, one could multiply the respective stress contributions to the rate of reaction. The model is closely related to the Arrhenius model and is based on the fact that the logarithm of the reaction rate is inversely proportional to absolute temperature (Equation (1)).
According to Eyring’s thermal activation flow theory, the strain rate (or the characteristic time) is given by the relationship
ε ˙ = 1 t = A 1 exp ( − E a − γ σ R T )
where A1 (s−1) is a material constant and γ is the coefficient linked to the activation volume; σ is the applied stress. Eyring’s activated flow theory is widely used to assess plasticity-controlled failure in thermoplastic polymers and composites [14][52][53][54][55][56][57][58][59][60][61][62][63].

3. Zhurkov’s Model

Zhurkov developed the kinetic theory of strength of solids using temperature and tensile stress [15][64]. The relationship for calculation of the fracture lifetime tf is similar to Equation (3), while the coefficient γ referred to as the lethargy coefficient is linked to lattice structure and defects in it. In the general case of nonisothermal tests and σ varying in time (e.g., creep and fatigue tests), the fracture probability with account of the linear damage accumulation concept is given by the following equation [15][58][65]:
∫ 0 t f d t t 0 exp ( E a − γ ( σ ( t ) ) R T ( t ) ) = 1
where t0 is the time constant.
Zhurkov’s model initially developed for metals often could not give accurate lifetime predictions for polymers owing to the sensitiveness of their mechanical properties to strain rate and uncertain distinctions between the elastic and plastic ranges. As a result, the parameters involved in Equation (4) are interrelated stress, temperature, and strain-rate dependent functions. The kinetic concept of strength is applied to model fatigue damage evolution [15][66]. Hur et al. developed a modified Zhurkov’s fatigue life model introducing strain-rate-dependent lethargy coefficient and applied it to polypropylene reinforced with glass fibres [15]. The stress-based failure cycles in the ranges of low- and high-cycle fatigue were predicted and successfully validated by the proposed modified strain-rate model. The kinetic strength model applied to lifetime predictions of biodegradable polymers is discussed in the review paper by Laycock et al. [67]. For this type of material, Zhurkov’s equation is coupled with broader biodegradation models enabling assessment of stress effects on the lifetime via lowering the activation energy for chain scission.

References

  1. Collins, D.H.; Freels, J.K.; Huzurbazar, A.V.; Warr, R.L.; Weaver, B.P. Accelerated Test Methods for Reliability Prediction. J. Qual. Technol. 2013, 45, 244–259.
  2. Plota, A.; Masek, A. Lifetime Prediction Methods for Degradable Polymeric Materials—A Short Review. Materials 2020, 13, 4507.
  3. Wang, J.; GangaRao, H.; Liang, R.; Liu, W. Durability and prediction models of fiber-reinforced polymer composites under various environmental conditions: A critical review. J. Reinf. Plast. Compos. 2015, 35, 179–211.
  4. Davalos, J.F.; Chen, Y.; Ray, I. Long-term durability prediction models for GFRP bars in concrete environment. J. Compos. Mater. 2011, 46, 1899–1914.
  5. Silva, M.A.G.; da Fonseca, B.S.; Biscaia, H. On estimates of durability of FRP based on accelerated tests. Compos. Struct. 2014, 116, 377–387.
  6. Guo, R.; Xian, G.; Li, C.; Hong, B.; Huang, X.; Xin, M.; Huang, S. Water uptake and interfacial shear strength of carbon/glass fiber hybrid composite rods under hygrothermal environments: Effects of hybrid modes. Polym. Degrad. Stab. 2021, 193, 109723.
  7. Wu, G.; Dong, Z.-Q.; Wang, X.; Zhu, Y.; Wu, Z.-S. Prediction of Long-Term Performance and Durability of BFRP Bars under the Combined Effect of Sustained Load and Corrosive Solutions. J. Compos. Constr. 2015, 19, 04014058.
  8. Zhou, J.; Chen, X.; Chen, S. Durability and service life prediction of GFRP bars embedded in concrete under acid environment. Nucl. Eng. Des. 2011, 241, 4095–4102.
  9. Gagani, A.I.; Monsås, A.B.; Krauklis, A.E.; Echtermeyer, A.T. The effect of temperature and water immersion on the interlaminar shear fatigue of glass fiber epoxy composites using the I-beam method. Compos. Sci. Technol. 2019, 181, 107703.
  10. Hota, G.; Barker, W.; Manalo, A. Degradation mechanism of glass fiber/vinylester-based composite materials under accelerated and natural aging. Constr. Build. Mater. 2020, 256, 119462.
  11. Krauklis, A.E.; Akulichev, A.G.; Gagani, A.; Echtermeyer, A.T. Time–Temperature–Plasticization Superposition Principle: Predicting Creep of a Plasticized Epoxy. Polymers 2019, 11, 1848.
  12. Starkova, O.; Gaidukovs, S.; Platnieks, O.; Barkane, A.; Garkusina, K.; Palitis, E.; Grase, L. Water absorption and hydrothermal ageing of epoxy adhesives reinforced with amino-functionalized graphene oxide nanoparticles. Polym. Degrad. Stab. 2021, 191, 109670.
  13. Idrisi, A.; Mourad, A.-H.; Abdel-Magid, B.; Shivamurty, B. Investigation on the Durability of E-Glass/Epoxy Composite Exposed to Seawater at Elevated Temperature. Polymers 2021, 13, 2182.
  14. Spathis, G.; Kontou, E. Creep failure time prediction of polymers and polymer composites. Compos. Sci. Technol. 2012, 72, 959–964.
  15. Hur, S.H.; Doh, J.; Yoo, Y.; Kim, S.; Lee, J. Stress-life prediction of 25°C polypropylene materials based on calibration of Zhurkov fatigue life model. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1784–1799.
  16. Feng, C.-W.; Keong, C.-W.; Hsueh, Y.-P.; Wang, Y.-Y.; Sue, H. Modeling of long-term creep behavior of structural epoxy adhesives. Int. J. Adhes. Adhes. 2005, 25, 427–436.
  17. Nunes, S.G.; Saseendran, S.; Joffe, R.; Amico, S.C.; Fernberg, P.; Varna, J. On Temperature-Related Shift Factors and Master Curves in Viscoelastic Constitutive Models for Thermoset Polymers. Mech. Compos. Mater. 2020, 56, 573–590.
  18. Böckenhoff, P.; Gundlach, C.; Kästner, M. Experimental characterization and modeling of the material behavior of an epoxy system. SN Appl. Sci. 2020, 2, 1–13.
  19. Luo, W.; Wang, C.; Hu, X.; Yang, T. Long-term creep assessment of viscoelastic polymer by time-temperature-stress superposition. Acta Mech. Solida Sin. 2012, 25, 571–578.
  20. Starkova, O.; Aniskevich, A. Application of time-temperature superposition to energy limit of linear viscoelastic behavior. J. Appl. Polym. Sci. 2009, 114, 341–347.
  21. Starkova, O.; Papanicolaou, G.C.; Xepapadaki, A.G.; Aniskevich, A. A method for determination of time- and temperature-dependences of stress threshold of linear-nonlinear viscoelastic transition: Energy-Based Approach. J. Appl. Polym. Sci. 2011, 121, 2187–2192.
  22. Amiri, A.; Hosseini, N.; Ulven, C.A. Long-Term Creep Behavior of Flax/Vinyl Ester Composites Using Time-Temperature Superposition Principle. J. Renew. Mater. 2015, 3, 224–233.
  23. Goertzen, W.; Kessler, M. Creep behavior of carbon fiber/epoxy matrix composites. Mater. Sci. Eng. A 2006, 421, 217–225.
  24. Rafiee, R.; Mazhari, B. Modeling creep in polymeric composites: Developing a general integrated procedure. Int. J. Mech. Sci. 2015, 99, 112–120.
  25. Miyano, Y.; Nakada, M.; Sekine, N. Accelerated testing for long-term durability of GFRP laminates for marine use. Compos. Part B Eng. 2004, 35, 497–502.
  26. Miyano, Y.; Nakada, M. Accelerated testing methodology for durability of CFRP. Compos. Part B Eng. 2020, 191, 107977.
  27. Aniskevich, K.; Starkova, O.; Jansons, J.; Aniskevich, A. Long-Term Deformability and Aging of Polymer Matrix Composites; Nova Science Publishers: New York, NY, USA, 2011; ISBN 978-1-61470-406-5.
  28. Aniskevich, K.; Krastev, R.; Hristova, Y. Effect of long-term exposure to water on the viscoelastic properties of an epoxy-based composition. Mech. Compos. Mater. 2009, 45, 137–144.
  29. Li, H.; Luo, Y.; Hu, D.; Jiang, D. Effect of hydrothermal aging on the dynamic mechanical performance of the room temperature-cured epoxy adhesive. Rheol. Acta 2019, 58, 9–19.
  30. Ishisaka, A.; Kawagoe, M. Examination of the time-water content superposition on the dynamic viscoelasticity of moistened polyamide 6 and epoxy. J. Appl. Polym. Sci. 2004, 93, 560–567.
  31. Xian, G.; Karbhari, V.M. Segmental relaxation of water-aged ambient cured epoxy. Polym. Degrad. Stab. 2007, 92, 1650–1659.
  32. Huber, F.; Etschmaier, H.; Walter, H.; Urstöger, G.; Hadley, P. A time–temperature–moisture concentration superposition principle that describes the relaxation behavior of epoxide molding compounds for microelectronics packaging. Int. J. Polym. Anal. Charact. 2020, 25, 467–478.
  33. Aiello, M.A.; Leone, M.; Aniskevich, A.N.; Starkova, O.A. Moisture Effects on Elastic and Viscoelastic Properties of CFRP Rebars and Vinylester Binder. J. Mater. Civ. Eng. 2006, 18, 686–691.
  34. Plushchik, O.A.; Aniskevich, A.N. Effects of temperature and moisture on the mechanical properties of polyester resin in tension. Mech. Compos. Mater. 2000, 36, 233–240.
  35. Fabre, V.; Quandalle, G.; Billon, N.; Cantournet, S. Time-Temperature-Water content equivalence on dynamic mechanical response of polyamide 6,6. Polymers 2018, 137, 22–29.
  36. Nakada, M.; Miyano, Y. Accelerated testing for long-term fatigue strength of various FRP laminates for marine use. Compos. Sci. Technol. 2009, 69, 805–813.
  37. Starkova, O.; Yang, J.; Zhang, Z. Application of time–stress superposition to nonlinear creep of polyamide 66 filled with nanoparticles of various sizes. Compos. Sci. Technol. 2007, 67, 2691–2698.
  38. Zhao, R.G.; Luo, W.B.; Li, Q.F.; Chen, C.Z. Application of Time-Ageing Time and Time-Temperature-Stress Equivalence to Nonlinear Creep of Polymeric Materials. Mater. Sci. Forum 2008, 575-578, 1151–1156.
  39. Luo, W.B.; Wang, C.H.; Zhao, R.G. Application of Time-Temperature-Stress Superposition Principle to Nonlinear Creep of Poly(methyl methacrylate). Key Eng. Mater. 2007, 340–341, 1091–1096.
  40. Amjadi, M.; Fatemi, A. Creep behavior and modeling of high-density polyethylene (HDPE). Polym. Test. 2021, 94, 107031.
  41. Jazouli, S.; Luo, W.; Bremand, F.; Vu-Khanh, T. Application of time–stress equivalence to nonlinear creep of polycarbonate. Polym. Test. 2005, 24, 463–467.
  42. Wang, B.; Fancey, K.S. Application of time-stress superposition to viscoelastic behavior of polyamide 6,6 fiber and its “true” elastic modulus. J. Appl. Polym. Sci. 2017, 134, 44971.
  43. Chevali, V.; Dean, D.R.; Janowski, G. Flexural creep behavior of discontinuous thermoplastic composites: Non-linear viscoelastic modeling and time–temperature–stress superposition. Compos. Part A Appl. Sci. Manuf. 2009, 40, 870–877.
  44. Chang, F.-C.; Lam, F.; Kadla, J.F. Application of time–temperature–stress superposition on creep of wood–plastic composites. Mech. Time-Depend. Mater. 2013, 17, 427–437.
  45. Guedes, R.M. A systematic methodology for creep master curve construction using the stepped isostress method (SSM): A numerical assessment. Mech. Time-Depend. Mater. 2017, 22, 79–93.
  46. Giannopoulos, I.P.; Burgoyne, C.J. Prediction of the long-term behaviour of high modulus fibres using the stepped isostress method (SSM). J. Mater. Sci. 2011, 46, 7660–7671.
  47. Hadid, M.; Guerira, B.; Bahri, M.; Zouani, A. Assessment of the stepped isostress method in the prediction of long term creep of thermoplastics. Polym. Test. 2014, 34, 113–119.
  48. Fonseca, E.; da Silva, V.D.; Amico, S.C.; Pupure, L.; Joffe, R.; Schrekker, H.S. Time-dependent properties of epoxy resin with imidazolium ionic liquid. J. Appl. Polym. Sci. 2021, 138, 51369.
  49. Li, H.; Xiao, R. Glass Transition Behavior of Wet Polymers. Materials 2021, 14, 730.
  50. Miyano, Y.; Nakada, M.; Ichimura, J.; Hayakawa, E. Accelerated testing for long-term strength of innovative CFRP laminates for marine use. Compos. Part B Eng. 2008, 39, 5–12.
  51. Saseendran, S.; Wysocki, M.; Varna, J. Evolution of viscoelastic behavior of a curing LY5052 epoxy resin in the glassy state. Adv. Manuf. Polym. Compos. Sci. 2016, 2, 74–82.
  52. Pastukhov, L.V.; Mercx, F.P.M.; Peijs, T.; Govaert, L.E. Long-term performance and durability of polycarbonate/carbon nanotube nanocomposites. Nanocomposites 2018, 4, 223–237.
  53. van Erp, T.B.; Reynolds, C.T.; Peijs, T.; van Dommelen, J.A.W.; Govaert, L.E. Prediction of yield and long-term failure of oriented polypropylene: Kinetics and anisotropy. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 2026–2035.
  54. Erartsın, O.; van Drongelen, M.; Govaert, L.E. Identification of plasticity-controlled creep and fatigue failure mechanisms in transversely loaded unidirectional thermoplastic composites. J. Compos. Mater. 2021, 55, 1947–1965.
  55. Pastukhov, L.; Govaert, L. Plasticity-controlled failure of fibre-reinforced thermoplastics. Compos. Part B Eng. 2021, 209, 108635.
  56. Kanters, M.J.; Kurokawa, T.; Govaert, L.E. Competition between plasticity-controlled and crack-growth controlled failure in static and cyclic fatigue of thermoplastic polymer systems. Polym. Test. 2016, 50, 101–110.
  57. Parodi, E.; Peters, G.W.M.; Govaert, L.E. Structure–Properties Relations for Polyamide 6, Part 1: Influence of the Thermal History during Compression Moulding on Deformation and Failure Kinetics. Polymers 2018, 10, 710.
  58. Guedes, R.M. Lifetime predictions of polymer matrix composites under constant or monotonic load. Compos. Part A Appl. Sci. Manuf. 2006, 37, 703–715.
  59. Duan, X.; Yuan, H.; Tang, W.; He, J.; Guan, X. A Phenomenological Primary–Secondary–Tertiary Creep Model for Polymer-Bonded Composite Materials. Polymers 2021, 13, 2353.
  60. Boumakis, I.; Nincevic, K.; Vorel, J.; Wan-Wendner, R. Creep rate based time-to-failure prediction of adhesive anchor systems under sustained load. Compos. Part B Eng. 2019, 178, 107389.
  61. Eftekhari, M.; Fatemi, A. On the strengthening effect of increasing cycling frequency on fatigue behavior of some polymers and their composites: Experiments and modeling. Int. J. Fatigue 2016, 87, 153–166.
  62. Eftekhari, M.; Fatemi, A. Fatigue behaviour and modelling of talc-filled and short glass fibre reinforced thermoplastics, including temperature and mean stress effects. Fatigue Fract. Eng. Mater. Struct. 2016, 40, 333–348.
  63. Starkova, O.; Aniskevich, K.; Sevcenko, J.; Bulderberga, O.; Aniskevich, A. Relationship between the residual and total strain from creep-recovery tests of polypropylene/multiwall carbon nanotube composites. J. Appl. Polym. Sci. 2021, 138, 49957.
  64. Zhurkov, S.N. Kinetic concept of the strength of solids. Int. J. Fract. 1984, 26, 295–307.
  65. Doh, J.; Lee, J. Bayesian estimation of the lethargy coefficient for probabilistic fatigue life model. J. Comput. Des. Eng. 2017, 5, 191–197.
  66. Mishnaevsky, L.; Brøndsted, P. Modeling of fatigue damage evolution on the basis of the kinetic concept of strength. Int. J. Fract. 2007, 144, 149–158.
  67. Laycock, B.; Nikolić, M.; Colwell, J.M.; Gauthier, E.; Halley, P.; Bottle, S.; George, G. Lifetime prediction of biodegradable polymers. Prog. Polym. Sci. 2017, 71, 144–189.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Mechanical
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Olesja Starkova
View Times: 1.4K
Revisions: 9 times (View History)
Update Date: 25 Mar 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback