Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Violeta Carvalho
 + 1415 word(s) 1415 2021-02-01 07:56:07 |
2 format correct
Dean Liu
 -11 word(s) 1404 2021-02-07 09:49:38 | |
3 format correct
Dean Liu
 Meta information modification 1404 2021-02-08 03:24:34 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Carvalho, V.; Lima, R.; Pinho, D.; Teixeira, S. Blood Flow Modeling. Encyclopedia. Available online: https://encyclopedia.pub/entry/7044 (accessed on 19 April 2024).
Carvalho V, Lima R, Pinho D, Teixeira S. Blood Flow Modeling. Encyclopedia. Available at: https://encyclopedia.pub/entry/7044. Accessed April 19, 2024.
Carvalho, Violeta, Rui Lima, Diana Pinho, Senhorinha Teixeira. "Blood Flow Modeling" Encyclopedia, https://encyclopedia.pub/entry/7044 (accessed April 19, 2024).
Carvalho, V., Lima, R., Pinho, D., & Teixeira, S. (2021, February 04). Blood Flow Modeling. In Encyclopedia. https://encyclopedia.pub/entry/7044
Carvalho, Violeta, et al. "Blood Flow Modeling." Encyclopedia. Web. 04 February, 2021.
Blood Flow Modeling
Edit
This entry is adapted from the peer-reviewed paper 10.3390/fluids6020053

Blood flow modeling consists of using computational techniques to investigate the blood flow behavior in a rapid and accurate fashion. This has become an area of extensive research due to the prevalence of cardiovascular diseases, responsible for a critical number of deaths every year worldwide, most of which are associated with atherosclerosis, a disease that causes unusual hemodynamic conditions in arteries. In the present review,  the application of computational simulations by using different physiological conditions of blood flow, several rheological models, and boundary conditions, were discussed.

atherosclerosis coronary arteries hemodynamics numerical methods

1. Introduction

Despite the progress done in experimental studies and blood flow measurement techniques, there are still some challenges associated with them[1]. For instance, in vitro wall shear stress (WSS) measurements are extremely difficult to perform and the velocity measurements have high associated errors. These, combined with other complications of directly measuring quantities of interest, have motivated the use of computer simulations to predict them in silico[2].

The earliest numerical detailed studies solving the flow problem in constricted tubes were conducted by Lee and Fung (1970)[3]. After that, other studies in this field conducted by Caro et al., (1971)[4], Glagov et al., (1989)[5], and Ku et al., (1985)[6] are important references in this area and should be highlighted. Ever since, CFD approaches have been progressively adopted by most researchers as the preferred technique for numerical modeling of hemodynamics. Owing to the continued growth of computational power, these have become an increasingly reliable tool for measuring biomechanical factors vital for clinical decision-making and surgical planning. However, the proper selection of the flow boundary conditions has to be done, otherwise, the findings can be considered uncertain, weak, and unrealistic[7]. In this regard, the different geometries, boundary conditions, and flow characteristics applied by some researchers in the last ten years are summarized in Table 1.

Table 1. Numerical studies of hemodynamics and the respective assumptions for numerical simulations.

Geometry Schematic Representation Modeling Approaches Fluid Boundary Conditions Authors
Wall Inlet Outlet
Idealized 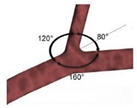Fluids 06 00053 i001 Laminar Non-Newtonian (Carreau-Yasuda) Rigid Time-dependent velocity profile Zero gauge pressure Kashyap et al., (2020) [8]
Idealized Fluids 06 00053 i002 Laminar Newtonian Rigid Time-dependent mass flow profile Zero surface tension Biglarian et al., (2019) [9]
Idealized Fluids 06 00053 i003 Laminar Non-Newtonian (Cross model) Rigid and Flexible Constant inlet velocity Constant pressure outlet (10 kPa) Mulani et al., (2015) [10]
Idealized Fluids 06 00053 i004 Laminar Newtonian Rigid and Flexible Time-dependent flowrate profile Time-dependent pressure profile Wu et al., (2015) [11]
Idealized Fluids 06 00053 i005 Laminar Newtonian Rigid Constant inlet velocity (fully developed parabolic profile) Constant pressure outlet (13 kPa) Kenjereš et al., (2019) [12]
Idealized Fluids 06 00053 i006 Laminar Newtonian Rigid Constant inlet velocity Zero gauge pressure Carvalho et al., (2020) [13]
Idealized Fluids 06 00053 i007 k-ω turbulent model Non-Newtonian (Carreau model) Rigid Spiral boundary conditionwith a parabolic velocity profile Zero gauge pressure Kabir et al., (2018) [14]
Idealized Fluids 06 00053 i008 k-ω turbulent model (SST) Non-Newtonian (Carreau model) Rigid Time-dependent velocity profile Zero gauge pressure Carvalho et al., (2020) [15]
Idealized Fluids 06 00053 i009 k-ω turbulent model (SST) Non-Newtonian (Carreau model) Rigid Time-dependent velocity profile Zero gauge pressure Carvalho et al., (2020) [16][17]
Idealized Fluids 06 00053 i010 N.A1 Newtonian Flexible Time-dependent velocity profile Time-dependent pressure profile Jahromi et al., (2019) [18]
Idealized Fluids 06 00053 i011 Laminar Newtonian Rigid Time-dependent velocity profile Flow partition implied in Murray’s law Doutel et al., (2018) [19]
Patient-specific 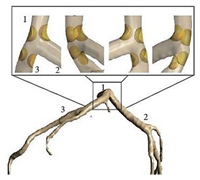Fluids 06 00053 i012 Laminar Non-Newtonian (Generalized power-law model) and Newtonian Rigid Time-dependent flow rate profile Time-dependent pressure profile Chaichana et al., (2012) [20]
Patient-specific Fluids 06 00053 i013 Laminar Non-Newtonian (Carreau model) Rigid Time-dependent velocity profile Time-dependent pressure profile Liu et al., (2015) [21]
Patient-specific Fluids 06 00053 i014 Laminar Newtonian Rigid and Flexible Time-dependent pressure profile Parabolic velocity profile Siogkas et al., (2014) [22]
Patient-specific 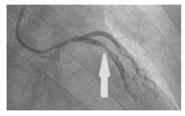Fluids 06 00053 i015 N.A Newtonian Rigid Time-dependent pressure profile Constant pressure outlet (9.85 kPa) Zhao et al., (2019) [23]
Patient-specific Fluids 06 00053 i016 Laminar Non-Newtonian (Carreau model) Rigid Time-dependent velocity profile Flow partition implied in Murray’s law Pandey et al., (2020) [24]
Patient-specific Fluids 06 00053 i017 Laminar Non-Newtonian (Carreau model) Rigid Various time-dependent velocity profiles Flow partition implied in Murray’s law Rizzini et al., (2020) [7]
Patient-specific 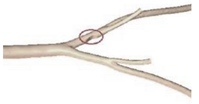Fluids 06 00053 i018 N.A Non-Newtonian (Power-law model) Rigid Time-dependent velocity profile Pressure outlet (N.A) Zhang et al., (2020) [25]
Patient-specific Fluids 06 00053 i019 k-ω turbulent model (SST) Non-Newtonian (Bird-Carreau model) Rigid Time-dependent velocity profile Constant pressure outlet (10 kPa) Kamangar et al., (2019) [26]
Patient-specific Fluids 06 00053 i020 Laminar Newtonian Rigid Time-dependent flow rate profile Two-Element Windkessel Model Lo et al., (2019) [27]
Patient-specific and Idealized 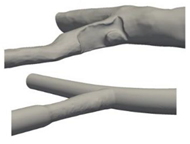Fluids 06 00053 i021 Laminar Newtonian and Non-Newtonian (Carreau model) Rigid Constant inlet velocity and Time-dependent velocity profile N.A Doutel et al., (2019) [28]
Patient-specific and Idealized Fluids 06 00053 i022 k-ω turbulent model (SST) Non-Newtonian (Carreau model) Rigid Time-dependent velocity profile Outflow condition Mahalingam et al., (2016) [29]
Patient-specific and Idealized 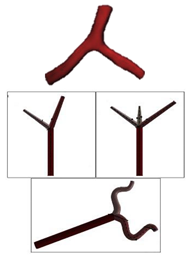Fluids 06 00053 i023 N.A Non-Newtonian (Carreau model) Rigid Time-dependent velocity profile Constant pressure outlet (10 kPa) Rabbi et al., (2020)[30]
Patient-specific and Idealized 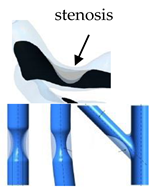Fluids 06 00053 i024 Laminar Newtonian Rigid Constant inlet mass flow and Time-dependent flow rate Zero gauge pressure Malota et al., (2018) [31]

N.A—Not available. All images were adapted from [8][19][15][24][13][10][11][16][20][26][7][9][12][14][17][18][21][22][23][25][27][28][29][30][31]

In general, from the above-mentioned investigations, it can be seen that, regardless of the type of geometry, the majority of authors consider that the blood is a non-Newtonian fluid, usually approximated by the Carreau model, with a laminar behavior. Regarding the boundary conditions, in most cases, the wall is considered rigid, and at the inlet, a pulsatile velocity is applied. At the outlet, the condition set mainly depends on the study, but either the default conditions are maintained, or pressures are applied, time-dependent or constant values. In the following section, the main observations drawn from these studies are presented.

2. Concluding Remarks and Future Perspectives

Although huge advancements have been made in imaging techniques to obtain patient-specific images, this step is time-consuming, and it is still a challenging task for all researchers. For this reason, nowadays, idealized models continue to be widely used by researchers, since these allow to obtain important and relevant results, without requiring much computational time and without the need to collect the medical images, which is highly time-consuming. In this regard, a promising study was proposed by Doutel et al., (2018) wherein artificial, but realistic stenosis can be generated.

It was also noted that, although the modelling of blood as a Newtonian fluid is a good approximation for large vessels with high shear rates, the assumption of non-Newtonian behavior of blood flow has been increasingly used in the presence of stenosis. From the overall studies, the most used models are the Carreau and the Carreau-Yasuda, and these have also been indicated as the most appropriate to simulate the blood rheology by Razavi et al., (2011) . Nevertheless, currently, one cannot say which is the right model, because there is not yet enough evidence in the literature to prove which model fully expresses the complex nature of blood rheology and its dependence on many biological factors . Accordingly, it is of great importance to obtain proper models for CFD analysis that take into account the non-Newtonian behavior of blood. For this purpose, more experimental studies are needed. Regarding the boundary conditions, few studies have evaluated the impact of using different inlet and outlet boundary conditions , and therefore, it would be interesting, in future studies, to investigate what are the profiles more adequate to study the blood flow behavior in coronary arteries.

Despite the great efforts that have been made so far, the blood has been mainly modeled as a single-phase fluid. However, blood is a mixture of plasma, red blood cells, white blood cells, and platelets. Therefore, the consideration of multiphase models is of great importance when modeling atherosclerotic lesions. Although some studies have already applied these models , the research is still in the beginning. Moreover, it should be also noted that the use of these models is a promising option for studying nanoparticle-mediated targeted drug delivery treatment of atherosclerosis. In this context, a promising study was conducted by Zhang et al., (2020). The authors used an Eulerian-Lagrangian approach coupled with FSI to investigate the impact of plaque morphology on magnetic nanoparticles targeting under the action of an external field.

Due to the continuous improvements acquired in computational methods, in the following years more amazing and complex hemodynamic studies will be performed. The work of Zhao et al. (2019) should be highlighted since their numerical approach has a great potential to achieve more realistic simulations. They have simulated 4D hemodynamic profiles of time-resolved blood flow. The results proved that these simulations can provide extensive information about blood flow, both qualitatively and quantitatively that may be advantageous for future investigations of clinical diagnosis and treatment of atherosclerosis.

To conclude, although computational methods have been extensively used for atherosclerosis investigations in recent years, they are expected to become more popular and more effective to simulate the blood flow in the cardiovascular system, and consequently, they will promote medical innovation at an affordable cost. However, to this end, active collaborations between engineers and medical staff are needed to assure the successful application of this technique in atherosclerosis treatment.

References

  1. Carvalho, V.; Maia, I.; Souza, A.; Ribeiro, J.; Costa, P.; Puga, H.; Teixeira, S.F.C.F.; Lima, R.A. In vitro stenotic arteries to perform blood analogues flow visualizations and measurements: A Review. Open Biomed. Eng. J. 2020, 14, 87–102.
  2. Kissas, G.; Yang, Y.; Hwuang, E.; Witschey, W.R.; Detre, J.A.; Perdikaris, P. Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2020, 358, 112623.
  3. Lee, J.; Fung, Y. Flow in Locally Constricted Tubes at Low Reynolds Numbers. J. Appl. Mech. 1970, 37, 9–16.
  4. Caro, C.G.; Fitz-Gerald, J.M.; Schroter, R.C. Atheroma and arterial wall shear. Observation, correlation and proposal of a shear dependent mass transfer mechanism for atherogenesis. Proc. R. Soc. London Ser. B Biol. Sci. 1971, 177, 109–159.
  5. Glagov, S.; Zarins, C.K.; Giddens, D.P.; Ku, D.N. Mechanical Factors in the Pathogenesis, Localization and Evolution of Atherosclerotic Plaques. In Diseases of the Arterial Wall; Springer: Berlin/Heidelberg, Germany, 1989; pp. 217–239.
  6. Ku, D.N.; Giddens, D.P.; Zarins, C.K.; Glagov, S. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low and oscillating shear stress. Arterioscler. Thromb. Vasc. Biol. 1985, 5, 293–302.
  7. Lodi Rizzini, M.; Gallo, D.; De Nisco, G.; D’Ascenzo, F.; Chiastra, C.; Bocchino, P.P.; Piroli, F.; De Ferrari, G.M.; Morbiducci, U. Does the inflow velocity profile influence physiologically relevant flow patterns in computational hemodynamic models of left anterior descending coronary artery? Med. Eng. Phys. 2020, 82, 58–69.
  8. Kashyap, V.; Arora, B.B.; Bhattacharjee, S. A computational study of branch-wise curvature in idealized coronary artery bifurcations. Appl. Eng. Sci. 2020, 4, 100027.
  9. Biglarian, M.; Larimi, M.M.; Afrouzi, H.H.; Moshfegh, A.; Toghraie, D.; Javadzadegan, A.; Rostami, S.; Momeni, M.; Hassanzadeh, H.; Moshfegh, A.; et al. Computational investigation of stenosis in curvature of coronary artery within both dynamic and static models. Comput. Methods Program. Biomed. 2020, 185, 105170.
  10. Mulani, S.S.; Jagad, P.I. Analysis of the Effects of Plaque Deposits on the Blood Flow through Human Artery. Int. Eng. Res. J. 2015, 41, 2319–3182.
  11. Wu, J.; Liu, G.; Huang, W.; Ghista, D.N.; Wong, K.K.L. Transient blood flow in elastic coronary arteries with varying degrees of stenosis and dilatations: CFD modelling and parametric study. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 1835–1845.
  12. Kenjereš, S.; van der Krieke, J.P.; Li, C. Endothelium resolving simulations of wall shear-stress dependent mass transfer of LDL in diseased coronary arteries. Comput. Biol. Med. 2019, 114.
  13. Carvalho, V.; Rodrigues, N.; Ribeiro, R.; Costa, P.F.; Lima, R.A.; Teixeira, S.F.C.F. 3D Printed Biomodels for Flow Visualization in Stenotic Vessels: An Experimental and Numerical Study. Micromachines 2020, 11, 549.
  14. Kabir, M.A.; Alam, M.F.; Uddin, M.A. A numerical study on the effects of reynolds number on blood flow with spiral velocity through regular arterial stenosis. Chiang Mai J. Sci. 2018, 45, 2515–2527.
  15. Carvalho, V.; Rodrigues, N.; Ribeiro, R.; Costa, P.; Teixeira, J.C.F.; Lima, R.; Teixeira, S.F.C.F. Hemodynamic study in 3D printed stenotic coronary artery models: Experimental validation and transient simulation. Comput. Methods Biomech. Biomed. Eng. 2020, 1–14.
  16. Carvalho, V.; Rodrigues, N.; Lima, R.A.; Teixeira, S.F.C.F. Modeling blood pulsatile turbulent flow in stenotic coronary arteries. Int. J. Biol. Biomed. Eng. 2020, 14, 1998–4510.
  17. Carvalho, V.; Rodrigues, N.; Lima, R.A.; Teixeira, S. Numerical simulation of blood pulsatile flow in stenotic coronary arteries: The effect of turbulence modeling and non-Newtonian assumptions. In Proceedings of the International Conference on Applied Mathematics & Computer Science, Athens, Greece, 2–4 June 2020.
  18. Jahromi, R.; Pakravan, H.A.; Saidi, M.S.; Firoozabadi, B. Primary stenosis progression versus secondary stenosis formation in the left coronary bifurcation: A mechanical point of view. Biocybern. Biomed. Eng. 2019, 39, 188–198.
  19. Doutel, E.; Carneiro, J.; Campos, J.B.L.M.; Miranda, J.M. Experimental and numerical methodology to analyze flows in a coronary bifurcation. Eur. J. Mech. B Fluids 2018, 67, 341–356.
  20. Chaichana, T.; Sun, Z.; Jewkes, J. Computational Fluid Dynamics Analysis of the Effect of Plaques in the Left Coronary Artery. Comput. Math. Methods Med. 2012, 2012, 504367.
  21. Liu, B.; Zheng, J.; Bach, R.; Tang, D. Influence of model boundary conditions on blood flow patterns in a patient specific stenotic right coronary artery. Biomed. Eng. Online 2015, 14, S6.
  22. Siogkas, P.K.; Papafaklis, M.I.; Sakellarios, A.I.; Stefanou, K.A.; Bourantas, C.V.; Athanasiou, L.S.; Exarchos, T.P.; Naka, K.K.; Michalis, L.K.; Parodi, O.; et al. Patient-specific simulation of coronary artery pressure measurements: An in vivo three-dimensional validation study in humans. Biomed Res. Int. 2014, 2015, 628416.
  23. Zhao, Y.; Ping, J.; Yu, X.; Wu, R.; Sun, C.; Zhang, M. Fractional flow reserve-based 4D hemodynamic simulation of time-resolved blood flow in left anterior descending coronary artery. Clin. Biomech. 2019, 70, 164–169.
  24. Pandey, R.; Kumar, M.; Srivastav, V.K. Numerical computation of blood hemodynamic through constricted human left coronary artery: Pulsatile simulations. Comput. Methods Program. Biomed. 2020, 197, 105661.
  25. Zhang, X.; Luo, M.; Wang, E.; Zheng, L.; Shu, C. Numerical simulation of magnetic nano drug targeting to atherosclerosis: Effect of plaque morphology (stenosis degree and shoulder length). Comput. Methods Program. Biomed. 2020, 195, 105556.
  26. Kamangar, S.; Salman Ahmed, N.J.; Badruddin, I.A.; Al-Rawahi, N.; Husain, A.; Govindaraju, K.; Yunus Khan, T.M. Effect of stenosis on hemodynamics in left coronary artery based on patient-specific CT scan. Biomed. Mater. Eng. 2019, 30, 463–473.
  27. Lo, E.W.C.; Menezes, L.J.; Torii, R. Impact of inflow boundary conditions on the calculation of CT-based FFR. Fluids 2019, 4, 60.
  28. Doutel, E.; Viriato, N.; Carneiro, J.; Campos, J.B.L.M.; Miranda, J.M. Geometrical effects in the hemodynamics of stenotic and non-stenotic left coronary arteries—Numerical and in vitro approaches. Int. J. Numer. Method. Biomed. Eng. 2019, 35, 1–18.
  29. Mahalingam, A.; Gawandalkar, U.U.; Kini, G.; Buradi, A.; Araki, T.; Ikeda, N.; Nicolaides, A.; Laird, J.R.; Saba, L.; Suri, J.S. Numerical analysis of the effect of turbulence transition on the hemodynamic parameters in human coronary arteries. Cardiovasc. Diagn. Ther. 2016, 6, 208–220.
  30. Rabbi, M.F.; Laboni, F.S.; Arafat, M.T. Computational analysis of the coronary artery hemodynamics with different anatomical variations. Inform. Med. Unlocked 2020, 19, 100314.
  31. Malota, Z.; Glowacki, J.; Sadowski, W.; Kostur, M. Numerical analysis of the impact of flow rate, heart rate, vessel geometry, and degree of stenosis on coronary hemodynamic indices. BMC Cardiovasc. Disord. 2018, 18, 1–16. 
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Others
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Violeta Carvalho
,
Rui Lima
,
Diana Pinho
,
Senhorinha Teixeira
View Times: 1.5K
Entry Collection: Hypertension and Cardiovascular Diseases
Revisions: 3 times (View History)
Update Date: 10 Apr 2021
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback