Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Bisrat Ayalew Yifru
 -- 1476 2024-02-26 01:32:50 |
2 layout
Jessie Wu
 -2 word(s) 1474 2024-02-26 02:01:22 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Yifru, B.A.; Lim, K.J.; Lee, S. Watershed Processes and Streamflow Prediction. Encyclopedia. Available online: https://encyclopedia.pub/entry/55418 (accessed on 16 November 2024).
Yifru BA, Lim KJ, Lee S. Watershed Processes and Streamflow Prediction. Encyclopedia. Available at: https://encyclopedia.pub/entry/55418. Accessed November 16, 2024.
Yifru, Bisrat Ayalew, Kyoung Jae Lim, Seoro Lee. "Watershed Processes and Streamflow Prediction" Encyclopedia, https://encyclopedia.pub/entry/55418 (accessed November 16, 2024).
Yifru, B.A., Lim, K.J., & Lee, S. (2024, February 26). Watershed Processes and Streamflow Prediction. In Encyclopedia. https://encyclopedia.pub/entry/55418
Yifru, Bisrat Ayalew, et al. "Watershed Processes and Streamflow Prediction." Encyclopedia. Web. 26 February, 2024.
Watershed Processes and Streamflow Prediction
Edit
This entry is adapted from the peer-reviewed paper 10.3390/su16041376

Accurate streamflow prediction (SFP) is crucial for water resource management, flood and drought forecasting, and reservoir operations. However, complex interactions between surface and subsurface processes in watersheds make predicting extreme events challenging. This work highlights the importance of incorporating physical understanding and process knowledge into data-driven SFP models for reliable and robust predictions, especially during extreme events.

baseflow data-driven modeling streamflow prediction physically consistent hybrid modeling

1. Introduction

Streamflow—a vital element of the hydrological system—constitutes a pivotal nexus between the sustenance of diverse aquatic ecosystems and the fulfillment of fundamental human needs across agriculture, industry, and societal well-being [1][2][3]. It also plays a significant role in riverine processes, influencing erosion, transportation, and deposition. Additionally, streamflow serves as a critical indicator of climatic and environmental changes [4][5]. Therefore, accurate understanding and prediction of streamflow are essential for drought monitoring, infrastructure design, reservoir management, flood forecasting, water quality control, and water resource management [6][7]. However, despite advances in streamflow prediction (SFP) methods, accurate prediction remains challenging due to the complex interplay between natural and human influences on a watershed’s response to precipitation [6][8][9][10]. Land-use changes, water withdrawals, infrastructure development, topography, soil characteristics, and vegetation cover create a dynamic and interdependent system that challenges accurate modeling. Data limitations and measurement uncertainties further complicate the task [11][12].
Process-based models have been used to comprehend complex hydrological processes at the watershed scale, while data-driven modeling (DDM) has been used to predict streamflow by leveraging input–output relationships. DDM ranges from traditional statistical methods to complex artificial intelligence (AI)-based models, while process-based models encompass conceptual and physically based models [8][9][13]. Although less physically based, DDM often outperforms PBM in terms of predictive accuracy [14][15][16]. Developing physically based models is slow and requires extensive data, making DDM an attractive solution to the challenge of relating input and output variables in complex systems [17]. Moreover, DDM has the potential to avoid several sources of uncertainty in the modeling process, such as downscaling errors, hydrological model errors, and parameter uncertainty [12].
However, many operational forecasting agencies do not use DDM for SFP [18]. This may be due, in part, to the “black box” nature of DDMs, making it difficult to interpret predictions and diagnose errors [19]. Overfitting is also a significant concern in this paradigm, as the complexity of the models can lead to spurious relationships with the data [20][21]. In fact, both DDM and PBM paradigms have difficulty capturing extreme events, such as floods or prolonged droughts. While the inherent complexity and non-stationary nature of these events pose a significant challenge for any prediction model, the simplified hydrological processes often used in PBM frameworks further limit their accuracy [22]. For example, simplified representations of groundwater modules in watershed models or neglecting certain physical processes can hinder the models’ ability to capture the intricate dynamics of extreme events [23][24].
To improve SFP, several options, including domain knowledge, advanced data preprocessing techniques, multi-model integration, and metaheuristic algorithms, have been explored. While most of these techniques aim primarily to enhance prediction accuracy, PBM and domain knowledge-based approaches aim to improve prediction accuracy, interpretability, and physical consistency in a DDM framework. Incorporating domain knowledge as additional information about the mechanisms responsible for generating streamflow can help to build physically consistent models and improve model performance [14][25][26]. Additionally, integrating process-based models with data-driven models is recognized as a way to create a streamflow model that is both physically consistent and interpretable.

2. Overview of Basic Watershed Processes

In the modeling paradigm, particularly within the context of PBM, detailed analysis and discussion of the distinct water balance segments and hydrological processes, along with comprehensive mathematical justifications and expert insights drawn from both the water balance and intimate familiarity with a study region, are crucial for strengthening the modeling procedures. Conversely, DDM can assist in circumventing certain modeling chain steps that involve uncertainty. Given the growing prevalence of the combined data-driven and PBM approach [12][27], this section provides an overview of both methods.

2.1. Streamflow Generation Processes

Several factors influence streamflow generation, such as climate, hydrogeology, soil properties, vegetation, management scenarios, and antecedent conditions. Precipitation undergoes interception by vegetation, infiltration into the soil, or surface runoff into streams. Evapotranspiration (ET) and subsurface processes, especially baseflow and lateral flow, significantly contribute to streamflow generation. From a watershed hydrology perspective, the generation is depicted based on their relation to surface processes, rootzone processes, and groundwater flow (Figure 1). However, conceptualizing and modeling streamflow has long been an intricate environmental challenge due to the significant subsurface flow mechanisms occurring in soil and bedrock, which researchers have limited capacity to quantify and evaluate [28].
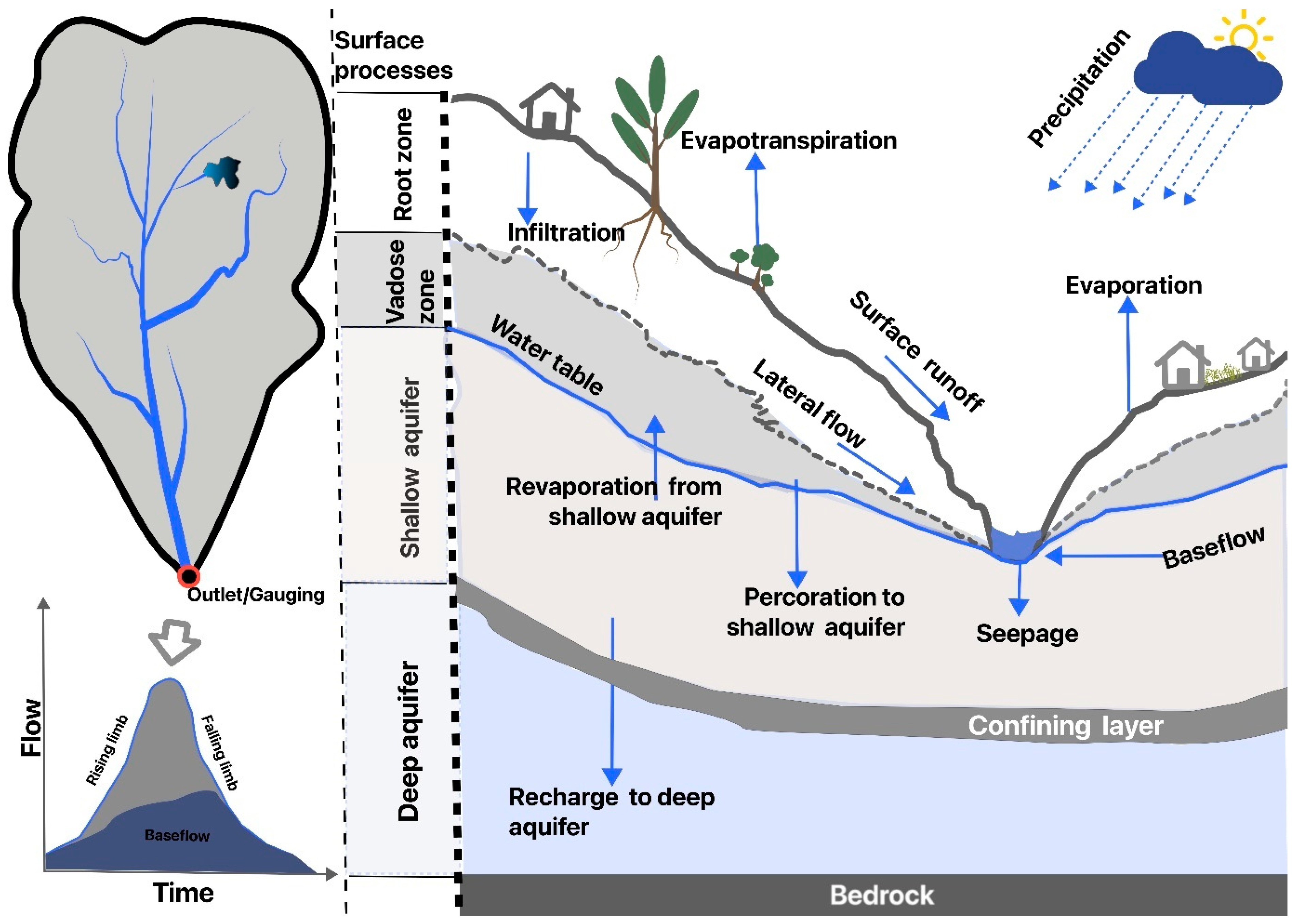
Sustainability 16 01376 g001
Figure 1. Basic watershed surface and subsurface hydrological processes and simplified diagram of the hydrograph.

2.2. Streamflow Prediction

PBM is typically used when there is a good understanding of the fundamental processes driving the system, and the goal is to create a model that accurately captures those processes. On the other hand, data-driven hydrological models use statistical or soft computing methods to map inputs to outputs without considering the physical hydrological processes involved in the transformation. The DDM approach is discussed further. Examples of widely utilized PBM include the Soil and Water Assessment Tool (SWAT), HBV (Hydrologiska Byråns Vattenbalansavdelning) [29], GR4J (Génie Rural à 4 paramètres Journalier) [30], Variable Infiltration Capacity (VIC) [31], the Hydrologic Engineering Center–Hydrologic Modeling System (HEC-HMS) [32], and the Precipitation-Runoff Modeling System (PRMS) [33]. Next, researchers described the key hydrological processes and equations used in the SWAT model as an example of PBM.
The SWAT model ET computation relies on potential evapotranspiration (PET) and has multiple options. The selection of a method primarily depends on the availability of data. For instance, the Penman–Monteith method [34] necessitates measurements of solar radiation, air temperature, relative humidity, and wind speed, whereas the Hargreaves method [35] requires only air temperature data.

2.3. Basic Processes in Data-Driven Streamflow Prediction

DDM can be broadly classified into two types: conventional data-driven techniques and AI-based models [36][37]. Conventional techniques, such as multiple linear regression (MLR), autoregressive integrated moving average (ARIMA), autoregressive-moving average (ARMA), and autoregressive-moving average with the exogenous term (ARMAX), are preferred in SFP due to their simplicity. In contrast, AI-based models offer more advanced capabilities and higher accuracy [37][38]. The most widely utilized AI-based data-driven models fall into four categories: evolutionary algorithms, fuzzy-logic algorithms, classification methods, and artificial network techniques [10][38].
The basic steps in DDM include data preprocessing, selecting suitable inputs and architecture, parameter estimation, and model validation [39][40][41]. This procedure unfolds in four key steps: data collection and cleaning, feature selection and engineering, model selection and building, and prediction (Figure 2). Effective data preprocessing, which typically involves essential steps such as data cleaning to detect and correct anomalies or inconsistencies, is critical for DDM as it significantly impacts subsequent analysis accuracy and efficiency [40]. To ensure the model’s ability to generalize to real-world scenarios, a crucial step is to divide the available data into three distinct subsets: training, testing, and validation [42]. This strategic division allows the model to learn from the majority of the data during training, undergo a rigorous evaluation on a separate testing set, and finally, have its ability to generalize to unseen data confidently validated [43].
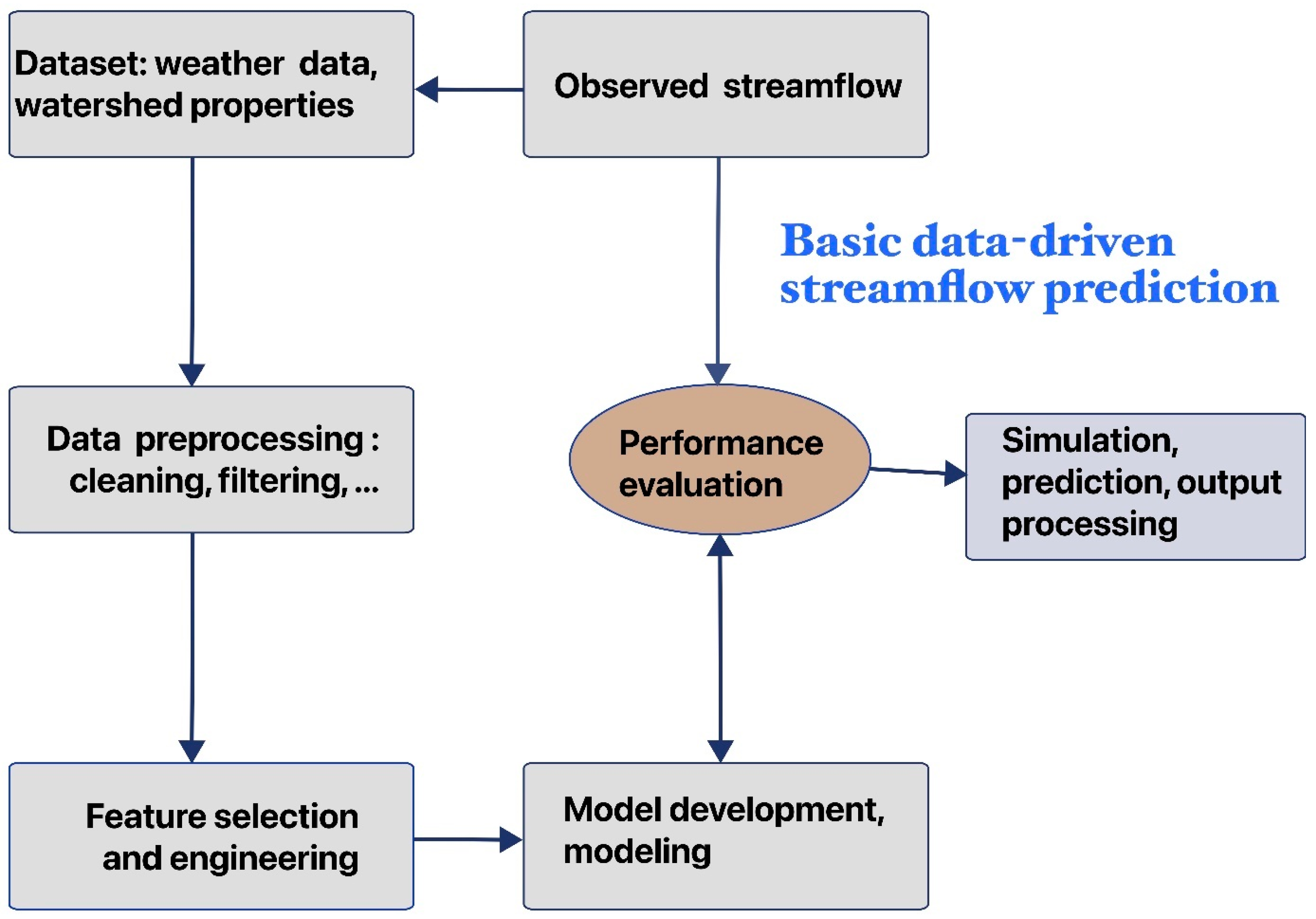
Sustainability 16 01376 g002
Figure 2. The fundamental data-driven prediction process.
Utilizing multiple input variables in hydrologic and water resources applications poses a challenge in identifying the most relevant or significant ones [41][44]. Selecting the most pertinent features can enhance model accuracy, mitigate overfitting, and improve the interpretability of natural processes [40][44][45]. Feature selection encompasses a variety of techniques, including filtering, wrapper, and embedded methods, which are broadly classified into model-free and model-based approaches [45][46][47].
An ideal input selection algorithm should exhibit flexibility for modeling, computational efficiency for handling high-dimensional datasets, scalability with respect to input dimensionality, and redundancy minimization [45]. A primary drawback of the model-based method lies in its computational demands, as it necessitates numerous calibration and validation processes to identify the optimal input combination. This renders the method unsuitable for large datasets [47]. Moreover, the input selection outcome hinges on the predetermined model class and architecture. Nonetheless, model-based approaches generally achieve superior performance due to their fine-tuning to the specific interactions between the model class and the data.
Feature engineering, the process of preparing input data before training a neural network, offers several benefits: reduced error in estimated outcomes, shorter training times, and equal attention to all data [48]. Effective normalization involves converting data to a linear scale, where equal relative changes correspond to identical absolute values [49]. Data are typically adjusted to fit within ranges like [–1, 1], [0.1, 0.9], or [0, 1] [49][50].
A comprehensive evaluation of a hydrological prediction model’s performance requires both graphical and numerical analyses of its error relative to observed data, including the selection of appropriate performance criteria and careful interpretation of the results [51]. For a more holistic assessment, it is recommended to use at least one goodness-of-fit measure, such as the Nash–Sutcliffe Efficiency Coefficient (NSE) [52], and one absolute error measure, such as root mean square error (RMSE) [53]. Specifically, for DDM, the relative correlation coefficient is recommended as an alternative to conventional evaluation measures such as NSE [53].

References

  1. Gleeson, T.; Wang-Erlandsson, L.; Porkka, M.; Zipper, S.C.; Jaramillo, F.; Gerten, D.; Fetzer, I.; Cornell, S.E.; Piemontese, L.; Gordon, L.J.; et al. Illuminating Water Cycle Modifications and Earth System Resilience in the Anthropocene. Water Resour. Res. 2020, 56, e2019WR024957.
  2. Carlisle, D.M.; Wolock, D.M.; Meador, M.R. Alteration of Streamflow Magnitudes and Potential Ecological Consequences: A Multiregional Assessment. Front. Ecol. Environ. 2011, 9, 264–270.
  3. Quang, N.H.; Viet, T.Q.; Thang, H.N.; Hieu, N.T.D. Long-Term Water Level Dynamics in the Red River Basin in Response to Anthropogenic Activities and Climate Change. Sci. Total Environ. 2024, 912, 168985.
  4. Depetris, P.J. The Importance of Monitoring River Water Discharge. Front. Water 2021, 3, 745912.
  5. Al Sawaf, M.B.; Kawanisi, K. Assessment of Mountain River Streamflow Patterns and Flood Events Using Information and Complexity Measures. J. Hydrol. 2020, 590, 125508.
  6. Bourdin, D.R.; Fleming, S.W.; Stull, R.B. Streamflow Modelling: A Primer on Applications, Approaches and Challenges. Atmos.-Ocean 2012, 50, 507–536.
  7. Mai, J.; Craig, J.R.; Tolson, B.A.; Arsenault, R. The Sensitivity of Simulated Streamflow to Individual Hydrologic Processes across North America. Nat. Commun. 2022, 13, 455.
  8. Solomatine, D.P.; Ostfeld, A. Data-Driven Modelling: Some Past Experiences and New Approaches. J. Hydroinform. 2008, 10, 3–22.
  9. Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007.
  10. Yaseen, Z.M.; El-shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial Intelligence Based Models for Stream-Flow Forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844.
  11. Zhang, B.; Govindaraju, R.S. Prediction of Watershed Runoff Using Bayesian Concepts and Modular Neural Networks. Water Resour. Res. 2000, 36, 753–762.
  12. Nearing, G.S.; Kratzert, F.; Sampson, A.K.; Pelissier, C.S.; Klotz, D.; Frame, J.M.; Prieto, C.; Gupta, H.V. What Role Does Hydrological Science Play in the Age of Machine Learning? Water Resour. Res. 2021, 57, e2020WR028091.
  13. Li, K.; Huang, G.; Wang, S.; Razavi, S. Development of a Physics-Informed Data-Driven Model for Gaining Insights into Hydrological Processes in Irrigated Watersheds. J. Hydrol. 2022, 613, 128323.
  14. Xie, K.; Liu, P.; Zhang, J.; Han, D.; Wang, G.; Shen, C. Physics-Guided Deep Learning for Rainfall-Runoff Modeling by Considering Extreme Events and Monotonic Relationships. J. Hydrol. 2021, 603, 127043.
  15. Zemzami, M.; Benaabidate, L. Improvement of Artificial Neural Networks to Predict Daily Streamflow in a Semi-Arid Area. Hydrol. Sci. J. 2016, 61, 1801–1812.
  16. Kim, T.; Yang, T.; Gao, S.; Zhang, L.; Ding, Z.; Wen, X.; Gourley, J.J.; Hong, Y. Can Artificial Intelligence and Data-Driven Machine Learning Models Match or Even Replace Process-Driven Hydrologic Models for Streamflow Simulation?: A Case Study of Four Watersheds with Different Hydro-Climatic Regions across the CONUS Daily Streamflow. J. Hydrol. 2021, 598, 126423.
  17. Dawson, C.W.; Wilby, R.L. Hydrological Modelling Using Artificial Neural Networks. Prog. Phys. Geogr. 2001, 25, 80–108.
  18. Abrahart, R.J.; Anctil, F.; Coulibaly, P.; Dawson, C.W.; Mount, N.J.; See, L.M.; Shamseldin, A.Y.; Solomatine, D.P.; Toth, E.; Wilby, R.L. Two Decades of Anarchy? Emerging Themes and Outstanding Challenges for Neural Network River Forecasting. Prog. Phys. Geogr. Earth Environ. 2012, 36, 480–513.
  19. Boucher, M.-A.; Quilty, J.; Adamowski, J. Data Assimilation for Streamflow Forecasting Using Extreme Learning Machines and Multilayer Perceptrons. Water Resour. Res. 2020, 56, e2019WR026226.
  20. Cho, K.; Kim, Y. Improving Streamflow Prediction in the WRF-Hydro Model with LSTM Networks. J. Hydrol. 2022, 605, 127297.
  21. Lu, D.; Konapala, G.; Painter, S.L.; Kao, S.-C.; Gangrade, S. Streamflow Simulation in Data-Scarce Basins Using Bayesian and Physics-Informed Machine Learning Models. J. Hydrometeorol. 2021, 22, 1421–1438.
  22. Brunner, M.I.; Slater, L.; Tallaksen, L.M.; Clark, M. Challenges in Modeling and Predicting Floods and Droughts: A Review. WIREs Water 2021, 8, e1520.
  23. Bailey, R.T.; Wible, T.C.; Arabi, M.; Records, R.M.; Ditty, J. Assessing Regional-Scale Spatio-Temporal Patterns of Groundwater-Surface Water Interactions Using a Coupled SWAT-MODFLOW Model. Hydrol. Process. 2016, 143, 103662.
  24. El Hassan, A.A.; Sharif, H.O.; Jackson, T.; Chintalapudi, S. Performance of a Conceptual and Physically Based Model in Simulating the Response of a Semi-urbanized Watershed in San Antonio, Texas. Hydrol. Process. 2013, 27, 3394–3408.
  25. Tongal, H.; Booij, M.J. Simulated Annealing Coupled with a Naïve Bayes Model and Base Flow Separation for Streamflow Simulation in a Snow Dominated Basin. Stoch. Environ. Res. Risk Assess. 2022, 37, 89–112.
  26. Corzo, G.; Solomatine, D. Baseflow Separation Techniques for Modular Artificial Neural Network Modelling in Flow Forecasting. Hydrol. Sci. J. 2007, 52, 491–507.
  27. Mohammadi, B.; Safari, M.J.S.; Vazifehkhah, S. IHACRES, GR4J and MISD-Based Multi Conceptual-Machine Learning Approach for Rainfall-Runoff Modeling. Sci. Rep. 2022, 12, 12096.
  28. Beven, K. Rainfall-Runoff Modelling, 2nd ed.; Wiley: Chichester, UK, 2012; ISBN 9780470714591.
  29. Seibert, J.; Vis, M.J.P. Teaching Hydrological Modeling with a User-Friendly Catchment-Runoff-Model Software Package. Hydrol. Earth Syst. Sci. 2012, 16, 3315–3325.
  30. Perrin, C.; Michel, C.; Andréassian, V. Improvement of a Parsimonious Model for Streamflow Simulation. J. Hydrol. 2003, 279, 275–289.
  31. Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A Simple Hydrologically Based Model of Land Surface Water and Energy Fluxes for General Circulation Models. J. Geophys. Res. 1994, 99, 14415.
  32. Hydrologic Engineering Center. Hydrologic Engineering Center. Hydrologic Modeling System Technical Reference Manual. In Hydrologic Modeling System HEC-HMS: Technical Reference Manual; Hydrologic Engineering Center: Davis, CA, USA, 2000; p. 148.
  33. Regan, R.S.; Markstrom, S.L.; Hay, L.E.; Viger, R.J.; Norton, P.A.; Driscoll, J.M.; Lafontaine, J.H. Description of the National Hydrologic Model for Use with the Precipitation-Runoff Modeling System (PRMS); U.S. Geological Survey: Reston, VA, USA, 2018.
  34. Monteith, J.L. Evaporation and Environment. In Proceedings of the Symposia of the Society for Experimental Biology; Volume 19, pp. 205–234. Available online: https://repository.rothamsted.ac.uk/item/8v5v7 (accessed on 2 January 2024).
  35. Hargreaves, G.H.; Samani, Z.A. Samani Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99.
  36. Solomatine, D.; See, L.M.; Abrahart, R.J. Data-Driven Modelling: Concepts, Approaches and Experiences. In Practical Hydroinformatics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 17–30.
  37. Zhang, Z.; Zhang, Q.; Singh, V.P. Univariate Streamflow Forecasting Using Commonly Used Data-Driven Models: Literature Review and Case Study. Hydrol. Sci. J. 2018, 63, 1091–1111.
  38. Zounemat-Kermani, M.; Matta, E.; Cominola, A.; Xia, X.; Zhang, Q.; Liang, Q.; Hinkelmann, R. Neurocomputing in Surface Water Hydrology and Hydraulics: A Review of Two Decades Retrospective, Current Status and Future Prospects. J. Hydrol. 2020, 588, 125085.
  39. Sudheer, K.P.; Nayak, P.C.; Ramasastri, K.S. Improving Peak Flow Estimates in Artificial Neural Network River Flow Models. Hydrol. Process. 2003, 17, 677–686.
  40. Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods Used for the Development of Neural Networks for the Prediction of Water Resource Variables in River Systems: Current Status and Future Directions. Environ. Model. Softw. 2010, 25, 891–909.
  41. Taormina, R.; Galelli, S.; Karakaya, G.; Ahipasaoglu, S.D. An Information Theoretic Approach to Select Alternate Subsets of Predictors for Data-Driven Hydrological Models. J. Hydrol. 2016, 542, 18–34.
  42. Zheng, F.; Maier, H.R.; Wu, W.; Dandy, G.C.; Gupta, H.V.; Zhang, T. On Lack of Robustness in Hydrological Model Development Due to Absence of Guidelines for Selecting Calibration and Evaluation Data: Demonstration for Data-Driven Models. Water Resour. Res. 2018, 54, 1013–1030.
  43. Wu, W.; May, R.J.; Maier, H.R.; Dandy, G.C. A Benchmarking Approach for Comparing Data Splitting Methods for Modeling Water Resources Parameters Using Artificial Neural Networks. Water Resour. Res. 2013, 49, 7598–7614.
  44. Reis, G.B.; da Silva, D.D.; Fernandes Filho, E.I.; Moreira, M.C.; Veloso, G.V.; Fraga, M.d.S.; Pinheiro, S.A.R. Effect of Environmental Covariable Selection in the Hydrological Modeling Using Machine Learning Models to Predict Daily Streamflow. J. Environ. Manag. 2021, 290, 112625.
  45. Galelli, S.; Castelletti, A. Tree-Based Iterative Input Variable Selection for Hydrological Modeling. Water Resour. Res. 2013, 49, 4295–4310.
  46. Taormina, R.; Chau, K.W. Data-Driven Input Variable Selection for Rainfall-Runoff Modeling Using Binary-Coded Particle Swarm Optimization and Extreme Learning Machines. J. Hydrol. 2015, 529, 1617–1632.
  47. May, R.J.; Maier, H.R.; Dandy, G.C.; Fernando, T.M.K.G. Non-Linear Variable Selection for Artificial Neural Networks Using Partial Mutual Information. Environ. Model. Softw. 2008, 23, 1312–1326.
  48. Sola, J.; Sevilla, J. Importance of Input Data Normalization for the Application of Neural Networks to Complex Industrial Problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468.
  49. Isik, S.; Kalin, L.; Schoonover, J.E.; Srivastava, P.; Graeme Lockaby, B. Modeling Effects of Changing Land Use/Cover on Daily Streamflow: An Artificial Neural Network and Curve Number Based Hybrid Approach. J. Hydrol. 2013, 485, 103–112.
  50. Nourani, V.; Baghanam, A.H.; Adamowski, J.; Gebremichael, M. Using Self-Organizing Maps and Wavelet Transforms for Space–Time Pre-Processing of Satellite Precipitation and Runoff Data in Neural Network Based Rainfall–Runoff Modeling. J. Hydrol. 2013, 476, 228–243.
  51. Teegavarapu, R.S.V.; Sharma, P.J.; Lal Patel, P. Frequency-Based Performance Measure for Hydrologic Model Evaluation. J. Hydrol. 2022, 608, 127583.
  52. Nash, J.E.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290.
  53. Hwang, S.H.; Ham, D.H.; Kim, J.H. A New Measure for Assessing the Efficiency of Hydrological Data-Driven Forecasting Models. Hydrol. Sci. J. 2012, 57, 1257–1274.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Water Resources; Environmental Sciences
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Bisrat Ayalew Yifru
,
Kyoung Jae Lim
,
Seoro Lee
View Times: 438
Revisions: 2 times (View History)
Update Date: 26 Feb 2024
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback