| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Emmanuel Ebinyu | -- | 4348 | 2023-11-21 12:18:23 | | | |
| 2 | Jason Zhu | -2 word(s) | 4369 | 2023-11-22 02:23:56 | | | | |
| 3 | Jason Zhu | -2 word(s) | 4367 | 2023-12-29 06:51:51 | | |
Video Upload Options
Changes are being implemented in the electrical power grid to accommodate the increased penetration of renewable energy sources interfaced with grid-connected inverters. The grid-forming (GFM) control paradigm of inverters in active power grids has emerged as a technique through which to tackle the effects of the diminishing dominance of synchronous generators (SGs) and is preferred to the grid-following (GFL) control for providing system control and stability in converter-dominated grids.
1. Introduction
2. Droop Control
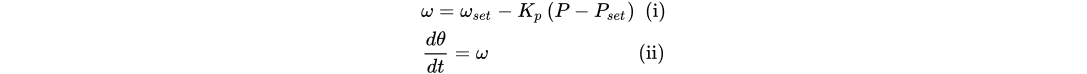 where 𝜔 is the instantaneous angular frequency, 𝜔𝑠𝑒𝑡 is the angular frequency reference, 𝑃 is the power output of the converter, 𝑃𝑠𝑒𝑡 is the reference power, 𝐾𝑝 is the 𝑃−𝜔 droop coefficient, and 𝜃 is the power angle.
where 𝜔 is the instantaneous angular frequency, 𝜔𝑠𝑒𝑡 is the angular frequency reference, 𝑃 is the power output of the converter, 𝑃𝑠𝑒𝑡 is the reference power, 𝐾𝑝 is the 𝑃−𝜔 droop coefficient, and 𝜃 is the power angle.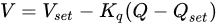
where 𝜃𝑠𝑒𝑡 is the set value of the power angle, 𝑃 is the real power output of the inverter, 𝑃𝑠𝑒𝑡 is the reference power value, and 𝐾𝑝 is the 𝑃−𝜃 droop coefficient.

where 𝑉 is the instantaneous voltage, 𝑉𝑠𝑒𝑡 is the voltage reference, 𝑄 is the instantaneous reactive power, and 𝑄𝑠𝑒𝑡 is the reference reactive power.
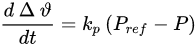
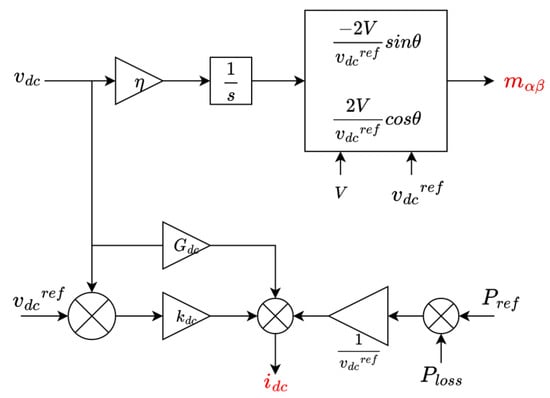
3. Power Synchronisation Control (PSC)

where 𝜗 is the electrical angle, 𝑘𝑝 is the controller gain, 𝑃 is the instantaneous active power, and 𝑃𝑟𝑒𝑓 is the reference of active power.
4. Synchronous Machine Emulation Controllers
4.1. Virtual Synchronous Generator (VSG) Control
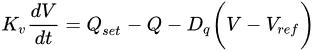
where 𝜔 is the angular frequency, 𝜔0 is the set value of angular frequency, 𝜃 is the electrical angle, 𝐽 is the inertia constant, 𝐷𝑝 is the damping coefficient of the rotor dynamics, 𝐾𝑝 is governor stiffness factor, 𝑃𝑒 is the electrical power supplied, 𝑃𝑠𝑒𝑡 is the set value of power, and 𝑃𝑟𝑒𝑓 is a variable calculated in the controller, derived as shown in Figure 1.
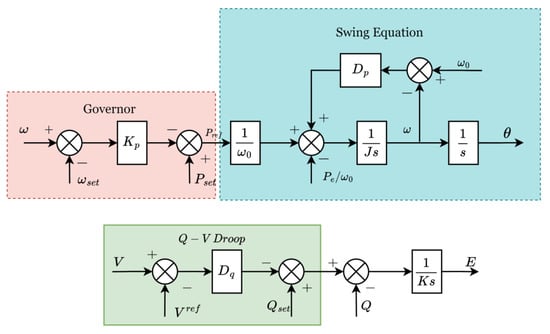

where 𝐾𝑣 is the voltage integral gain, 𝑄 is the instantaneous reactive power and 𝑄𝑠𝑒𝑡 its set value, and 𝐷𝑝 is the 𝑄−𝑉 droop coefficient of the controller.
4.2. Synchronverter
where 𝜃 is the electrical angle, with 𝜃¨=𝑑2𝜃𝑑𝑡2, 𝜃˙=𝑑𝜃𝑑𝑡; 𝐽 is the moment of inertia, 𝐷𝑝 is the damping factor, also designed for droop functionality [50]; 𝑇𝑚 is the mechanical torque; 𝑇𝑒 is the electrical torque; 〈.,.〉 represents the inner product; 𝑀𝑓 is the mutual inductance; 𝑖𝑓 is the excitation current of the stator; 𝑒 is the electromotive force; 𝑃 is the real power; 𝑄 is the reactive power; and 𝑖 is the stator current.

where 𝑃0 and 𝜔0 are the nominal values for real power and angular frequency.
5. Matching Control

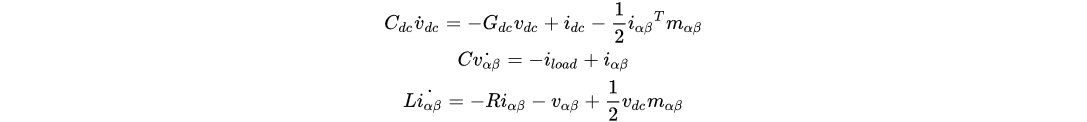
where 𝑥˙=𝑑x𝑑𝑡 for an arbitrary variable 𝑥.
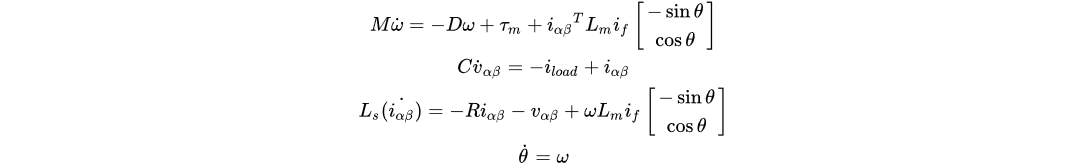
where M is the rotor inertia, 𝐷 is the damping coefficient, 𝜏𝑚 is the mechanical torque, 𝐿𝑚 is mutual inductance of the machine, 𝑖𝑓 is rotor current, 𝜃 is the electrical angle, 𝐶 is the capacitance at the output, 𝑖𝛼𝛽 and 𝑣𝛼𝛽 are the output inductance current and output voltage expressed in the 𝛼𝛽− frame, 𝑖𝑙𝑜𝑎𝑑 is the load current, 𝐿𝑠 is the stator inductance, 𝑅 is the stator resistance, and 𝜔 is the angular frequency.
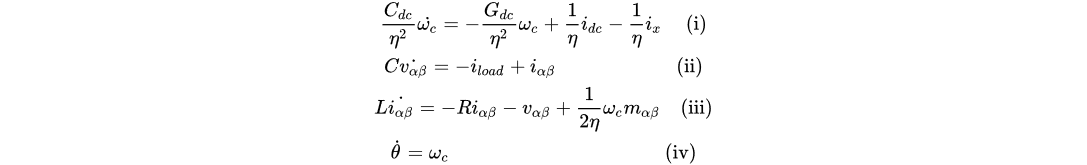
5. Virtual Oscillator Control (VOC)

-
Parallel 𝐿𝐶 tank, which determines the resonant frequency that sets the system frequency.
-
𝑔(𝑣𝑐) represents a voltage-dependent source. The value of its maximum slope, 𝜎, is related to the resistance, 𝑅, used for damping. The constant 𝜐 is the voltage scaling factor related to the grid RMS value, and 𝜑 and 𝑘𝑖 are used to ensure that the voltage of the inverter is within the limits for safe supply to load. 𝜅 is related to the power rating of the GFM in proportion to other inverters within the network.
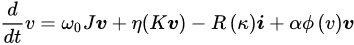 where 𝑣=[𝑣𝛼,𝑣𝛽]𝑇 is the terminal voltage in the 𝛼𝛽− frame, 𝑖=[𝑖𝛼,𝑖𝛽]𝑇 is the measured inverter current, 𝜂,𝛼>0 are positive constants, and 0<𝜅<𝜋, 𝑅(𝜅)=[cos𝜅sin𝜅−sin𝜅cos𝜅], 𝐽=𝑅(𝜋/2), 𝐾=1𝑉02𝑅(𝜅)[𝑃0−𝑄0𝑄0𝑃0], and 𝜙(𝑣)=𝑉02−‖𝑣‖2𝑉02, where ‖𝑣‖ is the Euclidean norm. 𝑃0, 𝑄0, and 𝑉0 are the active power, reactive power, and voltage set points, respectively. 𝜅 caters for the line parameters, i.e., 0 for resistive and 𝜋2 for inductive lines. The dVOC controller is shown in Figure 13b.
where 𝑣=[𝑣𝛼,𝑣𝛽]𝑇 is the terminal voltage in the 𝛼𝛽− frame, 𝑖=[𝑖𝛼,𝑖𝛽]𝑇 is the measured inverter current, 𝜂,𝛼>0 are positive constants, and 0<𝜅<𝜋, 𝑅(𝜅)=[cos𝜅sin𝜅−sin𝜅cos𝜅], 𝐽=𝑅(𝜋/2), 𝐾=1𝑉02𝑅(𝜅)[𝑃0−𝑄0𝑄0𝑃0], and 𝜙(𝑣)=𝑉02−‖𝑣‖2𝑉02, where ‖𝑣‖ is the Euclidean norm. 𝑃0, 𝑄0, and 𝑉0 are the active power, reactive power, and voltage set points, respectively. 𝜅 caters for the line parameters, i.e., 0 for resistive and 𝜋2 for inductive lines. The dVOC controller is shown in Figure 13b.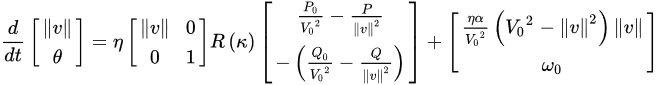 Assuming 𝜅=𝜋2 (for inductive impedance) and 𝑉0≈𝑉 for small voltage deviations in the steady state,
Assuming 𝜅=𝜋2 (for inductive impedance) and 𝑉0≈𝑉 for small voltage deviations in the steady state,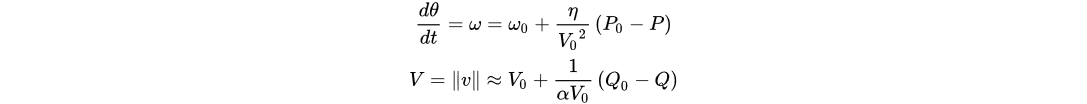 The authors of [76] tested the validity of the dVOC approach for inverters, showing its abilities for dynamic synchronisation, droop characteristics, black start, voltage regulation, and dynamic load sharing in an inverter-dominated grid.
The authors of [76] tested the validity of the dVOC approach for inverters, showing its abilities for dynamic synchronisation, droop characteristics, black start, voltage regulation, and dynamic load sharing in an inverter-dominated grid.
References
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-Forming Converters: Control Approaches, Grid-Synchronization, and Future Trends—A Review. IEEE Open J. Ind. Appl. 2021, 2, 93–109.
- Li, Z. Advanced Control of Grid-Forming Inverters under Uncertain Operating Conditions in AC Microgrids. Ph.D. Thesis, The Hong Kong Polytechnic University, Hongkong, China, 2021. Available online: https://theses.lib.polyu.edu.hk/handle/200/11693 (accessed on 17 July 2023).
- Dokus, M.; Mertens, A. On the Coupling of Power-Related and Inner Inverter Control Loops of Grid-Forming Converter Systems. IEEE Access 2021, 9, 16173–16192.
- Pereira, A.T.; Pinheiro, H. Inner Loop Controllers for Grid-Forming Converters. In Proceedings of the 2022 14th Seminar on Power Electronics and Control (SEPOC), Santa Maria, Brazil, 12–15 November 2022; pp. 1–6.
- Buso, S.; Caldognetto, T.; Liu, Q. Analysis and Experimental Characterization of a Large-Bandwidth Triple-Loop Controller for Grid-Tied Inverters. IEEE Trans. Power Electron. 2019, 34, 1936–1949.
- Gursoy, M.; Mirafzal, B. Direct vs. Indirect Control Schemes for Grid-Forming Inverters–Unveiling a Performance Comparison in a Microgrid. IEEE Access 2023, 11, 75023–75036.
- Pogaku, N.; Prodanovic, M.; Green, T.C. Modeling, Analysis and Testing of Autonomous Operation of an Inverter-Based Microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625.
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; Wiley: Hoboken, NJ, USA, 2010.
- Unruh, P.; Nuschke, M.; Strauß, P.; Welck, F. Overview on Grid-Forming Inverter Control Methods. Energies 2020, 13, 2589.
- Zhang, H.; Xiang, W.; Lin, W.; Wen, J. Grid Forming Converters in Renewable Energy Sources Dominated Power Grid: Control Strategy, Stability, Application, and Challenges. J. Mod. Power Syst. Clean Energy 2021, 9, 1239–1256.
- Abdel-Rahim, O.; Funato, H.; Junnosuke, H. Droop method based on model predictive control for DC microgrid. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–6.
- Majumder, R.; Ledwich, G.; Ghosh, A.; Chakrabarti, S.; Zare, F. Droop Control of Converter-Interfaced Microsources in Rural Distributed Generation. IEEE Trans. Power Deliv. 2010, 25, 2768–2778.
- D’Arco, S.; Suul, J.A. Virtual Synchronous Machines—Classification of Implementations and Analysis of Equivalence to Droop Controllers for Microgrids. In Proceedings of the 2013 IEEE Powertech Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–7.
- D’Arco, S.; Suul, J.A. Equivalence of Virtual Synchronous Machines and Frequency-Droops for Converter-Based MicroGrids. IEEE Trans. Smart Grid 2013, 5, 394–395.
- Sun, Y.; Hou, X.; Yang, J.; Han, H.; Su, M.; Guerrero, J.M. New Perspectives on Droop Control in AC Microgrid. IEEE Trans. Ind. Electron. 2017, 64, 5741–5745.
- Du, W.; Chen, Z.; Schneider, K.P.; Lasseter, R.H.; Nandanoori, S.P.; Tuffner, F.K.; Kundu, S. A Comparative Study of Two Widely Used Grid-Forming Droop Controls on Microgrid Small-Signal Stability. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 963–975.
- Shi, Y.; Gu, X.; Yin, X.; Feng, S.; Zhang, S. Design of droop controller in islanded microgrids using multi-objective optimisation based on accurate small-signal model. IET Power Electron. 2022, 15, 1093–1109.
- Eberlein, S.; Rudion, K. Small-signal stability modelling, sensitivity analysis and optimization of droop controlled inverters in LV microgrids. Int. J. Electr. Power Energy Syst. 2021, 125, 106404.
- Eberlein, S.; Rudion, K. Optimisation, benchmark testing and comparison of droop control variants in microgrids. IET Smart Grid 2021, 4, 536–548.
- Belal, E.K.; Yehia, D.M.; Azmy, A.M. Effective Power Management of DC Microgrids Using Adaptive Droop Control. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 905–910.
- Gurugubelli, V.; Ghosh, A.; Panda, A.K.; Rudra, S. Implementation and comparison of droop control, virtual synchronous machine, and virtual oscillator control for parallel inverters in standalone microgrid. Int. Trans. Electr. Energy Syst. 2021, 31, e12859.
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820.
- Ahmed, H.Y.; Abdel-Rahim, O.; Ali, Z.M. New High-Gain Transformerless DC/DC Boost Converter System. Electronics 2022, 11, 734.
- Zhang, L.; Harnefors, L.; Nee, H.-P. Interconnection of Two Very Weak AC Systems by VSC-HVDC Links Using Power-Synchronization Control. IEEE Trans. Power Syst. 2011, 26, 344–355.
- Sepehr, A.; Gomis-Bellmunt, O.; Pouresmaeil, E. Employing Machine Learning for Enhancing Transient Stability of Power Synchronization Control During Fault Conditions in Weak Grids. IEEE Trans. Smart Grid 2022, 13, 2121–2131.
- Zhang, L.; Nee, H.-P.; Harnefors, L. Analysis of Stability Limitations of a VSC-HVDC Link Using Power-Synchronization Control. IEEE Trans. Power Syst. 2011, 26, 1326–1337.
- Harnefors, L.; Hinkkanen, M.; Riaz, U.; Rahman, F.M.M.; Zhang, L. Robust Analytic Design of Power-Synchronization Control. IEEE Trans. Ind. Electron. 2019, 66, 5810–5819.
- Xiong, X.; Zhou, Y.; Luo, B.; Cheng, P.; Blaabjerg, F. Analysis and Suppression Strategy of Synchronous Frequency Resonance for Grid-Connected Converters with Power-Synchronous Control Method. IEEE Trans. Power Electron. 2023, 38, 6945–6955.
- Wu, H.; Wang, X. Design-Oriented Transient Stability Analysis of Grid-Connected Converters with Power Synchronization Control. IEEE Trans. Ind. Electron. 2019, 66, 6473–6482.
- Yazdani, S.; Davari, M.; Ferdowsi, M.; Shamsi, P. Internal Model Power Synchronization Control of a PV-Based Voltage-Source Converter in Weak-Grid and Islanded Conditions. IEEE Trans. Sustain. Energy 2021, 12, 1360–1371.
- Yazdani, S.; Ferdowsi, M.; Shamsi, P. Power Synchronization PID Control Method for Grid-Connected Voltage-Source Converters. In Proceedings of the 2020 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 13–14 July 2020; pp. 1–6.
- Driesen, J.; Visscher, K. Virtual synchronous generators. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–3.
- Liu, J.; Miura, Y.; Bevrani, H.; Ise, T. Enhanced Virtual Synchronous Generator Control for Parallel Inverters in Microgrids. IEEE Trans. Smart Grid 2017, 8, 2268–2277.
- Li, B.; Zhou, L.; Yu, X.; Zheng, C.; Liu, J. Improved power decoupling control strategy based on virtual synchronous generator. IET Power Electron. 2017, 10, 462–470.
- Shuai, Z.; Shen, C.; Liu, X.; Li, Z.; Shen, Z.J. Transient Angle Stability of Virtual Synchronous Generators Using Lyapunov’s Direct Method. IEEE Trans. Smart Grid 2019, 10, 4648–4661.
- Chen, M.; Zhou, D.; Blaabjerg, F. Enhanced Transient Angle Stability Control of Grid-Forming Converter Based on Virtual Synchronous Generator. IEEE Trans. Ind. Electron. 2022, 69, 9133–9144.
- Xiong, X.; Wu, C.; Hu, B.; Pan, D.; Blaabjerg, F. Transient Damping Method for Improving the Synchronization Stability of Virtual Synchronous Generators. IEEE Trans. Power Electron. 2021, 36, 7820–7831.
- Sadeque, F.; Fateh, F. On Control Schemes for Grid-Forming Inverters. In Proceedings of the 2022 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 25–26 April 2022; pp. 1–6.
- Shintai, T.; Miura, Y.; Ise, T. Oscillation Damping of a Distributed Generator Using a Virtual Synchronous Generator. IEEE Trans. Power Deliv. 2014, 29, 668–676.
- Wang, L.; Zhou, H.; Hu, X.; Hou, X.; Su, C.; Sun, K. Adaptive Inertia and Damping Coordination (AIDC) Control for Grid-Forming VSG to Improve Transient Stability. Electronics 2023, 12, 2060.
- Cheema, K.M.; Chaudhary, N.I.; Tahir, M.F.; Mehmood, K.; Mudassir, M.; Kamran, M.; Milyani, A.H.; Elbarbary, Z.S. Virtual synchronous generator: Modifications, stability assessment and future applications. Energy Rep. 2022, 8, 1704–1717.
- Li, J.; Li, Y.; Du, Z.; Xu, Z.; Dong, Z. Damping Turning Rule of Virtual Synchronous Generator for Global Stability. IEEE Trans. Power Deliv. 2023, 38, 2650–2660.
- Li, C.; Yang, Y.; Cao, Y.; Wang, L.; Blaabjerg, F.; Dragicevic, T. Frequency and Voltage Stability Analysis of Grid-Forming Virtual Synchronous Generator Attached to Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2662–2671.
- Chen, S.; Sun, Y.; Han, H.; Fu, S.; Luo, S.; Shi, G. A Modified VSG Control Scheme with Virtual Resistance to Enhance Both Small-Signal Stability and Transient Synchronization Stability. IEEE Trans. Power Electron. 2023, 38, 6005–6014.
- Miranbeigi, M.; Kandula, P.; Divan, D. A New Representation based on Virtual Capacitor for Virtual Synchronous Generators. In Proceedings of the 2020 IEEE 11th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Dubrovnik, Croatia, 28 September–1 October 2020; pp. 205–210.
- Suvorov, A.; Askarov, A.; Bay, Y.; Maliuta, B.; Achitaev, A.; Suslov, K. Comparative small-signal stability analysis of voltage-controlled and enhanced current-controlled virtual synchronous generators under weak and stiff grid conditions. Int. J. Electr. Power Energy Syst. 2023, 147, 108891.
- Yang, Y.; Xu, J.; Li, C.; Zhang, W.; Wu, Q.; Wen, M.; Blaabjerg, F. A New Virtual Inductance Control Method for Frequency Stabilization of Grid-Forming Virtual Synchronous Generators. IEEE Trans. Ind. Electron. 2023, 70, 441–451.
- Lu, S.; Zhu, Y.; Dong, L.; Na, G.; Hao, Y.; Zhang, G.; Zhang, W.; Cheng, S.; Yang, J.; Sui, Y. Small-Signal Stability Research of Grid-Connected Virtual Synchronous Generators. Energies 2022, 15, 7158.
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267.
- Tayyebi, A.; Dörfler, F.; Kupzog, F.; Miletic, Z.; Hribernik, W. Grid-Forming Converters—Inevitability, Control Strategies and Challenges in Future Grids Application. In Proceedings of the CIRED 2018 Ljubljana Workshop, Ljubljana, Slovenia, 7–8 June 2018.
- Rosso, R.; Engelken, S.; Liserre, M. A Generalized Formulation of Active Power Synchronization Based Control Algorithms for Grid Connected Converters. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 883–888.
- Zhong, Q.-C.; Nguyen, P.-L.; Ma, Z.; Sheng, W. Self-Synchronized Synchronverters: Inverters Without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 2014, 29, 617–630.
- Natarajan, V.; Weiss, G. Synchronverters with Better Stability Due to Virtual Inductors, Virtual Capacitors, and Anti-Windup. IEEE Trans. Ind. Electron. 2017, 64, 5994–6004.
- Lorenzetti, P.; Kustanovich, Z.; Shivratri, S.; Weiss, G. The Equilibrium Points and Stability of Grid-Connected Synchronverters. IEEE Trans. Power Syst. 2022, 37, 1184–1197.
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Babu, T.S.; Pouryekta, A. Synchronverter: A Comprehensive Review of Modifications, Stability Assessment, Applications and Future Perspectives. IEEE Access 2020, 8, 131565–131589.
- Gomes, L.D.N.; Abrantes-Ferreira, A.J.G.; Dias, R.F.d.S.; Rolim, L.G.B. Synchronverter-Based STATCOM With Voltage Imbalance Compensation Functionality. IEEE Trans. Ind. Electron. 2022, 69, 4836–4844.
- Remon, D.; Cantarellas, A.M.; Rakhshani, E.; Candela, I.; Rodriguez, P. An active power synchronization control loop for grid-connected converters. In Proceedings of the IEEE Power & Energy Society General Meeting, National Harbor, MD, USA, 27–31 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–5.
- Arghir, C.; Jouini, T.; Dörfler, F. Grid-forming control for power converters based on matching of synchronous machines. Automatica 2018, 95, 273–282.
- Curi, S.; Gross, D.; Dorfler, F. Control of low-inertia power grids: A model reduction approach. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 5708–5713.
- Jouini, T.; Arghir, C.; Dörfler, F. Grid-Friendly Matching of Synchronous Machines by Tapping into the DC Storage. IFAC-Pap. Online 2016, 49, 192–197.
- Arghir, C.; Dorfler, F. The Electronic Realization of Synchronous Machines: Model Matching, Angle Tracking, and Energy Shaping Techniques. IEEE Trans. Power Electron. 2020, 35, 4398–4410.
- Dörfler, F.; Chertkov, M.; Bullo, F. Synchronization in complex oscillator networks and smart grids. Proc. Natl. Acad. Sci. USA 2013, 110, 2005–2010.
- Torres, L.A.B.; Hespanha, J.P.; Moehlis, J. Synchronization of Identical Oscillators Coupled Through a Symmetric Network with Dynamics: A Constructive Approach with Applications to Parallel Operation of Inverters. IEEE Trans. Autom. Control 2015, 60, 3226–3241.
- Johnson, B.B.; Dhople, S.V.; Hamadeh, A.O.; Krein, P.T. Synchronization of Parallel Single-Phase Inverters with Virtual Oscillator Control. IEEE Trans. Power Electron. 2014, 29, 6124–6138.
- Dhople, S.V.; Johnson, B.B.; Hamadeh, A.O. Virtual Oscillator Control for voltage source inverters. In Proceedings of the 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–4 October 2013; pp. 1359–1363.
- Aghdam, S.A.; Agamy, M. Virtual oscillator-based methods for grid-forming inverter control: A review. IET Renew. Power Gener. 2022, 16, 835–855.
- Sinha, M.; Dorfler, F.; Johnson, B.B.; Dhople, S.V. Virtual Oscillator Control subsumes droop control. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 2353–2358.
- Lu, M.; Dutta, S.; Purba, V.; Dhople, S.; Johnson, B. A Grid-compatible Virtual Oscillator Controller: Analysis and Design. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 2643–2649.
- Johnson, B.B.; Sinha, M.; Ainsworth, N.G.; Dorfler, F.; Dhople, S.V. Synthesizing Virtual Oscillators to Control Islanded Inverters. IEEE Trans. Power Electron. 2016, 31, 6002–6015.
- Sinha, M.; Dorfler, F.; Johnson, B.B.; Dhople, S.V. Uncovering Droop Control Laws Embedded Within the Nonlinear Dynamics of Van der Pol Oscillators. IEEE Trans. Control Netw. Syst. 2017, 4, 347–358.
- Luo, S.; Wu, W.; Koutroulis, E.G.; Chung, H.S.-H.; Blaabjerg, F.G. A New Virtual Oscillator Control Without Third-Harmonics Injection For DC/AC Inverter. IEEE Trans. Power Electron. 2021, 36, 10879–10888.
- Awal, M.A.; Yu, H.; Husain, I.; Yu, W.; Lukic, S.M. Selective Harmonic Current Rejection for Virtual Oscillator Controlled Grid-Forming Voltage Source Converters. IEEE Trans. Power Electron. 2020, 35, 8805–8818.
- Raisz, D.; Thai, T.T.; Monti, A. Power Control of Virtual Oscillator Controlled Inverters in Grid-Connected Mode. IEEE Trans. Power Electron. 2019, 34, 5916–5926.
- Colombino, M.; Gros, D.; Dorfler, F. Global phase and voltage synchronization for power inverters: A decentralized consensus-inspired approach. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 5690–5695.
- Colombino, M.; Groz, D.; Brouillon, J.-S.; Dorfler, F. Global Phase and Magnitude Synchronization of Coupled Oscillators with Application to the Control of Grid-Forming Power Inverters. IEEE Trans. Autom. Control 2019, 64, 4496–4511.
- Seo, G.-S.; Colombino, M.; Subotic, I.; Johnson, B.; Gros, D.; Dorfler, F. Dispatchable Virtual Oscillator Control for Decentralized Inverter-dominated Power Systems: Analysis and Experiments. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 561–566.
- Lu, M.; Dhople, S.V.; Johnson, B. Benchmarking Nonlinear Oscillators for Grid-Forming Inverter Control. IEEE Trans. Power Electron. 2022, 37, 10250–10266.
- Ali, M.; Nurdin, H.I.; Fletcher, J.E. Dispatchable Virtual Oscillator Control for Single-Phase Islanded Inverters: Analysis and Experiments. IEEE Trans. Ind. Electron. 2021, 68, 4812–4826.
- Lu, M. Virtual Oscillator Grid-Forming Inverters: State of the Art, Modeling, and Stability. IEEE Trans. Power Electron. 2022, 37, 11579–11591.
- He, X.; Haberle, V.; Subotic, I.; Dorfler, F. Nonlinear Stability of Complex Droop Control in Converter-Based Power Systems. IEEE Control Syst. Lett. 2023, 7, 1327–1332.
- Awal, M.A.; Yu, H.; Tu, H.; Lukic, S.M.; Husain, I. Hierarchical Control for Virtual Oscillator Based Grid-Connected and Islanded Microgrids. IEEE Trans. Power Electron. 2020, 35, 988–1001.
- Lu, M.; Dutta, S.; Johnson, B. Self-Synchronizing Cascaded Inverters with Virtual Oscillator Control. IEEE Trans. Power Electron. 2022, 37, 6424–6436.
- Kong, L.; Xue, Y.; Qiao, L.; Wang, F. Enhanced Synchronization Stability of Grid-Forming Inverters with Passivity-Based Virtual Oscillator Control. IEEE Trans. Power Electron. 2022, 37, 14141–14156.
- Li, J.; Fletcher, J.E.; Holmes, D.; McGrath, B. Developing a machine equivalent inertial response for a Virtual Oscillator Controlled Inverter in a machine-inverter based microgrid. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 4314–4321.
- Awal, M.A.; Husain, I. Unified Virtual Oscillator Control for Grid-Forming and Grid-Following Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4573–4586.
- Ajala, O.; Lu, M.; Johnson, B.B.; Dhople, S.V.; Dominguez-Garcia, A. Model Reduction for Inverters with Current Limiting and Dispatchable Virtual Oscillator Control. IEEE Trans. Energy Convers. 2022, 37, 2250–2259.
- Ghosh, R.; Tummuru, N.R.; Rajpurohit, B.S. Modified VOC Using Three Symmetrical Components for Grid-Supporting Operation During Unbalanced Grid Voltages and Grid-Forming Operation in Hybrid Single-Phase/Three-Phase Microgrid. IEEE Trans. Ind. Electron. 2023, 70, 11276–11286.
- Ghosh, R.; Tummuru, N.R.; Rajpurohit, B.S. A New Virtual Oscillator-Based Grid-Forming Controller with Decoupled Control Over Individual Phases and Improved Performance of Unbalanced Fault Ride-Through. IEEE Trans. Ind. Electron. 2023, 70, 12465–12474.