Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Yung-Fu Chen
 -- 3551 2023-10-07 12:05:40 |
2 format
Jason Zhu
 Meta information modification 4081 2023-10-08 04:32:52 | |
3 format
Jason Zhu
 Meta information modification 4081 2023-10-19 03:56:55 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Chen, Y.; Lin, S.; Chang, R.; Yu, Y.; Liang, H. Two-Dimensional Quantum Billiards. Encyclopedia. Available online: https://encyclopedia.pub/entry/49903 (accessed on 03 May 2024).
Chen Y, Lin S, Chang R, Yu Y, Liang H. Two-Dimensional Quantum Billiards. Encyclopedia. Available at: https://encyclopedia.pub/entry/49903. Accessed May 03, 2024.
Chen, Yung-Fu, Song-Qing Lin, Ru-Wei Chang, Yan-Ting Yu, Hsing-Chih Liang. "Two-Dimensional Quantum Billiards" Encyclopedia, https://encyclopedia.pub/entry/49903 (accessed May 03, 2024).
Chen, Y., Lin, S., Chang, R., Yu, Y., & Liang, H. (2023, October 07). Two-Dimensional Quantum Billiards. In Encyclopedia. https://encyclopedia.pub/entry/49903
Chen, Yung-Fu, et al. "Two-Dimensional Quantum Billiards." Encyclopedia. Web. 07 October, 2023.
Two-Dimensional Quantum Billiards
Edit
This entry is adapted from the peer-reviewed paper 10.3390/sym15101809

Two-dimensional quantum billiards are one of the most important paradigms for exploring the connection between quantum and classical worlds. Researchers are mainly focused on nonintegrable and irregular shapes to understand the quantum characteristics of chaotic billiards. The emergence of the scarred modes relevant to unstable periodic orbits (POs) is one intriguing finding in nonintegrable quantum billiards. On the other hand, stable POs are abundant in integrable billiards. The quantum wavefunctions associated with stable POs have been shown to play a key role in ballistic transport. 

integrable quantum billiards classical periodic orbits level clustering

1. Introduction

Harmonic oscillators are universally recognized as one of the most important paradigms for exploring quantum-classical correspondence. Under the paraxial approximation, the transverse part of the wave equation for spherical cavities can be mathematically analogous to the Schrödinger equation for two-dimensional (2D) harmonic oscillators [1]. Accordingly, various high-order transverse modes can be generated with the specially designed spherical laser cavities to analogously manifest the quantum wave function. The eigenfunctions of 2D quantum harmonic oscillators can be solved as the Hermite–Gaussian (HG) functions in rectangular coordinates or the Laguerre–Gaussian (LG) functions in polar coordinates [2]. The selectively diode-end-pumped solid-state lasers have been widely employed to generate both HG and LG functions from ground order to very high order [3][4][5][6][7]. Additionally, the same laser technology was exploited to generate the so-called geometric modes in the degenerate cavities, which clearly revealed the ray-wave duality in the spatial domain [8][9]. In mesoscopic quantum phenomena, the degeneracy of energy levels was found to play an important role in the connection between the conductance fluctuation and the classical periodic orbits (POs) [10]. Similarly, the emergence of geometric modes was verified to originate from the degeneracy of eigenfrequencies in laser resonators [11][12]. The Lissajous stationary modes are one of the most remarkable geometric modes generated from the astigmatic laser cavities. Theoretically, the Schrödinger coherent state for the one-dimensional (1D) harmonic oscillator can be straightforwardly extended to the 2D harmonic oscillator to obtain the stationary coherent states that exactly spatially correspond to the Lissajous figures.
Additionally, 2D quantum billiards are another pedagogical model for comprehending the connection between quantum and classical worlds. Various dynamical features can be straightforwardly studied from the model of quantum billiards by changing the geometry. One main branch of research on billiard systems is focused on nonintegrable and irregular shapes to understand the characteristics in the field of quantum chaos [13][14][15][16][17][18][19][20]. Classically, the chaotic nature renders all the orbits in a chaotic system as being unstable. An interesting finding in nonintegrable quantum billiards is the emergence of eigenstates on unstable POs, called scarred modes [21][22][23]. Quantum scars have been searched and analyzed in mesoscopic systems [24][25][26][27][28][29][30][31][32][33][34]. Due to the similarity of the equations for different types of waves, scars have been observed in microwaves [35][36][37][38][39][40][41]. Quantum scars have not only been confirmed from the accumulation of spin–orbit-coupled atomic gases for specific energies [42] but also generated in the 2D harmonic oscillators with local impurities [43][44][45]. Furthermore, quantum many-body scars have been hypothesized to cause weak ergodicity breaking and the unexpectedly slow thermalization of cold atoms [46][47][48][49][50][51][52][53][54][55]. The similar phenomenon dynamical scar has also been experimentally found in a driven fraction system [56]. Nevertheless, the overall number of scarred modes is quite few. The eigenstates in nonintegrable billiards are mostly widely distributed in the coordinate space [13], often exhibiting common features of quasi-linear ridge structures [57].
Compared with non-integrable billiards, stable POs are generally abundant in integrable billiards with symmetrical shapes [11][16][58][59][60][61][62][63][64][65][66][67][68][69][70][71][72][73][74][75]. The quantum wavefunctions associated with stable POs have been found to play a key role in ballistic transport [76][77][78][79], quantum pointer states and decoherence [80][81][82][83][84][85][86][87][88][89][90][91][92][93][94][95], universal conductance fluctuations [95][96][97][98][99], and chaos-assisted quantum tunneling [100][101][102][103][104]. Ballistic transport means that the mean free path of the particle is significantly longer than the size of the medium through which the particle travels. In addition to microwave cavities, quantum billiards can be analogously explored with the wave systems including optical fibers [105][106], optical resonators [107][108][109][110][111][112][113][114][115][116], vibrating plates and acoustic waves [117][118][119][120][121][122][123], and liquid surface waves [123][124][125][126][127][128]. Noticeably, it has been confirmed that the vertical-cavity surface-emitting lasers (VCSELs) with a unique longitudinal wave vector kz and the lateral oxide confinements can be modeled as 2D wave billiards with hard walls. To be brief, theoretical research on quantum billiards was intensively performed in the last century, and later, some researchers’ interests shifted to applied fields such as laser resonators.

2. Quantum Billiards

The quantum analogy of a classical billiard is called a quantum billiard. For the classical billiard with the 2D region denoted by R, the corresponding potential in quantum mechanics is given as
V ( x , y ) = 0   in   R ∞   otherwise
The time-independent Schrödinger equation for the potential defined in Equation (1) can be expressed as the Helmholtz equation:
∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + k 2 ψ ( x , y ) = 0   in   R ψ ( x , y ) = 0   on   the   boundary   of   R
where 𝑘=(2𝜇𝐸/ℏ)1/2; E and 𝜇 are energy and mass of the particle, and ℏ is the reduced Planck’s constant. The homogeneous Dirichlet boundary condition is given due to the condition of 𝑉=∞. To be brief, quantum billiard is defined using the Helmholtz equation in R with the Dirichlet boundary condition.

3. Square Billiard

The spatial distributions of quantum wave functions corresponding to classical POs [76][77][78][79] have been an intriguing phenomenon in open ballistic cavities. Semiclassical PO theory has been used to explain the scarred wave functions in chaotic billiards [21][22][23]. Nevertheless, it is pedagogically useful for comprehending the quantum-classical correspondence in mesoscopic physics to fully develop the connection between quantum eigenfunctions and classical POs in integrable systems. One of the simplest integrable billiards is the square billiard [11]. In a square billiard, each family of POs can be specified with three parameters (p, q, and ϕ), where p and q are two positive integers describing the number of reflections with the horizontal and vertical boundaries, and ϕ (−π < ϕ < π) is associated with the wall positions of specular reflection points [11][65]. Alternatively, the parameter ϕ may also be linked to the starting point of the classical particle. Figure 1 depicts some examples for POs in a square billiard. The trajectory can be seen to constitute a single, non-repeated orbit when p and q are co-prime. When p and q have a common factor m, the trajectory is an orbit family that corresponds to m primitive POs with indices of (p/m, q/m, and ϕ/m).
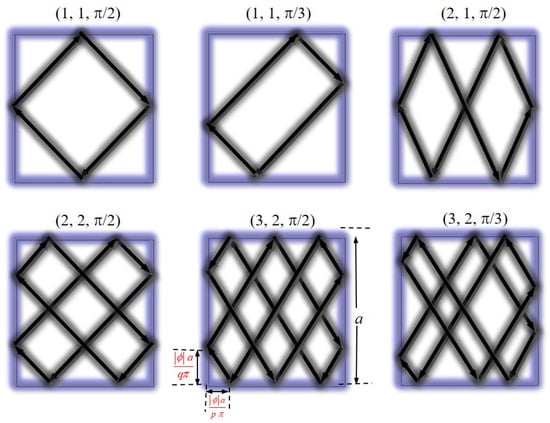
Symmetry 15 01809 g001
Figure 1. Some examples of orbit families in square billiard.
For a square billiard with the region in 0≤𝑥,𝑦≤𝑎, the eigenfunctions are given as
ψ m , n ( x , y ) = 2 a sin m π a x sin n π a y
where the quantum numbers m and n are positive integers. The eigenvalues corresponding to the eigenfunctions 𝜓𝑚,𝑛(𝑥,𝑦) are given using 𝐸(𝑚,𝑛)=ℏ2𝑘2𝑚,𝑛/(2𝜇), where the wave numbers 𝑘𝑚,𝑛 are expressed as
k m , n = π a m 2 + n 2
Figure 2 shows the wave patterns |𝜓𝑚,𝑛(𝑥,𝑦)|2 for several sets of quantum numbers (𝑚,𝑛).
From Bohr’s correspondence principle, the classical limit of a quantum system should be asymptotically obtained when the quantum numbers are sufficiently large. However, the conventional eigenfunctions of a square billiard cannot reveal the features of classical POs no matter how large the quantum numbers are. The quantum states relevant to the classical POs have been verified to be the superpositions of the nearly degenerate eigenstates. For a given central order (𝑚𝑜,𝑛𝑜), the nearly degenerate condition can be derived from the differential of the eigenvalue function 𝐸(𝑚,𝑛) given as
𝑑𝐸(𝑚,𝑛)|𝑚𝑜,𝑛𝑜=(∂𝐸/∂𝑚|𝑚𝑜,𝑛𝑜)𝑑𝑚+(∂𝐸/∂𝑛|𝑚𝑜,𝑛𝑜)𝑑𝑛
Symmetry 15 01809 g002
Figure 2. Wave patterns for eigenstates |𝜓𝑚,𝑛(𝑥,𝑦)|2 for several sets of quantum numbers (𝑚,𝑛) of square billiard.
Setting 𝑑𝐸(𝑚,𝑛)|𝑚𝑜,𝑛𝑜=0 leads the tangent of the constant-energy contour as
−𝑑𝑛𝑑𝑚=∂𝐸/∂𝑚|𝑚𝑜,𝑛𝑜∂𝐸/∂𝑛|𝑚𝑜,𝑛𝑜=𝑚𝑜𝑛𝑜
Since both quantum numbers (𝑚,𝑛) are positive integers, the slope −𝑑𝑛/𝑑𝑚 must be a rational number. From Equation (6), the nearly degenerate condition can be generalized as 𝑚𝑜/𝑛𝑜=𝑞/𝑝, where p and q are coprime positive integers. Figure 3 depicts the spectrum 𝑘𝑚,𝑛 as a function of the ratio 𝑚/𝑛 for a square billiard with 1≤𝑚,𝑛≤700. The spectrum conspicuously reveals that the eigenvalues are clustered in the vicinity of 𝑚/𝑛=𝑞/𝑝 to form valley structures. Clustering means that levels with very different quantum numbers have very similar energies. From the condition 𝑚𝑜/𝑛𝑜=𝑞/𝑝, the central eigenstate for the coherent superposition can be in terms of a single parameter N as 𝑚𝑜=𝑞𝑁 or 𝑛𝑜=𝑝𝑁. The slope −𝑑𝑛/𝑑𝑚=𝑞/𝑝 signifies that the quantum numbers for the nearly degenerate eigenstates around the central mode can be given using 𝑚=𝑞𝑁+𝑝𝐾 and 𝑛=𝑝𝑁−𝑞𝐾 with the integer index K in a small range. Consequently, the coherent superposition of the nearly degenerate eigenstates around the central mode can be generalized as
Ψ N , M ( p , q ) ( x , y ; ϕ ) = 1 2 M + 1 ∑ K = − M M e i K ϕ ψ q N + p K , p N − q K ( x , y )
where 𝜙 is the phase factor in the range of −𝜋≤𝜙≤𝜋 and (2𝑀+1) means the total number of the superposed eigenstates. Note that the parameter ϕ corresponds to the starting point of the classical particle shown in Figure 1. Under the circumstance of 𝑁>>𝑀, the eigen-energies of the superposed eigenstates can be confirmed to be close to a constant energy. Figure 4 illustrates the wave patterns |Ψ(𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)|2 calculated using Equation (7) with N = 100, M = 5, and 𝜙=𝜋/2 for eigenstates clustered around the indices (p,q) shown in Figure 3. The wave patterns of |Ψ(𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)|2 are evidently localized on the classical POs. The velocity direction of the trajectory can be straightforwardly determined with the relation of 𝑘𝑥/𝑘𝑦=𝑚/𝑛=𝑞/𝑝. By way of explanation, the wave function in Equation (7) is not a strictly stationary state since the eigenstate components are not exactly degenerate for the Hamiltonian H. Nevertheless, Δ𝐻/<𝐻> will rapidly approach to zero as 𝑁→∞
for a small M. Therefore, the coherent state in Equation (7) can be regarded as a quasi-stationary state in the mesoscopic region.
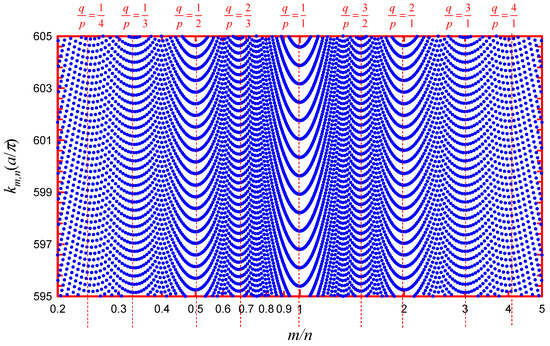
Symmetry 15 01809 g003
Figure 3. Directionally resolved level distribution 𝑘𝑚,𝑛 as a function of the ratio 𝑚/𝑛 with 1≤𝑚,𝑛≤700 for manifesting the level clustering relevant to classical POs.
Symmetry 15 01809 g004
Figure 4. Wave patterns for quasi-stationary coherent states |Ψ(𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)|2 calculated using Equation (6) with N = 100, M = 5, and 𝜙=𝜋/2 for eigenstates clustered around the indices (p, q).
The trajectorial equations for POs can be derived from the quantum coherent state in Equation (7) for the central maximum of the wave intensity. Using the identity sin𝜃=(𝑒𝑖𝜃−𝑒−𝑖𝜃)/(2𝑖), the representation of the coherent state in Equation (7) can be organized as
Ψ(𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)=12𝑎[𝑒𝑖𝑁Θ−𝑔(𝑥,𝑦)𝐷𝑀(Θ+𝑡(𝑥,𝑦)+𝜙)+𝑒−𝑖𝑁Θ−𝑔(𝑥,𝑦)𝐷𝑀(Θ+𝑡(𝑥,𝑦)−𝜙)]−12𝑎[𝑒𝑖𝑁Θ+𝑔(𝑥,𝑦)𝐷𝑀(Θ−𝑡(𝑥,𝑦)+𝜙)+𝑒−𝑖𝑁Θ+𝑔(𝑥,𝑦)𝐷𝑀(Θ−𝑡(𝑥,𝑦)−𝜙)]
where
D M ( θ ) = 1 2 M + 1 ∑ K = − M M e i K θ
Θ±𝑔(𝑥,𝑦)=𝜋(𝑞𝑥±𝑝𝑦)/𝑎 and Θ±𝑡(𝑥,𝑦)=𝜋(𝑝𝑥±𝑞𝑦)/𝑎. The function 𝐷𝑀(𝜃) in Equation (9) is the Dirichlet kernel that exhibits the periodic maxima of the intensity at 𝜃=2𝑛𝜋 for any integer n. Using the periodic maximal characteristic of the Dirichlet kernel, the parametric equations for the central maxima of the intensity |Ψ(𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)|2 can be generalized as 𝐴 𝑥+𝐵 𝑦±𝜙=2𝑛𝜋, where −𝐴 /𝐵 =𝜂 represents the slope. From Equation (8) and Θ±𝑡(𝑥,𝑦)=𝜋(𝑝𝑥±𝑞𝑦)/𝑎, the slopes for all parametric equations can be found to be two cases of 𝜂=±𝑝/𝑞. Furthermore, all parametric equations can be confirmed to exactly correspond to the trajectorial lines of classical POs in a square billiard. The initial position (𝑥𝑜,𝑦𝑜) and the velocity (𝑣𝑥,𝑣𝑦) in classical dynamics can be linked to Equation (8) using the condition of 𝐴 𝑥𝑜+𝐵 𝑦𝑜±𝜙=2𝑛𝜋 as well as 𝑣𝑦/𝑣𝑥=(𝑑𝑦/𝑑𝑡)/(𝑑𝑥/𝑑𝑡)|𝑥𝑜,𝑦𝑜=𝜂. From the result of 𝜂=±𝑝/𝑞, the velocity (𝑣𝑥,𝑣𝑦) can be verified to be consistent with the classical dynamics 𝑣𝑦/𝑣𝑥=𝑝/𝑞. To sum up, the trajectorial equations for the classical POs can be analytically extracted from the quantum coherent states in Equation (7). It is worthwhile to mention that the lines of the phase functions Θ±𝑔(𝑥,𝑦) and the lines of the trajectorial functions Θ±𝑡(𝑥,𝑦) in Equation (8) are mutually orthogonal.

4. Equilateral Triangular Billiard

Square billiard is a classically separable and integrable system, whereas the equilateral triangle billiard is an integrable but non-separable system. In theory, the correlation between the quantum level clustering and the classical POs was deeply discussed from the representation of the quantum coherent states. In experiments, the oxide-confined VCSEL devices were fabricated in the shape of an equilateral triangle to analogously manifest the quantum level distribution and the spatial features of the wave functions. For an equilateral-triangular billiard with three vertices at (0,0), (𝑎/2,3−−√𝑎/2), and (−𝑎/2,3−−√𝑎/2), the eigenfunctions are given using [62][129]
𝜓(𝑒)𝑚,𝑛(𝑥,𝑦)=16𝑎233√−−−−√{cos[2𝜋3𝑎(2𝑚−𝑛)𝑥]sin(2𝜋3√𝑎𝑛𝑦)−cos[2𝜋3𝑎(2𝑛−𝑚)𝑥]sin(2𝜋3√𝑎𝑚𝑦)+cos[−2𝜋3𝑎(𝑚+𝑛)𝑥]sin[2𝜋3√𝑎(𝑚−𝑛)𝑦]}
𝜓(𝑜)𝑚,𝑛(𝑥,𝑦)=16𝑎233√−−−−√{sin[2𝜋3𝑎(2𝑚−𝑛)𝑥]sin(2𝜋3√𝑎𝑛𝑦)−sin[2𝜋3𝑎(2𝑛−𝑚)𝑥]sin(2𝜋3√𝑎𝑚𝑦)+sin[−2𝜋3𝑎(𝑚+𝑛)𝑥]sin[2𝜋3√𝑎(𝑚−𝑛)𝑦]}
where the quantum numbers m and n are nonnegative integers, and the superscripts (o) and (e) denote the two types of degenerate modes with odd and even symmetries, respectively. The eigenvalues corresponding to the eigenfunctions 𝜓(𝑒)𝑚,𝑛(𝑥,𝑦) and 𝜓(𝑜)𝑚,𝑛(𝑥,𝑦) are given using 𝐸(𝑚,𝑛)=ℏ2𝑘2𝑚,𝑛/(2𝜇), where the wave numbers 𝑘𝑚,𝑛 are expressed as
k m , n = 4 π 3 a m 2 + n 2 − m n
Figure 5 shows the wave patterns of |𝜓(𝑒)𝑚,𝑛(𝑥,𝑦)|2 for several sets of quantum numbers (𝑚,𝑛). Since the wave patterns for |𝜓(𝑒)𝑚,𝑛(𝑥,𝑦)|2 and |𝜓(𝑜)𝑚,𝑛(𝑥,𝑦)|2 are the same in the spatial patterns, only the case of |𝜓(𝑒)𝑚,𝑛(𝑥,𝑦)|2 is presented in Figure 5. Due to the setting of the equilateral triangle, all wave patterns can be found to be symmetric with respect to the y axis. Like the results for a square billiard, the conventional eigenstates for an equilateral-triangular billiard cannot exhibit the spatial properties of classical POs, even in the correspondence limit of large quantum numbers.
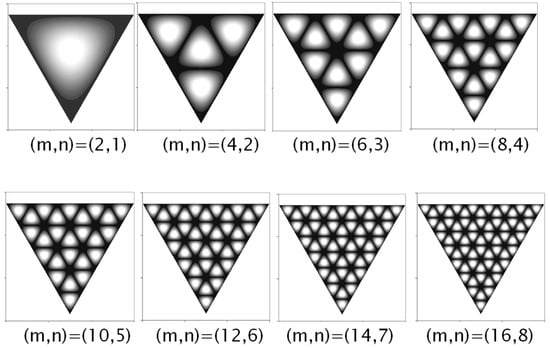
Symmetry 15 01809 g005
Figure 5. Wave patterns for eigenstates |𝜓(𝑒)𝑚,𝑛(𝑥,𝑦)|2 for several sets of quantum numbers (𝑚,𝑛) in equilateral triangle billiard.
The eigenfunctions 𝜓(𝑒)𝑚,𝑛(𝑥,𝑦) and 𝜓(𝑜)𝑚,𝑛(𝑥,𝑦) in Equations (10) and (11) are the standing-wave representation. The traveling-wave representation is more convenient for constructing the coherent states relevant to classical POs. In terms of 𝜓(𝑒)𝑚,𝑛(𝑥,𝑦) and 𝜓(𝑜)𝑚,𝑛(𝑥,𝑦), the traveling-wave representation is given using 𝜓(±)𝑚,𝑛(𝑥,𝑦)=𝜓(𝑒)𝑚,𝑛(𝑥,𝑦)±𝑖𝜓(𝑜)𝑚,𝑛(𝑥,𝑦) , where the symbols (+) and (−) denote the forward and backward characteristics, respectively. Consequently, the wave functions for 𝜓(±)𝑚,𝑛(𝑥,𝑦) can be given using
ψ m , n ( ± ) ( x , y ) = 16 a 2 3 3 exp ±   i 2 π 3 a ( 2 m − n ) x sin 2 π 3 a n y − exp ±   i 2 π 3 a ( 2 n − m ) x sin 2 π 3 a m y + exp ∓   i 2 π 3 a ( m + n ) x sin 2 π 3 a ( m − n ) y
Note that 𝜓(+)𝑚,𝑛 and 𝜓(−)𝑚,𝑛 form a conjugate pair with identical spatial patterns. Again, the quantum coherent states related to the classical POs can be formed via superposition of the nearly degenerate eigenstates. As discussed in the case of square billiard, the nearly degenerate condition for equilateral triangle billiards with the central order (𝑚𝑜,𝑛𝑜) can be given using
− d n d m = ∂ E / ∂ m m o , n o ∂ E / ∂ n m o , n o = 2 m o − n o 2 n o − m o
Since the slope −𝑑𝑛/𝑑𝑚
needs to be a rational number, the nearly degenerate condition in Equation (14) can be generalized as (2𝑚𝑜−𝑛𝑜)/(2𝑛𝑜−𝑚𝑜)=𝑞/𝑝 with p and q being coprime positive integers. Figure 6 depicts the spectrum 𝑘𝑚,𝑛 as a function of the ratio (2𝑚−𝑛)/(2𝑛−𝑚) for an equilateral triangle billiard with 1≤𝑚,𝑛≤700. The eigenvalues can be seen to be clustered in the vicinity of (2𝑚−𝑛)/(2𝑛−𝑚)=𝑞/𝑝 to display the valley structures. Obviously, the level clustering is certainly accompanied by the emergence of the gap. From the condition (2𝑚𝑜−𝑛𝑜)/(2𝑛𝑜−𝑚𝑜)=𝑞/𝑝, the central eigenstate for the coherent superposition can be given by 𝑚𝑜=(2𝑞+𝑝)𝑁 and 𝑛𝑜=(2𝑝+𝑞)𝑁 with a single parameter N. Combining with −𝑑𝑛/𝑑𝑚=𝑞/𝑝 from Equation (14), the coherent superposition of nearly degenerate eigenstates around the central mode can be expressed as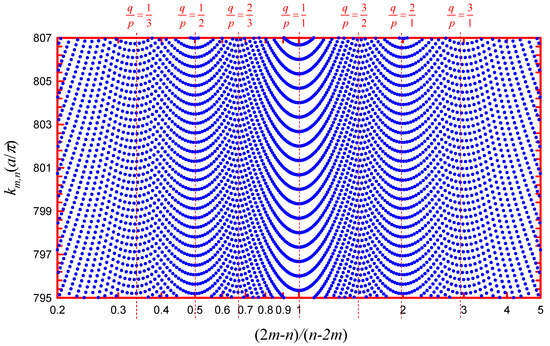
Ψ N , M ( ± , p , q ) ( x , y ; ϕ ) = 1 2 M + 1 ∑ K = − M M e ± i K ϕ ψ ( 2 q + p ) N + p K , ( 2 p + q ) N − q K ( ± ) ( x , y )
where 𝜙 is the phase factor in the range of −𝜋≤𝜙≤𝜋. Under the circumstance of 𝑁>>𝑀, the eigen-energies of the superposed eigenstates can be found to be nearly a constant energy of
E ( m , n ) ≈ 9 ℏ 2 π 2 8 μ a 2 5 ( p 2 + q 2 ) + 8 p q N 2
Symmetry 15 01809 g006
Figure 6. Directionally resolved level distribution 𝑘𝑚,𝑛 as a function of the ratio (2𝑚−𝑛)/(2𝑛−𝑚) with 1≤𝑚,𝑛≤700 for manifesting the level clustering relevant to classical POs.
Figure 7 illustrates the wave patterns of |Ψ(±,𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)|2 calculated using Equation (15) with N = 100, M = 5, and 𝜙=𝜋/2 for eigenstates with the indices (𝑝,𝑞) shown in Figure 6. The wave patterns of |Ψ(+,𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)|2 can be seen to be precisely concentrated on the classical POs. Since Ψ(+,𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙) and Ψ(−,𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙) form a conjugate pair, the spatial patterns are completely identical.
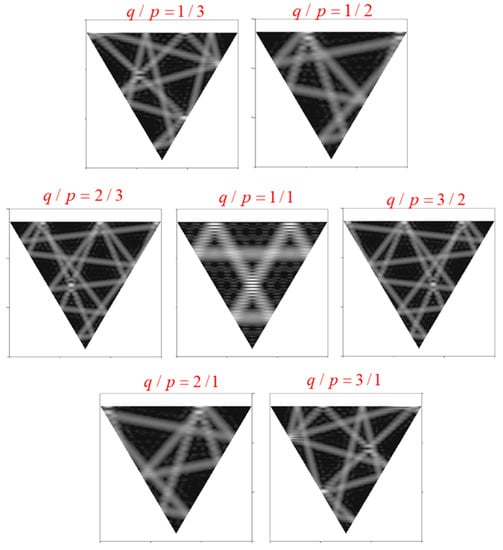
Symmetry 15 01809 g007
Figure 7. Wave patterns for quasi-stationary coherent states |Ψ(±,𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)|2 calculated using Equation (15) with N = 100, M = 5, and 𝜙=𝜋/2 for eigenstates clustered around the indices (p, q).
The same as in the case of a square billiard, the trajectory equations for POs can be derived from Equation (15) from the central maximum of the wave intensity. Using sin𝜃=(𝑒𝑖𝜃−𝑒−𝑖𝜃)/(2𝑖), the representation in Equation (15) can be organized as
Ψ N , M ( + , p , q ) ( x , y ; ϕ ) = 16 a 2 3 3 1 2 i e i N Θ g 1 + ( x , y ) D M Θ t 1 + ( x , y , ϕ ) − e i N Θ g 1 − ( x , y ) D M Θ t 1 − ( x , y , ϕ ) − e i N Θ g 2 + ( x , y ) D M Θ t 2 + ( x , y , ϕ ) + e i N Θ g 2 − ( x , y ) D M Θ t 2 − ( x , y , ϕ ) + e i N Θ g 3 + ( x , y ) D M Θ t 3 + ( x , y , ϕ ) − e i N Θ g 3 − ( x , y ) D M Θ t 3 − ( x , y , ϕ )
where
Θ g 1 ± ( x , y ) = 2 π a q x ± ( 2 p + q ) 3 y
Θ g 2 ± ( x , y ) = 2 π a p x ± ( 2 q + p ) 3 y
Θ g 3 ± ( x , y ) = 2 π a − ( p + q ) x ± ( q − p ) 3 y
Θ t 1 ± ( x , y , ϕ ) = 2 π 3 a ( 2 p + q ) 3 x ∓ q y + ϕ
Θ t 2 ± ( x , y , ϕ ) = 2 π 3 a − ( 2 q + p ) 3 x ± p y + ϕ
Θ t 3 ± ( x , y , ϕ ) = 2 π 3 a ( q − p ) 3 x ± ( p + q ) y + ϕ
The representation for Ψ(−,𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙) can be given using the conjugate of Ψ(+,𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙). Using the maximal feature of the Dirichlet kernel, the parametric equations for the central maxima of |Ψ(+,𝑝,𝑞)𝑁,𝑀| can be deduced as Θ±𝑡 𝑗(𝑥,𝑦,𝜙)=2𝑛𝜋 with 𝑗=1,2,3. Consequently, the classical POs of the equilateral-triangular billiard can be confirmed to be constituted by six independent line equations with different slopes. Using the form 𝐴𝑗𝑥+𝐵𝑗𝑦+𝜙=2𝑛𝜋 to express the trajectory equations, the slopes can be generalized as −𝐴𝑗/𝐵𝑗=±𝜂𝑗 with 𝜂1=(2𝑝+𝑞)/3−−√𝑞, 𝜂2=(𝑝+2𝑞)/3−−√𝑝, and 𝜂3=(𝑝−𝑞)/3−−√(𝑝+𝑞). Similar to the quantum coherent state for a square billiard, the lines of the phase functions Θ±𝑔 𝑗(𝑥,𝑦) and the lines of the trajectorial functions Θ±𝑡 𝑗(𝑥,𝑦) in Equation (17) are mutually orthogonal for 𝑗=1,2,3, respectively.

5. Circular Billiard

Circular billiard is another pedagogical paradigm in classically separable and integrable systems. The azimuthal and radial components of the eigenfunctions of a circular billiard are the form of exp(imϕ) and the Bessel function of the first kind, respectively. Helically phased light beams with the azimuthal phase form of exp(imϕ) are well known to carry an orbital angular momentum (OAM) of mη per photon, where m is an integer [130][131]. In ray dynamics, the function of a circular billiard is the same as the transverse confinement of a cylindrical waveguide for light. Consequently, the propagation-invariant solutions of the Helmholtz equation in a cylindrical waveguide can be in terms of the Bessel beams with well-defined OAM [132]. The OAM or optical vortex (OV) of light has been widely used in numerous applications, such as generating OAM-entangled photon pairs [133][134], trapping and rotating micron and submicron objects [135][136][137], generating astrophysical OAM light [138], assembling DNA biomolecules [139], OAM-based microscopy and imaging [140], super-diffraction limit imaging [141], and optical communication [142].
The eigenstates in polar coordinates for a circular billiard with radius R are given using
ψ m , n ( r , θ ) = 2 R 2 J m + 1 2 k m , n R 1 / 2 J m k m , n r 1 2 π e i m θ
where 𝑚∈𝛧, 𝑛∈𝛮, and 𝐽𝑚(•) are the Bessel functions of the first kind with order m. The quantum numbers m and n are the quantization of the azimuthal and radial oscillations, respectively. The eigenvalues for 𝜓𝑚,𝑛(𝑟,𝜃) are given using 𝑘𝑚,𝑛=𝑥𝑚,𝑛/𝑅 with 𝑅=𝑎/2, where 𝑥𝑚,𝑛 is the nth zero of 𝐽𝑚(𝑥) and a is the billiard diameter. Figure 8 shows the wave patterns for the function |Re[𝜓𝑚,𝑛(𝑟,𝜃)]|2 with different quantum numbers (m, n). Here, the real part of the eigenfunction 𝜓𝑚,𝑛(𝑟,𝜃) is purposely used for revealing the nodal structures in the radial and azimuthal directions associated with the indices n and m, respectively.
Symmetry 15 01809 g008
Figure 8. Wave patterns for the functions of Re[𝜓𝑚,𝑛(𝑟,𝜃)] with different quantum numbers (m, n) for circular billiard.
Unlike square and equilateral triangular billiards, the nearly degenerate condition for a circular billiard cannot be straightforwardly derived from the eigenvalues 𝑘𝑚,𝑛
determined with 𝐽𝑚(𝑘𝑚,𝑛𝑅). The Wentzel–Kramers–Brillouin (WKB) method was nicely used to analytically obtain the nearly degenerate condition for a circular billiard. The eigenvalues 𝑘𝑚,𝑛 derived from the WKB method is given using [143]
k m , n 2 ( R 2 − R o 2 ) − m cos − 1 R o R = n + 3 4 π ,
where 𝑅𝑜 is the shortest distance to the center for a wave inside the billiard. The relationship between 𝑅𝑜 and 𝑘𝑚,𝑛 can be connected from both the quantum and classical OAM theories. From the quantum momentum ℏ𝑘𝑚,𝑛, the semiclassical OAM can be expressed as 𝐿𝑧=𝑅𝑜(ℏ𝑘𝑚,𝑛). On the other hand, the quantum OAM can be directly in terms of the azimuthal quantum number as 𝐿𝑧=𝑚ℏ. Consequently, the relationship between 𝑅𝑜 and 𝑘𝑚,𝑛 can be given using 𝑅𝑜𝑘𝑚,𝑛=𝑚. In classical ray dynamics, the distance 𝑅𝑜 for a periodic orbit with indices (p, q) can be found to be 𝑅𝑜=𝑅cos(𝑝𝜋/𝑞), where q is the number of turning points at the boundary during one period and p is the number of windings during one period. Using 𝑅𝑜=𝑅cos(𝑝𝜋/𝑞) and 𝑅𝑜𝑘𝑚,𝑛=𝑚, Equation (25) can be rewritten as
𝑘𝑚,𝑛𝑅sin(𝑝𝜋/𝑞)=(𝑝𝑞𝑚+𝑛+34)𝜋
Equation (26) indicates that the eigenstates 𝜓𝑚𝑜−𝑞𝐾,𝑛𝑜+𝑝𝐾 with 𝐾∈𝛧 can constitute a family of nearly degenerate states for 𝑚𝑜>>|𝑞𝐾|. From 𝑅𝑜=𝑅cos(𝑝𝜋/𝑞), 𝑅𝑜𝑘𝑚,𝑛=𝑚, and 𝑅=𝑎/2, the relationship between the ratio 𝑝/𝑞 and 𝑘𝑚,𝑛 can be given using
1 π cos − 1 2 m k m , n a = p q
In other words, the parameter 𝜋−1cos−1[2𝑚/(𝑘𝑚,𝑛𝑎)] can be used to manifest the connection of the quantum level distribution and the classical POs. Figure 9 illustrates the spectrum 𝑘𝑚,𝑛 versus the parameter 𝜋−1cos−1[2𝑚/(𝑘𝑚,𝑛𝑎)] for a circular billiard with 1≤𝑚,𝑛≤700. The spectrum 𝑘𝑚,𝑛 can be found to be clustered with the conditions in Equation (27) to be satisfied. Just like square and equilateral triangle billiards, the level clustering is certainly accompanied by the appearance of the level gap. Namely, the eigenvalues 𝑘𝑚,𝑛 constitute the structure of energy shells in each neighborhood of the central state with 𝑘𝑚𝑜,𝑛𝑜=𝑚𝑜/[𝑅cos(𝑝𝜋/𝑞)]
, corresponding to the emergence of sharp peaks in the density of states [144].
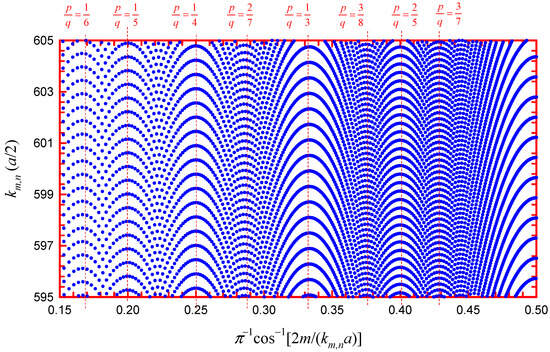
Symmetry 15 01809 g009
Figure 9. Directionally resolved level distribution 𝑘𝑚,𝑛 versus 𝜋−1cos−1[2𝑚/(𝑘𝑚,𝑛𝑎)] with 1≤𝑚,𝑛≤700 for manifesting the level clustering relevant to classical POs.
Once again, the manifestation of classical POs in quantum systems can be fulfilled by exploiting a coherent superposition of the eigenstates belonging to the same shell of the spectrum. In terms of the nearly degenerate eigenstates 𝜓𝑚𝑜−𝑞𝐾,𝑛𝑜+𝑝𝐾 and the phase factor ϕ, the coherent states for circular billiards can be expressed as
Ψ m o , M ( p , q ) ( r , θ ; ϕ ) = 1 2 M + 1 ∑ K = − M M e i   q K   ϕ   ψ m o − q K , n o + p K r , θ .
Figure 10 shows the wave patterns |Ψ(𝑝,𝑞)𝑚𝑜,𝑀(𝑟,𝜃;𝜙)|2 calculated with mo = 100, M = 2, and the different sets of parameters (𝑝,𝑞) and 𝜙=0. As expected, all the wave patterns |Ψ(𝑝,𝑞)𝑚𝑜,𝑀(𝑟,𝜃;𝜙)|2 of the coherent states are precisely concentrated on the classical POs.
Symmetry 15 01809 g010
Figure 10. Wave patterns for quasi-stationary coherent states |Ψ(𝑝,𝑞)𝑚𝑜,𝑀(𝑟,𝜃;𝜙)|2 calculated with mo = 100, M = 2, and different sets of parameters (𝑝,𝑞) and 𝜙=0.
Logically, the trajectory equations for classical POs can be extracted from the quantum coherent states in Equation (28). However, the extraction cannot be the same as the cases of square and equilateral triangular billiards to be reached straightforwardly. The derivation for the trajectory equations needs to be skillfully used for the integral representation, the asymptotic form, and the boundary condition for the Bessel functions. The integral representation for the Bessel functions of the first kind is given using [145]
J m ( ρ ) = 1 2 π ∫ − π π e i ρ sin ϑ e − i m ϑ d ϑ
Using the boundary condition 𝐽𝑚(𝑘𝑚,𝑛𝑅)=0 and the asymptotic form 𝐽𝑚(𝑧)≈(2/𝜋𝑧)−−−−−−√cos[𝑧−(2𝑚+1)𝜋/4] for 𝑧→∞, the coefficient related to the normalization constant in Equation (24) for high-order modes can be approximated as
2 R 2 J m + 1 2 k m , n R 1 / 2 1 2 π = k m , n 2 R
Substituting Equations (29) and (30) into Equation (24), the high-order eigenstates 𝜓𝑚,𝑛(𝑟,𝜃)
can be expressed as
ψ m , n ( r , θ ) = k m , n 2 R 1 2 π ∫ − π π e   i   k m , n r sin ϑ e i m ( θ − ϑ ) d ϑ
Note that the eigenfunctions in Equation (31) are still exact for a circular billiard, and the only one approximation is the normalization constant. In substitution of Equation (31) into Equation (28), the quantum coherent states can be expressed as
Ψ m o , M ( p , q ) ( r , θ ; ϕ ) = k m , n 2 R 1 2 π ∫ − π π e i k m o , n o r   sin ξ + θ − ϕ   e − i m o ξ − ϕ   D M ( q ξ ) d ξ
where the integration variable is changed to be 𝜉=𝜗−𝜃+𝜙, and 𝐷𝑀(𝑞𝜉) is the Dirichlet kernel given using Equation (9). Since 𝐷𝑀(𝑞𝜉) is a periodic pulse function with period 2𝜋/𝑞 for the variable 𝜉, the integration in Equation (32) on the range [−𝜋,𝜋] can be divided into q segments with the integration interval shortened on the range [−𝜋/𝑞,𝜋/𝑞]. Consequently, the quantum coherent state in Equation (32) can be rewritten as
Ψ m o , M ( p , q ) ( r , θ ; ϕ ) = k m , n 2 R 1 2 π   ∑ s = 0 q − 1 ∫ − π / q π / q e i k m o , n o r   sin ξ + θ + 2 π s q − ϕ   e − i m o ξ + 2 π s q − ϕ   D M ( q ξ ) d ξ
As long as (2𝑀+1)𝑞>>1, the 𝐷𝑀(𝑞𝜉) can display a narrow peak concentrated in a small region of −Δ≤𝜉≤Δ with the effective width of Δ=𝜋/[𝑞(2𝑀+1)]. By using the small angle approximation, the sine term in Equation (31) can be given by
sin ξ + θ + 2 π s q − ϕ ≈ ξ cos θ + 2 π s q − ϕ + sin θ + 2 π s q − ϕ
From Equation (34) and the relation 𝑘𝑚𝑜,𝑛𝑜=𝑚𝑜/𝑅𝑜, the quantum coherent state in Equation (33) can be organized as
Ψ m o , M ( p , q ) ( r , θ ; ϕ ) = k m , n 2 R 1 2 π ∑ s = 0 q − 1   e   i   m o Θ g , s ( r , θ ; ϕ ) ∫ − π / q π / q e   i   m o   ξ   Θ t , s ( r , θ ; ϕ )   D M ( q ξ ) d ξ
where
Θ g , s ( r , θ ; ϕ ) = r R o sin θ + 2 π s q − ϕ − 2 π s q − ϕ
Θ t , s ( r , θ ; ϕ ) = r R o cos θ + 2 π s q − ϕ − 1
To derive an analytical form, the kernel 𝐷𝑀(𝑞𝛼) is further approximated as a gate function whose values are unified in the interval [−Δ,Δ] and vanish outside. Accordingly, the integration in Equation (35) can be simplified as
Ψ m o , M ( p , q ) ( r , θ ; ϕ ) = m o 2 2 M + 1 R R o q 2 × ∑ s = 0 q − 1 e i m o Θ g , s ( r , θ ; ϕ ) sin c m o   π q 2 M + 1 Θ t , s ( r , θ ; ϕ )
where sinc(𝜒)=sin(𝜒)/𝜒 is the sinc function. Since the central maximum of the sinc(𝜒) function occurs at 𝜒=0, the parametric equations for the central maxima of the quantum coherent states in Equation (38) can be confirmed using Θ𝑡,𝑠(𝑟,𝜃;𝜙)=0. Therefore, the trajectory equations for classical POs of a circular billiard can be specifically given using 𝑟cos(𝜃+𝜃𝑠−𝜙)=𝑅𝑜 with 𝜃𝑠=2𝜋𝑠/𝑞 and 𝑠=0,1,…,𝑞−1.

References

  1. Haus, H.A. Waves and Fields in Optoelectronics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984.
  2. Boyd, G.D.; Kogelnik, H. Generalized confocal resonator theory. Bell Syst. Tech. J. 1962, 41, 1347–1369.
  3. Laabs, H.; Ozygus, B. Excitation of Hermite Gaussian modes in end-pumped solid-state laser via off axis pumping. Opt. Laser Technol. 1996, 28, 213–214.
  4. Flood, C.J.; Giuliani, G.; van Driel, H.M. Preferential operation of an end-pumped Nd:YAG laser in high-order Laguerre–Gauss modes. Opt. Lett. 1990, 15, 215–217.
  5. Bisson, J.F.; Senatsky, Y.; Ueda, K.I. Generation of Laguerre-Gaussian modes in Nd:YAG laser using diffractive optical pumping. Laser Phys. Lett. 2005, 2, 327–333.
  6. Kim, J.W.; Clarkson, W.A. Selective generation of Laguerre–Gaussian (LG0n) mode output in a diode-laser pumped Nd:YAG laser. Optics Commun. 2013, 296, 109–112.
  7. Lee, A.J.; Omatsu, T.; Pask, H.M. Direct generation of a first-Stokes vortex laser beam from a self-Raman laser. Opt. Express 2013, 21, 12401–12409.
  8. Dingjan, J.; van Exter, M.P.; Woerdman, J.P. Geometric modes in a single-frequency Nd:YVO4 laser. Opt. Commun. 2001, 188, 345–351.
  9. Barré, N.; Romanelli, M.; Lebental, M.; Brunel, M. Waves and rays in plano-concave laser cavities: I. Geometric modes in the paraxial approximation. Eur. J. Phys. 2017, 38, 034010.
  10. Courtois, J.; Mohamed, A.; Romanini, D. Degenerate astigmatic cavities. Phys. Rev. A 2013, 88, 043844.
  11. Brack, M.; Bhaduri, R.K. Semiclassical Physics; Addison-Wesley: Reading, MA, USA, 1997.
  12. Habraken, S.J.M.; Nienhuis, G. Modes of a twisted optical cavity. Phys. Rev. A 2007, 75, 033819.
  13. Mcdonald, S.W.; Kaufman, A.N. Spectrum and eigenfunctions for a Hamiltonian with stochastic trajectories. Phys. Rev. Lett. 1979, 42, 1189–1191.
  14. Tomsovic, S.; Heller, E.J. Semiclassical dynamics of chaotic motion: Unexpected long-time accuracy. Phys. Rev. Lett. 1991, 67, 664–667.
  15. Zaslavsky, G.M. Chaos in Dynamic Systems; Harwood: Reading, MA, USA, 1985.
  16. Gutzwiller, M.C. Chaos in Classical and Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1990.
  17. Müller, S.; Heusler, S.; Braun, P.; Haake, F.; Altland, A. Periodic-orbit theory of universality in quantum chaos. Phys. Rev. E 2005, 72, 046207.
  18. Tomsovic, S.; Heller, E.J. Long-time semiclassical dynamics of chaos: The stadium billiard. Phys. Rev. E 1993, 47, 282–299.
  19. Tomsovic, S.; Heller, E.J. Semiclassical construction of chaotic eigenstates. Phys. Rev. Lett. 1993, 70, 1405–1408.
  20. Berry, M.V. Regular and irregular semiclassical wavefunctions. J. Phys. A Math. Gen. 1997, 10, 2083.
  21. Heller, E.J. Bound-state eigenfunctions of classically chaotic Hamiltonian systems—Scars of periodic-orbits. Phys. Rev. Lett. 1984, 53, 1515–1518.
  22. Stöckmann, H.J. Quantum Chaos: An Introduction; Cambridge University Press: Cambridge, UK, 2000.
  23. Haake, F. Quantum Signatures of Chaos; Springer: New York, NY, USA, 2010.
  24. Fromhold, T.M.; Wilkinson, P.B.; Sheard, F.W.; Eaves, L.; Miao, J.; Edwards, G. Manifestations of classical chaos in the energy level spectrum of a quantum well. Phys. Rev. Lett. 1995, 75, 1142–1145.
  25. Wilkinson, P.B.; Fromhold, T.M.; Eaves, L.; Sheard, F.W.; Miura, N.; Takamasu, T. Observation of ‘scarred’ wavefunctions in a quantum well with chaotic electron dynamics. Nature 1996, 380, 608–610.
  26. Monteiro, T.S.; Delande, D.; Connerade, J.P. Have quantum scars been observed? Nature 1997, 387, 863–864.
  27. Akis, R.; Ferry, D.K.; Bird, J.P. Wave function scarring effects in open stadium shaped quantum dots. Phys. Rev. Lett. 1997, 79, 123–126.
  28. Narimanov, E.E.; Stone, A.D. Origin of strong scarring of wave functions in quantum wells in a tilted magnetic field. Phys. Rev. Lett. 1998, 80, 49–52.
  29. Bird, J.P.; Akis, R.; Ferry, D.K.; Vasileska, D.; Cooper, J.; Aoyagi, Y.; Sugano, T. Lead-orientation-dependent wave function scarring in open quantum dots. Phys. Rev. Lett. 1999, 82, 4691–4694.
  30. Crook, R.; Smith, C.G.; Graham, A.C.; Farrer, I.; Beere, H.E.; Ritchie, D.A. Imaging fractal conductance fluctuations and scarred wave functions in a quantum billiard. Phys. Rev. Lett. 2003, 91, 246803.
  31. LeRoy, B.J.; Bleszynski, A.C.; Aidala, K.E.; Westervelt, R.M.; Kalben, A.; Heller, E.J.; Shaw, S.E.J.; Maranowski, K.D.; Gossard, A.C. Imaging electron interferometer. Phys. Rev. Lett. 2005, 94, 126801.
  32. Brunner, R.; Akis, R.; Ferry, D.K.; Kuchar, F.; Meisels, R. Coupling-induced bipartite pointer states in arrays of electron billiards: Quantum Darwinism in action? Phys. Rev. Lett. 2008, 101, 024102.
  33. Burke, A.M.; Akis, R.; Day, T.E.; Speyer, G.; Ferry, D.K.; Bennett, B.R. Periodic scarred states in open quantum dots as evidence of quantum Darwinism. Phys. Rev. Lett. 2010, 104, 176801.
  34. Aoki, N.; Brunner, R.; Burke, A.M.; Akis, R.; Meisels, R.; Ferry, D.K.; Ochiai, Y. Direct imaging of electron states in open quantum dots. Phys. Rev. Lett. 2012, 108, 136804.
  35. Sridhar, S. Experimental observation of scarred eigenfunctions of chaotic microwave cavities. Phys. Rev. Lett. 1991, 67, 785–788.
  36. Sridhar, S.; Hogenboom, D.O.; Willemsen, B.A. Microwave experiments on chaotic billiards. J. Stat. Phys. 1992, 68, 239–258.
  37. Jensen, R.V. Quantum chaos. Nature 1992, 355, 311–318.
  38. Jensen, R.V. Quantum mechanics—Bringing order out of chaos. Nature 1992, 355, 591–592.
  39. Stein, J.; Stöckmann, H.J. Experimental determination of billiard wave functions. Phys. Rev. Lett. 1992, 68, 2867–2870.
  40. Sridhar, S.; Heller, E.J. Physical and numerical experiments on the wave mechanics of classically chaotic systems. Phys. Rev. A 1992, 46, R1728–R1731.
  41. Kudrolli, A.; Kidambi, V.; Sridhar, S. Experimental studies of chaos and localization in quantum wave functions. Phys. Rev. Lett. 1995, 75, 822–825.
  42. Larson, J.; Anderson, B.M.; Altland, A. Chaos-driven dynamics in spin–orbit-coupled atomic gases. Phys. Rev. A 2013, 87, 013624.
  43. Luukko, P.J.J.; Drury, B.; Klales, A.; Kaplan, L.; Heller, E.J.; Räsänen, E. Strong quantum scarring by local impurities. Sci. Rep. 2016, 6, 37656.
  44. Keski-Rahkonen, J.; Luukko, P.J.J.; Kaplan, L.; Heller, E.J.; Räsänen, E. Controllable quantum scars in semiconductor quantum dots. Phys. Rev. B 2017, 96, 094204.
  45. Keski-Rahkonen, J.; Ruhanen, A.; Heller, E.J.; Räsänen, E. Quantum Lissajous scars. Phys. Rev. Lett. 2019, 123, 214101.
  46. Turner, C.J.; Michailidis, A.A.; Abanin, D.A.; Serbyn, M.; Papić, Z. Weak ergodicity breaking from quantum many-body scars. Nat. Phys. 2018, 14, 1.
  47. Turner, C.J.; Michailidis, A.A.; Abanin, D.A.; Serbyn, M.; Papić, Z. Quantum scarred eigenstates in a Rydberg atom chain: Entanglement, breakdown of thermalization, and stability to perturbations. Phys. Rev. B 2018, 98, 155134.
  48. Moudgalya, S.; Regnault, N.; Bernevig, B.A. Entanglement of exact excited states of Affleck–Kennedy–Lieb–Tasaki models: Exact results, many-body scars, and violation of the strong eigenstate thermalization hypothesis. Phys. Rev. B 2018, 98, 235156.
  49. Ho, W.W.; Choi, S.; Pichler, H.; Lukin, M.D. Periodic orbits, entanglement, and quantum many-body scars in constrained models: Matrix product state approach. Phys. Rev. Lett. 2019, 122, 040603.
  50. Choi, S.; Turner, C.J.; Pichler, H.; Ho, W.W.; Michailidis, A.A.; Papić, Z.; Serbyn, M.; Lukin, M.D.; Abanin, D.A. Emergent SU(2) dynamics and perfect quantum many-body scars. Phys. Rev. Lett. 2019, 122, 220603.
  51. Lin, C.J.; Motrunich, O.I. Exact quantum many-body scar states in the Rydberg-blockaded atom chain. Phys. Rev. Lett. 2019, 122, 173401.
  52. Mamaev, M.; Kimchi, I.; Perlin, M.A.; Nandkishore, R.M.; Rey, A.M. Quantum entropic self-localization with ultracold fermions. Phys. Rev. Lett. 2019, 123, 130402.
  53. Schecter, M.; Iadecola, T. Weak ergodicity breaking and quantum many-body scars in spin-1 xy magnets. Phys. Rev. Lett. 2019, 123, 147201.
  54. Wilming, H.; Goihl, M.; Roth, I.; Eisert, J. Entanglement ergodic quantum systems equilibrate exponentially well. Phys. Rev. Lett. 2019, 123, 200604.
  55. Iadecola, T.; Schecter, M.; Xu, S. Quantum many-body scars from magnon condensation. Phys. Rev. 2019, 100, 184312.
  56. Pai, S.; Pretko, M. Dynamical scar states in driven fraction systems. Phys. Rev. Lett. 2019, 123, 136401.
  57. O’Connor, P.; Gehlen, J.; Heller, E.J. Properties of random superpositions of plane waves. Phys. Rev. Lett. 1987, 58, 1296–1298.
  58. Robinett, R.W. Isolated versus non-isolated periodic orbits in variants of the two-dimensional square and circular wells. J. Math. Phys. 1999, 40, 101–122.
  59. Robinett, R.W.; Heppelmann, S. Quantum wave packet revivals in circular billiards. Phys. Rev. A 2002, 65, 062103–062113.
  60. Robinett, R.W. Energy eigenvalues and periodic orbits for the circular disk or annular infinite well. Surf. Rev. Lett. 1998, 5, 519–526.
  61. Doncheski, M.A.; Heppelmann, S.; Robinett, R.W.; Tussey, D.C. Wave packet construction in two-dimensional quantum billiards: Blueprints for the square, equilateral triangle, and circular cases. Am. J. Phys. 2003, 71, 541–557.
  62. Doncheski, M.A.; Robinett, R.W. Quantum mechanical analysis of the equilateral triangle billiard: Periodic orbit theory and wave packet revivals. Ann. Phys. 2002, 299, 208–227.
  63. Lin, S.L.; Gao, F.Z.; Hong, P.; Du, M.L. Quantum spectra and classical orbits in two-dimensional equilateral triangle billiards. Chin. Phys. Lett. 2005, 22, 9–11.
  64. Styer, D.F. Quantum revivals versus classical periodicity in the infinite square well. Am. J. Phys. 2001, 69, 56–62.
  65. Robinett, R.W. Visualizing classical periodic orbits from the quantum energy spectrum via the Fourier transform: Simple infinite well examples. Am. J. Phys. 1997, 65, 1167–1175.
  66. Robinett, R.W. Quantum mechanics of the two-dimensional circular billiard plus baffle system and half-integral angular momentum. Eur. J. Phys. 2003, 24, 231–243.
  67. Wright, M.C.M.; Ham, C.J. Periodic orbit theory in acoustics: Spectral fluctuations in circular and annular waveguides. J. Acoust. Soc. Am. 2007, 121, 1865–1872.
  68. Robinett, R.W. Periodic orbit theory of a continuous family of quasi-circular billiards. J. Math. Phys. 1998, 39, 278–298.
  69. Lu, J. From quantum spectra to classical orbits: Varying rectangular billiards. Prog. Nat. Sci. 2008, 18, 927–930.
  70. Matzkin, A. Bohmian mechanics, the quantum-classical correspondence and the classical limit: The case of the square billiard. Found. Phys. 2009, 39, 903–920.
  71. Fonte, G.; Zerbo, B. Classical billiards and double-slit quantum interference. Eur. Phys. J. Plus 2012, 127, 8–19.
  72. Robinett, R.W. Periodic orbit theory analysis of the circular disk or annular billiard: Non-classical effects and the distribution of energy eigenvalues. Am. J. Phys. 1999, 67, 67–78.
  73. Macek, M.; Cejnar, P.; Jolie, J.; Heinze, S. Evolution of spectral properties along the O(6)-U(5) transition in the interacting boson model. II. Classical trajectories. Phys. Rev. C 2006, 73, 014307.
  74. Lee, W.K. Degeneracy in the particle-in-a-square problem. Am. J. Phys. 1982, 50, 666.
  75. Robinett, R.W. Quantum wave packet revivals. Phys. Rep. 2004, 392, 1–119.
  76. Marcus, C.M.; Rimberg, A.J.; Westervelt, R.M.; Hopkins, P.F.; Gossard, A.C. Conductance fluctuations and chaotic scattering in ballistic microstructures. Phys. Rev. Lett. 1992, 69, 506–509.
  77. Marcus, C.M.; Westervelt, R.M.; Hopkins, P.F.; Gossard, A.C. Conductance fluctuations and quantum chaotic scattering in semiconductor microstructures. Chaos 1993, 3, 643–653.
  78. Taylor, R.P.; Newbury, R.; Sachrajda, A.S.; Feng, Y.; Coleridge, P.T.; Dettmann, C.; Zhu, N.; Guo, H.; Delage, A.; Kelly, P.J.; et al. Self-similar magnetoresistance of a semiconductor Sinai billiard. Phys. Rev. Lett. 1997, 78, 1952–1955.
  79. Sachrajda, A.S.; Ketzmerick, R.; Gould, C.; Feng, Y.; Kelly, P.J.; Delage, A.; Wasilewski, Z. Fractal conductance fluctuations in a soft-wall stadium and a Sinai billiard. Phys. Rev. Lett. 1998, 80, 1948–1951.
  80. Blanchard, P.; Olkiewicz, R. Decoherence-induced continuous pointer states. Phys. Rev. Lett. 2003, 90, 010403.
  81. Ferry, D.K.; Akis, R.; Bird, J.P. Einselection in action: Decoherence and pointer states in open quantum dots. Phys. Rev. Lett. 2004, 93, 026803.
  82. Ferry, D.K.; Huang, L.; Yang, R.; Lai, Y.C.; Akis, R. Open quantum dots in graphene: Scaling relativistic pointer states. J. Phys. Conf. Ser. 2010, 220, 012015.
  83. Wang, W.G.; He, L.; Gong, J. Preferred states of decoherence under intermediate system-environment coupling. Phys. Rev. Lett. 2012, 108, 070403.
  84. Yang, Y.B.; Wang, W.G. A phenomenon of decoherence induced by chaotic environment. Chin. Phys. Lett. 2015, 32, 030301.
  85. Lee, P.A.; Stone, A.D. Universal conductance fluctuations in metals. Phys. Rev. Lett. 1985, 55, 1622–1625.
  86. Kaplan, S.B.; Hartstein, A. Universal conductance fluctuations in narrow Si accumulation layers. Phys. Rev. Lett. 1986, 56, 2403–2406.
  87. Skocpol, W.J.; Mankiewich, P.M.; Howard, R.E.; Jackel, L.D.; Tennant, D.M.; Stone, A.D. Universal conductance fluctuations in silicon inversion-layer nanostructures. Phys. Rev. Lett. 1986, 56, 2865–2868.
  88. Iida, S.; Weidenmüller, H.A.; Zuk, J.A. Wave propagation through disordered media and universal conductance fluctuations. Phys. Rev. Lett. 1990, 64, 583–586.
  89. Kharitonov, M.Y.; Efetov, K.B. Universal conductance fluctuations in graphene. Phys. Rev. B 2008, 78, 033404.
  90. Tomsovic, S.; Ullmo, D. Chaos-assisted tunneling. Phys. Rev. E 1994, 50, 145–162.
  91. Dembowski, C.; Gräf, H.D.; Heine, A.; Hofferbert, R.; Rehfeld, H.; Richter, A. First experimental evidence for chaos-assisted tunneling in a microwave annular billiard. Phys. Rev. Lett. 2000, 84, 867–870.
  92. Steck, D.A.; Oskay, W.H.; Raizen, M.G. Observation of chaos-assisted tunneling between islands of stability. Science 2001, 293, 274–878.
  93. Tomsovic, S. Tunneling and chaos. Phys. Scr. T 2001, 90, 162–165.
  94. de Moura, A.P.S.; Lai, Y.C.; Akis, R.; Bird, J.; Ferry, D.K. Tunneling and nonhyperbolicity in quantum dots. Phys. Rev. Lett. 2002, 88, 236804.
  95. Bäcker, A.; Ketzmerick, R.; Monastra, A.G. Flooding of chaotic eigenstates into regular phase space islands. Phys. Rev. Lett. 2005, 94, 054102.
  96. Bäcker, A.; Ketzmerick, R.; Löck, S.; Robnik, M.; Vidmar, G.; Höhmann, R.; Kuhl, U.; Stöckmann, H.J. Dynamical tunneling in mushroom billiards. Phys. Rev. Lett. 2008, 100, 174103.
  97. Bäcker, A.; Ketzmerick, R.; Löck, S.; Schilling, L. Regular-to-chaotic tunneling rates using a fictitious integrable system. Phys. Rev. Lett. 2008, 100, 104101.
  98. Rong, S.; Hai, W.; Xie, Q.; Zhu, Q. Chaos enhancing tunneling in a coupled Bose–Einstein condensate with a double driving. Chaos 2009, 19, 033129.
  99. Löck, S.; Bäcker, A.; Ketzmerick, R.; Schlagheck, P. Regular-to-chaotic tunneling rates: From the quantum to the semiclassical regime. Phys. Rev. Lett. 2010, 104, 114101.
  100. Pecora, L.M.; Lee, H.; Wu, D.H.; Antonsen, T.; Lee, M.J.; Ott, E. Chaos regularization of quantum tunneling rates. Phys. Rev. E 2011, 83, 065201.
  101. Lee, M.J.; Antonsen, T.M.; Ott, E.; Pecora, L.M. Theory of chaos regularization of tunneling in chaotic quantum dots. Phys. Rev. E 2012, 86, 056212.
  102. Ni, X.; Huang, L.; Lai, Y.C.; Pecora, L.M. Effect of chaos on relativistic quantum tunneling. Europhys. Lett. 2012, 98, 50007.
  103. Ni, X.; Huang, L.; Ying, L.; Lai, Y.C. Relativistic quantum tunneling of a Dirac fermion in nonhyperbolic chaotic systems. Phys. Rev. B 2013, 87, 224304.
  104. Ying, L.; Wang, G.; Huang, L.; Lai, Y.C. Quantum chaotic tunneling in graphene systems with electron-electron interactions. Phys. Rev. B 2014, 90, 224301.
  105. Doya, V.; Legrand, O.; Mortessagne, F.; Miniatura, C. Light scarring in an optical fiber. Phys. Rev. Lett. 2001, 88, 014102.
  106. Michel, C.; Doya, V.; Legrand, O.; Mortessagne, F. Selective amplification of scars in a chaotic optical fiber. Phys. Rev. Lett. 2007, 99, 224101.
  107. Slusher, R.; Weisbuch, C. Optical microcavities in condensed matter systems. Solid State Commun. 1994, 92, 149–158.
  108. Gmachl, C.; Capasso, F.; Narimanov, E.E.; Nockel, J.U.; Stone, A.D.; Faist, J.; Sivco, D.L.; Cho, A.Y. Highpower directional emission from microlasers with chaotic resonators. Science 1998, 280, 1556–1564.
  109. Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846.
  110. Lee, S.B.; Yang, J.; Moon, S.; Lee, S.Y.; Shim, J.B.; Kim, S.W.; Lee, J.H.; An, K. Observation of an exceptional point in a chaotic optical microcavity. Phys. Rev. Lett. 2009, 103, 134101.
  111. Song, Q.; Fang, W.; Liu, B.; Ho, S.T.; Solomon, G.S.; Cao, H. Chaotic microcavity laser with high quality factor and unidirectional output. Phys. Rev. A 2009, 80, 041807.
  112. Peng, B.; Oezdemir, S.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity-time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398.
  113. Wang, L.; Lippolis, D.; Li, Z.; Jiang, X.; Gong, Q.; Xiao, Y. Statistics of chaotic resonances in an optical microcavity. Phys. Rev. E 2016, 93, 040201.
  114. Jiang, X.; Shao, L.; Zhang, S.; Yi, X.; Wiersig, J.; Wang, L.; Gong, Q.; Loncar, M.; Yang, L.; Xiao, Y. Chaos-assisted broadband momentum transformation in optical microresonators. Science 2017, 358, 344–347.
  115. Bittner, S.; Guazzotti, S.; Zeng, Y.; Hu, X.; Yilmaz, H.; Kim, K.; Oh, S.S.; Wang, Q.J.; Hess, O.; Cao, H. Suppressing spatiotemporal lasing instabilities with wave-chaotic microcavities. Science 2018, 361, 1225–1231.
  116. Guidry, M.A.; Song, Y.; Lafargue, C.; Sobczyk, R.; Decanini, D.; Bittner, S.; Dietz, B.; Huang, L.; Zyss, J.; Grigis, A.; et al. Three-dimensional micro-billiard lasers: The square pyramid. Europhys. Lett. 2019, 126, 64004.
  117. Chinnery, P.A.; Humphrey, V.F. Experimental visualization of acoustic resonances within a stadium-shaped cavity. Phys. Rev. E 1996, 53, 272–276.
  118. Legrand, O.; Schmit, C.; Sornette, D. Quantum chaos methods applied to high-frequency plate vibrations. Europhys. Lett. 1992, 18, 101–106.
  119. Mortessagne, F.; Legrand, O.; Sornette, D. Transient chaos in room acoustics. Chaos 1993, 3, 529–541.
  120. Ellegaard, C.; Guhr, T.; Lindemann, K.; Lorensen, H.Q.; Nygård, J.; Oxborrow, M. Spectral statistics of acoustic resonances in aluminum blocks. Phys. Rev. Lett. 1995, 75, 1546–1549.
  121. Ellegaard, C.; Guhr, T.; Lindemann, K.; Nygård, J.; Oxborrow, M. Symmetry breaking and spectral statistics of acoustic resonances in quartz blocks. Phys. Rev. Lett. 1996, 77, 4918–4921.
  122. Leitner, D.M. Effects of symmetry breaking on statistical properties of near-lying acoustic resonances. Phys. Rev. E 1997, 56, 4890–4891.
  123. Bogomolny, E.; Hugues, E. Semiclassical theory of flexural vibrations of plates. Phys. Rev. E 1998, 57, 5404–5424.
  124. Blümel, R.; Davidson, I.H.; Reinhardt, W.P.; Lin, H.; Sharnoff, M. Quasilinear ridge structures in water surface waves. Phys. Rev. A 1992, 45, 2641–2644.
  125. Kudrolli, A.; Abraham, M.C.; Gollub, J.P. Scarred patterns in surface waves. Phys. Rev. E 2001, 63, 026208.
  126. Agam, O.; Altshuler, B.L. Scars in parametrically excited surface waves. Phys. A 2001, 302, 310–317.
  127. Lindelof, P.E.; Norregaard, J.; Hanberg, J. New light on the scattering mechanisms in Si inversion layers by weak localization experiments. Phys. Scr. T 1986, 14, 17–26.
  128. Nunez-Fernandez, Y.; Trallero-Giner, C.; Buchleitner, A. Liquid surface waves in parabolic tanks. Phys. Fluids 2008, 20, 117106.
  129. Práger, M. Eigenvalues and eigenfunctions of the Laplace operator on an equilateral triangle. Appl. Math. 1998, 43, 311–320.
  130. Nye, J.F.; Berry, M.V. Dislocations in wave trains. Proc. R Soc. A Math. Phys. Eng. Sci. 1974, 336, 165–190.
  131. Bazhenov, V.Y.; Soskin, M.S.; Vasnetsov, M.V. Screw dislocations in light wavefronts. J. Mod. Opt. 1992, 39, 985–990.
  132. Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1502.
  133. Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316.
  134. Molina-Terriza, G.; Torres, J.P.; Torner, L. Twisted photons. Nat. Phys. 2007, 3, 305–310.
  135. Paterson, L.; MacDonald, M.P.; Arlt, J.; Sibbett, W.; Bryant, P.E.; Dholakia, K. Controlled rotation of optically trapped microscopic particles. Science 2001, 292, 912–914.
  136. MacDonald, M.P.; Paterson, L.; Volke-Sepulveda, K.; Arlt, J.; Sibbett, W.; Dholakia, K. Creation and manipulation of three-dimensional optically trapped structures. Science 2002, 296, 1101–1103.
  137. Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816.
  138. Harwit, M. Photon orbital angular momentum in astrophysics. Astrophys. J. 2003, 597, 1266–1270.
  139. Zhuang, X.W. Unraveling DNA condensation with optical tweezers. Science 2004, 305, 188–190.
  140. Fürhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694.
  141. Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh criterion limit with optical vortices. Phys. Rev. Lett. 2006, 97, 163903.
  142. Barreiro, J.T.; Wei, T.C.; Kwiat, P.G. Beating the channel capacity limit for linear photonic superdense coding. Nat. Phys. 2008, 4, 282–286.
  143. Friedrich, H.; Trost, J. Accurate WKB wave functions for weakly attractive inverse-square potential. Phys. Rev. A 1999, 59, 1683–1686.
  144. De Heer, W.A. The physics of simple metal clusters: Experimental aspects and simple models. Rev. Mod. Phys. 1993, 65, 611.
  145. Lebedev, N.N. Special Functions & Their Applications; Dover: New York, NY, USA, 1972.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Quantum Science & Technology
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Yung-Fu Chen
,
Song-Qing Lin
,
Ru-Wei Chang
,
Yan-Ting Yu
,
Hsing-Chih Liang
View Times: 303
Revisions: 3 times (View History)
Update Date: 19 Oct 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback