Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 1 by Yung-Fu Chen and Version 3 by Jason Zhu.
Two-dimensional quantum billiards are one of the most important paradigms for exploring the connection between quantum and classical worlds. Researchers are mainly focused on nonintegrable and irregular shapes to understand the quantum characteristics of chaotic billiards. The emergence of the scarred modes relevant to unstable periodic orbits (POs) is one intriguing finding in nonintegrable quantum billiards. On the other hand, stable POs are abundant in integrable billiards. The quantum wavefunctions associated with stable POs have been shown to play a key role in ballistic transport.
- integrable quantum billiards
- classical periodic orbits
- level clustering
1. Introduction
Harmonic oscillators are universally recognized as one of the most important paradigms for exploring quantum-classical correspondence. Under the paraxial approximation, the transverse part of the wave equation for spherical cavities can be mathematically analogous to the Schrödinger equation for two-dimensional (2D) harmonic oscillators [1]. Accordingly, various high-order transverse modes can be generated with the specially designed spherical laser cavities to analogously manifest the quantum wave function. The eigenfunctions of 2D quantum harmonic oscillators can be solved as the Hermite–Gaussian (HG) functions in rectangular coordinates or the Laguerre–Gaussian (LG) functions in polar coordinates [2]. The selectively diode-end-pumped solid-state lasers have been widely employed to generate both HG and LG functions from ground order to very high order [3][4][5][6][7][3,4,5,6,7]. Additionally, the same laser technology was exploited to generate the so-called geometric modes in the degenerate cavities, which clearly revealed the ray-wave duality in the spatial domain [8][9][8,9]. In mesoscopic quantum phenomena, the degeneracy of energy levels was found to play an important role in the connection between the conductance fluctuation and the classical periodic orbits (POs) [10]. Similarly, the emergence of geometric modes was verified to originate from the degeneracy of eigenfrequencies in laser resonators [11][12][11,12]. The Lissajous stationary modes are one of the most remarkable geometric modes generated from the astigmatic laser cavities. Theoretically, the Schrödinger coherent state for the one-dimensional (1D) harmonic oscillator can be straightforwardly extended to the 2D harmonic oscillator to obtain the stationary coherent states that exactly spatially correspond to the Lissajous figures.
Additionally, 2D quantum billiards are another pedagogical model for comprehending the connection between quantum and classical worlds. Various dynamical features can be straightforwardly studied from the model of quantum billiards by changing the geometry. One main branch of research on billiard systems is focused on nonintegrable and irregular shapes to understand the characteristics in the field of quantum chaos [13][14][15][16][17][18][19][20][13,14,15,16,17,18,19,20]. Classically, the chaotic nature renders all the orbits in a chaotic system as being unstable. An interesting finding in nonintegrable quantum billiards is the emergence of eigenstates on unstable POs, called scarred modes [21][22][23][21,22,23]. Quantum scars have been searched and analyzed in mesoscopic systems [24][25][26][27][28][29][30][31][32][33][34][24,25,26,27,28,29,30,31,32,33,34]. Due to the similarity of the equations for different types of waves, scars have been observed in microwaves [35][36][37][38][39][40][41][35,36,37,38,39,40,41]. Quantum scars have not only been confirmed from the accumulation of spin–orbit-coupled atomic gases for specific energies [42] but also generated in the 2D harmonic oscillators with local impurities [43][44][45][43,44,45]. Furthermore, quantum many-body scars have been hypothesized to cause weak ergodicity breaking and the unexpectedly slow thermalization of cold atoms [46][47][48][49][50][51][52][53][54][55][46,47,48,49,50,51,52,53,54,55]. The similar phenomenon dynamical scar has also been experimentally found in a driven fraction system [56]. Nevertheless, the overall number of scarred modes is quite few. The eigenstates in nonintegrable billiards are mostly widely distributed in the coordinate space [13], often exhibiting common features of quasi-linear ridge structures [57].
Compared with non-integrable billiards, stable POs are generally abundant in integrable billiards with symmetrical shapes [11][16][58][59][60][61][62][63][64][65][66][67][68][69][70][71][72][73][74][75][11,16,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75]. The quantum wavefunctions associated with stable POs have been found to play a key role in ballistic transport [76][77][78][79][76,77,78,79], quantum pointer states and decoherence [80][81][82][83][84][85][86][87][88][89][90][91][92][93][94][95][80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95], universal conductance fluctuations [95][96][97][98][99][95,96,97,98,99], and chaos-assisted quantum tunneling [100][101][102][103][104][100,101,102,103,104]. Ballistic transport means that the mean free path of the particle is significantly longer than the size of the medium through which the particle travels. In addition to microwave cavities, quantum billiards can be analogously explored with the wave systems including optical fibers [105][106][105,106], optical resonators [107][108][109][110][111][112][113][114][115][116][107,108,109,110,111,112,113,114,115,116], vibrating plates and acoustic waves [117][118][119][120][121][122][123][117,118,119,120,121,122,123], and liquid surface waves [123][124][125][126][127][128][123,124,125,126,127,128]. Noticeably, it has been confirmed that the vertical-cavity surface-emitting lasers (VCSELs) with a unique longitudinal wave vector kz and the lateral oxide confinements can be modeled as 2D wave billiards with hard walls. To be brief, theoretical research on quantum billiards was intensively performed in the last century, and later, some researchers’ interests shifted to applied fields such as laser resonators.
2. Quantum Billiards
The quantum analogy of a classical billiard is called a quantum billiard. For the classical billiard with the 2D region denoted by R, the corresponding potential in quantum mechanics is given as 𝑉(𝑥,𝑦)={0 in 𝑅∞ otherwise
⎧⎩⎨(∂2∂𝑥2+∂2∂𝑦2+𝑘2)𝜓(𝑥,𝑦)=0 in 𝑅𝜓(𝑥,𝑦)=0 on the boundary of 𝑅
3. Square Billiard
The spatial distributions of quantum wave functions corresponding to classical POs [76][77][78][79][76,77,78,79] have been an intriguing phenomenon in open ballistic cavities. Semiclassical PO theory has been used to explain the scarred wave functions in chaotic billiards [21][22][23][21,22,23]. Nevertheless, it is pedagogically useful for comprehending the quantum-classical correspondence in mesoscopic physics to fully develop the connection between quantum eigenfunctions and classical POs in integrable systems. One of the simplest integrable billiards is the square billiard [11]. In a square billiard, each family of POs can be specified with three parameters (p, q, and ϕ), where p and q are two positive integers describing the number of reflections with the horizontal and vertical boundaries, and ϕ (−π < ϕ < π) is associated with the wall positions of specular reflection points [11][65][11,65]. Alternatively, the parameter ϕ may also be linked to the starting point of the classical particle. Figure 1 depicts some examples for POs in a square billiard. The trajectory can be seen to constitute a single, non-repeated orbit when p and q are co-prime. When p and q have a common factor m, the trajectory is an orbit family that corresponds to m primitive POs with indices of (p/m, q/m, and ϕ/m).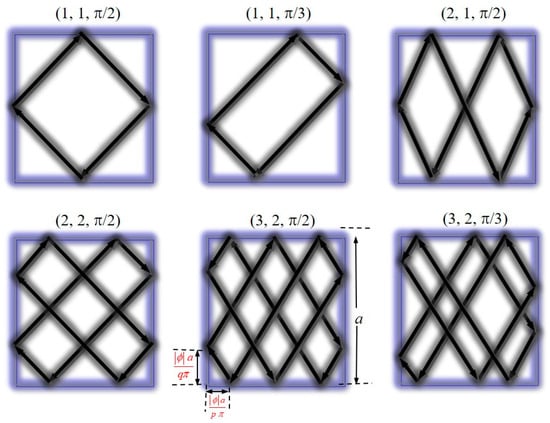
Figure 1.
Some examples of orbit families in square billiard.
𝜓𝑚,𝑛(𝑥,𝑦)=2𝑎sin(𝑚𝜋𝑎𝑥)sin(𝑛𝜋𝑎𝑦)
𝑘𝑚,𝑛=𝜋𝑎𝑚2+𝑛2−−−−−−−√
Figure 2
shows the wave patterns |𝜓𝑚,𝑛(𝑥,𝑦)|2 for several sets of quantum numbers
for several sets of quantum numbers (𝑚,𝑛).
From Bohr’s correspondence principle, the classical limit of a quantum system should be asymptotically obtained when the quantum numbers are sufficiently large. However, the conventional eigenfunctions of a square billiard cannot reveal the features of classical POs no matter how large the quantum numbers are. The quantum states relevant to the classical POs have been verified to be the superpositions of the nearly degenerate eigenstates. For a given central order
. From Bohr’s correspondence principle, the classical limit of a quantum system should be asymptotically obtained when the quantum numbers are sufficiently large. However, the conventional eigenfunctions of a square billiard cannot reveal the features of classical POs no matter how large the quantum numbers are. The quantum states relevant to the classical POs have been verified to be the superpositions of the nearly degenerate eigenstates. For a given central order (𝑚𝑜,𝑛𝑜)
, the nearly degenerate condition can be derived from the differential of the eigenvalue function 𝐸(𝑚,𝑛) given as
given as𝑑𝐸(𝑚,𝑛)|𝑚𝑜,𝑛𝑜=(∂𝐸/∂𝑚|𝑚𝑜,𝑛𝑜)𝑑𝑚+(∂𝐸/∂𝑛|𝑚𝑜,𝑛𝑜)𝑑𝑛

Figure 2.
Wave patterns for eigenstates
|𝜓𝑚,𝑛(𝑥,𝑦)|2
for several sets of quantum numbers
(𝑚,𝑛)
of square billiard.
−𝑑𝑛𝑑𝑚=∂𝐸/∂𝑚|𝑚𝑜,𝑛𝑜∂𝐸/∂𝑛|𝑚𝑜,𝑛𝑜=𝑚𝑜𝑛𝑜
Ψ(𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)=12𝑀+1−−−−−−√∑𝐾=−𝑀𝑀𝑒𝑖𝐾𝜙𝜓𝑞𝑁+𝑝𝐾,𝑝𝑁−𝑞𝐾(𝑥,𝑦)
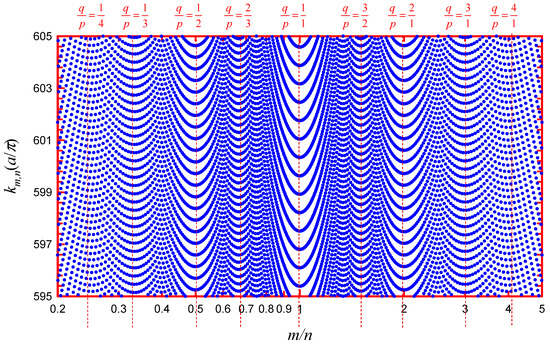
Figure 3. Directionally resolved level distribution 𝑘𝑚,𝑛 as a function of the ratio 𝑚/𝑛 with 1≤𝑚,𝑛≤700 for manifesting the level clustering relevant to classical POs.

Figure 4. Wave patterns for quasi-stationary coherent states |Ψ(𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)|2 calculated using Equation (6) with N = 100, M = 5, and 𝜙=𝜋/2 for eigenstates clustered around the indices (p, q).
The trajectorial equations for POs can be derived from the quantum coherent state in Equation (7) for the central maximum of the wave intensity. Using the identity sin𝜃=(𝑒𝑖𝜃−𝑒−𝑖𝜃)/(2𝑖), the representation of the coherent state in Equation (7) can be organized as
Ψ(𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)=12𝑎[𝑒𝑖𝑁Θ−𝑔(𝑥,𝑦)𝐷𝑀(Θ+𝑡(𝑥,𝑦)+𝜙)+𝑒−𝑖𝑁Θ−𝑔(𝑥,𝑦)𝐷𝑀(Θ+𝑡(𝑥,𝑦)−𝜙)]−12𝑎[𝑒𝑖𝑁Θ+𝑔(𝑥,𝑦)𝐷𝑀(Θ−𝑡(𝑥,𝑦)+𝜙)+𝑒−𝑖𝑁Θ+𝑔(𝑥,𝑦)𝐷𝑀(Θ−𝑡(𝑥,𝑦)−𝜙)]
𝐷𝑀(𝜃)=12𝑀+1−−−−−−√∑𝐾=−𝑀𝑀𝑒𝑖𝐾𝜃
4. Equilateral Triangular Billiard
Square billiard is a classically separable and integrable system, whereas the equilateral triangle billiard is an integrable but non-separable system. In theory, the correlation between the quantum level clustering and the classical POs was deeply discussed from the representation of the quantum coherent states. In experiments, the oxide-confined VCSEL devices were fabricated in the shape of an equilateral triangle to analogously manifest the quantum level distribution and the spatial features of the wave functions. For an equilateral-triangular billiard with three vertices at (0,0), (𝑎/2,3−−√𝑎/2), and (−𝑎/2,3−−√𝑎/2), the eigenfunctions are given using [62][129][62,130]𝜓(𝑒)𝑚,𝑛(𝑥,𝑦)=16𝑎233√−−−−√{cos[2𝜋3𝑎(2𝑚−𝑛)𝑥]sin(2𝜋3√𝑎𝑛𝑦)−cos[2𝜋3𝑎(2𝑛−𝑚)𝑥]sin(2𝜋3√𝑎𝑚𝑦)+cos[−2𝜋3𝑎(𝑚+𝑛)𝑥]sin[2𝜋3√𝑎(𝑚−𝑛)𝑦]}
𝜓(𝑜)𝑚,𝑛(𝑥,𝑦)=16𝑎233√−−−−√{sin[2𝜋3𝑎(2𝑚−𝑛)𝑥]sin(2𝜋3√𝑎𝑛𝑦)−sin[2𝜋3𝑎(2𝑛−𝑚)𝑥]sin(2𝜋3√𝑎𝑚𝑦)+sin[−2𝜋3𝑎(𝑚+𝑛)𝑥]sin[2𝜋3√𝑎(𝑚−𝑛)𝑦]}
𝑘𝑚,𝑛=4𝜋3𝑎𝑚2+𝑛2−𝑚𝑛−−−−−−−−−−−√
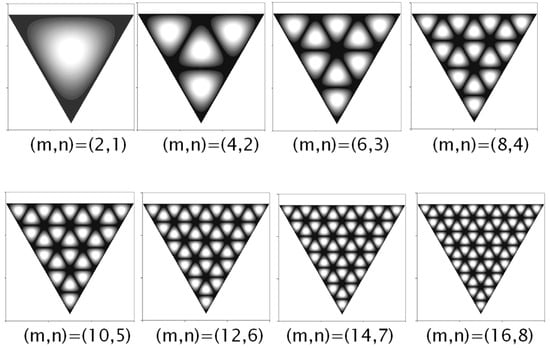
Figure 5. Wave patterns for eigenstates |𝜓(𝑒)𝑚,𝑛(𝑥,𝑦)|2 for several sets of quantum numbers (𝑚,𝑛) in equilateral triangle billiard.
𝜓(±)𝑚,𝑛(𝑥,𝑦)=16𝑎233√−−−−√{exp[± 𝑖2𝜋3𝑎(2𝑚−𝑛)𝑥]sin(2𝜋3√𝑎𝑛𝑦)−exp[± 𝑖2𝜋3𝑎(2𝑛−𝑚)𝑥]sin(2𝜋3√𝑎𝑚𝑦)+exp[∓ 𝑖2𝜋3𝑎(𝑚+𝑛)𝑥]sin[2𝜋3√𝑎(𝑚−𝑛)𝑦]}
−𝑑𝑛𝑑𝑚=∂𝐸/∂𝑚|𝑚𝑜,𝑛𝑜∂𝐸/∂𝑛|𝑚𝑜,𝑛𝑜=2𝑚𝑜−𝑛𝑜2𝑛𝑜−𝑚𝑜
Ψ(±,𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)=12𝑀+1−−−−−−√∑𝐾=−𝑀𝑀𝑒±𝑖𝐾𝜙𝜓(±)(2𝑞+𝑝)𝑁+𝑝𝐾,(2𝑝+𝑞)𝑁−𝑞𝐾(𝑥,𝑦)
𝐸(𝑚,𝑛)≈9ℏ2𝜋28𝜇𝑎2[5(𝑝2+𝑞2)+8𝑝𝑞]𝑁2
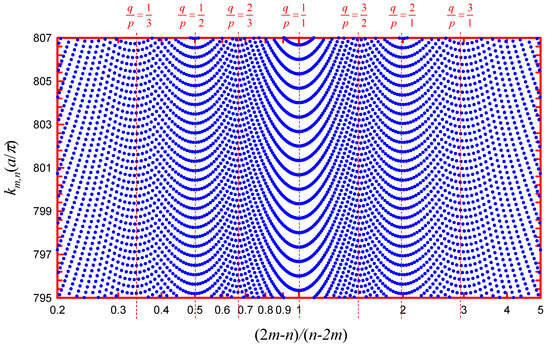
Figure 6. Directionally resolved level distribution 𝑘𝑚,𝑛 as a function of the ratio (2𝑚−𝑛)/(2𝑛−𝑚) with 1≤𝑚,𝑛≤700 for manifesting the level clustering relevant to classical POs.
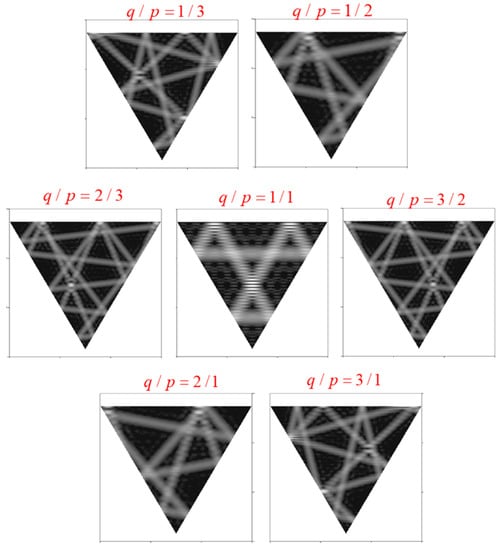
Figure 7. Wave patterns for quasi-stationary coherent states |Ψ(±,𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)|2 calculated using Equation (15) with
N
M
𝜙=𝜋/2
p
q).
The same as in the case of a square billiard, the trajectory equations for POs can be derived from Equation (15) from the central maximum of the wave intensity. Using sin𝜃=(𝑒𝑖𝜃−𝑒−𝑖𝜃)/(2𝑖), the representation in Equation (15) can be organized as
Ψ(+,𝑝,𝑞)𝑁,𝑀(𝑥,𝑦;𝜙)=16𝑎233√−−−−√12𝑖[𝑒𝑖𝑁Θ+𝑔1(𝑥,𝑦)𝐷𝑀(Θ+𝑡1(𝑥,𝑦,𝜙))−𝑒𝑖𝑁Θ−𝑔1(𝑥,𝑦)𝐷𝑀(Θ−𝑡1(𝑥,𝑦,𝜙))−𝑒𝑖𝑁Θ+𝑔2(𝑥,𝑦)𝐷𝑀(Θ+𝑡2(𝑥,𝑦,𝜙))+𝑒𝑖𝑁Θ−𝑔2(𝑥,𝑦)𝐷𝑀(Θ−𝑡2(𝑥,𝑦,𝜙))+𝑒𝑖𝑁Θ+𝑔3(𝑥,𝑦)𝐷𝑀(Θ+𝑡3(𝑥,𝑦,𝜙))−𝑒𝑖𝑁Θ−𝑔3(𝑥,𝑦)𝐷𝑀(Θ−𝑡3(𝑥,𝑦,𝜙))]
Θ±𝑔1(𝑥,𝑦)=2𝜋𝑎[𝑞𝑥±(2𝑝+𝑞)3−−√𝑦]
Θ±𝑔2(𝑥,𝑦)=2𝜋𝑎[𝑝𝑥±(2𝑞+𝑝)3−−√𝑦]
Θ±𝑔3(𝑥,𝑦)=2𝜋𝑎[−(𝑝+𝑞)𝑥±(𝑞−𝑝)3−−√𝑦]
Θ±𝑡1(𝑥,𝑦,𝜙)=2𝜋3−−√𝑎[(2𝑝+𝑞)3−−√𝑥∓𝑞𝑦]+𝜙
Θ±𝑡2(𝑥,𝑦,𝜙)=2𝜋3−−√𝑎[−(2𝑞+𝑝)3−−√𝑥±𝑝𝑦]+𝜙
Θ±𝑡3(𝑥,𝑦,𝜙)=2𝜋3−−√𝑎[(𝑞−𝑝)3−−√𝑥±(𝑝+𝑞)𝑦]+𝜙
5. Circular Billiard
Circular billiard is another pedagogical paradigm in classically separable and integrable systems. The azimuthal and radial components of the eigenfunctions of a circular billiard are the form of exp(imϕ) and the Bessel function of the first kind, respectively. Helically phased light beams with the azimuthal phase form of exp(imϕ) are well known to carry an orbital angular momentum (OAM) of mη per photon, where m is an integer [130][131][131,132]. In ray dynamics, the function of a circular billiard is the same as the transverse confinement of a cylindrical waveguide for light. Consequently, the propagation-invariant solutions of the Helmholtz equation in a cylindrical waveguide can be in terms of the Bessel beams with well-defined OAM [132][133]. The OAM or optical vortex (OV) of light has been widely used in numerous applications, such as generating OAM-entangled photon pairs [133][134][134,135], trapping and rotating micron and submicron objects [135][136][137][136,137,138], generating astrophysical OAM light [138][139], assembling DNA biomolecules [139][140], OAM-based microscopy and imaging [140][141], super-diffraction limit imaging [141][142], and optical communication [142][143]. The eigenstates in polar coordinates for a circular billiard with radius R are given using 𝜓𝑚,𝑛(𝑟,𝜃)=⎡⎣⎢2𝑅2𝐽2𝑚+1(𝑘𝑚,𝑛𝑅)⎤⎦⎥1/2𝐽𝑚(𝑘𝑚,𝑛𝑟)12𝜋−−−√𝑒𝑖𝑚𝜃

Figure 8. Wave patterns for the functions of Re[𝜓𝑚,𝑛(𝑟,𝜃)] with different quantum numbers (m, n) for circular billiard.
𝑘2𝑚,𝑛(𝑅2−𝑅2𝑜)−−−−−−−−−−−√−𝑚cos−1(𝑅𝑜𝑅)=(𝑛+34)𝜋,
𝑘𝑚,𝑛𝑅sin(𝑝𝜋/𝑞)=(𝑝𝑞𝑚+𝑛+34)𝜋
1𝜋cos−1(2𝑚𝑘𝑚,𝑛𝑎)=𝑝𝑞
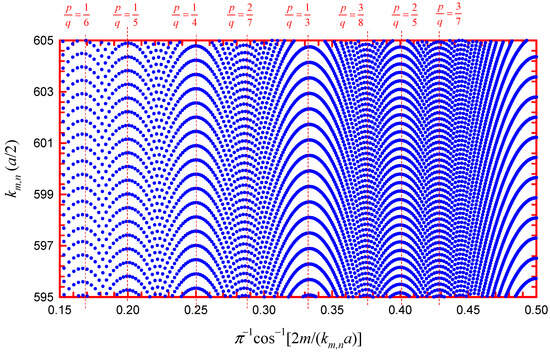
Figure 9. Directionally resolved level distribution 𝑘𝑚,𝑛 versus
𝜋−1cos−1[2𝑚/(𝑘𝑚,𝑛𝑎)]
1≤𝑚,𝑛≤700 for manifesting the level clustering relevant to classical POs.
Once again, the manifestation of classical POs in quantum systems can be fulfilled by exploiting a coherent superposition of the eigenstates belonging to the same shell of the spectrum. In terms of the nearly degenerate eigenstates 𝜓𝑚𝑜−𝑞𝐾,𝑛𝑜+𝑝𝐾
and the phase factor ϕ, the coherent states for circular billiards can be expressed as
Ψ(𝑝,𝑞)𝑚𝑜,𝑀(𝑟,𝜃;𝜙)=12𝑀+1−−−−−−√∑𝐾=−𝑀𝑀𝑒𝑖 𝑞𝐾 𝜙 𝜓𝑚𝑜−𝑞𝐾,𝑛𝑜+𝑝𝐾(𝑟,𝜃).

Figure 10. Wave patterns for quasi-stationary coherent states |Ψ(𝑝,𝑞)𝑚𝑜,𝑀(𝑟,𝜃;𝜙)|2 calculated with mo = 100, M = 2, and different sets of parameters (𝑝,𝑞) and 𝜙=0.
Logically, the trajectory equations for classical POs can be extracted from the quantum coherent states in Equation (28). However, the extraction cannot be the same as the cases of square and equilateral triangular billiards to be reached straightforwardly. The derivation for the trajectory equations needs to be skillfully used for the integral representation, the asymptotic form, and the boundary condition for the Bessel functions. The integral representation for the Bessel functions of the first kind is given using [145][146]
Using the boundary condition 𝐽𝑚(𝑘𝑚,𝑛𝑅)=0
and the asymptotic form 𝐽𝑚(𝑧)≈(2/𝜋𝑧)−−−−−−√cos[𝑧−(2𝑚+1)𝜋/4] for 𝑧→∞, the coefficient related to the normalization constant in Equation (24) for high-order modes can be approximated as
𝐽𝑚(𝜌)=12𝜋∫𝜋−𝜋𝑒𝑖𝜌sin𝜗𝑒−𝑖𝑚𝜗𝑑𝜗
⎡⎣⎢2𝑅2𝐽2𝑚+1(𝑘𝑚,𝑛𝑅)⎤⎦⎥1/212𝜋−−−√=𝑘𝑚,𝑛2𝑅−−−−√
𝜓𝑚,𝑛(𝑟,𝜃)=𝑘𝑚,𝑛2𝑅−−−−√12𝜋∫𝜋−𝜋𝑒 𝑖 𝑘𝑚,𝑛𝑟sin𝜗𝑒𝑖𝑚(𝜃−𝜗)𝑑𝜗
Ψ(𝑝,𝑞)𝑚𝑜,𝑀(𝑟,𝜃;𝜙)=𝑘𝑚,𝑛2𝑅−−−−√12𝜋[∫𝜋−𝜋𝑒𝑖𝑘𝑚𝑜,𝑛𝑜𝑟 sin(𝜉+𝜃−𝜙) 𝑒−𝑖𝑚𝑜(𝜉−𝜙) 𝐷𝑀(𝑞𝜉)𝑑𝜉]
Ψ(𝑝,𝑞)𝑚𝑜,𝑀(𝑟,𝜃;𝜙)=𝑘𝑚,𝑛2𝑅−−−−√12𝜋⎡⎣⎢⎢ ∑𝑠=0𝑞−1∫𝜋/𝑞−𝜋/𝑞𝑒𝑖𝑘𝑚𝑜,𝑛𝑜𝑟 sin(𝜉+𝜃+2𝜋𝑠𝑞−𝜙) 𝑒−𝑖𝑚𝑜(𝜉+2𝜋𝑠𝑞−𝜙) 𝐷𝑀(𝑞𝜉)𝑑𝜉⎤⎦⎥⎥
sin(𝜉+𝜃+2𝜋𝑠𝑞−𝜙)≈𝜉cos(𝜃+2𝜋𝑠𝑞−𝜙)+sin(𝜃+2𝜋𝑠𝑞−𝜙)
Ψ(𝑝,𝑞)𝑚𝑜,𝑀(𝑟,𝜃;𝜙)=𝑘𝑚,𝑛2𝑅−−−−√12𝜋∑𝑠=0𝑞−1 [𝑒 𝑖 𝑚𝑜Θ𝑔,𝑠(𝑟,𝜃;𝜙)∫𝜋/𝑞−𝜋/𝑞𝑒 𝑖 𝑚𝑜 𝜉 Θ𝑡,𝑠(𝑟,𝜃;𝜙) 𝐷𝑀(𝑞𝜉)𝑑𝜉]
Θ𝑔,𝑠(𝑟,𝜃;𝜙)=𝑟𝑅𝑜sin(𝜃+2𝜋𝑠𝑞−𝜙)−(2𝜋𝑠𝑞−𝜙)
Θ𝑡,𝑠(𝑟,𝜃;𝜙)=𝑟𝑅𝑜cos(𝜃+2𝜋𝑠𝑞−𝜙)−1
Ψ(𝑝,𝑞)𝑚𝑜,𝑀(𝑟,𝜃;𝜙)=𝑚𝑜2(2𝑀+1)𝑅𝑅𝑜𝑞2−−−−−−−−−−√×∑𝑠=0𝑞−1𝑒𝑖𝑚𝑜Θ𝑔,𝑠(𝑟,𝜃;𝜙)sinc[𝑚𝑜 𝜋𝑞(2𝑀+1)Θ𝑡,𝑠(𝑟,𝜃;𝜙)]
