Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
John Van Boxel
 -- 2878 2023-05-12 16:36:42 |
2 Gramatic and content changes regarding to the chosed part of text
Vukašin Rončević
 Meta information modification 2878 2023-05-13 09:16:01 | |
3 Reference format revised.
Lindsay Dong
 + 2 word(s) 2880 2023-05-15 11:07:53 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Rončević, V.; Živanović, N.; Van Boxel, J.H.; Iserloh, T.; Štrbac, S. Dripping Rainfall Simulators for Soil Research. Encyclopedia. Available online: https://encyclopedia.pub/entry/44212 (accessed on 16 November 2024).
Rončević V, Živanović N, Van Boxel JH, Iserloh T, Štrbac S. Dripping Rainfall Simulators for Soil Research. Encyclopedia. Available at: https://encyclopedia.pub/entry/44212. Accessed November 16, 2024.
Rončević, Vukašin, Nikola Živanović, John H. Van Boxel, Thomas Iserloh, Snežana Štrbac. "Dripping Rainfall Simulators for Soil Research" Encyclopedia, https://encyclopedia.pub/entry/44212 (accessed November 16, 2024).
Rončević, V., Živanović, N., Van Boxel, J.H., Iserloh, T., & Štrbac, S. (2023, May 12). Dripping Rainfall Simulators for Soil Research. In Encyclopedia. https://encyclopedia.pub/entry/44212
Rončević, Vukašin, et al. "Dripping Rainfall Simulators for Soil Research." Encyclopedia. Web. 12 May, 2023.
Dripping Rainfall Simulators for Soil Research
Edit
This entry is adapted from the peer-reviewed paper 10.3390/w15071314

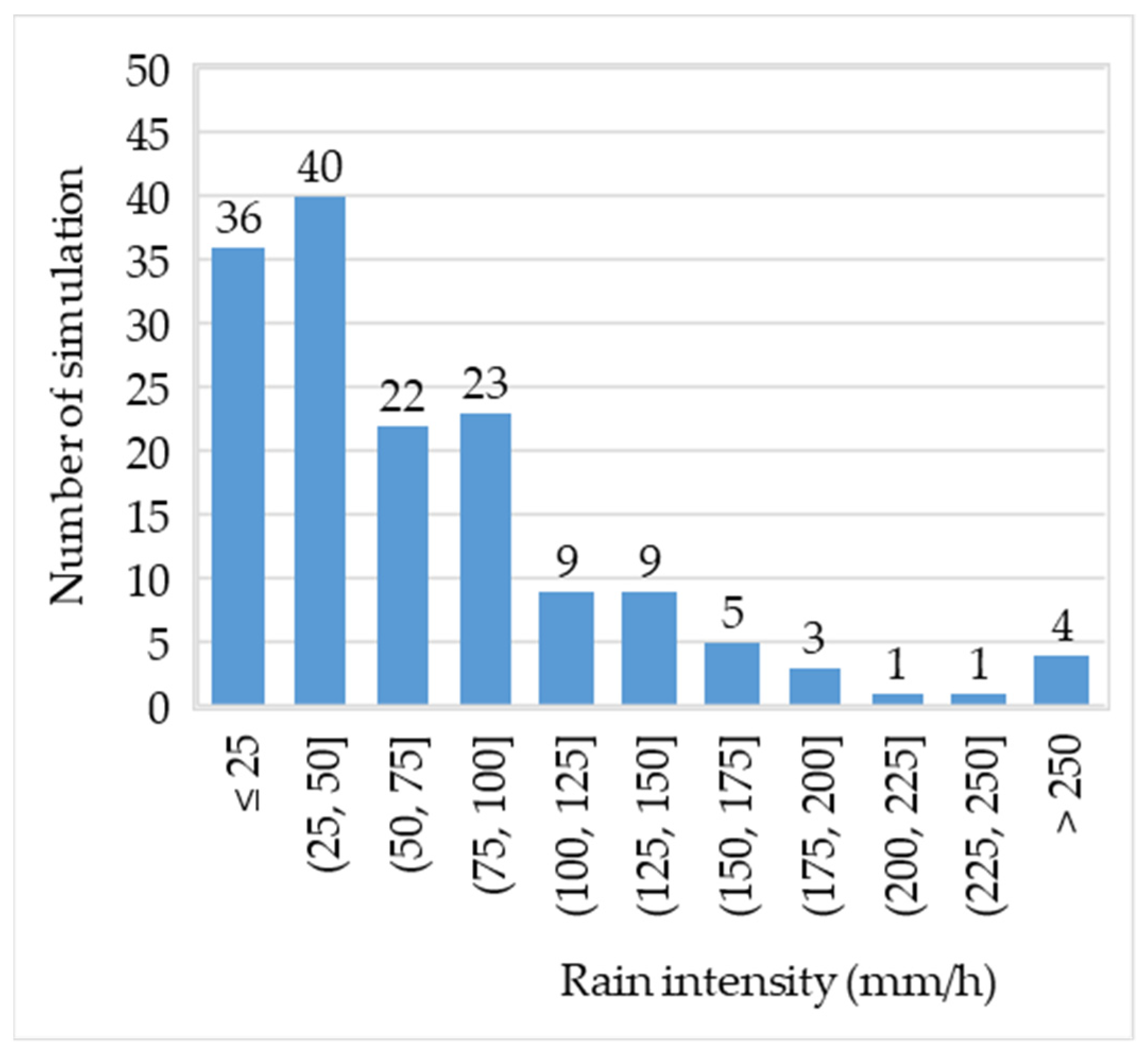
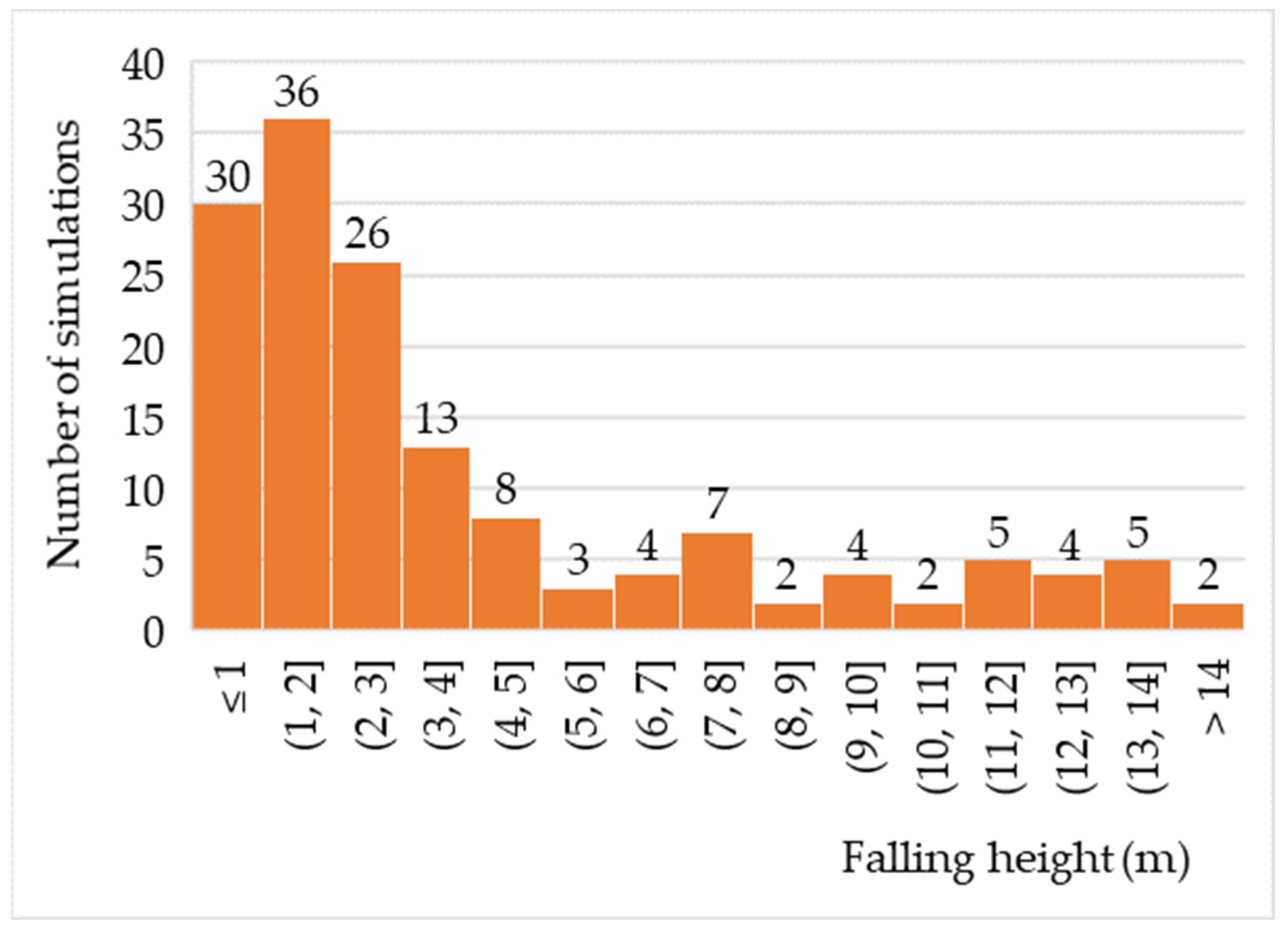
Rainfall simulators represent often-used equipment for soil research. Depending on their performance, they could be appropriate for some soil research or not. Dripping rainfall simulators (DRS) can provide rainfall that corresponds to natural rainfall, except in terms of the drop size distribution and wetted area. However, usually there are more factors that do not correspond to natural rainfall, such as the median drop size, volume and kinetic energy. The sizes of the drops generated by the simulator drippers are mostly in the range between 2 and 6 mm, while the number of drops smaller than 2 mm is relatively small. The intensity and duration of the simulated rain can be successfully produced to match natural values, with the most frequently simulated short-term rainfall of a high intensity. Most simulations were conducted at a fall height of up to 2 m, and then their number gradually decreases as the height gets closer to 5 m. Most simulations (58.6%) occur in the range between 20–90% KE, then 33.0% in a range of 90–100%, with only 8.4% lower than 20% KE.

dripping rainfall simulators drippers simulator performance soil research

1. Introduction

Rainfall simulators represent often-used equipment for soil research. According to the process of the formation of water drops, rainfall simulators can be divided into simulators that generate drops by spraying (Spraying Rainfall Simulators—SRS) [1][2][3][4][5] and by dripping (Dripping Rainfall Simulators—DRS) [6][7][8][9]. In addition to the mentioned groups, there is also a group of simulators that generate drops using the combined action of the two processes (Combined Rainfall Simulators—CRS). They usually involve nozzles or drippers that primarily create precipitation and different metal meshes, modifying the precipitation. They are created in an attempt to compensate for the shortcomings of simulators from the two previously mentioned groups [10][11][12][13][14][15]. Rainfall factors that are significant in terms of their impact on soil are the amount, intensity, duration and regime of precipitation [16][17][18][19], distribution raindrop sizes [20][21][22], spatial distribution [23], raindrop size, falling speed [24][25], direction of fall [26][27], direction of movement [18], kinetic energy [28], momentum [29] temperature [30] and chemical composition of rainfall [31].
It is important to keep in mind that simulator design and performance are mutually conditional, so to understand the simulator design it is necessary to analyze their performance as well [32]. By analyzing the rainfall simulators and comparing them with each other, the main differences in their performance were noted. SRS provide a distribution of water drop sizes that is more similar to natural precipitation, enable the establishment of the terminal velocity of the drops at a lower height and are advantageous in terms of the ease of manufacture, portability, the surface they can cover, handling and the price of the simulator [33][34]. On the other hand, DRS generate precipitation in a wider range of intensity, with the possibility of changing the intensity of precipitation without a significant change in the size of the drops and achieving greater uniformity of the spatial distribution of precipitation [9][34][35][36]. Simulators with only one dripper, by their design, enable a special analytical approach in the study of soil with the individual erosive action of drops on the soil [22][37][38][39][40][41][42].

2. DRS for Soil Research Performances

2.1. Wetted Area

The wetted area of dripping rainfall simulators with more than one dripper (DRS>1) represents the surface of the experimental plot that is exposed to simulated rainfall. The shape is most often rectangular but can also be round, and its dimensions are determined by the shape and dimensions of the projected drippers surface [7][43][44][45][46].
In the analysis, two sets of data were combined: the exact and approximate wetted area. The first set represents explicitly stated values of the area or dimensions of the wetted area. The second dataset represents the wetted area data based on the assumption that the dimensions or a covered area of the water tank with drippers above correspond to the dimensions and area of the wetted area below. The second dataset gives values that are usually slightly overestimated; however, for a general analysis, this can be neglected.
The largest number of simulators covers a wetted area between 0.2 and 0.6 m2. A smaller number of simulators have a wet surface area below 0.2 m2 and in the range of 0.8–1.0 m2, while the number of simulators with a wetted area larger than 1.0 m2 is significantly lower. One rainfall simulator had a wetted area of 36 m2 [9]. Wetted areas covered by rain simulators of a modular design were not included in the analysis, but only the wetted areas were covered by separate modules.

2.2. Drop Size

Natural or simulated rainfall drop size is defined by the diameter of a sphere whose volume is identical to the drop volume, although raindrop shape usually is not entirely spherical [47][48][49]. The choice of drippers for the DRS is often based on the experience of previous research or personal empirical knowledge, under the assumption that drippers in the form of tubes and holes with a smaller internal diameter (ID) generate drops of a smaller diameter and vice versa, neglecting other factors that affect the size of the drops. However, when fitting logarithmic functions, the dripper diameter of metal and plastic tubes (MT and PT) showed a strong relation for the dripper’s outer diameter (OD), while the relation for the dripper’s ID is moderate-to-weak (Figure 1a,b). For some of the drippers, both the ID and OD values were available, so their pairs can be noticed in the graph.
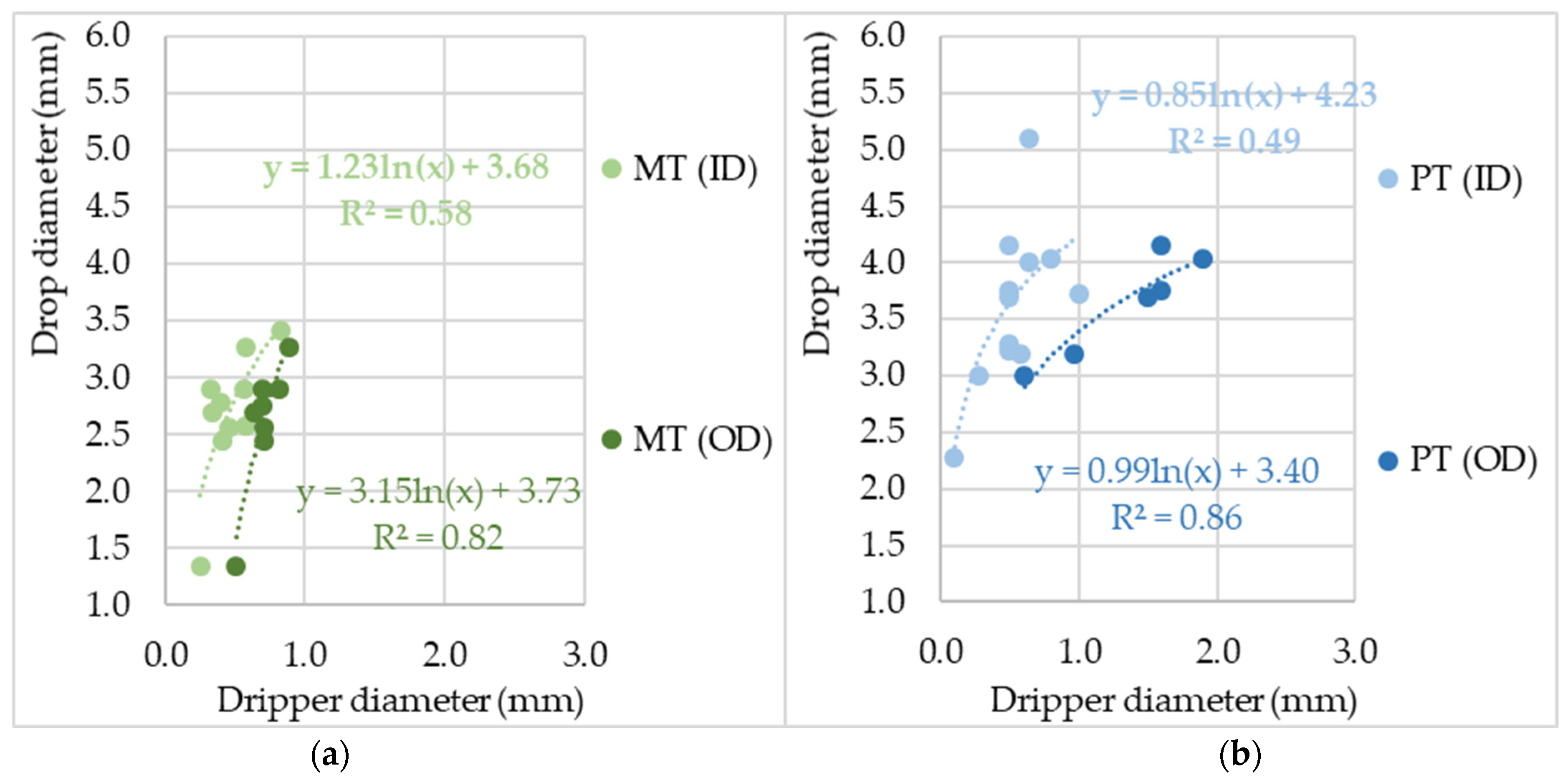
/media/item_content/202305/6461e7fdde2e9water-15-01314-g002.png
Figure 1. The influence of MT (a) and PT (b) drippers OD and ID on the drop diameter. Note: drippers whose corresponding drop diameter sizes were modified by the action of air, vibrations and inserted threads, and drops and drippers whose diameters were given in a range, were excluded from the analysis.
However, when increasing the range of the MT drippers’ diameter size the relation becomes very strong, R2 = 0.96 and 0.97, for both the ID and OD. Additionally, the logarithmic function that describes that relation is in accordance with data obtained by [50], where water drops were generated using hypodermic needles (Figure 2). On the other hand, observations by [51] showed that as the dripper diameter increased, the detached drop weight became less dependent on the dripper diameter.
/media/item_content/202305/6461e8772bbafwater-15-01314-g003.png
Figure 2. The influence of MT and PT drippers’ ID and OD size on the drop’s diameter with expanded diameter range (groups A, B and C) of MT drippers [52] in comparison to research of [50] Note: drippers whose corresponding drop diameters size were modified by the action of air, vibrations and inserted threads, and drops and drippers for which the diameter was given in a range, were excluded from the analysis. The equations shown exclude the data from the research of [50].
In general, the relation between drippers and drop diameter, described using the logarithmic equation, shows a very strong relation for the dripper’s OD, and a weaker but still strong relation for the ID (Figure 3). That is in accordance with [12], who roughly estimated that at the same water pressure, the OD size of the dripper determines the size of the drop.
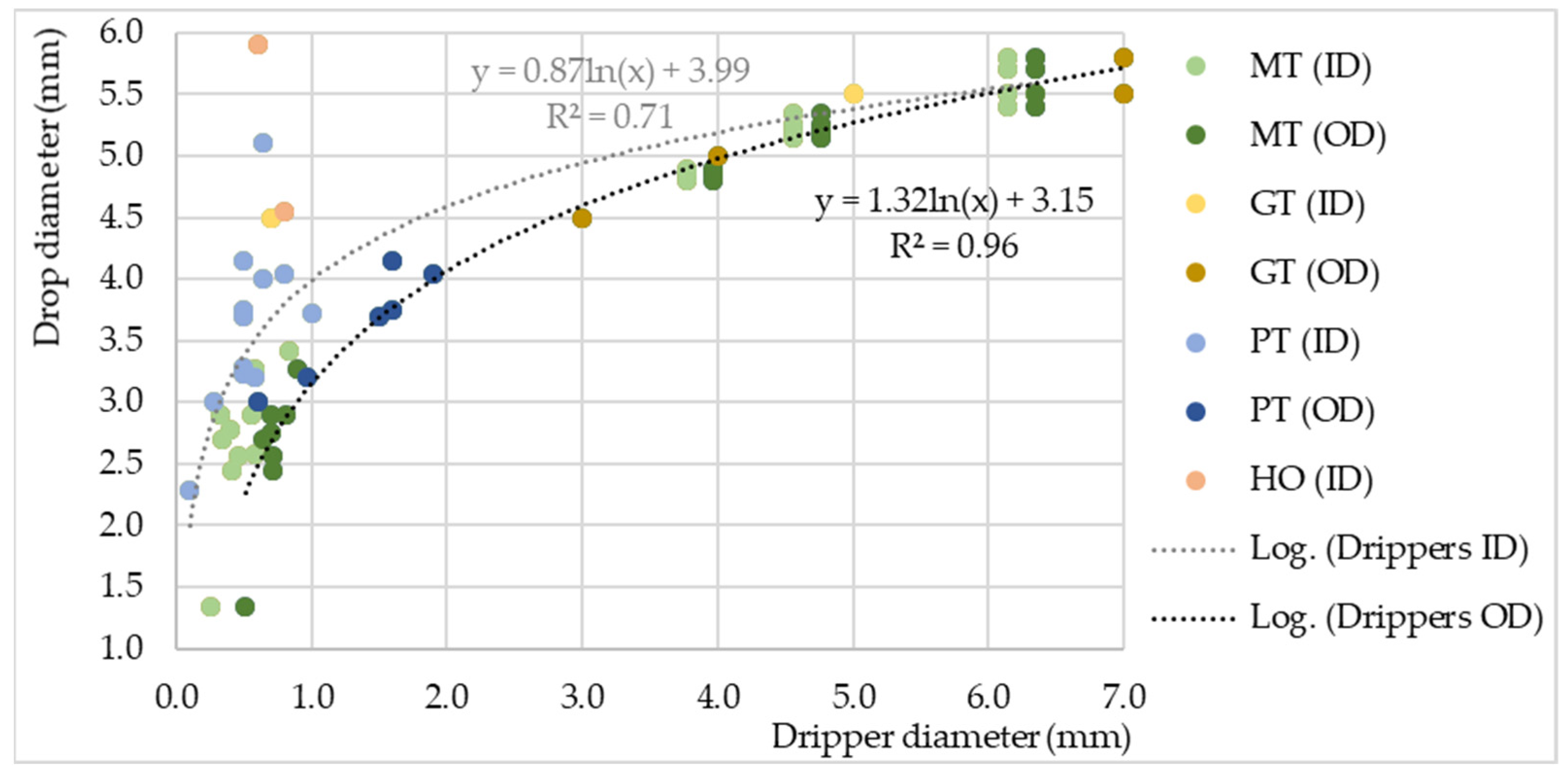
/media/item_content/202305/6461e84b2dbfawater-15-01314-g004.png
Figure 3. The influence of different types of drippers’ ID and OD on drop diameter size (GT—glass tubes, and HO—holes in boards and tubes). Note: drippers whose corresponding drops diameter size were modified by the action of air, vibrations and inserted threads, and drop and dripper diameters given in a range, were excluded from the analysis.

It is obvious that with the increase in the ID of the plastic tubes, the relation deviates from the logarithmic curve that represents all drippers together. Additionally, there are HO drippers whose values deviate from the logarithmic curve too, but they are specific because they have an almost infinite outer diameter (Figure 3). It is suggested that a possible reason for such a deviation could be the dripper material. However, based on the research of [68–72], drippers made from different materials such as glass, brass, stainless steel, Teflon, all show no significant difference in drop size. The material type rather determines the thickness of the tube wall. Therefore, when describing the relation between the dripper diameter and drop size, the assumption is that metal tube drippers have a different logarithmic distribution than plastic or glass tubes, because of their thinner wall (Figures 1a,b and 3), regardless of whether they are sharp or blunt.

However, drop size is not exclusively correlated with dripper diameter, surface tension or dripper tip geometry. The size of the drop depends on numerous other factors; among them are dripping intensity, dripping tip position and geometry, length-to-diameter ratio, water temperature and environmental atmosphere condition [52][53][54]. In addition to the dripper diameter and type, the dripping speed is also a factor that was taken into account for soil research using rainfall simulators. [25]. With the rise in the dripping speed, the drop size of the MT drippers rises too, until it starts to decline at some point [50].

Additionally, the influence of water temperature on the size of the generated drop is significant [54]. Water used in rainfall simulations with DRS can be distilled water [37][39][55][56] or water available from the environment, which is most often water from the water supply network [57][58][59][60][61][62]. 
Modifications of dripper performance via air flow and vibration were carried out in order to expand the range of drop sizes, primarily with the aim of also generating drops with smaller diameters [63][64]. Additionally, threads inserted in drippers were applied primarily to achieve capillary movement of water in the dripper and reduce flow, despite the fact that they change the diameter of the generated drop [65][66]. 
The sizes of the drops generated by the drippers are mostly in the range between 2 and 6 mm, while the number of drops smaller than 2 mm is relatively small (Figure 4). Although it is stated that the diameter of the drops of natural precipitation can reach 6, 7 and even 8 mm, it rarely exceeds 4 mm [67][68][69]. Falling drops are stable at terminal velocity until they reach a diameter of 4.6 mm, after which they break up into smaller ones due to the air resistance encountered during their fall, becoming definitely unstable with a diameter above 5.5 mm [70]. On the other hand, the maximum value of the median volume diameter (D0) of natural precipitation is only 2.0–2.5 mm at an intensity of 25–200 mm/h [98], which is in agreement with the observations of other researchers [21,99], whereas higher values have been reported also [100–102]. However, these D0 values refer most often to rains of a relatively high intensity, while rains of a lower intensity occur more often and achieve relatively lower D0 values [103].

/media/item_content/202305/6461e89c2edddwater-15-01314-g007.png

Figure 4. Type and subtype (modified performance drippers) of drippers and corresponding sizes of generated drops used in previous rainfall simulations (GT—glass tubes, GT wire—glass tubes with threads, HO—holes in dripper reservoir, HO wire—holes in dripper reservoir with threads, IRD—irrigation drippers, MT—metal tubes, MT air—metal tubes under the influence of air flow, MT vib—metal tubes under the influence of vibration, MT wire air—metal tubes with threads under the influence of air flow, PT—plastic tubes, PT wire—plastic tubes with threads, YA—hanging yarn and UN—unspecified dripper type). Note: for markers located on a horizontal line with a value of 0, the diameter of the generated drops was not specified [32]. Also, dotted lines represent simulated drop diameter values that are given in a range.

2.3. Rainfall Intensity and Duration

The rainfall intensity of DRS is regulated by regulating the pressure or water flow in the hydraulic system of the simulator [32][71][72][73][74].
The most common values of simulated rainfall intensities range up to 50 mm/h, and then their number gradually decreases for the ranges of 50–100 mm/h, 100–150 mm/h and over 150 mm/h, with a maximum value of over 1600 mm/h (Figure 5).
/media/item_content/202305/6461e8b265343water-15-01314-g008.png
Figure 5. Number of simulations at different intensities of simulated precipitation. Note: simulations with a single dropper or those for which intensity values are given in a range are not included in the analysis.
Rainfall intensity is correlated with drop size median volume (D0), which, as suggested by [75], is the best parameter for representing the drop size distribution of rainfall. However, the relationship is site specific [76] (Figure 6). With an increase in the intensity of precipitation, the value of D0 also increases [75][77][78][79][80][81]. However, some researchers state that after reaching a rainfall intensity of about 70–100 mm/h, the D0 hardly changes and stabilizes [82][83][84][85][86][87], while some even report that the D0 decreases [83][88][89][90] (Figure 6).
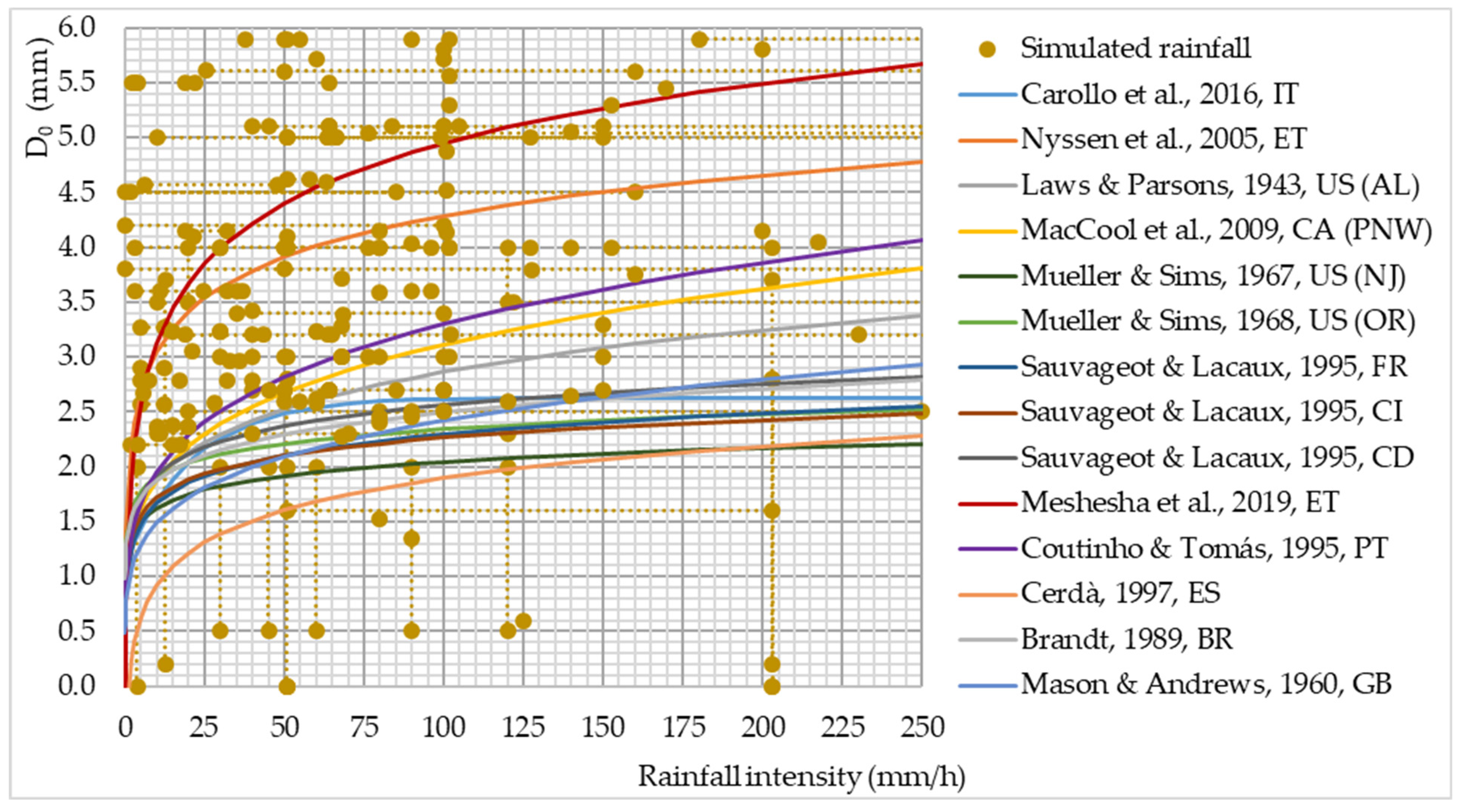
/media/item_content/202305/6461f318b1b2ewater-15-01314-g009.png
Figure 6. D0 as a function of intensity for natural and simulated rainfalls. Note: two capital letters after reference represent the ISO Alpha-2 country code that designates countries in which measurements have been conducted [21][77][78][91][92][93][94][95][96][97][98][99]. Note: dotted lines represent simulated D0 and rainfall intensity values that are given in a range.
Given that DRS>1 generate precipitation whose drop size uniformity coefficient is theoretically 100% (in practice it will be somewhat lower), the values of the D0 should correspond to the diameter of any such generated drop. Although it is possible using DRS>1 to generate precipitation intensity in the range of the D0 that occurs in nature, there is a relatively small number of simulated precipitations that corresponds to natural precipitation. D0 values usually rise until a rainfall intensity between 50–75 mm/h is reached, achieving maximum D0 values ranging from 2.0–2.7 mm at a precipitation intensity ranging from 75–200 mm/h (Figure 6).
The duration of the simulated rainfall is determined by the availability of water necessary for the simulation and the intensity of the rainfall. If the water necessary for the simulation is available in unlimited quantities, the duration of the simulation is also unlimited, while on the other hand, if the amount of water is limited, the duration of the simulation directly depends on the intensity of precipitation [32]. The largest number of simulations was conducted for a duration of less than 30 min, then the number of simulations gradually decreased to a duration of 2 h, while only a few simulations were conducted for a duration longer than 2 h.

In addition to the D0, rainfall intensity is also correlated with rainfall duration. The simulated and natural precipitation intensity for the return period of 1–5 years for different geographical areas mostly coincides (Figure 7).


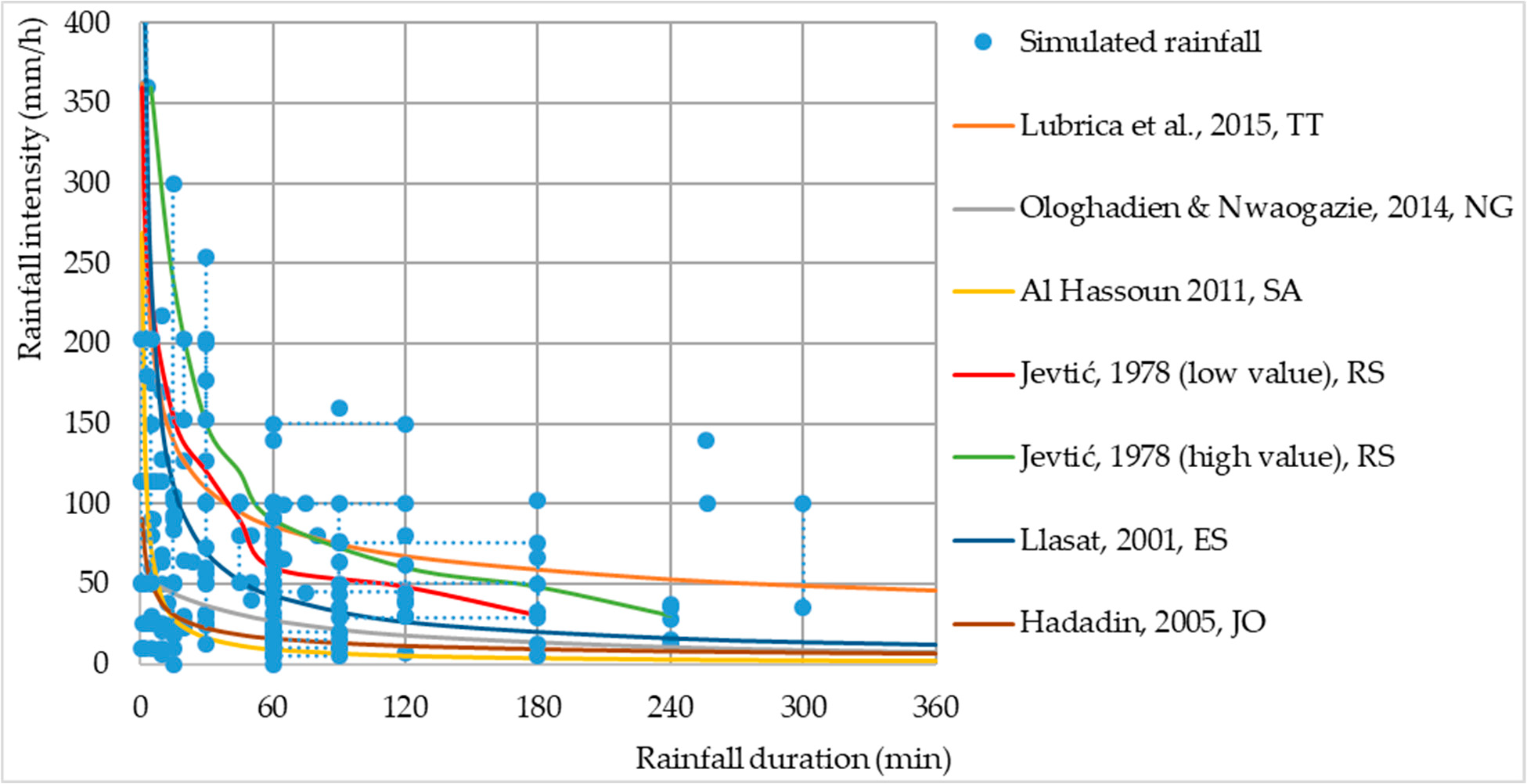
Figure 7. Rainfall intensity as a function of the duration of natural and simulated rainfalls. Note:
two capital letters after reference represent the ISO Alpha-2 country code that designates countries in which measurements have been conducted [23,129–133]. Note: dotted lines represent simulated rainfall duration and rainfall intensity values that are given in a range.

2.4. Kinetic Energy (KE)

The KE of rainfall is determined by the size distribution of raindrops and their falling speed. Since the diameter of the drop and the height of the fall are known for DRS>1, it is possible to calculate the KE of such precipitation. There are several works that determined the terminal velocity of drops of different diameters under given conditions [100][101][102][103][104] however, during simulations, due to the insufficient height at which the drops were placed, terminal velocities were often not reached. Given that the change in drop velocity does not occur linearly with the change in drop height and is different for drops of different diameters, there is no single equation that could represent this relationship [100]. For the purposes of the research, a mathematical model by [100] for determining the terminal and achieving the speed of drops of different diameters at different heights of drops was applied for the determination of the achieved speed, i.e., the KE of drops in the previous simulations (Figure 8).
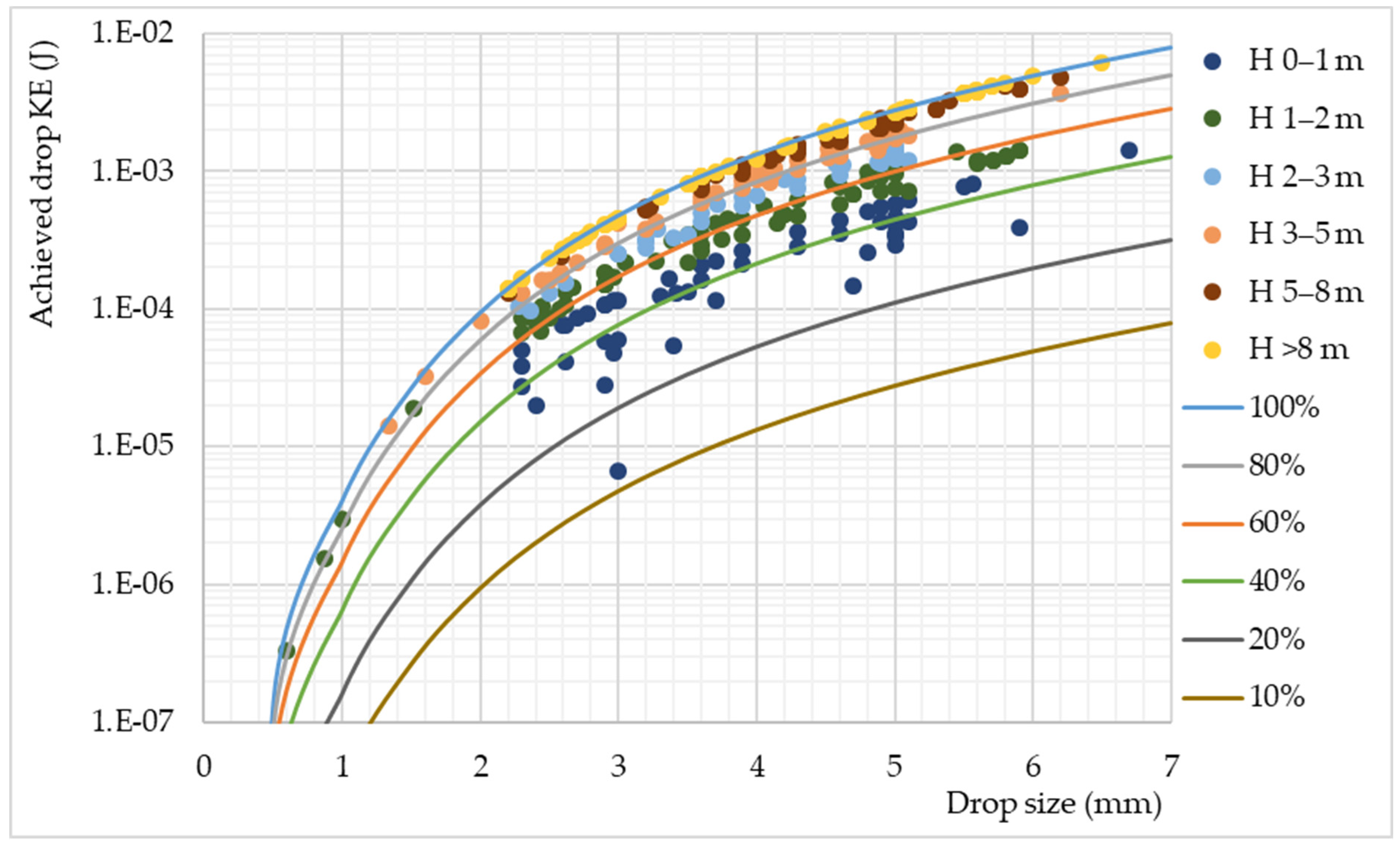
/media/item_content/202305/6461f5935d7f9water-15-01314-g012.png
Figure 8. Achieved drop KE of simulated precipitations for different heights based on the mathematical model of [100]. Note: the analysis did not include simulations for which drop height values were given in a range.
For 1-mm drops, the required height to achieve 90% of terminal velocity would be proximately 1.5 m, and for 2-mm drops it would be about 4.0 m, after which it increases to about 5.5 m for bigger drops [100]. Figure 9 shows the representation of different fall heights during the simulations, where it can be seen that most simulations were conducted at a fall height of up to 2 m (43.7%), and then the percentage decreases gradually as the height gets closer to 5 m (31.1%). Falling heights over 5 m occupy 25.2% of all simulations and occur relatively equally, while the highest recorded falling height is 14 m. However, depending on the diameter of the drop, the presented values of the drop height may or may not be satisfactory in terms of achieving the terminal drop speed [100].
/media/item_content/202305/6461f5a63e513water-15-01314-g013.png
Figure 9. Number of simulations at different heights of simulated precipitation [32]. Note: data whose values are given in ranges are not included in the analysis.
The number of simulations with a KE lower than 30% have a steep rise within categories, after which their number slowly falls with the increase in the KE until reaching the category of 90-100%, which comprises 33.0% of simulations. Most the simulations (58.6%) occur in the range between 20 and 90% KE, while only 8.4% are lower than 20% KE. Drops smaller or equal to 2-mm diameter achieved a KE in a range of 60-80% in 28.6% of the simulations, while 71.4% of the simulations achieved over 85% of the KE.
/media/item_content/202305/6461f5b4c9966water-15-01314-g014.png
Figure 9. The number of simulations at different values of the achieved KE in relation to falling drops of different diameters. Note: data whose values of drop diameter or fall height are given in ranges are not included in the analysis.

3. Conclusions

DRS can provide rainfall that corresponds well with natural rainfall, except in terms of the drop size distribution and wetted area, which can be cited as the biggest shortcoming of DRS; on the other hand, usually there are more factors that do not correspond to the natural conditions, such as the median drop size volume and kinetic energy.

References

  1. Bryan, R.B. An Improved Rainfall Simulator for Use in Erosion Research. Can. J. Earth Sci. 1970, 7, 1552–1561.
  2. Ogunye, F.O.; Boussabaine, H. Development of a Rainfall Test Rig as an Aid in Soil Block Weathering Assessment. Constr. Build. Mater. 2002, 16, 173–180.
  3. Alves Sobrinho, T.; Gómez-Macpherson, H.; Gómez, J.A. A Portable Integrated Rainfall and Overland Flow Simulator. Soil Use Manag. 2008, 24, 163–170.
  4. Gabrić, O. Eksperimentalno Istraživanje Procesa Na Slivu: Padavine, Oticaj I Erozija Tla; University of Novi Sad: Subotica, Serbia, 2014.
  5. Živanović, N.; Rončević, V.; Spasić, M.; Ćorluka, S.; Polovina, S. Construction and Calibration of a Portable Rain Simulator Designed for the in Situ Research of Soil Resistance to Erosion. Soil Water Res. 2022, 17, 158–169.
  6. Te Chow, V.; Harbaugh, T.E. Raindrop Production for Laboratory Watershed Experimentation. J. Geophys. Res. 1965, 70, 6111–6119.
  7. Meeuwig, R.O. Infiltration and Water Repellency in Granitic Soils. In Intermountain Forest & Range Experiment Station; US Department of Agriculture, Forest Service: Ogden, UT, USA, 1971; volume 111.
  8. Battany, M.C.; Grismer, M.E. Development of a Portable Field Rainfall Simulator for Use in Hillside Vineyard Runoff and Erosion Studies. Hydrol. Process. 2000, 14, 1119–1129.
  9. Naves, J.; Anta, J.; Suárez, J.; Puertas, J. Hydraulic, Wash-off and Sediment Transport Experiments in a Full-Scale Urban Drainage Physical Model. Sci. Data 2020, 7, 44.
  10. De Ploey, J.; Moeyersons, J. Runoff Creep of Coarse Debris: Experimental Data and Some Field Observations. Catena 1975, 2, 275–288.
  11. Imeson, A.C. A Simple Field-Portable Rainfall Simulator for Difficult Terrain. Earth Surf. Process. 1977, 2, 431–436.
  12. Bowyer-Bower, T.A.S.; Burt, T.P. Rainfall Simulators for Investigating Soil Response to Rainfall. Soil Technol. 1989, 2, 1–16.
  13. Wan, Y.; El-Swaify, S.A. Characterizing Interrill Sediment Size by Partitioning Splash and Wash Processes. Soil Sci. Soc. Am. J. 1998, 62, 430–437.
  14. Watanabe, H.; Grismer, M.E. Diazinon Transport through Inter-Row Vegetative Filter Strips: Micro-Ecosystem Modeling. J. Hydrol. 2001, 247, 183–199.
  15. Böker, J.; Zanzinger, H.; Bastian, M.; Németh, E.; Eppel, J. Surface Erosion Control Investigations for a Test Field on a Steep Embankment of German Autobahn A3. In Proceedings of the EuroGeo5, Valencia, Spain, 16–19 September 2012.
  16. Flanagan, D.C.; Foster, G.R.; Moldenhauer, W.C. Storm pattern effect on infiltration, runoff, and erosion. Trans. ASAE 1988, 31, 414–420.
  17. Römkens, M.J.; Helming, K.; Prasad, S.N. Soil erosion under different rainfall intensities, surface roughness, and soil water regimes. Catena 2002, 46, 103–123.
  18. Ran, Q.; Su, D.; Li, P.; He, Z. Experimental Study of the Impact of Rainfall Characteristics on Runoff Generation and Soil Erosion. J. Hydrol. 2012, 424–425, 99–111.
  19. Mohamadi, M.A.; Kavian, A. Effects of rainfall patterns on runoff and soil erosion in field plots. Int. Soil Water Conserv. Res. 2015, 3, 273–281.
  20. Caracciolo, C.; Napoli, M.; Porcù, F.; Prodi, F.; Dietrich, S.; Zanchi, C.; Orlandini, S. Raindrop size distribution and soil erosion. J. Irrig. Drain. Eng. 2012, 138, 461–469.
  21. Carollo, F.G.; Ferro, V.; Serio, M.A. Estimating Rainfall Erosivity by Aggregated Drop Size Distributions. Hydrol. Process. 2016, 30, 2119–2128.
  22. Yakubu, M.L.; Yusop, Z.; Fulazzaky, M.A. The Influence of Rain Intensity on Raindrop Diameter and the Kinetics of Tropical Rainfall: Case Study of Skudai, Malaysia. Hydrol. Sci. J. 2016, 61, 944–951.
  23. Jevtić, L.J. Hidrologija Bujičnih Tokova; Šumarski Fakultet Univerziteta u Beogradu: Belgrade, Serbia, 1978.
  24. Bisal, F. The Effect of Raindrop Size and Impact Velocity on Sand-Splash. Can. J. Soil Sci. 1960, 40, 242–245.
  25. Bubenzer, G.D.; Jones, B.A. Drop Size and Impact Velocity Effects on the Detachment of Soils Under Simulated Rainfall. Trans. ASAE 1971, 14, 625–628.
  26. Helming, K. Wind speed effects on rain erosivity. In Proceedings of the Sustaining the global farm-Selected papers from the 10th International Soil Conservation Organization Meeting, West Lafayette, IN, USA, 24–29 May 1999; pp. 771–776.
  27. Erpul, G.; Norton, L.D.; Gabriels, D. The effect of wind on raindrop impact and rainsplash detachment. Trans. ASAE 2003, 46, 51.
  28. Mineo, C.; Ridolfi, E.; Moccia, B.; Russo, F.; Napolitano, F. Assessment of rainfall kinetic-energy-intensity relationships. Water 2019, 11, 1994.
  29. Sanchez-Moreno, J.F.; Mannaerts, C.M.; Jetten, V.; Löffler-Mang, M. Rainfall kinetic energy-intensity and rainfall momentum-intensity relationships for Cape Verde. J. Hydrol. 2012, 454–455, 131–140.
  30. Akinola, A.I.; Wynn-Thompson, T.; Olgun, C.G.; Mostaghimi, S.; Eick, M.J. Fluvial erosion rate of cohesive streambanks is directly related to the difference in soil and water temperatures. J. Environ. Qual. 2019, 48, 1741–1748.
  31. Forti, M.C.; Melfi, A.J.; Astolfo, R.; Fostier, A.H. Rainfall chemistry composition in two ecosystems in the northeastern Brazilian Amazon (Amapá State). J. Geophys. Res. Atmos. 2000, 105, 28895–28905.
  32. Rončević, V.; Živanović, N.; Ristić, R.; van Boxel, J.H.; Kašanin-Grubin, M. Dripping Rainfall Simulators for Soil Research—Design Review. Water 2022, 14, 3309.
  33. Ries, J.B.; Iserloh, T. Rainfall Simulation: Methods, Research Questions and Challenges. In Proceedings of the EGU General Assembly, Vienna, Austria, 22–27 April 2012; p. 13866.
  34. Yakubu, M.L.; Yusop, Z. Adaptability of Rainfall Simulators as a Research Tool on Urban Sealed Surfaces—A Review. Hydrol. Sci. J. 2017, 62, 996–1012.
  35. Meyer, L.D.; Harmon, W.C. Multiple-Intensity Rainfall Simulator for Erosion Research on Row Sideslopes. Trans. ASAE 1979, 22, 0100–0103.
  36. Dunkerley, D.L. Intra-Storm Evaporation as a Component of Canopy Interception Loss in Dryland Shrubs: Observations from Fowlers Gap, Australia. Hydrol. Process. 2008, 22, 1985–1995.
  37. McCalla, T.M. Water-Drop Method of Determining Stability of Soil Structure. Soil Sci. 1944, 58, 117–122.
  38. Gunn, R.; Kinzer, G.D. The Terminal Velocity of Fall for Water Droplets in Stagnant Air. J. Meteorol. 1949, 6, 243–248.
  39. Bruce-Okine, E.; Lal, R. Soil Erodibility as Determined by Raindrop Technique. Soil Sci. 1975, 119, 149–157.
  40. Cousen, S.M.; Farres, P.J. The Role of Moisture Content in the Stability of Soil Aggregates from a Temperate Silty Soil to Raindrop Impact. Catena 1984, 11, 313–320.
  41. Sharma, P.P.; Gupta, S.C. Sand Detachment by Single Raindrops of Varying Kinetic Energy and Momentum. Soil Sci. Soc. Am. J. 1989, 53, 1005–1010.
  42. Mouzai, L.; Bouhadef, M. Water Drop Erosivity: Effects on Soil Splash. J. Hydraul. Res. 2003, 41, 61–68.
  43. Malekuti, A.; Gifford, G.F. Natural Vegetation as a Source of Diffuse Salt within the Colorado River Basin. J. Am. Water Resour. Assoc. 1978, 14, 195–205.
  44. Kamphorst, A. A Small Rainfall Simulator for the Determination of Soil Erodibility. Neth. J. Agric. Sci. 1987, 35, 407–415.
  45. Harden, C.P.; Mathews, L. Rainfall Response of Degraded Soil Following Reforestation in the Copper Basin, Tennessee, USA. Environ. Manag. 2000, 26, 163–174.
  46. Iserloh, T.; Pegoraro, D.; Schlösser, A.; Thesing, H.; Seeger, M.; Ries, J.B. Rainfall Simulation Experiments: Influence of Water Temperature, Water Quality and Plot Design on Soil Erosion and Runoff. In Proceedings of the EGU General Assembly, Vienna, Austria, 12–17 April 2015.
  47. Green, T.; Houk, D.F. The Mixing of Rain with Near-Surface Water. J. Fluid Mech. 1979, 90, 569.
  48. Agassi, M.; Bloem, D.; Ben-Hur, M. Effect of Drop Energy and Soil and Water Chemistry on Infiltration and Erosion. Water Resour. Res. 1994, 30, 1187–1193.
  49. Xiao, H.; Liu, G.; Abd-Elbasit, M.A.M.; Zhang, X.C.; Liu, P.L.; Zheng, F.L.; Zhang, J.Q.; Hu, F.N. Effects of Slaking and Mechanical Breakdown on Disaggregation and Splash Erosion: Effects of Splash Erosion on Aggregate Breakdown. Eur. J. Soil Sci. 2017, 68, 797–805.
  50. Rončević, V.; Živanović, N.; Boxel, J.H.V.; Iserloh, T.; Antić, N. Measuring the Size of Pendant Water Drop Generated by Hypodermic Needles for Construction of Rainfall Simulator for Soil Research. Water 2023. manuscript in preparation.
  51. Boucher, E.A.; Evans, M.J.B. Pendent Drop Profiles and Related Capillary Phenomena. Proc. R. Soc. London. A. Math. Phys. Sci. 1975, 346, 349–374.
  52. Mutchler, C.K.; Moldenhauer, W.C. Applicator for Laboratory Rainfall Simulator. Trans. ASAE 1963, 6, 0220–0222.
  53. Lee, B.-B.; Ravindra, P.; Chan, E.-S. A Critical Review: Surface and Interfacial Tension Measurement by the Drop Weight Method. Chem. Eng. Commun. 2008, 195, 889–924.
  54. Portuguez, E.; Alzina, A.; Michaud, P.; Oudjedi, M.; Smith, A. Evolution of a Water Pendant Droplet: Effect of Temperature and Relative Humidity. Nat. Sci. 2017, 9, 1–20.
  55. Barry, P.V.; Turco, R.F.; Stott, D.E.; Bradford, J.M. Organic Polymers’ Effect on Soil Shear Strength and Detachment by Single Raindrops. Soil Sci. Soc. Am. J. 1991, 55, 799–804.
  56. Bissonnais, Y.L.; Singer, M.J. Crusting, Runoff, and Erosion Response to Soil Water Content and Successive Rainfalls. Soil Sci. Soc. Am. J. 1992, 56, 1898–1903.
  57. Black, P.E. Runoff from Watershed Models. Water Resour. Res. 1970, 6, 465–477.
  58. Houk, D.; Green, T. A Note on Surface Waves Due to Rain. J. Geophys. Res. 1976, 81, 4482–4484.
  59. Moss, A.J.; Green, T.W. Erosive Effects of the Large Water Drops (Gravity Drops) That Fall from Plants. Soil Res. 1987, 25, 9.
  60. Robinson, D.A.; Naghizadeh, R. The Impact of Cultivation Practice and Wheelings on Runoff Generation and Soil Erosion on the South Downs: Some Experimental Results Using Simulated Rainfall. Soil Use Manag. 1992, 8, 151–156.
  61. Ao, C.; Yang, P.; Zeng, W.; Chen, W.; Xu, Y.; Xu, H.; Zha, Y.; Wu, J.; Huang, J. Impact of Raindrop Diameter and Polyacrylamide Application on Runoff, Soil and Nitrogen Loss via Raindrop Splashing. Geoderma 2019, 353, 372–381.
  62. Wang, L.; Fang, N.F.; Yue, Z.J.; Shi, Z.H.; Hua, L. Raindrop Size and Flow Depth Control Sediment Sorting in Shallow Flows on Steep Slopes. Water Resour. Res. 2018, 54, 9978–9995.
  63. Magarvey, R.H.; Taylor, B.W. Apparatus for the Production of Large Water Drops. Rev. Sci. Instrum. 1956, 27, 944–947.
  64. Brakensiek, D.L.; Rawls, W.J.; Hamon, W.R. Application of an Infiltrometer System for Describing Infiltration into Soils. Trans. ASAE 1979, 22, 320–325.
  65. McQueen, I.S. Development of a Hand Portable Rainfall-Simulator Infiltrometer. Geological Survey; United States Department of the Interior: Washington, DC, USA, 1963; Volume 482.
  66. Bhardwaj, A.; Singh, R. Development of a Portable Rainfall Simulator Infiltrometer for Infiltration, Runoff and Erosion Studies. Agric. Water Manag. 1992, 22, 235–248.
  67. Cerdà, A.; Ibáñez, S.; Calvo, A. Design and Operation of a Small and Portable Rainfall Simulator for Rugged Terrain. Soil Technol. 1997, 11, 163–170.
  68. Ristić, R.; Malošević, D. Hidrologija Bujičnih Tokova; Univerzitet u Beogradu, Šumarski Fakultet: Belgrade Serbia, 2011.
  69. Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation. Nature 2012, 284, 88.
  70. Blanchard, D.C. The Behavior of Water Drops at Terminal Velocity in Air. Trans. Am. Geophys. Union 1950, 31, 836.
  71. Rose, C.W. Soil Detachment Caused by Rainfall. Soil Sci. 1960, 89, 28–35.
  72. Roth, C.H.; Meyer, B.; Frede, H.-G. A Portable Rainfall Simulator for Studying Factors Affecting Runoff, Infiltration and Soil Loss. Catena 1985, 12, 79–85.
  73. Thompson, A.L.; James, L.G. Water Droplet Impact and Its Effect on Infiltration. Trans. ASAE 1985, 28, 1506–1510.
  74. Regmi, T.P.; Thompson, A.L. Rainfall Simulator for Laboratory Studies. Appl. Eng. Agric. 2000, 16, 641–647.
  75. Brandt, C.J. Simulation of the Size Distribution and Erosivity of Raindrops and Throughfall Drops. Earth Surf. Process. Landf. 1990, 15, 687–698.
  76. Carollo, F.G.; Ferro, V.; Serio, M.A. Predicting Rainfall Erosivity by Momentum and Kinetic Energy in Mediterranean Environment. J. Hydrol. 2018, 560, 173–183.
  77. Nyssen, J.; Vandenreyken, H.; Poesen, J.; Moeyersons, J.; Deckers, J.; Haile, M.; Salles, C.; Govers, G. Rainfall Erosivity and Variability in the Northern Ethiopian Highlands. J. Hydrol. 2005, 311, 172–187.
  78. Laws, J.O.; Parsons, D.A. The Relation of Raindrop-Size to Intensity. Trans. Am. Geophys. Union 1943, 24, 452.
  79. Atlas, D. OPTICAL EXTINCTION by RAINFALL. J. Meteorol. 1953, 10, 486–488.
  80. Zanchi, C.; Torri, D. Evaluation of Rainfall Energy in Central Italy. Assessment of Erosion; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 1980; pp. 133–142.
  81. Jayawardena, A.W.; Rezaur, R.B. Drop Size Distribution and Kinetic Energy Load of Rainstorms in Hong Kong. Hydrol. Process. 2000, 14, 1069–1082.
  82. Hudson, N.W. Soil Conservation; Scientific Publishers: New Delhi, India, 2015.
  83. Carter, C.E.; Greer, J.D.; Braud, H.J.; Floyd, J.M. Raindrop Characteristics in South Central United States. Trans. ASAE 1974, 17, 1033–1037.
  84. Kinnell, P.I.A. Rainfall Intensity-Kinetic Energy Relationships for Soil Loss Prediction1. Soil Sci. Soc. Am. J. 1981, 45, 153.
  85. Rosewell, C.J. Rainfall Kinetic Energy in Eastern Australia. J. Clim. Appl. Meteorol. 1986, 25, 1695–1701.
  86. Brown, L.C.; Foster, G.R. Storm Erosivity Using Idealized Intensity Distributions. Trans. ASAE 1987, 30, 0379–0386.
  87. Carollo, F.G.; Ferro, V.; Serio, M.A. Reliability of Rainfall Kinetic Power-Intensity Relationships. Hydrol. Process. 2017, 31, 1293–1300.
  88. Hudson, N.W. The Influence of Rainfall on the Mechanics of Soil Erosion: With Particular Reference to Southern Rhodesia; University of Cape Town: Cape Town, South Africa, 1965.
  89. Assouline, S.; Mualem, Y. The Similarity of Regional Rainfall: A Dimensionless Model of Drop Size Distribution. Trans. ASAE 1989, 32, 1216–1222.
  90. Van Dijk, A.I.J.M.; Bruijnzeel, L.A.; Rosewell, C.J. Rainfall Intensity-Kinetic Energy Relationships: A Critical Literature Appraisal. J. Hydrol. 2002, 261, 1–23.
  91. Cerdá, A. Rainfall Drop Size Distribution in the Western Mediterranean Basin, València, Spain. CATENA 1997, 30, 169–182.
  92. Brandt, C.J. The Size Distribution of Throughfall Drops under Vegetation Canopies. CATENA 1989, 16, 507–524.
  93. Coutinho, M.A.; Tomás, P.P. Characterization of Raindrop Size Distributions at the Vale Formoso Experimental Erosion Center. CATENA 1995, 25, 187–197.
  94. Meshesha, D.T.; Tsunekawa, A.; Haregeweyn, N. Influence of Raindrop Size on Rainfall Intensity, Kinetic Energy, and Erosivity in a Sub-Humid Tropical Area: A Case Study in the Northern Highlands of Ethiopia. Theor. Appl. Climatol. 2019, 136, 1221–1231.
  95. Mueller, E.A.; Sims, A.L. Raindrop Distributions at Island Beach, New Jersey; Atmospheric Sciences Laboratory, US Army Electronics Command: Fort Monmouth, NJ, USA, 1967.
  96. Mueller, E.A.; Sims, A.L. Raindrop Distributions at Corvallis, Oregon; US Army Electronics Command: Fort Monmouth, NJ, USA, 1968.
  97. Mason, B.J.; Andrews, J.B. Drop-Size Distributions from Various Types of Rain. Q. J. R. Meteorol. Soc. 1960, 86, 346–353.
  98. Sauvageot, H.; Lacaux, J.-P. The Shape of Averaged Drop Size Distributions. J. Atmos. Sci. 1995, 52, 1070–1083.
  99. McCool, D.K.; Williams, J.D.; Morse, J.R. Raindrop Characteristics in the Pacific Northwest. In Proceedings of the ASABE Annual International Meeting, Reno, NV, USA, 21–14 June 2009.
  100. Van Boxel, J.H. Numerical Model for the Fall Speed of Rain Drops in a Rain Fall Simulator. In Proceedings of the Workshop on Wind and Water Erosion, Ghent, Belgium, 17–18 November 1997; pp. 77–85.
  101. Laws, J.O. Measurements of the Fall-Velocity of Water -Drops and Raindrops. Trans. Am. Geophys. Union 1941, 22, 709.
  102. Best, A.C. The Size Distribution of Raindrops. Q. J. R. Meteorol. Soc. 1950, 76, 16–36.
  103. Beard, K.V.; Pruppacher, H.R. A Determination of the Terminal Velocity and Drag of Small Water Drops by Means of a Wind Tunnel. J. Atmos. Sci. 1969, 26, 1066–1072.
  104. Uplinger, W.G. A New Formula for Raindrop Terminal Velocity. In Proceedings of the 20th Conference on Radar Meteorology, Boston, MA, USA, 30 November–3 December 1981; pp. 389–391.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Soil Science
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Vukašin Rončević
,
Nikola Živanović
,
John H. van Boxel
,
Thomas Iserloh
,
Snežana Štrbac
View Times: 925
Revisions: 3 times (View History)
Update Date: 15 May 2023
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback