Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Xingxing Wang
 -- 2683 2023-05-09 11:48:06 |
2 layout
Camila Xu
 Meta information modification 2683 2023-05-10 03:05:59 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Wang, X.; Ye, P.; Liu, S.; Zhu, Y.; Deng, Y.; Yuan, Y.; Ni, H. Battery Life Prediction Methods Based on Electrochemical Models. Encyclopedia. Available online: https://encyclopedia.pub/entry/44031 (accessed on 24 July 2024).
Wang X, Ye P, Liu S, Zhu Y, Deng Y, Yuan Y, et al. Battery Life Prediction Methods Based on Electrochemical Models. Encyclopedia. Available at: https://encyclopedia.pub/entry/44031. Accessed July 24, 2024.
Wang, Xingxing, Peilin Ye, Shengren Liu, Yu Zhu, Yelin Deng, Yinnan Yuan, Hongjun Ni. "Battery Life Prediction Methods Based on Electrochemical Models" Encyclopedia, https://encyclopedia.pub/entry/44031 (accessed July 24, 2024).
Wang, X., Ye, P., Liu, S., Zhu, Y., Deng, Y., Yuan, Y., & Ni, H. (2023, May 09). Battery Life Prediction Methods Based on Electrochemical Models. In Encyclopedia. https://encyclopedia.pub/entry/44031
Wang, Xingxing, et al. "Battery Life Prediction Methods Based on Electrochemical Models." Encyclopedia. Web. 09 May, 2023.
Battery Life Prediction Methods Based on Electrochemical Models
Edit
This entry is adapted from the peer-reviewed paper 10.3390/en16093858

Remaining useful life prediction is of great significance for battery safety and maintenance. The remaining useful life prediction method, based on a physical model, has wide applicability and high prediction accuracy, which is the research hotspot of the next generation battery life prediction method. An electrochemical model is a model built by simulating the electrochemical reaction process of a battery. It describes the laws of the cell from the point of view of internal physical and chemical processes including kinetic parameters, mass conversion processes, thermodynamic properties, mechanical, thermal, and electrical properties of materials.

lithium-ion battery residual life physical model prediction method

1. Introduction

Lithium-ion batteries have the advantages of high energy density, high output power, no pollution, no memory effect, small self-discharge, etc., and has become the main battery type of current new energy vehicles [1]. Common lithium-ion batteries on the market include lithium cobaltate, lithium manganate, and lithium iron carbonate batteries [2]. Lithium cobalt-acid batteries are the most widely used and have high specific energy, but the production of raw materials is more expensive; lithium manganate batteries have excellent multiplier performance and stability, but low energy density and poor safety [3]; lithium iron carbonate batteries have high energy density and good cycling performance, but poor low-temperature discharge performance [4]. There are many factors to measure the performance of the above lithium-ion batteries, and battery life is one of the key indicators and an important factor to be considered by users when purchasing electric vehicles [5]. During long-term use, the lithium-ion battery undergoes a series of electrochemical reactions and physical changes that degrade the performance and capacity until the end of its life [6].
State of health (SOH) estimation and remaining useful life (RUL) prediction are the basic problems of battery health management [7]. SOH represents the aging degree of lithium-ion batteries, which is mostly defined as the percentage of the capacity released by the battery from the full charge state to the cut-off voltage and the rated capacity of the battery under certain conditions [8]. RUL is a parameter that characterizes the deterioration of the battery to obtain the operating time from the beginning of the prediction to the end of the battery life [9]. The accurate prediction and estimation of SOH and RUL can effectively judge their future working capacity and identify problems in time to avoid unnecessary problems and losses [10].
RUL prediction methods based on the model from the perspective of the first principles are given a full explanation of the cell aging process, applicable to almost all of the conditions and operation mode. The analysis of a battery control strategy is also more detailed and accurate than other methods, which should be paid attention to and further developed in the process of RUL prediction research [11]. 
RUL refers to the number of charge point cycles a battery can perform before its life ends. There are many factors that affect the battery life, from the physical level including temperature, charging current, charging voltage, battery structure, etc. [12] and on the chemical level including the electrode material, electrolyte, battery resistance, etc. [13]. Generally, when the capacity of a battery is lower than 80% of the factory capacity, the battery is considered to be invalid. A common RUL definition is shown in Formula (1) below:
R U L = C E O L − C i
where CEOL represents the number of charging and discharging cycles that can be carried out when the service life terminates, and Ci represents the number of charging and discharging cycles at the current moment [14].
In this entry, the existing model-based lithium-ion battery life prediction methods at home and abroad were divided into three categories: the electrochemical model-based method, equivalent circuit-based method, and empirical model based method [15][16], as shown in Figure 1.
Energies 16 03858 g001
Figure 1. Battery life prediction method based on the physical model.

2. Methods Based on Electrochemical Models

An electrochemical model is a model built by simulating the electrochemical reaction process of a battery [17]. It describes the laws of the cell from the point of view of internal physical and chemical processes including kinetic parameters, mass conversion processes, thermodynamic properties, mechanical, thermal, and electrical properties of materials [18]. It can provide a reference for battery research and development, so electrochemical models are often used for the analysis of battery principles and for battery research and development [19]. Electrochemical models include pseudo two-dimensional (P2D), single particle (SP) models, and coupled electrochemical models developed based on both.

2.1. P2D Model

The P2D model is shown in Figure 2. The battery was divided into three areas: negative electrode, diaphragm, and positive electrode [20]. Several governing equations were established in the P2D model to describe the diffusion of lithium ions in solid particles, mass transfer in the liquid phase, and the electrochemical reaction on the particle surface. Among these control equations, the most important is the Butler–Volmer kinetic response equation, as shown in Equation (2):
j = i 0 e x p α a F R T η − e x p − α c F R T η
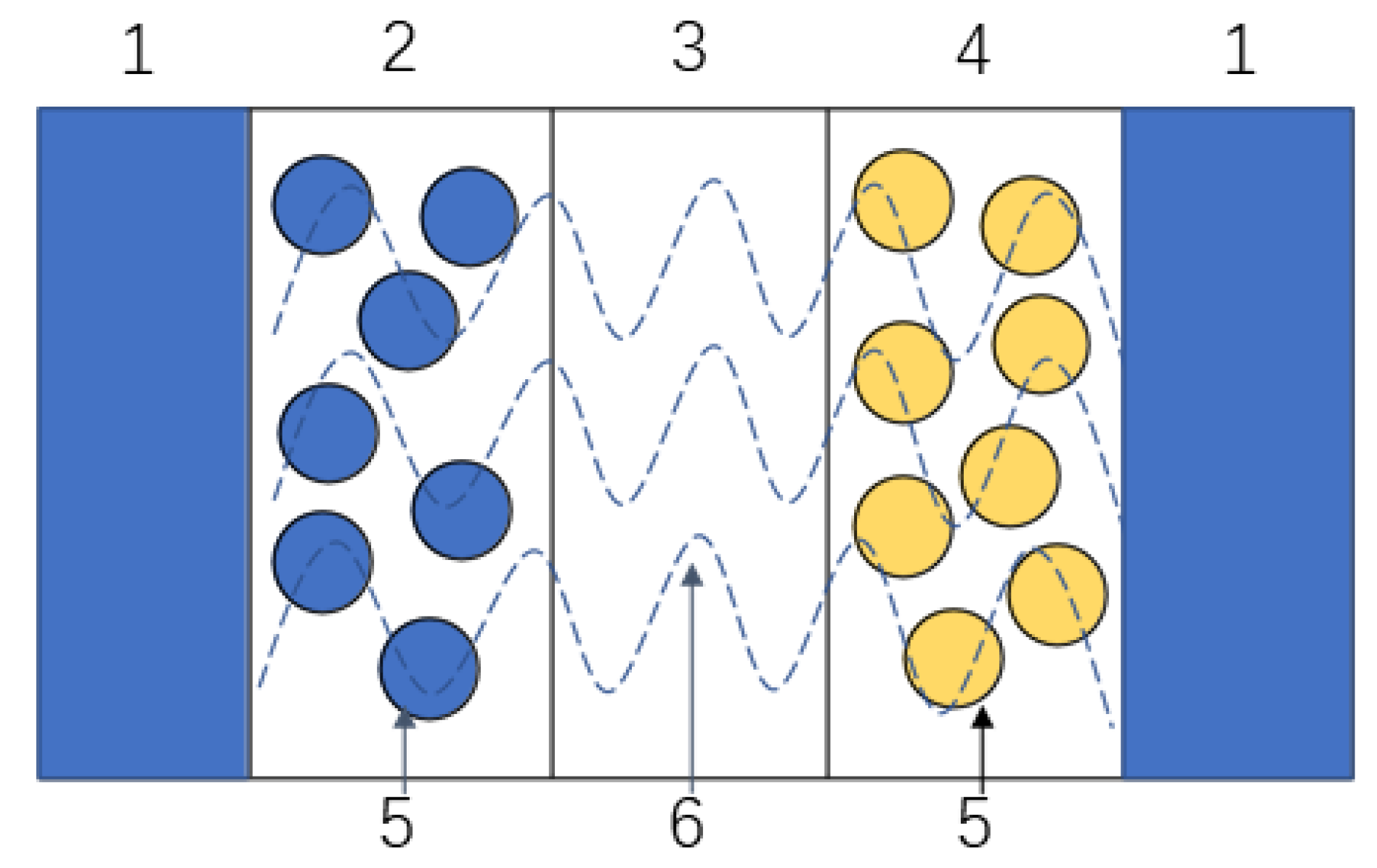
Energies 16 03858 g002
Figure 2. Structural diagram of the electrochemical model of a lithium-ion battery. (1) Liquid collector. (2). Negative electrode. (3) Diaphragm. (4) Positive electrode. (5) Active material. (6) Electrolyte.
In the formula, i0 is the exchange current density, αa is the anode transfer coefficient, usually taken as 0.5, F is the Faraday constant, R is the molar gas constant, T is the cell temperature, η is the spherical particle surface overpotential, and αc is the cathode transfer coefficient, usually taken as 0.5.
The P2D model can deeply understand the mass transfer and kinetic reaction inside the battery, and lay a foundation for the degradation mechanism of the reactive battery and the optimal solution control of the battery [21]. In order to improve the prediction efficiency and accuracy of the model, researchers have optimized it from two aspects, one of which is to simplify the P2D model. Li et al. [22] used the finite difference method to discretely degrade the P2D model and obtained a simplified pseudo-two-dimensional model. On this basis, the electrochemical decay model (ADME) was proposed based on the decay aging phenomenon caused by the side reaction between the cathode and the anode. By comparing the experimental results, it was concluded that the model is simpler, and the maximum errors of predicting the terminal voltage variation trend under the hybrid pulse power characterization (HPPC) condition and 0.33 C constant current and constant power experiment were reduced by 3.92% and 3.94%, respectively. Compared with the simplified pseudo-two-dimensional model, the prediction accuracy was improved by 76% and 55%, respectively. Deng et al. [23] simplified the P2D model by polynomial approximation and proposed a polynomial approximation pseudo-two-dimensional (PP2D) model. The number of operations of this model was only one sixtieth of that of the P2D model. The calculation time of each step was less than 2 ms, which greatly improved the calculation efficiency. Another approach is to simplify electrolyte diffusion. Li et al. [24] combined the simplified electrolyte diffusion process and other kinetic processes of a lithium-ion battery, and a complete five-state diagonal system was obtained, which improved the prediction accuracy of the electrolyte concentration, electrolyte diffusion overpotential, and terminal voltage. All of these methods can simplify the P2D model. After obtaining the simplified model, the researchers optimized the parameter identification stage. Kim et al. [25] proposed a practical method to identify and select valid P2D model parameters, which changed significantly with battery aging. The average error of the P2D model output voltage between the experimental data and identification parameters was only 18.79 mV, which had high accuracy. Li et al. [26] used the heuristic algorithm for parameter identification, adopted a divide and conquer strategy, divided the P2D model parameter set into two groups, and identified each group of parameters separately. The complete identification of the P2D model can be completed within 10 h, which is 50% more efficient than the traditional identification method. Laue et al. parameterized the most prevalent electrochemical P2D model for Li-ion batteries [27]. A three-step technique was performed with quasi-static electrode measurements of open-circuit potentials, C-rate testing, and electrochemical impedance spectroscopy all taking place. Each step’s identifiability was thoroughly addressed, and basic guidelines for future parameterizations were generated. According to the findings, open-circuit potentials and C-rate measurements are insufficient to properly parameterize electrochemical models. To address the ambiguity of diffusion and electrical processes in quasi-static circumstances, highly dynamic tests such as impedance spectroscopy are required. The findings of this research offer recommendations for the usage of electrochemical models in applied science and industry. To parameterize the most often used electrochemical pseudo-two-dimensional model, Xu et al. [28] suggested a unique nondestructive parameter identification approach. First, the sensitivity of the model parameters was examined and divided into three groups based on the situations under which the parameters were most sensitive. Second, for these unknown values, a deep learning technique was utilized to provide plausible first predictions. Finally, two alternative approaches for parameter identification were coupled in order to progressively estimate the parameters with great sensitivity. The results indicate that utilizing both the simulation and experimental data, one electrochemical parameter could be properly calculated in 14 h. The root-mean-square error of the model forecast voltage was less than 14 mV after evaluating the model parameters.

2.2. SP Model

Compared with other electrochemical models, the single-particle model is widely used because of its simple construction and fast prediction speed [29]. In the literature, the SP model was simplified to degrade to improve the calculation speed and prediction accuracy of the model [30][31]. At the same time, various factors that may affect the battery were taken into account in the model, and internal indicators were selectively extracted to track the battery health status [32][33]. Sadabadi et al. [34] proposed a RUL prediction algorithm based on single particle model parameter estimation. The algorithm uses the moles of circulating lithium and battery resistance as indicators of the state of health, and uses the derived composite SOH metric to design particle filter-based RUL predictions [35], where the greater the SOH-related estimates, the more accurate the RUL estimate. Based on the SP model, Li et al. [36] proposed an improved simplified model, obtained physical parameters with the aging mechanism, and selected new health indicators by analyzing the relationship between the physical parameters and battery health status [37], which is helpful in accurately predicting the remaining life of the battery, and has important theoretical significance and practical value for improving the level of battery management technology. Prasad et al. [38] simplified the model by two key parameters, battery resistance, and cathode solid-phase diffusion time [39]. The model uses the gradient parameter real-time update method under the excitation of the HPPC current [40]. Within 200 s, the estimated value of the total battery resistance and diffusion time could converge to the optimal value within 99%. The calculation speed was fast, and can be used for the online estimation of the remaining life of the car battery. Deng et al. [23] employed a sequence of polynomial functions to simulate the electrolyte phase concentration profile, the solid phase concentration profile, and the nonuniform reaction flow profile, respectively, to simplify the P2D model. The accuracy of the second- and third-order polynomial estimates for the reaction fluxes was compared, and the higher order’s more robust correctness was proven. The created model was simulated using a variety of constant flow rates, mixing pulses, and driving times, and the results were compared to the P2D model and the original SP model. The findings revealed that the proposed model captures the cell properties adequately while significantly reducing the computational complexity.

2.3. Electrochemical Coupling Model

The above electrochemical models can be optimized in their respective fields to compensate for deficiencies to a certain extent, but some deficiencies are inherent to the models themselves and cannot be eliminated. In this case, the integration with other models is needed to improve the accuracy. The P2D model is an isothermal model without considering the coupling relationship between heat generation and chemical reaction. In the actual charging and discharging process, the battery will inevitably generate heat. Kuangke et al. [41] put forward a kind of large capacity motor such as the lithium-ion battery electrochemistry-thermal coupling efficient modeling method through the classification of the parameters, and the measured/identification parameters for precise measurement and parameter identification, using pulse charging experiments under different temperature calibration solid phase diffusion coefficient of the DS and reaction rate constant k, further established the battery heat production model. The simulation data of the voltage and temperature agreed well with the test data, and the parameters of the model were more accurate at room temperature. The average voltage error was less than 10 mV, and the average temperature error was less than 1.1 °C. The established model had good accuracy and adaptability. Wang et al. [42] also developed an electrochemical-thermal model utilizing P2D and detailed how some parameters varied with temperature. The proportional mean square variance between the model’s anticipated and observed residual life was only 0.625%, which compensated for the simulation error caused by the temperature change. Zhang et al. [43] discovered that the P2D model’s impedance parameters were only consistent with the actual battery at low frequencies. It obtained high simulation precision in the wide bandwidth range from 10 mHz to 1 kHz by integrating the P2D model with the EIS model. Under the sinusoidal electrical excitation of 5 Hz, 10 Hz, and 20 Hz, the root mean square error of the improved model decreased by 24.8%, 30.6%, and 33.0%, respectively, when compared to the P2D model. Li et al. [36] found that the existing SP model did not consider the degradation mechanism, and proposed a new prediction model combining the capacity degradation model and SP model. This model could quickly predict the capacity attenuation and voltage distribution changes with the number of cycles and temperature. Compared with the experimental results, the root mean square error of the model prediction was 0.0103. A coupled electrochemical-thermal coupling (ECT) model of LiCoO batteries was proposed by Li et al. [44] to describe their charging and discharging behavior. Calculations of heat generation, conduction, and dissipation were added to the simplified electrochemical model by means of a total set thermal analysis and a rational reduction and recombination of the cell mechanism parameters to reduce the estimation complexity. Specifically designed identification conditions were used to obtain the mechanism parameters based on the excitation response analysis. The applicability of the model under different operating conditions was verified by simulations. The simulation results of the end voltage and surface temperature were in good agreement with the actual experimental measurements at lower C-rates and dynamic load currents. Jiang et al. [20] created a one-dimensional (1D) electricity generation-three-dimensional (3D) thermal connection model to investigate the heat transfer mechanism of hexagonal Li-ion cells cooled on various exterior surfaces. The simulation parameters studied were the forced convection cooling coefficient, h, the thermal diffusion surface area, and the dimension of the cell. The variation in temperature of the prismatic cells with conduction force cooling on tiny side surfaces was found to be more uniform than that of prismatic cells with massive front area cooling. The highest temperature differential of the prismatic cell with tiny side surface cooling was kept constant at h = 100 W/m2 K as the cell size rose. Furthermore, the influence of operating temperature on the capacity degradation of Li-ion batteries during cycling was examined. The greater the operating temperature, the faster the parasitic lithium/solvent reduction process, which resulted in the depletion of lithium ions and enhanced the rate of capacity degradation throughout cycling.

2.4. Comparison of Electrochemical Models

In order to more clearly show the advantages and disadvantages of the prediction methods based on electrochemical models, the prediction methods are summarized. In this entry, “★“ was used to indicate the accuracy and complexity of the prediction methods. The results are shown in Table 1.
Table 1. Electrochemical model.
Model Advantages Disadvantages Prediction Accuracy Complexity
P2D model It can describe the internal dynamic behavior of the battery, and has the advantages of accurate model and high calculation accuracy. There are many parameters in the model and the calculation is complicated and the efficiency is low. High
★★★★☆		 High
★★★★☆
SP model The modeling complexity is low and the calculation accuracy is high. The physical properties of electrolyte are ignored and the problem of order reduction is not considered. Higher
★★★★★		 Lower
★★☆☆☆
Electrochemical fusion model Strong robustness and high prediction accuracy. The model is complicated due to the large amount of calculation and many optimization parameters. High
★★★★☆		 High
★★★★☆

References

  1. Tian, J.; Gao, H.; Zhang, Y.; Wang, Y. Research of life prediction methods for power Li-ion battery in electric vehicles. J. Power Sources 2020, 44, 767–770.
  2. Song, K.; Hu, D.; Tong, Y.; Yue, X.G. Remaining life prediction of lithium-ion batteries based on health management: A review. J. Energy Storage 2023, 57, 106193.
  3. Zhao, J.H.; Zhu, Y.; Zhang, B.; Liu, M.Y.; Wang, J.X.; Liu, C.H.; Hao, X.W. Review of State Estimation and Remaining Useful Life Prediction Methods for Lithium-Ion Batteries. Sustainability 2023, 15, 5014.
  4. Shao, L.Y.; Zhang, Y.; Zheng, X.J.; He, X.; Zheng, Y.F.; Liu, Z.W. A Review of Remaining Useful Life Prediction for Energy Storage Components Based on Stochastic Filtering Methods. Energies 2023, 16, 1469.
  5. Deng, Y.; Li, J.; Li, T.; Gao, X.; Yuan, C. Life cycle assessment of lithium sulfur battery for electric vehicles. J. Power Sources 2017, 343, 284–295.
  6. Barre, A.; Deguilhem, B.; Grolleau, S. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689.
  7. Deng, Y.L.; Li, J.Y.; Li, T.H.; Zhang, J.Y.; Yang, F.; Yuan, C. Life cycle assessment of high capacity molybdenum disulfide lithium ion battery for electric vehicles. Energy. 2017, 123, 77–88.
  8. Hu, X.; Guo, Y.; Zhang, R. A Review of Lithium-ion Battery State of Health Estimation Methods. J. Power Supply 2021, 12, 113.
  9. Wu, L.; Fu, X.; Guan, Y. Review of the Remaining Useful Life Prognostics of Vehicle Lithium-Ion Batteries Using Data-Driven Methodologies. Appl. Sci. 2016, 6, 166.
  10. Wang, X.X.; Liu, S.R.; Zhang, Y.J.; Lv, S.S.; Ni, H.J.; Deng, Y.L.; Yuan, Y.N. A Review of the Power Battery Thermal Management System with Different Cooling, Heating and Coupling System. Energies 2022, 15, 1963.
  11. Hu, X.S.; Xu, L.; Lin, X.K. Battery Lifetime Prognostics. Joule 2020, 4, 310–346.
  12. Hasib, S.A.; Islam, S.; Chakrabortty, R.K.; Ryan, M.J.; Saha, D.K.; Ahamed, M.H.; Moyeen, S.I.; Das, S.K.; Ali, M.F.; Islam, M.R.; et al. A Comprehensive Review of Available Battery Datasets, RUL Prediction Approaches, and Advanced Battery Management. IEEE Access 2021, 9, 86166–86193.
  13. Pandey, S.V.; Parikh, N.; Prochowicz, D.; Akin, S.; Satapathi, S.; Tavakoli, M.M.; Kalam, A.; Yadav, P. Predicting the state parameters of lithium ion batteries: The race between filter-based and data driven approaches. Sustain. Energy Fuels 2023, 7, 598–628.
  14. Cai, Y.; Chen, W.; Su, Y.; Jiang, K.; Huang, H. Review of remaining useful life prediction for lithium ion batteries. J. Power Sources 2021, 45, 678–682.
  15. Wang, S.; Han, W.; Chen, L.; Su, X. Prediction of lithium ion batteries remaining useful life based on particle filtering method. J. Power Sources 2020, 44, 346–351.
  16. Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of simplified Pseudo-two-Dimensional models of lithium-ion batteries. J. Power Sources 2016, 327, 44–55.
  17. Guo, M.; Kim, G.; White, R. A three-dimensional multi-physics model for a Li-ion battery. J. Power Sources 2013, 240, 80–94.
  18. Zhou, J.; Xing, B.; Wang, C. A review of lithium ion batteries electrochemical models for electric vehicles. E3S Web Conf. 2020, 185, 04001.
  19. Kuchly, J.; Goussian, A.; Merveillaut, M.; Baghdadi, I.; Franger, S.; Nelson-Gruel, D.; Chamaillard, Y. Li-ion battery SOC estimation method using a neural network trained with data generated by a P2D model. IFAC Pap. 2021, 54, 336–343.
  20. Jiang, G.; Zhuang, L.; Hu, Q.; Liu, Z.; Huang, J. An investigation of heat transfer and capacity fade in a prismatic Li-ion battery based on an electrochemical-thermal coupling model. Appl. Therm. Eng. 2020, 171, 115080.
  21. Li, J.; Xiao, H. Review on modeling of lithium-ion battery. Energy Storage Sci. Technol. 2022, 11, 697–703.
  22. Li, X.; Yu, Y.; Zhang, Z.; Dong, X. Study on external characteristics of lithium-ion power battery based on ADME model. Acta Phys. Sin. 2022, 71, 345–353.
  23. Deng, Z.; Yang, L.; Deng, H. Polynomial approximation pseudo-two-dimensional battery model for online application in embedded battery management system. Energy 2018, 142, 838–850.
  24. Li, C.; Cui, N.; Wang, C. Reduced-order electrochemical model for lithium-ion battery with domain decomposition and polynomial approximation methods. Energy 2021, 221, 119662.
  25. Kim, J.; Chun, H.; Kim, M. Effective and practical parameters of electrochemical Li-ion battery models for degradation diagnosis. J. Energy Storage 2021, 42, 103077.
  26. Li, J.; Zou, L.; Tian, F. Parameter Identification of Lithium-Ion Batteries Model to Predict Discharge Behaviors Using Heuristic Algorithm. J. Electrochem. Soc. 2016, 163, A1646–A1652.
  27. Laue, V.; Röder, F.; Krewer, U. Practical identifiability of electrochemical P2D models for lithium-ion batteries. J. Appl. Electrochem. 2021, 51, 1253–1265.
  28. Xu, L.; Lin, X.; Xie, Y.; Hu, X. Enabling high-fidelity electrochemical P2D modeling of lithium-ion batteries via fast and non-destructive parameter identification. Energy Storage Mater. 2022, 45, 952–968.
  29. Cheng, Q.; Zhang, X.; Gao, Y.; Guo, B. Estimating state of Li-ion battery based on reduced-order electrochemical model. Battery 2021, 51, 110–113.
  30. Li, J.; Landers, R.; Park, J. A comprehensive single-particle-degradation model for battery state-of-health prediction. J. Power Sources 2020, 456, 227950.
  31. Cen, Z.; Kubiak, P. Lithium-ion battery SOC/SOH adaptive estimation via simplified single particle model. Int. J. Energy Res. 2020, 44, 12444–12459.
  32. Zhou, X.; Stein, J.; Ersal, T. Battery state of health monitoring by estimation of the number of cyclable Li-ions. Control Eng. Pract. 2017, 66, 51–63.
  33. Bi, Y.; Yin, Y.; Choe, S. Online state of health and aging parameter estimation using a physics-based life model with a particle filter. J. Power Sources 2020, 476, 228655.
  34. Sadabadi, K.; Jin, X.; Rizzoni, G. Prediction of remaining useful life for a composite electrode lithium ion battery cell using an electrochemical model to estimate the state of health. J. Power Sources 2021, 481, 228861.
  35. Li, J.; Wang, D.; Deng, L. Aging modes analysis and physical parameter identification based on a simplified electrochemical model for lithium-ion batteries. J. Energy Storage 2020, 31, 101538.
  36. Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.; Park, J. A single particle model with chemical/mechanical degradation physics for lithium ion battery State of Health (SOH) estimation. Appl. Energy 2018, 212, 1178–1190.
  37. Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015.
  38. Prasad, G.; Rahn, C. Model based identification of aging parameters in lithium ion batteries. J. Power Sources 2013, 232, 79–85.
  39. Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part II: Pseudo-two-dimensional model simplification and state of charge estimation. J. Power Sources 2015, 278, 814–825.
  40. Lin, C.; Tang, A. Simplification and efficient simulation of electrochemical model for Li-ion battery in EVs. Energy Procedia 2016, 104, 68–73.
  41. Kuang, K.; Sun, Y.; Ren, D.; Han, X.; Zheng, Y.; Geng, Z. Efficient Approach for Electrochemical-thermal Coupled Modeling of Large-format Lithium-ion Power Battery. J. Mech. Eng. 2021, 57, 10–22.
  42. Wang, D.; Zhang, Q.; Huang, H. An electrochemical–thermal model of lithium-ion battery and state of health estimation. J. Energy Storage 2021, 47, 103528.
  43. Zhang, Q.; Wang, D.; Yang, B. Electrochemical model of lithium-ion battery for wide frequency range applications. Electrochim. Acta 2020, 343, 136094.
  44. Li, J.; Wang, L.; Lyu, C.; Wang, H.; Liu, X. New method for parameter estimation of an electrochemical-thermal coupling model for LiCoO2 battery. J. Power Sources 2016, 307, 220–230.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Energy & Fuels
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Xingxing Wang
,
Peilin Ye
,
Shengren Liu
,
Yu Zhu
,
Yelin Deng
,
Yinnan Yuan
,
Hongjun Ni
View Times: 400
Revisions: 2 times (View History)
Update Date: 10 May 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback