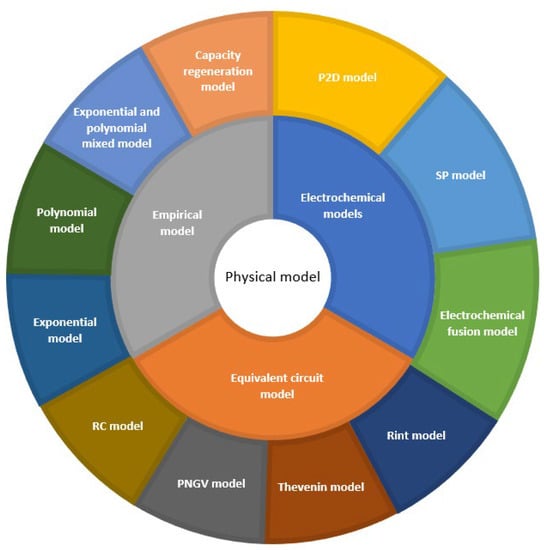
An electrochemical model is a model built by simulating the electrochemical reaction process of a battery [
17]. It describes the laws of the cell from the point of view of internal physical and chemical processes including kinetic parameters, mass conversion processes, thermodynamic properties, mechanical, thermal, and electrical properties of materials [
18]. It can provide a reference for battery research and development, so electrochemical models are often used for the analysis of battery principles and for battery research and development [
19]. Electrochemical models include pseudo two-dimensional (P2D), single particle (SP) models, and coupled electrochemical models developed based on both.
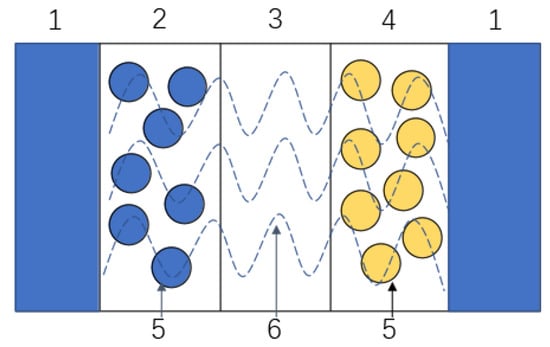
Figure 2. Structural diagram of the electrochemical model of a lithium-ion battery. (1) Liquid collector. (2). Negative electrode. (3) Diaphragm. (4) Positive electrode. (5) Active material. (6) Electrolyte.
In the formula, i0 is the exchange current density, αa is the anode transfer coefficient, usually taken as 0.5, F is the Faraday constant, R is the molar gas constant, T is the cell temperature, η is the spherical particle surface overpotential, and αc is the cathode transfer coefficient, usually taken as 0.5.
The P2D model can deeply understand the mass transfer and kinetic reaction inside the battery, and lay a foundation for the degradation mechanism of the reactive battery and the optimal solution control of the battery [
21]. In order to improve the prediction efficiency and accuracy of the model, researchers have optimized it from two aspects, one of which is to simplify the P2D model. Li et al. [
22] used the finite difference method to discretely degrade the P2D model and obtained a simplified pseudo-two-dimensional model. On this basis, the electrochemical decay model (ADME) was proposed based on the decay aging phenomenon caused by the side reaction between the cathode and the anode. By comparing the experimental results, it was concluded that the model is simpler, and the maximum errors of predicting the terminal voltage variation trend under the hybrid pulse power characterization (HPPC) condition and 0.33 C constant current and constant power experiment were reduced by 3.92% and 3.94%, respectively. Compared with the simplified pseudo-two-dimensional model, the prediction accuracy was improved by 76% and 55%, respectively. Deng et al. [
23] simplified the P2D model by polynomial approximation and proposed a polynomial approximation pseudo-two-dimensional (PP2D) model. The number of operations of this model was only one sixtieth of that of the P2D model. The calculation time of each step was less than 2 ms, which greatly improved the calculation efficiency. Another approach is to simplify electrolyte diffusion. Li et al. [
24] combined the simplified electrolyte diffusion process and other kinetic processes of a lithium-ion battery, and a complete five-state diagonal system was obtained, which improved the prediction accuracy of the electrolyte concentration, electrolyte diffusion overpotential, and terminal voltage. All of these methods can simplify the P2D model. After obtaining the simplified model, the researchers optimized the parameter identification stage. Kim et al. [
25] proposed a practical method to identify and select valid P2D model parameters, which changed significantly with battery aging. The average error of the P2D model output voltage between the experimental data and identification parameters was only 18.79 mV, which had high accuracy. Li et al. [
26] used the heuristic algorithm for parameter identification, adopted a divide and conquer strategy, divided the P2D model parameter set into two groups, and identified each group of parameters separately. The complete identification of the P2D model can be completed within 10 h, which is 50% more efficient than the traditional identification method. Laue et al. parameterized the most prevalent electrochemical P2D model for Li-ion batteries [
27]. A three-step technique was performed with quasi-static electrode measurements of open-circuit potentials, C-rate testing, and electrochemical impedance spectroscopy all taking place. Each step’s identifiability was thoroughly addressed, and basic guidelines for future parameterizations were generated. According to the findings, open-circuit potentials and C-rate measurements are insufficient to properly parameterize electrochemical models. To address the ambiguity of diffusion and electrical processes in quasi-static circumstances, highly dynamic tests such as impedance spectroscopy are required. The findings of this study offer recommendations for the usage of electrochemical models in applied science and industry. To parameterize the most often used electrochemical pseudo-two-dimensional model, Xu et al. [
28] suggested a unique nondestructive parameter identification approach. First, the sensitivity of the model parameters was examined and divided into three groups based on the situations under which the parameters were most sensitive. Second, for these unknown values, a deep learning technique was utilized to provide plausible first predictions. Finally, two alternative approaches for parameter identification were coupled in order to progressively estimate the parameters with great sensitivity. The results indicate that utilizing both the simulation and experimental data, one electrochemical parameter could be properly calculated in 14 h. The root-mean-square error of the model forecast voltage was less than 14 mV after evaluating the model parameters.
2.2. SP Model
Compared with other electrochemical models, the single-particle model is widely used because of its simple construction and fast prediction speed [
29]. In the literature, the SP model was simplified to degrade to improve the calculation speed and prediction accuracy of the model [
30,
31]. At the same time, various factors that may affect the battery were taken into account in the model, and internal indicators were selectively extracted to track the battery health status [
32,
33]. Sadabadi et al. [
34] proposed a RUL prediction algorithm based on single particle model parameter estimation. The algorithm uses the moles of circulating lithium and battery resistance as indicators of the state of health, and uses the derived composite SOH metric to design particle filter-based RUL predictions [
35], where the greater the SOH-related estimates, the more accurate the RUL estimate. Based on the SP model, Li et al. [
36] proposed an improved simplified model, obtained physical parameters with the aging mechanism, and selected new health indicators by analyzing the relationship between the physical parameters and battery health status [
37], which is helpful in accurately predicting the remaining life of the battery, and has important theoretical significance and practical value for improving the level of battery management technology. Prasad et al. [
38] simplified the model by two key parameters, battery resistance, and cathode solid-phase diffusion time [
39]. The model uses the gradient parameter real-time update method under the excitation of the HPPC current [
40]. Within 200 s, the estimated value of the total battery resistance and diffusion time could converge to the optimal value within 99%. The calculation speed was fast, and can be used for the online estimation of the remaining life of the car battery. Deng et al. [
23] employed a sequence of polynomial functions to simulate the electrolyte phase concentration profile, the solid phase concentration profile, and the nonuniform reaction flow profile, respectively, to simplify the P2D model. The accuracy of the second- and third-order polynomial estimates for the reaction fluxes was compared, and the higher order’s more robust correctness was proven. The created model was simulated using a variety of constant flow rates, mixing pulses, and driving times, and the results were compared to the P2D model and the original SP model. The findings revealed that the proposed model captures the cell properties adequately while significantly reducing the computational complexity.
2.3. Electrochemical Coupling Model
The above electrochemical models can be optimized in their respective fields to compensate for deficiencies to a certain extent, but some deficiencies are inherent to the models themselves and cannot be eliminated. In this case, the integration with other models is needed to improve the accuracy. The P2D model is an isothermal model without considering the coupling relationship between heat generation and chemical reaction. In the actual charging and discharging process, the battery will inevitably generate heat. Kuangke et al. [
41] put forward a kind of large capacity motor such as the lithium-ion battery electrochemistry-thermal coupling efficient modeling method through the classification of the parameters, and the measured/identification parameters for precise measurement and parameter identification, using pulse charging experiments under different temperature calibration solid phase diffusion coefficient of the DS and reaction rate constant k, further established the battery heat production model. The simulation data of the voltage and temperature agreed well with the test data, and the parameters of the model were more accurate at room temperature. The average voltage error was less than 10 mV, and the average temperature error was less than 1.1 °C. The established model had good accuracy and adaptability. Wang et al. [
42] also developed an electrochemical-thermal model utilizing P2D and detailed how some parameters varied with temperature. The proportional mean square variance between the model’s anticipated and observed residual life was only 0.625%, which compensated for the simulation error caused by the temperature change. Zhang et al. [
43] discovered that the P2D model’s impedance parameters were only consistent with the actual battery at low frequencies. It obtained high simulation precision in the wide bandwidth range from 10 mHz to 1 kHz by integrating the P2D model with the EIS model. Under the sinusoidal electrical excitation of 5 Hz, 10 Hz, and 20 Hz, the root mean square error of the improved model decreased by 24.8%, 30.6%, and 33.0%, respectively, when compared to the P2D model. Li et al. [
36] found that the existing SP model did not consider the degradation mechanism, and proposed a new prediction model combining the capacity degradation model and SP model. This model could quickly predict the capacity attenuation and voltage distribution changes with the number of cycles and temperature. Compared with the experimental results, the root mean square error of the model prediction was 0.0103. A coupled electrochemical-thermal coupling (ECT) model of LiCoO batteries was proposed by Li et al. [
44] to describe their charging and discharging behavior. Calculations of heat generation, conduction, and dissipation were added to the simplified electrochemical model by means of a total set thermal analysis and a rational reduction and recombination of the cell mechanism parameters to reduce the estimation complexity. Specifically designed identification conditions were used to obtain the mechanism parameters based on the excitation response analysis. The applicability of the model under different operating conditions was verified by simulations. The simulation results of the end voltage and surface temperature were in good agreement with the actual experimental measurements at lower C-rates and dynamic load currents. Jiang et al. [
20] created a one-dimensional (1D) electricity generation-three-dimensional (3D) thermal connection model to investigate the heat transfer mechanism of hexagonal Li-ion cells cooled on various exterior surfaces. The simulation parameters studied were the forced convection cooling coefficient, h, the thermal diffusion surface area, and the dimension of the cell. The variation in temperature of the prismatic cells with conduction force cooling on tiny side surfaces was found to be more uniform than that of prismatic cells with massive front area cooling. The highest temperature differential of the prismatic cell with tiny side surface cooling was kept constant at h = 100 W/m
2 K as the cell size rose. Furthermore, the influence of operating temperature on the capacity degradation of Li-ion batteries during cycling was examined. The greater the operating temperature, the faster the parasitic lithium/solvent reduction process, which resulted in the depletion of lithium ions and enhanced the rate of capacity degradation throughout cycling.
2.4. Comparison of Electrochemical Models
In order to more clearly show the advantages and disadvantages of the prediction methods based on electrochemical models, the prediction methods are summarized. In this paper, “★“ was used to indicate the accuracy and complexity of the prediction methods. The results are shown in Table 1.
Table 1. Electrochemical model.
| Model |
Advantages |
Disadvantages |
Prediction Accuracy |
Complexity |
| P2D model |
It can describe the internal dynamic behavior of the battery, and has the advantages of accurate model and high calculation accuracy. |
There are many parameters in the model and the calculation is complicated and the efficiency is low. |
High
★★★★☆ |
High
★★★★☆ |
| SP model |
The modeling complexity is low and the calculation accuracy is high. |
The physical properties of electrolyte are ignored and the problem of order reduction is not considered. |
Higher
★★★★★ |
Lower
★★☆☆☆ |
| Electrochemical fusion model |
Strong robustness and high prediction accuracy. |
The model is complicated due to the large amount of calculation and many optimization parameters. |
High
★★★★☆ |
High
★★★★☆ |