Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Amita Biswal
 -- 3552 2023-04-20 13:38:44 |
2 format change
Peter Tang
 Meta information modification 3552 2023-04-21 04:32:23 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Jwo, D.; Biswal, A.; Mir, I.A. Artificial Neural Networks for Navigation Systems. Encyclopedia. Available online: https://encyclopedia.pub/entry/43294 (accessed on 25 April 2024).
Jwo D, Biswal A, Mir IA. Artificial Neural Networks for Navigation Systems. Encyclopedia. Available at: https://encyclopedia.pub/entry/43294. Accessed April 25, 2024.
Jwo, Dah-Jing, Amita Biswal, Ilayat Ali Mir. "Artificial Neural Networks for Navigation Systems" Encyclopedia, https://encyclopedia.pub/entry/43294 (accessed April 25, 2024).
Jwo, D., Biswal, A., & Mir, I.A. (2023, April 20). Artificial Neural Networks for Navigation Systems. In Encyclopedia. https://encyclopedia.pub/entry/43294
Jwo, Dah-Jing, et al. "Artificial Neural Networks for Navigation Systems." Encyclopedia. Web. 20 April, 2023.
Artificial Neural Networks for Navigation Systems
Edit
This entry is adapted from the peer-reviewed paper 10.3390/app13074475

Several machine learning (ML) methodologies are gaining popularity as artificial intelligence (AI) becomes increasingly prevalent. An artificial neural network (ANN) may be used as a “black-box” modeling strategy without the need for a detailed system physical model. It is more reasonable to solely use the input and output data to explain the system’s actions. ANNs have been extensively researched, as artificial intelligence has progressed to enhance navigation performance. In some circumstances, the Global Navigation Satellite System (GNSS) can offer consistent and dependable navigational options. A key advancement in contemporary navigation is the fusion of the GNSS and inertial navigation system (INS). Numerous strategies have been put out to increase the accuracy for jamming, GNSS-prohibited environments, the integration of GNSS/INS or other technologies by means of a Kalman filter as well as to solve the signal blockage issue in metropolitan areas. A neural-network-based fusion approach is suggested to address GNSS outages. 

GNSS inertial navigation artificial neural networks Kalman filter

1. Introduction

Dead reckoning and position fixing are the two basic strategies of positioning classifications used in navigation. The inertial navigation system (INS) and the Global Positioning System (GPS), which is comprised of the Global Navigation Satellite System (GNSS), are the two most prevalent examples, respectively [1][2]. Over the past few decades, GPS and INS have been effectively integrated for real-world applications. Each does, however, have unique traits and limitations. A thorough examination of the existing literature on navigation systems is necessary because a significant amount of research has been conducted in the field of positioning systems. For instance, the GNSS navigation system offers accurate and semi-permanent position and speed data. Reduced accessibility and instability come from the threat to signal shadowing and multipath effects. A self-contained system that measures a vehicle’s linear and angular acceleration could serve as the guidance system. The drawback of INS is its drift error, which will continue to grow over time. As a result, the shortcomings of each technique are solved by the combination of the two systems.
GNSS is the most widely used approach in the disciplines of aviation, automatic craft technique and landing, land vehicle navigation and tracking, marine applications, and evaluation, among others. It is a navigational system that uses satellites to provide three-dimensional position and speed information. Despite being widely used, GNSS still must be able to provide consistent and accurate navigational solutions in some situations. The GNSS outage may occur whenever the vehicle travels through urban areas, tunnels, or enclosed spaces because the satellite signal is blocked. INS’s navigational accuracy decreases with time unless it is intermittently tagged by various sensors. Because of the inherent complementary operational characteristics of GNSS and INS systems, the combination of each method has provided the best possible resolution throughout the past decades. Furthermore, the combination of INS and an external navigation system, such as GNSS, could be a state-of-art technique for several application eventualities. In the integrated GNSS/INS navigation system, the GNSS resolution incorporates a consistent and semi-permanent stable accuracy that is employed to update the INS resolution. Furthermore, the INS settlement is subjected to bridging GNSS blackouts once a satellite signal is blocked. The GNSS/INS navigation system is becoming more and more fashionable because it offers consistent, accurate, and reliable navigation resolution. As long as the GNSS signals are usable, this navigation system calculates, estimates, and models the INS inaccuracy. As a result, it simultaneously provides accurate and fast navigation parameters.
For autonomous underwater vehicle (AUV) navigation, a navigation-grade INS in conjunction with a Doppler velocity log (DVL) is frequently employed. The precision of integrated navigation depends critically on whether or not the DVL can generate constant rate readings. Given the actual underwater working environment of AUVs, the DVL’s calculated value is subjected to outliers and even disruption. The well-trained network can forecast the velocity after the DVL fails, which can then be used for navigation in the future. Its benefit is that it enables time-varying noise adaptation and lessens outlier interference with the integrated navigation system. Figure 1 shows the different architectures for integrated navigation systems. The different methods of filtering approaches are the Kalman filter (KF), the extended Kalman filter (EKF), the unscented Kalman filter (UKF), the cubature Kalman filter (CKF), and the sequential Monte Carlo (SMC) approaches, among which the particle filter (PF) is the most well-known. The most fundamental and extensively used data fusion procedures in integrated navigation systems are KFs and their derivatives. The KF is an ideal estimate algorithm for Gaussian and linear approximations with the requirements of precise the system model and previous updated noise. Regrettably, the precision and robustness of conventional KFs are decreased by mistakes when modeling systems and the uncertainty of operating situations.
Figure 1. Example of integrated navigation systems: (a) GNSS/INS for air and land applications; (b) INS/DVL for underwater applications.
An adaptive Kalman filter (AKF) [3][4][5][6][7][8][9][10][11][12] can be used as the noise-adaptive filter for adjusting the noisy covariance matrices to satisfy the filter optimality criteria. The correlation- and covariance-matching techniques have made use of technological animations to predict the noise covariance. Making the inherent value of the covariance of the retained complies with its theoretical result is the fundamental tenet of the covariance-matching technique. To correct noisy estimates, the innovation-based estimation (IAE) [3][4][5][6][7][8] method has become quite effective. It combines fuzzy logic methodologies with membership functions created using the heuristic method. In contrast to sampling, the variational Bayesian (VB) [9][10][11][12] has been developed for a variety of models to achieve approximate posterior inference at a minimal computational cost.
Artificial neural networks (ANN) or neural networks (NN) [13] are built of straightforward components that work together. The quality and productivity of the NN enable it to estimate undetermined nonlinear input–output mapping. Due to the absence of estimators in the system model—i.e., it lacks the need for a mathematical model—NNs have been used to solve a wide range of issues. The NN has two unique characteristics: it can be generalized due to its nonlinearity, and it can be implemented in multi-input and multi-output arbitrary nonlinear mapping by altering the link weights. As a result, this makes the system’s real-time approximation more challenging. The deterministic methodology is a recognized and efficient technique for latency mitigation. Additionally, the NN’s widespread approximation property allows it to be used for the characterization of nonlinear systems. Like in nature, interconnections amongst constituents play a major role in networks’ function. The biological nervous system inspires these elements. By contrasting the outcome of an NN with the perceived target, an NN learns to fit the relationship. By changing the values of the connections (weights) between elements, an NN can be trained to carry out a certain task so that a different input leads to a particular target. Until the output of the network matches the target, the NN is changed based on a comparison between the output and the target. After that, it modifies the weight value until the error reaches the required accuracy.
The INS system can deliver precise navigational data quickly, and its accuracy will rapidly deteriorate over time. Therefore, it has been suggested that GNSS and INS be integrated to address their limitations. However, during GNSS process failures, the system will switch to a completely INS system navigation mode, and the effectiveness will be massively degraded. The features of the GNSS/INS integrated navigation system components in the situation of GNSS failures have been improved by using a variety of methods that have been presented to identify the GNSS signal outages. The addition of additional sensors to supply fresh reference data from other sources for the integrated navigation system, for which the odometer and maps are one remedy during GNSS failure. However, the price and size of the navigation system will rise correspondingly. Cornering, GNSS denial situations, the integration of employing KF, and several methods are also utilized to increase the perfection of GPS locations and to get over signal blockage in metropolitan areas. Neural networks are a popular choice for representing dynamic and complex processes since they have the potential to learn. To remove their influence from the estimation process, errors and noise are typically estimated using neural networks. In the event of a GPS signal failure, these strategies significantly improve GPS/INS integration. However, the localization systems are significantly impacted by severe multipath settings or prolonged non-line-of-sight (NLOS), and no improvement from its prior methodologies is realized. Although a few interesting implementations in complex visual detection and reduced AI computation have resulted from this research, a relatively intelligent mechanism has yet to be produced [14][15][16][17].

2. The Use of Neural Networks in the Global Positioning System

Machine learning (ML) enables artificial intelligence (AI) systems to learn from data. It is effective for nonlinear systems and is not reliant on the system’s mathematical model. The application overview of the ANN and NN in the navigation system has been subbmerized in Figure 2. The geometric dilution of precision (GDOP) approximation [13][14][15][16][17][18][19][20][21][22][23][24][25][26], GPS navigation processing [27][28][29], attitude determination using NNs [30], and prediction of differential DGPS correction message using NNs [31] are reviewed. It is a feature whose approaches—based on AI—may not ask for numerical methods of the system dynamics and observations, which is a key distinction between them and other forms of estimating methods. Figure 3 provides the overview of the NN training principle to approximate an unknown system model.
Figure 2. The outflow of ANN and NN in navigation system.
Figure 3. Overview of NN training principle.

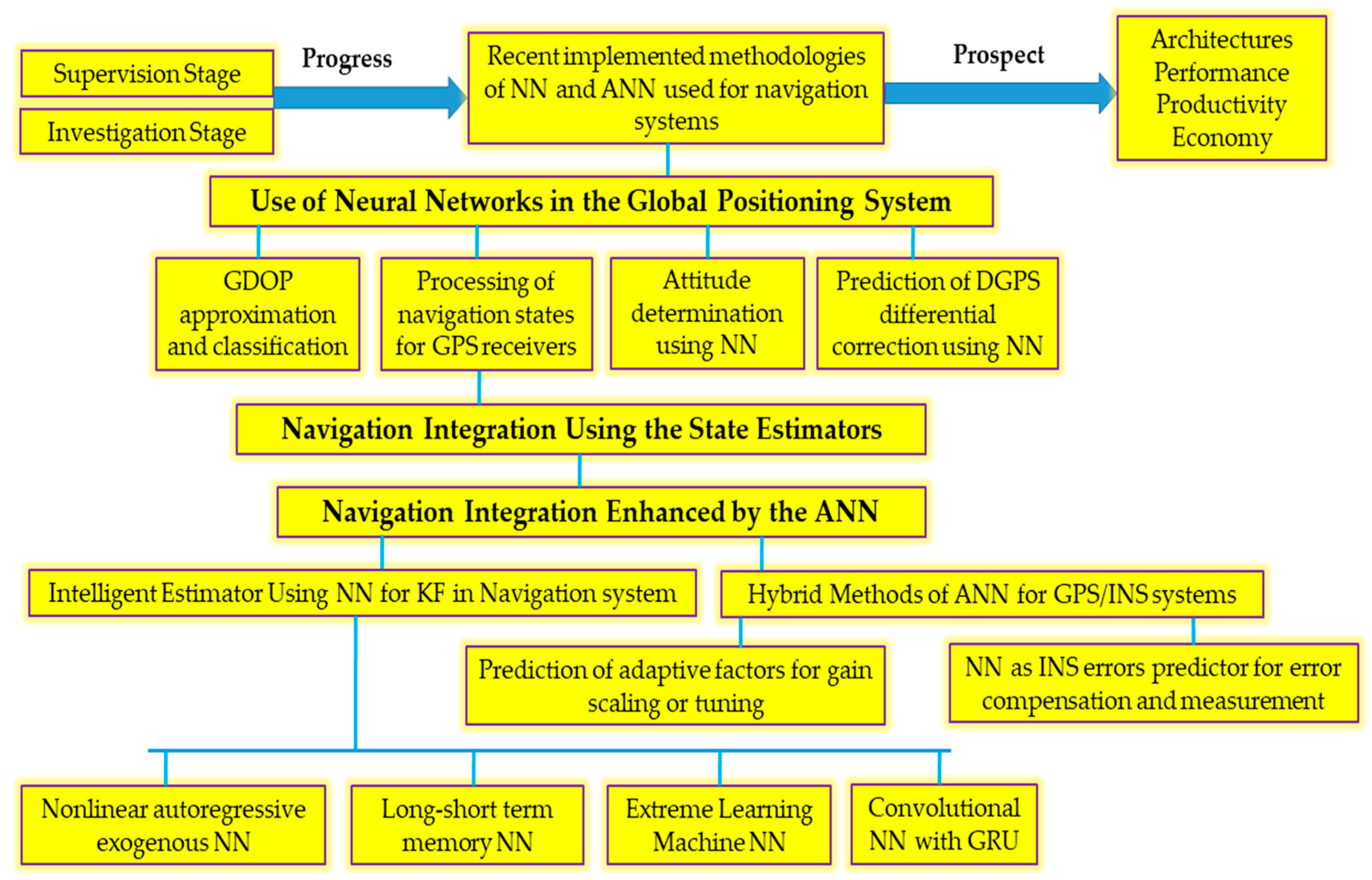
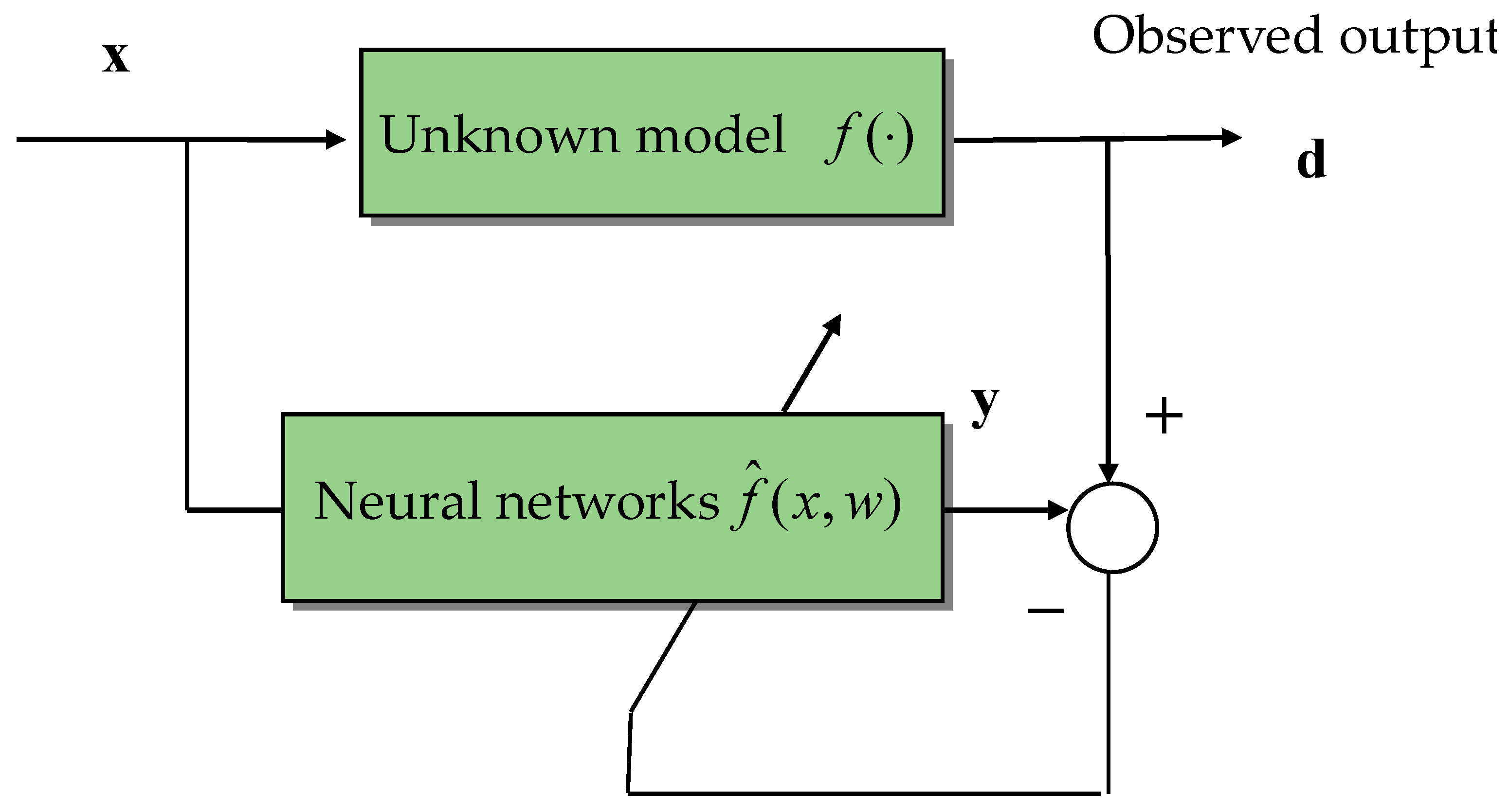
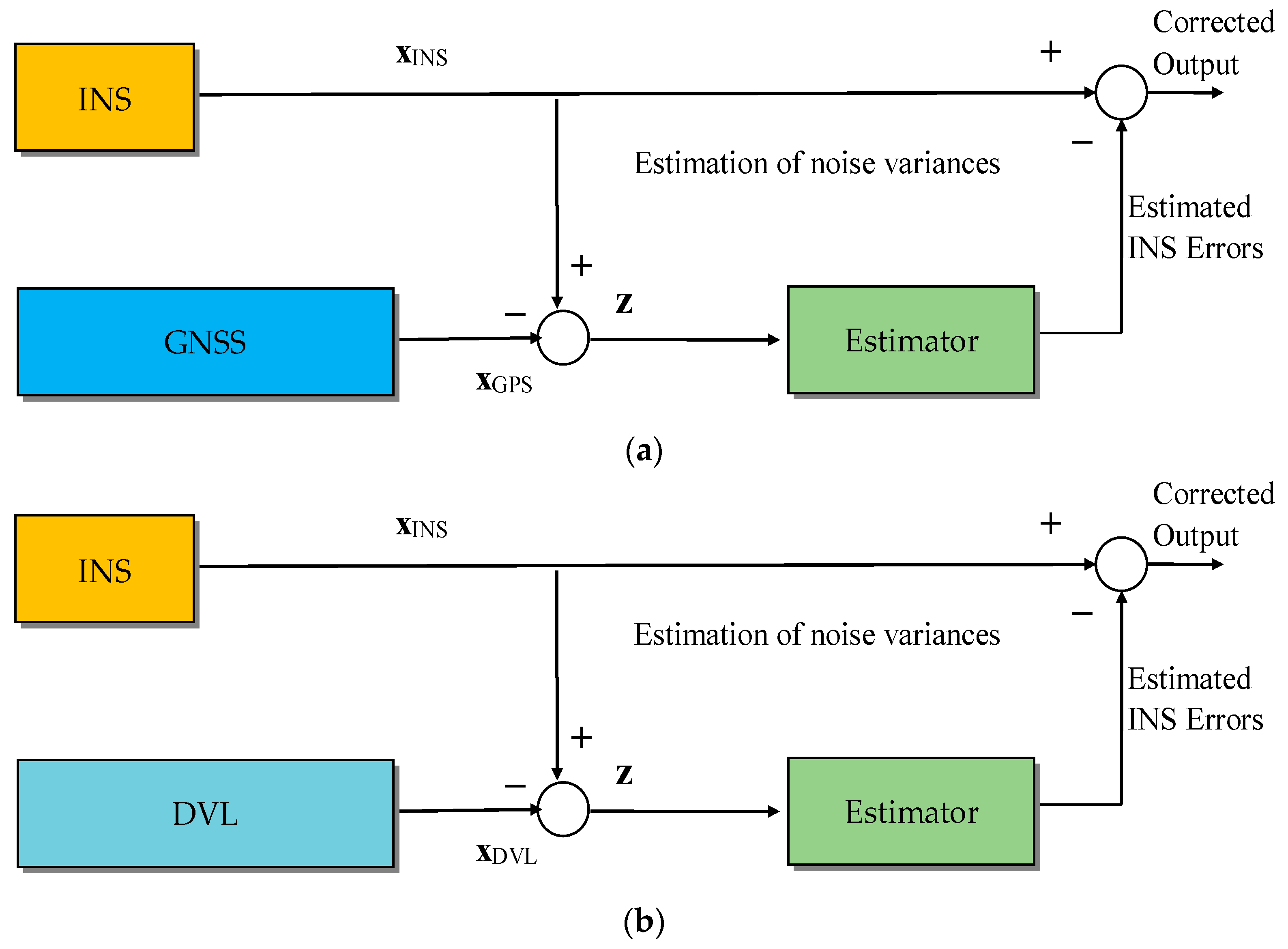
3. Navigation Integration Using the State Estimators

Navigation integration is typically carried out through the KF to estimate the system state variables and suppress the measurement noise. Different Bayesian filtering techniques, including the KF, EKF, UKF [32][33][34], CKF [35], and particle filter (PF) [34][36] techniques, are typically used in the data fusion algorithms of the INS/GPS-integrated navigation system to calibrate the navigation estimation error. In linear systems with white Gaussian noise, it is generally accepted that the KF makes use of the minimum mean square error (MMSE) as the best criterion. On the other hand, if the system’s dynamic and measurement models are accurately described, the KF leverages measurement updates to correct system state mistakes and restrict navigation solution errors. The noise statistics of the process provide the best estimates of a system’s states. Without measurement updates, the KF’s forecast diverges, and when GPS signals are not available, a combined GPS/INS navigation system’s performance may suffer quickly.
For nonlinear models, EKF employs an approximation technique to linearize the nonlinear system model. The state and observation equations are linearized using EKF using first-order Taylor reduction to enhance the conventional KF [36]. By constructing the linear differential equation, the nonlinear system is roughly approximated. It is straightforward to calculate the assessment in the Bayesian recursive formula since KF and EKF both turn the problem into a linear Gaussian model. The UKF is based on a method for mean and covariance propagation through a nonlinear mapping built using the unscented transform (UT) approach. The state vector is discretized as a minimum collection of sample points (sigma points), which approximates the second-order precision posterior mean and covariance of the random variable with a Gaussian distribution. To approximate the probability density distribution of a nonlinear function, UKF uses a set of predetermined samples. The EKF’s linearization method can only produce first-order accuracy. When the computing complexity is the same, the UKF performs better than the EKF. The aforementioned filtering algorithms for the high-dimensional process model are susceptible to a non-positive definite covariance matrix. Non-Gaussian noises, on the other hand, are commonly present in many real-world contexts and seriously degrade their functionality.
The KF, EKF, and UKF techniques have many significant flaws that prevent their application. They are unable to deal with the following two issues in particular: modeling non-Gaussian processes and observation noises and well as unidentified noise covariance matrices are the first two sources of noise. When the methods are coupled with colored noise, as is the case in several scenarios for practical implementation, the EKF cannot perform satisfactorily since the estimation outcomes are vulnerable to strong outliers and non-Gaussian noise. The CKF approximates the state mean and covariance of a nonlinear system with extra Gaussian noise using a collection of volume points based on the third-order spherical radial volume criteria. Theoretically, CKF is the approximation technique that comes closest to Bayesian filtering, and it is an effective tool for dealing with nonlinear system state estimates. For each integral point, CKF has the same weight, which is positive. Compared to UKF, CKF’s numerical stability is developing more rapidly. The resilience is decreased, and even the filter fails despite being impacted by the process model’s instability and the measured noise statics’ variability. In recent years, numerous academics have suggested enhanced CKF algorithms to address the aforementioned issues. The PF is computationally expensive for an online implementation even if it can handle the non-Gaussian, nonlinear system effectively.
The implementation of the Kalman family of filters needs a precise and logically valid statistical understanding of the process noise and measurement noise. Inadequate understanding of the noise statistics may cause filter divergence and substantially impair KF performance. Relativistic issues will arise if a filter’s theoretical operation and its real behavior do not correlate. The assumptions on the statistical database of disruption are violated in various of scenarios in which there are instabilities in the process model and noise characterization, because in many real-world scenarios, the availability of a well-defined model is unattainable because some observations are ignored in the modeling step and one approach for taking them into consideration is to consider an equivalent model influenced by uncertainty. Moreover, there are model assumptions in actual navigational applications that the continuous state-space model is unable to capture. Since the actual vehicle motions are the result of non-linear processes, the linear model contains modeling mistakes. It is necessary to predetermine the system model, the system’s beginning conditions, and the noise properties. It frequently happens that little prior knowledge of the operation is accessible.
The availability of a well-defined model is inappropriate in particular scenarios in which there are many uncertainties in the proposed system and noise interpretation. Predictions based on disruption statistics are violated due to a number of realistic applications, and some conditions are ignored in the modeling step. It is reasonable to suppose that an adaptive process will dynamically identify the system model uncertainties and modeling errors. Innovation-based adaptive estimating (IAE) and multiple-model-based adaptive estimation (MMAE), such as the interacting multiple models (IMM) [5][6][7][8] algorithm, are the two main approaches to AKFs that have been developed. The IMM algorithm has a configuration in which many model-matched state estimation filters operate in parallel and interact (exchange information) at each sampling period. By modifying the probabilities of each approach, which are utilized as weightings in the aggregate global state estimation, the algorithm performs soft switching between the various modes. The mode-conditioned forecast’s covariances as well as the variations between these estimates are taken into account in the covariance matrix linked to this combined estimate.
The noise data from the measurement sequence during the filtering process can be removed, and an IAE technique has been devised to estimate the process noise covariance Qk and/or measurement noise covariance Rk. A bank of KFs with various parameters operates concurrently in an MMAE approach, and the weights of every sub-filter are aggressively changed in response to fresh assessments. The sub-filter with well-known parameters wins after a thorough study. The MMAE method, however, requires more resources and may not completely account for the true system model. Another drawback is that the parameter estimation method for both IAE and MMAE systems requires a sliding window over the measurement sequence, which causes inaccuracy and delay. Consequently, adaptive filters introduce more sophisticated components in integrated navigation systems. The selection in integrated navigation systems’ adaptive filters frequently uses fuzzy logic techniques. Such a selection selects the best sensors or dynamically modifies the noise covariance matrix. Target tracking may be manipulated well using interactive multiple models. Then the more accurate noise covariance matrix was estimated using the IMM technique. When used in an underwater environment, the IMM-adaptive robust cubature Kalman filter technique may successfully address the issues of measurement noise and typical statistical inaccuracy.
The technique makes use of VB learning to give a robust tracking capacity for time-varying noise covariance as well as an approximation of the noise strength. The VB approach is an inferential technique that approximates the real posterior distribution of hidden variables using a straightforward distribution, typically presuming that the disguised variables are unrelated to one another. In contrast to sampling methods, the VB has been created for a several models to perform preliminary posterior inference with a minimal computing cost. The typical filters for navigational state estimation and their improved algorithms are summarized in Table 1.
Table 1. The navigation filters and their improved algorithms.

Navigation Fusion

Algorithm

Features

Linear Kalman filter algorithm

-

Simple calculation and easy implementation

Nonlinear filter algorithms, including the EKF, UKF, and CKF

-

Good processing capacity for nonlinear systems

Sequential Monte Carlo (SMC) approaches

-

Particle filter (PF) is the well-known realization of the SMC approach

Adaptive filter algorithms

-

Adapt to time-varying

-

Innovation-based adaptive estimating (IAE) and multiple-model-based adaptive estimation (MMAE) including the interacting multiple model (IMM) algorithm are the two main approaches.

-

The variational Bayesian (VB) learning algorithm analyzes the real posterior distribution of concealed parameters approximation using a straightforward distribution.

Neural-network-assisted filtering algorithm

-

Simple, easy to learn, no need for systematic mathematical models

-

Good network predictability with real-time performance.

Deep learning improvement algorithm

-

Improved accuracy

-

Good generalization capability.

4. Navigation Integration Enhanced by the ANN

In complicated and hidden situations, inertial navigation is an essential component of vehicle navigation systems. There has been widespread use of the GNSS/INS combined system for land and air applications and DVL/INS for underwater applications. In general, the integration task makes considerable use of the EKF to obtain an accurate and consistent estimated position. In contrast, the lack of readings from the GNSS/INS EKF in the event of a GNSS signals failure, signal blockage, or jamming causes the navigation system’s accuracy to rapidly decline. To increase the integrated navigation system’s accuracy while GNSS failures, several fusion techniques have been investigated [37][38][39][40][41][42][43][44][45][46][47][48][49][50][51][52][53][54][55][56][57][58][59][60][61][62]. Adding additional sensors to compensate for the lost GPS information and improve navigation accuracy is possible but comes at the cost of increased system complexity. Machine learning algorithms have become famous for mimicking the INS’s error propagation property and establishing a connection between updated vehicle dynamics and INS errors by using available GNSS signals to train the machine learning (ML) model. For the corrected INS mistakes caused by a lack of accurate measurements, such as GNSS failures, researchers have developed an error forecasting and compensating system based on artificial intelligence for GNSS/INS integration. The neural network has received considerable attention because of its useful nonlinear function estimation property and learning capacity. It has been frequently applied to integrated navigation error correction during GNSS failures. When GPS is unavailable, the neural network is used as an alternate integration mechanism to deliver superior navigational options.

5. Advantage and Disadvantages of ANN in Navigation System

Current developments in ML have produced ANNs that are significantly more complicated and simpler to train than their predecessors. The LSTM architecture is one of the most significant developments [63]. To identify patterns in sequences, the LSTM technique learns from knowledge segments and stores in the form of series in memory. A filter in navigation can be thought of as a function of a series of machine assessments and feeds to produce a series of state estimates. As a result, LSTM ANNs can act like filters, but they are developed through updating on empirical data rather than by customizing filters based on past experience. By enhancing an existing filter, ANNs facilitate and filter data. The advantages of the augmentations include keeping the functionality of a verified filter with obtaining a major improvement via ANN augmentation. The augmentations involve offering corrections, adding measurements, and adjusting filter settings. This connection can be used by the learning algorithm to enhance the filter. ANNs are one type of system that can be used to extract information from knowledge. This now improves filter efficiency by raising the a priori knowledge of the issue.
The state modifications of ANN might be updated simply by presenting the error at each step of the time as the objective for guided outcome and generating estimation from the filter at every time interval. The ANN would then pick up on the mistakes the filter made at each time step. The ANN will overstate the error made by the filter at runtime. Since the filter employs updated state projections at the beginning of every time period, the state estimates produced by the filter have less error. This feedback must be included in the ANN output target at each time step in order to prevent the ANN from overestimating the filter’s mistakes. The ANN estimator will finally appear at a minimal area or saddle point after repeating this process, producing the same corrections in each iteration. As a result, the output expectation for the next upgrade will not be considerably altered. The additional step of recalculating the ANN’s goal output can make this process more complex.

References

  1. Wellenhof, B.H.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems, GPS, GLONASS, Galileo, and More; Springer Wien: Vienna, Austria; New York, NY, USA, 2008.
  2. Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering; John Wiley & Sons: New York, NY, USA, 1997.
  3. Mehra, R.K. On-line Identification of Linear Dynamic Systems with Applications to Kalman Filtering. IEEE Trans. Autom. Control 1970, 16, 12–21.
  4. Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman Filtering for INS/GPS. J. Geod. 1999, 73, 193–203.
  5. Li, X.R.; Shalom, Y.B. Design of an Interacting Multiple Model Algorithm for Air Traffic Control Tracking. IEEE Trans. Control. Syst. Technol. 1993, 1, 186–194.
  6. Lin, X.; Kirubarajan, T.; Bar-Shalom, Y.; Li, X. Enhanced Accuracy GPS Navigation Using the Interacting Multiple Model Estimator. In Proceedings of the IEEE Aerospace Conference, Montana, CA, USA, 10–17 March 2001; Volume 4, pp. 1911–1923.
  7. Chen, G.; Harigae, M. Using IMM Adaptive Estimator in GPS Positioning. In Proceedings of the 40th SICE Annual Conference, SICE 2001, International Session Papers, Nagoya, Japan, 25–27 July 2001; pp. 25–27.
  8. Jwo, D.J.; Chung, F.C.; Yu, K.L. GPS/INS Integration Accuracy Enhancement Using the Interacting Multiple Model Nonlinear Filters. J. Appl. Res. Technol. 2013, 11, 496–509.
  9. Särkkä, S.; Nummenmaa, A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE Trans. Autom. Control 2009, 54, 596–600.
  10. Li, K.; Chang, L.; Hu, B. A variational Bayesian-based unscented Kalman filter with both adaptivity and robustness. IEEE Sens. J. 2016, 16, 6966–6976.
  11. Yun, P.; Wu, P.; He, S. An IMM-VB Algorithm for Hypersonic Vehicle Tracking with Heavy Tailed Measurement Noise. In Proceedings of the 2018 International Conference on Control, Automation and Information Sciences (ICCAIS), Hangzhou, China, 24–27 October 2018; pp. 169–174.
  12. Zhang, C.; Guo, C.; Zhang, D. Data fusion based on adaptive interacting multiple model for GPS/INS integrated navigation system. Appl. Sci. 2018, 8, 1682.
  13. Simon, D.; Sherief, H.E. Navigation Satellite Selection using Neural Networks. Neurocomputing 1995, 7, 247–258.
  14. Ham, D.; Park, H.; Hwang, S.; Kim, K. Neuromorphic electronics based on copying and pasting the brain. Nat. Electron. 2021, 4, 635–644.
  15. Deng, W.; Liu, H.; Xu, J.; Zhao, H.; Song, Y. An improved quantum-inspired differential evolution algorithm for deep belief network. IEEE Trans. Instrum. Meas. 2020, 69, 7319–7327.
  16. Ren, Z.; Zhen, X.; Jiang, Z.; Gao, Z.; Li, Y.; Shi, W. Underactuated control and analysis of single blade installation using a jackup installation vessel and active tugger line force control. Mar. Struct. 2023, 88, 103338.
  17. Zhao, H.; Yang, X.; Chen, B.; Chen, H.; Deng, W. Bearing fault diagnosis using transfer learning and optimized deep belief network. Meas. Sci. Technol. 2022, 33, 065009.
  18. Jwo, D.J.; Chin, K.P. Applying Back-propagation Neural Networks to GDOP Approximation. J. Navig. 2002, 54, 97–108.
  19. Jwo, D.J.; Lai, C.C. Neural Network-Based Geometry, Classification for Navigation Satellite Selection. J. Navig. 2003, 56, 291–304.
  20. Jwo, D.J.; Lai, C.C. Neural Network-based GPS GDOP Approximation and Classification. GPS Solut. 2007, 11, 51–60.
  21. Mosavi, M.R.; Sorkhi, M. An Efficient Method for Optimum Selection of GPS Satellites Set using Recurrent Neural Network. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 245–249.
  22. Mosavi, M.R.; Azami, H. Applying Neural Network Ensembles for Clustering of GPS Satellites. Int. J. Geoinformatics 2011, 7, 7–14.
  23. Tafazoli, S.; Mosavi, M.R. Performance Improvement of GPS GDOP Approximation Using Recurrent Wavelet Neural Network. J. Geogr. Inf. Syst. 2011, 3, 318–322.
  24. Azami, H.; Mosavi, M.R.; Sanei, S. Classification of GPS Satellites Using Improved Back Propagation Training Algorithms. Wirel. Pers. Commun. 2013, 71, 789–803.
  25. Zarei, N. Artificial Intelligence Approaches for GPS GDOP Classification. Int. J. Comput. Appl. 2014, 96, 16–21.
  26. Azarbad, M.; Azami, H.; Sanei, S.; Ebrahimzadeh, A. New Neural Network-based Approaches for GPS GDOP Classification based on Adaptive Neuro-Fuzzy Inference System, Radial Basis Function, and Improved Bee Algorithm. Appl. Soft Comput. 2014, 25, 285–292.
  27. Chansarkar, M. Neural Networks in GPS Navigation. GPS Solut. 2000, 4, 14–18.
  28. Mosavi, M.R. A Practical Approach for Accurate Positioning with L1 GPS Receivers using Neural Networks. Int. J. Intell. Fuzzy Syst. 2006, 17, 159–171.
  29. Mosavi, M.R. Precise Real-Time Positioning with a Low Cost GPS Engine using Neural Networks. Int. J. Surv. Rev. 2007, 39, 316–327.
  30. Jwo, D.J.; Pai, C.-F. Incorporation of Neural Network State Estimator for GPS Attitude Determination. J. Navig. 2004, 57, 117–134.
  31. Jwo, D.J. GPS Navigation Solutions by Analogue Neural Network Least-Squares Processors. J. Navig. 2005, 58, 105–118.
  32. Julier, S.J.; Uhlmann, J.K.; Durrant-whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 5, 477–482.
  33. Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269.
  34. Arulampalam, M.S.; Maksell, S.; Gordon, N.; Clapp, T. A tutorial of particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188.
  35. Wan, E.A.; Van der Merwe, R. The Unscented Kalman Filter for Nonlinear Estimation. In Proceedings of the IEEE Symposium 2000 (AS-SPCC), Lake Louise, AB, Canada, 1–4 October 2000; pp. 153–158.
  36. Simon, D. Optimal State Estimation: Kalman, H∞, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006.
  37. Benkouider, S.; Lagraa, N.; Yagoubi, M.B.; Lakas, A. Reducing Complexity of GPS/INS Integration Scheme through Neural Networks. In Proceedings of the 2013 9th International Wireless Communications and Mobile Computing Conference (IWCMC), Sardinia, Italy, 1–5 July 2013; pp. 53–58.
  38. Wang, C.-Z.; Kong, L.-W.; Jiang, J.; Lai, Y.-C. Machine learning-based approach to GPS anti jamming. GPS Solut. 2021, 25, 115.
  39. Krzykowska, K.; Krzykowski, M. Forecasting Parameters of Satellite Navigation Signal through Artificial Neural Networks for the Purpose of Civil Aviation. Int. J. Aerosp. Eng. 2019, 2019, 7632958.
  40. Khan, I.U.; Ali, T.; Farid, Z.; Scavino, E.; Rahman, M.A.A.; Hamdi, M.; Qiao, G. An improved hybrid indoor positioning system based on surface tessellation artificial neural network. Meas. Control 2020, 53, 1968–1977.
  41. Kaygisiz, B.H.; Erkmen, I.; Erkmen, A.M. GPS/INS Enhancement for Land Navigation using Neural Network. J. Navig. 2004, 57, 297–310.
  42. Gingras, D. An Overview of Positioning and Data Fusion Techniques Applied to Land Vehicle Navigation Systems. In Automotive Informatics and Communicative Systems: Principles in Vehicular Networks and Data Exchange; IGI Global: Hershey, PA, USA, 2009; pp. 219–246.
  43. Aftatah, M.; Lahrech, A.; Abdelouahed, A.; Soulhi, A. GPS/INS/Odometer Data Fusion for Land Vehicle Localization in GPS Denied Environment. Mod. Appl. Sci. 2017, 11, 62.
  44. Du, S.; Zhang, S.; Gan, X. A hybrid fusion strategy for the land vehicle navigation using MEMS INS, odometer and GNSS. IEEE Access 2020, 8, 152512–152522.
  45. Chen, Y.; Zhou, P.; Sheng, M.; Liu, K. Overview of the Integrated Navigation System Research Status and its Development Integrated with 5G Communication. In Proceedings of the 7th International Conference on Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS 2022), Wuhan, China, 18–19 March 2022; Volume XLVI-3/W1-2022, pp. 29–35.
  46. Wei, W.; Tan, L.; Jin, G.; Lu, L.; Sun, C. A Survey of UAV Visual Navigation Based on Monocular SLAM. In Proceedings of the 2018 IEEE 4th Information Technology and Mechatronics Engineering Conference (ITOEC 2018), Chongqing, China, 14–16 December 2018; pp. 1849–1853.
  47. Li, P.; Zhang, X.; Xu, X. Novel Terrain Integrated Navigation System Using Neural Network Aided Kalman Filter. In Proceedings of the Sixth International Conference on Natural Computation (ICNC), Yantai, China, 10–12 August 2010; pp. 445–448.
  48. Bao, J.; Li, D.; Qiao, X.; Rauschenbach, T. Integrated navigation for autonomous underwater vehicles in aquaculture: A review. Inf. Process. Agric. 2020, 7, 139–151.
  49. Zhang, X.; Mu, X.; Liu, H.; He, B.; Yan, T. Application of Modified EKF Based on Intelligent Data Fusion in AUV Navigation; IEEE Underwater Technology (UT): Kaohsiung, Taiwan, 2019.
  50. Shafie, A.E.; Noureldin, A. Sensor Integration for Satellite-Based Sensor Navigation Utilizing Neural Networks. IEEE Trans. Neural Netw. 2007, 18, 589–594.
  51. Noureldin, A.; Shafie, A.E.; Bayoumi, M. GPS/INS Integration Utilizing Dynamic Neural Networks for Vehicular Navigation. Inf. Fusion 2011, 12, 48–57.
  52. Chen, L.; Fang, J. A hybrid prediction method for bridging GPS outages in high-precision POS application. IEEE Trans. Instrum. Meas. 2014, 63, 1656–1665.
  53. Chiang, K.W.; Huang, Y.W. An intelligent navigator for seamless INS/GPS integrated land vehicle navigation applications. Appl. Soft Comput. 2008, 8, 722–733.
  54. Chiang, K.W.; Noureldin, A.; El-Sheimy, N. Constructive neural-networks-based MEMS/GPS integration scheme. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 582–594.
  55. Jwo, D.J.; Chang, C.-S.; Lin, C.-H. Neural Network Aided Adaptive Kalman Filtering for GPS Applications. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, The Hague, The Netherlands, 10–13 October 2004; pp. 3686–3691.
  56. Jwo, D.J.; Huang, H.-C. Neural Network Aided Adaptive Extended Kalman Filtering Approach for DGPS Positioning. J. Navig. 2004, 57, 449–463.
  57. Jwo, D.J.; Chen, J.J. GPS/INS navigation filter designs using neural network with optimization techniques. In Proceedings of the Advances in Natural Computation: Second International Conference, ICNC 2006, Xi’an, China, 24–28 September 2006; pp. 461–470.
  58. Wang, J.J.; Ding, W.; Wang, J. Improving Adaptive Kalman Filter in GPS/SDINS Integration with Neural Network. In Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 571–578.
  59. Wang, J.J.; Wang, J.; Sinclair, D.; Watts, L. Neural Network Aided Kalman Filtering for Integrated GPS/INS Geo-Referencing Platform. In Proceedings of the 5th International Symposium on Mobile Mapping Technology, Padua, Italy, 29–31 May 2007; pp. 1–6.
  60. Ibrahim, F.; Tascillo, A.; Holou, N.A. DGPS/INS Integration Using Neural Network Methodology. In Proceedings of the 12th IEEE Internationals Conference on Tools with Artificial Intelligence, ICTAI 2000, Vancouver, BC, Canada, 15 November 2000; pp. 114–121.
  61. Pukhov, E.; Cohen, H.I. Novel Approach to Improve Performance of Inertial Navigation System Via Neural Network. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 746–756.
  62. Brossard, M.; Barrau, A.; Bonnabel, S. AI-IMU Dead-reckoning. IEEE Trans. Intell. Veh. 2020, 5, 585–595.
  63. Liu, Y.; Luo, Q.; Liang, W.; Zhou, Y. GPS/INS Integrated Navigation with LSTM Neural Network. In Proceedings of the 2021 4th International Conference on Intelligent Autonomous Systems (ICoIAS), Wuhan, China, 14–16 May 2021; pp. 345–350.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Computer Science, Artificial Intelligence
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Dah-Jing Jwo
,
Amita Biswal
,
Ilayat Ali Mir
View Times: 685
Entry Collection: Remote Sensing Data Fusion
Revisions: 2 times (View History)
Update Date: 21 Apr 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback