Encyclopedia
Please note this is a comparison between Version 1 by Amita Biswal and Version 2 by Peter Tang.
Several machine learning (ML) methodologies are gaining popularity as artificial intelligence (AI) becomes increasingly prevalent. An artificial neural network (ANN) may be used as a “black-box” modeling strategy without the need for a detailed system physical model. It is more reasonable to solely use the input and output data to explain the system’s actions. ANNs have been extensively researched, as artificial intelligence has progressed to enhance navigation performance. In some circumstances, the Global Navigation Satellite System (GNSS) can offer consistent and dependable navigational options. A key advancement in contemporary navigation is the fusion of the GNSS and inertial navigation system (INS). Numerous strategies have been put out to increase the accuracy for jamming, GNSS-prohibited environments, the integration of GNSS/INS or other technologies by means of a Kalman filter as well as to solve the signal blockage issue in metropolitan areas. A neural-network-based fusion approach is suggested to address GNSS outages.
- GNSS
- inertial navigation
- artificial neural networks
- Kalman filter
1. Introduction
Dead reckoning and position fixing are the two basic strategies of positioning classifications used in navigation. The inertial navigation system (INS) and the Global Positioning System (GPS), which is comprised of the Global Navigation Satellite System (GNSS), are the two most prevalent examples, respectively [1][2][1,2]. Over the past few decades, GPS and INS have been effectively integrated for real-world applications. Each does, however, have unique traits and limitations. A thorough examination of the existing literature on navigation systems is necessary because a significant amount of research has been conducted in the field of positioning systems. For instance, the GNSS navigation system offers accurate and semi-permanent position and speed data. Reduced accessibility and instability come from the threat to signal shadowing and multipath effects. A self-contained system that measures a vehicle’s linear and angular acceleration could serve as the guidance system. The drawback of INS is its drift error, which will continue to grow over time. As a result, the shortcomings of each technique are solved by the combination of the two systems.
GNSS is the most widely used approach in the disciplines of aviation, automatic craft technique and landing, land vehicle navigation and tracking, marine applications, and evaluation, among others. It is a navigational system that uses satellites to provide three-dimensional position and speed information. Despite being widely used, GNSS still must be able to provide consistent and accurate navigational solutions in some situations. The GNSS outage may occur whenever the vehicle travels through urban areas, tunnels, or enclosed spaces because the satellite signal is blocked. INS’s navigational accuracy decreases with time unless it is intermittently tagged by various sensors. Because of the inherent complementary operational characteristics of GNSS and INS systems, the combination of each method has provided the best possible resolution throughout the past decades. Furthermore, the combination of INS and an external navigation system, such as GNSS, could be a state-of-art technique for several application eventualities. In the integrated GNSS/INS navigation system, the GNSS resolution incorporates a consistent and semi-permanent stable accuracy that is employed to update the INS resolution. Furthermore, the INS settlement is subjected to bridging GNSS blackouts once a satellite signal is blocked. The GNSS/INS navigation system is becoming more and more fashionable because it offers consistent, accurate, and reliable navigation resolution. As long as the GNSS signals are usable, this navigation system calculates, estimates, and models the INS inaccuracy. As a result, it simultaneously provides accurate and fast navigation parameters.
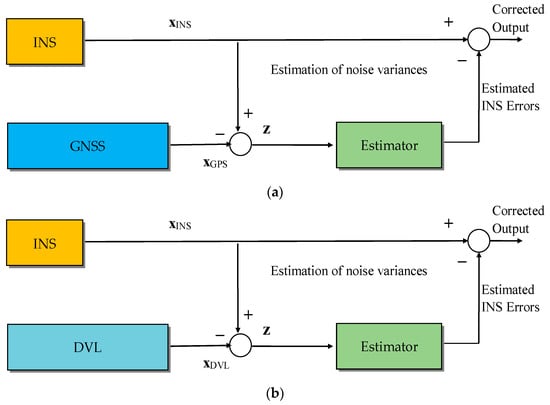
For autonomous underwater vehicle (AUV) navigation, a navigation-grade INS in conjunction with a Doppler velocity log (DVL) is frequently employed. The precision of integrated navigation depends critically on whether or not the DVL can generate constant rate readings. Given the actual underwater working environment of AUVs, the DVL’s calculated value is subjected to outliers and even disruption. The well-trained network can forecast the velocity after the DVL fails, which can then be used for navigation in the future. Its benefit is that it enables time-varying noise adaptation and lessens outlier interference with the integrated navigation system. Figure 1 shows the different architectures for integrated navigation systems. The different methods of filtering approaches are the Kalman filter (KF), the extended Kalman filter (EKF), the unscented Kalman filter (UKF), the cubature Kalman filter (CKF), and the sequential Monte Carlo (SMC) approaches, among which the particle filter (PF) is the most well-known. The most fundamental and extensively used data fusion procedures in integrated navigation systems are KFs and their derivatives. The KF is an ideal estimate algorithm for Gaussian and linear approximations with the requirements of precise the system model and previous updated noise. Regrettably, the precision and robustness of conventional KFs are decreased by mistakes when modeling systems and the uncertainty of operating situations.
Figure 1.
Example of integrated navigation systems: (
a
) GNSS/INS for air and land applications; (
b
) INS/DVL for underwater applications.
An adaptive Kalman filter (AKF) [3][4][5][6][7][8][9][10][11][12][3,4,5,6,7,8,9,10,11,12] can be used as the noise-adaptive filter for adjusting the noisy covariance matrices to satisfy the filter optimality criteria. The correlation- and covariance-matching techniques have made use of technological animations to predict the noise covariance. Making the inherent value of the covariance of the retained complies with its theoretical result is the fundamental tenet of the covariance-matching technique. To correct noisy estimates, the innovation-based estimation (IAE) [3][4][5][6][7][8][3,4,5,6,7,8] method has become quite effective. It combines fuzzy logic methodologies with membership functions created using the heuristic method. In contrast to sampling, the variational Bayesian (VB) [9][10][11][12][9,10,11,12] has been developed for a variety of models to achieve approximate posterior inference at a minimal computational cost.
Artificial neural networks (ANN) or neural networks (NN) [13] are built of straightforward components that work together. The quality and productivity of the NN enable it to estimate undetermined nonlinear input–output mapping. Due to the absence of estimators in the system model—i.e., it lacks the need for a mathematical model—NNs have been used to solve a wide range of issues. The NN has two unique characteristics: it can be generalized due to its nonlinearity, and it can be implemented in multi-input and multi-output arbitrary nonlinear mapping by altering the link weights. As a result, this makes the system’s real-time approximation more challenging. The deterministic methodology is a recognized and efficient technique for latency mitigation. Additionally, the NN’s widespread approximation property allows it to be used for the characterization of nonlinear systems. Like in nature, interconnections amongst constituents play a major role in networks’ function. The biological nervous system inspires these elements. By contrasting the outcome of an NN with the perceived target, an NN learns to fit the relationship. By changing the values of the connections (weights) between elements, an NN can be trained to carry out a certain task so that a different input leads to a particular target. Until the output of the network matches the target, the NN is changed based on a comparison between the output and the target. After that, it modifies the weight value until the error reaches the required accuracy.
The INS system can deliver precise navigational data quickly, and its accuracy will rapidly deteriorate over time. Therefore, it has been suggested that GNSS and INS be integrated to address their limitations. However, during GNSS process failures, the system will switch to a completely INS system navigation mode, and the effectiveness will be massively degraded. The features of the GNSS/INS integrated navigation system components in the situation of GNSS failures have been improved by using a variety of methods that have been presented to identify the GNSS signal outages. The addition of additional sensors to supply fresh reference data from other sources for the integrated navigation system, for which the odometer and maps are one remedy during GNSS failure. However, the price and size of the navigation system will rise correspondingly. Cornering, GNSS denial situations, the integration of employing KF, and several methods are also utilized to increase the perfection of GPS locations and to get over signal blockage in metropolitan areas. Neural networks are a popular choice for representing dynamic and complex processes since they have the potential to learn. To remove their influence from the estimation process, errors and noise are typically estimated using neural networks. In the event of a GPS signal failure, these strategies significantly improve GPS/INS integration. However, the localization systems are significantly impacted by severe multipath settings or prolonged non-line-of-sight (NLOS), and no improvement from its prior methodologies is realized. Although a few interesting implementations in complex visual detection and reduced AI computation have resulted from this research, a relatively intelligent mechanism has yet to be produced [14][15][16][17][14,15,16,17].
2. The Use of Neural Networks in the Global Positioning System
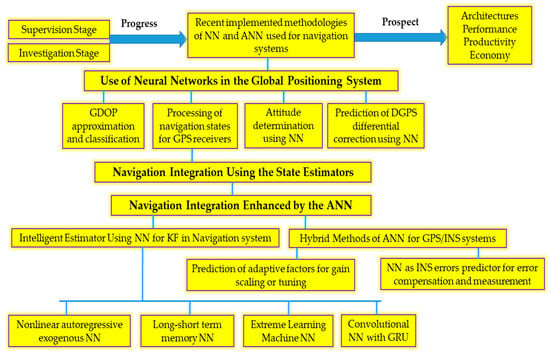
Machine learning (ML) enables artificial intelligence (AI) systems to learn from data. It is effective for nonlinear systems and is not reliant on the system’s mathematical model. The application overview of the ANN and NN in the navigation system has been subbmerized in Figure 2. The geometric dilution of precision (GDOP) approximation [13][14][15][16][17][18][19][20][21][22][23][24][25][26][13,14,15,16,17,18,19,20,21,22,23,24,25,26], GPS navigation processing [27][28][29][27,28,29], attitude determination using NNs [30], and prediction of differential DGPS correction message using NNs [31] are reviewed. It is a feature whose approaches—based on AI—may not ask for numerical methods of the system dynamics and observations, which is a key distinction between them and other forms of estimating methods. 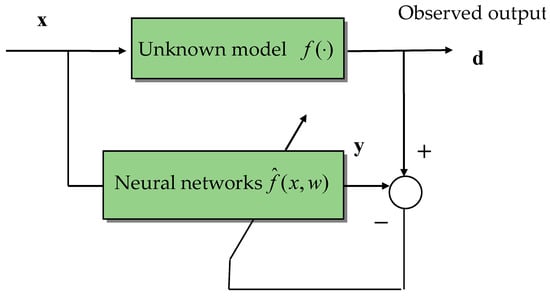Figure 3 provides the overview of the NN training principle to approximate an unknown system model.
Figure 2.
The outflow of ANN and NN in navigation system.
Figure 3.
Overview of NN training principle.
3. Navigation Integration Using the State Estimators
Navigation integration is typically carried out through the KF to estimate the system state variables and suppress the measurement noise. Different Bayesian filtering techniques, including the KF, EKF, UKF [32][33][34][34,35,36], CKF [35][37], and particle filter (PF) [34][36][36,38] techniques, are typically used in the data fusion algorithms of the INS/GPS-integrated navigation system to calibrate the navigation estimation error. In linear systems with white Gaussian noise, it is generally accepted that the KF makes use of the minimum mean square error (MMSE) as the best criterion. On the other hand, if the system’s dynamic and measurement models are accurately described, the KF leverages measurement updates to correct system state mistakes and restrict navigation solution errors. The noise statistics of the process provide the best estimates of a system’s states. Without measurement updates, the KF’s forecast diverges, and when GPS signals are not available, a combined GPS/INS navigation system’s performance may suffer quickly.
For nonlinear models, EKF employs an approximation technique to linearize the nonlinear system model. The state and observation equations are linearized using EKF using first-order Taylor reduction to enhance the conventional KF [36][38]. By constructing the linear differential equation, the nonlinear system is roughly approximated. It is straightforward to calculate the assessment in the Bayesian recursive formula since KF and EKF both turn the problem into a linear Gaussian model. The UKF is based on a method for mean and covariance propagation through a nonlinear mapping built using the unscented transform (UT) approach. The state vector is discretized as a minimum collection of sample points (sigma points), which approximates the second-order precision posterior mean and covariance of the random variable with a Gaussian distribution. To approximate the probability density distribution of a nonlinear function, UKF uses a set of predetermined samples. The EKF’s linearization method can only produce first-order accuracy. When the computing complexity is the same, the UKF performs better than the EKF. The aforementioned filtering algorithms for the high-dimensional process model are susceptible to a non-positive definite covariance matrix. Non-Gaussian noises, on the other hand, are commonly present in many real-world contexts and seriously degrade their functionality.
The KF, EKF, and UKF techniques have many significant flaws that prevent their application. They are unable to deal with the following two issues in particular: modeling non-Gaussian processes and observation noises and well as unidentified noise covariance matrices are the first two sources of noise. When the methods are coupled with colored noise, as is the case in several scenarios for practical implementation, the EKF cannot perform satisfactorily since the estimation outcomes are vulnerable to strong outliers and non-Gaussian noise. The CKF approximates the state mean and covariance of a nonlinear system with extra Gaussian noise using a collection of volume points based on the third-order spherical radial volume criteria. Theoretically, CKF is the approximation technique that comes closest to Bayesian filtering, and it is an effective tool for dealing with nonlinear system state estimates. For each integral point, CKF has the same weight, which is positive. Compared to UKF, CKF’s numerical stability is developing more rapidly. The resilience is decreased, and even the filter fails despite being impacted by the process model’s instability and the measured noise statics’ variability. In recent years, numerous academics have suggested enhanced CKF algorithms to address the aforementioned issues. The PF is computationally expensive for an online implementation even if it can handle the non-Gaussian, nonlinear system effectively.
The implementation of the Kalman family of filters needs a precise and logically valid statistical understanding of the process noise and measurement noise. Inadequate understanding of the noise statistics may cause filter divergence and substantially impair KF performance. Relativistic issues will arise if a filter’s theoretical operation and its real behavior do not correlate. The assumptions on the statistical database of disruption are violated in various of scenarios in which there are instabilities in the process model and noise characterization, because in many real-world scenarios, the availability of a well-defined model is unattainable because some observations are ignored in the modeling step and one approach for taking them into consideration is to consider an equivalent model influenced by uncertainty. Moreover, there are model assumptions in actual navigational applications that the continuous state-space model is unable to capture. Since the actual vehicle motions are the result of non-linear processes, the linear model contains modeling mistakes. It is necessary to predetermine the system model, the system’s beginning conditions, and the noise properties. It frequently happens that little prior knowledge of the operation is accessible.
The availability of a well-defined model is inappropriate in particular scenarios in which there are many uncertainties in the proposed system and noise interpretation. Predictions based on disruption statistics are violated due to a number of realistic applications, and some conditions are ignored in the modeling step. It is reasonable to suppose that an adaptive process will dynamically identify the system model uncertainties and modeling errors. Innovation-based adaptive estimating (IAE) and multiple-model-based adaptive estimation (MMAE), such as the interacting multiple models (IMM) [5][6][7][8][5,6,7,8] algorithm, are the two main approaches to AKFs that have been developed. The IMM algorithm has a configuration in which many model-matched state estimation filters operate in parallel and interact (exchange information) at each sampling period. By modifying the probabilities of each approach, which are utilized as weightings in the aggregate global state estimation, the algorithm performs soft switching between the various modes. The mode-conditioned forecast’s covariances as well as the variations between these estimates are taken into account in the covariance matrix linked to this combined estimate.
The noise data from the measurement sequence during the filtering process can be removed, and an IAE technique has been devised to estimate the process noise covariance Qk and/or measurement noise covariance Rk. A bank of KFs with various parameters operates concurrently in an MMAE approach, and the weights of every sub-filter are aggressively changed in response to fresh assessments. The sub-filter with well-known parameters wins after a thorough study. The MMAE method, however, requires more resources and may not completely account for the true system model. Another drawback is that the parameter estimation method for both IAE and MMAE systems requires a sliding window over the measurement sequence, which causes inaccuracy and delay. Consequently, adaptive filters introduce more sophisticated components in integrated navigation systems. The selection in integrated navigation systems’ adaptive filters frequently uses fuzzy logic techniques. Such a selection selects the best sensors or dynamically modifies the noise covariance matrix. Target tracking may be manipulated well using interactive multiple models. Then the more accurate noise covariance matrix was estimated using the IMM technique. When used in an underwater environment, the IMM-adaptive robust cubature Kalman filter technique may successfully address the issues of measurement noise and typical statistical inaccuracy.
The technique makes use of VB learning to give a robust tracking capacity for time-varying noise covariance as well as an approximation of the noise strength. The VB approach is an inferential technique that approximates the real posterior distribution of hidden variables using a straightforward distribution, typically presuming that the disguised variables are unrelated to one another. In contrast to sampling methods, the VB has been created for a several models to perform preliminary posterior inference with a minimal computing cost. The typical filters for navigational state estimation and their improved algorithms are summarized in Table 1.
Table 1.
The navigation filters and their improved algorithms.
|
Navigation Fusion Algorithm |
Features |
|---|---|
|
Linear Kalman filter algorithm |
|
|
Nonlinear filter algorithms, including the EKF, UKF, and CKF |
|
|
Sequential Monte Carlo (SMC) approaches |
|
|
Adaptive filter algorithms |
|
|
Neural-network-assisted filtering algorithm |
|
|
Deep learning improvement algorithm |
|
4. Navigation Integration Enhanced by the ANN
In complicated and hidden situations, inertial navigation is an essential component of vehicle navigation systems. There has been widespread use of the GNSS/INS combined system for land and air applications and DVL/INS for underwater applications. In general, the integration task makes considerable use of the EKF to obtain an accurate and consistent estimated position. In contrast, the lack of readings from the GNSS/INS EKF in the event of a GNSS signals failure, signal blockage, or jamming causes the navigation system’s accuracy to rapidly decline. To increase the integrated navigation system’s accuracy while GNSS failures, several fusion techniques have been investigated [37][38][39][40][41][42][43][44][45][46][47][48][49][50][51][52][53][54][55][56][57][58][59][60][61][62][39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]. Adding additional sensors to compensate for the lost GPS information and improve navigation accuracy is possible but comes at the cost of increased system complexity. Machine learning algorithms have become famous for mimicking the INS’s error propagation property and establishing a connection between updated vehicle dynamics and INS errors by using available GNSS signals to train the machine learning (ML) model. For the corrected INS mistakes caused by a lack of accurate measurements, such as GNSS failures, researchers have developed an error forecasting and compensating system based on artificial intelligence for GNSS/INS integration. The neural network has received considerable attention because of its useful nonlinear function estimation property and learning capacity. It has been frequently applied to integrated navigation error correction during GNSS failures. When GPS is unavailable, the neural network is used as an alternate integration mechanism to deliver superior navigational options.
