Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Ngo Anh Tuan
 -- 3144 2023-03-14 09:39:34 |
2 Reference format revised.
Lindsay Dong
Meta information modification 3144 2023-03-15 09:54:29 | |
3 Main text format revised.
Lindsay Dong
Meta information modification 3144 2023-03-15 09:55:32 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Ngo, T.A.; Nguyen, T.; Thang, T.C. Quantum Generative Adversarial Networks. Encyclopedia. Available online: https://encyclopedia.pub/entry/42160 (accessed on 08 July 2024).
Ngo TA, Nguyen T, Thang TC. Quantum Generative Adversarial Networks. Encyclopedia. Available at: https://encyclopedia.pub/entry/42160. Accessed July 08, 2024.
Ngo, Tuan Anh, Tuyen Nguyen, Truong Cong Thang. "Quantum Generative Adversarial Networks" Encyclopedia, https://encyclopedia.pub/entry/42160 (accessed July 08, 2024).
Ngo, T.A., Nguyen, T., & Thang, T.C. (2023, March 14). Quantum Generative Adversarial Networks. In Encyclopedia. https://encyclopedia.pub/entry/42160
Ngo, Tuan Anh, et al. "Quantum Generative Adversarial Networks." Encyclopedia. Web. 14 March, 2023.
Quantum Generative Adversarial Networks
Edit
This entry is adapted from the peer-reviewed paper 10.3390/electronics12040856

Quantum mechanics studies nature and its behavior at the scale of atoms and subatomic particles. By applying quantum mechanics, a lot of problems can be solved in a more convenient way thanks to its special quantum properties, such as superposition and entanglement. In the current noisy intermediate-scale quantum era, quantum mechanics finds its use in various fields of life. Following this trend, researchers seek to augment machine learning in a quantum way. The generative adversarial network (GAN), an important machine learning invention that excellently solves generative tasks, has also been extended with quantum versions. Since the first publication of a quantum GAN (QuGAN) in 2018, many QuGAN proposals have been suggested. A QuGAN may have a fully quantum or a hybrid quantum–classical architecture, which may need additional data processing in the quantum–classical interface. Similarly to classical GANs, QuGANs are trained using a loss function in the form of max likelihood, Wasserstein distance, or total variation. The gradients of the loss function can be calculated by applying the parameter-shift method or a linear combination of unitaries in order to update the parameters of the networks. 

quantum machine learning generative adversarial networks quantum GAN hybrid quantum–classical system

1. Introduction

Machine learning (ML) [1] has been a hot topic for researchers for a long time. Early ML works, such as artificial neurons [2], the perceptron [3], support-vector machines [4], recurrent neural networks [5], and convolutional neural networks [6] were developed and applied in all parts of the human society, such as education [7][8][9], agriculture [10][11], finance [12][13], and health care [14][15][16]. One of the important goals of ML is generative tasks, where ML programs have to generate new data based on some existing data. Through excellent empirical results, generative adversarial networks (GANs) [17] have been found a brilliant candidate to fulfill this task. In a GAN, a generator and a discriminator play an adversarial game against each other. The generator tries to generate new data that resemble some real data in order to fool the discriminator, while the discriminator aims to distinguish the generated data from the real data.
There has been a sharp increase in the number of GAN variants in the past few years [18]. Since their invention, GANs have been widely used in both semi-supervised and unsupervised learning. However, this type of network bears some issues, such as training instability, mode collapse, and non-convergence [19]. Researchers have been trying their best to improve the efficiencies of the networks, to overcome their shortcomings, and to expand their applications.
In recent years, quantum computing [20] has emerged and drawn a lot of attention from researchers. This new paradigm of computing can accomplish difficult tasks that traditional computing cannot solve. With the development of near-term quantum devices, quantum computing can make use of special properties, including superposition and entanglement, to even perform those tasks exponentially faster [21]. For example, quantum computers can search an unsorted dataset of N entries in time O(N−−√), whereas it takes time O(N)for classical computers to do the same task [22]. Thus, researchers seek to combine quantum computing with machine learning to develop quantum ML. The quantum counterparts of ML models, such as quantum reinforcement learning [23], quantum support vector machines [24], and quantum variational autoencoders [25], were in turn invented.
The generative tasks of ML are getting more and more complicated. Therefore, quantum GANs (QuGANs) were also developed. Basically, QuGANs may have different architectures with various components, in either classical or quantum forms. Instead of neural networks, the quantum parts of a QuGAN consist of variational quantum circuits which also depend on a set of parameters [26]. A certain loss or cost function can be formed, and its gradients with respect to the parameters are calculated for updating the parameters themselves. When an optimal status is reached, the network is able to generate a specific type of data that mimics the true data. The performance of the network can be evaluated using some metrics measuring the distances between these generated data and the real data [27][28][29][30].

1.1. Generative Adversarial Networks (GANs)

The idea of quantum GANs originates from classical GANs, which were first proposed by Goodfellow et al. [17]. A GAN aims at learning a target distribution, which can be a series of text or a collection of images or audio, and generating samples that have similar characteristics to the samples in the training distribution. The architecture of a typical GAN is depicted in Figure 1. A GAN typically consists of a generator G and a discriminator D. The generator and the discriminator are made from neural networks and are parameterized by θG and θD, respectively. The mission of G is to take noise vectors z from a noise source and produce data x′ that mimic the realistic data x as much as possible in order to fool D, which is supposed to distinguish whether a sample is taken from the real distribution or is generated by G. The distinguishing results y of D are then used to train both G and D iteratively; in other words, θG and θD are updated alternately until the network reaches its optimality. Ideally, this optimality, or Nash equilibrium [17], occurs when G can generate identical samples to those in the real distribution, and D is not able to determine which source the data belong to.
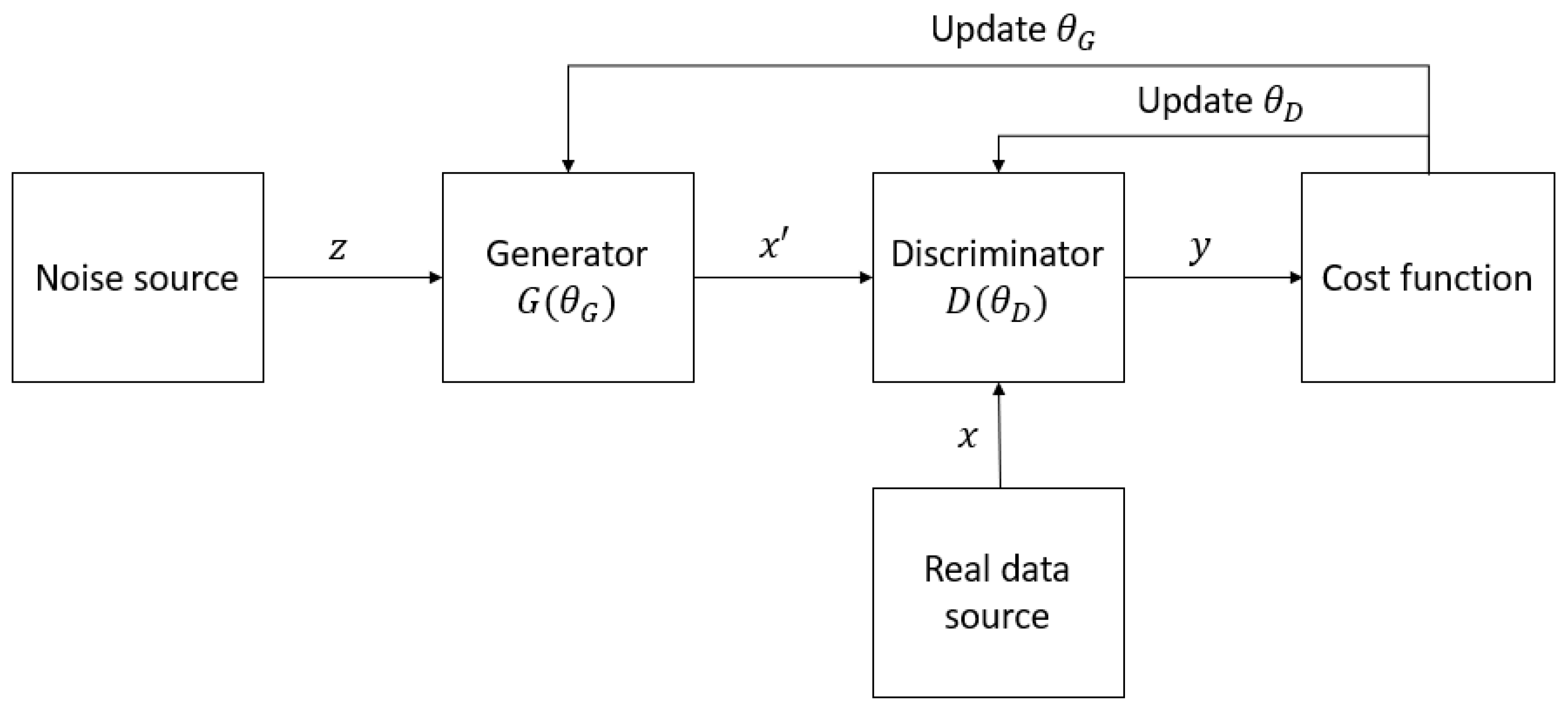
/media/item_content/202303/6411865c2148celectronics-12-00856-g001.png
Figure 1. The architecture of a typical GAN.
GANs are the most potential and popular types of networks used for generative tasks. They vary in terms of network architectures, optimization strategies, and purposes of use. Some notable variants of GANs include deep convolutional GAN [31], conditional GAN [32], Wasserstein GAN [33], boundary equilibrium GAN [34], Big GAN [35], Laplacian GAN [36], and information maximizing GAN [37]. Many GANs have been the basis of outstanding achievements. For example, StyleGAN3 [38] obtained a Fréchet inception distance of 3.07 on the FFHQ dataset, 4.40 on the AFHQv2 dataset, and 4.57 on the Beaches dataset. These networks have found their roles in image domains such as image synthesis [35][36][39][40], image inpainting [41][42], image blending [43][44], image superresolution [45][46], and image-to-image translation [47][48][49]; audio domains such as speech synthesis [50][51] and music composing [52][53]; and other fields such as autonomous driving [54], weather forecasting [55][56], and data augmentation [57][58]. GANs’ effectiveness and varied applications have been described in previous surveys of them [18][19][59].

1.2. Quantum–Classical Interface

As quantum machines only work with data stored in quantum states, classical data must be encoded into this form of data. Therefore, data encoding (or embedding) has also become an interesting field of research. There are various data encoding techniques that are used in quantum machine learning algorithms, but in quantum GANs, basis encoding, amplitude encoding, and angle encoding are the most popular [60]. Basis encoding is the simplest way to embed classical data into a quantum state. The inputs must be in binary form, and each of them corresponds with a computational basis of the qubit system. 

2. Structures of QuGAN

A QuGAN can be fully quantum, hybrid, or based on tensor networks. A diagram of quantum GAN categorization in terms of network architecture is sketched in Figure 2.
/media/item_content/202303/64118674cb8b3electronics-12-00856-g002.png
Figure 2. Quantum GAN structures.
In the fully quantum (or quantum-quantum) case, both the generator and the discriminator are quantum. Suppose the quantum generator produces fake data with a density matrix ρ, and the quantum discriminator must discriminate those fake data with true data described by a density matrix σ with a measurement operator D. The outcomes of D can be T (i.e., true, or the data are from the real data source), or F (i.e., false, or the data are generated by the generator). Since T and F are positive operators with a 1-norm less than or equal to 1, the set of them is convex, which means there must exist a minimum error measurement [26]. To reach this optimal measurement, the discriminator aims to maximize the probability that it correctly categorizes the data as real or fake by following the gradients of the probability with respect to its parameters to adjust its weights. After that, due to the fact that the set of ρ is convex, the generator also manages to adjust its own weights to maximize the probability that the discriminator fails to discriminate the data and produce an optimal density matrix ρ [26]. Similarly to the traditional GANs, after a number of iterations of adjusting the weights of both the generator and the discriminator, a quantum GAN can also approach the Nash equilibrium.
The mechanism is similar when only a part of the classical GAN is replaced by a quantum engine. However, not all hybrid structures are possible. In particular, the generator or the discriminator cannot be classical if the training dataset is generated by a quantum system, which has quantum supremacy. This means the classical generator can never generate the statistics of a dataset that are similar to those of a quantum data source [20]. Therefore, using the same strategy as in a fully quantum network, the quantum discriminator can always find a measurement to distinguish the true and the generated data. As a result, the probability that the discriminator makes wrong predictions will always be less than 12, and the Nash equilibrium will never happen [26]. On the contrary, in the case where the discriminator is classical, both the real data and the generated data which are fed into the discriminator are quantum.
When the target data are classical, either the generator or the discriminator can be classical. However, although possessing quantum supremacy, the quantum systems only act on data as quantum states and are unable to work with classical data directly. If the discriminator is quantum, both the training data and the fake data generated by the classical generator need to be encoded before being fed into the discriminator. On the contrary, if the generator is quantum, the generated data must be measured using some computational bases to produce classical generated samples [29][30].

3. Optimization of QuGAN

3.1. Loss Function

Just like the traditional GANs, the quantum version needs a function whose gradients it can trace along to adjust its weight so as to reach the Nash equilibrium. This function may involve different quantities. Some QuGANs make use of the quantum states of the generator and the discriminator, and some others involve a certain function estimated by the discriminator (in this case, it is called the critic). However, in most QuGANs, the discriminating results of the discriminator are used to determine the loss.

3.2. Gradient Computation

In quantum GANs, there are parametrized quantum circuits that build one or more parts of the network. That part can be the generator, or the discriminator, or both, or even the supplement components to assist the network in working more efficiently. These variational circuits consist of quantum gates or unitaries with tunable continuous parameters. Similarly to the classical counterparts, during the training process, the parameters are updated using a certain optimizing algorithm, such as gradient descent [61], Adam [62], or Adagrad [63]. All these approaches to adjusting the circuits to optimality require calculating the gradients of the cost function, including the partial derivatives with respect to the parameters of the circuits.

3.3. Optimization and Evaluation Strategies

A good strategy to optimize a quantum GAN is also an important research direction with a lot of interesting questions. For example, what is the order of training the generator and the discriminator that results in the most efficient optimization process? How much should one train the generator in comparison with the discriminator? How many steps of gradients should the network go through? How can the parameters of a network be initialized for the best performance? Additionally, how can one set or even adjust the learning rate to adapt to the change during the training process?
These problems matter when training a classical GAN, and they are certainly carried through to the quantum counterparts. With the exponential computational power and the more complicated algorithms, researchers should carefully set up the hyperparameters and determine the optimization strategy before conducting the training process.
The solutions to these issues, however, are rather indiscriminate, and due to the different structures of the networks and the elusiveness of quantum nature, there has been no rule to find out the best training strategy that can be applied for every quantum network in general, and for every quantum GAN in particular. To tackle the learning rate and the number of measurement shots, Huang et al. [29] simply performed a grid search to find the optimal hyperparameters. In the same manner, some researchers also set the hyperparameters and adjust them manually during the training process.

4. Quantum GAN Variants

4.1. Fully Quantum GANs

With fully quantum GANs, both generators and discriminators are constructed by quantum circuits, connected directly with the other, and they together apply to a system of qubits [27][28][29][64][65][66][67]. The target distributions can be quantum, which can be fed directly into the network, or classical, which must be encoded to some quantum states before being input into the network. The workflow of fully quantum GANs is depicted in Figure 3. The noise from latent space puts the quantum system in the state |z⟩. After being applied by the generator, the system is in state |ψ⟩. At this time, in the case the real data are used, the real quantum data source outputs state |x⟩ from the quantum system. The discriminator is then applied, and it changes the state to |y⟩. The states |y⟩ in the cases where the discriminator’s input is real or generated will then be used for the cost function and updating the parameters in the circuits.
/media/item_content/202303/641186aae1856electronics-12-00856-g004.png
Figure 3. The workflow of a fully quantum network in the cases where the target data are (a) quantum and (b) classical.

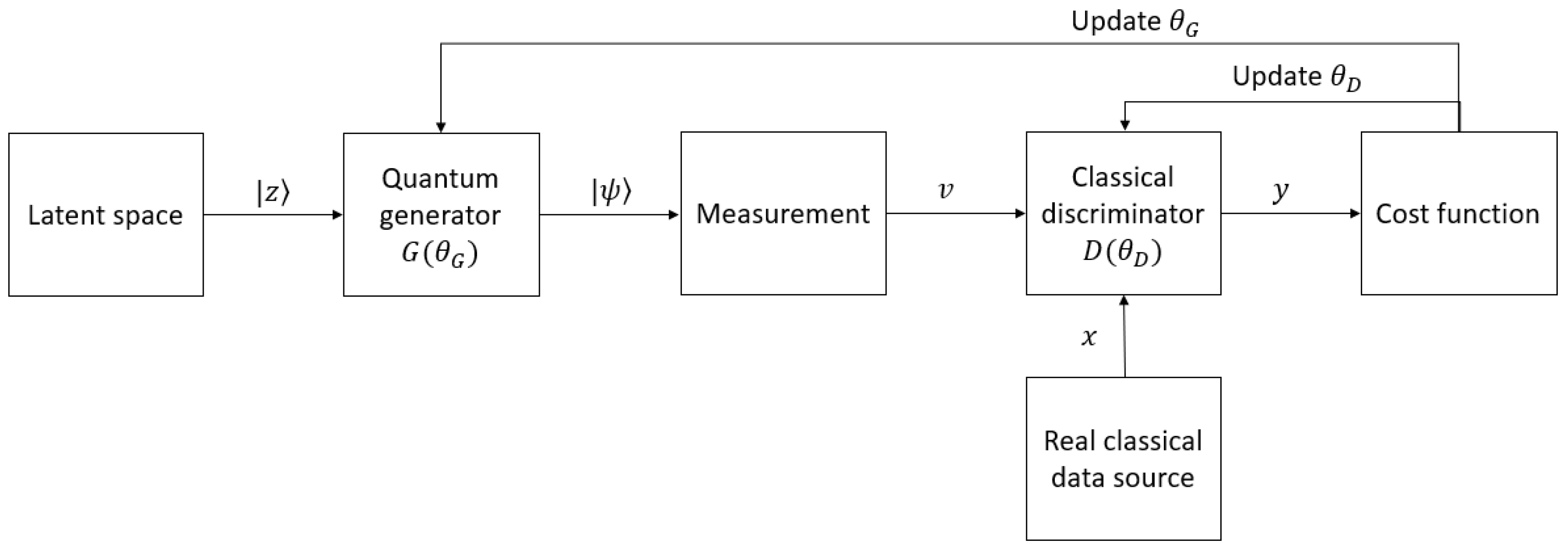
4.2. Hybrid Quantum–Classical GANs

A GAN could be a combination of a quantum and a classical module. In practice, a GAN with a classical generator and a quantum discriminator is never used. As stated in [26], if the target distribution is quantum, it is impossible for the classical generator to estimate and learn such a distribution. On the other hand, if the target data are classical, the generator is able to generate such data, but it can always be beaten by the quantum discriminator. In this way, the generator never reaches its convergence. Hence, a hybrid quantum–classical GAN has a quantum generator and a classical discriminator. The architecture of a hybrid quantum–classical GAN is illustrated in Figure 4. This variant of quantum GANs is used to generate classical data with extraordinary performance in comparison with traditional GANs. Since the discriminator is also classical, the target data do not need encoding. However, the states of the quantum system after the generator must be measured to be transformed into classical statistics, which are readable for the discriminator. The classical discriminator can be made of a fully connected neural network [29][30][68], with its output being 0 or 1, corresponding with real and fake examples, respectively.
/media/item_content/202303/641186cbcaadfelectronics-12-00856-g005.png
Figure 4. The workflow of a hybrid quantum–classical GAN.

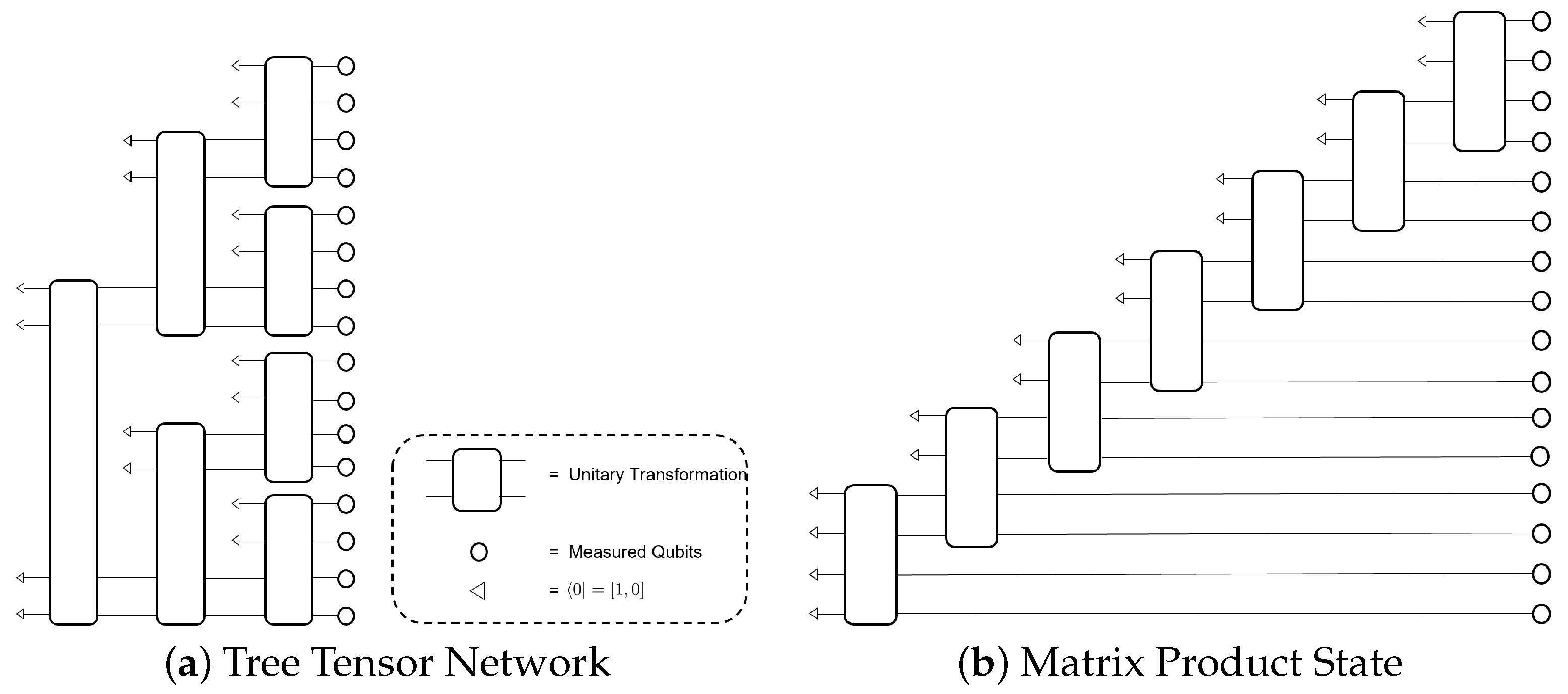
4.3. Tensor-Network-Based GANs

Tensor networks have recently been considered as a promising design for many generative learning tasks [69][70][71]. In [69], the authors considered two families of tensor networks, namely, matrix product states and tree tensor networks, to model a generative circuit. Their architectures are shown in Figure 5. Rather than applying the universal unitary operators of all qubits, tensor-network-based generative models consider some specific patterns by choosing a subset of qubits for each unitary transformation. The algorithms begin by initializing 2V qubits in one subset in a reference computational basis state ⟨0|⊗2V , then transform these qubits by a unitary operator. Another subset of 2V qubits is prepared in ⟨0|⊗2V, and half of them will be entangled with V qubits from the first subset by another unitary operator. The process continues until the total number of qubits reaches the desired output dimensionality. Figure 5 shows examples of the designs of generators based on tree tensor network (a) and matrix product states (b) with V = 2.
/media/item_content/202303/641186e382e50electronics-12-00856-g006.png
Figure 5. Generative models with tensor networks.

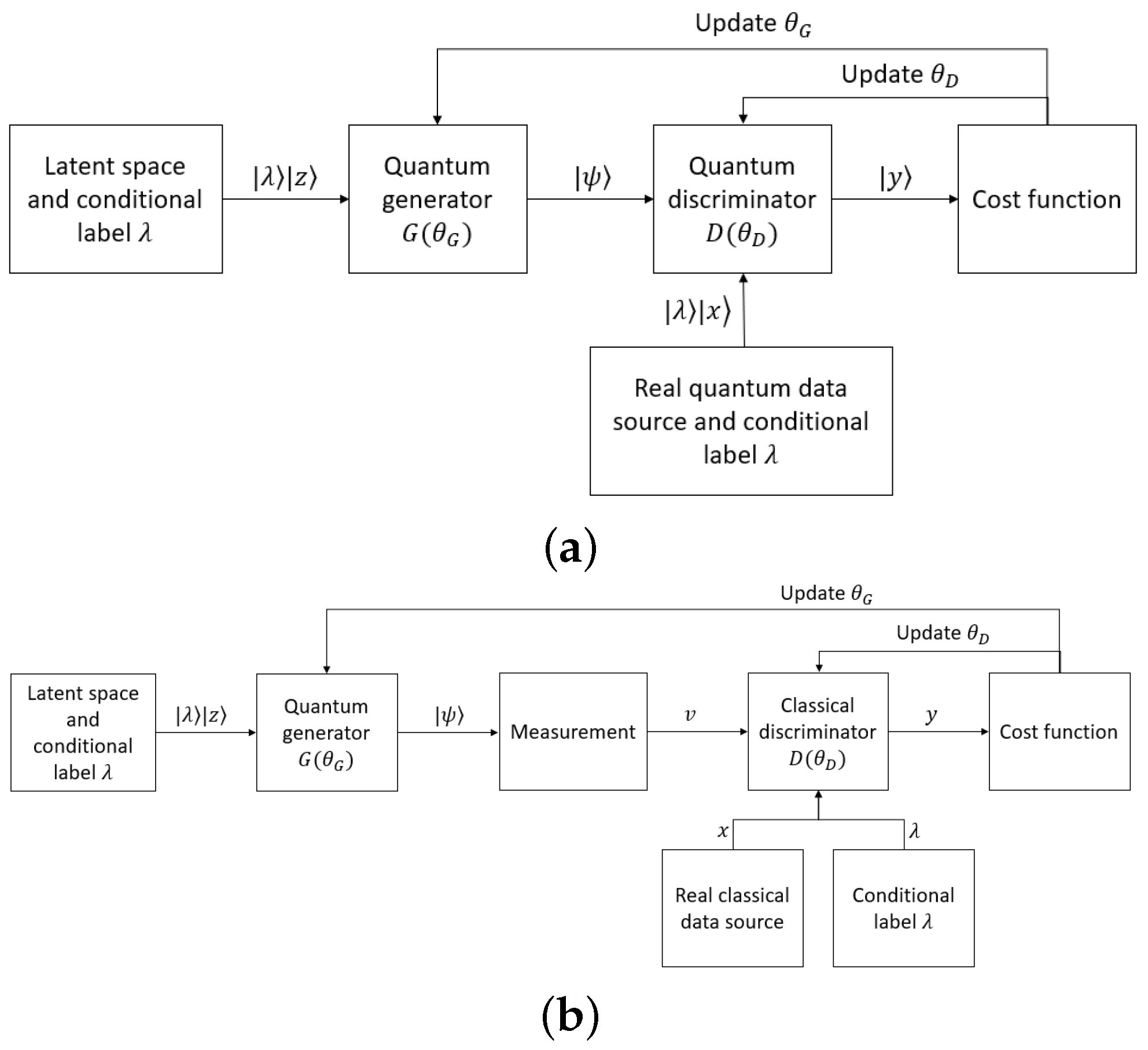
4.4. Quantum Conditional GANs

In classical generative tasks, the input of the generator is random, so one has no control over the generated output. To force the network to produce the examples with desired classes, one conditional constraint about the label is added [32]. Both the generator and the discriminator are aware of this constraint. In addition to discriminating whether the sample comes from a real or generated distribution, the discriminator has to evaluate whether the sample has the characteristics corresponding to the right label or not. This is the same approach when it comes to the quantum scenario. The conditional label λ is also encoded in the form of quantum states. The schematic of quantum conditional GANs is shown in Figure 6.
/media/item_content/202303/641186fada504electronics-12-00856-g007.png
Figure 6. The workflow of (a) a quantum conditional GAN generating quantum data and (b) that of a hybrid conditional GAN generating classical data.

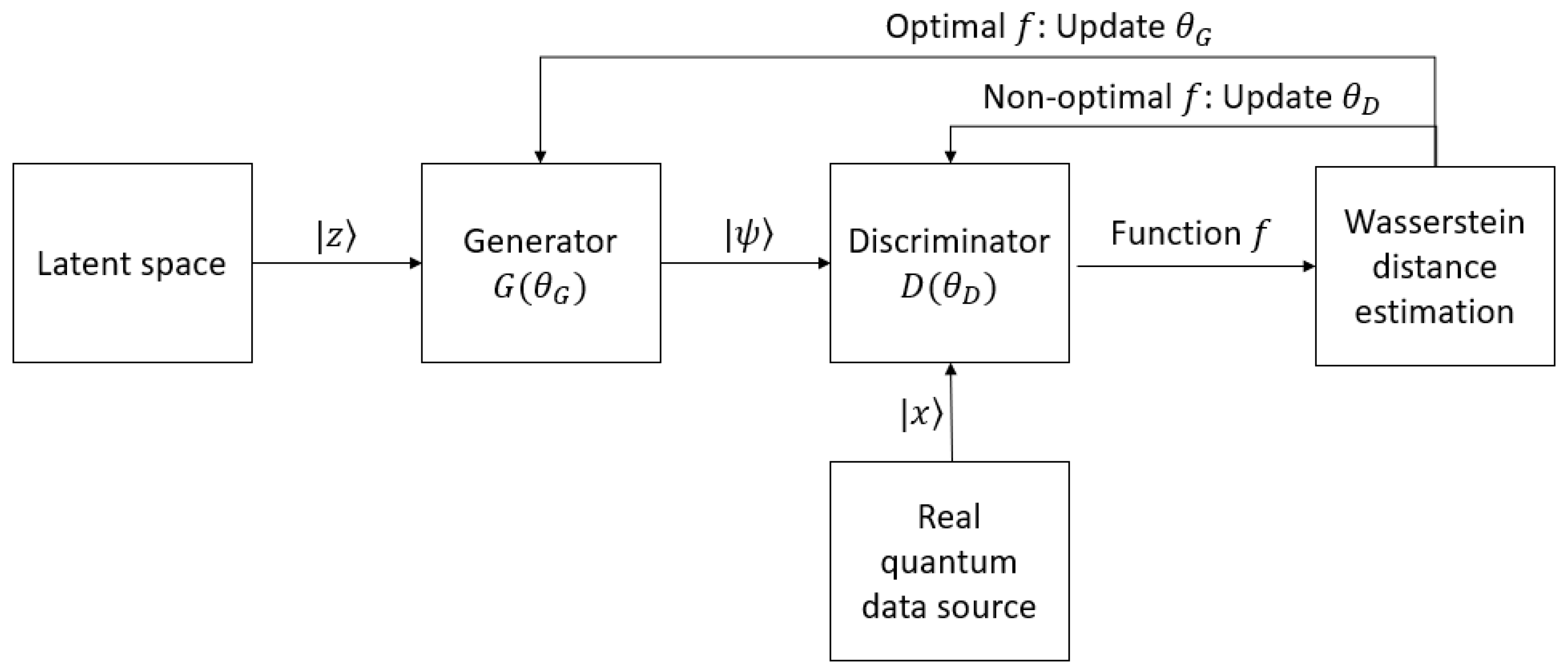
4.5. Quantum Wasserstein GANs

Quantum Wasserstein GANs are the quantum GANs that use Wasserstein distance, or Earth mover’s distance (EMD), as their cost functions. Differently from other quantum GANs variants, the mission of the discriminator in Wasserstein GANs (WGANs) is not to distinguish between the real and the generated data. Due to the fact that Wasserstein distance contains a function that satisfies the Lipschitz condition, the discriminator acts as an estimator that finds out the optimal function for calculating the distance. After the distance is computed, it is used to update the parameters in the generator. The workflow of quantum WGANs is illustrated in Figure 7.
/media/item_content/202303/641187134d50aelectronics-12-00856-g008.png
Figure 7. The general workflow of a quantum WGAN.

4.6. Quantum Patch GANs Using Multiple Sub-Generators

For a classical dataset with M dimensions, whichever encoding method is used, each sample requires at least N=logM qubits to be represented. To deal with the case there are limited quantum resources, i.e., the number of available qubits, Huang et al. suggested a quantum patch GAN [29]. This network consists of T quantum sub-generators and a classical discriminator. The sub-generators are identical, and each is responsible for a portion of the high-dimensional data. The outputs of the sub-generators are measured and concatenated together to form a classical vector, which then can be fed into the discriminator. Thanks to dividing the data into small parts for each sub-generator, the training can be carried out on distributed quantum devices parallelly or on a single quantum device sequentially.

4.7. Quantum GANs Using Quantum Fidelity for a Cost Function

This fully quantum GAN variant was suggested by Stein et al. [28]. The architectures of the generator and the discriminator, the gradient calculation method, and the training strategy stay the same as other fully quantum GANs, but there is a modification in the cost function. The outcomes of the discriminator when the input is real (x) and fake (x′), i.e., D(x) and D(x'), are alternated by the fidelities of the state generated by encoding the real samples (ξ) and the state after applying by the generator (γ), respectively, with the state after applying the discriminator (δ). 

5. Conclusions

Quantum GAN is a new and potential field of research in quantum machine learning. This kind of quantum generative network is inspired by classical GANs, which have already proved their effectiveness and wide applications. In addition to the outstanding nature of GANs, quantum GANs even perform with higher efficiency due to their unique quantum properties and exponential computing power.

References

  1. Mitchell, T.; Buchanan, B.; DeJong, G.; Dietterich, T.; Rosenbloom, P.; Waibel, A. Machine Learning. Annu. Rev. Comput. Sci. 1990, 4, 417–433.
  2. McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133.
  3. Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408.
  4. Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297.
  5. Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558.
  6. LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444.
  7. Alam, M.M.; Mohiuddin, K.; Das, A.K.; Islam, M.K.; Kaonain, M.S.; Ali, M.H. A Reduced Feature Based Neural Network Approach to Classify the Category of Students. In Proceedings of the 2nd International Conference on Innovation in Artificial Intelligence, Shanghai, China, 9–12 March 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 28–32.
  8. Luckin, R.; Holmes, W.; Griffiths, M.; Forcier, L.B. Intelligence Unleashed: An Argument for AI in Education; Pearson Education: London, UK, 2016.
  9. Djambic, G.; Krajcar, M.; Bele, D. Machine learning model for early detection of higher education students that need additional attention in introductory programming courses. Int. J. Digit. Technol. Econ. 2016, 1, 1–11.
  10. Amatya, S.; Karkee, M.; Gongal, A.; Zhang, Q.; Whiting, M.D. Detection of cherry tree branches with full foliage in planar architecture for automated sweet-cherry harvesting. Biosyst. Eng. 2016, 146, 3–15.
  11. Pantazi, X.E.; Moshou, D.; Bravo, C. Active learning system for weed species recognition based on hyperspectral sensing. Biosyst. Eng. 2016, 146, 193–202.
  12. Bouri, E.; Gkillas, K.; Gupta, R.; Pierdzioch, C. Forecasting Realized Volatility of Bitcoin: The Role of the Trade War. Comput. Econ. 2021, 57, 29–53.
  13. Lussange, J.; Lazarevich, I.; Bourgeois-Gironde, S.; Palminteri, S.; Gutkin, B. Modelling Stock Markets by Multi-agent Reinforcement Learning. Comput. Econ. 2021, 57, 113–147.
  14. Sughasiny, M.; Rajeshwari, J. Application of Machine Learning Techniques, Big Data Analytics in Health Care Sector—A Literature Survey. In Proceedings of the 2018 2nd International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC), Palladam, India, 30–31 August 2018; pp. 741–749.
  15. Hazra, A.; Kumar, S.; Gupta, A. Study and Analysis of Breast Cancer Cell Detection using Naïve Bayes, SVM and Ensemble Algorithms. Int. J. Comput. Appl. 2016, 145, 39–45.
  16. Otoom, A.; Abdallah, E.; Kilani, Y.; Kefaye, A.; Ashour, M. Effective diagnosis and monitoring of heart disease. Int. J. Softw. Eng. Its Appl. 2015, 9, 143–156.
  17. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K., Eds.; Curran Associates: New York, NY, USA, 2014; Volume 27.
  18. Farajzadeh-Zanjani, M.; Razavi-Far, R.; Saif, M.; Palade, V. Generative Adversarial Networks: A Survey on Training, Variants, and Applications. In Generative Adversarial Learning: Architectures and Applications; Razavi-Far, R., Ruiz-Garcia, A., Palade, V., Schmidhuber, J., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 7–29.
  19. Pradhyumna, P.; Mohana. A Survey of Modern Deep Learning based Generative Adversarial Networks (GANs). In Proceedings of the 2022 6th International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 29–31 March 2022; pp. 1146–1152.
  20. Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79.
  21. Harrow, A.W.; Montanaro, A. Quantum computational supremacy. Nature 2017, 549, 203–209.
  22. Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202.
  23. Dong, D.; Chen, C.; Li, H.; Tarn, T.J. Quantum Reinforcement Learning. IEEE Trans. Syst. Man Cybern. Part B 2008, 38, 1207–1220.
  24. Rebentrost, P.; Mohseni, M.; Lloyd, S. Quantum Support Vector Machine for Big Data Classification. Phys. Rev. Lett. 2014, 113, 130503.
  25. Khoshaman, A.; Vinci, W.; Denis, B.; Andriyash, E.; Sadeghi, H.; Amin, M.H. Quantum variational autoencoder. Quantum Sci. Technol. 2018, 4, 14001.
  26. Lloyd, S.; Weedbrook, C. Quantum Generative Adversarial Learning. Phys. Rev. Lett. 2018, 121, 40502.
  27. Dallaire-Demers, P.L.; Killoran, N. Quantum generative adversarial networks. Phys. Rev. A 2018, 98, 12324.
  28. Stein, S.A.; Baheri, B.; Chen, D.; Mao, Y.; Guan, Q.; Li, A.; Fang, B.; Xu, S. QuGAN: A Quantum State Fidelity based Generative Adversarial Network. In Proceedings of the 2021 IEEE International Conference on Quantum Computing and Engineering (QCE), Broomfield, CO, USA, 17–22 October 2021; IEEE: Piscataway, NJ, USA, 2021.
  29. Huang, H.L.; Du, Y.; Gong, M.; Zhao, Y.; Wu, Y.; Wang, C.; Li, S.; Liang, F.; Lin, J.; Xu, Y.; et al. Experimental Quantum Generative Adversarial Networks for Image Generation. Phys. Rev. Appl. 2021, 16, 24051.
  30. Zoufal, C.; Lucchi, A.; Woerner, S. Quantum Generative Adversarial Networks for learning and loading random distributions. NPJ Quantum Inf. 2019, 5, 103.
  31. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates: New York, NY, USA, 2012; Volume 25.
  32. Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014, arXiv:1411.1784.
  33. Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875.
  34. Berthelot, D.; Schumm, T.; Metz, L. BEGAN: Boundary Equilibrium Generative Adversarial Networks. arXiv 2017, arXiv:1703.10717.
  35. Brock, A.; Donahue, J.; Simonyan, K. Large Scale GAN Training for High Fidelity Natural Image Synthesis. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019.
  36. Denton, E.; Chintala, S.; Szlam, A.; Fergus, R. Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks. arXiv 2015, arXiv:1506.05751.
  37. Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets. arXiv 2016, arXiv:1606.03657.
  38. Karras, T.; Aittala, M.; Laine, S.; Härkönen, E.; Hellsten, J.; Lehtinen, J.; Aila, T. Alias-Free Generative Adversarial Networks. arXiv 2021, arXiv:2106.12423.
  39. Tang, X.; Wang, Z.; Luo, W.; Gao, S. Face Aging with Identity-Preserved Conditional Generative Adversarial Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7939–7947.
  40. Wu, X.; Xu, K.; Hall, P. A survey of image synthesis and editing with generative adversarial networks. Tsinghua Sci. Technol. 2017, 22, 660–674.
  41. Dolhansky, B.; Ferrer, C.C. Eye In-Painting with Exemplar Generative Adversarial Networks. arXiv 2017, arXiv:1712.03999.
  42. Demir, U.; Unal, G. Patch-Based Image Inpainting with Generative Adversarial Networks. arXiv 2018, arXiv:1803.07422.
  43. Wu, H.; Zheng, S.; Zhang, J.; Huang, K. GP-GAN: Towards Realistic High-Resolution Image Blending. arXiv 2017, arXiv:1703.07195.
  44. Chen, B.C.; Kae, A. Toward Realistic Image Compositing With Adversarial Learning. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8407–8416.
  45. Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Loy, C.C.; Qiao, Y.; Tang, X. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. arXiv 2018, arXiv:1809.00219.
  46. Ding, Z.; Liu, X.Y.; Yin, M.; Kong, L. TGAN: Deep Tensor Generative Adversarial Nets for Large Image Generation. arXiv 2019, arXiv:1901.09953.
  47. Wang, C.; Xu, C.; Wang, C.; Tao, D. Perceptual Adversarial Networks for Image-to-Image Transformation. IEEE Trans. Image Process. 2018, 27, 4066–4079.
  48. Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks. arXiv 2017, arXiv:1703.10593.
  49. Liu, M.Y.; Breuel, T.; Kautz, J. Unsupervised Image-to-Image Translation Networks. arXiv 2017, arXiv:1703.00848.
  50. Kong, J.; Kim, J.; Bae, J. HiFi-GAN: Generative Adversarial Networks for Efficient and High Fidelity Speech Synthesis. arXiv 2020, arXiv:2010.05646.
  51. Oord, A.v.d.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. WaveNet: A Generative Model for Raw Audio. arXiv 2016, arXiv:1609.03499.
  52. Dong, H.W.; Hsiao, W.Y.; Yang, L.C.; Yang, Y.H. MuseGAN: Multi-track Sequential Generative Adversarial Networks for Symbolic Music Generation and Accompaniment. arXiv 2017, arXiv:1709.06298.
  53. Engel, J.; Agrawal, K.K.; Chen, S.; Gulrajani, I.; Donahue, C.; Roberts, A. GANSynth: Adversarial Neural Audio Synthesis. arXiv 2019, arXiv:1902.08710.
  54. Uřičář, M.; Křížek, P.; Hurych, D.; Sobh, I.; Yogamani, S.; Denny, P. Yes, we GAN: Applying adversarial techniques for autonomous driving. Electron. Imaging 2019, 2019, 48-1–48-17.
  55. Jeong, C.H.; Yi, M.Y. Correcting rainfall forecasts of a numerical weather prediction model using generative adversarial networks. J. Supercomput. 2022, 79, 1289–1317.
  56. Besombes, C.; Pannekoucke, O.; Lapeyre, C.; Sanderson, B.; Thual, O. Producing realistic climate data with generative adversarial networks. Nonlinear Process. Geophys. 2021, 28, 347–370.
  57. Sandfort, V.; Yan, K.; Pickhardt, P.J.; Summers, R.M. Data augmentation using generative adversarial networks (CycleGAN) to improve generalizability in CT segmentation tasks. Sci. Rep. 2019, 9, 16884.
  58. Frid-Adar, M.; Diamant, I.; Klang, E.; Amitai, M.; Goldberger, J.; Greenspan, H. GAN-based synthetic medical image augmentation for increased CNN performance in liver lesion classification. Neurocomputing 2018, 321, 321–331.
  59. Cheng, J.; Yang, Y.; Tang, X.; Xiong, N.; Zhang, Y.; Lei, F. Generative Adversarial Networks: A Literature Review. KSII Trans. Internet Inf. Syst. 2020, 14, 4625–4647.
  60. Schuld, M. Supervised quantum machine learning models are kernel methods. arXiv 2021, arXiv:2101.11020.
  61. Lemaréchal, C. Cauchy and the gradient method. Doc. Math. Extra 2012, 251, 10.
  62. Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980.
  63. Lydia, A.; Francis, S. Adagrad—An optimizer for stochastic gradient descent. Int. J. Inf. Comput. Sci 2019, 6, 566–568.
  64. Shrivastava, N.; Puri, N.; Gupta, P.; Krishnamurthy, B.; Verma, S. OpticalGAN: Generative Adversarial Networks for Continuous Variable Quantum Computation. arXiv 2019, arXiv:1909.07806.
  65. Hu, L.; Wu, S.H.; Cai, W.; Ma, Y.; Mu, X.; Xu, Y.; Wang, H.; Song, Y.; Deng, D.L.; Zou, C.L.; et al. Quantum generative adversarial learning in a superconducting quantum circuit. Sci. Adv. 2019, 5, eaav2761.
  66. Benedetti, M.; Grant, E.; Wossnig, L.; Severini, S. Adversarial quantum circuit learning for pure state approximation. New J. Phys. 2019, 21, 43023.
  67. Du, Y.; Hsieh, M.H.; Tao, D. Efficient Online Quantum Generative Adversarial Learning Algorithms with Applications. arXiv 2019, arXiv:1904.09602.
  68. Situ, H.; He, Z.; Wang, Y.; Li, L.; Zheng, S. Quantum generative adversarial network for generating discrete distribution. Inf. Sci. 2020, 538, 193–208.
  69. Huggins, W.; Patil, P.; Mitchell, B.; Whaley, K.B.; Stoudenmire, E.M. Towards quantum machine learning with tensor networks. Quantum Sci. Technol. 2019, 4, 24001.
  70. Han, Z.Y.; Wang, J.; Fan, H.; Wang, L.; Zhang, P. Unsupervised Generative Modeling Using Matrix Product States. Phys. Rev. X 2018, 8, 031012.
  71. Guo, C.; Jie, Z.; Lu, W.; Poletti, D. Matrix product operators for sequence-to-sequence learning. Phys. Rev. E 2018, 98, 042114.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Computer Science, Artificial Intelligence; Computer Science, Information Systems
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Tuan Anh Ngo
,
Tuyen Nguyen
,
Truong Cong Thang
View Times: 696
Revisions: 3 times (View History)
Update Date: 15 Mar 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback