Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Chengkai Tang
 -- 2420 2022-12-02 03:53:18 |
2 format correct
Vivi Li
+ 1 word(s) 2421 2022-12-02 07:41:35 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Tang, C.;  Wang, Y.;  Zhang, L.;  Zhang, Y.;  Song, H. Multisource Fusion UAV Cluster Cooperative Positioning. Encyclopedia. Available online: https://encyclopedia.pub/entry/37709 (accessed on 20 May 2024).
Tang C,  Wang Y,  Zhang L,  Zhang Y,  Song H. Multisource Fusion UAV Cluster Cooperative Positioning. Encyclopedia. Available at: https://encyclopedia.pub/entry/37709. Accessed May 20, 2024.
Tang, Chengkai, Yuyang Wang, Lingling Zhang, Yi Zhang, Houbing Song. "Multisource Fusion UAV Cluster Cooperative Positioning" Encyclopedia, https://encyclopedia.pub/entry/37709 (accessed May 20, 2024).
Tang, C.,  Wang, Y.,  Zhang, L.,  Zhang, Y., & Song, H. (2022, December 02). Multisource Fusion UAV Cluster Cooperative Positioning. In Encyclopedia. https://encyclopedia.pub/entry/37709
Tang, Chengkai, et al. "Multisource Fusion UAV Cluster Cooperative Positioning." Encyclopedia. Web. 02 December, 2022.
Multisource Fusion UAV Cluster Cooperative Positioning
Edit
This entry is adapted from the peer-reviewed paper 10.3390/rs14215491

Due to the functional limitations of a single UAV, UAV clusters have become an important part of smart cities, and the relative positioning between UAVs is the core difficulty in UAV cluster applications. Existing UAVs can be equipped with satellite navigation, radio navigation, and other positioning equipment, but in complex environments, such as urban canyons, various navigation sources cannot achieve full positioning information due to occlusion, interference, and other factors, and existing positioning fusion methods cannot meet the requirements of these environments. Therefore, demand exists for the real-time positioning of UAV clusters. Aiming to solve the above problems, multisource fusion UAV cluster cooperative positioning using information geometry (UCP-IG), which converts various types of navigation source information into information geometric probability models and reduces the impact of accidental errors is proposed, and the Kullback–Leibler divergence minimization (KLM) fusion method to achieve rapid fusion on geometric manifolds and creatively solve the problem of difficult fusion caused by different positioning information formats and parameters is presented.

cooperative positioning multisource fusion information geometry UAV

1. Introduction

The UAV has the characteristics of not being affected by terrain, fast speed, small size, etc. Therefore, it has shown great development prospects in the fields of logistics transportation, security monitoring, information collection, and traffic guidance in smart cities [1]. However, due to load limitations and the occlusion effect of urban canyons, a single UAV provides low coverage, which greatly limits its application in smart cities. While a lightweight UAV cluster has attracted more attention because of its wide coverage and high transportation efficiency, the main direction of UAV development is towards applications in cities [2]. However, unlike a single UAV, the positioning between UAVs in a cluster is the core difficulty in the application of UAV clusters. Compared with traditional node positioning, UAV cluster positioning has the characteristics of a three-dimensional position, large dynamics, and easy interference. The main positioning information of a UAV cluster comes from satellite navigation and inertial navigation, supplemented by wireless base station navigation, laser navigation, visual navigation, and other technologies. Due to inherent problems, various types of navigation sources cannot realize the positioning service of a UAV cluster in the whole area and environment. For example, navigation satellites are easily blocked by urban canyons, resulting in the loss of UAV navigation signals [3]; wireless base stations have limited navigation transmission distance and cannot provide positioning services outside the area [4]; LiDAR is greatly affected by weather and atmosphere; the beam is narrow, and performance drops significantly in cloudy, rainy, and foggy environments [5]; and visual navigation requires a huge amount of image processing in complex and dynamic environments, exhibits poor real-time performance, and has a large impression of the light-receiving environment [6]. Therefore, using the relative position of a UAV cluster to realize the rapid fusion of distributed multisource navigation system information is the main problem of UAV cluster positioning.
The existing distributed node positioning method mainly realizes cooperative information fusion positioning through ranging, direction finding, and information interaction. This fusion method mainly includes two categories. The first category is the fusion of positioning data represented by neural networks [7][8][9], and the other is the fusion of localization results represented by the Kalman filter [10][11][12]. Both types of algorithms have problems of high computational complexity and poor real-time performance, and thus they are not suitable for the cooperative positioning of UAV clusters. Therefore, using the various types of navigation sources independently distributed in the UAV cluster to achieve fast and high-stability fusion is the main problem of the coordinated positioning of the UAV cluster.
As the current mainstream positioning information fusion algorithm, the Kalman filter and its extended series of filtering algorithms [13] can not only estimate the time domain information of stationary random processes but can also estimate nonstationary random processes. However, the positioning information is output by different types of navigation sources. The format and frequency of the parameters are completely different, resulting in high computational complexity and a long fusion time, which cannot meet the needs of UAV clusters for performing the rapid fusion of different types of navigation sources. With the rapid development of artificial intelligence, intelligent information fusion by neural networks has also developed rapidly, and these can realize the rapid fusion of various types of navigation information, but they also have the problems of requiring a large amount of data and exhibiting poor real-time performance. To solve the problem of difficulty in fusion positioning caused by factors such as the time-space asynchrony of distributed multitype navigation source information in UAV clusters, the loss of navigation source information, and the rapid movement of UAV clusters, this entry proposes a multisource information geometry-based approach. The main innovation points of the fusion UAV cluster positioning method are as follows:
  • The information from various navigation sources carried by the UAV cluster is creatively transformed into an information probability model, the time and frequency parameters of various types of navigation information of the UAV cluster are unified, and a simulation scenario is established to verify the model.
  • A multisource fusion UAV cluster localization method based on information geometry is proposed. The method utilizes the correlation between the information probability of the UAV navigation sources and the positioning accuracy, calculates the accuracy probability function of the navigation source information, establishes the probability geometric manifold of the navigation source information, and fuses multiple probability density functions to obtain the positioning result.
  • Simulation tests of the proposed UCP-IG model in ideal scenarios, sudden loss of navigation information scenarios, and random motion scenarios are carried out. The test results show that the UCP-IG method proposed in this entry can effectively improve the stability of UAV clusters. In the case of a loss of human–machine navigation information, errors can also be effectively suppressed.

2. UAV Cooperative Positioning

With the application of UAVs in unmanned transportation applications, traffic management, and other basic core projects of smart cities, the relative positioning between UAV clusters has become the core basis for UAV cluster applications [14]. With the improvement of the accuracy of the GNSS system and the enhancement of the navigation signal by low-orbit communication satellite systems, satellite navigation has become the main method of the cluster positioning of UAVs. However, due to the serious occlusion of urban environments, the signals of some UAVs will always be lost during the flight of a UAV cluster. The development of the coordinated navigation and positioning of UAV clusters has become a hot topic for UAV cluster applications.
UAV cooperative positioning mainly evolved from wireless sensor network cooperative positioning. Early UAV cooperative positioning methods mainly achieved cooperative positioning through the LS method [15], MSE method [16], etc. This kind of method has the advantage of fast positioning speed, but it is easily disturbed by environmental errors.
Due to the jittery characteristics of UAVs, reducing the error has become the main problem of UAV positioning. Techniques such as Bayesian estimation [17] and non-Bayesian estimation [18] are used for UAV cooperative positioning, but the disadvantage of Bayesian estimation methods is the large communication and computational overhead required. The research work discussed in [19] proposed a cooperative positioning fusion technique based on a particle filter (PF), but it is difficult to solve the problem of particle degradation and depletion [20]. To this end, [21] and [22] proposed a positioning estimation method based on the extended Kalman filter (EKF) and unscented Kalman filter (UKF), respectively. Non-Bayesian estimation cooperative positioning methods mainly include the least squares (LS) [23] estimation method and the maximum likelihood (ML) [24] method. The research work discussed in [25] uses weight compensation combined with the LS method to achieve UAV cluster positioning, which can reduce the impact of environmental errors. The study proposes a new hybrid cooperative positioning scheme based on distance and angle measurement; that is, a modification of the TOA-AOA-based and AOA-RSS-based linear least squares (LLS) hybrid scheme. Based on the ranging information between the man–machine and base station, an optimized version of LLS estimation was proposed, which further improves the positioning performance but limits the scope of use. Tomic S et al. [26] proposed a new method based on received signal strength (RSS) and convex optimization. By deriving nonconvex estimates, the search problem of the global optimal solution was solved, but it could not meet the high mobility characteristics of UAVs, and the stability of positioning accuracy was poor.
In recent years, neural networks have also been used in the field of cooperative positioning due to their advantages of arbitrary nonlinear mapping of input and output. The research work discussed in [27] used BP neural-network-assisted EKF and UKF to achieve cooperative positioning, and the results showed that using a BP neural network to optimize nonlinear filtering could improve filter estimation performance. The research work discussed in [28] proposes a layered sensor fusion method with an artificial neural network (ANN) to solve the self-localization problem of mobile robots. This method uses octagonal sonar, digital compass, and wireless network signal strength measurement to determine the position of autonomous mobile robots. Multi-layer perceptron (MLP) is used in combination with supervised learning and back-propagation techniques to train the network by layered fusion steps and determine the robot’s position on the map. However, this type of method needs to train various parameters and the calculation amount and time are too large, so it cannot meet the real-time requirements of UAV cluster cooperative positioning.
Therefore, how to realize the cooperative positioning of UAV clusters in an unknown, complex, and dynamic environment and how to maximize the real-time performance of the algorithm and reduce the amount of calculation require further research. For this reason, an increasing number of scholars have introduced graph theory knowledge into cooperative positioning. For instance, Ihler A proposed the nonparametric belief propagation algorithm [29]. The basic idea of this algorithm is a method based on a graph model, which models the localization problem as an inference problem, allowing it to perform a distributed estimation process, but it has problems of high computational complexity and poor real-time performance. Starting from estimation theory and factor graphs [30][31][32], Wymeersch H et al. proposed a distributed cooperative positioning algorithm, SPAWN (sum-product algorithm over a wireless network), which transformed the node localization problem in cooperative networks into variables. The approximate edge posterior distribution of variable nodes is obtained by updating and transmitting confidence information on the factor graph. However, the algorithm requires a large amount of computation and large communication bandwidth and has poor positioning performance in dynamic scenarios. On the basis of graph theory, information geometry is widely used as an effective tool for solving nonlinear and random problems. Compared with the mathematical theory of the Euclidean framework, information geometry theory can more effectively solve some nonlinear and random problems in the information field. Information geometry methods have made considerable progress in statistical signal processing, parameter estimation, and filtering. Reference [33] refers to the concept of information geometry to radar signal processing and proposes a corresponding radar signal detection method, but how to use the information geometry distance to realize multi-UAV cooperative positioning is currently unaddressed. This entry takes advantage of the unified parameters of the information geometric model, combined with the K–L fusion method, which can effectively improve the positioning stability of the UAV cluster and the ability to suppress mutation errors.

3. System Model

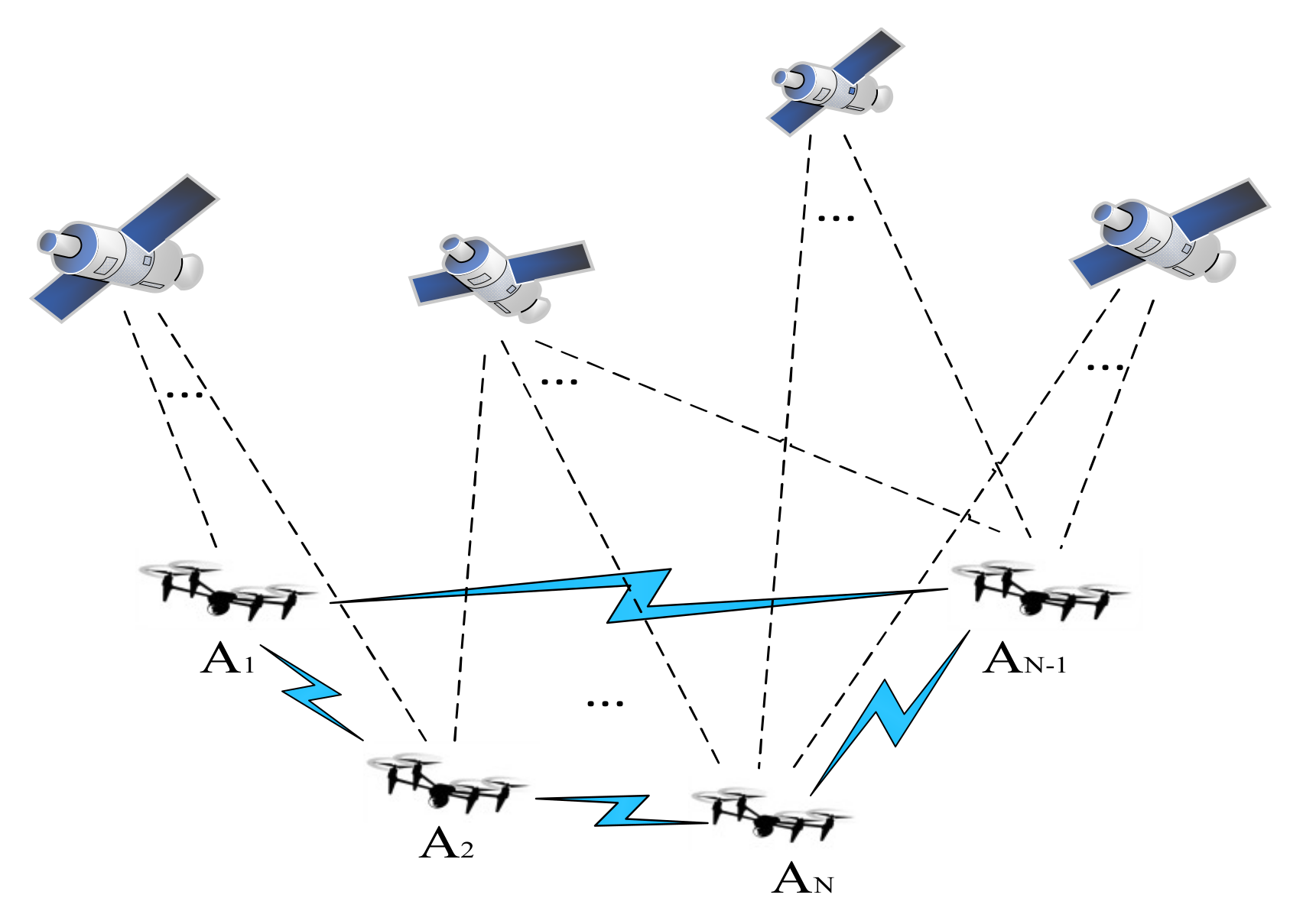
Due to the limited transportation weight and quantity of a single UAV, distributed UAV clusters can greatly improve transportation efficiency and reduce costs, but the mutual distance and control between clusters require high-precision, real-time positioning information support. The cooperative positioning network of the UAV cluster studied in this entry is shown in Figure 1.
Figure 1. Cooperative positioning network of a UAV cluster.
In Figure 1, A1, A2, AN-1, and AN all represent UAVs, while AN represents the n-th UAV. UAV positioning can be realized by a base station or cluster UAV. In the figure, the blue link represents the ranging communication link between UAVs. Meanwhile, the UAV is equipped with a satellite receiver and inertial measurement unit (IMU), which can receive satellite navigation signals and information such as speed and acceleration.
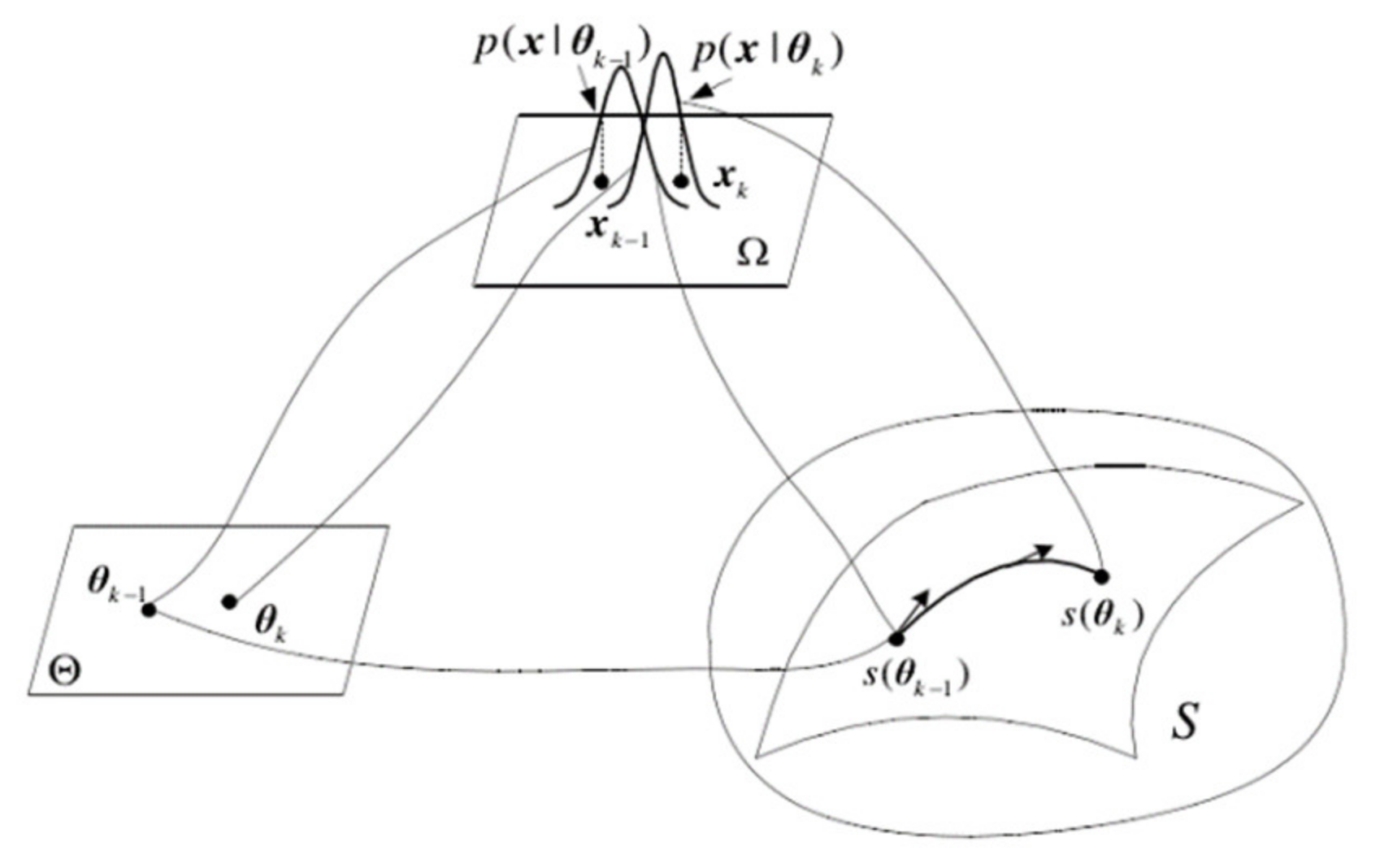
The essence of information geometry is to study the intrinsic geometric properties of probability distribution manifolds. The basic problems of probability theory and information theory are geometrized by using the differential geometry method. Different types of probability distribution function families have corresponding statistical manifolds with certain structures. A statistical manifold can be understood as a surface in the parameter space of the probability density function. Every point on it corresponds to a specific probability distribution, and the coordinates of points are related to the parameters of the probability distribution. The form of each probability distribution function determines the relationship between its neighboring probability distribution function and the spatial structure it constitutes. The relationship between the probability distribution and statistical manifold is shown in Figure 2. In Figure 2, is the sample space of navigation source information, its probability density function is , is the parameter vector of , is the vector space of parameter , and is the statistical manifold with the parameter as the coordinate.
Figure 2. Schematic diagram of the statistical manifold.
In the multisource fusion scenario, combined with information geometry theory, the probability distribution functions of multiple UAV navigation information sources can be mapped to the Riemannian space as a family of functions to form a statistical manifold, and each point on the statistical manifold represents a probability distribution function. The multisource fusion algorithm based on information geometry theory can process heterogeneous data with better real-time performance, fault tolerance, and positioning accuracy.
The information fusion of a target UAV includes two parts: the target UAV’s own information fusion and the cooperative information fusion from its neighboring UAVs. Each UAV merges the location information of its own multiple navigation sources, and then the target UAV iterates the information fusion through the location information provided by the neighbor UAVs and combines the ranging information to reduce the error. Figure 3 shows the multisource fusion process based on information geometry. Assume that UAV A1 is the target UAV that needs to obtain positioning information. First, each information source of UAV A1 is processed, a statistical manifold is established, the navigation information is mapped to the manifold, and the probability density function of each information source is obtained. Then, combined with the probability density function of location information provided by each neighboring UAV, the multisource fusion algorithm based on information geometry replaces the geodesic distance of the correlation matrix of the two probability density functions on the manifold by K–L divergence, obtains the lower bound of the fused objective function, and the real-time positioning result of target UAV A1 is finally obtained.
Figure 3. Flow chart of UAV cluster multisource fusion based on information geometry.

References

  1. Estrada, M.A.R.; Ndoma, A. The uses of unmanned aerial vehicles—UAV’s-(or drones) in social logistic: Natural disasters response and humanitarian relief aid. Procedia Comput. Sci. 2019, 149, 375–383.
  2. Song, B.D.; Park, K.; Kim, J. Persistent UAV delivery logistics: MILP formulation and efficient heuristic. Comput. Ind. Eng. 2018, 120, 418–428.
  3. Mo, Y.; Zhang, Z.; Meng, W.; Ma, L.; Wang, Y. A Spatial Division Clustering Method and Low Dimensional Feature Extraction Technique Based Indoor Positioning System. Sensors 2014, 14, 1850–1876.
  4. Sivakumar, A. UAV swarm coordination and control for establishing wireless. In Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), Toronto, ON, Canada, 10–14 May 2010; pp. 1157–1164.
  5. Gualda, D.; Ureña, J.; García, J.C.; Pérez, M.C.; Díaz, E. Study of cooperative position estimations of mobile robots. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 1–7.
  6. Lin, Q.; Wang, X.; Wang, Y. Cooperative Formation and Obstacle Avoidance Algorithm for Multi-UAV System in 3D Environment. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 6943–6948.
  7. Zhou, Y.; Wan, J.; Li, Z.; Song, Z. GPS/INS integrated navigation with BP neural network and Kalman filter. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 2515–2520.
  8. Pulford, G.W. Taxonomy of Multiple Target Tracking Methods. IEE Proc.-Radar Sonar Navig. 2005, 152, 291–304.
  9. Rajchl, M.; Baxter, J.S.; McLeod, A.J.; Yuan, J.; Qiu, W.; Peters, T.M.; Khan, A.R. Hierarchical max-flow segmentation framework for multi-atlas segmentation with Kohonen self-organizing map based Gaussian mixture modeling. Med. Image Anal. 2016, 27, 45–56.
  10. Kiani, M.; Pourtakdoust, S.H. Concurrent orbit and attitude estimation using minimum sigma point unscented Kalman filter. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 801–819.
  11. Jwo, D.J.; Wang, S.H. Adaptive Fuzzy Strong Tracking Extended Kalman Filtering for GPS Navigation. IEEE Sens. J. 2007, 7, 778–789.
  12. Kalman, R.E. A New Approach to Linear Filtering and Prediction Problem. J. Basic Eng (ASME) 1960, 82, 35–45.
  13. Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269.
  14. Patwari, N.; Ash, J.N.; Kyperountas, S.; Hero, A.O.; Moses, R.L.; Correal, N.S. Locating the nodes: Cooperative localization in wireless sensor networks. IEEE Signal Process. Mag. 2005, 22, 54–69.
  15. Nguyen, T.V.; Jeong, Y.; Shin, H.; Win, M.Z. Least Square Cooperative Localization. IEEE Trans. Veh. Technol. 2015, 64, 1318–1330.
  16. Panzieri, S.; Pascucci, F.; Sciavicco, L.; Setola, R. Distributed Cooperative Localization. J. Inf. Technol. Res. 2015, 6, 49–67.
  17. Nguyen, T.L.T.; Septier, F.; Rajaona, H.; Peters, G.W.; Nevat, I.; Delignon, Y. A Bayesian Perspective on Multiple Source Localization in Wireless Sensor Networks. IEEE Trans. Signal Process. 2016, 64, 1684–1699.
  18. Garello, R.; Samson, J.; Spirito, M.A.; Wymeersch, H. Peer-to-Peer Cooperative Positioning Part II: Hybrid Devices with GNSS & Terrestrial Ranging Capability. Inside GNSS 2015, 7, 56–64.
  19. Sun, C.; Zhang, Y.; Wang, G.; Gao, W. A New Variational Bayesian Adaptive Extended Kalman Filter for Cooperative Navigation. Sensors 2018, 18, 2538.
  20. Kwok, C.; Fox, D.; Meila, M. Real-time particle filters. Proc. IEEE 2004, 92, 469–484.
  21. Kia, S.S.; Rounds, S.; Martinez, S. Cooperative Localization for Mobile Agents: A Recursive Decentralized Algorithm Based on Kalman-Filter Decoupling. IEEE Control Syst. Mag. 2016, 36, 86–101.
  22. Hai, N.; Zhao, Q.; Wan, Q. UKF algorithm based on optimized weighting data fusion. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015; pp. 1–4.
  23. Abd El Aziz, M. Source localization using TDOA and FDOA measurements based on modified cuckoo search algorithm. Wirel. Netw. 2017, 23, 487–495.
  24. Nguyen, H.D.; Wood, I.A. A Block Successive Lower-Bound Maximization Algorithm for the Maximum Pseudo-Likelihood Estimation of Fully Visible Boltzmann Machines. Neural Comput. 2016, 28, 485–492.
  25. Khan, M.W.; Salman, N.; Kemp, A.H. Optimised hybrid localisation with cooperation in wireless sensor networks. IET Signal Process. 2017, 11, 341–348.
  26. Tomic, S.; Beko, M.; Dinis, R. RSS-Based Localization in Wireless Sensor Networks Using Convex Relaxation: Noncooperative and Cooperative Schemes. IEEE Trans. Veh. Technol. 2015, 64, 2037–2050.
  27. Li, S.; Wang, S.L. Research of nonlinear filtering algorithm based on BP neural network. Electron. Meas. Technol. 2018, 41, 34–39.
  28. Magrin, C.E.; Todt, E. Multi-Sensor Fusion Method Based on Artificial Neural Network for Mobile Robot Self-Localization. In Proceedings of the 2019 Latin American Robotics Symposium (LARS), 2019 Brazilian Symposium on Robotics (SBR) and 2019 Workshop on Robotics in Education (WRE), Rio Grande, Brazil, 23–25 October 2019; pp. 138–143.
  29. Ihler, A.T.; Fisher, J.W.; Moses, R.L.; Willsky, A.S. Nonparametric belief propagation for self-localization of sensor networks. IEEE J. Sel. Areas Commun. 2005, 23, 809–819.
  30. Kschischang, F.R.; Frey, B.J.; Loeliger, H. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519.
  31. Loeliger, H.A. An introduction to factor graphs. IEEE Signal Process. Mag. 2004, 21, 28–41.
  32. Caceres, M.A.; Penna, F.; Wymeersch, H.; Garello, R. Hybrid Cooperative Positioning based on Distributed Belief Propagation. IEEE J. Sel. Areas Commun. 2011, 29, 1948–1958.
  33. Cheng, Y.; Wang, X.; Caelli, T.; Li, X.; Moran, B. On Information Resolution of Radar Systems. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3084–3102.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Computer Science, Information Systems
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Chengkai Tang
,
Yuyang Wang
,
Lingling Zhang
,
Yi Zhang
,
Houbing Song
View Times: 395
Entry Collection: Remote Sensing Data Fusion
Revisions: 2 times (View History)
Update Date: 02 Dec 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback