1. Single-Precision 32-bit

A single-precision binary floating-point number (called "short" by IBM) is stored in a 32-bit word:

In this format the initial bit is not suppressed, and the radix point is set to the left of the significand (fraction in IBM documentation and the figures) in increments of 4 bits.

Since the base is 16, the exponent in this form is about twice as large as the equivalent in IEEE 754, in order to have similar exponent range in binary, 9 exponent bits would be required.

1.1. Example

Consider encoding the value −118.625 as an IBM single-precision floating-point value.

The value is negative, so the sign bit is 1.

The value 118.625₁₀ in binary is 1110110.101₂. This value is normalized by moving the radix point left four bits (one hexadecimal digit) at a time until the leftmost digit is zero, yielding 0.01110110101₂. The remaining rightmost digits are padded with zeros, yielding a 24-bit fraction of .0111 0110 1010 0000 0000 0000₂.

The normalized value moved the radix point two digits to the left, yielding a multiplier and exponent of 16⁺². A bias of +64 is added to the exponent (+2), yielding +66, which is 100 0010₂.

Combining the sign, exponent plus bias, and normalized fraction produces this encoding:

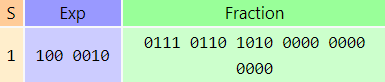
In other words, the number represented is −0.76A000₁₆ × 16^{66 − 64} = −0.4633789… × 16⁺² = −118.625

1.2. Largest Representable Number

The number represented is +0.FFFFFF₁₆ × 16^{127 − 64} = (1 − 16⁻⁶) × 16⁶³ ≈ +7.2370051 × 10⁷⁵

1.3. Smallest Positive Normalized Number

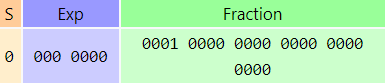
The number represented is +0.1₁₆ × 16^{0 − 64} = 16⁻¹ × 16⁻⁶⁴ ≈ +5.397605 × 10⁻⁷⁹.

1.4. Zero

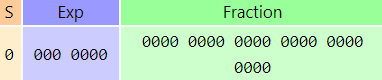
Zero (0.0) is represented in normalized form as all zero bits, which is arithmetically the value +0.0₁₆ × 16^{0 − 64} = +0 × 16⁻⁶⁴ ≈ +0.000000 × 10⁻⁷⁹ = 0. Given a fraction of all-bits zero, any combination of positive or negative sign bit and a non-zero biased exponent will yield a value arithmetically equal to zero. However, the normalized form generated for zero by CPU hardware is all-bits zero. This is true for all three floating-point precision formats.

1.5. Precision Issues

Since the base is 16, there can be up to three leading zero bits in the binary significand. That means when the number is converted into binary, there can be as few as 21 bits of precision. Because of the "wobbling precision" effect, this can cause some calculations to be very inaccurate.

A good example of the inaccuracy is representation of decimal value 0.1. It has no exact binary or hexadecimal representation. In hexadecimal format, it is represented as 0.19999999...₁₆ or 0.0001 1001 1001 1001 1001 1001 1001...₂, that is:

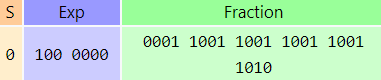
This has only 21 bits, whereas the binary version has 24 bits of precision.

Six hexadecimal digits of precision is roughly equivalent to six decimal digits (i.e. (6 − 1) log₁₀(16) ≈ 6.02). A conversion of single precision hexadecimal float to decimal string would require at least 9 significant digits (i.e. 6 log₁₀(16) + 1 ≈ 8.22) in order to convert back to the same hexadecimal float value.

2. Double-precision 64-bit

The double-precision floating-point format (called "long" by IBM) is the same as the "short" format except that the fraction field is wider and the double-precision number is stored in a double word (8 bytes):

The exponent for this format covers only about a quarter of the range as the corresponding IEEE binary format.

14 hexadecimal digits of precision is roughly equivalent to 17 decimal digits. A conversion of double precision hexadecimal float to decimal string would require at least 18 significant digits in order to convert back to the same hexadecimal float value.

3. Extended-precision 128-bit

Called extended-precision by IBM, a quadruple-precision floating-point format was added to the System/370 series and was available on some S/360 models (S/360-85, -195, and others by special request or simulated by OS software). The extended-precision fraction field is wider, and the extended-precision number is stored as two double words (16 bytes):

28 hexadecimal digits of precision is roughly equivalent to 32 decimal digits. A conversion of extended precision hexadecimal float to decimal string would require at least 35 significant digits in order to convert back to the same hexadecimal float value.

4. Arithmetic Operations

Most arithmetic operations truncate like simple pocket calculators. Therefore, 1 − 16⁻⁷ = 1. In this case, the result is rounded away from zero.^[1]

5. IEEE 754 on IBM Mainframes

Starting with the S/390 G5 in 1998,^[2] IBM mainframes have also included IEEE binary floating-point units which conform to the IEEE 754 Standard for Floating-Point Arithmetic. IEEE decimal floating-point was added to IBM System z9 GA2^[3] in 2007 using millicode^[4] and in 2008 to the IBM System z10 in hardware.^[5]

Modern IBM mainframes support three floating-point radices with 3 hexadecimal (HFP) formats, 3 binary (BFP) formats, and 3 decimal (DFP) formats. There are two floating-point units per core; one supporting HFP and BFP, and one supporting DFP; there is one register file, FPRs, which holds all 3 formats. Starting with the z13 in 2015, processors have added a vector facility that includes 32 vector registers, each 128 bits wide; a vector register can contain two 64-bit or four 32-bit floating-point numbers.^[6] The traditional 16 floating-point registers are overlaid on the new vector registers so some data can be manipulated with traditional floating-point instructions or with the newer vector instructions.

6. Special Uses

The IBM floating-point format is used in:

• SAS 5 Transport files (.XPT) as required by the Food and Drug Administration (FDA) for New Drug Application (NDA) study submissions,^[7]
• GRIB (GRIdded Binary) data files to exchange the output of weather prediction models (IEEE single-precision floating-point format in current version),
• GDS II (Graphic Database System II) format files (OASIS is the replacement), and
• SEG Y (Society of Exploration Geophysicists Y) format files (IEEE single-precision floating-point was added to the format in 2002).^[8]

As IBM is the only remaining provider of hardware (and only in their mainframes) using their non-standard floating-point format, no popular file format requires it; Except the FDA requires the SAS file format and "All floating-point numbers in the file are stored using the IBM mainframe representation. [...] Most platforms use the IEEE representation for floating-point numbers. [...] To assist you in reading and/or writing transport files, we are providing routines to convert from IEEE representation (either big endian or little endian) to transport representation and back again."^[7] Code for IBM's format is also available under LGPLv2.1.^[9]

7. Systems That Use the IBM Floating-point Format

• IBM System/360
• RCA Spectra 70
• English Electric System 4
• GEC 4000 series minicomputers
• Interdata 16-bit and 32-bit computers
• Texas Instruments 990/12
• Data General minicomputers