Computational Simulations of Heart Valves

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Milan Toma	--	2509	2022-05-09 16:57:38	\|
2	layout	Camila Xu	-36 word(s)	2473	2022-05-10 04:05:51	\|

This entry is adapted from the peer-reviewed paper 10.3390/ma15093302

Computational methods are a cost-effective tool that can be used to evaluate the flow parameters of heart valves. Valve repair and replacement have long-term stability and biocompatibility issues, highlighting the need for a more robust method for resolving valvular disease. For example, while fluid–structure interaction analyses are still scarcely utilized to study aortic valves, computational fluid dynamics is used to assess the effect of different aortic valve morphologies on velocity profiles, flow patterns, helicity, wall shear stress, and oscillatory shear index in the thoracic aorta. It has been analyzed that computational flow dynamic analyses can be integrated with other methods to create a superior, more compatible method of understanding risk and compatibility.

heart valves mitral valve tricuspid valve aortic valve

1. Introduction

The art of heart valve repairs is constantly developing. Leonardo da Vinci conducted studies in animals and did more than 30 human dissections to accurately interpret the anatomy of fresh specimens and the motion of blood in the beating heart through small metallic tracers. Over half a millennia later, researchers are still investigating the movement of blood in the beating heart, albeit by means not available to Leonardo. Noteworthy technological improvements ^[1] have facilitated the evolution of computational methods for heart valve modeling.

The four heart valves include the mitral valve (MV), tricuspid valve (TV), aortic valve (AV), and pulmonary valve (PV). The configurations of the mitral and tricuspid valves are similar, comprising two and three valve leaflets, respectively, with inserted chordae tendineae and anchored to the ventricle walls via papillary muscles. On the other hand, the aortic and pulmonary valves are comprised of three equally sized semilunar cusps or leaflets, which are bound at three commissures. The pressure gradient across each valve controls its opening and closing dynamics. In heart valve disruptions, the design of the valve may be compromised, leading to stenosis (narrowing of the valve) or regurgitation (leakage of the valve). Treatment of these conditions can be surgical, transcatheter, or percutaneous, and include repair or replacement therapies.

Validated using in vitro models, e.g., ^[2], computational models can be used to (i) aid in the development of diagnostic tools, therapeutic instruments, and innovative prostheses for the treatment of heart valve ailments; (ii) indicate surgical consequences for repair or replacement procedures available for heart valve pathologies, or support pre-procedural planning of appropriate transcatheter or percutaneous therapies; (iii) provide help in medical device regulatory recommendations, and (iv) explain the cause-and-effect associations between cardiovascular biology and hemodynamics ^[3]. The latter has the prospect to extend the knowledge of disease evolution and progression, thereby allowing the expansion of new translational technologies, diagnoses, devices, and treatment alternatives ^[4]^[5].

Computational fluid dynamic (CFD) investigations are a cost-effective mechanism that can be used for the high-resolution evaluation of clinically pertinent flow parameters, e.g., wall shear stress and blood damage. These parameters are of interest during the creation and optimization of manufactured heart valves but are challenging to measure in vivo and/or in vitro. Thus, CFD can be used to augment the understanding gained from clinical and empirical reviews of artificial heart valves. To guide in conducting computational studies of transcatheter heart valve prostheses, a position paper was disseminated by an ISO working group ^[6], while more recently, the FDA has formulated procedures for evaluating the credibility of computational modeling and simulation in medical device recommendations ^[7]. Patient-specific modeling has been earning awareness because of its prospect to tailor possible therapies and enhance patient outcomes (e.g., ^[8]^[9]). However, there is presently no traditional practice for the patient-specific evaluation of artificial heart valve performance using CFD. Fully patient-specific computational simulations are fairly new and not yet exhaustively validated for a wide spectrum of applications. Similarly, the use of CFD for heart valve modeling is challenged by the intricacy of the interaction between blood flow and the anatomical and/or device configurations concerned, oftentimes necessitating the usage of more costly and convoluted fluid–structure interaction (FSI) models.

1.1. Heart Valve Repairs/Devices

Numerous studies have been executed to investigate the impact of medical devices on decreasing the stress in diverse MV regions ^[10]^[11]^[12]. While the physio ring is regarded as an improved rendition of the traditional rigid ring, and the physio ring is more widely employed, long-term results of repair for degenerative MV disease with the classic and physio rings are equivalent ^[12]. However, the low incidence of reoperation and late cardiac events indicates that the physio ring, with its intrinsic flexibility, presents an indisputable benefit in the application of remodeling strategies in MV reconstruction ^[13]. Some therapies of choice for chronic ischemic mitral regurgitation annul active annular movement and immobilize the posterior leaflet. In a model of chronic ischemic mitral regurgitation, septal–lateral annular cinching sought to uphold regular annular and leaflet dynamics was tested ^[14]. A decrease of the annulus with an undersized ring has once seemed to be the select surgical choice to rectify ischemic mitral incompetence ^[15]^[16]. Nonetheless, numerous investigations uncovered substantial residual and repeat rates of mild to severe mitral incompetence in 30% of patients within 6 months of surgery ^[17]^[18]^[19]^[20]^[21]. Mitral valve replacement strategies in patients with left ventricular dysfunction are often chaperoned with other techniques for more promising left ventricular remodeling compared with total retention of the mitral subvalvular apparatus during MV replacement ^[22]. Surgical repair is the most routine procedure used to rectify mitral regurgitation. However, the effectiveness of other techniques is still examined. The efficacy of a procedure is specified using an immense combination of factors, such as the durability of the repaired valve as well as the valve’s function and hemodynamics under stress states. Thus, a myriad of studies are carried out to assess these parameters at follow-ups ^[23]^[24]^[25]^[26]. By approximating edge-to-edge repair (to repair ruptured/elongated chords) with chordal replacement, it was discovered that edge-to-edge repair and chordal replacement are sufficiently suited for the restoration of both the anterior and posterior leaflets ^[27]. Regardless, among patients experiencing transcatheter MV edge-to-edge repair with the MitraClip device, a pertinent ratio (2–6%) requires open MV surgery within 1 year after unsuccessful clip implantation ^[28]. Both in vivo and in silico examinations evaluated the combined force transfer from the papillary muscle tips to the MV via the chordae tendineae, and thereby quantified the force shared through the papillary–chordal complex to augment left ventricular ejection ^[29]^[30].

1.2. Repair versus Replacement

The outcomes underscore the significance of early detection and research of mitral regurgitation ^[31]. The most satisfactory short-term and long-term results are gained in asymptomatic patients worked on in state-of-the-art repair centers with low operative mortality and high repair rates ^[32]. The durability of a successful mitral reconstruction for degenerative MV condition is not consistent, and this should be accepted when asymptomatic patients are proposed early MV repair ^[33]. Early diagnosis and surgery are paramount as a life-saving standard for infants with acute MV chordal rupture ^[25]^[34]. The unique vision of staging of the valvular diseases, newer predictors, and controversy of “watchful waiting” versus “early surgical intervention” for severe, asymptomatic, primary mitral regurgitation are examined in a study that outlines the current interpretation of primary, degenerative mitral regurgitation concerning etiology, complete examination, natural history, and control ^[35]. Based upon a sounder knowledge of the natural history of mitral regurgitation, the unsatisfactory effects of medical therapies, the adverse consequence of anomalous left ventricular dimensions and function, and manifestations of long-term survival, a directive presently exists for early surgical repair of mitral regurgitation before the start of symptoms and considerable left ventricular dysfunction ^[36]. New valve pathology after a repair oftentimes results in recurrent mitral regurgitation. Successive mitral re-repair is conducted in nearly half of patients and is associated with outstanding survival, enhanced ejection fraction, and more significant regression in ventricular proportions compared with valve replacement ^[37]^[38]. However, an observational analysis found that MV repair in coronary artery bypass grafting patients with ischaemic mitral regurgitation and depressed left ventricular ejection fraction is not incomparable to mitral valve replacement concerning operative early mortality and mid-term survival ^[39]. A meta-analysis of randomized controlled trials and adjusted observational studies demonstrated that for patients with ischemic mitral regurgitation, MV repair seems to be unassociated with a noteworthy reduction in both early and late all-cause mortality compared with MV replacement ^[40]. The mechanisms of MV repair failure as well as aspects that meaningfully impact the probability of a successful re-repair can be located in ^[41]. When comparing MV re-repair versus replacement following failed initial repair, it was uncovered that they are associated with comparable postoperative outcomes ^[42]. Repair of rheumatic MVs has been met with narrow success. Due to residual diseased leaflet tissue, the hemodynamic obstruction continually endures after repair. An assertive strategy to rheumatic MV repair with extreme excision of the diseased leaflets area, and subvalvular apparatus and subsequent reconstruction, intending to extract all diseased valvular tissue, was devised and executed ^[43]. Data comparing processes of MV repair and replacement for ischemic mitral regurgitation are primarily restricted to small, non-randomized retrospective trials ^[44]. The only randomized trial data to investigate this topic indicated no distinction in mortality with either replacement or repair; however, the replacement was shown to be invariably associated with higher rates of mitral regurgitation recurrence ^[44]. Regardless, the use of replacement heart valves persists to grow due to the raised preponderance of valvular heart disorders resulting from an aging population ^[45].

2. Computational Simulations

To determine the coupling between the fluid and structural domains, FSI strategies are utilized. Particularly in computational simulations meant to imitate the functions inside the human body, intricate dynamics are present, e.g., heart valves opening and closing every second interacting with blood flow. Consequently, for physiologically authentic simulations, the fluid dynamics associated with the valves, the structural mechanics of the valves, and tissue characteristics, should be modeled concurrently. Nonetheless, standard FSI studies present several challenges, e.g., considerable extra computation time.

FSI simulations can be separated into three significant classifications: (1) Pseudo-state simulations are generally used to investigate the downstream flow domains of heart valves under the supposition that the valve is unmoving, and they can be modeled utilizing ordinary computational fluid dynamics strategies for flow fields ^[46]. (2) One-way FSI lets heart valves move under a stipulated geometric deformation. The prescribed structure dynamic movement impacts the fluid flow but not contrariwise. In two-way FSI (3), the most demanding type of FSI simulation, the structural and fluid fields influence one another. The structural model of a two-way FSI solver requires adequately representing material properties and the interaction between the leaflets and the surrounding fluid. Naturally, most two-way FSI solvers can solve one-way FSI problems.

Two techniques are utilized for the coupling between the fluid and structure domains. (A) Partitioned technique: The fluid and solid domains are treated individually with two separate solvers (Figure 1a). Communication between the two solvers is passed along their domain interface. Since each domain is solved employing a different solver, autonomous numerical algorithms can be involved to solve the fluid and solid equations. Consequently, less memory storage is demanded compared to the monolithic approach. However, in the FSI heart valves simulations, which typically include large deformations, this technique tends to face converge issues due to stability problems ^[46]. (B) Monolithic approach: The fluid and structural domains are solved simultaneously by discretizing the problem into a single system of equations employing a single numerical algorithm ^[47]. This generates fewer convergence issues since the joint impact of the two domains on one another is incorporated directly. However, for extensive 3D problems, with a high number of degrees of freedom, a prohibitive quantity of memory storage is required.

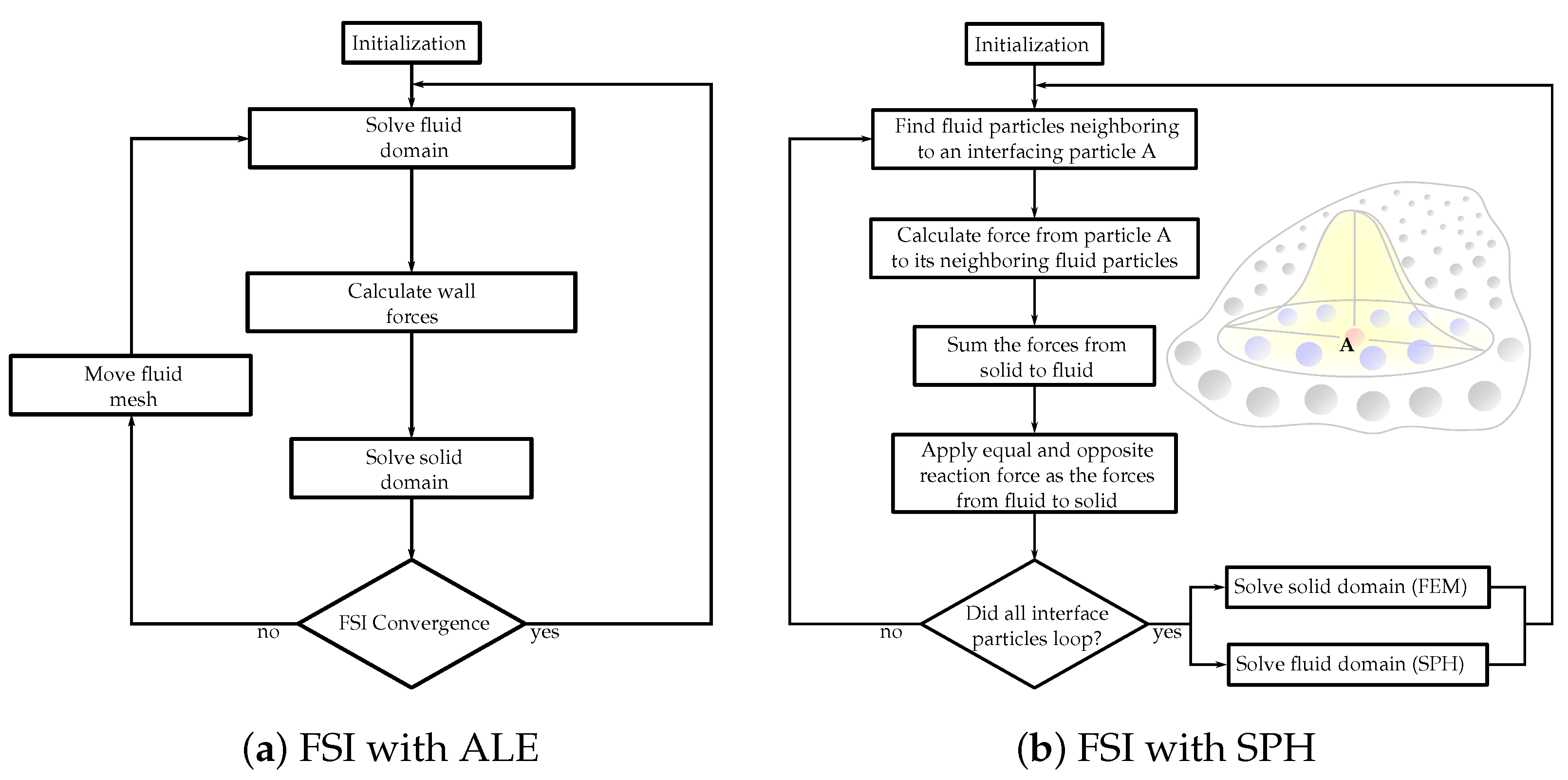Figure 1. Flowcharts of the FSI solution algorithms with (a) arbitrary Lagrangian–Eulerian (ALE) and (b) smoothed-particle hydrodynamics (SPH) methods.

An alternative method to classify FSI techniques is to (1) body-fitted and (2) non-body-fitted methods. This categorization depends on whether the computational fluid domain mesh conforms to the borders of the computational solid domain mesh. The Arbitrary Lagrangian–Eulerian (ALE) approach is an illustration of a body-fitted method, and the Immersed-Boundary (IB) method is one of the non-body-fitted methods. The IB approach is an efficient way of modeling fluid–structure interactions. Numerical simulations employing coupled MV and left ventricle models are devised utilizing IB and finite element methods (FEM) ^[48]. An FSI model of the left atrium and MV employing an IB-FEM framework is utilized in ^[49] to examine the impacts of diverse pathological conditions. Regardless, it bears two major constraints: namely, the difficulty of use and capacity to model static loading. Additionally, one other thing can be detected in all the IB analyses, i.e., 3D models employed seem to be geometrically streamlined with the purpose of evading computational instability and convergence problems.

Thus far, the ALE approach is the most traditional technique embraced in industrial applications. This conforming mesh method divides the computational domains associated with the structure and fluid. Considering the extensive deformation of the heart valve structures together with the connection between the fluid and solid elements, it demands mesh adaptations for the fluid domain, which significantly diminishes computational efficiency and results in poor mesh quality. Since remeshing is essential, it may result in artificial diffusivity and instabilities. The IB method embeds the structure to the static fluid mesh implicitly, which delivers a significant benefit for simulating largely moving/morphing structures. Nevertheless, the near-wall flow resolution of the leaflets of the IB approach may be inadequate to the ALE method.

Peskin et al., in 1997, presented FSI simulations in prosthetic and biological heart valve models with the muscular heart wall retained. Their models depicted the capacity to apply Navier–Stokes equations to moving solid immersed boundaries ^[50]. In 2003, Tang et al. employed a 3D thick-wall model to imitate blood flow in the carotid arteries and presented asymmetric stenosis to quantify the impact of stenosis while mimicking the pressure conditions on blood flow and artery contraction ^[51]. This strategy was then expanded upon, including geometries reconstructed from CT scans well resembling the intricate anatomy of the human artery ^[52]^[53]. The usage of traditional mesh-based numerical procedures for biomedical applications remains a challenge, and it is nevertheless the standard approach to streamline the computational models by skipping the fluid domain ^[54]. However, lately, studies can be encountered demonstrating the benefit of smoothed-particle hydrodynamics (SPH) techniques, as shown in Figure 1b, for accurately executing simulations even within the context of blood flow and thrombosis ^[55]. A more thorough overview of FSI algorithms employed to simulate heart valves can be found in ^[56].

The intricacy of computational simulations that involve heart valves (e.g., complex geometries and large deformations) makes SPH well suited to execute these FSI calculations, namely SPH methods mixed with high-order FEM. Employing SPH methods brings numerical stability because the communication between the solid and fluid domains is fairly straightforward to treat numerically. Moreover, it is more manageable to parallelize SPH. Consequently, it is achievable to run FSI simulations with convoluted geometries, i.e., conserving all their geometrical details; and, at the same time, maintaining the simulations numerically steady, accurate, and parallelized on a standard GPU workstation. Thus, the user can run these complicated simulations “under the table” rather than on large supercomputers, with the typical runtime being only hours/days as opposed to weeks/months.

References

Fedele, M.; Quarteroni, A. Polygonal surface processing and mesh generation tools for the numerical simulation of the cardiac function. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3435.
Stephens, S.E.; Kammien, A.J.; Paris, J.C.; Applequist, A.P.; Ingels, N.B.; Jensen, H.K.; Rodgers, D.E.; Cole, C.R.; Wenk, J.F.; Jensen, M.O. In Vitro Mitral Valve Model with Unrestricted Ventricular Access: Using Vacuum to Close the Valve and Enable Static Trans-Mitral Pressure. J. Cardiovasc. Transl. Res. 2022, 1–10.
Atkins, S.; McNally, A.; Sucosky, P. Mechanobiology in Cardiovascular Disease Management: Potential Strategies and Current Needs. Front. Bioeng. Biotechnol. 2016, 4, 79.
Dasi, L.P.; Sucosky, P.; De Zelicourt, D.; Sundareswaran, K.; Jimenez, J.; Yoganathan, A.P. Advances in Cardiovascular Fluid Mechanics: Bench to Bedside. Ann. N. Y. Acad. Sci. 2009, 1161, 1–25.
Toma, M.; Addepalli, D.; Chan-Akeley, R. The Intricacies of Computational Medical Research: An Advanced Study Approach. Recent Dev. Med. Med. Res. 2021, 4, 71–83.
Wei, Z.A.; Sonntag, S.J.; Toma, M.; Singh-Gryzbon, S.; Sun, W. Computational Fluid Dynamics Assessment Associated with Transcatheter Heart Valve Prostheses: A Position Paper of the ISO Working Group. Cardiovasc. Eng. Technol. 2018, 9, 289–299.
Food and Drug Administration. Assessing the Credibility of Computational Modeling and Simulation in Medical Device Submissions, Draft Guidance for Industry and Food and Drug Administration Staff; U.S. Department of Health and Human Services Food and Drug Administration Center for Devices and Radiological Health: Rockville, MD, USA, 2022.
Ammarullah, M.I.; Afif, I.Y.; Maula, M.I.; Winarni, T.I.; Tauviqirrahman, M.; Akbar, I.; Basri, H.; van der Heide, E.; Jamari, J. Tresca Stress Simulation of Metal-on-Metal Total Hip Arthroplasty during Normal Walking Activity. Materials 2021, 14, 7554.
Jamari, J.; Ammarullah, M.; Saad, A.; Syahrom, A.; Uddin, M.; van der Heide, E.; Basri, H. The Effect of Bottom Profile Dimples on the Femoral Head on Wear in Metal-on-Metal Total Hip Arthroplasty. J. Funct. Biomater. 2021, 12, 38.
Toma, M.; Einstein, D.R.; Kohli, K.; Caroll, S.L.; Iv, C.H.B.; Cochran, R.P.; Kunzelman, K.S.; Yoganathan, A.P.; Bloodworth, C. Effect of Edge-to-Edge Mitral Valve Repair on Chordal Strain: Fluid-Structure Interaction Simulations. Biology 2020, 9, 173.
Jimenez, J.H.; Liou, S.W.; Padala, M.; He, Z.; Sacks, M.; Gorman, R.C.; Gorman, J.H.; Yoganathan, A.P. A saddle-shaped annulus reduces systolic strain on the central region of the mitral valve anterior leaflet. J. Thorac. Cardiovasc. Surg. 2007, 134, 1562–1568.
Sidiki, A.I.; Faybushevich, A.G.; Lishchuk, A.N.; Koltunov, A.N.; Roshchina, E.A. The Carpentier-Edwards Classic And Physio Annuloplasty Rings in Repair of Degenerative Mitral Valve Disease: A Retrospective Study. J. Saudi Heart Assoc. 2020, 32, 224–232.
Accola, K.D.; Scott, M.L.; Thompson, P.A.; Palmer, G.J.; Sand, M.E.; Ebra, G. Midterm Outcomes Using the Physio Ring in Mitral Valve Reconstruction: Experience in 492 Patients. Ann. Thorac. Surg. 2005, 79, 1276–1283.
A Tibayan, F.; Rodriguez, F.; Langer, F.; Zasio, M.K.; Bailey, L.; Liang, D.; Daughters, G.T.; Ingels, N.B.; Miller, D. Does septal-lateral annular cinching work for chronic ischemic mitral regurgitation? J. Thorac. Cardiovasc. Surg. 2004, 127, 654–663.
2006 WRITING COMMITTEE MEMBERS; Bonow, R.O.; Carabello, B.A.; Chatterjee, K.; De Leon, A.C.; Faxon, D.P.; Freed, M.D.; Gaasch, W.H.; Lytle, B.W.; Nishimura, R.A.; et al. 2008 Focused Update Incorporated Into the ACC/AHA 2006 Guidelines for the Management of Patients with Valvular Heart Disease. Circulation 2008, 118, e523–e661.
Romano, A.M.; Bolling, S.F. Mitral valve repair as an alternative treatment for heart failure patients. Heart Fail. Monit. 2003, 4, 7–12.
McGee, E.C.; Gillinov, A.M.; Blackstone, E.H.; Rajeswaran, J.; Cohen, G.; Najam, F.; Shiota, T.; Sabik, J.F.; Lytle, B.W.; McCarthy, P.M.; et al. Recurrent mitral regurgitation after annuloplasty for functional ischemic mitral regurgitation. J. Thorac. Cardiovasc. Surg. 2004, 128, 916–924.
Hung, J.; Papakostas, L.; Tahta, S.A.; Hardy, B.G.; Bollen, B.A.; Duran, C.M.; Levine, R.A. Mechanism of Recurrent Ischemic Mitral Regurgitation After Annuloplasty. Circulation 2004, 110, II-85–II-90.
Matsunaga, A.; A Tahta, S.; Duran, C.M. Failure of reduction annuloplasty for functional ischemic mitral regurgitation. J. Heart Valve Dis. 2004, 13, 390–398.
Gelsomino, S.; Lorusso, R.; De Cicco, G.; Capecchi, I.; Rostagno, C.; Caciolli, S.; Romagnoli, S.; Da Broi, U.; Stefàno, P.; Gensini, G.F. Five-year echocardiographic results of combined undersized mitral ring annuloplasty and coronary artery bypass grafting for chronic ischaemic mitral regurgitation. Eur. Heart J. 2007, 29, 231–240.
A Tahta, S.; Oury, J.H.; Maxwell, J.M.; Hiro, S.P.; Duran, C.M.G. Outcome after mitral valve repair for functional ischemic mitral regurgitation. J. Heart Valve Dis. 2002, 11, 11–18.
Yousefnia, M.A.; Mandegar, M.H.; Roshanali, F.; Alaeddini, F.; Amouzadeh, F. Papillary Muscle Repositioning in Mitral Valve Replacement in Patients With Left Ventricular Dysfunction. Ann. Thorac. Surg. 2007, 83, 958–963.
Minardi, G.; Manzara, C.; Pulignano, G.; Luzi, G.; Maselli, D.; Casali, G.; Musumeci, F. Rest and Dobutamine stress echocardiography in the evaluation of mid-term results of mitral valve repair in Barlow’s disease. Cardiovasc. Ultrasound 2007, 5, 17.
Seeburger, J.; Borger, M.; Doll, N.; Walther, T.; Passage, J.; Falk, V.; Mohr, F.W. Comparison of outcomes of minimally invasive mitral valve surgery for posterior, anterior and bileaflet prolapse. Eur. J. Cardio-Thorac. Surg. 2009, 36, 532–538.
Minami, K.; Kado, H.; Sai, S.; Tatewaki, H.; Shiokawa, Y.; Nakashima, A.; Fukae, K.; Hirose, H. Midterm results of mitral valve repair with artificial chordae in children. J. Thorac. Cardiovasc. Surg. 2005, 129, 336–342.
Croft, L.R.; Jimenez, J.H.; Gorman, R.C.; Gorman, J.H.; Yoganathan, A.P. Efficacy of the Edge-to-Edge Repair in the Setting of a Dilated Ventricle: An In Vitro Study. Ann. Thorac. Surg. 2007, 84, 1578–1584.
Espino, D.M.; Hukins, D.W.L.; Shepherd, D.E.T.; Buchan, K.G. Mitral valve repair: An in-vitro comparison of the effect of surgical repair on the pressure required to cause mitral valve regurgitation. J. Heart Valve Dis. 2006, 15, 375–381.
Melillo, F.; Baldetti, L.; Beneduce, A.; Agricola, E.; Margonato, A.; Godino, C. Mitral valve surgery after a failed MitraClip procedure. Interact. Cardiovasc. Thorac. Surg. 2020, 32, 380–385.
Askov, J.B.; Honge, J.L.; Jensen, M.O.; Nygaard, H.; Hasenkam, J.M.; Nielsen, S.L. Significance of force transfer in mitral valve–left ventricular interaction: In vivo assessment. J. Thorac. Cardiovasc. Surg. 2013, 145, 1635–1641.e1.
Toma, M.; Jensen, M.; Einstein, D.R.; Yoganathan, A.P.; Cochran, R.P.; Kunzelman, K.S. Fluid–Structure Interaction Analysis of Papillary Muscle Forces Using a Comprehensive Mitral Valve Model with 3D Chordal Structure. Ann. Biomed. Eng. 2015, 44, 942–953.
Dalrymple-Hay, M.J.; Bryant, M.; A Jones, R.; Langley, S.M.; A Livesey, S.; Monro, J.L. Degenerative mitral regurgitation: When should we operate? Ann. Thorac. Surg. 1998, 66, 1579–1583.
Enriquez-Sarano, M.; Akins, C.W.; Vahanian, A. Mitral regurgitation. Lancet 2009, 373, 1382–1394.
Flameng, W.; Herijgers, P.; Bogaerts, K. Recurrence of Mitral Valve Regurgitation After Mitral Valve Repair in Degenerative Valve Disease. Circulation 2003, 107, 1609–1613.
Asakai, H.; Kaneko, Y.; Kaneko, M.; Misaki, Y.; Achiwa, I.; Hirata, Y.; Kato, H. Acute Progressive Mitral Regurgitation Resulting From Chordal Rupture in Infants. Pediatr. Cardiol. 2011, 32, 634–638.
Maslow, A.D.; Poppas, A.; Apostolidou, E. Primary mitral valve regurgitation: Update and review. Glob. Cardiol. Sci. Pract. 2017, 2017, e201703.
Northrup, W.F. Mitral valve repair: We must do a better job. Curr. Cardiol. Rep. 2005, 7, 94–100.
Suri, R.M.; Schaff, H.V.; Dearani, J.A.; Sundt, T.M.; Daly, R.C.; Mullany, C.J.; Enriquez-Sarano, M.; Orszulak, T.A. Recurrent mitral regurgitation after repair: Should the mitral valve be re-repaired? J. Thorac. Cardiovasc. Surg. 2006, 132, 1390–1397.
Aphram, G.; De Kerchove, L.; Mastrobuoni, S.; Navarra, E.; Solari, S.; Tamer, S.; Baert, J.; Poncelet, A.; Rubay, J.; Astarci, P.; et al. Re-repair of the failed mitral valve: Insights into aetiology and surgical management. Eur. J. Cardio-Thorac. Surg. 2018, 54, 774–780.
Lio, A.; Miceli, A.; Varone, E.; Canarutto, D.; Di Stefano, G.; Della Pina, F.; Gilmanov, D.; Murzi, M.; Solinas, M.; Glauber, M. Mitral valve repair versus replacement in patients with ischaemic mitral regurgitation and depressed ejection fraction: Risk factors for early and mid-term mortality. Interact. Cardiovasc. Thorac. Surg. 2014, 19, 64–69.
Takagi, H.; Umemoto, T. Similar Survival After Repair vs Replacement for Ischemic Mitral Regurgitation. Semin. Thorac. Cardiovasc. Surg. 2016, 28, 748–756.
A Moore, R.; Gillinov, A.M.; Burns, D.J.; Pettersson, G.B.; Wierup, P. Techniques for Mitral Valve Re-repair. Oper. Tech. Thorac. Cardiovasc. Surg. 2021, 26, 42–65.
Veerappan, M.; Cheekoty, P.; Sazzad, F.; Kofidis, T. Mitral valve re-repair vs replacement following failed initial repair: A systematic review and meta-analysis. J. Cardiothorac. Surg. 2020, 15, 304.
El Oumeiri, B.; Boodhwani, M.; Glineur, D.; De Kerchove, L.; Poncelet, A.; Astarci, P.; Pasquet, A.; Vanoverschelde, J.-L.; Verhelst, R.; Rubay, J.; et al. Extending the Scope of Mitral Valve Repair in Rheumatic Disease. Ann. Thorac. Surg. 2009, 87, 1735–1740.
Sharma, A.; Agrawal, S.; Goel, S.; Borer, J.S. Surgical Treatment of Ischemic Mitral Regurgitation: Valve Repair Versus Replacement. Curr. Cardiol. Rep. 2017, 19, 3.
Soares, J.S.; Feaver, K.R.; Zhang, W.; Kamensky, D.; Aggarwal, A.; Sacks, M.S. Biomechanical Behavior of Bioprosthetic Heart Valve Heterograft Tissues: Characterization, Simulation, and Performance. Cardiovasc. Eng. Technol. 2016, 7, 309–351.
Ge, L.; Jones, S.C.; Sotiropoulos, F.; Healy, T.M.; Yoganathan, A.P. Numerical Simulation of Flow in Mechanical Heart Valves: Grid Resolution and the Assumption of Flow Symmetry. J. Biomech. Eng. 2003, 125, 709–718.
Toma, M.; Oshima, M.; Takagi, S. Decomposition and parallelization of strongly coupled fluid-structure interaction linear subsystems based on the Q1/P0 discretization. J. Comput. Struct. 2016, 173, 84–94.
Gao, H.; Feng, L.; Qi, N.; Berry, C.; Griffith, B.; Luo, X. A coupled mitral valve—left ventricle model with fluid–structure interaction. Med. Eng. Phys. 2017, 47, 128–136.
Feng, L.; Gao, H.; Griffith, B.; Niederer, S.A.; Luo, X. Analysis of a coupled fluid-structure interaction model of the left atrium and mitral valve. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3254.
Peskin, C.S. Numerical analysis of blood flow in the heart. J. Comput. Phys. 1977, 25, 220–252.
Tang, D.; Yang, C.; Kobayashi, S.; Zheng, J.; Vito, R.P. Effect of Stenosis Asymmetry on Blood Flow and Artery Compression: A Three-Dimensional Fluid-Structure Interaction Model. Ann. Biomed. Eng. 2003, 31, 1182–1193.
Wong, K.; Fong, F.; Wang, D. Computational evaluation of smoothed particle hydrodynamics for implementing blood flow modelling through CT reconstructed arteries. J. Ray Sci. Technol. 2017, 25, 213–232.
Nasar, A. Eulerian and Lagrangian Smoothed Particle Hydrodynamics as Models for the Interaction of Fluids and Flexible Structures in Biomedical Flows. Ph.D. Thesis, The University of Manchester (United Kingdom), PQDT-UK & Ireland, Manchester, UK, 2016.
Hron, J.; Mádlík, M. Fluid-structure interaction with applications in biomechanics. Nonlinear Anal. Real World Appl. 2007, 8, 1431–1458.
Al-Saad, M.; Suarez, C.A.; Obeidat, A.; Bordas, S.P.A.; Kulasegaram, S. Application of Smooth Particle Hydrodynamics Method for Modelling Blood Flow with Thrombus Formation. Comput. Model. Eng. Sci. 2020, 122, 831–862.
Le, T.B.; Usta, M.; Aidun, C.; Yoganathan, A.; Sotiropoulos, F. Computational Methods for Fluid-Structure Interaction Simulation of Heart Valves in Patient-Specific Left Heart Anatomies. Fluids 2022, 7, 94.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Engineering, Biomedical; Physics, Mathematical; Cardiac & Cardiovascular Systems

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

View Times: 681

Entry Collection: Hypertension and Cardiovascular Diseases

Update Date: 10 May 2022

Table of Contents

Video Upload Options

Confirm