Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Zongwei Liang	--	2056	2022-04-19 09:44:11	\|
2	Adjust the reference format	Lindsay Dong	+ 934 word(s)	2990	2022-04-20 03:24:27	\| \|
3	Adjust the Latex format	Lindsay Dong	-3 word(s)	2987	2022-04-20 03:34:00	\| \|
4	Adjust figure legend	Lindsay Dong	Meta information modification	2987	2022-04-20 03:41:31	\| \|
5	Adjust the Latex format	Lindsay Dong	Meta information modification	2987	2022-04-21 08:13:52	\| \|
6	Reference format revised.	Lindsay Dong	Meta information modification	2987	2022-04-21 08:16:42	\|

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?

No, upload directly Yes

Confirm

Are you sure to Delete?

Yes No

Cite

If you have any further questions, please contact Encyclopedia Editorial Office.

Select a Style

Liang, Z.; Yang, J.; Liu, H.; Huang, K.; , . SeAttE—Embedding Model Based on Knowledge Graph Completion. Encyclopedia. Available online: https://encyclopedia.pub/entry/21920 (accessed on 26 December 2024).

Liang Z, Yang J, Liu H, Huang K, . SeAttE—Embedding Model Based on Knowledge Graph Completion. Encyclopedia. Available at: https://encyclopedia.pub/entry/21920. Accessed December 26, 2024.

Liang, Zongwei, Jun-An Yang, Hui Liu, Keju Huang, . "SeAttE—Embedding Model Based on Knowledge Graph Completion" Encyclopedia, https://encyclopedia.pub/entry/21920 (accessed December 26, 2024).

Liang, Z., Yang, J., Liu, H., Huang, K., & , . (2022, April 19). SeAttE—Embedding Model Based on Knowledge Graph Completion. In Encyclopedia. https://encyclopedia.pub/entry/21920

Liang, Zongwei, et al. "SeAttE—Embedding Model Based on Knowledge Graph Completion." Encyclopedia. Web. 19 April, 2022.

SeAttE—Embedding Model Based on Knowledge Graph Completion

Edit

This entry is adapted from the peer-reviewed paper 10.3390/electronics11071058

SeAttE is a novel tensor ecomposition model based on Separating Attribute space for knowledge graph completion. SeAttE is the first model among the tensor decomposition family to consider the attribute space separation task. Furthermore, SeAttE transforms the learning of too many parameters for the attribute space separation task into the structure’s design. This operation allows the model to focus on learning the semantic equivalence between relations, causing the performance to approach the theoretical limit.

NLP knowledge graphs knowledge representation link prediction attribute space

1. Introduction

Knowledge Graphs (KGs) are collections of large-scale triples, such as Freebase ^[1], YAGO ^[2] and DBpedia ^[3]. KGs play a crucial role in applications such as question answering services, search engines, and smart medical care. Although there are billions of triples in KGs, they are still incomplete. These incomplete knowledge bases will bring limitations to practical applications ^[4].

Researchers recently tried to solve the task of link prediction through knowledge graph embedding. Knowledge graph embedding models map entities and relations into low-dimensional vectors (or matrices, tensors), measure the rationality of triples through specific score functions between entities and relations, and rank the triples with scores. TransE ^[1] first proposes to utilize relation vectors as the geometric distance between entities. Then many variants emerge.

The tensor decomposition models ^[5]^[6]^[7]^[8]^[9]^[10]^[11] are a family of which the inference performance is relatively good among these variants. RESCAL ^[5] is the basic tensor decomposition model, which is the first tensor decomposition model. Since RESCAL ^[5] represents the relations as a matrix, the large number of parameters makes it difficult for the model to learn effectively. So DisMult ^[6] directly diagonalizes the matrix, which takes the relations as vectors. This operation significantly reduces the number of parameters. There are a large number of complex relation types in the knowledge graphs. However, DisMult is an over-simplified model, which cannot describe complex relations. Then subsequent variants are invented to describe more types of relations, such as asymmetric and hierarchical relations, which are equivalent to designing unique structures for description of specific types of relations. For example, ComplEx ^[7], similarly to DistMult ^[6], forces each relation embedding to be a diagonal matrix but extends such formulation in the complex space. Analogy ^[12] aims at modeling analogical reasoning, which is crucial for any knowledge induction. It employs the general bilinear scoring function but adds two main constraints inspired by analogical structures. TuckER ^[8] relies on the Tucker decomposition ^[13], which factorizes a tensor into a set of vectors and a smaller shared core. SimplE ^[9] forces relation embeddings to be diagonal matrices, similarly to DistMult ^[6], but extends it by associating two separate embeddings with each entity and associating two separate diagonal matrices with each relation. These models mainly explore particular regularization to improve performance. No matter how sophisticated the design of such tensor decomposition models is, they find it difficult to surpass the basic tensor decomposition model theoretically. In addition, the previous tensor decomposition models do not consider the problem of attribute separation. The unnoticed task of attribute separation in the traditional models is just handed over to the training. However, the amount of parameters for this task is tremendous, and the model is prone to overfitting.

In practice, entities are collections of attributes, and different entities can contain various semantic attributes. Comparing triples with different relations should only select specific attributes for comparison. Figure 1 shows the comparison of boxes with the same shape and different colors. A novel model—a tensor decomposition model based on separating attribute space for knowledge graph completion (SeAttE) was proposed. SeAttE transfers the large-parameter learning for the attribute space separation task in traditional tensor decomposition models to the model structure design.

/media/item_content/202204/625f597f92b04electronics-11-01058-g001.png

Figure 1. Comparison of boxes with the same shape and different colors.

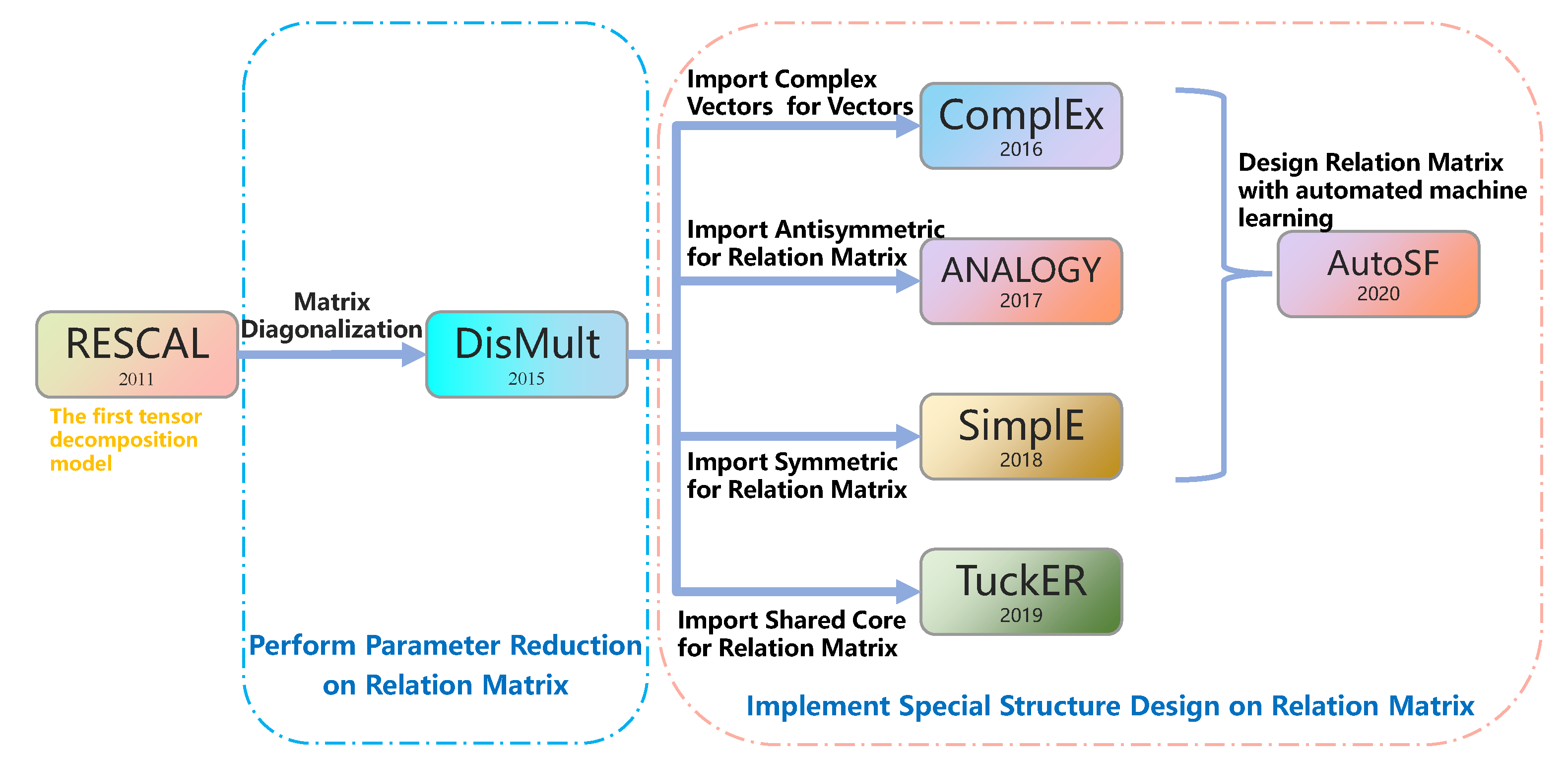
2. Related Work and Critical Differences

Tensor Decomposition Models. These models implicitly consider triples as tensor decomposition. DistMult ^[6] constrains all relation embeddings to be diagonal matrices, which reduces the space of parameters to access a more accessible model to train. RESCAL ^[5] represents each relationship with a total rank matrix. ComplEx ^[7] extends the KG embeddings to the complex space to better model asymmetric and inverse relations. Analogy ^[12] employs the general bilinear scoring function but adds two main constraints inspired by analogical structures. Based on the Tucker decomposition, TuckER ^[8] factorizes a tensor into a set of vectors and a smaller shared core matrix. SimplE ^[9] is a simple enhancement of CP to allow the two embeddings of each entity to be learned dependently. HolE ^[11] is a multiplicative model that is isomorphic to ComplEx ^[7]. Inspired by the recent success of automated machine learning (AutoML), AutoSF ^[10] proposes to automatically design scoring functions for distinct KGs by the AutoML techniques. QuatDE ^[14] captures the variety of relational patterns and separates different semantic information of the entity, using transition vectors to adjust the point position of the entity embedding vectors in the quaternion space via Hamilton product, enhancing the feature interaction capability between elements of the triplet. DensE ^[15] develops a novel knowledge graph embedding method to provide an improved modeling scheme for the complex composition patterns of relations.

Geometric Models. Geometric Models interpret relations as geometric transformations in the latent space. TransE ^[1] is the first translation-based method, which treats relations as translation operations from the head entities to the tail entities. Along with TransE ^[1], multiple variants, including TransH ^[16], TransR ^[17] and TransD ^[18], are proposed to improve the embedding performance of KGs. Recently, RotatE ^[19] defines each relation as a rotation from head entities to tail entities. Inspired by the fact that concentric circles in the polar coordinate system can naturally reflect the hierarchy, HAKE ^[20] maps entities into the polar coordinate system. HAKE ^[20] can effectively model the semantic hierarchies in knowledge graphs. OTE ^[21] proposes a distance-based knowledge graph embedding. First, OTE extends the modeling of RotatE from 2D complex domain to high dimensional space with orthogonal relation transforms. Second, graph context is proposed to integrate graph structure information into the distance scoring function to measure the plausibility of the triples during training and inference.

Deep Learning Models. Deep Learning Models use deep neural networks to perform knowledge graph completion. ConvE ^[22] and ConvKB ^[23] employ convolutional neural networks to define score functions. CapsE ^[24] embeds entities and relations into one-dimensional vectors under the basic assumption that different embeddings encode homologous aspects in the same positions. CompGCN ^[25] utilizes graph convolutional networks to update the knowledge graph embedding. Neural Tensor Network (NTN) combines E-MLP with several bilinear parts. Nathani ^[26] proposes a novel attention-based feature embedding that captures both entity and relation features in any given entity’s neighborhood. RLH ^[27] is inspired by the hierarchical structure through which a human being handles cognitionally ambiguous cases. The whole reasoning process is decomposed into a hierarchy of two-level Reinforcement Learning policies for encoding historical information and learning structured action space. R2D2 ^[28] is a novel method for automatic reasoning on knowledge graphs based on debate dynamics. R2D2 is to frame the task of triple classification as a debate game between two reinforcement learning agents which extract arguments-paths in the knowledge graph—with the goal to promote the fact being true (thesis) or the fact being false (antithesis), respectively. RNNLogic ^[29] is a probabilistic model. RNNLogic treats logic rules as a latent variable, and simultaneously trains a rule generator as well as a reasoning predictor with logic rules. MADLINK ^[30] introduces an attentive encoder–decoder-based link prediction approach considering both structural information of the KG and the textual entity descriptions.

There are also other models, such as DURA ^[31], which are proposed to solve overfitting. RuleGuider ^[32] leverages high-quality rules generated by symbolic-based methods to provide reward supervision for walk-based agents. SFBR ^[33] provides a relation-based semantic filter to extract the attributes that need to be compared and suppress the irrelevant attributes of entities. Together, most of the above studies intend to find a more robust representing approach. Measuring the effectiveness of certain triples is to compare the matching degree of specific attributes based on relations. Only a few models, such as TransH ^[16], TransR ^[17], and TransD ^[18], consider that entities in different triples should have different representation. However, these variants require many resources occupations and are limited to particular models.

3. Background

3.1. KG Completion and Notations

KGs are collections of factual triples $K = \{(h, r, t), h, t \in E, r \in R\}$ , where $(h, r, t)$ represents a triple in the knowledge graph, $h, t, r$ are head, tail entities and relations, respectively. Scholars associates the entities $h, t$ and relations r with vectors $h, t, r \in R^{d}$ in knowledge graph embedding. Then scholars design an appropriate scoring function $d_{r} (h, t)$ , to map the embedding of the triple to a certain score. For a particular question $(h, r, ?)$ , the task of KG completion is ranking all possible answers and obtain the preference of prediction.

Using $W_{r} \in R^{d \times d}$ and $r \in R^{d}$ to distinguish matrix representation and vector representation of the relations, respectively. T, ⟨⋅⟩ and ∘ denote the operation of transpose, the generalized dot product and the Hadamard product, respectively. Especially, scholars utilize $r_{S e A t t E}$ to represent the matrix of relation in SeAttE. Let ∥∥, $diag$ () and $Re$ () denote the $L_{2}$ norm, matrix diagonalization and the real part of complex vectors.

3.2. Basic Models

Tensor Factorization Models. Models in this family interpret link prediction as a task of tensor decomposition, where triples are decomposed into a combination (e.g., a multi-linear product) of low-dimensional vectors for entities and relations. CP ^[34] represents triples with canonical decomposition. Note that the same entity has different representations at the head and tail of the triplet. The score function can be expressed as:

$\begin{matrix} d_{r} (h, t) = ∥h^{T} rt∥ \end{matrix}$

where $h, r, t \in R^{k}$ .

RESCAL ^[5] represents a relation as a matrix $W_{r} \in R^{d \times d}$ that describes the interactions between latent representations of entities. The score function is defined as:

$\begin{matrix} d_{r} (h, t) = ∥h^{T} W_{r} t∥ \end{matrix}$

DistMult ^[6] forces all relations to be diagonal matrices, which consistently reduces the space of parameters to be learned, resulting in a much easier model to train. On the other hand, this makes the scoring function commutative, which amounts to treating all relations as symmetric.

$\begin{matrix} d_{r} (h, t) = ∥h^{T} W_{r} t∥ \end{matrix}$

where $W_{r} = diag (w_{1}, w_{2}, \dots, w_{n})$ .

ComplEx ^[7] extends the real space to complex spaces and constrains the embeddings for relation to be a diagonal matrix. The bilinear product becomes a Hermitian product in complex spaces. The score function can be expressed as:

$\begin{matrix} d_{r} (h, t) = Re (h^{T} diag (r) t) \end{matrix}$

where $h, r, t \in C^{k}$ .

4. SeAttE Model

4.1. Motivation and Design of SeAttE

4.1.1. Motivation

As shown in Figure 2, RESCAL is the basic tensor decomposition model. Since RESCAL represents the relations as a matrix, the large number of parameters makes it difficult for the model to learn effectively. So DisMult directly diagonalizes the matrix, significantly reducing the number of parameters. However, over-simplified models limit the performance. Subsequently, variants are invented for describing specific types of relations, such as asymmetric and hierarchical relations, which are equivalent to designing unique structures for describing specific types of relationships. Such models need to look for special functions to precisely fit different relations categories. Some relations can be well characterized in models, while some are not. This design from a specific relationship type is challenging to cover all relations. No matter how sophisticated the design of such models is, it is difficult to surpass the RESCAL model theoretically. Moreover, the previous tensor decomposition model did not consider the problem of attribute separation. The unnoticed task of attribute separation in the traditional models is just handed over to the training. However, the amount of parameters for this task is tremendous, and the model is prone to overfitting.

/media/item_content/202204/625f5e4c17e72electronics-11-01058-g002.png

Figure 2. The research routes of current tensor decomposition models.

It is widely accepted that each entity contains different attributes, and the relations describe the association of entities on specific attributes. When comparing the plausibility of triples, the first step is to pick out the semantic dimension that the relation compares and filter out irrelevant dimensions. In the second step, scholars compare the correlation of the attributes of heads and tails under specific attributes, whether it satisfies the triples. It is essential to separate the dimensions that need to be compared from those unrelated dimensions. However, existing tensor decomposition models ignore the isolation of attribute dimensions, and these models combine these two steps for training. These models simultaneously complete the separation of attributes and the learning of semantic equivalence. This combination will result in too many parameters for learning. Therefore, scholars make a unique design for the relation matrix based on the subspace theory so that the different semantic spaces will not overlap. The model implements the isolation of different attributes in the structural design.

As shown in Figure 3, the left is the traditional entity vector and relation matrix; the right is the entity vector and the relation matrix with the separation of attribute spaces. Scholars perform vector subspace separation on the relation matrix of tensor decomposition models. As shown in Equation (5), the task of attribute isolation is transferred to the model structure design. This operation allows the model to focus on learning the semantic equivalence between relations, resulting in better performance. Since the model is a new embedding model that separates attribute space for knowledge graph completion, scholars name the model SeAttE.

\begin{matrix} d_{r} (h, t) = ∥h \times r \times t∥ \\ \Rightarrow d_{r} (h, t) = ∥h \times r_{S e A t t E} \times t∥ \end{matrix}

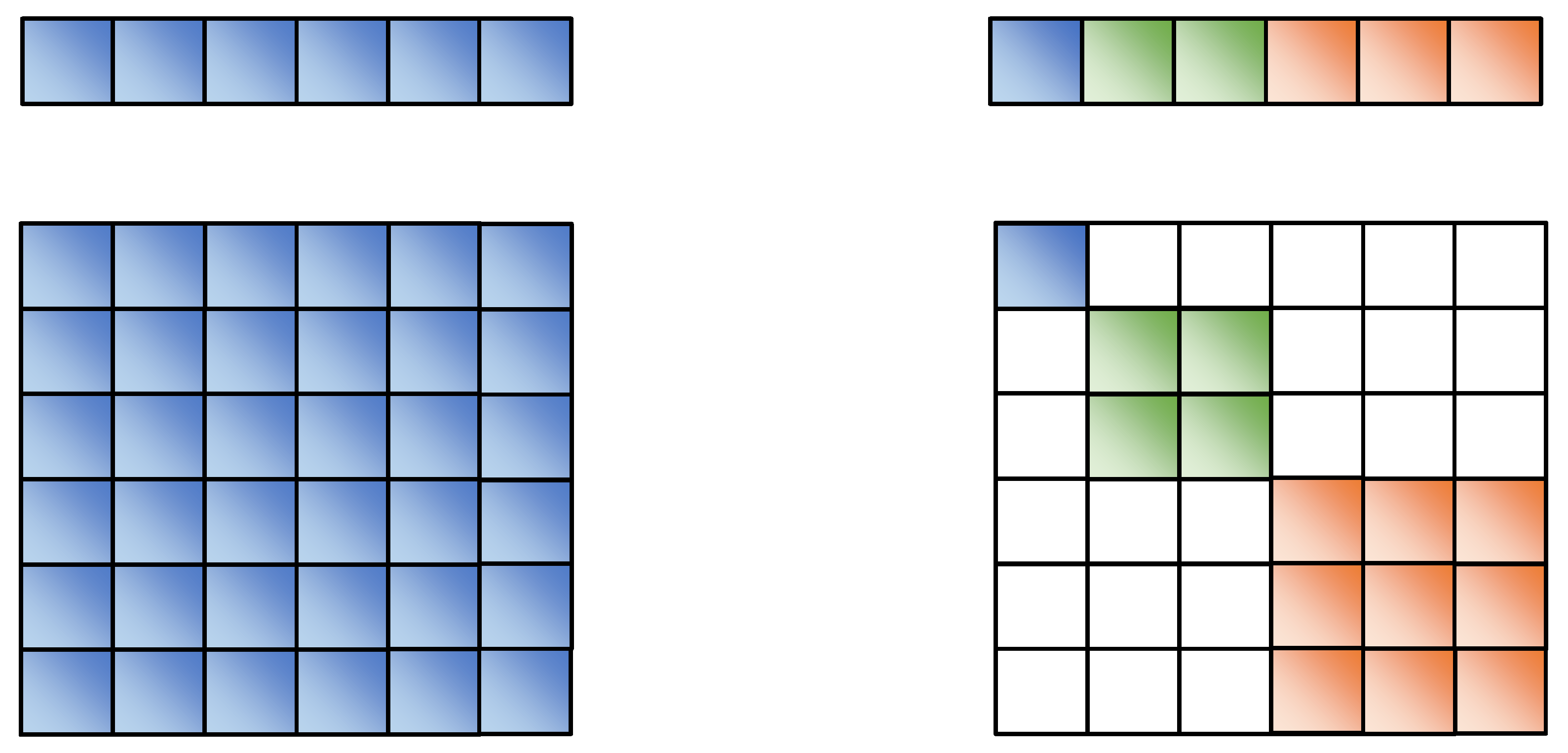
/media/item_content/202204/625f5e798890delectronics-11-01058-g003.png

Figure 3. The left is the traditional entity vector and relation matrix, the right is the entity vector and the relation matrix with the separation of attribute spaces.

4.1.2. Design

In theory, the subspace separation should be related to the actual relations, which cannot be designed in advance. Scholars design the structure of attribute subspace segmentation to reduce the model’s workload in learning segmentation tasks of different semantic dimensions.

In order to facilitate the design and implementation of the model, SeAttE adopts the exact size of attribute subspace design. Assuming that the dimension of each entity vector is d and the dimension of each attribute subspace is k, each entity contains d/k attribute spaces.

r_{S e A t t E} = |\begin{matrix} W_{1} & 0 & 0 & 0 \\ 0 & W_{2} & 0 & 0 \\ 0 & 0 & \dots & 0 \\ 0 & 0 & 0 & W_{k} \end{matrix}|

where

r_{S e A t t E} \in R^{d}

and

h = d / k

As shown in the left part of Figure 4, the dimension of each entity vector d is eight, and the dimension of each attribute subspace k is two, then the entity contains four attributes subspaces. As shown in the right part of Figure 4, when the dimension of each attribute subspace d is two and the dimension of each subspace k is four, the entity contains two attributes subspaces.

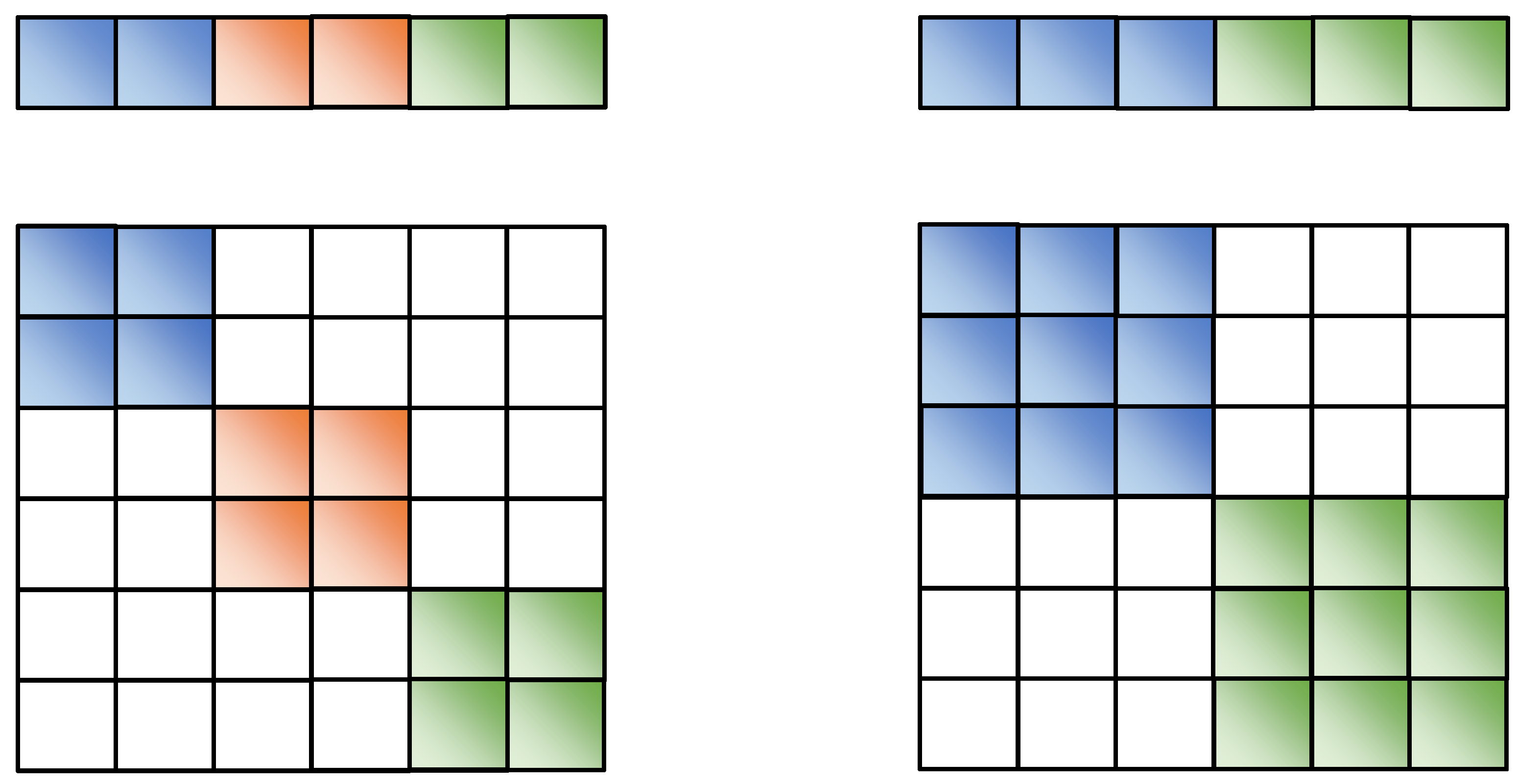
/media/item_content/202204/625f5ee97ba54electronics-11-01058-g004.png

Figure 4. Different attribute subspace sizes under the same entity dimension. The dimension of each attribute subspace is set to 2 in the left and 3 in the right.

SeAttE realizes the division of knowledge graph attribute space by setting the max dimension of the attribute subspace. The model avoids a large number of parameter learning for attribute separations by setting the parameter of the maximum semantic space dimension.

4.2. Relation to Previous Tensor Factorization Models

RESCAL is the basic tensor decomposition model. Due to the tremendous amount of parameters of this model, the dimension of the entity cannot be well expanded. When the dimension of the attribute subspace of SeAttE satisfies $k = d$ , SeAttE is equivalent to RESCAL.

$r_{S e A t t E} = |W_{1}|$

where $k = d$ and $h = 1$ .

DisMult is the simplest tensor decomposition model, which diagonalizes all relation matrices. When the max dimension of the attribute subspace of SeAttE k is set to 1, then $W_{k}$ is a 1-dimensional matrix, that is, a numerical value. The relationship matrix is equivalent to the diagonal. Under these circumstances, SeAttE is equivalent to DisMult.

$\begin{matrix} r_{S e A t t E} & = |\begin{matrix} W_{1} & 0 & 0 & 0 \\ 0 & W_{2} & 0 & 0 \\ 0 & 0 & \dots & 0 \\ 0 & 0 & 0 & W_{h} \end{matrix}| \\ = d i a g (W_{1}, W_{2}, \dots, W_{h}) \end{matrix}$

where $W_{k} \in R$ .

ComplEx imports complex representations to characterize symmetric and antisymmetric relations.

$\begin{matrix} d_{r} (s, o) & = Re (⟨w_{r}, e_{s}, e_{o}⟩) \\ = Re (\sum_{k = 1}^{K} w_{r k} e_{s k} {\bar{e}}_{o k}) \\ = Re (w_{r}) Re (e_{s}) {Re}^{T} (e_{o}) + Re (w_{r}) Im (e_{s}) {Im}^{T} (e_{o}) \\ + Im (w_{r}) Re (e_{s}) {Im}^{T} (e_{o}) - Im (w_{r}) Im (e_{s}) {Re}^{T} (e_{o}) \\ = [Re (e_{s}) | | Im (e_{s})] W_{r} {[Re (e_{o}) | | Im (e_{o})]}^{T} \\ = {e^{'}}_{s} W_{r} {({e^{'}}_{o})}^{T} \end{matrix}$

$W_{r} = [\begin{matrix} d i a g (Re (w_{r})) & d i a g (Im (w_{r})) \\ d i a g (- Im (w_{r})) & d i a g (Re (w_{r})) \end{matrix}]$

where $e_{s}^{'}, {e_{o}}^{'} \in R^{2 K}$ and $W_{r} \in R^{2 K \times 2 K}$ .

From the above formula, it can find that ComplEx is equivalent to RESCAL with $d = 2 k$

The model performs a particular regularization for each relation matrix, which only retains the diagonal elements of the four sub-matrices of the matrix, and the remaining elements are set to 0.

When the dimension of the attribute subspace of the SeAttE model k is set to 2, the relation matrix can also be expressed as the following.

\begin{matrix} r_{S e A t t E} & = |\begin{matrix} W_{1} & O & O & O \\ O & W_{2} & O & O \\ O & O & \dots & O \\ O & O & O & W_{h} \end{matrix}| \\ = |\begin{matrix} \begin{matrix} W_{11} & W_{12} & 0 & 0 \\ W_{13} & W_{14} & 0 & 0 \\ 0 & 0 & W_{21} & W_{22} \\ 0 & 0 & W_{23} & W_{24} \end{matrix} & O \\ O & \begin{matrix} \dots & \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} & \begin{matrix} W_{h 1} & W_{h 2} \\ W_{h 3} & W_{h 4} \end{matrix} \end{matrix} \end{matrix}| \\ = H * |\begin{matrix} d i a g (W_{11}, W_{21}, \dots, W_{h 1}) & d i a g (W_{12}, W_{22}, \dots, W_{h 2}) \\ d i a g (W_{13}, W_{23}, \dots, W_{h 3}) & d i a g (W_{14}, W_{24}, \dots, W_{h 4}) \end{matrix}| * G \end{matrix}

where

H = h_{2_n + 1} \times h_{3_n + 2} \times \dots \times h_{n_2 n - 1}

is obtained by exchanging the i-th row and the k-th row of the identity matrix, that is, performing elementary row transformation on the matrix W. Where

G = g_{2_n + 1} \times g_{3_n + 2} \times \dots \times g_{n_2 n - 1}

is obtained by exchanging the i-th column and the k-th column of the identity matrix, that is, performing elementary column transformation on the matrix W.

References

Bordes, A.; Usunier, N.; García-Durán, A.; Weston, J.; Yakhnenko, O. Translating Embeddings for Modeling Multi-relational Data. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems 2013, Lake Tahoe, NV, USA, 5–8 December 2013; Burges, C.J.C., Bottou, L., Ghahramani, Z., Weinberger, K.Q., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2013; pp. 2787–2795.
Suchanek, F.M.; Kasneci, G.; Weikum, G. YAGO: A Large Ontology from Wikipedia and WordNet. J. Web Semant. 2008, 6, 203–217.
Auer, S.; Bizer, C.; Kobilarov, G.; Lehmann, J.; Cyganiak, R.; Ives, Z.G. DBpedia: A Nucleus for a Web of Open Data. In The Semantic Web, 6th International Semantic Web Conference, 2nd Asian Semantic Web Conference, ISWC 2007 + ASWC 2007, Busan, Korea, 11–15 November 2007; Aberer, K., Choi, K., Noy, N.F., Allemang, D., Lee, K., Nixon, L.J.B., Golbeck, J., Mika, P., Maynard, D., Mizoguchi, R., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4825, pp. 722–735.
Socher, R.; Chen, D.; Manning, C.D.; Ng, A.Y. Reasoning With Neural Tensor Networks for Knowledge Base Completion. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 926–934.
Nickel, M.; Tresp, V.; Kriegel, H. A Three-Way Model for Collective Learning on Multi-Relational Data. In Proceedings of the ICML’11: Proceedings of the 28th International Conference on International Conference on Machine Learning, Washington, DC, USA, 28 June–2 July 2011.
Yang, B.; tau Yih, W.; He, X.; Gao, J.; Deng, L. Embedding Entities and Relations for Learning and Inference in Knowledge Bases. In Proceedings of the 28th International Conference on Machine Learning, ICML 2011, Washington, DC, USA, 28 June–2 July 2011.
Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex Embeddings for Simple Link Prediction. arXiv 2016, arXiv:1606.06357.
Balazevic, I.; Allen, C.; Hospedales, T.M. TuckER: Tensor Factorization for Knowledge Graph Completion. arXiv 2019, arXiv:1901.09590.
Kazemi, S.M.; Poole, D. SimplE Embedding for Link Prediction in Knowledge Graphs. In Proceedings of the Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, Montréal, QC, Canada, 3–8 December 2018; 2018; Bengio, S., Wallach, H.M., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; pp. 4289–4300.
Zhang, Y.; Yao, Q.; Dai, W.; Chen, L. AutoSF: Searching Scoring Functions for Knowledge Graph Embedding. In Proceedings of the 36th IEEE International Conference on Data Engineering, ICDE 2020, Dallas, TX, USA, 20–24 April 2020; pp. 433–444.
Nickel, M.; Rosasco, L.; Poggio, T.A. Holographic Embeddings of Knowledge Graphs. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Schuurmans, D., Wellman, M.P., Eds.; AAAI Press: Palo Alto, CA, USA, 2016; pp. 1955–1961.
Liu, H.; Wu, Y.; Yang, Y. Analogical Inference for Multi-relational Embeddings. arXiv 2017, arXiv:1705.02426.
Hitchcock, F.L. The Expression of a Tensor or a Polyadic as a Sum of Products. J. Math. Phys. 1927, 6, 164–189.
Gao, H.; Yang, K.; Yang, Y.; Zakari, R.Y.; Owusu, J.W.; Qin, K. QuatDE: Dynamic Quaternion Embedding for Knowledge Graph Completion. arXiv 2021, arXiv:2105.09002.
Lu, H.; Hu, H.; Lin, X. DensE: An enhanced non-commutative representation for knowledge graph embedding with adaptive semantic hierarchy. Neurocomputing 2022, 476, 115–125.
Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge Graph Embedding by Translating on Hyperplanes. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec, QC, Canada, 27–31 July 2014.
Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning Entity and Relation Embeddings for Knowledge Graph Completion. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015.
Ji, G.; He, S.; Xu, L.; Liu, K.; Zhao, J. Knowledge Graph Embedding via Dynamic Mapping Matrix. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing, Beijing, China, 15 July 2015.
Sun, Z.; Deng, Z.; Nie, J.Y.; Tang, J. RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space. arXiv 2019, arXiv:1902.10197.
Zhang, Z.; Cai, J.; Zhang, Y.; Wang, J. Learning Hierarchy-Aware Knowledge Graph Embeddings for Link Prediction. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, 7–12 February 2020; AAAI Press: Palo Alto, CA, USA, 2020; pp. 3065–3072.
Tang, Y.; Huang, J.; Wang, G.; He, X.; Zhou, B. Orthogonal Relation Transforms with Graph Context Modeling for Knowledge Graph Embedding. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Virtual Event, 5–10 July 2020; Jurafsky, D., Chai, J., Schluter, N., Tetreault, J.R., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 2713–2722.
Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2D Knowledge Graph Embeddings. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018.
Nguyen, D.Q.; Nguyen, T.; Nguyen, D.Q.; Phung, D.Q. A Novel Embedding Model for Knowledge Base Completion Based on Convolutional Neural Network. arXiv 2018, arXiv:1712.02121.
Nguyen, D.Q.; Vu, T.; Nguyen, T.; Nguyen, D.Q.; Phung, D.Q. A Capsule Network-based Embedding Model for Knowledge Graph Completion and Search Personalization. arXiv 2019, arXiv:1808.04122.
Vashishth, S.; Sanyal, S.; Nitin, V.; Talukdar, P. Composition-based Multi-Relational Graph Convolutional Networks. arXiv 2020, arXiv:1911.03082.
Nathani, D.; Chauhan, J.; Sharma, C.; Kaul, M. Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs. In Proceedings of the 57th Conference of the Association for Computational Linguistics, ACL 2019, Florence, Italy, 28 July–2 August 2019; Volume 1: Long Papers. Korhonen, A., Traum, D.R., Màrquez, L., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; Volume 1, pp. 4710–4723.
Wan, G.; Pan, S.; Gong, C.; Zhou, C.; Haffari, G. Reasoning Like Human: Hierarchical Reinforcement Learning for Knowledge Graph Reasoning. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 11–17 July 2020; pp. 1926–1932.
Hildebrandt, M.; Serna, J.A.Q.; Ma, Y.; Ringsquandl, M.; Joblin, M.; Tresp, V. Reasoning on Knowledge Graphs with Debate Dynamics. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, 7–12 February 2020; AAAI Press: Palo Alto, CA, USA, 2020; pp. 4123–4131.
Qu, M.; Chen, J.; Xhonneux, L.A.C.; Bengio, Y.; Tang, J. RNNLogic: Learning Logic Rules for Reasoning on Knowledge Graphs. In Proceedings of the 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, 3–7 May 2021.
Biswas, R.; Alam, M.; Sack, H. MADLINK: Attentive Multihop and Entity Descriptions for Link Prediction in Knowledge Graphs; IOS Press: Amsterdam, The Netherlands, 2021.
Zhang, Z.; Cai, J.; Wang, J. Duality-Induced Regularizer for Tensor Factorization Based Knowledge Graph Completion. arXiv 2020, arXiv:2011.05816.
Lei, D.; Jiang, G.; Gu, X.; Sun, K.; Mao, Y.; Ren, X. Learning Collaborative Agents with Rule Guidance for Knowledge Graph Reasoning. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing, EMNLP 2020, Virtual Event, 16–20 November 2020; Webber, B., Cohn, T., He, Y., Liu, Y., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 8541–8547.
Liang, Z.; Yang, J.; Liu, H.; Huang, K. A Semantic Filter Based on Relations for Knowledge Graph Completion. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, Virtual Event, 7–11 November 2021; Moens, M., Huang, X., Specia, L., Yih, S.W., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2021; pp. 7920–7929.
Lacroix, T.; Usunier, N.; Obozinski, G. Canonical Tensor Decomposition for Knowledge Base Completion. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 2869–2878.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Computer Science, Artificial Intelligence

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

View Times: 653

Update Date: 21 Apr 2022

Table of Contents

1000/1000

Hot Most Recent