Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Yangyang Zou
 + 1610 word(s) 1610 2022-03-04 12:03:09 |
2 Format correct
Vicky Zhou
+ 4 word(s) 1614 2022-03-15 01:28:20 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Zou, Y. Bidirectional Reflection Distribution Function. Encyclopedia. Available online: https://encyclopedia.pub/entry/20562 (accessed on 18 May 2024).
Zou Y. Bidirectional Reflection Distribution Function. Encyclopedia. Available at: https://encyclopedia.pub/entry/20562. Accessed May 18, 2024.
Zou, Yangyang. "Bidirectional Reflection Distribution Function" Encyclopedia, https://encyclopedia.pub/entry/20562 (accessed May 18, 2024).
Zou, Y. (2022, March 14). Bidirectional Reflection Distribution Function. In Encyclopedia. https://encyclopedia.pub/entry/20562
Zou, Yangyang. "Bidirectional Reflection Distribution Function." Encyclopedia. Web. 14 March, 2022.
Bidirectional Reflection Distribution Function
Edit
This entry is adapted from the peer-reviewed paper 10.3390/s22051739

The bidirectional reflection distribution function (BRDF) is among the most effective means to study the phenomenon of light–object interaction. It can precisely describe the characteristics of spatial reflection of the target surface, and has been applied to aerial remote sensing, imaging technology, materials analysis, and computer rendering technology. 

BRDF traditional measurement fast measurement developmental trends

1. Introduction

The interaction between electromagnetic waves and the surface of objects consists of three processes: reflection, absorption, and transmission. The reflection of electromagnetic waves by the object is related to the roughness of its surface and the wavelength of the waves. The surfaces of all objects in nature are neither ideally smooth, like a mirror, nor ideally Lambertian. Reflection in these cases cannot be described simply by specular reflection or diffuse reflection, but by the scattering of light with both specular and diffuse components in hemispheric space. Nicodemus proposed the bidirectional reflectance distribution function (BRDF) in 1965 to characterize the properties of spatial reflectance of the target surface [1]. The BRDF combines specular and diffuse reflections to provide a more realistic and accurate description of the characteristics of spatial reflection off the surface of the target object.
In remote sensing, the calculation of surface albedo refers to the ratio of the total reflected light flux in each direction to the total incident light flux. The surface Lambeau hypothesis leads to a 45% error in albedo calculations [2], Stroeve et al. [3] found in their study that the inversion accuracy of illumination could be improved by combining spectral data with multi-angle BRDF data. Currently, landmark albedo products in-orbit, such as POLDER, MISR, MOIDS, and MERIS [4][5][6][7], are estimated based on surface bidirectional reflection characteristics.
In environment and Earth science, vegetation canopy structure parameters are key input parameters of ecosystem productivity models, global climate, and hydrological models. The surface reflectance of different vegetation is anisotropic due to its structural distribution. For example, BRDF distribution tests on wheat leaves [8], sorghum [9], maple leaves, and other leaves [10] can be found that different vegetation has different BRDF characteristic models. Therefore, based on the sensitivity of multi-angle BRDF data observation to vegetation structure, BRDF data can improve the accuracy of vegetation classification to 91% [11], which can improve the assessment of the ecological environment in different regions.
In optical research, stray light is a non-negligible aspect of all optical design, and its suppression is the basis for obtaining high-quality images. BRDF/BTDF (Bi-directional Transmittance Distribution Function) data can be used to quantify the scattering characteristics, and BRDF/BTDF spatial distribution data on the surface of optical elements can be used in stray light modeling in FRED, ASAP, Zemax, and other optical software [12][13][14]. As for stray light suppression materials required in some space optical systems, their inhibitory effect on stray light can also be judged by analyzing their BRDF data [15][16].
In computer model rendering and imaging, performance in terms of processing the microstructure of a given surface based on BRDF data can be used to determine the degree of ‘realism’ in areas such as special effects and 3D animation. As visual attributes, gloss and texture are the physical information of BRDF distribution in hemispherical space [17][18][19]. The authenticity of human skin in animation production can be realized through a large amount of BRDF model data. In 2006, T. Weyrich et al. [20] measured and estimated skin BRDF data of people of different genders and races. L. Hanssen et al. [21] and G.S. Won et al. [22] also carried out a lot of work on the establishment of BRDF data of human skin, providing data support for rendering technology of the human model.
The use and calibration of basic measurement devices in meteorology, such as the Transmission Visibility Meter (TVM) and the Forward Scattering Visibility Meter (FSVM), are based on atmospheric scattering characteristics. The calibration of TVM is achieved by using the scattering characteristics of standard scatterers [23][24], while the FSVM measures atmospheric visibility by measuring the scattering coefficient in the fixed direction of the atmosphere [25][26].

2. Trend of Development of BRDF Measurement Devices

2.1. Summary of Development Status

The initial structure used for BRDF measurement was simple and rough [27][28][29][30][31]. It was later automated to improve the accuracy and stability of the measurements. Further advances have included the enrichment of light sources [32][33][34][35][36][37] (multi-spectral, and polarization), new detectors (photoelectric detection, and Charge Coupled Device (CCD) imaging), and the emergence of devices for fast measurement [38][39][40][41][42][43][44][45]. BRDF measurement devices are developing with the aims of being able to handle large amounts of data, and having higher accuracy, higher efficiency, and greater stability. In accordance with the history of BRDF measurements, the measurement devices can be divided into those for “traditional measurement” and “fast measurement,” as shown in Figure 1.
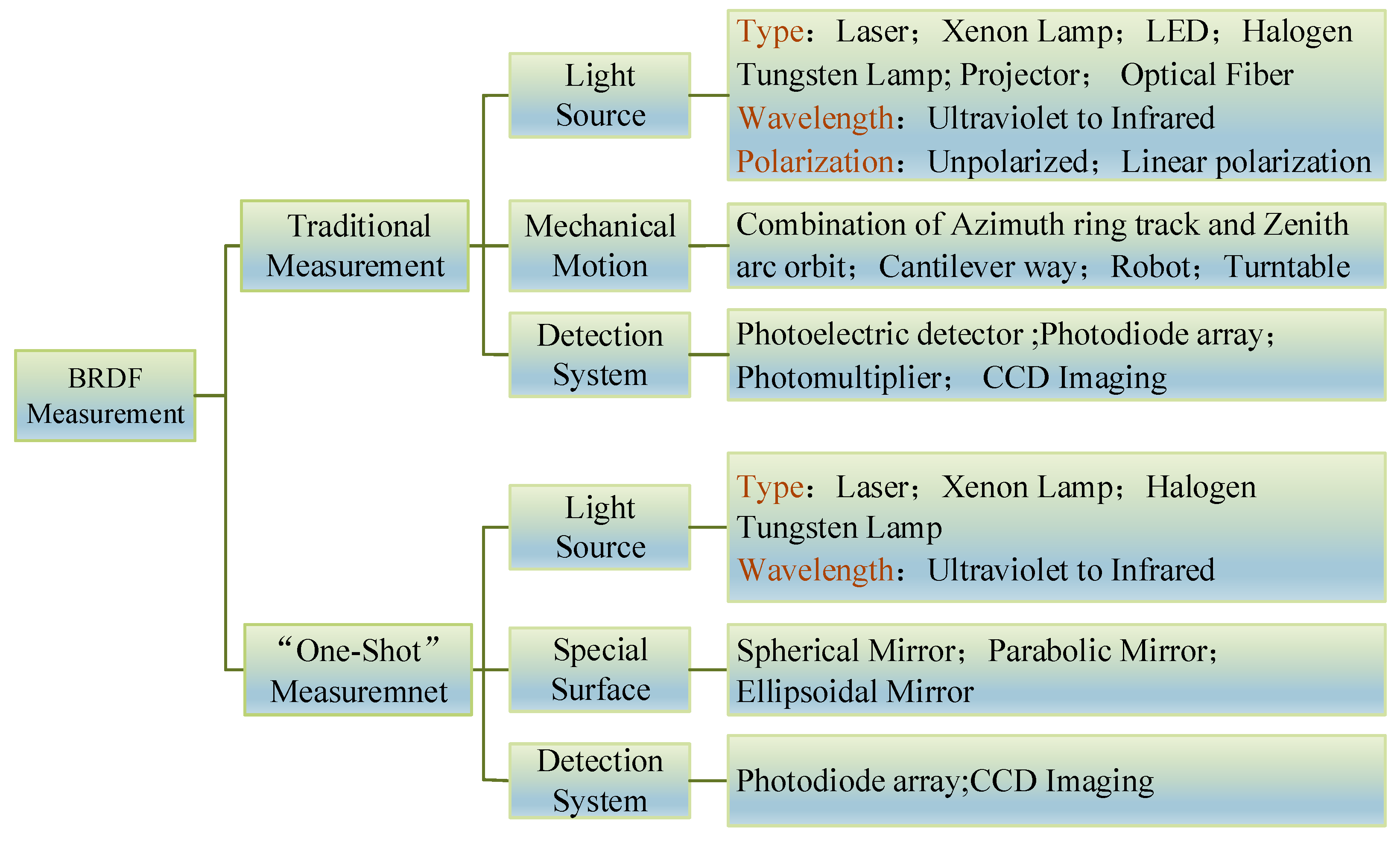Figure 1. Classification of BRDF measurement devices and system components.
Traditional measurement devices measure the sample by using a mechanical structure to rotate the detector and the light source around it at a certain spatial angle. The most common structural form of such a device features a combination of the zenith of the motion structure, the azimuthal circular track [46][47][48][49][50][51][52], and a cantilever structure forms [53][35][54][55][56][57][58][59][60] for BRDF measurements. With the development of robotics, the advantages of automated measurements have been expanded by combining robots with BRDF measurement devices [39][61].
Devices capable of fast measurement are used to determine the reflective properties of the sample in hemispheric space in one shot, with the aid of the optical properties of special surfaces, special optical devices, and optical imaging techniques [62][63][38][39][40][41][42][43][64][65][66][67][45][68], or by increasing the area of the detector [69][70][71]. The measurement device uses a special surface reflector to eliminate part of the mechanical motion or increase the area of detection to measure the characteristics of reflection of the sample in hemispheric space at once. The device for fast measurement can use optics to consider the imaging device as an array of detectors to capture multiple reflections in one snapshot. This approach improves the stability of the measurement system, and, most importantly, the efficiency of the measurement. The measurement data that would take hours or even tens of hours to obtain with a traditional measuring device can be obtained in seconds or minutes with a fast measurement device.

2.2. Current Problems and Development Trends

An analysis of measurement devices reveals the following problems with current BRDF measurements:
(a) Unachievable of time-varying BRDF detection for traditional measurement;
Traditional devices perform measurements in a point-by-point manner using mechanical motion in the hemispheric space of the BRDF distribution, and even sparse sampling requires tens of hours regardless of the form of mechanical motion. Moreover, during the measurement process, the relative positional accuracy of the light source, sample, and detector has a significant influence on the measurement results, and mechanical motion introduces large instability to the measurement system. Moreover, the instability of the light source during measurement can cause intuitive errors in the BRDF data. For special samples, e.g., oxidation on the surface of objects at high temperatures or on liquids with dynamic scattered light, traditional measuring devices cannot provide BRDF measurements in variable environments over long testing periods.
(b) Lack of devices for fast measurement;
The devices for fast measurements can overcome the problems of instability and low measurement efficiency in traditional measurement devices while avoiding errors due to power fluctuations in the light source and variations in the sensitivity of the detector. They can also significantly reduce the acquisition time and capture multiple reflected light signals in the sample hemisphere space in one snapshot. However, they are limited by their mechanical structure, which can lead to missing BRDF data in a fixed direction in the hemisphere space, and the resolution of their optical system is lower than that of the traditional mechanical structure. Most importantly, the reflection outside the specular reflection area of the “one-shot” measurement is weak, and the system has a low signal-to-noise ratio, so a highly sensitive, high-precision, hyperspectral detector with a large dynamic range is needed.
(c) Lack of means to fuse and reconstruct BRDF data;
The ultimate goal of the distribution of BRDF measurements in a hemisphere is to fuse them with multi-angle information on the scattered light field to obtain the characteristics of the target, and then to invert them. However, no study to date has examined the means of fusion and reconstruction of information on the scattered light field.
(d) Incomplete analysis of factors affecting BRDF data.
The results of BRDF measurements are affected by many factors, including but not limited to the wavelength of light, angle of incidence, surface morphology of the target object, and temperature. Some studies have analysed the wavelength, angle of incidence, and observation angle but no systematic research has been devoted to the other factors.
In summary, a method to quickly measure the BRDF is needed that can simultaneously measure the multi-angle light field without requiring moving mechanical parts. It needs to also be at least as accurate as traditional measurement devices.

3. Conclusions

As an important means of describing the distribution of spatial optical properties on the surface of an object, the BRDF has been widely used in many fundamental and prospective research fields. In recent years, major work on the BRDF has focused on the development and application of measurement devices along two directions. It is showed that through an analysis of the entire developmental history of BRDF measurement devices, that the two major types of measurement devices used have their respective advantages and limitations. The foundation of the use of BRDF data is their accurate measurement, because of which research in the area is focusing on developing measurement devices with increasingly higher precision, efficiency, and stability. This can provide the basis for developing a rich database of BRDF measurements to meet the demands of many fields. Moreover, factors affecting the BRDF data and their applications need to be studied in more detail.

References

  1. Nicodemus, F.E. Directional reflectance and emissivity of an opaque surface. Appl. Opt. 1965, 4, 767–775.
  2. Kimes, D.S.; Sellers, P.J.; Diner, D.J. Extraction of spectral hemispherical reflectance (albedo) of surfaces from nadir and directional reflectance data. Int. J. Remote Sens. 1987, 8, 1727–1746.
  3. Stroeve, J.C.; Nolin, A.W. New methods to infer snow albedo from the MISR instrument with applications to the Greenland ice sheet. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1616–1625.
  4. Pokrovsky, I.; Pokrovsky, O.; Roujean, J.L. Development of an operational procedure to estimate surface albedo from the SEVIRI/MSG observing system in using polder BRDF measurements. Remote Sens. Environ. 2003, 87, 198–214.
  5. Chen, Y.M.; Wang, J.D.; Liang, S.L.; Wang, D.W.; Ma, B.; Bo, Y.C. The bidirectional reflectance signature of typical land surfaces and comparison of MISR and MODIS BRDF products. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008.
  6. Wu, H.; Liang, S.; Ling, T.; Tao, H. Snow BRDF characteristics from MODIS and MISR data. In Proceedings of the Geoscience & Remote Sensing Symposium IEEE, Vancouver, BC, Canada, 24–29 July 2011.
  7. Samain, O.; Geiger, B.; Roujean, J.L. Spectral normalization and fusion of optical sensors for the retrieval of BRDF and albedo: Application to VEGETATION, MODIS, and MERIS data sets. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3166–3179.
  8. Comar, A.; Baret, F.; Viénot, F.; Yan, L.; De Solan, B. Wheat leaf bidirectional reflectance measurements: Description and quantification of the volume, specular and hot-spot scattering features. Remote Sens. Environ. 2012, 121, 26–35.
  9. Comar, A.; Baret, F.; Obein, G.; Simonot, L.; Meneveaux, D.; Vienot, F.; de Solan, B. ACT: A leaf BRDF model taking into account the azimuthal anisotropy of monocotyledonous leaf surface. Remote Sens. Environ. 2014, 143, 112–121.
  10. Roth, B.D.; Saunders, M.G.; Bachmann, C.M.; van Aardt, J.A. On leaf BRDF estimates and their fit to microfacet models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 99, 1761–1771.
  11. Hyman, A.H.; Barnsley, M.J. On the potential for land cover mapping from multiple-view-angle (MVA) remotely sensed images. Int. J. Remote Sens. 1997, 18, 2471–2475.
  12. Schrder, S.; Finck, A.; Katsir, D.; Duparre, A. Light scattering characterization of optical components: BRDF, BTDF, and scatter losses. In Proceedings of the Optical Design & Testing VI International Society for Optics and Photonics, Bejing, China, 5 November 2014.
  13. Lu, X.; Gross, H. Efficient simulation of surface scattering in symmetry-free optical systems. Opt. Express 2020, 28, 39368–39386.
  14. Lu, C.; Li, L. Application of BRDF data in stray light analysis. In Proceedings of the Tenth International Conference On Information Optics And Photonics, CIOP100, Bejing, China, 8–11 July 2018.
  15. Mo, D.; Wang, Y.; Liu, D.; Chen, J.; Xu, L. Research of suppressing stray light of cold shield with different black coating. Metasurface Wave Planar Opt. 2019, 10841, 17.
  16. Zeidler, S.; Akutsu, T.; Torii, Y.; Aso, Y. Measuring scattering light distributions on high-absorptive surfaces for stray-light reduction in gravitational-wave detectors. Opt. Express 2019, 27, 16890.
  17. Löw, J.; Kronander, J.; Ynnerman, A.; Unger, J. BRDF models for accurate and efficient rendering of glossy surfaces. Comput. Graph. 2012, 31, 1–14.
  18. Schwartz, C.; Sarlette, R.; Weinmann, M.; Rump, M.; Klein, R. Design and implementation of practical bidirectional texture function measurement devices focusing on the developments at the university of bonn. Sensors 2014, 14, 7753–7819.
  19. Wojciech, M.; Hanspeter, P.; Matthew, B.; Leonard, M. Efficient isotropic BRDF measurement. The Eurographics Association. 2003. Available online: http://www.csbio.unc.edu/mcmillan/pubs/egsr03_matusik.pdf (accessed on 10 September 2021).
  20. Weyrich, T.; Matusik, W.; Pfister, H.; Bickel, B.; Donner, C.; Tu, C.; McAndless, J.; Lee, J.; Ngan, A.; Jensen, H.W.; et al. Analysis of Human Faces using a Measurement-Based Skin Reflectance Model. ACM Trans. Graph. 2006, 25, 1013–1024. Available online: https://www.merl.com/publications/docs/TR2006-071.pdf (accessed on 17 January 2022).
  21. Hanssen, L.M.; Bintz, J.R.; Mendenhall, M.J.; Marciniak, M.A.; Bulter, S.D.; Lloyd, J.T. A novel image-based BRDF measurement system and its application to human skin. In Proceedings of the Society of Photo-optical Instrumentation Engineers, Reflection, Scattering, and Diffraction from Surfaces V, San Diego, CA, USA, 26 September 2016; Volume 996108.
  22. Method for Rendering Skin Material Based on BRDF and Its Apparatus. K.R. Patent KR20100062860(A), 10 June 2010. Available online: https://patentimages.storage.googleapis.com/6e/e8/ad/47b531d4ef6137/KR20100062860A.pdf (accessed on 17 January 2022).
  23. Hongda, T.; Zibo, Z.; Lihui, J.; Dong, S. Visibility measurement in an atmospheric environment simulation chamber. Curr. Opt. Photonics 2017, 3, 186–195.
  24. Park, S.; Lee, D.H.; Kim, Y.G. SI-traceable calibration of a transmissometer for meteorological optical range (MOR) observation. Hankook Kwanghak Hoeji 2015, 26, 73–82.
  25. Bloemink, H.I. KNMI visibility standard for calibration of scatterometers. In Proceedings of the 4th ICEAWS International Conference on Experiences with Automatic Weather Stations, Lisboa, Portugal, 24–26 May 2006.
  26. Chong, W.; Bian, Z.Q.; Chu, J.H.; He, X.L.; Jiang, D.D. A method for calibrating forward scatterometers indoors. Metrologia 2020, 57, 065030.
  27. Hsia, J.J.; Richmond, J.C. Bidirectional reflectometry (Part I) A high resolution laser bidirectional reflectometer with results on several optical coatings. J. Res. Natl. Inst. Stand. Technol. 1976, 80A, 189–205.
  28. Mainguy, S.; Olivier, M.; Josse, M.A.; Guidon, M. Description and calibration of a fully automated infrared scatterometer. Proc Spie. 1991, 1530, 269–282.
  29. Schiff, T.F.; Knighton, M.W.; Wilson, D.J.; Cady, F.M.; Stover, J.C.; Bulter, J.J. Design review of a high-accuracy UV to near-IR scatterometer. Opt. Scatt. Appl. Meas. Theory II. Int. Soc. Opt. Photonics 1993, 1995, 121–130.
  30. Castonguay, R.J.; Stover, J.C. New generation high-speed high-resolution hemispherical scatterometer. In Proceedings of the SPIE-The International Society for Optical Engineering, San Diego, CA, USA, 1 December 1993.
  31. Mcguckin, B.T.; Haner, D.A.; Menzies, R.T.; Esproles, C.; Brothers, A.M. Directional reflectance characterization facility and measurement methodology. Appl. Opt. 1996, 35, 4827–4834.
  32. Drolen, B.L. Bidirectional reflectance and specularity of twelve spacecraft thermal control materials. J. Thermophys. Heat Transf. 1992, 6, 672–679.
  33. Li, H.; Torrance, K.E. Validation of the Gonioreflectometer; Beijing Institute of Technology: Bejing, China, 2005.
  34. Li, H.; Foo, S.C.; Torrance, K.E.; Westin, S.H. Automated three-axis gonioreflectometer for computer graphics applications. Opt. Eng. 2006, 45, 043605.
  35. Zhao, Z.; Chao, Q.; Dai, J. Design of multi-spectrum BRDF measurement system. Chin. Opt. Lett. 2007, 5, 168–171.
  36. Roy, S.; Bang, S.Y.; Modest, M.F.; Vladimir, S.S. Measurement of spectral, directional reflectivities of solids at high temperatures between 9 and 11 μm. Appl. Opt. 1993, 32, 3550–3558.
  37. Barnes, P.Y.; Proctor, J.E. NIST high accuracy reference reflectometer-spectrophotometer. Natl. Inst. Stand. Technol. 1996, 101, 619–627.
  38. McNeil, J.R.; Wilson, S.R. Two-Dimensional Optical Scatterometer Apparatus and Process. U.S. Patent 5,241,369, 31 August 1993.
  39. Hatab, Z.R.; McNeil, J.R.; Naqvi, S.S.H. Sixteen-megabit dynamic random access memory trench depth characterization using two-dimensional diffraction analysis. Vac. Sci. Technol. B. 1995, 13, 174–181.
  40. Kautz, J. Shading and shadows. Fast, arbitrary BRDF shading for low-frequency lighting using spherical harmonics. In Proceedings of the 13th Eurographics Workshop on Rendering, Pisa, Italy, 26–28 June 2002.
  41. Han, J.Y.; Perlin, K. Measuring bidirectional texture reflectance with a kaleidoscope. ACM Trans. Graph. 2003, 22, 741–748.
  42. Achutha, S. BRDF Acquisition with Basis Illumination. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 2006.
  43. Mukaigawa, Y.; Sumino, K.; Yagi, Y. High-speed measurement of BRDF using an ellipsoidal mirror and a projector. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007.
  44. Meyen, S.; Sutter, F.; Heller, P.; Oschepkov, A. A new instrument for measuring the reflectance distribution function of solar reflector materials. Proc. Sol. Int. Conf. Energy Procedia 2014, 49, 2145–2153.
  45. Ohno, H. One-shot three-dimensional measurement method with color mapping of light direction. OSA Continuum. 2021, 4, 840–848.
  46. Murray-Coleman, J.F.; Smith, A.M. The automated measurement of BRDFs and their application to luminaire modeling. J. Illum. Eng. Soc. 1990, 19, 87–99.
  47. Zaworski, J.R.; Welty, J.R.; Drost, M.K. Measurement and use of bi-directional reflectance. Int. J. Heat Mass Transf. 1996, 39, 1149–1156.
  48. White, D.R.; Saunders, P.; Bonsey, S.J.; Ven, J.V.D.; Edgar, H. Reflectometer for measuring the bidirectional reflectance of rough surfaces. Appl. Opt. 1998, 37, 3450–3454.
  49. Sandmeier, S.R. Acquisition of bidirectional reflectance factor data with field goniometers. Remote Sens. Environ. 2000, 73, 257–269.
  50. Coburn, C.A.; Peddle, D.R. A low-cost field and laboratory goniometer system for estimating hyper spectral bidirectional reflectance. Can J Remote Sens. 2006, 32, 244–253.
  51. Ma, L.; Zhang, L. BRDF measuring device design and pointing accuracy analysis. Infrared Laser Eng. 2019, 48, 31–36.
  52. Ma, W.J.H. The Measurement and modeling investigation on the spectral polarized BRDF of brass. Opt. Rev. 2020, 27, 380–390.
  53. Shen, Y.J.; Zhu, Q.Z.; Zhang, Z.M. A scatterometer for measuring the bidirectional reflectance and transmittance of semiconductor wafers with rough surfaces. Rev. Sci. Instrum. 2003, 74, 4885–4892.
  54. Feng, X.; Schott, J.R.; Gallagher, T. Comparison of methods for generation of absolute reflectance-factor values for bidirectional reflectance-distribution function studies. Appl. Opt. 1993, 32, 1234–1242.
  55. Foo, S.C. A Gonioreflectometer for Measuring the Bidirectional Reflectance of Material for Use in Illumination Computation. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2001.
  56. Suomalainen, J.; Hakala, T.; Peltoniemi, J.; Puttonen, E. Polarized multi-angular reflectance measurements using the finish geodetic institute field goniospectro-meter. Sensors 2009, 9, 3891–3907.
  57. Yan, G.; Ren, H.; Hu, R.; Hu, R.H.; Yan, K.; Zhang, W.M. A portable Multi-Angle Observation System. In Proceedings of the International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012.
  58. Bachmann, C.M.; Gray, D.; Abelev, A.; Philpot, W.; Montes, M.J.; Fusina, R.; Musser, J.; Li, R.-R.; Vermillion, M.; Smith, G.; et al. Linking goniometer measurements to hyperspectral and multisensory imagery for retrieval of beach properties and coastal characterization. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII, Baltimor, MD, USA, 23–27 April 2012.
  59. Buchhorn, M.; Petereit, R.; Heim, B. A Manual transportable instrument platform for ground-based spectro-directional observations (ManTIS) and the resultant hyperspectral field goniometer system. Sensors 2013, 13, 16105–16128.
  60. Li, H.; Chen, M.; Deng, C.; Liao, N.; Rao, Z. Versatile four-axis gonio-reflectometer for bidirectional reflectance distribution function measurements on anisotropic material surfaces. Opt. Eng. 2019, 58, 82–91.
  61. Hünerhoff, D.; Grusemann, U.; Hope, A. New robot-based gonio-reflectometer for measuring spectral diffuse reflection. Metrologia 2006, 43, 11–16.
  62. Ward, G.J. Measuring and modeling anisotropic reflection. Acm Siggraph Comput. Graph. 1992, 26, 265–272.
  63. Dana, K.J. BRDF/BTF measurement device. In Proceedings of the IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; pp. 6197–6206.
  64. Ju, R.; Zhao, J. Measurement of a bidirectional reflectance distribution and system achievement based on a hemi-parabolic mirror. Opt. Lett. 2010, 35, 1458–1460.
  65. Ju, R.; Zhao, J. Measurement of surface bidirectional reflectance distribution based on parabolic mirror. In Proceedings of the SPIE-The International Society for Optical Engineering, Shangai, China, 20 November 2009; Volume 75111H, pp. 1–8.
  66. Boher, P.; Leroux, T.; Collomb-Patton, V.; Bignon, T. Fast spectral BRDF & BTDF measurements for characterization of displays and components. IEICE Trans. Electron. 2016, 99, 1255–1263.
  67. Luo, D.B.; Qian, L.L.; Dong, L.W.; Shao, P.; Qin, Y. Simultaneous measurement of liquid surface tension and contact angle by light reflection. Opt. Express 2019, 27, 16703–16712.
  68. Ohno, H.; Kamikawa, T. One-shot BRDF imaging system to obtain surface properties. Opt Rev. 2021, 28, 655–661.
  69. Ben-Ezra, M.; Wang, J.; Wilburn, B.; Li, X.; Le, M. An LED-only BRDF measurement device. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008.
  70. Ren, J.; Zhao, J.L. Measurement of surface bidirectional reflectance distribution based on optical fiber array in hemispheric space. Chin. J. Lasers 2009, 36, 3011–3014.
  71. Yashika, A.; Swathi, R.; Roy, C.S. An optimal reflection photoplethysmographic sensor system based on skin optics. IEEE Sens. J. 2018, 18, 7233–7241.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Instruments & Instrumentation
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Yangyang Zou
View Times: 813
Entry Collection: Remote Sensing Data Fusion
Revisions: 2 times (View History)
Update Date: 15 Mar 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback