Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Kifayat Ullah
 + 1217 word(s) 1217 2022-02-17 07:55:10 |
2 format correct
Vivi Li
 + 97 word(s) 1314 2022-03-03 04:07:42 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Ullah, K. Robust Speed Control Techniques. Encyclopedia. Available online: https://encyclopedia.pub/entry/20125 (accessed on 17 November 2024).
Ullah K. Robust Speed Control Techniques. Encyclopedia. Available at: https://encyclopedia.pub/entry/20125. Accessed November 17, 2024.
Ullah, Kifayat. "Robust Speed Control Techniques" Encyclopedia, https://encyclopedia.pub/entry/20125 (accessed November 17, 2024).
Ullah, K. (2022, March 03). Robust Speed Control Techniques. In Encyclopedia. https://encyclopedia.pub/entry/20125
Ullah, Kifayat. "Robust Speed Control Techniques." Encyclopedia. Web. 03 March, 2022.
Robust Speed Control Techniques
Edit
This entry is adapted from the peer-reviewed paper 10.3390/en15031235

The permanent magnet synchronous motor (PMSM) is a highly efficient energy saving machine. Due to its simple structural characteristics, good heat radiation capability, and high efficiency, PMSMs are gradually replacing AC induction motors in many industrial applications. The PMSM has a nonlinear system and lies on parameters that differ over time with complex high-class dynamics. To achieve the excessive performance operation of a PMSM, it essentially needs a speed controller for providing accurate speed tracking, slight overshoot, and robust disturbance repulsion. 

robust speed controller PMSM speed regulation H∞ robust control SMC control current controller

1. Introduction

The permanent magnet synchronous motor (PMSM) has outstanding advantages over brush-type motors and is progressively replacing induction motors in many fields because of their benefits, i.e., simple structure, fast dynamic response, high efficiency, high air-gap flux density, and high torque-to-inertia ratio [1]. Due to their vast application prospects, these kinds of motors are broadly used for operation in low and medium power applications. Furthermore, they are used in high-performance electric drives such as electric vehicles, robotics, aeronautical spaceframes, and machine tools [2][3]. However, the motor model is nonlinear and sensitive to many uncertainties inside and outside the speed control system during operation, making it difficult for the conventional PI control topology to convene the excessive performance control requirements of the system. Therefore, the question of how to suppress the uncertainty of the speed control system to improve the robustness of the system has become a hotspot for scholars [3][4].
Since the discovery of AC motors for speed regulation, vector control methods are the most popular, and among these methods, direct torque control (DTC) [5][6] and field-oriented control (FOC) are commonly used [7][8]. Due to the rapid and full decoupling control of torque and flux, the FOC has been widely used in PMSM motors. In the FOC method, due to their simple design structure, proportional integration (PI) controllers are typically implemented for current and speed control [9]. PI controller gain is usually determined by nominal motor parameters to assemble motor performance specifications [10]. Based on the specified model parameters and time separation assumptions, there is no guarantee of stability if there is uncertainty, load changes, or input saturation constraints. However, where high performance and precision are required, this type of controller is not applicable [11][12].
For PMSM speed control, the control structure typically uses cascade control loops, including an external speed control loop and two internal current loops [13][14]. The benefits of the cascading control topology are enhanced disturbance resistance and superior point of tuning response performance [15]. In speed current cascading control, the relationship between the output speed and the four-axis reference current is usually defined by the first-order model. However, given that closed-loop performance may decline due to the disappearance of the relative difference in control cycles between the two loops, a second-order model relationship is also proposed [8][16]. For high-speed PMSM applications, the integration speed and current controller have been used to address the nonlinear coupling between speed and current. In [17], the authors describe the particle swarm optimization (PSO) technique for the speed control of sensorless PMSM motors.
Therefore, many advanced nonlinear control topologies have been developed in recent years to progress the speed regulation performance of PMSM motors in different applications. These methods include neural network control [18], backstepping control [19], automatic disturbance rejection control [20], fuzzy logic control (FLC) [21], predictive control [5], artificial intelligence-incorporated control [22], sliding mode control (SMC) [23], adaptive control [24], variable structure control (VSC) [25], predictive current control (PCC) [20], disturbance observer (DOB) [26], and extended state observer (ESO) [27][28]. Furthermore, for the speed regulation of the PMSM, as alternative to the conventional PI control method, H∞ control is in operational use. In H∞ control, external disturbances are assumed to be indeterminate parameters with bounded energy [29]. A robust speed controller based on mixed sensitivity can be used to progress the speed control for each molding in PMSM systems, as in [30][31]. An adaptive control scheme with a pre-determined H∞ property is implemented for the PMSM control in [32]. Using the robust control principle based on signal compensation, the design method of the robust speed control system with PMSM is proposed in [33]. To comprehend PMSM speed control, a robust predictive controller is proposed [34]. Several of these methods have been used successfully in practical applications.

2. H∞ Robust Control

Hamilton–Jacobi Inequality (HJI) system theory provides several possible control techniques for the academic circles of nonlinear disciplines and has attracted great devotion from PMSM nonlinear system scholars [35]. In the entry, several main control approaches to robust control are developed, such as quantitative feedback theory, Kharitonov, H∞, μ theory, and Lyapunov [36]. The H∞ robust current control strategy based on (HJI) is proposed in [37], which improves the robustness of the current control. This method effectively solves the effect of voltage fluctuation on current control performance, but the robustness of load variation is not ideal. To control the motor drive electromagnetic synchronization, H∞ control is used in [29][38]. However, some measurement errors still occur in the system, such as fixed space lagging and inertia that can indicate high frequency chatter. The Linear Matrix Inequality (LMI) related theory is applied to the PMSM speed control system in [39]. A robust optimal position control strategy, combined with linear quadratic regulator (LQR) and LMI theory, is proposed, resulting in optimal controller gain to ensure system robustness. The robust H∞ sliding mode control strategy based on LMI is proposed [40], which solves the problem of mismatch interference in the system. Although this control method’s effect is good, there may be changes in the system parameters caused by the controller, as well as system parameters mismatch problems, which will affect the controller’s performance [41]. The decisive controller is designed through an interconnect and damping arrangement based on the main principle of energy formative and port series Hamiltonian systems [42]. In addition, the H∞-based current controller is proposed to suppress the voltage variation of the current loop, which improves the current control robustness [43][44]. For linear time disguise problems, the Kharitonov and H∞ are used; however, there is lack of theoretical evidence. On a theoretical basis, the Lyapunov method is applicable to self-sufficient nonlinear systems [45]. To efficiently suppress the disturbance of system mismatch, the robust H∞-SMC controller, based on LMI, is proposed in [40][46]. However, it also provides new ideas for resolving parameter mismatch between the PMSM motor and its control system.

2.1. H∞ Robust Current Controller Design

The formula to obtain the H∞ robust current controller is given below [27].
{ x ˙ = f ( x ) + Z ( x ) ξ y = h ( x )
(1)
where h(x) and f(x) are nonlinear. HJI is given below, when E(x) ≥ 0 (E(x*) = 0).
E ˙ ( x ) = x T A x + x T B { − B − 1 [ A 2 x + 1 2 ( 1 + 1 γ 2 ) x ] }

(2)

E ˙ ( x ) = x T A 1 − 1 2 ( 1 + 1 γ 2 ) x T x < 0 (3)

2.2. Design of Robust H∞ Sliding Mode Speed Controller

2.2.1. Design of H∞ Sliding Surface

The H∞ slide surface refers to the system state that has robust stability and H∞ disturbance attenuation γ on the slide surface [47]. Rewrite the motion equation of the SPMSM under the d-q rotation coordinate system in the form of an error, that is given below [48].
e ˙ ω m = − B 0 J e ω m − 3 p n ψ f 2 J i q + 1 J T L 0 + B 0 J ω ˙ m (4)
At the same time, the external disturbance and parameter perturbation are considered, and the state space expression is obtained.
x ˙ ′ = A ′ x ′ + B ′ u ′ + M ′ δ (5)
y ′ = C ′ x ′ (6)

2.2.2. Robust H∞ Design of the Sliding Mode Speed Control Law

For the system state to reach the slide face within a limited time, set the robust H∞ slip mode speed control law:
u ′ = − ( Ξ B ′ ) − 1 ( ‖ Ξ A ′ ‖ ‖ x ′ ‖ + ‖ Ξ M ′ ‖ δ 0 + β ) × s i g m o i d ( s ) (7)
where β＞0, ijmoid(s) = 2/(1-e-as)-1, and α＞o construct the Lyapunov function as:
V s ( t ) = 1 2 s 2 (8)
V ˙ s ( t ) = s s ˙ = s Ξ ( A ′ x ′ + M ′ δ ) + s Ξ B ′ u ′ (9)
By substituting Equations (7) into (9), researchers can get the final equation of sliding mode speed control law. A diagram of the basic operation of the H∞ controller is described in Figure 1.
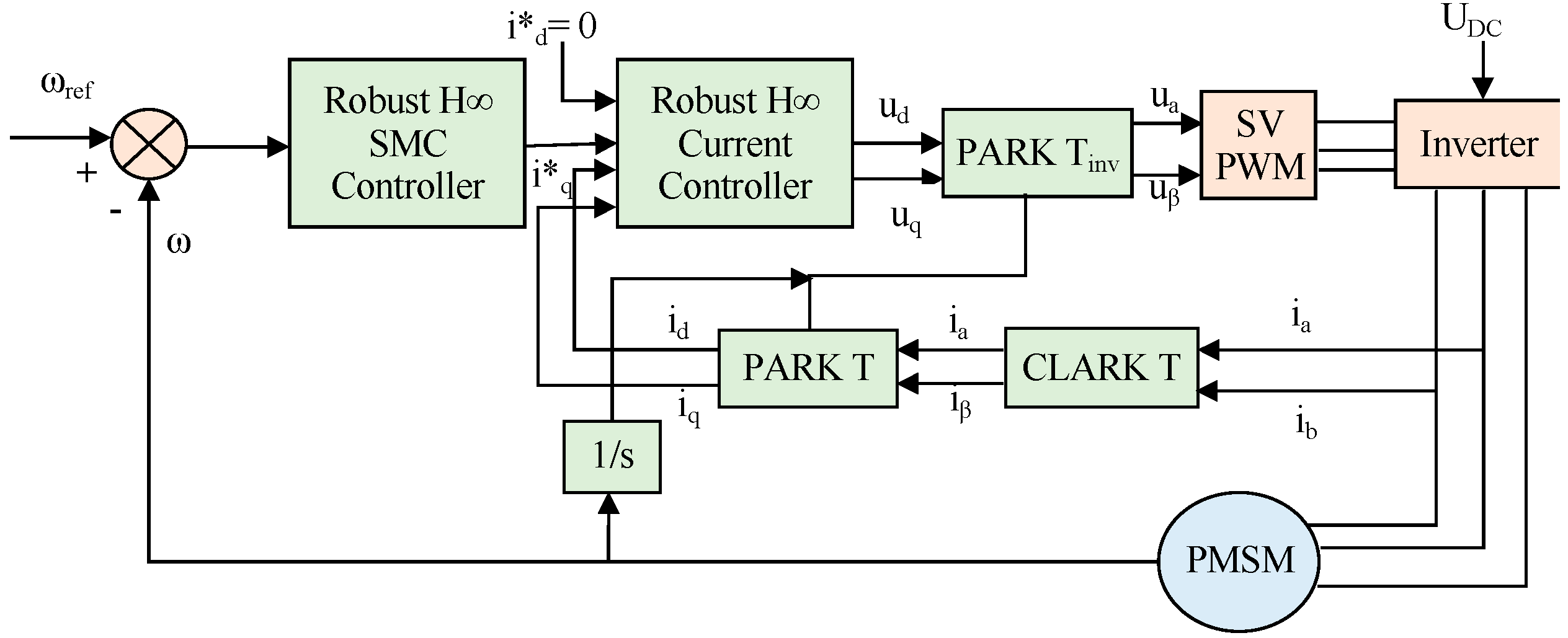
Figure 1. Principal diagram of PMSM speed regulation based on H∞ robust controller.

References

  1. Fan, S.; Tong, C. Model predictive current control method for PMSM drives based on an improved prediction model. J. Power Electron. 2020, 20, 1456–1466.
  2. Wang, W.; Shen, H.; Hou, L.; Gu, H. H∞ Robust Control of Permanent Magnet Synchronous Motor Based on PCHD. IEEE Access 2019, 7, 49150–49156.
  3. Ma, Y.; Li, Y. Active Disturbance Compensation Based Robust Control for Speed Regulation System of Permanent Magnet Synchronous Motor. Appl. Sci. 2020, 10, 709.
  4. Zheng, Y.; Zhao, H.; Zhen, S.; Sun, H. Fuzzy-set theory based optimal robust constraint-following control for permanent magnet synchronous motor with uncertainties. Control Eng. Pract. 2021, 115, 104911.
  5. Zhen, S.; Peng, X.; Liu, X.; Li, H.; Chen, Y.-H. A new PD based robust control method for the robot joint module. Mech. Syst. Signal Process. 2021, 161, 107958.
  6. Wu, H.; Zheng, L.; Li, Y.; Zhang, Z.; Yu, Y. Robust Control for Active Suspension of Hub-Driven Electric Vehicles Subject to in-Wheel Motor Magnetic Force Oscillation. Appl. Sci. 2020, 10, 3929.
  7. Pillay, P.; Krishnan, R. Modeling, simulation, and analysis of permanent-magnet motor drives. I. The permanent-magnet synchronous motor drive. IEEE Trans. Ind. Appl. 1989, 25, 265–273.
  8. Kim, S.-K.; Lee, J.-S.; Lee, K.-B. Robust speed control algorithm with disturbance observer for uncertain PMSM. Int. J. Electron. 2018, 105, 1300–1318.
  9. Sudwilai, P.; Oka, K.; Sano, A.; Hirokawa, Y. 2A12 Vibration Control with Linear Actuator Permanent Magnet System using Robust Control. In Proceedings of the Symposium on the Motion and Vibration Control, Tokyp, Japan, 17–20 August 2010; pp. _2A12-1_–_2A12-11_.
  10. Hassaine, S.; Moreau, S.; Ogab, C.; Mazari, B. Robust Speed Control of PMSM using Generalized Predictive and Direct Torque Control Techniques. In Proceedings of the 2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 1213–1218.
  11. Chou, H.-H.; Cheng, S.; Ting, C.-M. 2A23 H∞ Observer for Sensorless Velocity Control of Permanent Magnet Synchronous Motors. In Proceedings of the Symposium on the Motion and Vibration Control, Tokyp, Japan, 17–20 August 2010; pp. _2A23-1_–_2A23-10_.
  12. Mayo, P.; Saenz-Aguirre, A.; Martín, F.; Vadillo, J. FOC-Droop control strategy for PMSM fed paralleled multi-inverter power systems oriented to aeronautical applications. Electr. Power Syst. Res. 2020, 185, 106369.
  13. Wang, X.; Suh, C.S. A nonlinear time–frequency control based FOC for permanent magnet synchronous motors. Int. J. Dyn. Control 2020, 9, 179–189.
  14. Cai, R.; Zheng, R.; Liu, M.; Li, M. Optimal selection of PI parameters of FOC for PMSM using structured H∞-synthesis. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 5–8 November 2017; pp. 8602–8607.
  15. Zhang, W.; Cao, B.; Nan, N.; Li, M.; Chen, Y. An adaptive PID-type sliding mode learning compensation of torque ripple in PMSM position servo systems towards energy efficiency. ISA Trans. 2020, 110, 258–270.
  16. Nazelan, A.; Osman, M.K.; Samat, A.; Salim, N.A. PSO-Based PI Controller for Speed Sensorless Control of PMSM. J. Phys. Conf. Ser. 2018, 1019, 012027.
  17. Elhafyani, M.L.; Fadil, H. Fuzzy-PI controller applied to PMSM speed controller: Design and experimental evaluation. Int. J. Power Electron. 2020, 11, 102.
  18. Pyrkin, A.; Bobtsov, A.; Ortega, R.; Vedyakov, A.; Cherginets, D.; Ovcharov, A.; Petranevsky, I. Robust nonlinear observer design for permanent magnet synchronous motors. IET Control Theory Appl. 1994, 2, 524.
  19. Xu, D.; Gao, Y. A simple and robust speed control scheme of permanent magnet synchronous motor. J. Control Theory Appl. 2004, 2, 165–168.
  20. Pyrkin, A.; Vedyakov, A.; Bobtsov, A.; Bazylev, D.; Sinetova, M.; Ovcharov, A.; Vladislav, A. Adaptive Full State Observer for Nonsalient PMSM with Noised Measurements of the Current and Voltage: The work was written with the support of the Ministry of Science and Higher education of the Russian Federation, project unique identifier RFMeFI57818X0271. IFAC-PapersOnLine 2020, 53, 1652–1657.
  21. De Soricellis, M.; Da Ru, D.; Bolognani, S. A Robust Current Control Based on Proportional-Integral Observers for Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Appl. 2017, 54, 1437–1447.
  22. Ahmed, W.A.E.M.; Adel, M.M.; Taha, M.; Saleh, A.A. PSO technique applied to sensorless field-oriented control PMSM drive with discretized RL-fractional integral. Alex. Eng. J. 2021, 60, 4029–4040.
  23. Jie, H.; Zheng, G.; Zou, J.; Xin, X.; Guo, L. Adaptive Decoupling Control Using Radial Basis Function Neural Network for Permanent Magnet Synchronous Motor Considering Uncertain and Time-Varying Parameters. IEEE Access 2020, 8, 112323–112332.
  24. Sheng, L.; Xiaojie, G.; Lanyong, Z. Robust Adaptive Backstepping Sliding Mode Control for Six-Phase Permanent Magnet Synchronous Motor Using Recurrent Wavelet Fuzzy Neural Network. IEEE Access 2017, 5, 14502–14515.
  25. Liu, X.; Zhang, Q. Robust Current Predictive Control-Based Equivalent Input Disturbance Approach for PMSM Drive. Electronics 2019, 8, 1034.
  26. Girovský, P. Fuzzy control of synchronous motor with permanent magnet. Acta Electrochim. Inform. 2016, 16, 17–20.
  27. Yang, J.-Z.; Li, Y.-X.; Tong, S. Adaptive NN finite-time tracking control for PMSM with full state constraints. Neurocomputing 2021, 443, 213–221.
  28. Zaihidee, F.M.; Mekhilef, S.; Mubin, M. Robust Speed Control of PMSM Using Sliding Mode Control (SMC)—A Review. Energies 2019, 12, 1669.
  29. Pewmaikam, C.; Srisertpol, J.; Khajorntraidet, C. Adaptive Fuzzy Logic Compensator for Permanent Magnet Synchronous Motor Torque Control System. Int. J. Model. Optim. 2012, 2, 141–146.
  30. Xiong, J.; Gu, H. Research on a Sliding Mode Variable Structure Control FOC of PMSM for Electric Vehicles. In Proceedings of the 2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 23–25 November 2018; pp. 1088–1091.
  31. Ma, X.; Zhang, J.; Huang, R. Disturbance observer based adaptive sliding mode controllers for fuzzy systems with mismatched disturbance. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 3391–3396.
  32. Wang, Y.; Yu, H.; Che, Z.; Wang, Y.; Zeng, C. Extended State Observer-Based Predictive Speed Control for Permanent Magnet Linear Synchronous Motor. Processes 2019, 7, 618.
  33. Jon, R.; Wang, Z.; Luo, C.; Jong, M. Adaptive robust speed control based on recurrent elman neural network for sensorless PMSM servo drives. Neurocomputing 2017, 227, 131–141.
  34. Benfriha, E.; Mansouri, A.; Bendiabdellah, A.; Boufadene, M. Nonlinear adaptive observer for sensorless passive control of permanent magnet synchronous motor. J. King Saud Univ.-Eng. Sci. 2019, 32, 510–517.
  35. Zhao, N.; Ge, B.-M. H∞ robust control of permanent magnet synchronous motor used in electric vehicle. Electr. Mach. Control 2007, 5, 462–466.
  36. Zhou, B.; Xia, Y. H∞ control for speed control of permanent magnet synchronous motor based on Matlab. In Proceedings of the 2012 International Conference on System Simulation (ICUSS 2012), Shanghai, China, 12–15 June 2012; p. 147.
  37. Gambhire, S.J.; Kishore, D.R.; Londhe, P.S.; Pawar, S.N. Review of sliding mode based control techniques for control system applications. Int. J. Dyn. Control 2020, 9, 363–378.
  38. Majidabad, S.S.; Zafari, Y. Robust flux observer and robust block controller design for interior permanent magnet synchronous motor under demagnetisation fault. Int. J. Model. Identif. Control 2018, 30, 206.
  39. Lee, Y.; Lee, S.-H.; Chung, C.C. LPV H∞ Control with Disturbance Estimation for Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2017, 65, 488–497.
  40. Liu, B. Research on H infinity Robust Tracking Controller for Permanent Magnet Synchronous Motor Servo System. In Proceedings of the 2009 International Conference on Information Engineering and Computer Science, Wuhan, China, 31 March–2 April 2009; pp. 1–5.
  41. Vadivel, R.; Joo, Y.H. Reliable fuzzy H∞ control for permanent magnet synchronous motor against stochastic actuator faults. IEEE Trans. Syst. Man Cybern. Syst. 2019.
  42. Mousavi, M.H.; Karami, M.E.; Ahmadi, M.; Sharafi, P.; Veysi, F. Robust speed controller design for permanent magnet synchronous motor based on gain-scheduled control method via LMI approach. SN Appl. Sci. 2020, 2, 1–15.
  43. Khodamoradi, A.; Heydari, M.; Hasanzadeh, S. Design of Robust H∞ Controller based on Nonlinear Observer for Sensorless PMSM using LMIs. In Proceedings of the 7th International Conference on Control, Instrumentation and Automation (ICCIA), Tabriz, Iran, 23–24 February 2021.
  44. Ghafarri-Kashani, A.R.; Yazdanpanah, M.J.; Faiz, J. Robust speed control of pmsm using mixed nonlinear h∞/smc techniques. IFAC Proc. 2008, 41, 8413–8418.
  45. Huang, G.; Li, J.; Fukushima, E.F.; Zhang, C.; He, J.; Zhao, K. An improved equivalent-input-disturbance approach for PMSM drive with demagnetization fault. ISA Trans. 2020, 105, 120–128.
  46. Choi, J.; Nam, K.; Bobtsov, A.; Pyrkin, A.; Ortega, R. Robust Adaptive Sensorless Control for Permanent-Magnet Synchronous Motors. IEEE Trans. Power Electron. 2016, 32, 3989–3997.
  47. Lee, H.; Lee, Y.; Shin, D.; Chung, C.C. H∞ control based on LPV for load torque compensation of PMSM. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Korea, 13–16 October 2015.
  48. Yang, J.; Fa, N.; Chen, R. H∞ Robust Controller Based on Local Feedback Recurrent Neural Network for Permanent Magnet Linear Synchronous Motor. In Proceedings of the 2006 CES/IEEE 5th International Power Electronics and Motion Control Conference, Shanghai, China, 14–16 August 2006.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Electrical & Electronic
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Kifayat Ullah
View Times: 1.1K
Revisions: 2 times (View History)
Update Date: 03 Mar 2022
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback