Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1 Surfactant/oil/water system have resulted in formulation concepts labeled hydrophilic-lipophilic balance (HLB), Winsor’s ratio (R = Aco/Acw), phase inversion temperature (PIT), or more recently the hydrophilic-lipophilic deviation (HLD).
Jean-Louis Salager
+ 4565 word(s) 4565 2020-08-17 06:27:49 |
2 Equation numbers
Jean-Louis Salager
Meta information modification 4565 2020-08-21 21:56:26 | |
3 References
Jean-Louis Salager
-4 word(s) 4561 2020-08-21 22:06:24 | |
4 Typo
Jean-Louis Salager
-5 word(s) 4560 2020-08-21 22:36:12 | |
5 typos
Jean-Louis Salager
-5 word(s) 4560 2020-08-21 22:59:00 | |
6 typo
Jean-Louis Salager
-5 word(s) 4560 2020-08-21 23:00:01 | |
7 Typo
Jean-Louis Salager
+ 9 word(s) 4574 2020-08-22 02:53:18 | |
8 Typo
Jean-Louis Salager
+ 10 word(s) 4575 2020-08-22 02:59:27 | |
9 typos
Jean-Louis Salager
+ 10 word(s) 4575 2020-08-22 03:19:28 | |
10 spaces
Jean-Louis Salager
+ 10 word(s) 4575 2020-08-22 03:20:15 | |
11 Typo
Jean-Louis Salager
Meta information modification 4575 2020-08-22 18:55:48 | |
12 Image
Jean-Louis Salager
Meta information modification 4575 2020-08-23 21:12:10 | |
13 Cover
Jean-Louis Salager
Meta information modification 4575 2020-08-23 21:15:06 | |
14 format correct
Camila Xu
 -14 word(s) 4561 2020-08-24 08:21:49 | |
15 format correct
Camila Xu
 Meta information modification 4561 2020-12-11 02:40:10 | |
16 Link at the end unintended erased
Jean-Louis Salager
+ 5 word(s) 4566 2021-07-03 20:11:16 | |
17 Typo
Jean-Louis Salager
-1 word(s) 4565 2021-08-10 20:28:16 | |
18 Authors
Jean-Louis Salager
+ 31 word(s) 4596 2021-08-14 04:03:10 | |
19 authors
Jean-Louis Salager
+ 33 word(s) 4598 2021-08-14 07:15:48 | |
20 typo
Jean-Louis Salager
+ 33 word(s) 4598 2021-08-14 07:16:48 | |
21 update layout
Rita Xu
-33 word(s) 4565 2021-08-17 05:25:03 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Salager, J.; Antón, R.; Bullón, J.; Forgiarini, A.; Marquez, R. Multivariable Formulation of Surfactant-Oil-Water Systems. Encyclopedia. Available online: https://encyclopedia.pub/entry/1772 (accessed on 26 April 2024).
Salager J, Antón R, Bullón J, Forgiarini A, Marquez R. Multivariable Formulation of Surfactant-Oil-Water Systems. Encyclopedia. Available at: https://encyclopedia.pub/entry/1772. Accessed April 26, 2024.
Salager, Jean-Louis, Raquel Antón, Johnny Bullón, Ana Forgiarini, Ronald Marquez. "Multivariable Formulation of Surfactant-Oil-Water Systems" Encyclopedia, https://encyclopedia.pub/entry/1772 (accessed April 26, 2024).
Salager, J., Antón, R., Bullón, J., Forgiarini, A., & Marquez, R. (2020, August 21). Multivariable Formulation of Surfactant-Oil-Water Systems. In Encyclopedia. https://encyclopedia.pub/entry/1772
Salager, Jean-Louis, et al. "Multivariable Formulation of Surfactant-Oil-Water Systems." Encyclopedia. Web. 21 August, 2020.
Multivariable Formulation of Surfactant-Oil-Water Systems
Edit

Surfactant-Oil-Water (SOW) systems are found in nature and synthetic products. They usually result in two immiscible phases, e.g., for two liquids, a water phase (often a brine), and an oily phase (which could be extremely complex as petroleum). Surfactant partitions between the two phases according to some physicochemical rules due to molecular interactions. There is a very particular formulation case in which SOW systems can form three immiscible phases, that is, two excess phases (water and oil) in equilibrium with a  so-called middle phase (because of an intermediate density that places it in the middle of a test tube). This middle phase is a so-called bicontinuous microemulsion which has no droplets dispersed in an external phase as a typical emulsion, but a complex single-phase structure similar to a disordered liquid crystal. When stirred, SOW systems can form multiple dispersed systems that can be described as macroemulsions or nanoemulsions depending on the drop size (O/W or W/O) or multiple emulsions (w/O/W or o/W/O) with droplets inside larger drops. Since the beginnings of the 20th century with Bancroft’s rule, the properties of these systems have been related to many thermodynamic variables, generally with one effect at a time. Nowadays, the generalized physicochemical concept of SOW systems with many formulation variables involved allows to make predictions in various application cases, even for very complex systems, as in enhanced oil recovery (EOR), crude oil dehydration, paints, foods, cosmetics and pharmaceutical formulations, that requires the control on 6-8 variables or even more. This is mainly because of the presence of mixtures of oils from linear alkanes to triglycerides or complex molecules perfumes, or a mixture of salts with cations from sodium to calcium or aluminum, and anions like chloride to phosphate. The complexity is even worse with mixtures of very different surface-active species, resulting in non-linear interactions.

surfactant-oil-water (SOW) systems physicochemical formulation phase behavior micro/macro-emulsion properties
 

1. Surfactants

Surfactants are amphiphilic molecules going to surfaces and interfaces to produce specific effects. Typical interfaces are the limits between two immiscible phases, e.g., two fluids like water/air and water/oil, or solid/liquid. Surfactants tend to crucially influence the properties of the equilibrated systems (surface and interfacial tension, adsorption, association, bulk solution solubilization, and phase behavior) [1], as well as those of multiphasic dispersions (e.g., macro-, mini-, nano-, and micro-emulsions, foams, and suspensions), which vary with the selected surfactant(s) and with the nature of the other ingredients [2].

Surfactants are used in hundreds of household and industrial applications dealing with surfaces and interfaces, e.g., detergency and cleaning, personal care products, pharmaceutical and cosmetic vehicles, foods and beverages, paints, corrosion inhibitors, wastewater treatment, paper making, ore separation and concentration, and lubrication.

Surfactants are classified according to its behavior in water (i.e., soluble or insoluble, ionic or nonionic); however, this classification is too simple and often insufficient in practical cases. A useful classification must be related to some determinant behavior, or some attained characteristic property of interest, in a water solution or a multiphase system, such as those containing oil and water, or solid and liquid [1].

2. Physicochemical formulation parameters

The first and simplest way to describe the effect of surfactants from the physicochemical point of view was first considered analyzing the surfactant behavior in the system, independently of the nature of the other ingredients [11][12][13]. Surfactant properties include (i) the phase behavior in one solvent fluid, in particular, the concept of cloud point for nonionic surfactants; (ii) self-association in a solvent fluid, e.g., the formation of micelles or other aggregates, either in aqueous or oily phases and (iii) the association of surfactants with two immiscible fluids, e.g., oil and water, as in arrangements like microemulsions, liquid crystals, vesicles, liposomes, etc.

The physicochemical properties of SOW systems depend on the surfactant behavior and also on the other ingredients (aqueous brine, oil, additives) and certain conditions (temperature and pressure). The other ingredients, in particular in petroleum, food, detergency, pharmaceutical and cosmetic applications, involve the use of several variables to describe their composition, such as water (from an aqueous solution of sodium chloride to different salts composition as in petroleum reservoir brine, wastewater, or blood). As far as the oil phase is concerned, it can vary from pure n-alkane to plant terpenes, edible triglyceride oils, chlorinated solvents, or even crude oils, as well as more or less water-soluble alcohol cosurfactants. In all these cases, the temperature exerts an influence on many different phenomena, and, in petroleum reservoirs, as well as in system containing dissolved gas, the pressure may also be critical.

Physicochemical behavior of SOW systems was first described in the pioneering proposals such as Bancroft’s rule in 1915 [14], Langmuir’s wedge theory in 1917 [15], and Griffin’s hydrophilic-lipophilic balance (HLB) proposed in 1949 with an additional explanation on its use and limits in 1954 [4][5]. Then, as the surfactant systems have become more sophisticated, more complete approaches were proposed. The most significant step in that direction took into account many formulation variables, but was still a qualitative description; it was the Winsor’s R ratio, proposed in the 1950s [16][17], and its extension by Beerbower in 1976 as the cohesive energy ratio (CER) [18], based on the solubility parameters proposed by Hansen in 1967 [19], as well as the geometrical approach of Israelachvili’s critical packing parameter (CPP) [20]. After that, concepts that are more directed for application have been developed, among them, the phase inversion temperature (PIT), the surfactant affinity difference (SAD), and more recently, the hydrophilic-lipophilic deviation (HLD) and its more specific form HLDN [1].

2.1. Hydrophilic lipophilic balance (HLB) and Phase Inversion Temperature (PIT)

In 1950, Griffin introduced the hydrophilic-lipophilic balance number (HLB) by mixing two surfactants to attain a high stability of emulsion. HLB was firstly taken as 20% of the weight percent of the hydrophilic part of the surfactant, in particular, the ethylene oxide chain in polyethoxylated alcohols. General information is clearly found in Griffin’s original proposal [4][5], as well as with many publications [6], indicating for HLB the 12–18 range to attain stable O/W emulsions and a 4–5 short interval for W/O ones, both depending on the oil phase characterized by a so-called required HLB value. The neutral zone with no stable emulsion was in the 8–12 range on the Griffin scale, while it was in the 6–8 range in a proposal from Davies, which was more theoretical but also quite inexact in practice [7].

The HLB proposal from Griffin was helpful, but it was quite inaccurate for formulations used in many different applications, in particular for foods, cosmetics and pharmaceuticals [10]. This is because SOW systems physicochemical behavior depend on many other properties as the surfactant molecular weight [8], the nature of the hydrophilic group and the branching of the lipophilic tail, or some other specificities like the aromaticity of the oil, the presence of electrolyte in water, the usual addition of alcohol and other cosurfactants, the temperature, and the pressure [9].

After Griffin’s proposal, which comprised only the effect of the surfactant at constant temperature, Shinoda proposed in 1964 the phase inversion temperature (PIT) approach [21][22][23], independently described as a concept similar to Winsor’s R but with a temperature characteristic value. Even if it was limited to systems containing polyethoxylated nonionic surfactants, it was the first numerical approximation, and it has applicability even today in some processes, as emulsion inversion and nanoemulsion formation in temperature-sensitive systems.

2.2. One-Dimensional Scan with Typical Formulation Variables and the Winsor R relationship.

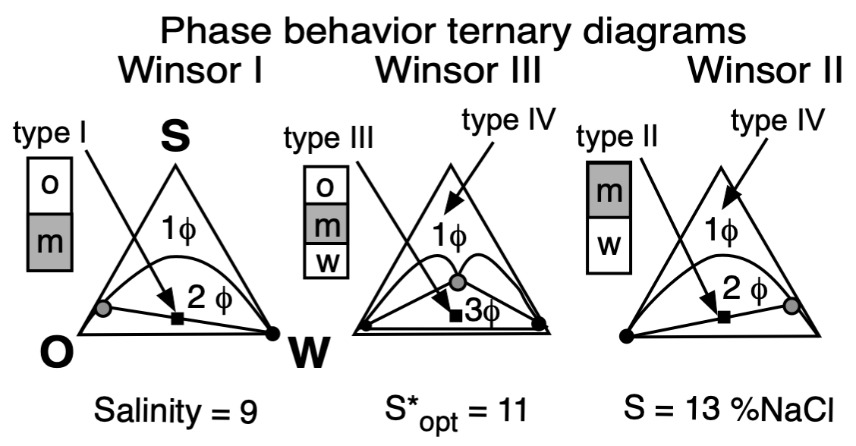
The basic technique to study the phase behavior of a SOW system was the one proposed by Winsor 70 years ago [16][40], which consisted of three cases very well described, which are depicted in Figure 5 according to Winsor’s ternary diagrams.

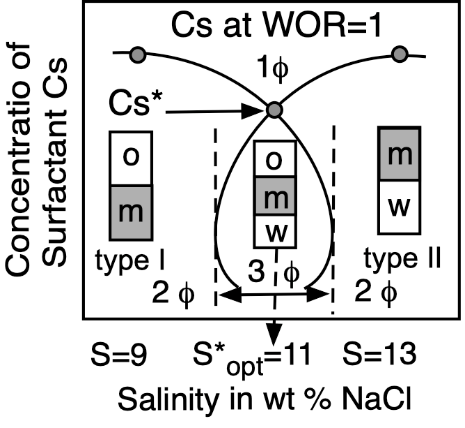
Figure 5. Top: Phase behavior at constant formulation cut for three cases of salinity (Winsor’s diagrams). Bottom: Solubilization as CS surfactant concentration to attain a single-phase microemulsion at constant WOR = 1 cut (vertical fish diagram). In both cases, the formulation scan is carried out by a change in salinity.

In the most elemental SOW ternary case containing a pure surfactant, an aqueous brine and an immiscible oil, the variables that affect physicochemical formulation were found to be the following: the surfactant characteristic features depending on at least two different aspects (i.e., its head group hydrophilicity and its tail lipophilicity), the salinity S of the water phase, and the nature of the oil, typically the alkane carbon number (ACN) for the most simple oil case, as well as the temperature and pressure.

In Winsor’s type I phase behavior, the surfactant exhibits more dominating attractive forces or interactions with water, and thus solubilizes oil in this phase micelles, with a very low concentration in the excess oil phase (essentially just above the CMC). In type II, it is the same but in the reversed way, when the surfactant has more interactions with the oil phase, thus forming inversed micelles solubilizing water inside.

In type III, the structured middle phase has an intermediate density because it contains similar amounts of oil and water. Winsor proposed for this middle phase a lamellar, more or less jellylike structure, because of some birefringence, but he mentioned that it was not necessarily a perfectly plane liquid crystal. He suggested that it might be distorted or could contain twisted lamellae with both types of micelles not necessarily spherical, nor really fully organized, but somehow linked or connected, and that it may be in a permanently changing situation. This was a very early vision from Winsor of the currently accepted bicontinuous microemulsion structure, proposed by Scriven in his excellent description [43].

Type IV is essentially a case in which there is enough surfactant (a very large concentration in practice, such as more than 20%) to cosolubilize both oil and water to produce a single phase.

In his 1954 book and final review paper [17], Winsor proposed to relate the type of SOW system with the ratio of interactions of the surfactant located at the oil and water limit. Winsor’s formulation parameter was defined according to the value of the ratio

R = Aco/Acw     (1)

where the molecular attractive forces Aco and Acw are between the adsorbed surfactant molecule and the nearby oil (O) and water (W) molecules. R indicates the ratio of the tendency of the interface layer to become convex towards O (R > 1) or towards W (R < 1). When R = 1, the situation corresponds to an average zero curvature at the O–W limit, which could be a flat lamellar structure or complex bicontinuous arrangements of both types of swollen micelles.

It should be noted that the R ratio is only qualitative since it is not known how many oil and water molecules actually interact with a single surfactant molecule, i.e., what are the coefficients before Aco and Acw, as well as other interactions appearing in R [32][45].

2.3. Hydrophilic Lipophilic Deviation (HLD)

The six or seven variables complex situation of a SOW was analyzed during the intensive research drive in enhanced oil recovery with surfactants in the late 1970s [25]. A study on bi- and multidimensional scans produced an empirical relationship that was interpreted as a physicochemical correlation for the attainment of three-phase behavior, high solubilization and a minimum interfacial tension [26] for ionic and nonionic surfactants [27][28].

The generality of the correlation for the occurrence of a so-called optimum formulation and related phenomena was expressed as the surfactant affinity difference (SAD) in 1983 [29], and its dimensionless equivalent, so-called hydrophilic-lipophilic deviation (HLD) in 2000 [30]. Conceptually, HLD is some kind of logarithmical expression of R, i.e., it is negative (respectively positive) if R < 1 (respectively R > 1). As will be more discussed later [11], HLD has the advantage of being easier to calculate because interaction energies are generally handled as summations and subtractions of chemical potential terms instead of their ratio. Hence, the so-called generalized formulation criterion, or hydrophilic-lipophilic deviation (HLD), is the difference between the numerator and denominator of R, i.e.,

HLD = Aco − Acw     (2)

By continuously changing one of the variables influencing R or HLD, through one of the interactions Aco or Acw, a so-called “formulation scan” is said to be carried out.

For instance, if the length of a surfactant alkyl tail is increased, without changing anything else, then the term Aco is going to increase, thus increasing R and HLD. If the size of a polyethoxylated surfactant head group is increased, it is now the Acw term, which is increased; thus, R and HLD are decreased. If the second change is carried out to exactly return to the HLD = 0 situation of three-phase behavior, then their effects are exactly compensated from the numerical point of view.

When the salinity of the aqueous phase increases, the Acw term decreases because the saltwater is a less hydrophilic solvent, and it thus results in a lower interaction of the aqueous phase with the surfactant head group. The Aww interaction is also decreasing, and the denominator definitively decreases, and thus R and HLD increase [32].

When the temperature is changed, most molecular interactions are altered, and the discussion is not easy to handle. However, it is experimentally well known that the ionic surfactants are likely to become slightly more water-soluble when temperature increases, i.e., Acw generally increases. The opposite occurs with nonionic species whose ethoxylated part is systematically dehydrated when temperature increases, thus becoming less water-soluble. As a result, an increase in temperature tends to slightly decrease the R and HLD for ionic surfactants and to strongly increase them for nonionics.

Consequently, it may be said that along with any kind of change of a formulation variable, the R or HLD criterion increases or decreases, and that at some point of the scan, a specific R = 1 or HLD = 0 value will take place. This occurrence has been called the “optimum formulation” by the people working in enhanced oil recovery because it is where an (ultra-)low minimum interfacial tension occurs, and thus allows the crude oil displacement to happen because of the considerable modification of the capillary number [24].

At optimum formulation, the partition coefficient of the surfactant between the two excess phases in a type III system is unity, which corresponds to an equal interaction of the amphiphile molecule with the oil and water or very close to its critical micelle concentrations in the excess phases. The phase behavior change produced by an increase in brine salinity is usually shown as the diagram transition WI > WIII > WII, as indicated on the top of Figure 5.

An emulsion made by stirring an equilibrated SOW system also exhibits particular characteristics at optimum formulation [13][62][63]. It inverts, as indicated by a large change in conductivity, where it passes from O/W to W/O [91], as the phase behavior changes from type I to type II.

The emulsion stability passes through a very deep minimum at HLD = 0, i.e., the emulsion becomes very unstable, probably because the surfactant has a lower chemical potential in the microemulsion middle phase than at the oil-water interface, where it has to be to generate stabilization mechanisms. Consequently, it may be said that at optimum formulation, the surfactant seems to be trapped in the microemulsion and that the oil/water mixture dispersed as drops by the stirring would coalesce instantly in practice, as it would be in the complete absence of surfactant. This specific emulsion strong instability at optimum formulation has recently been found to match, and thus probably to result from, a very low interfacial rheology elasticity through a low dilational modulus  [64][65][66].

Additionally, emulsion viscosity is particularly low at optimum formulation, probably because the low tension favors the elongation of the drops when the emulsion is submitted to a shear. However, this viscosity minimum is not as accurate for detecting the optimum as the minimum stability.

The hydrophilic-lipophilic deviation from optimum formulation is formally similar to the empirical equation first proposed in 1979 for alkyl benzene sulfonates and other anionic and cationic surfactants likely to produce very low interfacial tension in EOR [27]. For systems containing ionic surfactants, the correlation was originally written as follows with a unit coefficient in front of the LnS term, essentially because it was the variable that was actually scanned in most experiments [27][32]. For this reason, here it will be called HLDLns

HLDLnS = LnS − KACN ACN + σ = 0     (3)

K is the coefficient of ACN, i.e., (∂lnS/∂ACN) in the original correlations (). K was found to be 0.16 for alkyl benzene sulfonates, 0.10 for alkyl carboxylates and sulfates, 0.17 for alkyl ammonium, and 0.19 for alkyl trimethyl ammonium and alkyl pyridinium. For extended surfactants containing a polypropylene oxide intermediate group between the ionic head and the alkyl tail, K was found to depend on PON, EON, the ionic group, and the tail branching (from 0.05 to 0.14) but with no general rule found yet [76][78][79][82][85][86].

The alcohol contribution was originally indicated as an extra term called −f(A) added in equation (2) because it is positive only for very short alcohols like ethanol or propanols and very small. For longer alcohols normally used, it is negative and linear, i.e., −f(A) = −KA CA, with CA being the concentration in vol % and KA a negative coefficient whose absolute value increases with the alcohol lipophilicity.

The following more complete correlation (3) includes the effect of temperature and pressure [87][88][89][90]. The temperature effect is small for ionic surfactants. The pressure effect reported only some time ago [90] has in most cases a very small Kp coefficient value in HLD; it is thus generally negligible at ambient conditions.

HLDLnS = Ln(S) − KACN (ACN) + σ − KACA − KT (T) − Kp (P) = 0     (4)

HLD equation can be generalized so as to use it as a single expression, dividing by the coefficient of the variable which has the same meaning, i.e., KACN, thus becoming the “normalized” HLDN, in which the surfactant contributing parameter SCP is also taken with a (+1) coefficient by definition.

HLDN = SCP − (ACN − ACNref) + kLnS LnS (or kS S) − kACA ± kT (T-Tref) − kp (P-Pref) = 0     (5)

In the references that are usually selected, the temperature and pressure are ambient values, i.e., Tref = 25 °C and Pref = 1 bar, while the salinity references are S = 0 for nonionics or S = 1 for ionic amphiphiles (as well as S = 1 for a mixture of ionic and nonionic surfactants), and in most cases without alcohol (CA = 0). In the current equation (11), the oil reference could be taken as ACNref = 0, so that, with the previously selected references, the HLDN = 0 equation can be simply be written as SCP = (P)CAN.

3. Relation of HLD Values with Micro-, Mini-, and Macroemulsion Properties

Emulsion persistence has been systematically studied in many reports describing the numerous phenomena involved [92][93][94]. No matter the ordinate stability scale, it happens that very close to the optimum formulation, in the narrow HLDN interval from −5 to +5, the emulsions are very unstable. The handling of HLD by changing one or two variables enables the emulsion manufacturer to be exactly in the desired stability or instability zone. This is why manipulating the HLD is an extremely useful technique for the practical use of formulation. At optimum formulation, SOW systems exhibit not only a very strong instability, but it also indicates that, at some distance from HLDN = 0, i.e., in the 10–20 unit range on both sides, there is a stable zone for the two types of emulsions.

3.1. The formulation-composition diagram

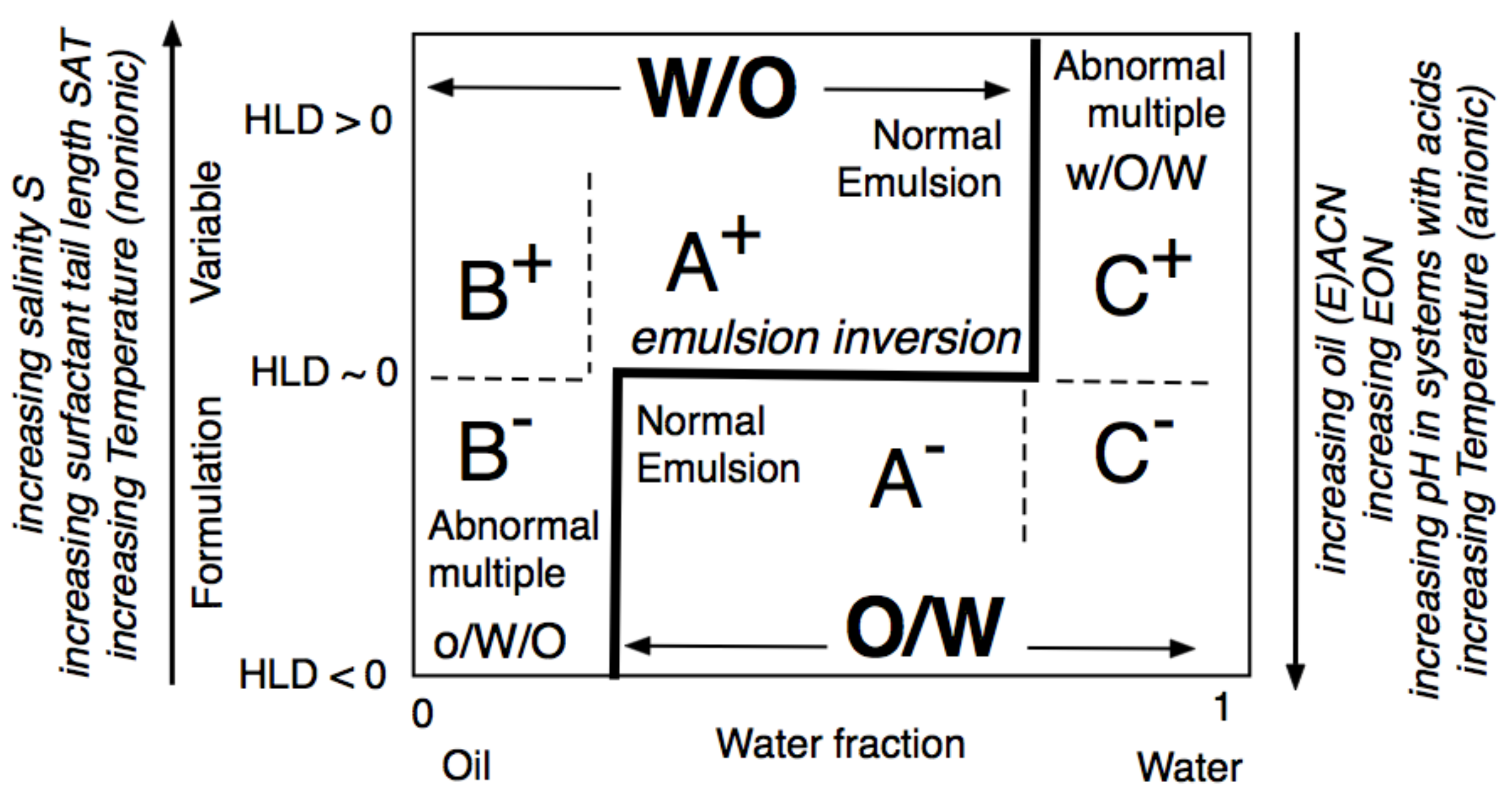
The formulation-composition or HLD-WOR (Water-Oil Ratio) diagram, depicted in Figure 16, is an important tool for understanding the changes that occur in SOW when variables are changed. The emulsion inversion is a horizontal line at HLDN ~ 0 with the WIII phase behavior in the WOR central part. In this range, the HLD is the unique criterion to attain O/W or W/O types so-called A+ and A- “normal” emulsions, in which the continuous phase is the one containing most of the surfactant. In the extreme WOR zones, called B and C, the normal emulsions occur when the HLD matches the occurrence of the continuous phase with most of the surfactant, i.e., B+ (respectively C-), which may be considered as the continuity of the A+ (respectively A-) zone with a high dilution, i.e., a large excess of the external phase.

Figure 16. Classical formulation-composition diagram (HLD-WOR) showing the inversion line and emulsion types.

On the contrary, the B– and C+ zones are said to be “abnormal” because most of the surfactant is not in the emulsion external phase. This is the reason why these zones are exhibiting “multiple” emulsions in some places, with droplets in drops forming the “internal” emulsion, and drops in a continuous phase forming the “external” one, i.e., o/W/O in B– and w/O/W in C+, with the low case letter indicating the phase of the smaller droplets inside the drops. The formation of multiple emulsion is due to a conflict between the formulation and the composition, and it depends on the way the emulsification process is carried out, in particular, it can be made in different steps or produced spontaneously [95][96][97][98].

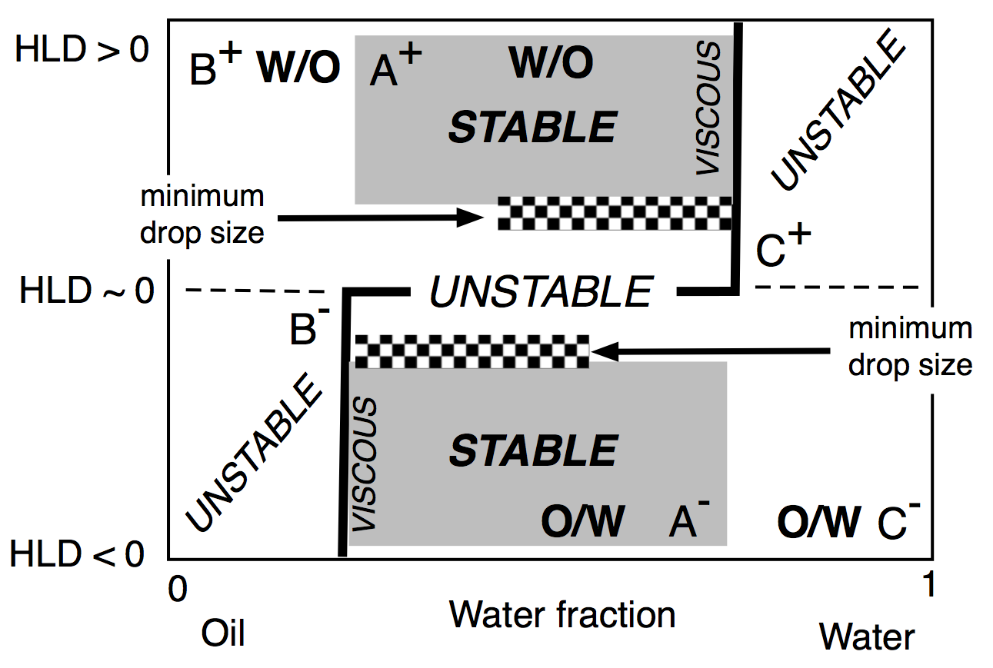
The two lateral branches of the inversion line, depicted in Figure 17, are mostly vertical, are due to the presence of different mechanisms that are independent of HLD. This type of inversion thus mainly depends on the WOR, with a strong tendency to have the one with the larger proportion as an external phase. This is why the inversion vertical line is on the right or the left side, depending on the HLD favoring a curvature matching a W/O or O/W emulsion. The vertical line position was also found to depend on other conditions which do not appear on this map, such as the mixing apparatus features that can influence the local WOR in the mixed zone, as well as the stirring energy and the intensity of shearing, and the relative viscosity of the phases. This inversion, which is so-called “catastrophic” because of its characteristics, is not necessarily the same in the two directions of change, i.e., when adding oil or adding water, and it can involve a hysteresis that tends to increase when the formulation deviates from HLD = 0. This hysteresis means that dynamic changes in WOR (i.e., adding water or adding oil when stirring) can produce delays, or somehow push the inversion occurrence, thus displacing its position. As a consequence, these vertical parts on the inversion line can be slanted in one direction or the other depending on the direction of WOR change.

Figure 17. Classical formulation-composition diagram (HLD-WOR) showing the basic properties (stability, drop size and viscosity) as described a long time ago [98].

In any case, this change in property from place to place in this kind of map indicates that dynamic processes are often a means to benefit from several favorable properties in a path on the map with a number of subsequent steps, often with a horizontal, vertical or slanted crossing of the inversion line [99][100][101][102][103][104][105].

4. The complex case of SOW non-linear mixtures

There are instances where the very straightforward case of HLDN linear relationship isn't apparent. These happen due to the occurrence of non-linear effects in mixtures of the components that are present in SOW systems. Some specific cases can be mentioned, particularly the effect of non-linearity in complex oil, salt or surfactant mixtures.

4.1. Equivalent Alquil Chain Number (EACN)

When the oil phase contains various substances, a linear mixing rule is generally valid if the species involved are not very different, in particular in their structure and polarity. For instance, a hexane-hexadecane mixture perfectly follows a linear equation with the number of carbon atoms in the oil, as can be seen in the next equation, where the Xi is the fraction (molar in theory but often simply volumetric) of the “i” specie in the mixture.

EACNMIX = ∑ Xi EACNi     (6)

Oils of diverse nature generate non-linear mixture rules. For example, when benzene is added to the tetradecane, the LnS* decreases very quickly, certainly because the benzene tends to accumulate close to the interface, and results in a strong change [106][107]. However, on the other side, when some tetradecane is added to benzene, the oil LnS* practically does not change because the tetradecane does not go close to the interface, where the benzene occupies almost all the volume.

4.2. Equivalent Salinity

In many cases, the aqueous phase contains different salts, in particular in a petroleum reservoir, in wastewater, and in blood. The HLD linear variation with salinity as LnS seems to be general for ionic surfactant systems, even if the concentration is not expressed in wt% but in mol/liter, i.e., with another scale, which only changes the salinity term coefficient in the HLDN expression.

The variation of the negative counter-ion (for instance, a change from sodium chloride to sodium sulfate or phosphate) can be taken into account with an equivalence coefficient 2/(1 + Z), where Z is the valency of the anions [75]. This term enters the constant in the HLDN equation, and the equivalence is easy to handle.

However, this is not the case for the variation of the cation (for instance, from sodium to calcium or aluminum chloride) and a general salinity equivalence is not available yet, although some trends have been proposed [108][109][110].

4.3. Equivalent SCP in Surfactant Mixtures

The use of surfactant mixtures is a very important subject, first because, in many systems, the S, (E)ACN, T and P values are fixed by the application. A required SCP value can thus be calculated to produce HLD = 0 in order to attain optimum formulation or a different goal, for instance, HLDN ~ −6 or −8 to produce an O/W small-drop nanoemulsion.

Since it is highly unlikely that a commercial product has the proper SCP to exactly attain the goal, a mixture of at least two surfactants is required. Back in 1979, the basic mixing rules were studied at the same time as the SAD/HLD concept for the EOR application [69]. These results were written as follows when the optimum was detected by a salinity scan for two or more similar ionic surfactants:

LnSMIX = X1 LnS1 + X2 LnS2 or LnSMIX = ∑ Xi LnSi     (7)

Or with EON scans for ethoxylated nonionics where ∂β/∂ACN = −∂EON/∂ACN slope K = −0.15

EONMIX = X1 EON1 + X2 EON2 or EONMIX = ∑ Xi EONi     (8)

This is equivalent to HLDMIX = ∑ Xi HLDi only if the K coefficient is the same for all the surfactants used, which is not always true in particular in a mixture of ionics with different Ks in front of ACN, and for ionic/nonionic mixtures where the definitions of K are different. To avoid this problem, it is absolutely necessary to use the normalized HLDN for such mixtures, and thus the surfactant contribution parameter SCP with the same coefficient as the real or virtual scan variable, i.e., SCP = NMIN, σ/K, β/K, Cc/K, PIT/K in the first generation of equations.

5. Final remarks

Using a sound knowledge of physicochemical formulation, HLDN parameter, a general HLD-WOR map, and carrying out a few experiments to generate the corresponding know-how, makes it possible to conduct a few effective trials to obtain an original solution for very complex SOW systems. Now, the possibilities are very numerous because the exact position of the frontiers also depends on some specificities of the surfactant(s), oil(s), and brine, as well as cosurfactants, and polymers.

This means that each research and development center which prepares an emulsion with a specific application needs to improve its understanding and build up appropriate know-how for its business. This is generally a matter of getting some practical training from a university working with the industrial sector. Then the research and development professionals have to start working on that, trial after trial, in equilibrated and dynamic processes, and, after ten years of accumulated experience, they will be able to provide an optimized solution in a few days only.

The entry is from 10.3390/cosmetics7030057

References

  1. Rosen, M.J. Surfactants and Interfacial Phenomena, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
  2. Rosen, M.J.; Dahanayake, M. Industrial Utilization of Surfactants. Principles and Practice; AOCS Press: Urbana, IL, USA, 2000; ISBN 893997111. [Google Scholar]
  3. Salager, J.L.; Bullon, J.; Pizzino, A.; Rondon-Gonzalez, M.; Tolosa, L. Emulsion Formulation Engineering for the Practitioner. In Encyclopedia of Surface and Colloid Science, 2nd ed.; Somasundaran, B., Ed.; Taylor & Francis: London, UK, 2010; Volume 1, Section 1; pp. 1–6. [Google Scholar] [CrossRef]
  4. Griffin, W.C. Classification of Surface Active Agents by HLB. J. Soc. Cosmet. Chem. 1949, 1, 311–326. [Google Scholar]
  5. Griffin, W.C. Calculation of HLB values of nonionic surfactants. J. Soc. Cosmet. Chem. 1954, 5, 249–256. [Google Scholar]
  6. Becher, P. Hydrophilic-lipophilic balance: An updated bibliography. In Encyclopedia of Emulsion Technology; Becher, P., Ed.; Marcel Dekker: New York, NY, USA, 1985; Volume 2, Chapter 8. [Google Scholar]
  7. Davies, J.T. A quantitative kinetic theory of emulsion type I: Physical chemistry of the emulsifying agent. In Gas/Liquid and Liquid/Liquid Interfaces. Proceedings of the 2nd International Congress of Surface Activity; Butterworths: London, UK, 1957; Volume 1, pp. 426–438. [Google Scholar]
  8. Marszall, L. Dependence of hydrophilic-lipophilic balance of nonionic surfactants on the size of the molecule. Kolloid Z Z Polym. 1973, 251, 609–610. [Google Scholar] [CrossRef]
  9. Balson, T.G. HLB: Is it a valuable concept or a curiosity? In Industrial Applications of Surfactants IV; Karsa, D.R., Ed.; Royal Society of Chemistry: London, UK, 1999; pp. 175–192. [Google Scholar]
  10. Ontiveros, J.F.; Pierlot, C.; Catte, M.; Molinier, V.; Salager, J.L.; Aubry, J.M. A simple method to assess the hydrophilic lipophilic balance of food and cosmetic surfactants using the phase inversion temperature of C10E4/n-octane/water emulsions. Colloids Surf. A 2014, 458, 32–39. [Google Scholar] [CrossRef]
  11. Salager, J.L. Quantifying the concept of physico-chemical formulation in surfactant-oil-water systems. Progr. Colloid Polym. Sci. 1996, 100, 137–142. [Google Scholar] [CrossRef]
  12. Salager, J.L. Formulation concepts for the emulsion makers. In Pharmaceutial Emulsions and Suspensionfs; Nielloud, F., Marti-Mestres, G., Eds.; Marcel Dekker: New York, NY, USA, 2000; Chapter 2; pp. 19–72. [Google Scholar] [CrossRef]
  13. Salager, J.L. Emulsion properties and related know-how to attain them. In Pharmaceutial Emulsions and Suspensionfs; Nielloud, F., Marti-Mestres, G., Eds.; Marcel Dekker: New York, NY, USA, 2000; Chapter 3; pp. 73–125. [Google Scholar] [CrossRef]
  14. Bancroft, W.D. The Theory of Emusification VI. J. Phys. Chem. 1915, 19, 275–309. [Google Scholar] [CrossRef]
  15. Langmuir, I. The constitution and fundamental properties of solids and liquids. J. Am. Chem. Soc. 1917, 39, 1848–1906. [Google Scholar] [CrossRef]
  16. Winsor, P. Solvent Properties of Amphiphilic Compounds; Butterworth: London, UK, 1954. [Google Scholar]
  17. Winsor, P. Binary and multicomponent Solutions of amphiphilic compounds. solubilization and the formation, structure, and theoretical significance of liquid crystalline solutions. Chem. Rev. 1968, 68, 1–40. [Google Scholar] [CrossRef]
  18. Holtzscherer, C.; Candau, F. Application of the cohesive energy ratio concept (CER) to the formation of polymerizable microemulsions. Colloids Surf. 1988, 29, 411–423. [Google Scholar] [CrossRef]
  19. Hansen, C. The Three Dimensional Solubility Parameter—Key to Paint Component Affinities: I.; Solvents, Plasticizers, Polymer, and Resins. J. Paint Technol. 1967, 39, 104–117. [Google Scholar]
  20. Israelavilich, J.N. The science and applications of emulsions—An overview. Colloids Surf. A 1994, 91, 1–8. [Google Scholar] [CrossRef]
  21. Shinoda, K.; Arai, H. The correlation between phase inversion temperature in emulsion and cloud point in solution of nonionic emulsifier. J. Phys. Chem. 1964, 68, 3485–3490. [Google Scholar] [CrossRef]
  22. Shinoda, K.; Arai, H. The effect of phase volume on the phase inversion temperature of the emulsions stabilized by nonionic surfactants. J. Colloid Interface Sci. 1967, 25, 429–431. [Google Scholar] [CrossRef]
  23. Shinoda, K.; Kunieda, H. Conditions to produce so-called microemulsions: Factors To increase the mutual solubility of oil and water by solubilizer. J. Colloid Interface Sci. 1973, 42, 381–387. [Google Scholar] [CrossRef]
  24. Reed, R.L.; Healy, R.N. Some physicochemical aspects of microemulsion flooding—A review. In Improved Oil Recovery by Surfactant and Polymer Flooding; Shah, D.O., Schechter, R.S., Eds.; Academic Press: New York, NY, USA, 1977; pp. 347–383. [Google Scholar]
  25. Wade, W.H.; Schechter, R.S.; Morgan, J.C.; Jacobson, J.K.; Salager, J.L. Interfacial tension and Phase Behavior of Surfactant Systems. Paper SPE 6844 presented in Proceedings 52nd Fall Meeting Society of Petroleum Engineering, Denver (1977). Soc. Petroleum Eng. J. 1978, 18, 242–252. [Google Scholar] [CrossRef]
  26. Salager, J.L. Physico-Chemical Properties of Surfactant-Water-Oil Mixtures: Phase Behavior, Microemulsion Formation and Interfacial Tension. Ph.D. Thesis, University of Texas, Austin, TX, USA, 24 December 1977. [Google Scholar]
  27. Salager, J.L.; Morgan, J.; Schechter, R.S.; Wade, W.H.; Vasquez, E. Optimum formulation of surfactant-oil-water systems for minimum tension and phase behavior. Soc. Pet. Eng. J. 1979, 19, 107–115. [Google Scholar] [CrossRef]
  28. Bourrel, M.; Salager, J.L.; Schechter, R.S.; Wade, W.H. A correlation for phase behavior of nonionic surfactants. J. Colloid Interface Sci. 1980, 75, 451–461. [Google Scholar] [CrossRef]
  29. Salager, J.L.; Miñana-Perez, M.; Perez-Sanchez, M.; Ramirez-Gouveia, M.; Rojas, C. Surfactant-Oil-Water systems near the affinity inversion—Part III: The two kinds of emulsion inversion. J. Dispers. Sci. Technol. 1983, 4, 313–329. [Google Scholar] [CrossRef]
  30. Salager, J.L.; Marquez, N.; Graciaa, A.; Lachaise, J. Partitioning of ethoxylated octylphenol surfactants in microemulsion-oil-water systems: Influence of temperature and relation between partitioning coefficient and physicochemical formulation. Langmuir 2000, 16, 5534–5539. [Google Scholar] [CrossRef]
  31. Shinoda, K.; Kunieda, H. Phase properties of emulsions: PIT and HLB. In Encyclopedia of Emulsion Technology; Basic Theory; Becher, P., Ed.; Marcel Dekker: New York, NY, USA, 1983; Volume 1, pp. 337–367. [Google Scholar]
  32. Bourrel, M.; Schechter, R.S. Microemulsions and Related Systems: Formulation, Solvency, and Physical Properties; Marcel Dekker: New York, NY, USA, 1988. [Google Scholar]
  33. Kunieda, H.; Solans, C. How to prepare microemulsions: Temperature insensitive microemulsions. In Industrial Applications of Microemulsions; Marcel Dekker: New York, NY, USA, 1997; ISBN 9780824797959. [Google Scholar]
  34. Stubenrauch, C. (Ed.) Microemulsions: Background, New Concepts, Applications and Perspectives; Wiley-Blackwell: Oxford, UK, 2009. [Google Scholar] [CrossRef]
  35. Shinoda, K.; Lindman, B. Organized surfactant systems: Microemulsions. Langmuir 1989, 3, 135–149. [Google Scholar] [CrossRef]
  36. Salager, J.L.; Forgiarini, A.; Bullon, J. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 1. Optimum formulation for simple surfactant-oil-water ternary systems. J. Surfactants Deterg. 2013, 16, 449–472. [Google Scholar] [CrossRef]
  37. Salager, J.L.; Forgiarini, A.; Marquez, L.; Manchego, L.; Bullon, J. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 2. Performance improvement trends from Winsor’s premise to currently proposed inter- and intramolecular mixtures. J. Surfactants Deterg. 2013, 16, 631–663. [Google Scholar] [CrossRef]
  38. Salager, J.L.; Forgiarini, A.; Rondon, M. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 3. Practical procedures to optimize the laboratory research according to the current state of the art in surfactant mixing. J. Surfactants Deterg. 2017, 20, 3–19. [Google Scholar] [CrossRef]
  39. Salager, J.L.; Anton, R.E.; Arandia, M.A.; Forgiarini, A. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 4. Robustness of optimum formulation zone through the insensibility to some variables and the occurrence of complex artifacts. J. Surfactants Deterg. 2017, 20, 987–1018. [Google Scholar] [CrossRef]
  40. Winsor, P. Hydrotropy, solubilization and related emulsification processs. Trans. Faraday Soc. 1948, 44, 376–382. [Google Scholar] [CrossRef]
  41. Hoar, T.P.; Schulman, J.H. Transparent water-in-oil dispersions: Oleopathic hydromicelle. Nature 1943, 182, 102–103. [Google Scholar] [CrossRef]
  42. Schulman, J.H.; Stoeckenius, W.; Prince, L.M. Mechanism of formation and structure of microemulsions by electron microscopy. J. Phys. Chem. 1959, 63, 1677–1680. [Google Scholar] [CrossRef]
  43. Scriven, L.E. Equilibrium bicontinuous structures. Nature 1976, 263, 123–125. [Google Scholar] [CrossRef]
  44. Clausse, M.; Peyrelasse, J.; Heil, J.; Boned, C.; Lagourette, B. Bicontinuous structure zones in microemulsions. Nature 1981, 293, 636–638. [Google Scholar] [CrossRef]
  45. Bourrel, M.; Verzaro, F.; Chambu, C. Effect of oil type on solubilization by amphiphiles. Soc. Pet. Eng. Reserv. Eng. 1987, 2, 41–53. [Google Scholar] [CrossRef]
  46. Kahlweit, M.; Strey, R. Phase Behavior of ternary systems of the type H20-oil-nonionic amphiphile microemulsions. Angew. Chem. Intern. Ed. Engl. 1988, 24, 654–668. [Google Scholar] [CrossRef]
  47. Kahlweit, M.; Strey, R.; Firman, P. Search for Tricritical points in ternary systems: Water-Oil-Nonionic amphiphile. J. Phys. Chem. 1986, 90, 671–677. [Google Scholar] [CrossRef]
  48. Lade, O.; Beizai, K.; Sottmann, T.; Strey, R. Polymerizable nonionic microemulsions: Phase Behavior of H2O-n-alkyl methacrylate-n-alkyl polyethylene glycol ether (CiEj). Langmuir 2000, 16, 4122–4130. [Google Scholar] [CrossRef]
  49. Lee, J.M.; Lim, K.H. Changes in two-phase emulsion morphology in temperature-amphiphile concentration or fish diagram for ternary amphiphile/oil/water systems. J. Colloid Interface Sci. 2005, 290, 241–249. [Google Scholar] [CrossRef] [PubMed]
  50. Pizzino, A.; Molinier, V.; Catte, M.; Salager, J.L.; Aubry, J.M. Bidimensional analysis of the phase behavior of a well-defined surfactant (C10E4)/oil (n-Octane)/water-temperature system. J. Phys. Chem. B 2009, 113, 16142–16150. [Google Scholar] [CrossRef] [PubMed]
  51. Pizzino, A.; Molinier, V.; Catte, M.; Ontiveros, J.F.; Salager, J.L.; Aubry, J.M. Relationship between phase behavior and emulsion inversion for a well-defined surfactant (C10E4)/n-octane/water ternary system at different temperatures and water/oil ratios. Ind. Eng. Chem. Res. 2013, 52, 4527–4538. [Google Scholar] [CrossRef]
  52. Burauer, S.; Sachert, T.; Sottmann, T.; Strey, R. On microemulsion phase behavior and the monomeric solubility of surfactant. Phys. Chem. Chem. Phys. 1999, 1, 4299–4306. [Google Scholar] [CrossRef]
  53. Solans, C.; Kunieda, H. (Eds.) Industrial Applications of Microemulsions; Marcel Dekker: New York, NY, USA, 1997. [Google Scholar]
  54. Kahlweit, M.; Lessner, E.; Strey, R. Phase behavior of quaternary systems of the type H2O-oil-nonionic surfactant inorganic electrolyte. J. Phys. Chem. 1984, 88, 1937–1944. [Google Scholar] [CrossRef]
  55. Strey, R. Microemulsion microstructure and interfacial curvature. Colloid Polym. Sci. 1994, 272, 1005–1019. [Google Scholar] [CrossRef]
  56. Graciaa, A.; Fortney, L.N.; Schechter, R.S.; Wade, W.H.; Yiv, S. Criteria for structuring surfactants to maximize solubilization of oil and water: Part 1—Commercial nonionics. Soc. Pet. Eng. J. 1982, 22, 743–749. [Google Scholar] [CrossRef]
  57. Barakat, Y.; Fortney, L.; Schechter, R.S.; Wade, W.H.; Yiv, S.H.; Graciaa, A. Criteria for structuring surfactants to maximize solubilization of oil and water. II. Alkyl benzene sodium sulfonates. J. Colloid Interface Sci. 1983, 92, 561–574. [Google Scholar] [CrossRef]
  58. Barakat, Y.; Fortney, L.; Schechter, R.S.; Wade, W.H. Alpha-Olefin sulfonates for oil recovery. In Proceedings of the 2nd European Symposium on Enhanced Oil Recovery, Paris, France, 8–10 November 1982. [Google Scholar]
  59. Huh, C. Interfacial tensions and solubilizing ability of a microemulsion phase that coexists with oil and brine. J. Colloid Interface Sci. 1979, 71, 408–426. [Google Scholar] [CrossRef]
  60. Salager, J.L.; Manchego, L.; Marquez, L.; Bullón, J.; Forgiarini, A. Trends to attain a lower interfacial tension in a revisited pure alkyl polyethyleneglycol surfactant-alkane-water ternary system. Basic concepts and straightforward guidelines for improving performance in enhanced oil recovery formulations. J. Surf. Deterg. 2014, 17, 199–213. [Google Scholar] [CrossRef]
  61. Salager, J.L.; Forgiarini, A.; Bullón, J. Surfactant formulation guidelines to reach an ultralow interfacial tension for enhanced oil recovery. In Topics in Colloidal Aggregation and Interfacial Phenomena; Garcia-Sucre, M., Lozsan, A., Castellanos-Suarez, A., Toro-Mendoza, J., Eds.; Research Signpost: Kerala, India, 2012; Chapter 5; pp. 125–160. ISBN 9788130804910. [Google Scholar]
  62. Salager, J.L.; Marquez, L.; Mira, I.; Peña, A.; Tyrode, E.; Zambrano, N. Principles of emulsion formulation engineering. In Adsorption and Aggregation of Surfactants in Solution; Surfactant Science Series; Mittal, K.L., Shah, D.O., Eds.; Marcel Dekker: New York, NY, USA, 2003; Volume 109, Chapter 24; pp. 501–524. [Google Scholar] [CrossRef]
  63. Salager, J.L.; Forgiarini, A.M.; Bullón, J. Progress over a century of designing emulsion properties—Emerging phenomenological guidelines from generalized formulation and prospects to transmute the knowledge into know-how. In Surfactant Science and Technology: Retrospects and Prospects; Romsted, L.S., Ed.; CRC Press: Boca Raton, FL, USA, 2014; Chapter 18; pp. 459–487. [Google Scholar] [CrossRef]
  64. Marquez, R.; Forgiarini, A.; Fernandez, J.; Langevin, D.; Salager, J.L. New interfacial rheology characteristics measured using a spinning-drop rheometer at the optimum formulation of a simple surfactant-oil-water system. J. Surf. Deterg. 2018, 21, 611–623. [Google Scholar] [CrossRef]
  65. Marquez, R.; Forgiarini, A.; Langevin, D.; Salager, J.L. Instability of emulsions made with surfactant-oil-water systems at optimum formulation with ultralow interfacial tension. Langmuir 2018, 34, 9252–9263. [Google Scholar] [CrossRef]
  66. Marquez, R.; Anton, R.E.; Vejar, F.; Salager, J.L.; Forgiarini, A. New Interfacial Rheology Characteristics Measured using a Spinning Drop Rheometer at the Optimum Formulation. Part 2. Surfactant-Oil-Water systems with a high volume of middle phase microemulsion. J. Surf. Deterg. 2019, 22, 177–188. [Google Scholar] [CrossRef]
  67. Cash, L.; Cayias, J.L.; Fournier, G.; MacAllister, D.; Shares, T.; Schechter, R.S.; Wade, W.H. The application of low interfacial tension scaling rules to binary hydrocarbon mixtures. J. Colloid Interface Sci. 1977, 59, 39–44. [Google Scholar] [CrossRef]
  68. Salager, J.L.; Anton, R.E.; Anderez, J.M.; Aubry, J.M. Formulation des micro-émulsions par la méthode HLD. Tech. Ing. Vol. Génie Procédés 2001, 157, 1–20. [Google Scholar]
  69. Salager, J.L.; Bourrel, M.; Schechter, R.S.; Wade, W.H. Mixing rules for optimum phase-behavior formulations of surfactant/oil/water systems. Soc. Pet. Eng. J. 1979, 19, 271–278. [Google Scholar] [CrossRef]
  70. Quintero, L.; Jones, T.A.; Clark, D.E.; Gabrysch, A.D.; Forgiarini, A.; Salager, J.L. Single Phase Microemulsions And in Situ Microemulsions for Cleaning Formation Damage. U.S. Patent 8,091,646 B2, 10 January 2012. [Google Scholar]
  71. Delgado-Linares, J.G.; Pereira, J.; Rondón, M.; Bullón, J.; Salager, J.L. Breaking of water-in-crude oil emulsions. 6. Estimating the demulsifier performance at optimum formulation from both the required dose and the attained instability. Energy Fuels 2016, 30, 5483–5491. [Google Scholar] [CrossRef]
  72. Delgado, J.G.; Alvarado, J.G.; Vejar, F.; Forgiarini, A.; Bullón, J.; Salager, J.-L. Breaking of water-in-crude oil emulsions. 7. Demulsifier performance at optimum formulation for various extended surfactant structures. Energy Fuels 2016, 30, 7065–7073. [Google Scholar] [CrossRef]
  73. Anton, R.E.; Anderez, J.M.; Bracho, C.; Vejar, F.; Salager, J.L. Practical surfactant mixing rules based on the attainment of microemulsion-oill-water three-phase behavior systems. In Interfacial Processes and Molecular Aggregation; Narayanan, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 218, pp. 83–113. [Google Scholar] [CrossRef]
  74. Bourrel, M.; Salager, J.L.; Schechter, J.L.; Wade, W.H. Properties of amphiphile oil-water systems at optimum formulation for phase behavior. In Proceedings of the 53rd Annual Fall Technical Conference Society Petroleum Engieneers, Preprints Paper SPE 7450, Houston, TX, USA, 1–3 October 1978. [Google Scholar] [CrossRef]
  75. Anton, R.E.; Salager, J.L. Effect of the electrolyte anion on the salinity contribution formulation of anionic surfactant microemulsions. J. Colloid Interface Sci. 1990, 1540, 75–81. [Google Scholar] [CrossRef]
  76. Witthayapanyanon, A.; Acosta, E.; Harwell, J.H.; Sabatini, D.A. Formulation of ultralow interfacial tension systems using extended surfactants. J. Surf. Deterg. 2006, 9, 331–339. [Google Scholar] [CrossRef]
  77. Salager, J.L.; Anton, R.E.; Sabatini, D.A.; Harwell, J.H.; Acosta, E.; Tolosa, L.I. Enhancing solubilization in microemulsion—State of the art and current trends. J. Surf. Deterg. 2005, 8, 3–21. [Google Scholar] [CrossRef]
  78. Witthayapanyanon, A.; Harwell, J.H.; Sabatini, D.A. Hydrophilic–Lipophilic deviation (HLD) method for characterizing conventional and extended surfactants. J. Colloid Interface Sci. 2008, 325, 259–266. [Google Scholar] [CrossRef]
  79. Solairaj, S.; Britton, C.; Lu, J.; Kim, D.H.; Weerasooriya, U.; Pope, G. New correlation to predict the optimum surfactant structure for EOR. Paper SPE 154262. In Proceedings of the 18th SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 14–18 April 2012. [Google Scholar] [CrossRef]
  80. Bourrel, M.; Koukounis, C.; Schechter, R.S.; Wade, W.H. Phase and interfacial tension behavior of nonionic surfactats. J. Dispers. Sci. Technol. 1980, 1, 13–35. [Google Scholar] [CrossRef]
  81. Anton, R.E.; Garces, N.; Yajure, A. A correlation for three-phase behavior of cationic surfactant-oil-water systems. J. Dispers. Sci. Technol. 1997, 18, 539–555. [Google Scholar] [CrossRef]
  82. Nguyen, T.T.; Morgan, C.; Poindexter, L.; Fernandez, J. Application of the Hydrophilic–Lipophilic Deviation concept to surfactant characterization and surfactant selection for enhanced oil recovery. J. Surf. Deterg. 2019, 22, 983–999. [Google Scholar] [CrossRef]
  83. Torrealba, V.A.; Johns, R.T. Partition coefficient relations in surfactant-oil-brine systems for improved description of microemulsion phase behavior. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, Muscat, Oman, 26–28 March 2016. [Google Scholar] [CrossRef]
  84. Torrealba, V.; Johns, R. Coupled interfacial tension and phase behavior model based on micellar curvatures. Langmuir 2017, 33, 13603–13614. [Google Scholar] [CrossRef]
  85. Miñana-Perez, M.; Graciaa, A.; Lachaise, J.; Salager, J.L. Solubilization of polar oils in microemulsion systems. Progr. Colloid Polym. Sci. 1995, 98, 177–179. [Google Scholar] [CrossRef]
  86. Hammond, C.; Acosta, E.; Jakobs-Sauter, B. Effect of hydrocarbon branching on the packing of extended surfactants at oil-water interfaces. In Proceedings of the 5th World Congress on Emulsion, Lyon, France, 12–14 October 2010. [Google Scholar]
  87. Fotland, P.; Skauge, A. Ultralow interfacial tension as a function of pressure. J. Dispers. Sci. Technol. 1986, 7, 563–579. [Google Scholar] [CrossRef]
  88. Skauge, A.; Fotland, P. Effect of pressure and temperature on the phase behavior of microemulsions. Soc. Pet. Reserv. Eng. 1990, 5, 601–608. [Google Scholar] [CrossRef]
  89. Austad, T.; Strand, S. Chemical flooding of oil reservoir. 4. Effects of temperature and pressure on the middle phase solubilization parameters close to optimum flood conditions. Colloid Surf. A 1996, 108, 243–252. [Google Scholar] [CrossRef]
  90. Ghosh, S.; Johns, R.T. An equation-of-state model to predict surfactant/oil/brine-phase behavior. Soc. Pet. Eng. J. 2016, 21, 1106–1125. [Google Scholar] [CrossRef]
  91. Jean-Louis Salager; Raquel Antón; Johnny Bullón; Ana Forgiarini; Ronald Marquez; How to Use the Normalized Hydrophilic-Lipophilic Deviation (HLDN) Concept for the Formulation of Equilibrated and Emulsified Surfactant-Oil-Water Systems for Cosmetics and Pharmaceutical Products. Cosmetics 2020, 7, 57, 10.3390/cosmetics7030057.
  92. Jeffreys, G.; Davies, A.C. Coalescence of liquid droplets and liquid dispersión. In Recent Advances in Liquid-Liquid Extraction; Hansen, C., Ed.; Pergamon Press: Oxford, UK, 1971; pp. 495–584. [Google Scholar] [CrossRef]
  93. Jones, T.J.; Neustadter, E.L.; Whittingham, K.P. Water-In-Crude oil emulsion stability and emulsion destabilization by chemical demulsifiers. J. Can. Pet. Technol. 1978, 17, 100–108. [Google Scholar] [CrossRef]
  94. Walstra, P. Formation of emulsions. In Encyclopedia of Emulsion Technology; Becher, P., Ed.; Marcel Dekker: New York, NY, USA, 1983; Chapter 2; pp. 57–127.
  95. Salager, J.L. Emulsion phase inversion phenomena. In Emulsions and Emulsion Stability, 2nd ed.; Sjoblöm, J., Ed.; Taylor & Francis: London, UK, 2006; Chapter 4; pp. 184–225. [Google Scholar]
  96. Aserin, A. (Ed.) Multiple Emulsions—Technology and Applications; Wiley: Hoboken, NJ, USA, 2008; ISBN 9780470170939. [Google Scholar]
  97. Frenkel, M.; Shwartz, R.; Garti, N. Multiple Emulsions. I. Stability: Inversion, apparent and weighted HLB. J. Colloid Interface Sci. 1983, 94, 174–178. [Google Scholar] [CrossRef]
  98. Garti, N. Double emulsions—Scope, limitations and new achievements. Colloids Surf. A 1997, 123, 233–246.
  99. Mendez, Z.; Anton, R.E.; Salager, J.L. Surfactant-Oil-Water systems near the affinity inversion. Part 11. pH sensitive emulsions containing carboxylic acids. J. Dispers. Sci. Technol. 1999, 20, 883–892.
  100. Salager, J.L.; Anton, R.E.; Bracho, C.; Briceño, M.I.; Peña, A.; Rondon, M.; Salager, S. Attainment of emulsion properties on design. A typical case of formulation engineering. Récent Progrès Génie des Procédés. 1999, 13, 133–140.
  101. Salager, J.L.; Forgiarini, A.; Lopez, J.C.; Marfisi, S.; Alvarez, G. Dynamics of near-zero energy emulsification. In Proceedings of the 6th World Surfactant Congress CESIO, Berlin, Germany, 21–23 June 2004. [Google Scholar]
  102. Perazzo, A.; Preziosi, V.; Guido, S. Phase inversion emulsification: Current understanding and applications. Adv. Colloid Interface Sci. 2015, 222, 581–599. [Google Scholar] [CrossRef]
  103. Salager, J.L.; Forgiarini, A.; Marquez, L.; Peña, A.; Pizzino, A.; Rodriguez, M.P.; Rondon-Gonzalez, M. Using emulsion inversion in industrial processes. Adv. Colloid Interface Sci. 2004, 108, 259–272. [Google Scholar] [CrossRef]
  104. Tyrode, E.; Mira, I.; Zambrano, N.; Marquez, N.; Rondon-Gonzalez, M.; Salager, J.L. Emulsion catastrophic inversion from abnormal to normal morphology. 3. Conditions for triggering the dynamic inversion and application to industrial processes. Ind. Eng. Chem. Res. 2003, 42, 4311–4318. [Google Scholar] [CrossRef]
  105. Forster, T.; Schambil, F.; von Rybinski, W. Production of fine dispersed and long-term stable oil-in-water emulsions by the phase inversion temperature. J. Dispers. Sci. Technol. 1992, 13, 183–193.
  106. Graciaa, A.; Lachaise, J.; Cucuphat, C.; Bourrel, M.; Salager, J.L. Interfacial segregation of an ethyl oleate/hexadecane oil mixture in microemulsion systems. Langmuir 1993, 9, 1473–1478.
  107. Ontiveros, J.F.; Pierlot, C.; Catte, M.; Molinier, V.; Pizzino, A.; Salager, J.L.; Aubry, J.M. Classification of ester oils according to their equivalent alkane carbon number (EACN) and asymmetry of fish diagrams of C10E4/ester oil/water systems. J. Colloid Interface Sci. 2013, 403, 67–76.
  108. Vera, R.; Salazar, F.; Marquez, R.; Forgiarini, A. How the influence of different salts on interfacial properties of surfactant-oil-water systems at optimum formulation matches the Hofmeister series ranking. J. Surfactants Deterg. 2020, 23, 603–615.
  109. Trotter, B.; Baradaran, S.; Kadhum, M.; Shiau, B.; Harwell, J. Specific ion effects in Winsor III microemulsions. In Proceedings of the AOCS Annual Meeting, Orlando, FL, USA, 30 April–4 May 2017.
  110. Vlachy, N.; Jagoda-Cwiklik, B.; Vácha, R.; Touraud, D.; Jungwirth, P.; Kunz, W. Hofmeister series and specific interactions of charged headgroups with aqueous ions. Adv. Colloid Interface Sci. 2009, 146, 42–47.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Chemistry, Physical; Materials Science, Coatings & Films; Others
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Jean-Louis Salager
,
Raquel Antón
,
Johnny Bullón
,
Ana Forgiarini
,
Ronald Marquez
View Times: 2.3K
Revisions: 21 times (View History)
Update Date: 17 Aug 2021
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback