Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1 In the majority of the literature on UAV routing the kinematics are neglected and the UAVs’ flight dynamics are neglected or simplified using assumptions.
Amila Thibbotuwawa
 + 6160 word(s) 6160 2020-07-10 11:55:21 |
2 Corrected the reference 1 in the text
Amila Thibbotuwawa
 Meta information modification 6160 2020-07-11 21:27:02 | |
3 format correct
Catherine Yang
 -5 word(s) 6155 2020-07-14 06:30:12 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Thibbotuwawa, A.; Bocewicz, G.; Nielsen, P.; Banaszak, Z. Unmanned Aerial Vehicle Routing Problems. Encyclopedia. Available online: https://encyclopedia.pub/entry/1310 (accessed on 15 November 2024).
Thibbotuwawa A, Bocewicz G, Nielsen P, Banaszak Z. Unmanned Aerial Vehicle Routing Problems. Encyclopedia. Available at: https://encyclopedia.pub/entry/1310. Accessed November 15, 2024.
Thibbotuwawa, Amila, Grzegorz Bocewicz, Peter Nielsen, Zbigniew Banaszak. "Unmanned Aerial Vehicle Routing Problems" Encyclopedia, https://encyclopedia.pub/entry/1310 (accessed November 15, 2024).
Thibbotuwawa, A., Bocewicz, G., Nielsen, P., & Banaszak, Z. (2020, July 11). Unmanned Aerial Vehicle Routing Problems. In Encyclopedia. https://encyclopedia.pub/entry/1310
Thibbotuwawa, Amila, et al. "Unmanned Aerial Vehicle Routing Problems." Encyclopedia. Web. 11 July, 2020.
Unmanned Aerial Vehicle Routing Problems
Edit
This entry is adapted from the peer-reviewed paper 10.3390/app10134504

Unmanned aerial vehicle (UAV) routing is transitioning from an emerging topic to a growing research area as the 3D flexible utilization of airspace, promogulated by UAVs, is a potential game-changer in solving the urban air mobility challenge by allowing to reshape transportation and logistics in the future. This has revealed a need to classify different types of research and examine the general characteristics of the research area. This research aims to assist in identifying the main topics and emerging research streams and provides a published overview of the current state and contributions to the area of the UAV routing problem (UAVRP) and a general categorization of the vehicle routing problem (VRP) followed by a UAVRP classification with a graphical taxonomy based on the analysis of UAVRP current status. To achieve this, an analysis of the existing research contributions promulgated in this domain is conducted. This analysis is used to identify the current state of UAVRP and the gaps related to the UAVs’ flight dynamics and weather conditions, which significantly influence the fuel consumption of the UAV when modeling the UAVRP.

unmanned aerial vehicles UAV routing and scheduling UAV routing vehicle routing problem

1. Introduction

Unmanned aerial vehicles (UAVs) have been the subject of immense interest in recent years and have developed into a mature technology applied in areas such as defense, search and rescue, agriculture, manufacturing, and environmental surveillance [1][2][3][4]. Without any required alterations to the existing infrastructure, for example, deployment stations on the wall or guiding lines on the floor, UAVs are capable of covering flexible wider areas in the field [5]. However, this advantage comes at a price. To utilize this flexible resource efficiently, there is a need to establish a coordination and monitoring system for the UAV or fleet of UAVs to determine their environment-based route and schedule in a safe, collision-free, and a time-efficient manner [3][6].

While the most common models of UAVs can be identified as quadcopters and the hexacopters, the most common types of UAVs are multi-rotors, fixed-wing, flapping wing, and hybrid systems, where the multi-rotor system is the most popular type of UAVs because it is used for versatile applications and the number of rotors can be in the range of 1 to 12 [7]. The fixed-wing UAV is used inaccurate mapping and monitoring applications due to its long flight endurance and high-altitude operability, which allows covering long distances and carrying equipment such as cameras and sensors [8]. Flapping-wing UAVs are often referred to as Ornithopter that simulates the mechanics of flying birds and insects to generate lift by using semi-rigid articulated wings. These UAVs are mainly used for research purposes due to the improved maneuverability and high flight efficiency when compared to both the multirotor and fixed-wing systems. The hybrid UAVs system is a combination of the multi-rotor and fixed-wing UAVs, and the combination of these two models has boosted its capabilities to allow vertical take-off and landing [8].

Following recent advancements in UAV technology, Amazon, DHL, Federal Express, and other large companies with an interest in package delivery have begun investigating the viability of incorporating UAV-based delivery into their commercial services [8][9]. UAVs have the potential to significantly reduce the cost and time required to deliver materials as, in general, they are less expensive to maintain than traditional delivery vehicles such as trucks and can lower labor costs by performing tasks autonomously [10][11][12][13][14]. To support this emerging area, a new problem category arises, the UAV routing problem (UAVRP). Despite the increasing focus on UAVs and the field’s status as an emerging technology, there is no comprehensive overview of the current state available in terms of the UAVRP characteristics and the methods used to solve UAVRP in the current state.

The main objectives of this paper are to identify the unique characteristics of the UAVRP and present the first overview of the current state of research. This is achieved by analyzing the existing research contributions promulgated in this domain. Based on the analysis, we identify the current state of UAVRP and the challenges in the current state of the general vehicle routing to address the specific nature of the UAVRP. Simultaneously, this paper also provides a published overview of the current state and contributions to the area of the UAVRP. The remainder of the paper is structured as follows: First, a general categorization of the vehicle routing problem (VRP) is presented. An overview of UAVRP based on the analysis of UAVRP current state follows next.

2. UAV Routing with an Emphasis on the Problem Type, Transportation Mode, and Degree of Automation

The basis of all routing literature is the VRP, which is a well-studied field and still very much applicable for the advancement of new technology [12][13][14]. VRPs have been applied to solve delivery problems [15], which could appear similar to the UAV routing as a VRP attempts to find the optimal routes for one or more vehicles to deliver commodities to a set of locations [16]. We identify three main dimensions that seem particularly relevant to apply when addressing the UAVRP:

1. The problem type: When classifying routing literature, it can be segregated based on the problem type with an emphasis on the VRP, which has given the major research contributions in the domain of vehicle routing [15][17] and is used as an input for all the routing problems in general.

2. The transportation mode: Routing literature can be partitioned according to the categories of transportation mode, as the characteristics of the modes (such as land, sea, and air) affect the routing methods. Transportation modes have different characteristics in terms of cost, transit time, accessibility, and environmental performance [18]. Compared to other transportation modes, UAVs can be a competitive alternative for delivery and pickup of time-sensitive items, regardless of the ground-level road conditions [19].

3. The degree of automation: The degree of automation in the transportation systems is a dimension as automated systems are discussed in dynamic vehicle routing [20][21], generalized vehicle routing [21], and real-time vehicle routing [22]. Technological advances in the area of UAV have been impressive, and this leads to an increased degree of automation of these systems [23]. In production systems, the majority of research has been focused on automated guided vehicles (AGVs) [24], mobile robot routing [25][26][27][28][29][30][31][32][33][34], or six degrees of freedom aerial robots [34], which are UAVs.

2.1. Different Types of Vehicle Routing Problems

In its simplest form, the VRP addresses the routing of a fleet of homogeneous vehicles to deliver identical packages from a depot to customer locations while minimizing the total travel cost [13]. The VRP definition is that a set of vehicles initially located at a depot are to deliver discrete quantities of goods to a set of customers determining the optimal route used by the set of vehicles when serving the set of customers [13][15][35][36][37][38][39]. The objective is to minimize the overall transportation cost, and the solution of the classical VRP problem is a set of routes that all begin and end in the depot, which satisfies the constraint that all the customers are served only once [13][15][35]. The transportation cost can be improved by reducing the total traveled distance and by reducing the number of required vehicles [13][37][38][39][40][41][42][43][44]. Several sub-categories of VRP exist, addressing a specific set of routing problems [15][35][36]:

  • Capacitated VRP (CVRP): Every vehicle has a limited capacity [37][38]. CVRP is important when using UAVs with limited capacities in delivering goods.
  • VRP with time windows (VRPTW): Every customer has to be supplied within a certain time window [39]. VRPTW is important when referencing using UAVs to deliver perishable goods.
  • Multiple Depot (MDVRP) VRP: The vendor uses many depots to supply the customers [40]. MDVRP is important when using UAVs with multiple depots to transport materials to customers.
  • VRP with Pick-Up and Delivering (VRPPD): Customers may return some goods to the depot [14][39]. VRPPD is important when using UAVs with multiple pick up and deliveries of goods.
  • Split Delivery VRP (SDVRP): Customers may be served by more than one vehicle [41]. SDVRP is important when using UAVs to delivering goods to customers where one vehicle can visit many customers and one customer can be visited by many UAVs.
  • Stochastic VRP (SVRP): Some parameters (like the number of customers, their demands, serve time, or travel time) are random [42][43]. SVRP is important when using UAVs in delivering goods to satisfy stochastic demands.
  • Time-dependent VRP with path flexibility (TDVRP-PF): Any arc between two customer nodes has multiple corresponding paths in the road network [44].
  • VRP with trailers and transshipments (VRPTT): In addition to depot and customer locations, this introduces transshipment locations [45]. VRPTT is important when using UAVs along with a fleet of trucks in delivering goods and in last-mile deliveries.
  • VRP with profits: A profit is associated with each customer that makes such a customer more or less attractive. Unlike to the most classical VRPs, in VRP with profits, the set of customers to serve is not given and different decisions have to be taken on which customers to serve and how to cluster the customers to be served in different routes and order the visits in each route [46][47].

These relate to the UAVRP as the different categories of VRP inspire the existing work in UAV routing. In solving the UAVRP, certain studies have used different VRP approaches.

2.2. Based on Modes of Transport

When studying routing literature, it is also apparent that it can be partitioned according to the transportation mode such as land-based, maritime, and air transport. However, the application of VRP is mainly visible in land-based and maritime-based transportation modes as described below, and the UAV routing falls under the domain of air transport along with typical airplanes used in airline industry.

2.2.1. Land-Based Transportation Modes (Vehicle Routing)

Trucks, delivery vehicles, AGVs, and other land-based transportation modes fall under this category, and much research has been carried out regarding route optimization [48][49]. The VRP can, in this context, typically be described as the problem of designing optimal delivery or collection routes from one or several depots to any number of geographically scattered cities or customers, subject to side constraints [36]. VRP plays a central role in the fields of physical distribution and logistics [42]. In this field, fuel models are seldom considered.

2.2.2. Maritime-Based Transportation (Vessel Routing)

The other relatively well-researched transportation mode is the vessel routing or maritime routing problems [49]. In maritime routing, in contrast to land-based modes of transportation, one generally must consider non-linear fuel-consumption models. The main concern with non-linear fuel-consumption models is that they make the solution of relevant models complicated [49][50]. In this area, one also often encounters network design problems [51] where the aim is to set up cyclical plans [52]. The same is often seen when designing, for example, airline flight schedules [53]. The focus of these is not dynamic routing such as covered by the traditional VRP and of particular relevance to the UAVRP.

2.3. Degree of Automation

This paper also considers the degree of automation of transportation as automation and autonomy play a large role in practical applications of the UAVRP [54][55][56]. Furthermore, they play an increasing role in various modes of transport. Driverless trains are already in operation; the degree of automation in cars is continuously rising, and even the air transport sector is discussing the use of pilotless aircraft [56]. It is observed that certain modes of transportation are fully automated and certain modes are semi-automated [56][57]. Automated guided transport (AGT) systems and AGVs fall under the fully automated modes of transportation and have been subjected to intense study in literature [24][25][27][58][59][60][61][62]. In maritime transport, automated vessel routing has been introduced and unmanned vessels will be the future of maritime transportation [62].

As UAVs flight and navigation tasks are increasingly automated to gain economies-of-scale and speed of operations and support the large-scale operations, UAV routing and execution are evolving from teams of operators managing a single UAV to a single operator managing multiple UAVs as illustrated in Figure 1. The increasing degree of autonomy and automation has created a continuous push for developing methods for managing complex UAV operations. Such systems will naturally require the development of advanced prediction, routing, and scheduling methods and implementation of various systems to support decision-makers in handling the complexity of operations [10][11][12][13]. It is also worth noting that most contributions focus on the VRP characteristics, specific or multimodal transportation modes, and to some degree, on the VRP for automated land-based transportation (typically indoor robotic solutions such as AGVs, mobile robots). While the classical VRP is well-studied, the methods and approaches found within this domain are still very much applicable for the advancement of new technology in the area of UAV operations [12].

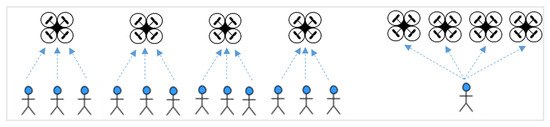
Applsci 10 04504 g001 550

Figure 1. Transitioning from teams of operators managing a single unmanned aerial vehicle (UAV) to a single operator managing multiple UAVs [13].

2.4. Significance of UAVRP

UAV routing problems involve a huge amount of stochastic information in contrast to VRPs in general, as UAVs should be able to change, adapt, modify, and optimize their routes in real-time. In contrast to general routing problems, several individual objective functions can be used in UAV routing such as reducing individual UAV costs, enhancing its profit, increasing safety in operations, reducing lead time, and increasing the load capacity of the entire system [63][64].

Influencing parameters for UAV routing includes numerous parameters and constraints in contrast to traditional VRP problems. UAVs’ nature is routing and scheduling in 3D environment [65], whereas land- and maritime-based transportation are 2D [66] and in UAV routing, changing weather conditions (wind speed, wind direction, air density) should be considered in solutions. Moreover, UAVs specifications, energy consumption affected by weather conditions, carrying payload of UAVs, and collision avoidance with respect to moving/fixed objects adds more complexity in finding solutions in the domain of UAV routing. All these elements emphasize the significance of UAV routing as it is challenging to develop models considering all the influencing aspects together.

Unlike the traditional routing problems, the UAV routing should address different decision layers in the system architecture (Figure 2), which includes the fleet level where the fleet is managed to provide delivery services using the UAV fleet and the platform level where it focuses on the individual functioning of the UAVs [13]. The current state of research is fragmented as shown in the layers illustrated in Figure 1 and neglects that different types of decisions are addressed at different abstraction levels [13].

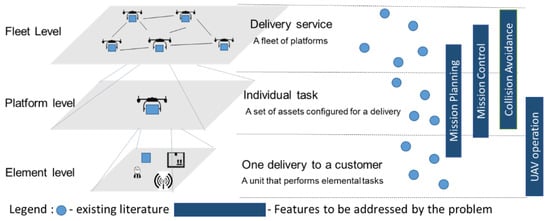
Applsci 10 04504 g002 550

Figure 2. Overall hierarchical representation of the systems related to the UAV routing problem (UAVRP) [13].

3. UAVRP Current State

Limited contributions have been presented [67][68][69] in the area of UAV routing in 3D environments. What has been accomplished in the field has focused on UAV routing for transporting materials and surveillance [10] without considering the stochastic conditions in weather and non-linear fuel consumption models [9]. Table 1 shows the top seven subject areas in UAV routing literature, where the majority of contributions are seen in engineering and computer science domains.

Table 1. Top seven subject areas.

Subject Area No of Papers
Engineering 173
Computer Science 83
Mathematics 41
Physics and Astronomy 25
Social Sciences 24
Materials Science 18
Decision Sciences 14
 

A literature review aims to map and evaluate the body of literature and identify potential research gaps highlighting the limitations of knowledge [70][71]. The search was conducted for the context keyword “UAV routing,” using the “article title, abstract, keywords” search in the Scopus database. Through the exhaustive search, we initially identified 396 papers published in UAV routing, and these papers were analyzed to identify the areas covered in addressing the UAV routing problem.

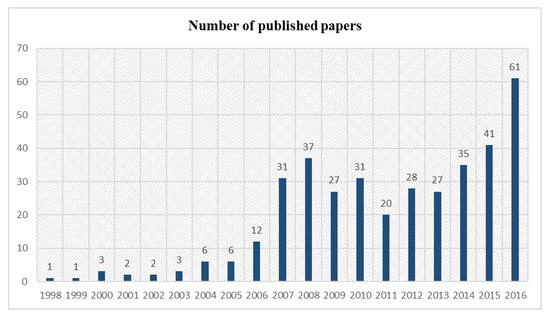
The first published research we were able to identify on the topic stems from 1998, and this work contains a Reactive Tabu Search (RTS) heuristic within a discrete-event simulation to solve routing problems for unmanned aerial vehicles (UAVs) [72]. The next contribution was in 1999 and proposes a variation of standard VRP that arises in routing UAVs in the presence of terrain obscuration, thus introducing visibility-constrained routing of UAVs [73]. From the timeline presented in Figure 3, it is apparent that the UAV routing theme is gaining increasing attention, especially from 2005 and onward, with a steadily increasing number of publications per year. After the year 2000, an increasing trend is visible with a focus on wireless sensor networking and ad-hoc sensor networking. The top journals and conferences contributing to UAV routing are identified in Figure 4 where publication sources with more than three contributions are included. From Figure 3, The International Society for Optical Engineering Conferences, IEEE Military Communications Conferences, and Journal of Intelligent and Robotic Systems have topped the list with the majority of contributions.

Applsci 10 04504 g003 550
Figure 3. The publishing trend in UAV routing as identified using Scopus [14][70].
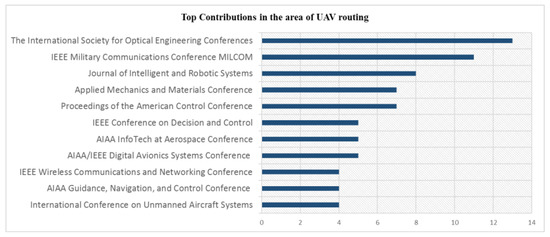
Applsci 10 04504 g004 550

Figure 4. Top journals/conferences contributing to the area of UAV routing [14].

To limit the detailed study of the literature to understand the current state of UAV routing, we chose to focus on all the relevant published journals and the top 10% cited conference papers. This list includes 51 journal papers and 21 conference papers and indicates that the clear majority (70%) of contributions on UAV routing to date have been disseminated through conferences rather than journals.

For the identified 72 main contributions, the keywords have been recorded, and Figure 3 shows a rich image of these and their prevalence. The illustration of the keywords presents the different areas of technologies, industries, and research areas linked to UAV routing. Most commonly used keywords are presented in larger fonts and we can see the various areas linked with UAV routing in Figure 5.

Applsci 10 04504 g005 550

Figure 5. Analysis of keyword frequency in UAV routing. 

4. Approaches and Domains in UAV Routing in Existing Literature

When considering the published literature both in terms of sources and keywords, it becomes clear that various approaches are used in addressing UAV routing. The contributions’ approaches are inspired primarily by different variants of the VRP and traveling salesman problem (TSP). The difference between TSP and VRP is that TSP considers finding the shortest path that connects an arbitrary number of nodes whose pairwise distances are known [73][74][75].

The most basic form of a VRP can be considered as a direct descendant of TSP [41][76] in which there are one salesman and one fixed depot; the rules are to visit all customers once and only once and end the route at the depot where it started [77]. Many approaches for the VRP were inherited from the huge and successful work done for the solutions of the TSP [39]. This UAVRP is similar to the traditional TSP if the UAV can arrive at or depart from each target only once with the objective of minimizing the total cruise distance [78]. This is relevant in UAV routing if one particular considers sense-and-avoid [79], where the objective is to move to the nearest safe point in a collision-free manner [3][79], or complete autonomy where the UAVs are self-navigating point-by-point [80][81]. The VRP considers a problem similar to the TSP but with a different context, as the VRP considers the problem of delivering goods located at a central depot to customers.

Based on the analysis in the existing literature, VRP approaches used for routing of UAVs can be grouped mainly in a few variants of VRP. These correspond with the general classifications of VRP stated in Section 2. Table 2 categorizes the different VRP approaches used to solve UAV routing. The majority of applied VRP approaches are the general VRP, dynamic VRP, VRP with time windows, and capacitated VRP.

Table 2. Distribution of papers with respect to various domains/approaches used in UAV routing.

Area/Approach No of Papers
Wireless networks 24
Scheduling 8
VRP 18
TSP 9
Other 13

Besides VRP approaches, the literature review also identified various other approaches. Chief among these approaches is formulating the problem as a TSP. Table 3 and Table 4 presents an overview of contributions in the literature that utilize the VRP and TSP approaches used in UAV routing. Several contributions use a combination of the variants of both TSP and VRP.

Table 3. Overview of (vehicle routing problem) VRP approaches used in UAV routing.

Author Approach Objective Experimental Data
[81] Shetty, Sudit, and Nagi, 2008 General VRP+ multi-vehicle TSP Maximize the total weighted service to the targets from the homogeneous fleet of UAVs TSPLIB (http://www.iwr.uni-heidelberg.de/groups/comopt/software)
[82] Xingyin Wang, Poikonen, and Golden, 2016 VRP Minimize the maximum duration of the routes (i.e., the completion time) Have considered two problems which have the same set of customers, but different homogeneous fleets
[83] Sundar and Rathinam, 2014 Single VRP To find a path for the UAV such that each target is visited at least once by the vehicle, the fuel constraint is never violated along the path for the UAV, and the total fuel required by the UAV is a minimum 50 instances of 10 targets to 25 targets with increments in steps of 5 in each problem size and all the targets are chosen randomly from a square area of 5000 × 5000 units
[84] David W. Casbeer, 2011 VRP with Precedence Constraints Minimize the total distance traveled by a homogeneous fleet of UAVs Five UAVs and ten targets placed randomly in the area of responsibility
[85] Karaman and Frazzoli, 2008 VRPTL-VRP with Temporal Logic Specifications Minimize the relative risk for using a homogeneous fleet of UAVs in the mission. A scenario with three UAVs, one launch site, two landing sites, and five targets
[86] Klein et al., 2013 Dynamic VRP Minimize the time required to determine the location of the source Have conducted a pair of flight tests where they deploy 6 sensors over a 1 km2 region and localize acoustic sources within the area
[87] Arsie and Frazzoli, 2008 Dynamic VRP Minimize the expected time between the appearance of a target point and the time it is visited by one of the agents -
       
[88] Murray and Chu, 2015 VRP+ Flying Sidekick TSP Minimize the latest time at which either the truck or the UAV returns to the depot 10 or 20 customers, such that 80%–90% of customers are UAV-eligible according to weight, while the truck and UAV speeds were fixed at 25 miles/h, with the UAV having a flight endurance of 30 min
[89] Kinney, Hill, and Moore, 2005 VRP with Pick-Up and Delivering (VRPPD) + TSP To find the shortest tour visiting all of the customers 56 test problems comprising the standard test set of Solomon were used in the testing
[74] Guerrero and Bestaoui, 2013 TSP+ Capacitated VRP (CVRP) Minimizes the sum of travel time among waypoints Have considered three 2D and two 3D example scenarios with different waypoints and home waypoints
[90] Wen, Zhang, and Wong, 2016 Capacitated VRP (CVRP) Minimize the total travel time and fleet size of the homogeneous fleet of UAVs Have considered nine instances according to different proportions between hot water and blood
[75] Savuran and Karakaya, 2016 Capacitated Mobile Depot VRP (C-MoDVRP) Maximize the total number of targets visited by the UAV The simulation tests are conducted using 16 of bench-mark problems from Heidelberg TSP Library (of Heidelberg 1995)
[91] Murray and Karwan, 2013 VRP with Time windows (VRPTW) Maximize the overall effectiveness of the mission, minimize changes to the initial mission plan, minimize total travel time, and minimize the use of resources, payloads, and “dummy” bases Test problems are created for a combination of different initial tasks, resources, pop-ups, time window scales, loiter times, and payloads for a battlespace area of size (∼unif(50,400)) × (∼unif(50,400))
[92] Lamont, Slear, and Melendez, 2007 VRP with Time Windows (VRPTW) Minimizing cost and risk generally associated with a three-dimensional VRP Three-element target packages are created along with a grid of real-world terrain and a realistic threat lay down
[67] Guerriero, Surace, Loscri, and Natalizio, 2014 VRP with Soft Time Windows (VRP-STW) Minimize the total distances traveled by the homogeneous fleet of UAVs, maximize the customer satisfaction and minimize the number of used UAVs Fleet of 6 homogeneous UAVs in a field of 110 × 80 m2 with different parameters for a sport event
[19] Kim, Lim, Cho, and Côté, 2017 Multi-Depot VRP (MDVRP) Minimizing the operating cost of a heterogeneous fleet of UAVs and to find the optimal number of UAV center locations Have considered 9 candidate sites for centers and 40 patients to be served by two types of UAVs
[93] Habib, Jamal, and Khan, 2013 Multiple-Depot VRP (MDVRP) Minimize the total distances traveled by a homogeneous fleet of UAVs Have considered 12 instances with different combinations of fleet size and targets (Max fleet size of 5 homogeneous fleets of UAVs and max targets of 101)

Table 4. Overview of traveling salesman problem (TSP) approaches used in UAV routing.

Author Approach Objective Experimental Data
[94] Oberlin, Rathinam, and Darbha, 2009 Heterogeneous, Multiple Depot, Multiple TSP (HMDMTSP) Minimize the total cost of traveling for the heterogeneous fleet of UAVs 6 UAVs with a minimum turning radius vary uniformly from 100 to 200 meters and uniformly generated targets [4][40] in a square of area 5 × 5 km2
[77] Liu, Gao, Guang, and Song, 2013 TSP Minimize the total traveling time for the homogeneous fleet of UAVs 6 UAV having cruise speed 100 km/h and maximum distance 200 km
[95] Babel, 2016 The curvature-constrained TSP with obstacles Minimize the total tour length One aerial vehicle with a cruise speed of 100 m/s covering an operational area of size 20 km × 20 km
[96]  Manyam et al., 2016 Asymmetric TSP Minimize the total traveling time for homogeneous fleet of UAVs 2 UAVs in a zone of size 30 × 30 units where targets are located randomly and 50 instances for each problem size with 10–40 targets
[97] Furini, Persiani, and Toth, 2016 Time-Dependent TSP in Controlled Airspace (TDTSPPCA) Minimize the total traveling time and the holding time over mission waypoints for homogeneous fleet of UAVs 5 scenarios 10–40 mission waypoints, randomly selected among the navigation points located within a circle having center in Milano Linate and ray of 80 NM
[98] Enright and Frazzoli, 2005 Dynamic Traveling Repairperson Problem (DTRP) Minimize the expected waiting time between the appearance of a target, and the time it is visited Simulated with a Single UAV with randomly generated targets
 [71] Ryan, Bailey, and Moore,

 

2013 Multi-vehicle TSP Maximize the expected target coverage 21-day simulation of the Sisson’s (1997) [100]notional Nari dataset

The rest of the papers found in UAV routing, other than VRP and TSP approaches, are mainly in the domain of wireless networks and scheduling. Most of these remaining contributions are related to wireless networks with a focus on contributions in the fields of ad-hoc networks and wireless sensor networks (WSN). Figure 4 presents an overview of these areas. The UAV routing taxonomy covering the four major areas of UAV routing with VRP approaches, UAV routing with TSP approaches, UAV routing in WNS, and UAV routing in scheduling problems are graphically illustrated in Figure 5.

There is a trend to use UAV routing in WSN domain for surveillance, exploring, and monitoring large regions [100][101][102][103][104][105][106][107][108][109][110][111][112][113][114][115]. The recent papers related to UAV routing in various wireless networks are presented in Figure 6. These systems can integrate information from ground with WSN, in atmosphere with the sensors of UAVs and Global Positioning System (GPS). These collaborative systems have been used for large-scale monitoring, increasing mobility, accessibility, and reaction time in case of emergencies [116]. WSNs and ad-hoc networks have been widely used for data collection using UAVs in both outdoor and indoor settings  and in numerous application domains, and WSNs have been enhanced with data processing abilities in the direction of on-board intelligence. Physical constraints of energy consumption, communication range and autonomy, data transmission, and processing capabilities have been analyzed literature in the domain of WSN design considerations of UAV routing [116][117][118][119][120].

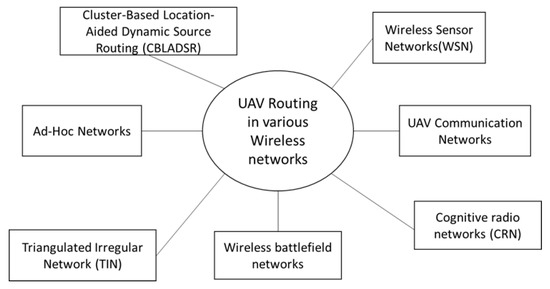
Applsci 10 04504 g006 550

Figure 6. UAV routing in various wireless networks.

UAV routing in scheduling problems mainly focuses on assigning tasks to UAVs in an approach that efficiently utilizes the fleet of UAVs [121][122][123][124]. UAV routing should be done to have a seamless flight during the operations and the required navigation control is derived from a command, which is provided by a scheduler [122][123][124][125]. Generally, these problems aim at assigning various tasks, and actions such as recharge, hover, and wait-on-ground are assigned to the UAVs at different execution times [4][126][127][128][129]. There is limited literature on UAV routing in the scheduling domain and a summary of related studies that focus on UAV scheduling is presented in Figure 7.

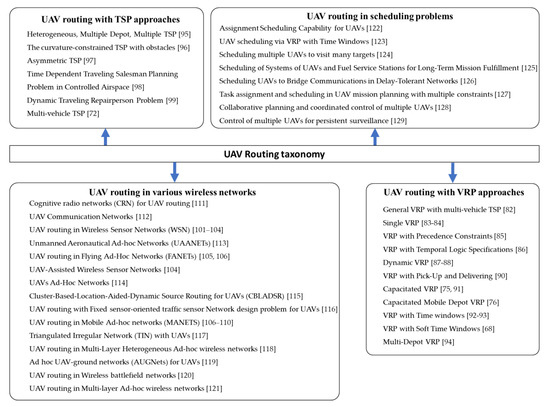
Applsci 10 04504 g007 550

Figure 7. UAV routing taxonomy.

From the overviews of UAV routing literature, the graphical representation of the UAV routing taxonomy is presented in Figure 7. This leads this domain of research to conclude that chief among them is the extensions of VRP and TSP, while the next major contributions are identified in wireless networks as UAV routing is linked with various types of wireless network communication methods.

5. Challenges in UAV Routing

What is noticeable is that there are some issues in the UAVRP that are unaddressed in the existing literature. Specifically, the authors have identified the following issues that are highly relevant. In outdoor route optimization for UAVs, we must deal with the following stochastic conditions, which have received limited attention in the current state. Stochastic conditions influencing the UAV routing can be identified under weather conditions [13][89][130][131][132], air traffic control [6][13][132][133][134], fuel consumption, and range [135][136][137][138][139][140].

These elements are not encountered in the general VRP or TSP and have some characteristics that can potentially greatly influence the solution strategy for the UAVRP. Ignoring the impact of weather will not provide more realistic solutions as flying with the wind could reduce energy consumption and cold temperatures may adversely affect battery performance [17]. As UAVs have fuel constraints, it may not be possible for a UAV to complete a mission before refueling at one of the depots [84]. Even though these challenges with regard to stochastic conditions and minimizing fuel consumption are studied for some years, they are different regarding the context of this paper as in UAVRP, it is different to typical stochastic VRPs where in UAVRP the routings are done in 3D environment with highly non-linear fuel consumption models and the stochastic behavior is not similar to typical stochastic VRPs. Weather makes the conditions time-dependent as changes in the weather conditions impact the fuel consumption and the flying dynamics of the UAVs. There are various approaches to address the time dependency in routing and, in UAV routing, more focus should be put on the sources of uncertainty and time dependency than on the particular manner in which this stochasticity and time dependencies are addressed.

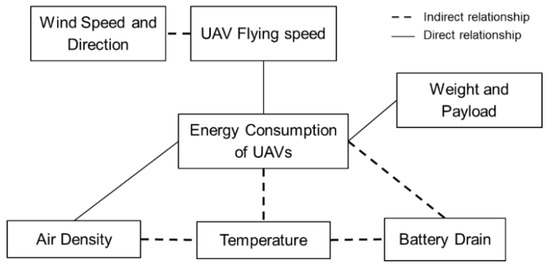
5.1. Weather Conditions

Weather is a critical feature for UAV routing as it affects the travel speed of the UAV, and the temperature in the atmosphere affects the energy consumption [13][16][140] of batteries used in UAVs. Figure 8 presents the relationships between different factors linked to the energy consumption of UAVs. Weather in various forms is critical for energy consumption as it affects the travel speed of the UAV, and the temperature in the atmosphere affects the energy capacity of batteries used in UAVs. Air density affects energy consumption, but that is a function of humidity, air pressure, and temperature. Flying with the wind could, for example, reduce energy consumption. Cold temperatures may adversely affect battery performance until the batteries warm-up [10][13][141].

Applsci 10 04504 g008 550
Figure 8. Factors that affect energy consumption of UAVs [13][138].

The current state of research has not considered the weather factors and ignores the impact of weather on performance [67][83][93]. Interestingly, this seems to add another type of SVRP that should be considered as weather is changing over time in a stochastic manner [133]. Rarely has research focused on considering wind conditions on energy consumption while simultaneously using that information in routing of UAVs [13][136][138].

5.2. Air Traffic Control

Many rules and regulations govern the movement of objects in the airspace. These lead to blocking and opening of flying zones [6]. Even though air traffic control has a significant impact on designing and implementing routes for UAVs, none of the current VRP approaches to solve UAV routing has considered this due to its complex nature. Countries have established systems for notifying blocks of airspace where particular limitations are placed on the flight of all types of UAVs. Such areas are typically either: Prohibited Areas, Restricted Areas, or Danger Areas such as military ranges. Other airspaces may have temporary restrictions imposed at specific times, either as a result of a longer-term pre-planned event or in reaction to a short notice occurrence, such as an emergency incident. Permanent Prohibited, Restricted, or Danger areas are marked on aviation ‘Visual Flight Rules’ (VFR) flight charts (maps), which are readily available for purchase online and proprietary VFR flight-planning and navigation software and apps contain such information in their mapping databases. UAVs around airfields or airports that are designated as ‘protected aerodromes’ are tightly restricted. UAVs of any size must not be flown within the Flight Restriction Zone (FRZ) of a protected aerodrome, without appropriate permission. This information about the restricted or controlled air space is taken as input data and used as constraints in UAV route planning. Furini et al. (2016) [97] uses the Time-dependent TSP in Controlled Airspace (TDTSPPCA), which consists of finding the best order of visit of a UAV over a set of waypoints, aiming at minimizing the operational cost and, at the same time, ensuring a minimum separation with respect to the planned air traffic. However, the technology already exists to build UAVs that can see electronically and avoid other aircraft [130].

5.3. Fuel Consumption and Range

From the airline industry we know that the fuel/energy consumption depends on certain factors such as maximum flight distance or the flight time of the UAV could be constrained by gross takeoff weight, empty weight, thrust to weight ratio [81], fuel weight, payload, and the number of battery units [115], thereby giving more emphasis to the criticality of focusing on fuel consumption.

The range of the UAV is also a crucial aspect where the existing literature has not to give attention and the range is not the same as fuel consumption, as the extent of this depends on many other conditions. How far a UAV can travel is described as range, and the range of a UAV is dependent on the amount of energy capacity of the UAV, endurance, flight speed, and aerodynamic performance [138][139]. Endurance for a UAV can be explained at the total time taken during the flight. For an electric fixed-wing aircraft or quadrotor, this is directly related to the capacity of the battery and the amount of current the motor produces to keep the aircraft in the air. There are many other aircraft parameters that determine the endurance for any UAV; however, the range of the UAV heavily depends on UAV dimensions, Weight, and Payload [138][139]. Any entity that is concerned about UAV security should be extremely concerned about the endurance and range capabilities of various types of UAV categories.

In routing algorithms, some studies have either assumed unlimited fuel capacities [134] in UAV routing or not considered the fuel at all in their approaches to solving UAV routing. Certain studies in UAV routing have considered fuel as a constraint [68][83], and introduce a fuel-constrained UAV routing problem (FCURP). This implies that, given a set of targets and depots and a UAV that is initially stationed at one of the depots, a path can be found for the UAV such that each target is visited at least once, the fuel constraint is never violated along the path for the UAV, and the travel cost for the vehicle is a minimum.

Although fuel consumption is typically considered in vessel routing [135], when it comes to UAVs, the fuel consumption models differ from vessels by depending on not only just speed but also weight or type of payload and weather conditions [136]. For vessels, the non-linear aspects are heavily dependent on the speed of the vessel [137]. Even though existing research uses linear approximations [11], we know from the industry that this is not a reasonable approach for UAVs where the weight of the payload is more critical when seen in combination with speed and weather conditions [138][139][140][141] From the airline industry, one can find comparable models for flight—such as available fuel models for multirotor helicopters [142][143]—that indicate that linear approximation of the energy consumption is not applicable for large variations of the payload carried [16].

6. Conclusions

In general, UAV routing is a novel topic. There has been a very limited number of research contributions published on UAV routing compared to the VRP and vessel routing. This paper identifies different VRP approaches to solve UAV routing, and most of them consist of variants of VRP and TSP. This paper provides a detailed overview of UAV routing literature with a general mathematical formulation for the UAVRP and presents a UAV routing taxonomy covering four areas of VRP-based UAV routing, TSP-based UAV routing, UAV scheduling problems, and UAV routing in wireless networks. The four areas of taxonomy are done considering the common attributes from the literature and the proposed taxonomy is applied to 54 recent papers.

In the majority of the literature on UAV routing the kinematics are neglected and the UAVs’ flight dynamics are neglected or simplified using assumptions. It is worth noting that a UAV’s performance is highly influenced by the payload it is carrying (weight and dimensions) and the weather conditions in which it is operating. Both significantly influence the fuel consumption of the UAV and, thus, they must be included when modeling the UAVRP. Such models will lead to computationally expensive formulations with more realistic solutions. There is seldom research done for a heterogeneous fleet of UAVs due to the complexity and the majority of the existing literature focuses on a homogeneous fleet of UAVs. This problem should be further derived by the non-linearity of the fuel consumption model, and it is also worth noting that the existing literature does give importance to stochastic conditions. Thus, modeling energy consumption must be further investigated by giving more focus to the literature. These models and their integration in the UAVRP seem like particularly relevant avenues of future research and development of efficient frameworks for solving UAVRPs addressing the challenges presented in this study need to be answered.

References

  1. Amila Thibbotuwawa; Grzegorz Bocewicz; P. Nielsen; Z. Banaszak; UAV Mission Planning Subject to Weather Forecast Constraints. Advances in Intelligent Systems and Computing 2019, 1004, 65-76, 10.1007/978-3-030-23946-6_8.
  2. Thibbotuwawa, A.; Bocewicz, G.; Nielsen, P.; Banaszak, Z. Planning deliveries with UAV routing under weather forecast and energy consumption constraints. IFAC-PapersOnLine 2019, 52, 820–825. [Google Scholar] [CrossRef]
  3. Khosiawan, Y.; Nielsen, I. A system of UAV application in indoor environment. Prod. Manuf. Res. 2016, 4, 2–22. [Google Scholar] [CrossRef]
  4. Barrientos, A.; Colorado, J.; Del Cerro, J.; Martinez, A.; Rossi, C.; Sanz, D.; Valente, J. Aerial remote sensing in agriculture: A practical approach to area coverage and path planning for fleets of mini aerial robots. J. Field Robot. 2011, 28, 667–689. [Google Scholar] [CrossRef]
  5. Zhang, M.; Su, C.; Liu, Y.; Hu, M.; Zhu, Y. Unmanned Aerial Vehicle Route Planning in the Presence of a Threat Environment Based on a Virtual Globe Platform. ISPRS Int. J. Geo-Inf. 2016, 5, 184. [Google Scholar] [CrossRef]
  6. Xiang, J.; Liu, Y.; Luo, Z. Flight safety measurements of UAVs in congested airspace. Chin. J. Aeronaut. 2016, 29, 1355–1366. [Google Scholar] [CrossRef]
  7. Klippstein, H.; Diaz De Cerio Sanchez, A.; Hassanin, H.; Zweiri, Y.; Seneviratne, L. Fused Deposition Modeling for Unmanned Aerial Vehicles (UAVs): A Review. Adv. Eng. Mater. 2017, 20, 1700552. [Google Scholar] [CrossRef]
  8. Popper, B. Drones could make Amazon’s dream of free delivery profitable—The Verge. 2016. Available online: http://www.theverge.com/33 (accessed on 11 April 2017).
  9. Radzki, G.; Thibbotuwawa, A.; Bocewicz, G. UAVs flight routes optimization in changing weather conditions—Constraint programming approach. Appl. Comput. Sci. 2019, 15, 5–17. [Google Scholar] [CrossRef]
  10. Bocewicz, G.; Nielsen, P.; Banaszak, Z.; Thibbotuwawa, A. A Declarative Modelling Framework for Routing of Multiple UAVs in a System with Mobile Battery Swapping Stations. In International Conference on Intelligent Systems in Production Engineering and Maintenance; Springer: Berlin, Germany, 2019; pp. 429–441. [Google Scholar] [CrossRef]
  11. Aasen, H.; Gnyp, M.L. Spectral comparison of low-weight and UAV- based hyperspectral frame cameras with portable spectroradiometers measurements. In Proceedings of the Work UAV-Based Remote Sensing Methods for Monitoring Vegetation, Cologne, Germany, 9–10 September 2013; pp. 1–6. [Google Scholar] [CrossRef]
  12. Chandran, B.; Raghavan, S. Modeling and Solving the Capacitated Vehicle Routing Problem on Trees. In Mathematics of Neural Networks; Springer Science and Business Media LLC: Berlin, Germany, 2008; Volume 43, pp. 239–261. [Google Scholar]
  13. Thibbotuwawa, A. Unmanned Aerial Vehicle Fleet Mission Planning Subject to Changing Weather Conditions. Ph.D. Thesis, Og Naturvidenskabelige Fakultet, Aalborg Universitet, Aalborg, Denmark, 2020. [Google Scholar]
  14. Sung, I.; Nielsen, P. Zoning a Service Area of Unmanned Aerial Vehicles for Package Delivery Services. J. Intell. Robot. Syst. 2019, 97, 719–731. [Google Scholar] [CrossRef]
  15. Ekşioglu, B.; Vural, A.V.; Reisman, A. The vehicle routing problem: A taxonomic review. Comput. Ind. Eng. 2009, 57, 1472–1483. [Google Scholar] [CrossRef]
  16. Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle Routing Problems for Drone Delivery. IEEE Trans. Syst. Man, Cybern. Syst. 2016, 47, 70–85. [Google Scholar] [CrossRef]
  17. Braekers, K.; Ramaekers, K.; Van Nieuwenhuyse, I. The vehicle routing problem: State of the art classification and review. Comput. Ind. Eng. 2016, 99, 300–313. [Google Scholar] [CrossRef]
  18. Toro, E.M.; Escobar, A.H.; Granada, E.M. Literature Review on the Vehicle Routing Problem in the Green Transportation Context. Luna Azul 2015, 362–387. [Google Scholar] [CrossRef]
  19. Kim, S.J.; Lim, G.J.; Cho, J.; Côté, M.J. Drone-Aided Healthcare Services for Patients with Chronic Diseases in Rural Areas. J. Intell. Robot. Syst. 2017, 88, 163–180. [Google Scholar] [CrossRef]
  20. Psaraftis, H.N. Dynamic vehicle routing: Status and prospects. Ann. Oper. Res. 1995, 61, 143–164. [Google Scholar] [CrossRef]
  21. Baldacci, R.; Bartolini, E.; Laporte, G. Some applications of the generalized vehicle routing problem. J. Oper. Res. Soc. 2010, 61, 1072–1077. [Google Scholar] [CrossRef]
  22. Ghiani, G.; Guerriero, F.; Laporte, G.; Musmanno, R. Real-time vehicle routing: Solution concepts, algorithms and parallel computing strategies. Eur. J. Oper. Res. 2003, 151, 1–11. [Google Scholar] [CrossRef]
  23. Le Ny, J.; Dahleh, M.; Feron, E. Multi-UAV dynamic routing with partial observations using restless bandit allocation indices. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; Institute of Electrical and Electronics Engineers (IEEE): Los Alamitos, CA, USA, 2008; pp. 4220–4225. [Google Scholar] [CrossRef]
  24. Kłosowski, G.; Gola, A.; Amila, T. Computational intelligence in control of AGV multimodal systems. Ifac-Papersonline 2018, 51(11), 1421–1427. [Google Scholar] [CrossRef]
  25. Dang, Q.-V.; Nielsen, I.; Steger-Jensen, K.; Madsen, O. Scheduling a single mobile robot for part-feeding tasks of production lines. J. Intell. Manuf. 2013, 25, 1271–1287. [Google Scholar] [CrossRef]
  26. Bocewicz, G.; Nielsen, P.; Banaszak, Z.; Thibbotuwawa, A. Routing and Scheduling of Unmanned Aerial Vehicles Subject to Cyclic Production Flow Constraints. In Proceedings of the 15th International Conference Distributed Computing and Artificial Intelligence, Toledo, Spain, 20–22 June 2018; pp. 75–86. [Google Scholar] [CrossRef]
  27. Nielsen, I.; Dang, Q.-V.; Bocewicz, G.; Banaszak, Z. A methodology for implementation of mobile robot in adaptive manufacturing environments. J. Intell. Manuf. 2015, 28, 1171–1188. [Google Scholar] [CrossRef]
  28. Dang, Q.-V.; Nielsen, I. Simultaneous scheduling of machines and mobile robots. e-Bus. Telecommun. Netw. 2013, 365, 118–128. [Google Scholar] [CrossRef]
  29. Zou, B.; Gong, Y.; Xu, X.; Yuan, Z. Assignment rules in robotic mobile fulfilment systems for online retailers. Int. J. Prod. Res. 2017, 55, 6175–6192. [Google Scholar] [CrossRef]
  30. Mann, M.; Zion, B.; Shmulevich, I.; Rubinstein, D. Determination of robotic melon harvesting efficiency: A probabilistic approach. Int. J. Prod. Res. 2015, 54, 3216–3228. [Google Scholar] [CrossRef]
  31. Djordjevich, A.; Tso, S.; Zhang, J. Extended range tactility in material handling. Int. J. Prod. Res. 2000, 38, 4357–4367. [Google Scholar] [CrossRef]
  32. Logendran, R.; Sriskandarajah, C. Sequencing of robot activities and parts in two-machine robotic cells. Int. J. Prod. Res. 1996, 34, 3447–3463. [Google Scholar] [CrossRef]
  33. Rembold, B.; Nof, S.Y. Modelling the performance of a mobile robot with RTM. Int. J. Prod. Res. 1991, 29, 967–978. [Google Scholar] [CrossRef]
  34. Franceschini, F.; Mastrogiacomo, L.; Pralio, B. An unmanned aerial vehicle-based system for large scale metrology applications. Int. J. Prod. Res. 2010, 48, 3867–3888. [Google Scholar] [CrossRef]
  35. Toth, P.; Vigo, D. The Vehicle Routing Problem; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar] [CrossRef]
  36. Sonmezocak, E.; Kurt, S. Optimum Route Planning and Scheduling for Unmanned Aerial Vehicles; Navel Postgraduate School: Monterey, CA, USA, 2010. [Google Scholar]
  37. Toth, P.; Tramontani, A. An Integer Linear Programming Local Search for Capacitated Vehicle Routing Problems. In The Vehicle Routing Problem: Latest Advances and New Challenges; Springer: Boston, MA, USA, 2008; pp. 275–295. [Google Scholar]
  38. Toth, P.; Vigo, D. Models, relaxations and exact approaches for the capacitated vehicle routing problem. Discret. Appl. Math. 2002, 123, 487–512. [Google Scholar] [CrossRef]
  39. Pisinger, D.; Ropke, S. A general heuristic for vehicle routing problems. Comput. Oper. Res. 2007, 34, 2403–2435. [Google Scholar] [CrossRef]
  40. Montoya-Torres, J.R.; Franco, J.L.; Isaza, S.N.; Jiménez, H.F.; Herazo-Padilla, N. A literature review on the vehicle routing problem with multiple depots. Comput. Ind. Eng. 2015, 79, 115–129. [Google Scholar] [CrossRef]
  41. Archetti, C.; Speranza, M.G. The Split Delivery Vehicle Routing Problem: A Survey. In The Vehicle Routing Problem: LATEST Advances and New Challenges; Springer: Boston, MA, USA, 2008; Volume 43, pp. 103–122. [Google Scholar]
  42. Gendreau, M.; Laporte, G.; Séguin, R. Stochastic vehicle routing. Eur. J. Oper. Res. 1996, 88, 3–12. [Google Scholar] [CrossRef]
  43. Pillac, V.; Gendreau, M.; Guéret, C.; Medaglia, A.L. A review of dynamic vehicle routing problems. Eur. J. Oper. Res. 2013, 225, 1–11. [Google Scholar] [CrossRef]
  44. Huang, Y.; Zhao, L.; Van Woensel, T.; Gross, J.-P. Time-dependent vehicle routing problem with path flexibility. Transp. Res. Part B Methodol. 2017, 95, 169–195. [Google Scholar] [CrossRef]
  45. Drexl, M. A Generic Heuristic for Vehicle Routing Problems with Multiple Synchronization Constraints; Gutenberg School of Management and Economics–Discussion Paper Series: Mainz, Germany, 2014; Volume 1412, p. 43. [Google Scholar] [CrossRef]
  46. Stavropoulou, F.; Repoussis, P.; Tarantilis, C. The vehicle routing problem with profits and consistency constraints. Eur. J. Oper. Res. 2019, 274, 340–356. [Google Scholar] [CrossRef]
  47. Archetti, C.; Speranza, M.G.; Vigo, D. Vehicle routing problems with profits. In Vehicle Routing: Problems, Methods, and Applications, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014; pp. 273–297. [Google Scholar]
  48. Ibarra-Rojas, O.J.; Delgado, F.; Giesen, R.; Muñoz, J.C. Planning, operation, and control of bus transport systems: A literature review. Transp. Res. Part B Methodol. 2015, 77, 38–75. [Google Scholar] [CrossRef]
  49. Kontovas, C.A. The Green Ship Routing and Scheduling Problem (GSRSP): A conceptual approach. Transp. Res. Part D Transp. Environ. 2014, 31, 61–69. [Google Scholar] [CrossRef]
  50. Wang, X. Operational Transportation Planning of Modern Freight Forwarding Companies: Vehicle Routing under Consideration of Subcontracting and Request Exchange; Springer Nature: Basel, Switzerland, 2015; pp. 1–161. [Google Scholar] [CrossRef]
  51. Hoff, A.; Andersson, H.; Christiansen, M.; Hasle, G.; Lokketangen, A. Industrial aspects and literature survey: Fleet composition and routing. Comput. Oper. Res. 2010, 37, 2041–2061. [Google Scholar] [CrossRef]
  52. Kjeldsen, K.H.; Ergun, O.; Lysgaard, J.; Erera, A. Rescheduling ships and cargo in liner shipping in the event of disruptions. Liner Shipp 2011, 105–133. [Google Scholar]
  53. Campbell, J.F.; O’Kelly, M.E. Twenty-Five Years of Hub Location Research. Transp. Sci. 2012, 46, 153–169. [Google Scholar] [CrossRef]
  54. Holden, J.; Goel, N. Fast-Forwarding to A Future of On-Demand Urban Air Transportation; Uber Elevate: San Francisco, CA, USA, 2016; Available online: https://www.uber.com/info/elevate (accessed on 14 April 2018).
  55. Esa, J.; Poikonen, E.; Hyvönen, M. Remote and Autonomous Ships: The Next Steps; AAWA Position Paper; Rolls Royce plc: London, UK, 2016. [Google Scholar]
  56. Zheng, F.; Wang, F.; Wu, J.; Zheng, X. A methodology of UAV route planning for fast image mosaicking. In Proceedings of the 2015 23rd International Conference on Geoinformatics, Wuhan, China, 19–21 June 2015; pp. 1–5. [Google Scholar] [CrossRef]
  57. Drones: High-Profile and Niche. Deloitte Touche Tohmatsu Ltd, London, UK. Available online: https://www2.deloitte.com/content/dam/Deloitte/global/Documents (accessed on 11 May 2019).
  58. Confessore, G.; Fabiano, M.; Liotta, G. A network flow based heuristic approach for optimising AGV movements. J. Intell. Manuf. 2011, 24, 405–419. [Google Scholar] [CrossRef]
  59. Ulusoy, G.; Bilge, Ü. Simultaneous scheduling of machines and automated guided vehicles. Int. J. Prod. Res. 1993, 31, 2857–2873. [Google Scholar] [CrossRef]
  60. Oboth, C.; Batta, R.; Karwan, M. Dynamic conflict-free routing of automated guided vehicles. Int. J. Prod. Res. 1999, 37, 2003–2030. [Google Scholar] [CrossRef]
  61. Qiu, L.; Hsu, W.-J.; Huang, S.Y.; Wang, H. Scheduling and routing algorithms for AGVs: A survey. Int. J. Prod. Res. 2002, 40, 745–760. [Google Scholar] [CrossRef]
  62. Wróbel, K.; Montewka, J.; Kujala, P. Towards the assessment of potential impact of unmanned vessels on maritime transportation safety. Reliab. Eng. Syst. Saf. 2017, 165, 155–169. [Google Scholar] [CrossRef]
  63. Coelho, B.N.; Coelho, V.N.; Coelho, I.M. A multi-objective green UAV routing problem. Comput. Oper. Res. 2017, 88, 306–315. [Google Scholar] [CrossRef]
  64. Enright, J.J.; Frazzoli, E.; Pavone, M.; Ketan, S. Selection of Appropriate Class UAS/Sensors to Support Fire Monitoring: Experiences in the United States; Handbook of UAVs; Springer Nature: Basel, Switzerland, 2015. [Google Scholar] [CrossRef]
  65. Goerzen, C.; Kong, Z.; Mettler, B. A survey of motion planning algorithms from the perspective of autonomous UAV guidance. J. Intell. Robot. Syst. 2009, 57, 65. [Google Scholar] [CrossRef]
  66. Karpenko, S.; Konovalenko, I.; Miller, A.; Miller, B.; Nikolaev, D. UAV Control on the Basis of 3D Landmark Bearing-Only Observations. Sensors 2015, 15, 29802–29820. [Google Scholar] [CrossRef]
  67. Guerriero, F.; Surace, R.; Loscrí, V.; Natalizio, E. A multi-objective approach for unmanned aerial vehicle routing problem with soft time windows constraints. Appl. Math. Model. 2014, 38, 839–852. [Google Scholar] [CrossRef]
  68. Sundar, K.; Venkatachalam, S.; Rathinam, S. An Exact Algorithm for a Fuel-Constrained Autonomous Vehicle Path Planning Problem. arXiv Preprint 2016, arXiv:1604.08464. [Google Scholar]
  69. Rojas-Viloria, D.; Solano-Charris, E.L.; Muñoz-Villamizar, A.; Montoya-Torres, J.R. Unmanned aerial vehicles/drones in vehicle routing problems: A literature review. Int. Trans. Oper. Res. 2020. [Google Scholar] [CrossRef]
  70. Perera, H.N.; Hurley, J.; Fahimnia, B.; Reisi, M. The human factor in supply chain forecasting: A systematic review. Eur. J. Oper. Res. 2019, 274, 574–600. [Google Scholar] [CrossRef]
  71. Ryan, J.L.; Bailey, T.G.; Moore, J.T.; Carlton, W.B. Reactive tabu search in unmanned aerial reconnaissance simulations. J. Chem. Inf. Model. 2013, 53, 1689–1699. [Google Scholar] [CrossRef]
  72. Buck, K.; Gassner, R.; Poore, A.B.; Yan, X. Visibility Constrained Routing of Unmanned Aerial Vehicles. Signal Processing, Sensor Fusion, and Target Recognition. Int. Soc. Opt. Photonics 1999, 3720, 256–266. [Google Scholar] [CrossRef]
  73. Laporte, G. The Vehicle Routing Problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 231–247. [Google Scholar] [CrossRef]
  74. Guerrero, J.A.; Bestaoui, Y. UAV path planning for structure inspection in windy environments. J. Intell. Robot Syst. 2012, 69, 297–311. [Google Scholar] [CrossRef]
  75. Savuran, H.; Karakaya, M. Efficient route planning for an unmanned air vehicle deployed on a moving carrier. Soft Comput. 2015, 20, 2905–2920. [Google Scholar] [CrossRef]
  76. Lawler, E.L. The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization; Wiley-Interscience Series in Discrete Mathematics: Hoboken, NJ, USA, 1985. [Google Scholar]
  77. Liu, X.; Gao, L.; Guang, Z.; Song, Y. A UAV Allocation Method for Traffic Surveillance in Sparse Road Network. J. Highw. Transp. Res. Dev. 2013, 7, 81–87. [Google Scholar] [CrossRef]
  78. Geyer, C.; Dey, D.; Singh, S. Prototype Sense-and-Avoid Sstemy for UAVs; Report 2009 Tech. Report, CMU-RI-TR-09-09; Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 2009. [Google Scholar]
  79. Fu, Y. New Development on Sense and Avoid Strategies for Unmanned Aerial Vehicles. Master’s Thesis, Concordia University, Montréal, QC, Canada, 2016. [Google Scholar]
  80. Imanberdiyev, N.; Fu, C.; Kayacan, E.; Chen, I.M. Autonomous navigation of UAV by using real-time model-based reinforcement learning. In Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), Phuket, Thailand, 13–15 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
  81. Shetty, V.K.; Sudit, M.; Nagi, R. Priority-based assignment and routing of a fleet of unmanned combat aerial vehicles. Comput. Oper. Res. 2008, 35, 1813–1828. [Google Scholar] [CrossRef]
  82. Wang, X.; Poikonen, S.; Golden, B. The vehicle routing problem with drones: Several worst-case results. Optim. Lett. 2016, 11, 679–697. [Google Scholar] [CrossRef]
  83. Sundar, K.; Rathinam, S. Algorithms for routing an unmanned aerial vehicle in the presence of refueling depots. IEEE Trans. Autom. Sci. Eng. 2013, 11, 287–294. [Google Scholar] [CrossRef]
  84. David, W.; Casbeer, R.H.C. Column generation for a UAV assignment problemwith precedence constraints David. Int. J. Robust Nonlinear Control 2011, 21, 1421–1433. [Google Scholar] [CrossRef]
  85. Karaman, S.; Frazzoli, E. Vehicle Routing Problem with Metric Temporal Logic Specifications. In Proceedings of the IEEE Conf Decis Control, San Diego, CA, USA, 13–15 December 2006; pp. 3953–3958. [Google Scholar] [CrossRef]
  86. Klein, D.J.; Venkateswaran, S.; Isaacs, J.T. Localization with sparse acoustic sensor network using UAVs as information-seeking data mules. ACM Trans. Sens. Netw. 2013, 9, 1–29. [Google Scholar] [CrossRef]
  87. Arsie, A.; Frazzoli, E. Efficient routing of multiple vehicles with no explicit communications. Int. J. Robust Nonlinear Control 2007, 18, 154–164. [Google Scholar] [CrossRef]
  88. Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
  89. Kinney, G.W.; Hill, R.R.; Moore, J.T. Devising a quick-running heuristic for an unmanned aerial vehicle (UAV) routing system. J. Oper. Res. Soc. 2005, 56, 776–786. [Google Scholar] [CrossRef]
  90. Wen, T.; Zhang, Z.; Wong, K.K.L. Multi-objective algorithm for blood supply via unmanned aerial vehicles to the wounded in an emergency situation. PLoS ONE 2016, 11, e0155176. [Google Scholar] [CrossRef] [PubMed]
  91. Murray, C.; Karwan, M. A Branch-and-Bound-Based Solution Approach for Dynamic Rerouting of Airborne Platforms. Nav. Res. Logist. 2013, 60, 141–159. [Google Scholar] [CrossRef]
  92. Lamont, G.B.; Slear, J.N.; Melendez, K. UAV swarm mission planning and routing using multi-objective evolutionary algorithms. In Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making, Honolulu, HI, USA, 1–5 April 2007; pp. 10–20. [Google Scholar] [CrossRef]
  93. Habib, D.; Jamal, H.; Khan, S.A. Employing multiple unmanned aerial vehicles for co-operative path planning. Int. J. Adv. Robot. Syst. 2013, 10(5), 235. [Google Scholar] [CrossRef]
  94. Oberlin, P.; Rathinam, S.; Darbha, S. A Transformation for a Heterogenous, Multiple Depot, Multiple Traveling Salesman Problem. Transformation 2003, 1292–1297. [Google Scholar] [CrossRef]
  95. Babel, L. Curvature-constrained traveling salesman tours for aerial surveillance in scenarios with obstacles. Eur. J. Oper. Res. 2017, 262, 335–346. [Google Scholar] [CrossRef]
  96. Manyam, S.G.; Rathinam, S.; Darbha, S. GPS Denied UAV Routing with Communication Constraints. J. Intell. Robot Syst. 2016, 84, 691–703. [Google Scholar] [CrossRef]
  97. Furini, F.; Persiani, C.A.; Toth, P. The Time Dependent Traveling Salesman Planning Problem in Controlled Airspace. Transp. Res. Part B Methodol. 2016, 90, 38–55. [Google Scholar] [CrossRef]
  98. Enright, J.J.; Frazzoli, E. UAV Routing in a Stochastic, Time-Varying Environment. IFAC Proc. 2005, 38, 295–300. [Google Scholar] [CrossRef]
  99. Sisson, M.R. Applying Tabu Heuristic to Wind Influenced, Minimum Risk and Maximum Expected Coverage Routes. Air Force Inst of Tech Wright-Patterson of School of Engineering. Master’s Thesis, Air Force Institute of Technology, Wright-Patterson AFB, OH, USA, 1997. [Google Scholar]
  100. Jawhar, I.; Mohamed, N.; Al-Jaroodi, J.; Zhang, S. A framework for using unmanned aerial vehicles for data collection in linear wireless sensor networks. J. Intell. Robot. Syst. 2013, 74, 437–453. [Google Scholar] [CrossRef]
  101. Antonio, P.; Grimaccia, F.; Mussetta, M. Architecture and methods for innovative heterogeneous wireless sensor network applications. Remote. Sens. 2012, 4, 1146–1161. [Google Scholar] [CrossRef]
  102. Mascarenas, D.; Flynn, E.; Farrar, C. A mobile host approach for wireless powering and interrogation of structural health monitoring sensor networks. IEEE Sens. J. 2009, 9, 1719–1726. [Google Scholar] [CrossRef]
  103. Say, S.; Inata, H.; Liu, J.; Shimamoto, S. Priority-Based Data Gathering Framework in UAV-Assisted Wireless Sensor Networks. IEEE Sens. J. 2016, 16, 5785–5794. [Google Scholar] [CrossRef]
  104. Sahingoz, O.K. Networking models in flying Ad-hoc networks (FANETs): Concepts and challenges. J. Intell. Robot. Syst. 2013, 74, 513–527. [Google Scholar] [CrossRef]
  105. Rosati, S.; Kruzelecki, K.; Heitz, G. Dynamic Routing for Flying Ad Hoc Networks. IEEE Trans. Veh. Technol. 2015, 65, 1690–1700. [Google Scholar] [CrossRef]
  106. Guo, Y.; Li, X.; Yousefi’zadeh, H.; Jafarkhani, H. UAV-aided cross-layer routing for MANETs. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Paris, France, 1–4 April 2012; pp. 2928–2933. [Google Scholar] [CrossRef]
  107. Sahingoz, O.K. Mobile networking with UAVs: Opportunities and challenges. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; Institute of Electrical and Electronics Engineers (IEEE): Los Alamitos, CA, USA, 2013; pp. 933–941. [Google Scholar] [CrossRef]
  108. Maxa, J.-A.; Ben Mahmoud, M.S.; Larrieu, N. Secure routing protocol design for UAV Ad hoc NETworks. In Proceedings of the IEEE/AIAA 34th Digital Avionics Systems Conference (DASC), Prague, Czech Republic, 13–17 September 2015; pp. 4A5-1–4A5-15. [Google Scholar] [CrossRef]
  109. Zhang, K.E.; Zhang, W.; Zeng, J.Z. Preliminary study of routing and date integrity in mobile Ad Hoc uav network. In Proceedings of the 2008 Int Conf Apperceiving Comput Intell Anal ICACIA, Boston, MA, USA, 7–11 July 2008; pp. 347–350. [Google Scholar] [CrossRef]
  110. Huang, X.; Wang, G.; Hu, F.; Kumar, S. Stability-Capacity-Adaptive Routing for High Mobility, Multi-Hop Cognitive Radio Networks. Communic Res. 2011, 60, 1–17. [Google Scholar]
  111. Gupta, L.; Jain, R.; Vaszkun, G. Survey of Important Issues in UAV Communication Networks. IEEE Commun. Surv. Tutor. 2015, 18, 1123–1152. [Google Scholar] [CrossRef]
  112. Li, Y.; Shirani, R.; St-Hilaire, M.; Kunz, T. Improving routing in networks of Unmanned Aerial Vehicles: Reactive-Greedy-Reactive. Wirel. Commun. Mob. Comput. 2012. [Google Scholar] [CrossRef]
  113. Alshabtat, A.; Dong, L.; Li, J.; Yang, F. Low latency routing algorithm for unmanned aerial vehicles ad-hoc networks. Electr. Comput. Eng. 2010, 6, 48–54. [Google Scholar]
  114. Shi, N.; Luo, X. A Novel Cluster-Based Location-Aided Routing Protocol for UAV Fleet Networks. Int. J. Digit. Content Technol. Its Appl. 2012, 6, 376–383. [Google Scholar] [CrossRef]
  115. Zhang, J.; Jia, L.; Niu, S. A space-time network-based modeling framework for dynamic unmanned aerial vehicle routing in traffic incident monitoring applications. Sensors 2015, 15, 13874–13898. [Google Scholar] [CrossRef]
  116. Casas, I.; Malik, A.; Delmelle, E.M. An automated network generation procedure for routing of Unmanned Aerial Vehicles (UAVs) in a GIS environment. Netw. Spat. Econ. 2006, 7, 153–176. [Google Scholar] [CrossRef]
  117. Gu, D.L.; Gerla, M.; Ly, H.; Xu, K.; Kong, J.; Hong, X. Design of multilevel heterogeneous ad-hoc wireless networks with UAVs. Wirel. Mob. Commun. 2001, 4586, 327–338. [Google Scholar] [CrossRef]
  118. Brown, T.X.; Argrow, B.; Dixon, C. Ad Hoc UAV-Ground Network, Test Bed. Test 2004, 1, 1–5. [Google Scholar]
  119. Xu, K.X.K.; Hong, X.H.X.; Gerla, M.G.M. Landmark routing in large wireless battlefield networks using UAVs. In Proceedings of the Proceedings Communications for Network-Centric Operations: Creating the Information (MILCOM), McLean, VA, USA, 28–31 October 2001; pp. 230–234. [Google Scholar] [CrossRef]
  120. Gu, D.; Pei, G.; Ly, H. Hierarchical routing for multi-layer ad-hoc wireless networks with UAVs. MILCOM 2000, 310–314. [Google Scholar] [CrossRef]
  121. Ahner, D.K.; Buss, A.H.; Ruck, J.; Ave, S. A discrete event simulation with optimization in the loop approach to solving. In Proceedings of the Winter Simulation Conference (WSC), Monterey, CA, USA, 3–6 December 2006; pp. 1349–1356. [Google Scholar]
  122. Weinstein, A.L.; Schumacher, C. UAV scheduling via the vehicle routing problem with time windows. In Proceedings of the AIAA Infotech Aerospace Conference and Exhibit, Rohnert Park, CA, USA, 7–10 May 2007. [Google Scholar] [CrossRef]
  123. Kim, Y.; Gu, D.W.; Postlethwaite, I. Real-time optimal mission scheduling and flight path selection. IEEE Trans. Autom. Control. 2007, 52, 1119–1123. [Google Scholar] [CrossRef]
  124. Kim, J.; Song, B.D.; Morrison, J.R. On the scheduling of systems of UAVs and fuel service stations for long-term mission fulfillment. J. Intell. Robot. Syst. 2012, 70, 347–359. [Google Scholar] [CrossRef]
  125. Kwon, J.; Hailes, S. Scheduling UAVs to bridge communications in delay-tolerant networks using real-time scheduling analysis techniques. In Proceedings of the IEEE/SICE International Symposium on System Integration, Tokyo, Japan, 13–14 December 2014; pp. 363–369. [Google Scholar] [CrossRef]
  126. Bocewicz, G.; Nielsen, P.; Banaszak, Z.; Thibbotuwawa, A. Deployment of Battery Swapping Stations for Unmanned Aerial Vehicles Subject to Cyclic Production Flow Constraints. In Biomedical Engineering Systems and Technologies; Springer: Cham, Switzerland, 2018; pp. 73–87. [Google Scholar] [CrossRef]
  127. Tso, K.S.; Tharp, G.K.; Zhang, W.; Tai, A.T. A multi-agent operator interface for unmanned aerial vehicles. In Proceedings of the 18th Digital Avionics Systems Conference, St. Louis, MO, USA, 24–29 October 1999. [Google Scholar] [CrossRef]
  128. Nigam, N.; Bieniawski, S.; Kroo, I.; Vian, J. Control of multiple UAVs for persistent surveillance: Algorithm and flight test results. IEEE Trans. Control. Syst. Technol. 2011, 20, 1236–1251. [Google Scholar] [CrossRef]
  129. Popescu, D.; Stoican, F.; Stamatescu, G.; Chenaru, O.; Ichim, L. A Survey of Collaborative UAV–WSN Systems for Efficient Monitoring. Sensors 2019, 19, 4690. [Google Scholar] [CrossRef]
  130. Baek, J.; Han, S.I.; Han, Y. Energy-Efficient UAV Routing for Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2020, 69, 1741–1750. [Google Scholar] [CrossRef]
  131. Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
  132. Holcombe, R.G. Integrating Drones into the US Air Traffic Control System; Working Paper; Mercatus Center at George Mason University: Arlington, WV, USA, 2016; Available online: https://www.mercatus.org/publications/technology-and-innovation (accessed on 13 February 2019).
  133. Wu, J.; Zhang, D.; Pei, D. Autonomous route planning for UAV when threats are uncertain. In Proceedings of the IEEE Chinese Guidance, Navigation and Control Conference, CGNCC, Yantai, China, 8–10 August 2014. [Google Scholar] [CrossRef]
  134. Frazzoli, E.; Bullo, F. Decentralized algorithms for vehicle routing in a stochastic time-varying environment. In Proceedings of the 43rd IEEE Conference on Decision and Control, Atlantis, Bahamas, 14–17 December 2004; Volume 4, pp. 3357–3363. [Google Scholar] [CrossRef]
  135. Zhang, J.; Zhao, Y.; Xue, W.; Li, J. Vehicle routing problem with fuel consumption and carbon emission. Int. J. Prod. Econ. 2015, 170, 234–242. [Google Scholar] [CrossRef]
  136. Thibbotuwawa, A.; Nielsen, P.; Zbigniew, B.; Bocewicz, G. Energy Consumption in Unmanned Aerial Vehicles: A Review of Energy Consumption Models and Their Relation to the UAV Routing. In Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin, Germany, 2019; pp. 173–184. [Google Scholar] [CrossRef]
  137. Feng, Y.; Zhang, R.; Jia, G. Vehicle Routing Problems with Fuel Consumption and Stochastic Travel Speeds. Math. Probl. Eng. 2017, 2017, 6329203. [Google Scholar] [CrossRef]
  138. Thibbotuwawa, A.; Nielsen, P.; Zbigniew, B.; Bocewicz, G. Factors Affecting Energy Consumption of Unmanned Aerial Vehicles: An Analysis of How Energy Consumption Changes in Relation to UAV Routing. In Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin, Germany, 2019; pp. 228–238. [Google Scholar] [CrossRef]
  139. Thibbotuwawa, A.; Bocewicz, G.; Zbigniew, B.; Nielsen, P. A Solution Approach for UAV Fleet Mission Planning in Changing Weather Conditions. Appl. Sci. 2019, 9, 3972. [Google Scholar] [CrossRef]
  140. Thibbotuwawa, A.; Bocewicz, G.; Radzki, G.; Nielsen, P.; Banaszak, Z. UAV Mission Planning Resistant to Weather Uncertainty. Sensors 2020, 20, 515. [Google Scholar] [CrossRef]
  141. Leishman, D.S. Principles of Helicopter Aerodynamics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
  142. Amila Thibbotuwawa; Grzegorz Bocewicz; Peter Nielsen; Zbigniew Banaszak; Unmanned Aerial Vehicle Routing Problems: A Literature Review. Applied Sciences 2020, 10, 4504, 10.3390/app10134504.
  143. Amila Thibbotuwawa; Grzegorz Bocewicz; P. Nielsen; Z. Banaszak; UAV Mission Planning Subject to Weather Forecast Constraints. Advances in Intelligent Systems and Computing 2019, 1004, 65-76, 10.1007/978-3-030-23946-6_8.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Mechanical
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Amila Thibbotuwawa
,
Grzegorz Bocewicz
,
Peter Nielsen
,
Zbigniew Banaszak
View Times: 1.5K
Revisions: 3 times (View History)
Update Date: 14 Jul 2020
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback