Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1 This method enables meaningful quantitative comparison of clustering patterns at various spatial scales and among different time spots, and it is a useful metric for understanding and quantifying the change in clustering through time.
G.-Fivos Sargentis
 + 2196 word(s) 2196 2020-09-28 11:48:12 |
2 format correct
Conner Chen
 Meta information modification 2196 2020-10-14 06:09:15 | |
3 Details added.
G.-Fivos Sargentis
 + 6 word(s) 2202 2020-10-15 08:03:13 | |
4 Format is changed
G.-Fivos Sargentis
 + 6 word(s) 2202 2020-10-15 08:05:22 | |
5 Format is changed
G.-Fivos Sargentis
 + 6 word(s) 2202 2020-10-15 08:06:52 | |
6 Format is changed
G.-Fivos Sargentis
 Meta information modification 2202 2020-10-15 18:50:32 | |
7 Type-writing errors
G.-Fivos Sargentis
 -2 word(s) 2200 2020-10-15 20:22:34 | |
8 format correct
Conner Chen
 Meta information modification 2200 2020-10-30 11:03:17 | |
9 format correct
Nora Tang
 Meta information modification 2200 2020-11-10 09:35:39 | |
10 format correct
Conner Chen
 Meta information modification 2200 2020-12-23 07:50:12 | |
11 format correct
Conner Chen
 Meta information modification 2200 2020-12-23 07:50:44 | |
12 Change the title to make it the same as the published entry
Dean Liu
 + 4 word(s) 2204 2021-10-28 08:13:51 | |
13 update the definition
Dean Liu
 + 49 word(s) 2249 2021-10-28 08:16:52 | |
14 format correct
Conner Chen
 -1772 word(s) 477 2022-04-14 07:42:43 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Sargentis, G.; Iliopoulou, T.; Sigourou, S.; Dimitriadis, P.; Koutsoyiannis, D. Spatial Hurst–Kolmogorov Clustering. Encyclopedia. Available online: https://encyclopedia.pub/entry/2568 (accessed on 20 April 2024).
Sargentis G, Iliopoulou T, Sigourou S, Dimitriadis P, Koutsoyiannis D. Spatial Hurst–Kolmogorov Clustering. Encyclopedia. Available at: https://encyclopedia.pub/entry/2568. Accessed April 20, 2024.
Sargentis, G.-Fivos, Theano Iliopoulou, Stavroula Sigourou, Panayiotis Dimitriadis, Demetris Koutsoyiannis. "Spatial Hurst–Kolmogorov Clustering" Encyclopedia, https://encyclopedia.pub/entry/2568 (accessed April 20, 2024).
Sargentis, G., Iliopoulou, T., Sigourou, S., Dimitriadis, P., & Koutsoyiannis, D. (2020, October 14). Spatial Hurst–Kolmogorov Clustering. In Encyclopedia. https://encyclopedia.pub/entry/2568
Sargentis, G.-Fivos, et al. "Spatial Hurst–Kolmogorov Clustering." Encyclopedia. Web. 14 October, 2020.
Peer Reviewed
Spatial Hurst–Kolmogorov Clustering
This is a peer-reviewed entry published in Encyclopedia Journal, full entry can be found at 10.3390/encyclopedia1040077

The stochastic analysis in the scale domain (instead of the traditional lag or frequency domains) is introduced as a robust means to identify, model and simulate the Hurst–Kolmogorov (HK) dynamics, ranging from small (fractal) to large scales exhibiting the clustering behavior (else known as the Hurst phenomenon or long-range dependence). The HK clustering is an attribute of a multidimensional (1D, 2D, etc.) spatio-temporal stationary stochastic process with an arbitrary marginal distribution function, and a fractal behavior on small spatio-temporal scales of the dependence structure and a power-type on large scales, yielding a high probability of low- or high-magnitude events to group together in space and time. This behavior is preferably analyzed through the second-order statistics, and in the scale domain, by the stochastic metric of the climacogram, i.e., the variance of the averaged spatio-temporal process vs. spatio-temporal scale.

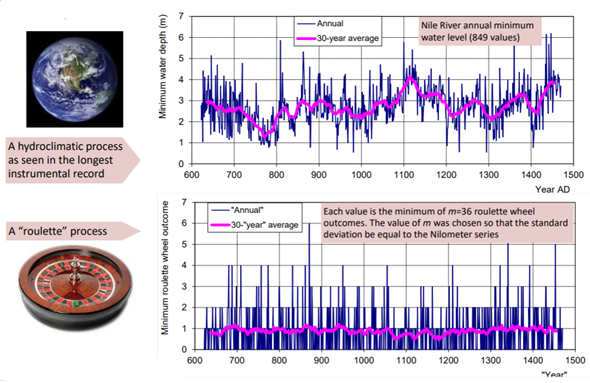
stochastic method clustering evolution of clustering

Clustering in nature has been first identified by H.E. Hurst (1951) [1] (Figure 1a) while studying the long-term behaviour in a variety of scales of the discharge timeseries of the Nile River in the framework of developing engineering projects in its basin.

Particularly, H.E. Hurst discovered a tendency of high-discharge years to cluster into high-flow periods, and low-discharge years to cluster into low-flow periods. This behaviour, also known as the Hurst phenomenon or Joseph effect (Mandelbrot, 1977) [2], has been verified in a variety of hydrological [3], hydrometeorological and turbulent processes [4] [5] and in other geophysical and alternate fields such as finance, medicine [6], and art [7] [8] [9].

All these processes are characterized by long-term persistence (LTP), which leads to high unpredictability in long-term scales due to the clustering of events as compared to the purely random process, i.e. white-noise (e.g. as in a fair dice game [10]), or other short-range dependence models (e.g., Markov).

(a) (b)

Figure 1: (a) In 1951 H.E. Hurst discovered the clustering behaviour in nature (b) A.N.Kolmogorov proposed a decade before a stochastic process that describes this clustering behaviour. 

The mathematical description of the Hurst phenomenon is attributed to A.N. Kolmogorov (Figure 1b) who developed it while studying turbulence in 1940 [11] (Figure 1b), inspiring D. Koutsoyiannis [12] to name the general behaviour of the Hurst phenomenon as Hurst-Kolmogorov (HK) dynamics (Figure 2), to give credit to both contributing scientists and to distinguish it from the Gaussian LTP processes (e.g., fractional-Gaussian-noise [13]), and to incorporate alternate short-range dependence (e.g., Markov-behaviour [14]). 


Figure 2. Hurst-Kolmogorov (HK) dynamics and the perpetual change of Earth’s climate

The HK dynamics has been recently also linked to the entropy maximization principle, and thus, to robust physical justification [15]. The stochastic simulation of the HK dynamics has been a mathematical challenge since it requires the explicit preservation of high-order moments  in a vast range of scales, affecting both the intermittent behaviour in small scales [16]  and the dependence in extremes [17] as well as the trends often appearing in geophysical timeseries [18].

References

  1. Hurst, H.E.. Long term storage capacities of reservoirs; Trans. Am. Soc. Civil Eng: USA, 1951; pp. 116.
  2. Mandelbrot B. B. . Fractals: Form, Chance and Dimension; W. H. Freeman and Co.: US, 1977; pp. 365.
  3. Koutsoyiannis D.; The Hurst phenomenon and fractional Gaussian noise made easy. Hydrological Sciences Journal 2002, 47, 573-595, 10.1080/02626660209492961.
  4. Koutsoyiannis D.; Dimitriadis P.; Lombardo F.; Stevens S., From fractals to stochastics: Seeking theoretical consistency in analysis of geophysical data, Advances in Nonlinear Geosciences, edited by A.A. Tsonis, 237–278, doi:10.1007/978-3-319-58895-7_14, Springer, 2018.
  5. Dimitriadis, P. Hurst-Kolmogorov Dynamics in Hydrometeorological Processes and in the Microscale of Turbulence. Ph.D. Thesis, Department of Water Resources and Environmental Engineering—National Technical University of Athens, Athens, Greece, 2017.
  6. Mandelbrot B.; Van Ness J.W.; Fractional Brownian motions, fractional noises and applications. J. Soc. Ind. Appl. Math.l 1968, 10, 422-437.
  7. Sargentis G.-F.; Dimitriadis P.; Koutsoyiannis D.; Aesthetical Issues of Leonardo Da Vinci’s and Pablo Picasso’s Paintings with Stochastic Evaluation. Heritage 2020, 3, 283-305, 10.3390/heritage3020017.
  8. Sargentis G.-F.; Ioannidis R.; Meletopoulos I.T.; Dimitriadis P.; Koutsoyiannis; D. ; Aesthetical issues with stochastic evaluation, European Geosciences Union General Assembly 2020, Geophysical Research Abstracts, Vol. 22, Online, EGU2020- 19832, https://doi.org/10.5194/egusphere-egu2020-19832, European Geosciences Union, 2020.
  9. Sargentis G.-F.; Dimitriadis P.; Iliopoulou T.; Ioannidis R.; Koutsoyiannis D.; Stochastic investigation of the Hurst-Kolmogorov behaviour in arts, European Geosciences Union General Assembly 2018, Geophysical Research Abstracts, Vol. 20, Vienna, EGU2018-17082, European Geosciences Union, 2018.
  10. Dimitriadis P.; Koutsoyiannis D.; Tzouka K.; Predictability in dice motion: how does it differ from hydrometeorological processes?. Hydrological Sciences Journal 2016, 61, 1611-1622, 10.1080/02626667.2015.1034128.
  11. Kolmogorov, A.N.. Wiener spirals and some other interesting curves in a Hilbert space. Selected Works of A. N. Kolmogorov ; Kluwer, Dordrecht, Eds.; Mathematics and Mechanics, Tikhomirov, V. M. : The Netherlands, 1991; pp. 303-307.
  12. Koutsoyiannis D.; A random walk on water. Hydrology and Earth System Sciences 2010, 14, 585–601.
  13. Mandelbrot, B. B.; A Fast Fractional Gaussian Noise Generator. Water Resour. Res. 1971, 7(3), 543–553..
  14. Gneiting T.; Schlather M.; Stochastic Models That Separate Fractal Dimension and the Hurst Effect. SIAM Review 2004, 46, 269-282, 10.1137/s0036144501394387.
  15. Koutsoyiannis D.; Hurst–Kolmogorov dynamics as a result of extremal entropy production. Physica A: Statistical Mechanics and its Applications 2011, 390, 1424-1432, 10.1016/j.physa.2010.12.035.
  16. Dimitriadis P.; Koutsoyiannis D.; Stochastic synthesis approximating any process dependence and distribution. Stochastic Environmental Research and Risk Assessment 2018, 32, 1493-1515, 10.1007/s00477-018-1540-2.
  17. Iliopoulou T.; Koutsoyiannis D.; Revealing hidden persistence in maximum rainfall records. Hydrological Sciences Journal 2019, 64, 1673-1689, 10.1080/02626667.2019.1657578.
  18. Iliopoulou T.; Koutsoyiannis D.; Projecting the future of rainfall extremes: Better classic than trendy. Journal of Hydrology 2020, 588, 125005, 10.1016/j.jhydrol.2020.125005.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Statistics & Probability
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
G.-Fivos Sargentis
,
Theano Iliopoulou
,
Stavroula Sigourou
,
Panayiotis Dimitriadis
,
Demetris Koutsoyiannis
View Times: 1.1K
Online Date: 14 Oct 2020
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback