| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Vladimir Fomin | + 14556 word(s) | 14556 | 2020-07-22 08:25:07 | | | |
| 2 | Vladimir Fomin | -302 word(s) | 14254 | 2020-10-30 04:16:49 | | | | |
| 3 | Vladimir Fomin | -11809 word(s) | 2445 | 2021-01-11 13:45:32 | | |
Video Upload Options
- Spin-dependent phenomena in semiconductors are analyzed starting from a theory of the dynamic nuclear polarization via numerous insightful findings in the realm of characterization and control through the nuclear spin polarization in nanoparticles and their aggregates into microparticles as potential contrast agents for magnetic resonance imaging (MRI) applications.
- Electron spin-dependent process of the photosensitized generation of singlet oxygen in porous silicon (Si) for photodynamic therapy application and design of Si-based nanoparticles with electron spin centers for MRI contrasting for cancer theranostics are discussed.
1. Description
Nanoparticles (NPs) of semiconductors exhibit interesting electronic, optical and magnetic properties, which depend on a preferential orientation of electron and nuclear spins. Spatial confinement of charge carriers (electron and holes) in a NP results in an increase of the spin-lattice relaxation time. Thus, going from itinerant to immobile, fully-localized electrons, while inducing the hyperfine dephasing, can be also beneficial in quenching the spin-lattice relaxation. The dynamic nuclear polarization in semiconductors opens fascinating prospects for creation of new efficient contrast agents (CAs) for the magnetic resonance imaging (MRI), which is a powerful diagnostic tool in biomedicine, e.g., silicon (Si) NPs and microparticles (MPs) are explored in hyperpolarized 29Si MRI. Furthermore, Si NPs with a large number of electron paramagnetic centers exhibit properties of a CA in conventional proton (1H) MRI. Si-based NPs and MPs prepared from porous Si can act as sensitizers of the singlet oxygen generation owing to the spin-dependent energy transfer from the excitons to oxygen molecules adsorbed on the surface of NPs and MPs. These properties are promising for biomedical applications in the therapy and diagnosis, including their combination called theranostics, of cancer [1].
2. History
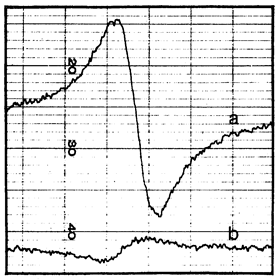
The most common ways to polarize nuclear spins are optical pumping, chemical reaction or direct transfer of spin angular momentum from electron to nuclear spins called dynamic nuclear polarization (DNP) [2]. At cryogenic temperatures, while typically less than 1% of nuclear spins are polarized under static magnetic fields of around 10 T, the polarization of electron spins is typically larger than 90% [3]. Thus, DNP is caused by aligning the nuclear spins induced by the electron spins alignment. The first demonstration of an enhanced DNP was obtained by optical pumping in very pure n-type crystalline silicon (c-Si) [4] (see Figure 1).Optically induced DNP in semiconductors can be achieved in two ways, i.e. (i) saturation of the electronic spin magnetization with unpolarized light and (ii) production of highly spin-polarized conduction electrons by irradiation with circularly polarized light [4].
Figure 1. (a) Signal proportional to the derivative of the 29Si nuclear magnetization obtained in a dc magnetic field 1 G after 21 h of irradiation with circularly polarized light at 77 K. (b) The same signal for 6 kG at 300 K. (Reprinted figure with permission from Ref. [4] © (1968) by the American Physical Society).
The optically induced DNP is covered by the Overhauser effect [5] and it occurs on 29Si nuclei in c-Si: the dynamic enhancement of the nuclear polarization, obtained by maintaining the electronic polarization off its equilibrium value. Two kinds of processes take place in the sample: (i) the relaxation drives the magnetization to its equilibrium value with a typical spin relaxation time T1 (ii) the alternating magnetic field induces more transitions with the photoinduced transition time \( \tau \) from the state with a higher population and therefore leads to a decrease of the magnetization. In the steady state, the both processes are counterbalancing each other, what gives rise to the electron spin magnetization. In the general case, a saturation parameter is
\( s={T_1\over{T_1+\tau}}.\hspace{5cm}(1) \)
The value of s changes from 0 when there is no alternating magnetic field to 1 when it is strong. The amplitude of the microwave field that is necessary to saturate the resonance is inversely proportional to the geometric mean value of the spin relaxation time T1 and the transverse relaxation time T2 [5]. The DNP is most efficiently performed via the hyperfine interaction with electrons localized on a donor impurity [6].Similar to the electron spins, the difference in numbers of nuclei (with spin I=1/2, like 29Si) possessing spins up and down is selected as a measure of the nuclear spin magnetization. The relative steady-state nuclear polarization expressed in terms of the gyromagnetic ratios of the electron \( \gamma_e \) and nucleus \( \gamma_n \) as follows (see Section IX.I C in [7]):
| \( {<{I_z}>\over {I_0}} =1- s{{|\gamma_e}|\over{\gamma_n}}, \hspace{5cm} (2) \) |
where s is given by Eq. (1) and \( |{\gamma_e|}/\gamma_n \)= 3310 for 29Si [1]. The nuclear magnetization produced by optical pumping in a field of 1G corresponded to the equilibrium polarization in a field of 28 kG at 77 K. Thus, the enhanced nuclear polarization as high as 2.8 \( \times \) 104 due to the optical pumping with circularly polarized light was experimentally found in c-Si with natural isotopic content (4.67% of 29Si) [4].The dynamic polarization of 29Si nuclei in c-Si:P was investigated [8,9]. During illumination the 29Si magnetization becomes gradually established, following the exponential law with a time constant Tl [9]. The main focus of solid-state optical pumping therefore shifted to direct bandgap semiconductors as GaxAl1-xAs [10], InP [11] and CdS [12]. By increasing the depth of the donor levels, a very significant nuclear polarization was achieved because of the increase of the electron spin relaxation time. The spin-to-charge conversion for hot photoexcited electrons was experimentally detected in Ge [13]. The successful optical generation of a net spin polarization of electrons was demonstrated in the strained Ge1-xSnx alloy, which manifested hybridization of the spin properties of Ge with the peculiar electronic states offered by \( \alpha \)-Sn [14].
3. Current Status
A combination of the DNP and photoexcitation is known as microwave-induced optical nuclear polarization [15]. The polarization from the electron triplet states is transferred via microwaves to the nuclear spins. The hyperpolarization of electron spins can be prepared at low magnetic fields, since it is generated due to selectivity in crossing from excited singlet states to hyperpolarized triplet states. Because the triplet states have a longer relaxation time as compared to the singlet state, the hyperpolarized nuclear spins can be generated by DNP at room temperature. Feasibility of the nuclear hyperpolarization at low magnetic fields and room temperature provides an advantage to microwave-induced optical nuclear polarization as compared to the DNP. The unpaired electron spins do not perturb the NMR signals because the decay time of the triplet state to the diamagnetic state is shorter than the relaxation time of the longitudinal nuclear magnetization [15]. The synthesis, materials characterization and DNP of amorphous and crystalline Si NPs for use as hyperpolarized CAs for MRI were reported [16].
In solid-state spin-1/2 materials, such as Si, the primary source of nuclear spin-lattice relaxation is the interaction with unbonded electrons or holes, which occur in the form of free charge carriers or paramagnetic centers either at lattice defect sites or at the surface. In pure materials, the nuclear spin polarization is protected from these sources of relaxation, resulting in bulk relaxation times of many hours [7,17,18]. A transition to the nanoscale results in the spin relaxation that depends on the particle size, purity and density of defects [17]. The colloidal synthesis of Si NPs with average diameters of 10 nm at room temperature provided spin relaxation times that exceed 600 s. This resulted in NPs with significantly longer size-adjusted 29Si relaxation times T1 than commercially available Si particles [17] and diamond NPs of similar sizes [19].
4. Applications
Si NPs are the smallest ones characterized for hyperpolarization applications. Due to their size and long T1 times, they are perspective as in vivo imaging agents, which are suitable for intracellular investigations and for crossing the blood-brain barrier [17]. High 29Si spin polarization was achieved using DNP in microcrystalline Si powder [20]. Unpaired electrons in the powder are related to Si DBs in the amorphous region of microcrystalline grains. Nuclei 29Si in the amorphous region become polarized by forced electron-nuclear spin flips induced by off-resonant microwave radiation. Nuclei in the crystalline region are polarized by spin diffusion across crystalline boundaries. Hyperpolarized Si MPs have long T1 and hence can be used as tracers for MRI [20]. In vivo imaging of hyperpolarized 29Si in Si MPs and NPs by MRI is perspective for gastrointestinal, intravascular and tumor perfusion imaging at sub-pm concentrations [21].
The hyperpolarized 29Si MRI was shown to provide a high contrast with little or no background signal [17]. To date, in vivo applications of pre-hyperpolarized materials have been limited by relatively short nuclear spin relaxation times. The nuclear spin relaxation time for a variety of Si NPs was found to be extremely long, ranging from many minutes to hours at room temperature, allowing hyperpolarized NPs to be transported, administered and imaged on practical time scales [17]. Additionally, Si NPs can be surface functionalized using techniques common to other biologically targeted NP systems. These results suggest that Si NPs can be used as a targetable, hyperpolarized MRI agent with a large range of potential applications. Micrometer-sized Si MPs, which reveal the longest known relaxation times up to 136 min at room temperature at 2.9 T [22], are difficult to administer and impossible to handle in vivo. A new window for MRI applications was opened in Ref. [23], where it was demonstrated that 29Si NPs in powder synthesized from a gas phase using a laser-assisted technique with average particle size of 55 ± 12 nm can be hyperpolarized with superior properties: maximal polarization about 12.6% with a long T1 relaxation time of 42.3 ± 0.1 min at room temperature. Such a long depolarization time enabled the observation of 29Si NMR signal more than 5 h after transfer to the imaging system. A further significant increase in the polarization level is proposed by lowering the temperature (to < 2 K) and at higher magnetic fields.
The same optical pumping of the electronic system of semiconductor NPs, which is used for the nuclear spin orientation, can also initiate the electron-spin-dependent processes, which are sensitive to the molecular environment of NPs. It was found that Si nanocrystals (nc-Si) with sizes of 1–10 nm in photoluminescent (PL) porous Si (por-Si) can act as a photosensitizer of the generation of singlet oxygen (1)O2 (the superscript indicates the electron spin degeneracy) [24]. The effect is covered by the spin-dependent energy transfer from excitons in nc-Si to O2 molecules adsorbed on the nc-Si surface [25,26]. The photosensitized generation of (1)O2 was confirmed by experiments in vitro, which showed that the number of living cells with added por-Si MPs decreased strongly after photoexcitation [27]. The photosensitized (1)O2, which is a strong oxidizer, resulted in an inhibition of the cancer cell proliferation due to the apoptosis mechanism [28].
Mesoporous Si NPs were used to enhance the photosensitized generation of (1)O2 with quantum yield of 17% in aqueous medium [29]. Such NPs with concentration of 0.1 g/L were added to cancer cell cultures followed with white light illumination that resulted in 45% decrease of cell number [29]. A stronger effect for the cancer cell suppression was observed for microporous Si NPs, which could enter cancer cells by endocytosis mechanism, resulting in ~70% cell death [30]. NPs prepared from meso- and microporous Si were shown to be efficient both as photosensitizers of (1)O2 generation and PL labels in bioimaging in vitro. The photosensitization ability of Si NPs is easily combined with their PL properties for bioimaging that makes them effective for cancer theranostics [31,32].
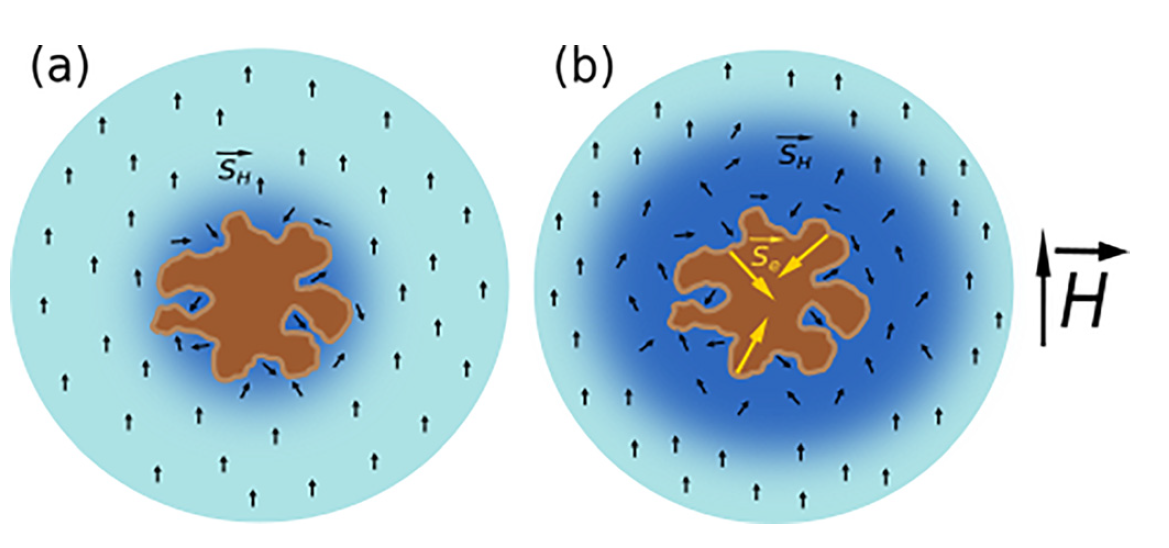
Si NPs with a high number of paramagnetic electron spin centers can act as CAs for the conventional biomedical MRI at the proton (1H) frequency [33]. The MRI contrast properties of Si NPs are explained by considering the magnetic dipole-dipole interaction between electron spins on the Si NPs’ surfaces and those of protons in surrounding water molecules [34] as shown in Figure 2. In general, a solid NP can increase the proton spin relaxation (Figure 2a), Si NPs (especially those prepared from por-Si) provide additional opportunities to increase the spin center density due to a huge specific surface area of small NPs. While the surface of electrochemically prepared por-Si is well passivated by hydrogen atoms [35], the number of paramagnetic centers as Si dangling bonds (DBs) can be significantly increased by physical and chemical treatments [34]. This strategy was used to improve the CA properties of por-Si NPs for MRI applications (Figure 2b).
Figure 2. (a) Schematic view of the shortening of proton spin relaxation in water (blue regions) nearby a NP (brown spot) without unpaired electron spins; (b) the same scheme for the NP with numerous unpaired electron spins centers on the NP surface. Black and yellow arrows correspond to the proton and electron spins, respectively. (Reprinted from Reference [34] by permission from John Wiley and Sons © 2018).
The MRI contrast properties of Si NPs can be characterized by their specific relaxation efficiency, called relaxivity, which is defined as the change in relaxation rate divided to the concentration of NPs. The transverse proton relaxivity can be expressed in the following way [34]:
\( r_2={{R_2}\over{C_{NP}}}, \hspace{5cm} (3) \)
where R2 is the proton relaxation rate governed by Si NPs and CNP is the mass concentration of those NPs. The value r2 ≈ 0.5 L/(g\( \cdot \)s) was determined for microporous Si NPs after thermal annealing in vacuum that resulted in the electron spin density ~1017 g−1 [34]. The transverse relaxivity normalized on the number of Si atoms in NPs is about 0.01 L/(mM\( \cdot \)s) that is still smaller than that of the standard CAs based on Gd3+ ions [36] and for superparamagnetic iron oxide NPs [37].
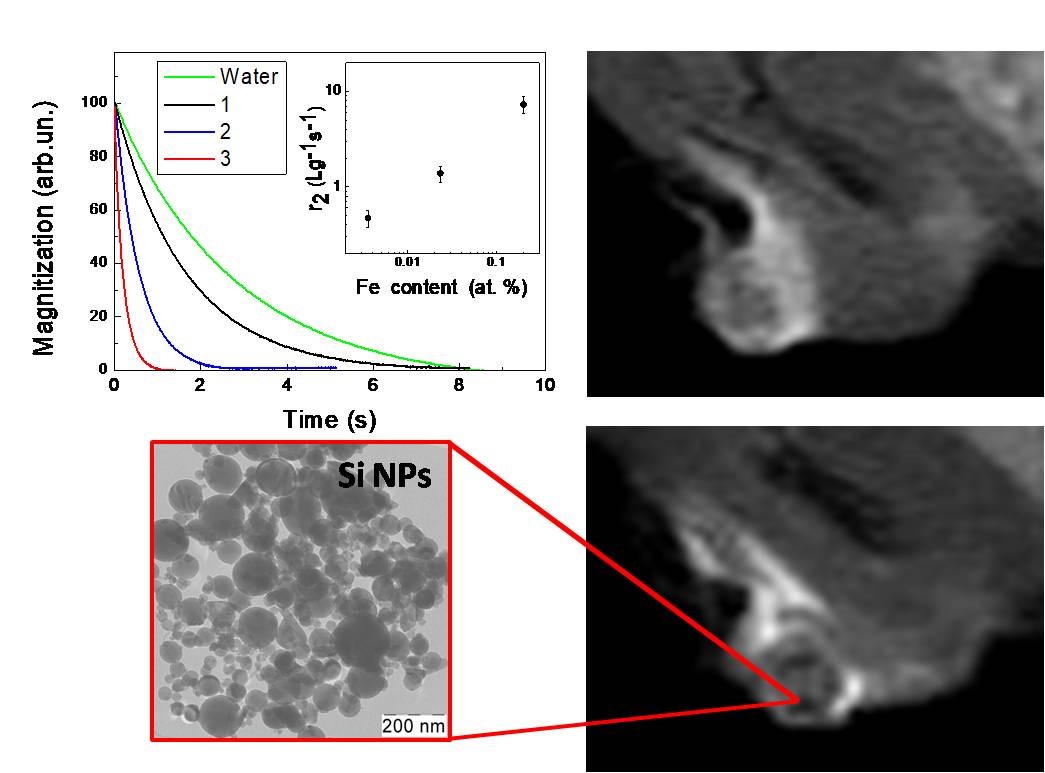
The contrasting property of Si-based NPs for 1H MRI was significantly improved by using incorporation of iron impurities [38]. The total concentration of electron spin centers in Si NPs with iron (0.2 at%) approached 1018 spin/g that resulted in r2 ≈ 7.3 L/(g\( \cdot \)s). The latter value corresponds to the molar relaxivity of 200 L/(mM\( \cdot \)s) [39], which is close to that for CAs based on superparamagnetic iron oxide NPs [37]. The MRI contrasting of cancer tumor with injected Si:Fe NPs was demonstrated in vivo [39] (see Figure 3).
Figure 3. Transients of the proton magnetization (inset shows the transverse relaxivity vs the iron content), typical TEM image of Si NPs with 0.2 at% of iron impurities and MRI images of cancer tumor before (upper image) and after (down image) injection of such NPs. (Reprinted from Reference [39] by permission from John Wiley and Sons © 2019).
Aqueous suspensions of Si NPs were also found to be a sensitizer of radiofrequency (RF) electromagnetic hyperthermia for mild cancer therapy [32,38]. Moreover, Si:Fe NPs were successfully used to suppress the cancer tumor growth in vivo and it was correlated with increasing the lifetime of mice [39]. The obtained results demonstrate perspectives for applications of Si-based NPs in both the MRI diagnostics and therapy of cancer. Additional promises in biomedical applications of Si NPs are related with multinuclear MRI diagnostics by using both the standard 1H mode and hyperpolarized 29Si nuclei as well as other biomedical nuclei, for example, 13C and 19F [4].
[1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16][17][18][19][20][21][22][23][24][25][26][27][28][29][30][31][32][33][34][35][36][37][38][39][40]
References
- Fomin, V.M.; Timoshenko, V.Yu. Spin-Dependent Phenomena in Semiconductor Micro- and Nanoparticles—From Fundamentals to Applications, Appl. Sci. 2020, 10, 4992, doi:10.3390/app10144992
- Abragam, A.; Goldman, M. Principles of dynamic nuclear polarisation. Rep. Prog. Phys. 1978, 41, 395–467, doi:10.1088/0034-4885/41/3/002.
- Kwiatkowski, G.; Polyhach, Y.; Jähnig, F.; Shiroka, T.; Starsich, F.H.L.; Ernst, M.; Kozerke, S. Exploiting Endogenous Surface Defects for Dynamic Nuclear Polarization of Silicon Micro- and Nanoparticles. J. Phys. Chem. C 2018, 122, 25668–25680, doi:10.1021/acs.jpcc.8b08926.
- Lampel, G. Nuclear Dynamic Polarization by Optical Electronic Saturation and Optical Pumping in Semiconductors. Phys. Rev. Lett. 1968, 20, 491–493, doi:10.1103/physrevlett.20.491.
- Overhauser, A.W. Polarization of Nuclei in Metals. Phys. Rev. 1953, 92, 411–415, doi:10.1103/physrev.92.411.
- Dyakonov, M.I.; Perel, V.I. Theory of Optical Spin Orientation of Electrons and Nuclei in Semiconductors. In: Optical Orientation; Meier, F., Zakharchenya, B.P., Eds.; Elsevier: Amsterdam, The Netherlands, 1984, doi:10.1016/B978-0-444-86741-4.50007-X.
- Abragam, A. The Principles of Nuclear Magnetism; Oxford University Press: Oxford, UK, 1961.
- Bagraev, N.T.; Vlasenko, L.S.; Zhitnikov, R.A. Optical orientation of 29Si nuclei in n-type silicon and its dependence on the pumping light intensity. Sov. Phys. JETP 1976, 44, 500–504
- Bagraev, N.T.; Vlasenko, L.S.; Zhitnikov, R.A. Influence of the depth of location of donor levels on the degree of optical orientation of 29Si nuclei in silicon. Sov. Phys. JETP Lett. 1976, 24, 366368.
- Ekimov, A.I.; Safarov, V.I. Optical detection of dynamic polarization of nuclei in semiconductors. JETP Lett. 1972, 15, 179181
- Tycko, R. Optical pumping in indium phosphide: 31P NMR measurements and potential for signal enhancement in biological solid state NMR. Solid State Nucl. Magn. Reson. 1998, 11, 1–9.
- Pietraß, T.; Tomaselli, M. Optically pumped NMR in CdS single crystals. Phys. Rev. B 1999, 59, 1986–1989, doi:10.1103/physrevb.59.1986.
- Zucchetti, C.; Bottegoni, F.; Isella, G.; Finazzi, M.; Rortais, F.; Vergnaud, C.; Widiez, J.; Jamet, M.; Ciccacci, F. Spin-to-charge conversion for hot photoexcited electrons in germanium. Phys. Rev. B 2018, 97, 17, doi:10.1103/PhysRevB.97.125203.
- De Cesari, S.; Balocchi, A.; Vitiello, E.; Jahandar, P.; Grilli, E.; Amand, T.; Marie, X.; Myronov, M.; Pezzoli, F. Spin-coherent dynamics and carrier lifetime in strained Ge1−xSnx semiconductors on silicon. Phys. Rev. B 2019, 99, 1–9, doi:10.1103/physrevb.99.035202.
- Fujiwara, T.; Ramamoorthy, A. How far can the sensitivity of NMR be increased? Annu. Rep. NMR Spectrosc. 2006, 58, 155–175, doi:10-1016/S0066-4013(05)58003-7.
- Atkins, T.M.; Cassidy, M.C.; Lee, M.; Ganguly, S.; Marcus, C.M.; Kauzlarich, S.M. Synthesis of Long T1 Silicon Nanoparticles for Hyperpolarized 29Si Magnetic Resonance Imaging. ACS Nano 2013, 7, 1609–1617, doi:10.1021/nn305462y.
- Aptekar, J.W.; Cassidy, M.C.; Johnson, A.C.; Barton, R.A.; Lee, M.; Ogier, A.C.; Vo, C.; Anahtar, M.N.; Ren, Y.; Bhatia, S.N.; et al. Silicon Nanoparticles as Hyperpolarized Magnetic Resonance Imaging Agents. ACS Nano 2009, 3, 4003–4008, doi:10.1021/nn900996p.
- Shulman, R.G.; Wyluda, B.J. Nuclear magnetic resonance of 29Si in n- and p-type silicon. Phys. Rev. 1956, 103, 11271129, doi:10.1103/PhysRev.103.1127.
- Casabianca, L.B.; Shames, A.I.; Panich, A.M.; Shenderova, O.; Frydman, L. Factors Affecting DNP NMR in Polycrystalline Diamond Samples. J. Phys. Chem. C 2011, 115, 19041–19048, doi:10.1021/jp206167j.
- Dementyev, A.E.; Cory, D.G.; Ramanathan, C. Dynamic Nuclear Polarization in Silicon Microparticles. Phys. Rev. Lett. 2008, 100, 1–4, doi:10.1103/physrevlett.100.127601.
- Cassidy, M.C.; Chan, H.R.; Ross, B.D.; Bhattacharya, P.K.; Marcus, C.M. In vivo magnetic resonance imaging of hyperpolarized silicon particles. Nat. Nanotechnol. 2013, 8, 363–368, doi:10.1038/nnano.2013.65.
- Lee, M.; Cassidy, M.C.; Ramanathan, C.; Marcus, C.M. Decay of nuclear hyperpolarization in silicon microparticles. Phys. Rev. B 2011, 84, 035304, doi:10.1103/physrevb.84.035304.
- Kwiatkowski, G.; Jähnig, F.; Steinhauser, J.; Wespi, P.; Ernst, M.; Kozerke, S. Nanometer size silicon particles for hyperpolarized MRI. Sci. Rep. 2017, 7, 1–6; https://www.nature.com/articles/s41598-017-08709-0.
- Kovalev, D.; Gross, E.; Künzner, N.; Koch, F.; Timoshenko, V.Y.; Fujii, M. Resonant Electronic Energy Transfer from Excitons Confined in Silicon Nanocrystals to Oxygen Molecules. Phys. Rev. Lett. 2002, 89, 1–4, doi:10.1103/physrevlett.89.137401.
- Gross, E.; Kovalev, D.; Künzner, N.; Diener, J.; Koch, F.; Timoshenko, V.Y.; Fujii, M. Spectrally resolved electronic energy transfer from silicon nanocrystals to molecular oxygen mediated by direct electron exchange. Phys. Rev. B 2003, 68, 1–11, doi:10.1103/physrevb.68.115405.
- Fujii, M.; Kovalev, D.; Goller, B.D.; Minobe, S.; Hayashi, S.; Timoshenko, V.Y. Time-resolved photoluminescence studies of the energy transfer from excitons confined in Si nanocrystals to oxygen molecules. Phys. Rev. B 2005, 72, 165321, doi:10.1103/physrevb.72.165321.
- Timoshenko, V.Y.; Kudryavtsev, A.A.; Osminkina, L.; Vorontsov, A.S.; Ryabchikov, Y.V.; Belogorokhov, I.A.; Kovalev, D.; Kashkarov, P.K. Silicon nanocrystals as photosensitizers of active oxygen for biomedical applications. JETP Lett. 2006, 83, 423–426, doi:10.1134/s0021364006090128.
- Timoshenko, V.Y.; Osminkina, L.; Vorontsov, A.S.; Ryabchikov, Y.V.; Gongalsky, M.; Efimova, A.I.; Konstantinova, E.A.; Bazylenko, T.Y.; Kashkarov, P.K.; Kudriavtsev, A.A. Silicon nanocrystals as efficient photosensitizer of singlet oxygen for biomedical applications. SPIE Proc. 2007, 6606, 66061E, doi:10.1117/12.729523.
- Xiao, L.; Gu, L.; Howell, S.B.; Sailor, M. Porous Silicon Nanoparticle Photosensitizers for Singlet Oxygen and Their Phototoxicity against Cancer Cells. ACS Nano 2011, 5, 3651–3659, doi:10.1021/nn1035262.
- Osminkina, L.; Tamarov, K.P.; Sviridov, A.P.; Galkin, R.A.; Gongalsky, M.B.; Solovyev, V.V.; Kudryavtsev, A.A.; Timoshenko, V.Y. Photoluminescent biocompatible silicon nanoparticles for cancer theranostic applications. J. Biophotonics 2012, 5, 529–535, doi:10.1002/jbio.201100112.
- Timoshenko, V.Y. Porous Silicon in Photodynamic and Photothermal Therapy. In: Handbook of Porous Silicon, 2nd ed.; Canham, L., Ed.; Springer: BerlinHeidelberg, Germany, 2018; pp. 1461–1469, doi:10.1007/978-3-319-71381-6_93.
- Kabashin, A.V.; Timoshenko, V.Y. What theranostic applications could ultrapure laser-synthesized Si nanoparticles have in cancer? Nanomedicine 2016, 11, 2247–2250, doi:10.2217/nnm-2016-0228.
- Gongalsky, M.B.; Kargina, Y.V.; Osminkina, L.; Perepukhov, A.M.; Gulyaev, M.; Vasiliev, A.; Pirogov, Y.A.; Maximychev, A.V.; Timoshenko, V.Y. Porous silicon nanoparticles as biocompatible contrast agents for magnetic resonance imaging. Appl. Phys. Lett. 2015, 107, 233702, doi:10.1063/1.4937731.
- Kargina, Y.V.; Gongalsky, M.B.; Perepukhov, A.M.; Gippius, A.A.; Minnekhanov, A.A.; Zvereva, E.A.; Maximychev, A.V.; Timoshenko, V.Y. Investigation of proton spin relaxation in water with dispersed silicon nanoparticles for potential magnetic resonance imaging applications. J. Appl. Phys. 2018, 123, 1–6, doi:10.1063/1.5006846.
- Cullis, A.G.; Canham, L.T.; Calcott, P.D.J. The structural and luminescence properties of porous silicon. J. Appl. Phys. 1997, 82, 909–965, doi:10.1063/1.366536.
- Rohrer, M.; Bauer, H.; Mintorovitch, J.; Requardt, M.; Weinmann, H.-J. Comparison of Magnetic Properties of MRI Contrast Media Solutions at Different Magnetic Field Strengths. Investig. Radiol. 2005, 40, 715–724, doi:10.1097/01.rli.0000184756.66360.d3.
- Araki, K.; Uchiyama, M.K.; Toma, S.; Rodrigues, S.F.; Shimada, A.L.B.; Loiola, R.A.; Rodríguez, H.J.C.; Oliveira, P.V.; Luz, M.S.; Rabbani, S.R.; et al. Ultrasmall cationic superparamagnetic iron oxide nanoparticles as nontoxic and efficient MRI contrast agent and magnetic-targeting tool. Int. J. Nanomed. 2015, 10, 4731–4746, doi:10.2147/IJN.S83150.
- Kargina, Y.V.; Perepukhov, A.M.; Kharin, A.Y.; Zvereva, E.A.; Koshelev, A.V.; Zinovyev, S.V.; Maximychev, A.V.; Alykova, A.F.; Sharonova, N.V.; Zubov, V.P.; et al. Silicon Nanoparticles Prepared by Plasma‐Assisted Ablative Synthesis: Physical Properties and Potential Biomedical Applications. Phys. Status Solidi A 2019, 216, 1800897, doi:10.1002/pssa.201800897.
- Kargina, Y.V.; Zinovyev, S.V.; Perepukhov, A.M.; Suslova, E.V.; Ischenko, A.A.; Timoshenko, V.Y. Silicon nanoparticles with iron impurities for multifunctional applications. Funct. Mater. Lett. 2020, 13, 2040007, doi:10.1142/s179360472040007x.
- Bouchoucha, M.; Van Heeswijk, R.B.; Gossuin, Y.; Kleitz, F.; Fortin, M.-A. Fluorinated Mesoporous Silica Nanoparticles for Binuclear Probes in 1H and 19F Magnetic Resonance Imaging. Langmuir 2017, 33, 10531–10542, doi:10.1021/acs.langmuir.7b01792.