2.1. Optically Induced DNP in Semiconductors

2.1.1. First Demonstration of DNP

Vividly developing applications of spintronics (see for example Reference [13]), in particular, in biomedicine, require a secure control over the spin polarization in semiconductors. The first demonstration of an enhanced DNP was obtained by optical pumping in very pure n-type Si (with the concentration 5 × 10¹⁶ m⁻³ of phosphorus atoms, which was much lower than the concentration 2 × 10¹⁷ m⁻³ of conduction electrons) [14,15] (see Figure 2). Optically induced DNP in semiconductors can be achieved in two ways—(i) saturation of the electronic spin magnetization with an unpolarized light, which generates an equal number of spins up and spins down and (ii) production of highly polarized conduction electrons by irradiation with circularly polarized light, which generates spin-polarized electrons and holes [14].

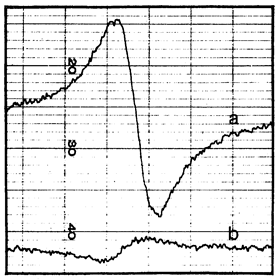
Figure 2. (a) Signal proportional to the derivative of the ²⁹Si nuclear magnetization obtained in a dc magnetic field 1 G after 21 h of irradiation with circularly polarized light at 77 K. (b) Signal proportional to the derivative of the equilibrium Si nuclear magnetization in a dc magnetic field 6 kG at 300 K. (Reprinted figure with permission from Reference [14] © (1968) by the American Physical Society).

2.1.2. Principle of DNP

The process of DNP occurred by off-center irradiation of the resonance of paramagnetic centers, which were present at low concentration in the sample [9]. Its importance was shown to far exceed that of the other methods of nuclear polarization.

Spin-temperature theory was initially suggested for the investigation of nuclear magnetism in solids and then evolved into an important tool for the explanation of NMR in solids. A first extension of the theory to extremely low temperatures, for systems of nuclear spins at normal concentrations, led to the understanding of nuclear magnetic cooperative ordering. A second extension of the spin-temperature theory, to dilute electronic spin systems both at high and low temperatures, led to the unveiling of several physical mechanisms contributing to dynamic polarization.

The basic hypothesis in the spin-temperature theory is that the evolution of an isolated system of a big number of interacting spins leads to an equilibrium state characterized by a temperature. In fact, spin systems are never completely isolated. Therefore, the concept of spin temperature is meaningful only if the rate of achievement of internal equilibrium in the spin system is much faster than the spin-lattice relaxation rate.

2.1.3. Fundamentals of the Optically Induced DNP

Photoexcitation of electrons in a semiconductor under irradiation with unpolarized light (the case of circular polarization is considered in Appendix) produces an equal number of electrons with spin up and down. After that, the Overhauser effect [16] occurs on ²⁹Si nuclei in the bulk crystalline silicon (c-Si): the dynamic enhancement of the nuclear polarization, obtained by maintaining the electronic polarization off its equilibrium value. The essence of the Overhauser effect consists in the following.

A metal sample is placed in a constant magnetic field, which creates the polarization of electron spins. The electron energy in this field has two eigenvalues, corresponding to spin-up and spin-down states. The electron spins tend to be aligned with the field. The resulting difference D in spatial density of electrons with spins down and up is selected as a measure of the electron spin magnetization In thermal equilibrium under relatively weak magnetic fields, the value of this difference D₀ is directly proportional to the constant magnetic field ([17], pp. 421 and 435). The metal sample is subjected, furthermore, to a perpendicular alternating magnetic field (in particular, of the microwave radiation)  whose frequency satisfies the electron spin resonance (electron paramagnetic resonance) criterion ([17], p. 488). Such a radiation leads to the transitions between electronic states.

As a consequence, two kinds of processes take place in the sample—first, relaxation drives the magnetization to its equilibrium value with a typical spin relaxation time T₁; second, the alternating field induces more transitions with the photoinduced relaxation time τ from the state with a higher population and therefore leads to a decrease of the magnetization. In a stationary state, the both processes are counterbalancing each other, what gives rise to the steady-state magnetization. At strong alternating magnetic fields, the resonance is saturated, that is D=0. In the general case, a saturation parameter s=T₁/τ /(1+ T₁/τ) changes from 0 when there is no alternating magnetic field to 1 when it is strong. The amplitude of the microwave field that is necessary to saturate the resonance is inversely proportional to the geometric mean value of the spin relaxation time T₁ and the transverse relaxation time T₂, which is determined by the integrated width of the resonance line w [16].

Using NMR of ²⁹Si, the spin-lattice relaxation time was determined as a function of mobile carrier concentration (sample resistivity) [18]. T₁ was established to be inversely proportional to the carrier concentration for the high-conductivity samples, approaching an asymptotic value in the purer samples.

Analysis of relaxation times in semiconductors [19] led to the conclusion that the relaxation of ²⁹Si in the exhaustion and intrinsic ranges should be accomplished by the hyperfine interaction between the nuclear spins and the spins of the mobile electrons or holes. However, there was a significant uncertainty in the density of mobile carriers. No differences were observed because of the crystal growth conditions (some crystals were pulled from quartz crucibles, some zone-refined without crucibles). The asymptotic values of p- and n-type Si were substantially different.

The low-field relaxation of nuclear hyperpolarization was studied in undoped and highly doped Si MPs at room temperature following removal from high field [20]. For nominally undoped particles (Figure 3a), two relaxation time scales were identified for ambient fields above 0.2 mT. The slower, T_1,s, was roughly independent of ambient field; the faster, T_1,f , decreased with increasing ambient field. A model assumed the nuclear spin relaxation to occur at the Si MPs surface via a 2-electron mechanism in a good agreement with the experimental data in what concerns the magnetic-field independence of the slow relaxation time. For boron-doped particles (Figure 3b), a single relaxation time scale was observed. This suggested that for doped particles, mobile carriers and bulk ionized acceptor sites, rather than paramagnetic surface states, were the dominant relaxation mechanisms. Relaxation times for the undoped particles were not affected by tumbling in a liquid solution [20].

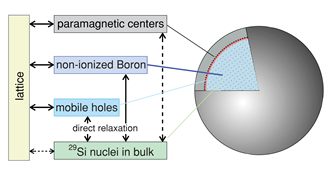
Figure 3. (a) Model showing the spin reservoirs and relaxation pathways in undoped silicon particles. Nuclei in the core region of the particle relax by transferring their magnetization to the nuclei in the shell region, nearer to the surface, by spin diffusion. The nuclei near the surface can relax quickly due to strong dipolar coupling to paramagnetic defects at the Si/SiO₂ interface. (b) Rate model showing dominant nuclear relaxation pathways of direct relaxation on mobile holes and short diffusion to non-ionized B (i.e., bound holes) throughout the bulk of the boron-doped particle. Long-distance spin diffusion to surface impurities is relatively slow and direct coupling of the nuclei to the lattice is weak. (Reprinted figures with permission from Reference [20] © (2011) by the American Physical Society).

Nuclear polarization is most efficiently performed via the hyperfine interaction with electrons localized in a donor impurity [21]. The key issue is the hyperfine dipolar interaction between the magnetic moments of electron and nucleus The action of the hyperfine interaction is twofold. (i) Every nucleus is subjected, next to the applied magnetic fields, to a magnetic field of polarized electron spins fluctuating due to the aforementioned processes of spin relaxation. The magnitude of this field is proportional to the average (over the fluctuations) electron spin. The nuclear spin relaxation time due to the hyperfine interaction is T₁’. (ii) Every electron is subjected, next to the applied magnetic fields, to the total magnetic field of all polarized nuclei. These two magnetic fields are comparable because electrons at low energy levels interact with a large number of nuclei. The electron spin relaxation time due to the hyperfine interaction is T₁’. As a consequence, there occurs a feedback, which leads to a steady-state polarization of both electron and nuclear spins. There has been a renewed interest in the hole-nuclei hyperfine interaction in semiconductor quantum dots [22]. The main effect arises from the coupling of the nuclear spin with the hole wavefunction within the same unit cell, that is, the short-range part of the dipole-dipole interaction [12]. The potential effect of large inhomogeneous elastic strain in nanostructures (like quantum dots) on the microscopic Bloch hole wave function is considered as a possible route to engineer the hyperfine coupling.

Similar to the electron spins, the difference Δ in numbers of nuclei (with spin I=1/2, like ²⁹Si) possessing spins up and down is selected as a measure of the nuclear spin magnetization. The thermal equilibrium value of the difference Δ₀ is directly proportional to the constant magnetic field [23]. The corresponding steady-state magnetization on nuclei with spin I=1/2 is I₀=Δ₀/2  In terms of the gyromagnetic ratios of the electron γ_e and the nucleus γ_n, the relative magnetization of nuclei takes on the form (Reference [12]):

⟨I_z⟩/I₀ = 1-s|γ_e|/γ_n.                  (1)   

In analogue to the Overhauser effect [16], the steady-state nuclear polarization is enhanced as if the nuclear gyromagnetic ratio γ_n would be increased by s|γ_e|. Near the saturation, when s is close to 1, this increase theoretically may be as large as |γ_e|/γ_n=3310 in ²⁹Si [17, p. 489]. The experimentally observed nuclear spin polarization enhancement extrapolated to an infinite time of continuous irradiation by an unpolarized light constitutes ⟨I_z⟩/I₀ = −5.6 [14]. According to Equation (1), this implies the saturation parameter s~2 × 10⁻³.

The nuclear magnetization (Figure 2a) produced by optical pumping in a field of 1G (extrapolated to infinite time of continuous irradiation) corresponded to the equilibrium polarization in a field of 28 kG at 77 K and constituted ⟨I_z⟩=3.7 × 10⁻⁶. Thus, the enhanced nuclear polarization as high as 2.8 × 10⁴ due to the optical pumping was experimentally demonstrated [14].

Polarized electronic spins are produced by optical pumping with circularly polarized light. Both spin directions are created in the conduction band. However, the unequal proportions G₊ and G₋ of transitions to spin-up and spin-down states lead to a net electronic polarization much larger than its equilibrium value (see Equation (VI.7) in Reference [15]):

⟨I_z⟩=I₀ +T₁/τ /(1+ T₁/τ)[(G₊ - G₋)/2-S0],               (2)

where the first term in the parentheses is due to the optical pumping, while the second one is the nuclear magnetization saturation term [14]. As long as under optical pumping the latter is much smaller than the former and I₀<< ⟨I_z⟩ and taking into account that T₁/τ<< 1 (it is typically 2 × 10⁻³), the steady-state nuclear spin polarization turns to

⟨I_z⟩≈T₁/τ (G₊ - G₋)/2.                (3)

It depends on matrix-element ratios describing electronic transitions between valence and conduction bands, as well as on electronic recombination and relaxation rates. Therefore, for this mechanism the value of the obtained nuclear spin polarization is of key importance rather than the enhancement of the relative nuclear spin polarization. A direct measurement of  performed in Reference [14] demonstrated that only 0.4% was achieved of the magnetization that could be expected if only one kind of electronic spin had been created. This was due to the matrix elements between the valence and conduction bands in Si, which is an indirect bandgap material.

A theory proposed in Reference [24] established the first link between the degrees of spin polarization of electrons and the circular polarization for each of the dominant phonon-assisted optical transitions, which was crucial for the subsequent development of applications. A method of hyperpolarizing Si MPs and NPs demonstrated an increase of the ²⁹Si MR signal by up to 3–5 orders of magnitude via the enhanced nuclear spin alignment, while retaining this improved signal for tens of minutes [25,26].

2.1.4. Optical Spin Orientation in Various Semiconductors

Since the first successful experiment [14], discussed in the previous Subsection, there has been a steady interest in theoretical and experimental investigation of optical spin orientation in various semiconductors. Among them, c-Si is an advantageous material for spintronics because of its long spin relaxation time and dominating technology. The dynamic polarization of ²⁹Si nuclei in phosphorus-doped (N_d=1.5 × 10¹³ cm⁻³) n-type c-Si induced by optical pumping was investigated in Reference [27]. During illumination of c-Si, the magnetization of ²⁹Si nuclei becomes gradually established, following an exponential law with a time constant equal to the spin-lattice relaxation time T1 of ²⁹Si nuclei. Limiting relative polarization of the ²⁹Si nuclei obeyed the following equation [27]:

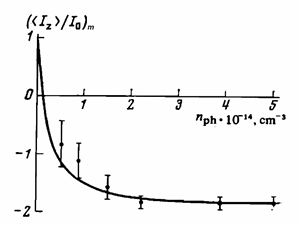
⟨I_z⟩/I₀ = 1-s|γ_e|/γ_n n_ph /(n₀ + n_ph) ,           (4)

with the concentrations n_ph of photoexcited and n₀ of thermal electrons, correspondingly. Without light, the nuclear magnetization equaled its equilibrium value. When the concentrations of photoexcited electrons was much higher than that of thermal electrons, the saturation value was described by Equation (13) in agreement with experiment (see Figure 4). The limiting degree of nuclear polarization was determined by the spin polarization of both the photoexcited and thermal electrons in the conduction band. The presence of rare earth impurities (Gd) in combination with shallow impurities (P) resulted in increased optical pumping efficiency, because the rare earth impurities increased the ionization energy of the shallow impurities [28]. More recently, the dynamic-nuclear-polarization capabilities of optical pumping at 4 K and a magnetic field of 7 T were investigated with a ²⁹Si-enriched sample. Using NMR spectroscopy, the ²⁹Si polarization as high as up to 0.25% was demonstrated [29]. The investigations of above-bandgap excitations look promising for further enhancement of ²⁹Si polarization in the sample area close to the exposed surface.

Figure 4. Limiting relative polarization of the ²⁹Si nuclei as a function of the concentration n_ph of photoexcited electrons in n-type Si irradiated with unpolarized light. (Reproduced from Reference [27], with the permission of American Institute of Physics).

However, c-Si is an indirect bandgap semiconductor and it was soon clear that higher nuclear polarizations could be generated in direct bandgap materials. The main focus of solid-state optical pumping therefore shifted to direct bandgap semiconductors soon after the pioneering experiment of Lampel [14], which was analyzed in Section 2.1.3. The stationary spin orientation of photoelectrons excited by circularly polarized light in Ga_xAl_1-xAs, as detected by the degree of the circular polarization of photoluminescence, was determined by the value of the nuclear magnetization [30]. The optical method manifested a very high sensitivity (signal-to-noise ratio of the order of 100:1 when the total number of photoelectrons constituted 10⁹) and could be applied to samples at microscale. Optically-pumped, directly-detected NMR experiments on the bulk crystalline InP (c-InP) were performed [31] by using irradiation of a sample of undoped c-InP wafer from a diode laser to enhance the spin polarization of ³¹P nuclei near the sample surface. The spin polarization was found to depend on the light polarization. The spin polarization magnitude and polarization transfer efficiency of the from the semiconductor substrate to the overlayer (Figure 5) were high enough to permit solid state NMR measurements on sub-nanomole quantities of molecules in the overlayer [31]. The optically induced dynamic nuclear polarization in CdS was observed by radio-frequency detection of the ¹¹³Cd nuclear magnetic resonance signal for T < 2 K. At this temperature, the optically induced spin polarization was negative when compared to the thermal polarization, irrespective of the helicity of the pumping light [32]. By increasing the depth of the donor levels, a very significant nuclear polarization was achieved because of the increase of the electron spin relaxation time.

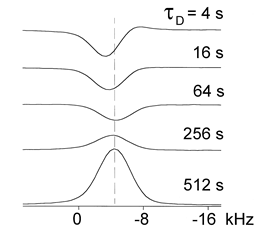
Figure 5. Dependence of the ³¹P optically-pumped nuclear magnetic resonance (NMR) lineshape on the period during which the shutter is closed τ_D, with the period during which the shutter is open τ_L=120 s. At short τ_D, the lineshape is dominated by signal from the optically-pumped surface layer. At long τ_D, the lineshape is dominated by signal from the bulk of the InP sample which increases due to spin-lattice relaxation. (Reprinted from Reference [31], © (1998), with permission from Elsevier).

The mechanism of optical pumping can be considerably more complicated and less well understood. Both contact hyperfine and dipolar hyperfine interactions can contribute appreciably to cross-relaxation. The spin polarization of the photoexcited electrons may depend on the pumping wavelength and the magnetic field. The precise nature of the photoexcitation that dominate optical pumping, which are expected to be localized excitations, may be unknown. The roles of photogenerated holes, doped carriers and radiationless transitions to a metastable excited state after the initial absorption of a photon are to be clarified [31].

A theory of the optical spin orientation under indirect optical injection of carriers and spins in bulk Si, proposed in Reference [33], predicted the maximum degree of spin polarization as high as 25% at low temperatures and 15% at high temperatures. These values of the degree of the spin polarization implied the term “optically induced spin hyperpolarization” for the phenomenon, which is the main objective of the present review. The theory of Reference [33] was immediately applied to analyze two-photon indirect optical injection of carriers and spins and two-color coherent control in bulk Si [34]. Measurements of the electron spin lifetime and optical orientation efficiency were also carried out in Ge by using electrical detection of radio frequency modulated spin polarization [35]. The optical spin injection and spin lifetime in Ge heterostructures were experimentally investigated in Reference [36]. Th valley-dependent spin polarization and long-lived electron spins were detected in Ge [37]. Spin-dependent optical properties were investigated as a function of strain in Si and Ge [38]. Theory of spin-dependent intravalley and intervalley electron-phonon scatterings was developed for Ge [39]. The optical spin-selection rules in bulk Si and Ge/Si quantum dots were experimentally unveiled in Reference [40]. Two optical routes of cold carrier injection in Si were revealed by time-resolved excitation spectroscopy [41]. The optical generation of pure spin currents was detected at the indirect gap of bulk Si [42]. Hot phonon and carrier relaxation in Si single crystalline wafers with the (100) crystallographic orientation were determined by transient extreme ultraviolet spectroscopy [43].

The spin-to-charge conversion for hot photoexcited electrons was experimentally detected in Ge [44]. The successful optical generation of a net spin polarization of electrons in the strained Ge_1-xSn_x alloy, which manifests hybridization of the spin properties of Ge with the peculiar electronic states offered by α-Sn, was demonstrated by recording PL spectra, the optical spin orientation being robust over a wide temperature range up to room temperature [45]. The spin coherence time of photoexcited spin-polarized electrons was found to decay from 12 ns to 6 ns when increasing the magnetic field from 0 to 53.5 mT owing to g-factor fluctuations as long as spin dephasing was triggered by the cooling process, during which optically generated electrons underwent momentum relaxation under random effective magnetic fields due to local changes in the alloy composition and strain [45].

2.2. Microwave-Irradiation-Induced Nuclear Polarization

2.2.1. Microwave-Induced Optical Nuclear Polarization

The hyperpolarization of ²⁹Si nuclear spins is usually generated by solid-state DNP at low temperatures and high magnetic fields to spin-polarize an electron to near unity. This spin polarization is then transferred to nearby nuclear spins through microwave-mediated dipolar interactions, similar to those occurring in the liquid phase with ¹³C [46].

A combination of the DNP and the photoexcitation of the electron-pair spin to the triplet state is known as microwave-induced optical nuclear polarization [47]. The polarization from the electron triplet states is transferred via microwaves to the nuclear spins. The hyperpolarization of electron spins can be prepared at low magnetic fields, since it is generated due to selectivity in crossing from excited singlet states to hyperpolarized triplet states. Because the triplet states have a longer relaxation time as compared to the singlet state, the hyperpolarized nuclear spins can be generated by DNP at room temperature. Feasibility of the nuclear hyperpolarization at low magnetic field and room temperature provides an advantage to microwave-induced optical nuclear polarization as compared to the DNP. The unpaired electron spins do not perturb the NMR signals because the decay time of the triplet state to the diamagnetic state is shorter than the relaxation time of the longitudinal nuclear magnetization [47]. While the microwave-induced optical nuclear polarization was demonstrated for organics as fluorene C₁₃H₁₀ crystals [48], it seems to be a possible mechanism for inorganic semiconductor systems as NP/MPs with nc-Si, where triplet excitonic state are rather probable (see Section 3).

2.2.2. ²⁹Si Surface-Enhanced NMR Spectroscopy

Fast characterization of the distribution of surface bonding modes and interactions in a series of functionalized materials was achieved via surface-enhanced nuclear magnetic resonance spectroscopy using DNP [49]. Surface-enhanced ²⁹Si DNP NMR spectra were obtained by using incipient wetness impregnation of the sample with a solution containing a polarizing radical (TOTAPOL). The bonding topology of functional groups was identified in materials obtained via a sol-gel process and in materials prepared by post-grafting reactions [49]. The remarkable gain in time provided by surface-enhanced NMR Spectroscopy using DNP, which is of the order of 400, allows for a facile acquisition of 2D correlation spectra for characterization of the distribution of the surface bonding modes/interactions in functionalized materials [49]. 

2.2.3. Long T₁ Nanoparticles for Hyperpolarized ²⁹Si MRI 

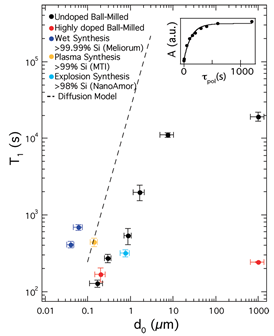
 The synthesis, materials characterization and DNP of amorphous and crystalline Si NPs for use as hyperpolarized MRI agents were represented in Reference [26]. The Si NPs of ~10 nm size were synthesized by a metathesis reaction and surface functionalized with a variety of passivating ligands. Because of the long size-adjusted nuclear spin-lattice relaxation time T₁ > 600 s (Figure 6), Si NPs can be hyperpolarized by low-temperature DNP and retain the polarization for > 300 s [26].

Figure 6. Nuclear spin relaxation (T₁) times at 2.9 T and 300 K as a function of particle diameter d for Si NPs. Previously reported T₁ measurements of other Si particles are shown as a reference. Simulations of the nuclear relaxation based on a spin diffusion model are also shown. Vertical error bars are from exponential fits to relaxation data; horizontal error bars are from size distributions. (Reprinted with permission from Reference [26]. © 2013 American Chemical Society).

In solid-state spin-1/2 materials, such as Si, the primary source of nuclear spin-lattice relaxation is the interaction with unbonded electrons or holes, which occur in the form of free charge carriers or paramagnetic centers either at lattice defect sites or at the surface. In pure materials, the nuclear spin polarization is to a significant extent protected from sources of relaxation, resulting in bulk relaxation times of many hours [11,12,18]. A transition to the nanoscale resulted in spin relaxation times that depend on the particle size, purity and density of defects [11]. The colloidal synthesis of Si NPs with average diameters of∼10 nm at room temperature provided spin relaxation times that exceed 600 s. This resulted in fabrication of NPs that revealed significantly longer size-adjusted ²⁹Si nuclear spin relaxation times T₁ than commercially available Si particles [11] and diamond NPs of similar sizes [50].These Si NPs are the smallest characterized for hyperpolarization applications. Due to their size and long T₁ times, they are perspective as in vivo imaging agents, which are suitable for intracellular investigations and for crossing the blood-brain barrier [26].

2.2.4. DNP in Si Microparticles

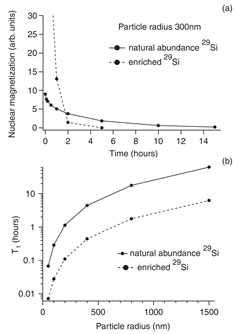
High ²⁹Si spin polarization was achieved using DNP in microcrystalline Si powder [51]. Unpaired electrons in the powder are related to Si DBs in the amorphous region of microcrystalline grains. Nuclei in the amorphous region become polarized by forced electron-nuclear spin flips induced by off-resonant microwave radiation. Nuclei in the crystalline region are polarized by spin diffusion across crystalline boundaries. Hyperpolarized Si MPs have long T₁ (Figure 7) and hence can be used as tracers for MRI [51].

Figure 7. (a) Simulations of the ²⁹Si magnetization decay due to spin diffusion and instantaneous relaxation at the surface for particles with 300 nm radius. (b) Simulated T₁ relaxation time as a function of the particle size. Solid line is for the naturally abundant ²⁹Si and dashed line is for the ²⁹Si enriched sample. (Reprinted figure with permission from Reference [51] © (2008) by the American Physical Society).

2.2.5. In Vivo MRI of Hyperpolarized Si Particles

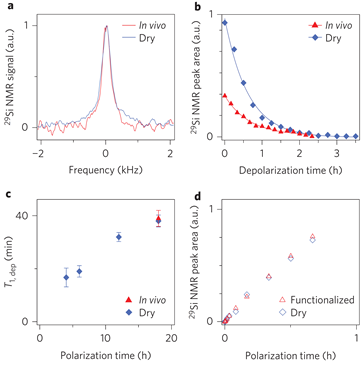
Natural physical properties of Si (Figure 8) provide surface electronic states for DNP, long depolarization times, insensitivity to the in vivo environment and surfaces favorable for functionalization. In vivo imaging of hyperpolarized ²⁹Si in Si MPs and NPs by MRI is perspective for applications to gastrointestinal, intravascular and tumor perfusion imaging at sub-picometer concentrations [25].

Figure 8. ²⁹Si nuclear spin dynamics in silicon particles. (a) ²⁹Si NMR spectrum of hyperpolarized particles recorded in vivo and dry at 30 min delay. (b) Decay of ²⁹Si nuclear polarization in hyperpolarized Si particles recorded in vivo and dry. Both plots show a characteristic decay of T_1,dep≈40 min for hyperpolarization time τ_pol=8 h using variable flip angle acquisition. The difference in absolute signal is mainly due to the reduced concentration within the active region of the coil. (c) Characteristic ²⁹Si depolarization time constants (T_1,dep) in dry particle phantoms recorded in the imager for polarization times of 4, 6, 12 and 18 h. (d) Time evolution of the ²⁹Si nuclear polarization under DNP conditions for particles with and without surface functionalization with polyethylene glycol. The signal is normalized by sample weight. (Reprinted by permission from Springer Nature [25], © (2013)).

2.2.6. Si Nanoparticles for Hyperpolarized MRI

MRI of hyperpolarized nuclei was shown to provide a very high image contrast with little or no background signal [11]. To date, in vivo applications of pre-hyperpolarized materials have been limited by relatively short nuclear spin relaxation times. Si NPs were proposed as a new type of hyperpolarized MRI agent. Nuclear spin relaxation times for a variety of Si NPs were found to be extremely long, ranging from many minutes to hours at room temperature (Figure 9), allowing hyperpolarized NPs to be transported, administered and imaged on practical time scales [11]. Additionally, Si NPs can be surface functionalized using techniques common to other biologically targeted NP systems. These results suggest that Si NPs can be used as a targetable, hyperpolarized MRI agent with a large range of potential applications.

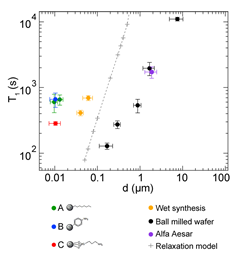
Figure 9. NMR Properties of Si particles. Nuclear spin relaxation (T₁) times at 2.9 T as a function of particle diameter d₀ for various Si particles. Vertical error bars are from exponential fits to relaxation data; horizontal error bars represent the dispersion of size distributions. Inset: Fourier-transform NMR peak amplitude, A, as a function of polarization time for the ball-milled high-resistivity particles with d₀ = 0.17 mm. T₁ values were measured using a saturation recovery spin echo pulse sequence. (Reprinted with permission from Reference [11]. © (2009) American Chemical Society).

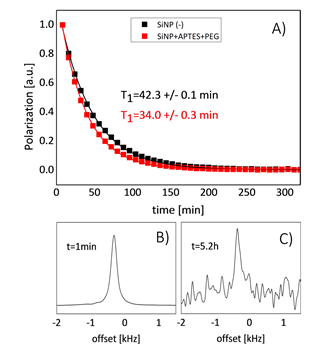
Micrometer-sized Si MPs, which reveal the longest known relaxation times up to 136 min at room temperature at 2.9 T [20], are difficult to administer and impossible to handle in-vivo. A new window for MRI applications was opened in Reference [52], where it was demonstrated that ²⁹Si NPs in powder synthesized from a gas phase using a laser-assisted technique, with average particle size of 55 ± 12 nm can be hyperpolarized with superior properties, that is, maximal polarization about 12.6% with a long T₁ relaxation time of 42.3 ± 0.1 min at room temperature (Figure 10A). Such a long depolarization time enabled the observation of ²⁹Si NMR signal more than 5 h after transfer to the imaging system (Figures 10B,C). The presence of PEG polymer on the surface of the nanoparticles resulted in shortening of T₁ relaxation times at room temperature from 42.3 ± 0.1 min to 34.0 ± 0.3 min (Figure 10A), while no change in the polarization level was observed. A further significant increase in the polarization level is proposed by lowering the temperature (to < 2 K) in the course of the DNP process, using a dedicated long-run helium bath or helium-free cryostat, boosting the obtainable ²⁹Si polarization. Conducting the DNP process at higher magnetic fields is also expected to increase final nuclear polarization. The limited availability of high-power microwave sources operating in the frequency range above 100 GHz is presently the major difficulty.

Figure 10. (A) Comparison of T₁ relaxation between pure (black) and PEG functionalized (red) silicon NPs. The Fourier-transformed free induction decay signal acquired at t = 1 min (B) and t = 5.2 h (C) at room temperature using a 9.4 T imaging system. (Reprinted from Reference [52], © (2017), Springer Nature. This article is licensed under a Creative Commons Attribution 4.0 International License http://creativecommons.org/licenses/by/4.0/).

Optimal physical and chemical conditions, including surface-defect concentration adjusted to the particle size, are necessary to achieve a high level of DNP enhancement [10]. Real-time MRI-guided catheter tracking using hyperpolarized ²⁹Si particles (polycrystalline/amorphous; average mean diameter ~2 μm) was demonstrated [53]. The increased signal of the ²⁹Si particles is generated via low-temperature, solid-state DNP and the particles retain their enhanced signal for ≥40 min, thus allowing imaging experiments over extended time durations in phantoms and live mice. The measured hyperpolarized relaxation rate of the ²⁹Si particles was ~25 min at 7 T and room temperature.

A variety of particle sizes (20 nm to 2 μm) were found to have hyperpolarized relaxation times ranging from ∼10 to 50 min [54,55]. The addition of different functional groups to the Si particle surface was shown to provide no effect on the hyperpolarization buildup or decay rates and allowed for in vivo imaging over long time-scales. Hyperpolarized Si particles were demonstrated to be available agents for targeted, noninvasive and nonradioactive molecular imaging of various cancer systems [54] and a powerful theragnostic deep tissue imaging platform [55]. In vivo studies examined diverse particle administration routes in mice, including intraperitoneal injection, rectal enema and oral gavage [54]. Incorporating exogenous radicals (e.g., 2,2,6,6-tetramethyl-1-piperidinyloxy (TEMPO)) into Si NPs suspensions is proposed order to improve the characteristics of hyperpolarization of ²⁹Si nuclear spins to levels sufficient for in vivo MRI [56]. Without any added radical, T₁ values ranged from ∼23 min (30 nm particles) to ∼36 min (200 nm particles). This size-dependence of T₁ is largely expected given the spin-diffusion model [20] for the relaxation of core nuclei to the surface. At optimal TEMPO concentrations (30−60 mM), the shortened T₁ values of the Si particles were overshadowed by the significant increase in the ²⁹Si MR signal [56].

3. Electron Spin-Dependent Processes in Si Nanocrystal Systems

3.1. Excitons in Si Nanocrystals

 The same optical pumping of the electronic system of semiconductor MPs and NPs, which is used for the nuclear spin orientation (see Section 2), can also initiate the electron-spin-dependent processes, which are highly sensitive to both the size of semiconductor particles and their molecular environment. Besides the quantum confinement effect, which results in an increase of the forbidden gap and optical transition energies in nc-Si of different dimensionality and characteristic sizes from 1 to 10 nm [57,58], the Coulomb interaction between photoexcited electrons and holes in nc-Si promotes the existence of excitons with relatively large binding energies up to 100–200 meV [57] that ensures stability for the excitons at room temperature. Furthermore, the exchange interaction in an exciton can remove the spin degeneracy for the exciton states [59]. It results in two possible spin configurations for the exciton states in nc-Si, i.e. the singlet state and triplet one. The latter is lowered in energy in respect to the singlet state because of the electron-hole exchange interaction as it was experimentally demonstrated for small nc-Si in electrochemically prepared porous Si (por-Si) [60]. Despite a small singlet-triplet splitting being in the range from 1 to 30 meV the main part of excitons in nc-Si can be in the threefold degenerated triplet state even at room temperature [61,62].

3.2. Photosensitized Generation of Singlet Oxygen

Since there is a similarity between the electronic structure of excitons in nc-Si and that of many organic molecules as dyes, the energy transfer through spin-split states of the latter can be also probable for the former. A bright example of the spin-dependent energy transfer from photoexcited dye molecules to molecular oxygen in its triplet state followed with its transformation into the singlet oxygen, that is, ⁽¹⁾O₂ where (1) in the superscript indicates the electron spin degeneracy, which is used in the photodynamic therapy (PDT) [63]. It was found that nc-Si in por-Si layer and powder can act as a photosensitizer of the ⁽¹⁾O₂ generation [64]. The observed photosensitization was explained by the spin-dependent energy transfer from excitons in nc-Si with sizes of 1–10 nm to O₂ molecules adsorbed on the nc-Si surface [65]. According to the quantum mechanics the relaxation of ⁽¹⁾O₂ back to the ground (triplet) state is “spin-forbidden” and thus a ⁽¹⁾O₂ molecule is characterized by rather long lifetime [66], which is favorable for transferring the excitation energy to oxidation reactions. The latter can be used for the detection and application of ⁽¹⁾O₂ [67]. The latter is known to be an electronically excited state of molecular oxygen [67] and it influences oxidative biochemical processes in living systems [68]. The ¹O₂-mediated reaction, which is employed in PDT of cancer, consists of a drug, that is, photosensitizer of ⁽¹⁾O₂, administration followed with resonant photoexcitation of the drug [63].

The efficient ¹O₂ photosensitization by nc-Si is promoted by its huge specific surface area up to 10³ m²/g [62] and by long radiative lifetimes (10⁻⁵-10⁻³ sec) of the triplet excitons confined in nc-Si [61]. The ⁽¹⁾O₂ generation by photoexcited nc-Si can be quantified by measuring the quenching of the exciton photoluminescence (PL) of nc-Si [64] and by analyzing the radiative decay of ⁽¹⁾O₂ molecules at 0.98 eV (1270 nm) as it is usually used for molecular sensitizer [68,69]. In fact, the ⁽¹⁾O₂ photosensitization by por-Si was successfully monitored by means of the PL spectroscopy of ⁽¹⁾O₂ emission at 0.98 eV [70]. While the ⁽¹⁾O₂ luminescence indicates a high efficiency of the photosensitization process [71], a strong deactivation (quenching) of ⁽¹⁾O₂ molecules in nc-Si assemblies is revealed from a comparison of the photosensitizing efficiency of the standard molecular sensitizer as porphyrin molecules and nc-Si [72]. It can be explained by considering a process of the nonradiative collisional quenching of ⁽¹⁾O₂ molecules on the nc-Si surfaces in por-Si layer and powder. The ⁽¹⁾O₂ quenching acts as a limiting factor to achieve high concentration of ⁽¹⁾O₂ due to the photosensitized generation in por-Si MPs [73].

A method of the electron paramagnetic resonance (EPR) is well known to detect ⁽¹⁾O₂ in gaseous ambient [67]. The conventional X-band EPR spectroscopy of photoexcited por-Si in O₂ atmosphere allowed us to estimate the ⁽¹⁾O₂ concentration photosensitized by nc-Si to be of the order of 10¹⁹ cm⁻³ under excitation with photon flux about 10²⁰ cm⁻² [74]. Similar results were obtained by means of the Q-band EPR spectroscopy, which demonstrated a conversion of about 30% of O₂ molecules in the singlet state upon excitation of por-Si powder in oxygen atmosphere [75]. The ⁽¹⁾O₂ photosensitization was shown to be also possible for por-Si dispersed in different oxygen-saturated organic and inorganic liquids [70] as well in water [76].

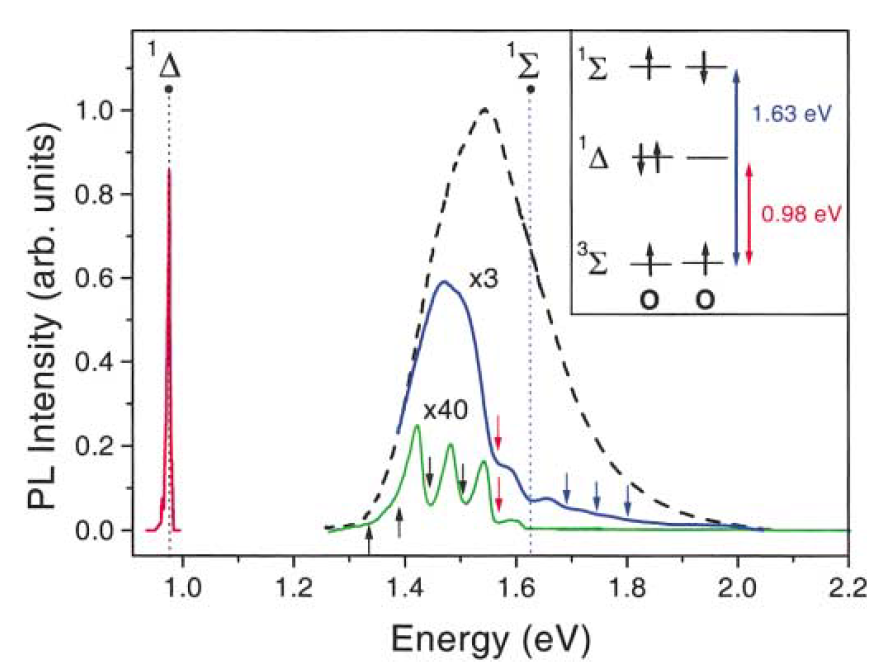
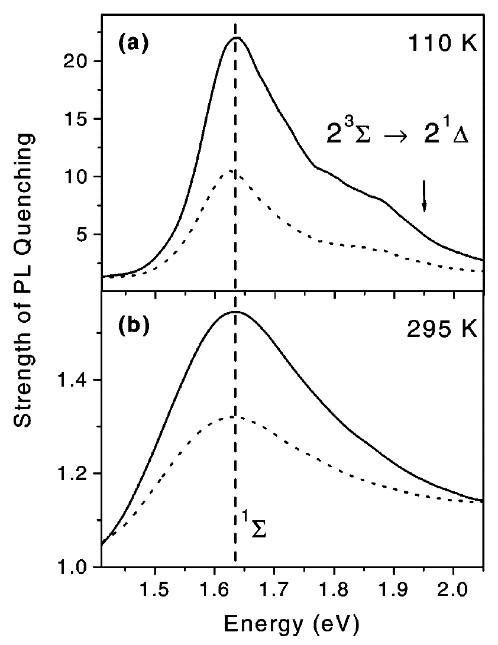
The strong interaction of oxygen molecules with photoexcited nc-Si in por-Si was observed by means of the PL spectroscpy at cryogenic temperatures [64] and it was studied in more details at different excitation conditions and temperatures including room temperature [65]. The investigated samples of por-Si were prepared by standard electrochemical etching of c-Si wafers in a solution of hydrofluoric acid [77]. Some of the free standing por-Si layers were dried in air for several hours and a part of the prepared por-Si was milled to get powder of MPs assembled from nc-Si and their agglomerates [65]. The samples were kept in a vacuum chamber in oil-free vacuum with a residual pressure of about 10^-5 Torr. The exciton PL spectrum of nc-Si measured in vacuum at low temperature is characterized by a broad, featureless emission band located in the visible region (Figure 11). The PL quenching by O₂ adsorption is stronger for the PL photon energies above 1.63 eV. The latter value corresponds to the ³Σ- ¹Σ transition energy in O₂ molecule. At the same time, the PL line at 0.98 eV, which is related to the radiative transition ¹Δ- ³Σ, appeared after oxygen adsorption in por-Si (inset in Figure 11). These spectroscopic data manifest the ⁽¹⁾O₂ photosensitization by the energy transfer from excitons in nc-Si [64,65].

Figure 11. PL spectra of por-Si in vacuum (dashed line) and those with adsorbed oxygen molecules (solid lines). Transition energies from the excited states (¹Δ, ¹Σ) of ⁽¹⁾O₂ to the ground state are indicated by dashed vertical lines. Inset shows the spin configuration and spectroscopic labeling of the oxygen states. Red line is related to the ¹Δ → ³Σ transition in O₂. Temperatures T = 5-50 K, excitation at 2.41 eV. (From Reference [64]).

Detailed description of the energy-transfer mechanism responsible for the photosensitized generation of ¹O₂ can be obtained from the spectral dependence of the PL quenching strength, which can be defined as follows [65]:

Q = I_PL^vac / I_PL^ox ,             (5)

where I_PL^vac and I_PL^ox are the exciton PL intensities of nc-Si in vacuum and in oxygen ambient, respectively.

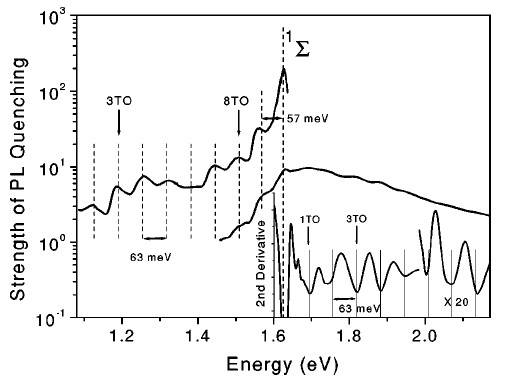
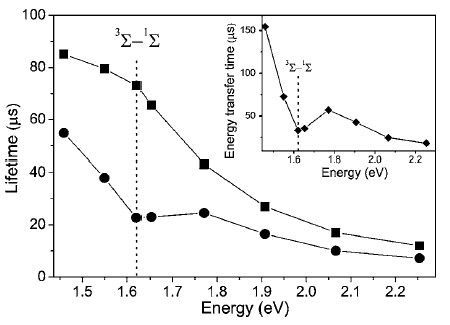
The spectra of Q(hν_PL) and its second derivative are shown in Figure 12. Besides the strongest quenching at 1.63 eV there is an additional maximum at hν_PL of about 57 meV below the ¹Σ state energy and numerous maxima separated by energy of about 63 meV. These maxima correspond to the energy transfer from nc-Si with band gaps, which do not satisfy to the resonance with the excitation energies of ⁽¹⁾O₂. A local maximum separated by 57 meV from the main maximum at 1.63 eV is an evidence of the indirect radiative transition in nc-Si, where the participation of the momentum conserving TO phonon with energy of 57 meV is required [61]. The excess of the exciton energy with respect to the energies of the ¹Δ and ¹Σ states is compensated by emission of the TO phonons with energy of 63 meV [65].

Figure 12. Spectral dependence of the PL quenching strength of por-Si with adsorbed O₂ molecules at T = 5 K. Inset shows the second derivative of the PL quenching strength. For convenient presentation, the data are partially scaled by the indicated multiplication factor. Vertical dotted lines are guide for the eye. (From Reference [65]).

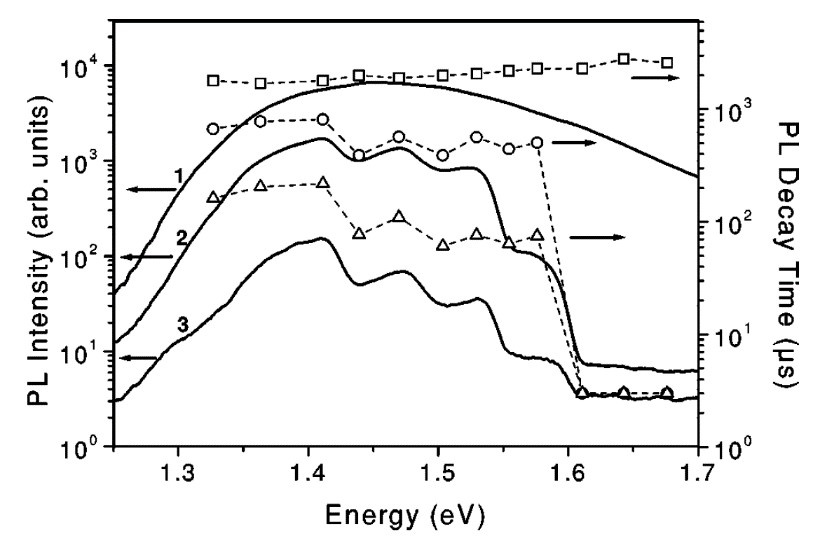
The dynamics of the energy transfer is deduced from the PL transients of por-Si in the presence of adsorbed O₂ molecules [65]. The PL spectra of por-Si at different quenching level by the energy transfer to O₂ at low temperatures and the corresponding PL decay times τ_PL are shown in Figure 23. In vacuum τ_PL is approximately equal to the radiative lifetime of excitons τ_ex of the order of 10⁻³ s and it does not depend on the photon energy (see Figure 13). The PL quenching by O₂ adsorption is accompanied by a significant decrease of the PL decay time because the adsorbed O₂ molecules on the nc-Si surface represent a channel for the nonradiative recombination of the excitons. The spectral dependence of τ_PL follows the quenching strength spectrum. The shortest τ_PL is observed at the PL photon energies, which correspond the strongest PL quenching. Increasing the concentration of adsorbed O₂ molecules results in a stronger PL quenching and further decrease of τ_PL [65]. The time resolved PL studies performed with nanosecond time resolution confirm this spectral behavior of the exciton lifetime [71].

Figure 13. PL spectra (curves) of por-Si and the corresponding spectral dependences of the PL decay time (symbols) for different strength of the quenching induced by O₂ molecule adsorption at T = 5 K: in vacuum (curve 1, squares), intermediate level of the quenching (curve 2, circles) and strong quenching (curve 3, triangles). (From Reference [65]).

The average time of the energy transfer from excitons in nc-Si assembly to O₂ molecules can be calculated from the following expression [65]:

τ_ET^-1= τ_PL^-1 - τ_ex^-1 .               (6)

In the regime of the strongest quenching the values of τ_ET for the ¹Δ and ¹Σ states are 50 to 100 µs and < 3 µs, respectively. A uniform concentration of O₂ molecules for all nc-Si would result in a quenching strength that scales as τ_ex/τ_PL. Obviously this simple relation is not valid. A decay time longer than that expected from the quenching strength is observed because of statistical fluctuations of the number of adsorbed O₂ molecules. While mainly the slowest PL emission from nc-Si with a small number of the adsorbed molecules contributes to the PL decay, the PL intensity spectrum consists of the emission of all nc-Si assembly [65]. 

A mechanism of the direct electron exchange between nc-Si and O₂ molecule is explained the triplet-triplet annihilation of excitons accompanied by spin-flip excitation of an O₂ molecule and followed by the ⁽¹⁾O₂ formation [65]. The energy transfer rate is supposed to be determined by the spatial overlap of the electronic wave functions of the interacting species and depends exponentially on the donor-acceptor distance [78]. The latter parameter controls the energy transfer probability, which is larger for nc-Si in as-prepared por-Si with hydrogen-terminated surface [65]. For oxidized nc-Si the increased spacing between confined excitons and adsorbed O₂ molecules is of the order of double the length of the Si-O bond (~3 Å). This critically affects the efficiency of the electron exchange interaction. Contrary to a strong coupling for hydrogen-terminated nanocrystals, the PL quenching efficiency is reduced by orders of magnitude if a thin oxide barrier is present. The degree of spatial overlap of the electronic wave functions of confined excitons and adsorbed oxygen molecules depends on the size of nc-Si. For smaller nc-Si the overlap becomes better and the probability for energy transfer is higher. On the other hand, for smaller NPs a larger number of emitted phonons is required to conserve the energy, which lowers the probability for energy exchange. The interplay between these two tendencies results in an almost spectrally constant efficiency of the energy transfer. While the involved transitions are spin forbidden in isolated nc-Si and O₂ molecules, they become allowed through exchange interaction [65].

To demonstrate the role of the electron spin statistics for the energy transfer rate, the magnetic-field dependence of the PL quenching efficiency was studied [65]. A magnetic field introduces the quantization axis for electron spins and it results in the lifting of the energy state degeneracy in both O₂ molecules and nc-Si. In general, the number of possible states participating in the electron exchange is reduced and the decreased energy transfer rate results in a weaker PL quenching. At low temperature the magnetic field results in preferential occupation of “spin-down” states for both O₂ and excitons, while to proceed with energy exchange “spin-up states” are required. The PL quenching was observed at temperature of 10 K in magnetic fields up to 10 T as shown in Figure 14. For the spectral region above the ¹Σ state, the high quenching level of the PL intensity prevented the observation of magnetic field effects within the experimental detection sensitivity.

Figure 14. PL spectra of por-Si with adsorbed O₂ molecules at various strength of magnetic field at T = 10 K. The magnetic-field increment is equal to 2 T. Inset: Sketch of the Zeeman splitting of the triplet states of excitons in nc-Si and the ground state ³Σ  of O₂. The spin orientation for electrons in the lowest-lying levels are indicated by arrows. (From Reference [65]).

Besides the quenching of exciton PL, the photosensitized generation of ⁽¹⁾O₂ can be observed by measuring the infrared PL related to the ⁽¹⁾O₂ radiative de-excitation [65]. The relevant time scale of the infrared PL was determined from time-resolved measurements. In the presence of adsorbed O₂ molecules the radiative decay of the ¹Δ state of ⁽¹⁾O₂ was observed at detection energy of 0.953 eV. The initial fast decay is attributed to the defect-related PL background. The slow component with the lifetime τ_Δ≈0.5 ms accounts for the ¹Δ→ ³Σ transition in O₂. This lifetime is significantly shorter that the radiative lifetime of a free O₂ molecule. The shortening of τ_D can be explained by the interaction of ⁽¹⁾O₂ with nc-Si surface. The same interaction should also influence the radiative lifetime τ_r of adsorbed ⁽¹⁾O₂ molecules. Firstly, the quantum yield η_r≈7×10^-5 of the radiative decay of the ¹Δ state is estimated from the comparison from the integral intensity of the exciton PL band. The radiative lifetime τ_r≈7 s  of ⁽¹⁾O₂ is obtained by using the simple relation τ_r=τ_D/η_r. On the one hand, the obtained τ_r is much shorter than the intrinsic radiative lifetime ~50 min. On the other hand, τ_r≈7 s is close to τ_D of ⁽¹⁾O₂ in different liquids. Therefore, the photoexcited nc-Si can contribute simultaneously  both to the photosensitization and to the quenching of ⁽¹⁾O₂ nc-Si systems.

3.3. Phenomenological Model of the Photosensitization by Si Nanocrystals

The photosensitized generation of ⁽¹⁾O₂ in nc-Si ensembles is quantitatively explained by using a model based on the rate equations for excitons and oxygen molecules [65,79]. In brief, the number of excitons in the nc-Si ensemble at low temperatures is limited due to the long radiative lifetime of excitons and efficient nonradiative Auger recombination in nc-Si [80]. According to the experimental data the PL intensity of por-Si in vacuum increases linearly with the excitation intensity up to 0.01 W/cm² as shown in Figure 15 [65]. At higher excitation intensity an occupation of each nc-Si by two electron-hole pairs can be achieved and the nonradiative Auger recombination results in a saturation behavior of the PL intensity vs excitation intensity (triangles in Figure 15). The model describes the experimental data both for por-Si in vacuum (curve 1) and after oxygen adsorption, which leads to the superlinear dependence I_PL on I_ex (curves 2,3). The fitting parameters correspond to the product of (β×n₀)⁻¹ = 200 µs, which is close to the experimentally determined τ_ET (see Figure 15). The fitting parameter β can be calculated by considering the microscopic mechanism of the energy transfer [78].

Figure 15. PL intensity of por-Si in vacuum (triangles, hν_PL = 1.47 and 1.5 eV) and with adsorbed O₂ molecules (closed circles, hν_PL = 1.47 eV and open circles, hν_PL = 1.5 eV) vs excitation intensity. Dashed line is a linear law approximation. The datasets are arbitrarily scaled for clarity. Solid lines are the fits by using Equations (16) and (17) with the following parameters: N = 10¹⁹ cm⁻³, σ = 10⁻¹⁵ cm², τ_ex = 0.8 ms, τ_D = 4 ms, β = 5×10⁻¹⁶ cm³/s and n = 0 (curve 1) and oxygen concentrations are taken as n=10¹⁹ sm⁻³ (curve 2), n=3×10¹⁹ cm⁻³ (curve 3). Excitation photon energy hν_exc = 2.41 eV, T = 5 K. (The experimental data are taken from Reference [65]. Reprinted from Reference [79] by permission from Springer Nature Customer Service Centre GmbH. Springer © 2007).

A coupled system, which consists of nc-Si and O₂ molecules, under optical excitation can be described by a simple set of the rate equations [79]:

             (7)

where N₀ and N₁ are the numbers of nc-Si containing 0 and 1 exciton, respectively, n₀ and n₁ are the numbers of O₂ molecules being in the ground ³Σ and singlet ¹Δ  states, respectively, τ_ex is the exciton lifetime, τ_D is the lifetime of the ¹Δ state, σ is the cross section of optical absorption in nc-Si, Φ is the photon flux density of exciting light, β is the coupling coefficient. The latter value describes the energy transfer probability of in nc-Si/O₂ system and the reciprocal product (βn₀)⁻¹ corresponds to the experimentally accessible energy-transfer time τ_ET.

To solve Equation (7) the following expressions for the total numbers of interacting species can be used:

             (8)

where N and n are the total numbers of nc-Si and O₂ molecules, respectively. The discussed phenomenological model does not account contributions of the upper excited states of nc-Si and O₂ molecules, the nonradiative recombination of excitons in nc-Si and the reverse energy transfer from ⁽¹⁾O₂ to nc-Si.

The exciton PL intensity of nc-Si is obtained from the steady state solution of Equations (7) and (8) and from the relation I_PL = N₁/ τ_ex. The time constants used in the model are obtained from the experimental data discussed above whereas σ is known from Reference [61]. Solutions of Equation (7) fit the experimental dependences of the PL intensity of por-Si on excitation intensity I_ex (solid lines in Figure 25).

The described model assumes that the larger number of adsorbed O₂ molecules results in shorter t_ET at the same conditions of the energy transfer. The energy transfer efficiency is described by β and it is obviously dependent on nc-Si size and surface conditions [79]. Hydrogen terminated nc-Si assembles with lowest number of nonradiative surface defects as Si DBs are preferable for the ⁽¹⁾O₂ photosensitization [81]. For por-Si aged in air at room temperature, the photosensitization process is additionally complicated by the thermally activated desorption of O₂ molecules as well as by the thermally activated exciton migration and nonradiative recombination. Besides, it should be analyzed both the generation rate and the quenching process of ⁽¹⁾O₂ via the interaction with internal surface of por-Si and ambient molecules. The quenching processes are especially important for por-Si suspended in different solvents. 

Spectra of the photosensitization efficiency of nc-Si in por-Si at different temperatures are shown in Figure 16 [65]. At intermediate temperatures (T = 110 K) the second quenching band in the spectral region of 1.75–1.95 eV is observed and it becomes better pronounced with increasing oxygen concentration (Figure 16a). This quenching band is attributed to the energy transfer from excitons confined in nc-Si to ⁽¹⁾O₂ dimers, that is, to the 2(¹Δ) state formation [65]. The energy transfer to the 2(¹Δ) states is enhanced at higher pressures due to increasing the probability of dimer formation. A decrease of the dimer-related quenching band is observed at higher temperature because the 2(¹Δ) formation is less probable. For temperatures above 250 K the energy transfer to the ⁽¹⁾O₂ dimers is hardly detected (see Figure 16b). This fact agrees with early reported results of the optical studies of ⁽¹⁾O₂ [67].

Figure 16. (a) Spectra of the PL quenching strength in por-Si with adsorbed O₂ molecules at T = 110 K, 100 mbar (solid line) and 2 mbar (dotted line). (b) the same spectra at T = 295 K, 1 bar (solid line) and 100 mbar (dotted line). (From Reference [65]).

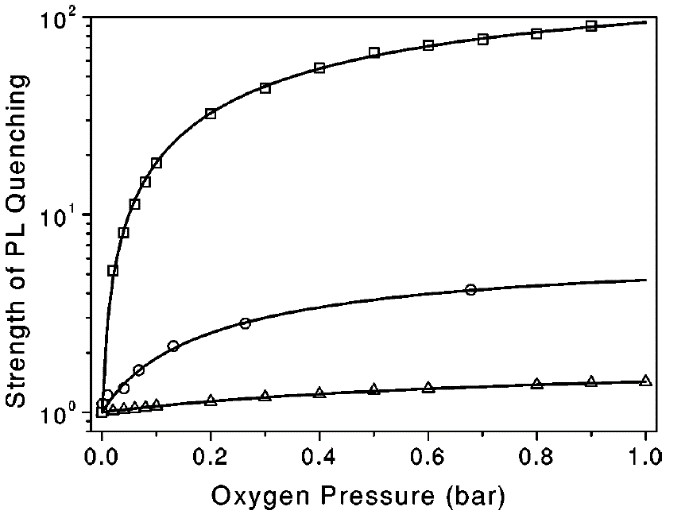
Dependence of the exciton PL quenching detected at 1.63 eV on the O₂ ambient pressure at different temperatures are shown in Figure 17 [65]. The pressure dependence is well described by using the Langmuir approach for molecular adsorption on a surface [82], that considers the dynamic equilibrium between the rates of adsorption and desorption by the following expression:

,               (9)

where K is the equilibrium constant, P_ox is the oxygen gas pressure and A is the part of exciton energy transferred to adsorbed O₂ molecules [65].

Figure 17. Dependences of the exciton PL quenching strength at 1.63 eV on oxygen pressure at different temperatures: T = 120 K (squares), T=200 K (circles), T=300 K (triangles). Solid lines are fits by Equation (9). (From Reference [65]).

The experimental pressure dependence of the photosensitization efficiency is well described by theoretical predictions (solid lines in Figure 17). As expected, in the entire pressure range a decrease of the temperature increases the mean number of adsorbed molecules and enhances the efficiency of energy transfer to O₂ molecules. The steady state concentration of ⁽¹⁾O₂ is a product of its generation rate and the collision-related deactivation one. Because both quantities are rising with oxygen ambient pressure [67], there is an optimal P_ox for the maximal steady state concentration of ⁽¹⁾O₂ [65].

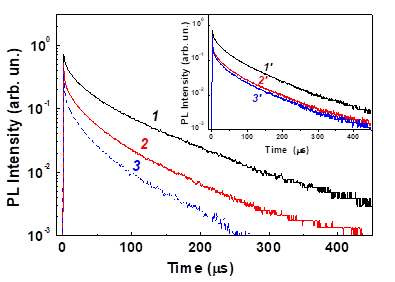
Additional information about the ⁽¹⁾O₂ photosensitization at room temperature is obtained from the PL transient measurements. Figure 18 presents several transients of the exciton PL of por-Si MPs in gaseous oxygen ambient. The inset of Figure 18 shows the transients after removal of oxygen molecules. The PL transients are not actually single exponential. However, they can be well fitted by single exponential decays for times about 50–70 ms after the excitation laser pulse [83]:

,                (10)

where τ_PL  is the PL lifetime and I_PL(0) is the PL intensity just after excitation. The values of τ_PL  for the samples in vacuum are found to be within a microsecond time scale that is in good agreement with the singlet lifetimes of excitons in nc-Si [60,61].

Figure 18. Transients of the exciton PL intensity of nc-Si in por-Si at 1.6 eV at oxygen pressures P_ox = 1 Torr (1), 100 Torr (2) and 200 Torr (3). Inset: the same PL transients in vacuum after oxygen adsorption at P_ox= 1 Torr (1’), 100 Torr (2’) and 200 Torr (3’). T = 300 K. (Reprinted from Reference [83] by permission from John Wiley and Sons © 2007).

The admission of O₂ causes a decrease of  and this effect is stronger at higher oxygen pressure (curve 3 in Figure 18). The PL lifetime shortening after oxygen adsorption with P_ox > 10 Torr is partially reversible (inset of Figure 18). The strongest lifetime shortening occurs at the PL energy of 1.6 eV, which correlates with the spectral maximum of the PL intensity quenching.

While the energy transfer time at room temperature can be obtained from the PL decay times by applying Equation (6), in which τ_ex has to be substituted by τ_PL in vacuum, the energy transfer efficiency is estimated by using the following expression [83]:

.               (11)

It is obvious that η≅1-Q^-1 where Q is described by Equation (5). If the PL quenching is not completely reversible due to the oxidation of nc-Si by photosensitized ⁽¹⁾O₂ [81], Equations (6) and (11) will give the lower and upper limits of the corresponding energy transfer time and photosensitization efficiency, respectively [83].

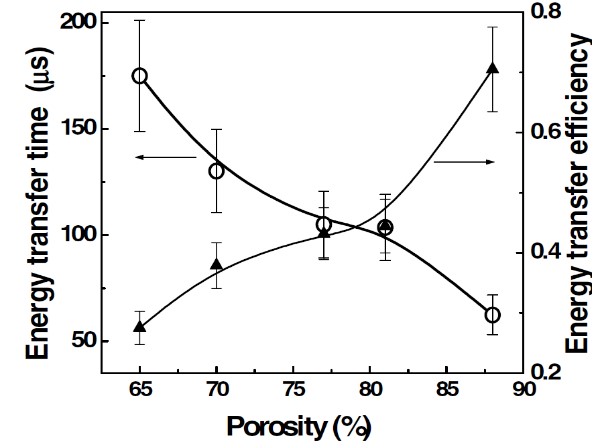
It was found that the photosensitization efficiency in por-Si layers and powder is strongly dependent on the porosity of nc-Si assemblies (Figure 19). The minimal value of τ_ET and maximal value of  are supposed for highly porous layers and powder of MPs, which consist of smallest nc-Si. The porosity dependence of  and τ_ET can be explained by considering the following reasons. The first one is a growth of the specific surface area of nc-Si with porosity increasing that promotes the O₂ adsorption and then the total rate of ⁽¹⁾O₂ photosensitization. The second reason is related to a decrease of the nonradiative recombination with increasing the porosity that results in an increase of the exciton concentration. In fact, the PL quantum yield increases in por-Si with high porosity that indicates the second reason impact [83].

Figure 19. Energy transfer time (circles) and energy transfer efficiency (triangles) vs porosity of por-Si. hν_exc = 3.7 eV, hν_PL = 1.6 eV, P_ox =1 bar, T = 300 K. (Reprinted from Reference [83] by permission from John Wiley and Sons © 2007).

Besides the characteristic energy of about 1.63 eV of the ¹Σ → ³Σ transition energy in O₂ molecule, the spectrum of the exciton PL intensity in por-Si at room temperature demonstrates an additional maximum at photon energy of 2.0–2.2 eV, which is related to the formation of superoxide radicals, that is, O^-₂ [76]. The PL quenching at 2.0–2.2 eV can be also explained by the charging of nc-Si due to the O^-₂ radical formation on the nc-Si surface [83] because the positively charged Si nanocrystals exhibit an enhanced rate of the nonradiative Auger recombination [61,80].

The infrared PL of nc-Si in por-Si MPs at room temperature was investigated to get information on the photosensitized generation of ⁽¹⁾O₂ [70]. Since the radiative transitions in ⁽¹⁾O₂ molecules are characterized by extremely low probability, the experimental observation of the ⁽¹⁾O₂ phosphorescence at 0.98 eV required very sensitive detection system and was possible only for por-Si with rather efficient generation of ⁽¹⁾O₂.  While the PL spectrum of por-Si powder in vacuum shows a featureless emission band related to defects states in nc-Si [61], the PL line of the ⁽¹⁾O₂ phosphorescence at 0.98 eV appears just after the admission of O₂ to por-Si powder. For several minutes after the O₂ admission the ⁽¹⁾O₂ phosphorescence intensity decreases, while the intensity of the defect-related band increases. The relative intensity of the ⁽¹⁾O₂ phosphorescence intensity was found to decrease in por-Si subjected to mechanical grinding, which resulted in increasing the defect-related PL [73].

Dependences of the intensity of ⁽¹⁾O₂ luminescence at 0.98 eV and defect-related PL at 0.94–0.95 eV for por-Si photoexcited at room temperature indicate formation of new defect states on the nc-Si surfaces due to the photosensitized generation of ⁽¹⁾O₂ [73]. Most probable reason of the defect formation is the photo-induced oxidation of nc-Si by ⁽¹⁾O₂, which is accompanied by irreversible quenching of the exciton PL [81]. The latter process induces decreasing the ⁽¹⁾O₂ photosensitization efficiency and then the ⁽¹⁾O₂ luminescence intensity drops down (see Figure 20). Therefore por-Si acts both as the photosensitizer and quencher of ⁽¹⁾O₂. The lifetime τ_D ≈15 ms was estimated from the comparison of ⁽¹⁾O₂ luminescence and exciton PL of nc-Si at room temperature at P_ox = 1 bar [73]. On the one hand, the estimated lifetime is significantly shorter than the radiative lifetime of ⁽¹⁾O₂ [67]. On the other hand, τ_D ≈15 ms is larger than the ⁽¹⁾O₂ lifetime in water (3 µs) or biosystems (<1 µs) [69]. This fact implies that nc-Si can be considered as a potential photosensitizer of ⁽¹⁾O₂ in liquids, including aqueous media [70,71].

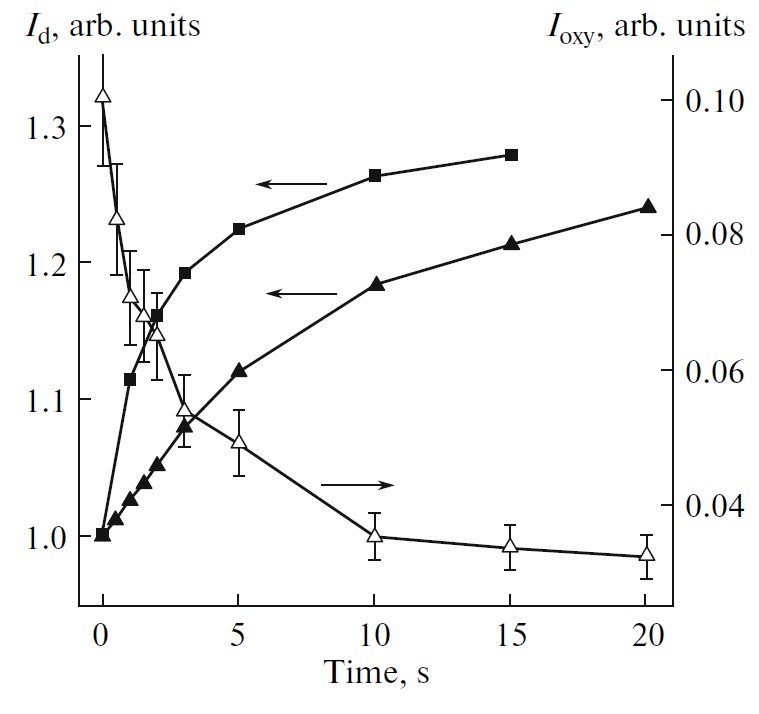
Figure 20. Dependences of the of ⁽¹⁾O₂ luminescence intensity, I_oxy, (open triangles) and defect-related PL, I_d, for initial por-Si (solid triangles) and por-Si powder (solid squares) for the photoexcitation time of por-Si powder in oxygen atmosphere at P_ox = 1 bar. hν_exc = 2.33 eV, I_exc=0.1 W/cm², T = 300 K. (Reprinted from Reference [73] by permission from Springer Nature Customer Service Centre GmbH: Springer © 2010.)

Together with the PL diagnostics the EPR technique was shown to be efficient for the quantitative analysis of the ⁽¹⁾O₂ photosensitization [84]. It is known that por-Si possesses intrinsic defects as Si DBs, which can act as spin labels for ⁽¹⁾O₂. Typical EPR spectra of por-Si are shown in Figure 21. The EPR signal is characterized by the effective g-factor of 2.0055 ± 0.0005. The corresponding paramagnetic defects are usually attributed to so-called P_b-like centers, which are Si DBs at Si/SiO₂ interface [85]. The EPR signal intensity (I_EPR) of por-Si in vacuum is the weakest at high microwave power because of the saturation effect of the microwave power absorbance by Si DBs [74]. The ¹O₂ can be also detected by monitoring a decrease of the concentration of paramagnetic ⁽³⁾O₂ [75].

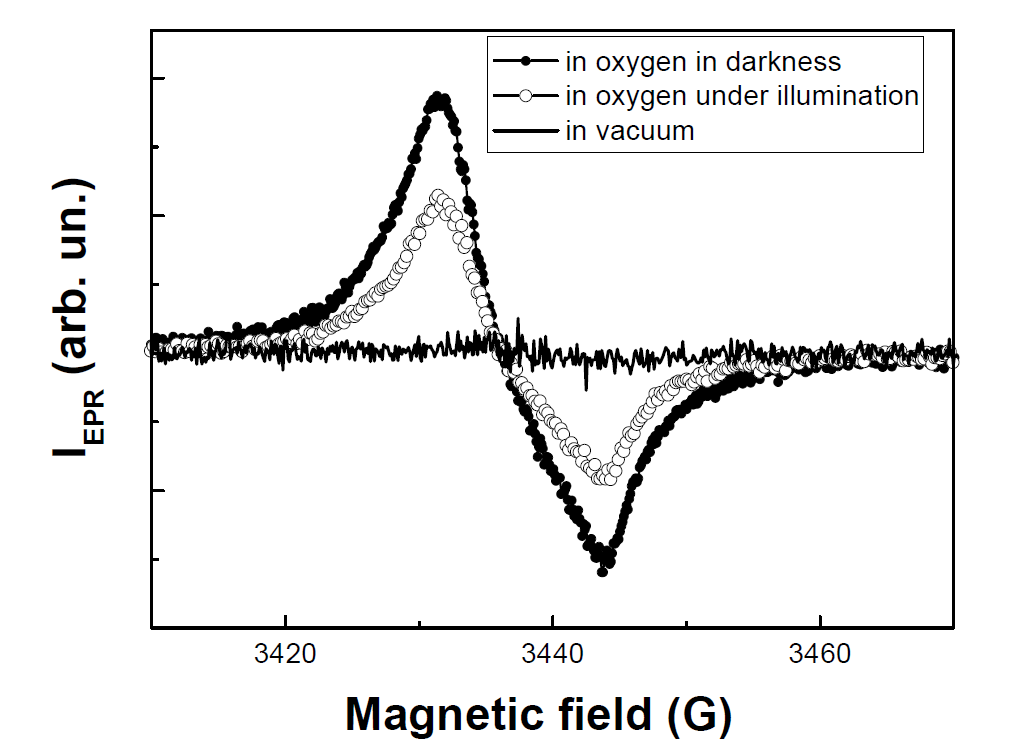
Figure 21. Electron paramagnetic resonance (EPR) spectra of por-Si powder in vacuum and in oxygen ambient (P_ox=760 Torr) in darkness and under illumination. Measurements were done at high microwave power of about 200 mW. (Reprinted from Reference [84] with permission from Elsevier).

It was found that por-Si in O₂ atmosphere was characterized by larger I_EPR in darkness than under illumination. Furthermore, I_EPR for the sample under short time illumination in O₂ atmosphere decreased almost reversibly [74]. Note, that prolonged intensive illumination led to an irreversible increase of I_EPR due to the defect formation under photo-oxidation [81]. The saturation effect of the EPR signal of por-Si results from relatively long time of the spin relaxation of P_b-centers [85]. In general, I_EPR depends on the number of paramagnetic centers (Si DBs in the case of nc-Si) and their relaxation time, which can be expressed in the following way [75]:

,               (12)

where T₁^DB  is the longitudinal relaxation time (spin-lattice relaxation) and T₂^DB is the transverse relaxation time, associated with spin-spin relaxation. For nc-Si systems with low defect density T₁^DB << T₂^DB and then T≈2T₁^DB. While the value of T₁ for bulk c-Si at the room temperature lies typically in the range of several microseconds [85], this time can be longer in small nc-Si because of a low density of phonon modes. Indeed, I_EPR for the sample in vacuum exhibits the strong saturation even at relatively low microwave power (Figure 22). The spectral shape of the EPR signal of the sample in vacuum does not change significantly under illumination [75]. Note, the factor of phonon mode depletion in nc-Si can also influence the longitudinal relaxation time of nuclear spin as ²⁹Si what is essential for the hyperpolarization method (see Section 2).

Figure 22. Dependences of the EPR signals of por-Si in vacuum (triangles) and in oxygen ambient (P_ox = 760 Torr) in darkness (solid circles) and under illumination (open circles). (Reprinted from Reference [84] with permission from Elsevier).

The T₂^DB value is reciprocal to the paramagnetic center concentration, which depends on the number of adsorbed ⁽³⁾O₂ molecules on nc-Si surface. The saturation of I_EPR at high microwave power can be absent when T₂^DB decreases due to the spin-spin relaxation. Indeed, there is no saturation of the I_EPR signal on microwave power for por-Si in oxygen atmosphere (Figure 22). Since I_EPR for the samples at P_ox = 760 Torr decreases by 40% under illumination with photon flux of about 10²⁰ cm⁻², the concentration of triplet O₂ molecules decreases by Δn≈0.4n₀, where n₀ is the initial O₂ concentration. The latter number at P_ox = 760 Torr is about 10¹⁹ cm⁻³ (the Avogadro number divided by the molar volume). From the comparison of I_EPR in the O₂ atmosphere in darkness and under illumination, one can estimate the ⁽¹⁾O₂ molecular concentration to be Δn≈4×10¹⁸ cm⁻³. The latter value is comparable with the number of nc-Si and it is by 2 orders of magnitude larger than the Si DBs concentration. This fact demonstrates that Si DBs are only probes to monitor the ⁽¹⁾O₂ photosensitization. The observed features of I_EPR for por-Si in oxygen atmosphere in darkness and under illumination were confirmed by means of the pulsed EPR technique and similar concentration of photosensitized ⁽¹⁾O₂ ~10¹⁸ cm⁻³ was detected by using the Q-band EPR [75].

While por-Si looks rather efficient photosensitizer of the ⁽¹⁾O₂ generation in gaseous atmosphere, the photosensitization by por-Si in liquids and, especially, in aqueous solutions is required for biomedical applications [86-90]. Unfortunately, the fast nonradiative relaxation of ⁽¹⁾O₂ in water complicates detection of the ⁽¹⁾O₂ luminescence. In this case the ⁽¹⁾O₂ photosensitization can be indirectly probed by monitoring the intensity and lifetime of the exciton PL of por-Si. Although the exciton PL quenching for nc-Si dispersed in water is weaker, its spectral shape is similar to that measured in gaseous ambient. Note, the relative contribution of the high-energy quenching at 2.0–2.2eV is stronger in water because of more efficient charging of the nc-Si surfaces followed with formation of O^-₂ radicals [76].

The lifetime of the exciton PL of por-Si MPs dispersed in water decreases after saturation of the solution by oxygen as shown in Figure 23 [91]. The energy transfer times determined from transients of the exciton PL by using Equation (6) are plotted in the inset of Figure 23. The spectral dependence of the energy transfer time is similar to that observed for por-Si in gaseous oxygen ambient [64,65]. A slightly longer energy transfer time correlates with weaker quenching of the PL intensity of por-Si in water than that in gaseous O₂. This fact indicates an influence of water molecules on the exciton recombination and/or energy transfer from the excitons to O₂ molecules. Indeed, the energy transfer is mostly efficient for nc-Si with S-H surface bonds, which are hydrophobic [77]. Therefore nc-Si dispersed in water should be partially oxidized that results in decreasing the ⁽¹⁾O₂ photosensitization efficiency [65]. The oxidation of nc-Si dispersed in water or aqueous solutions can be a limiting factor to achieve the stable and efficient ⁽¹⁾O₂ photosensitization. The oxidation process can be also stimulated during the photosensitization [81]. For biomedical applications of nc-Si in PDT it is obviously necessary to stabilize nc-Si surface against the ⁽¹⁾O₂ induced photooxidation. It can be done, for example, by using rapid thermal annealing or laser irradiation. For example, nearly spherical colloidal nc-Si obtained by femtosecond laser ablation of c-Si wafer in deuterated water (D₂O) water were found to photosensitize the ⁽¹⁾O₂ generation with a yield estimated at 10% of that of the standard molecular sensitizer - a photofrin [86].

Figure 23. Spectral dependences of the PL lifetime measured for por-Si MPs dispersed in degassed water (squares) and in oxygen-saturated water (circles). Inset: spectral dependence of the energy transfer time in oxygen-saturated water. hν_exc = 2.33 eV, T = 300 K. (From Reference [91]).

3.4. Si Nanocrystals as Photosensitizers of Singlet Oxygen Generation for Biomedical Applications

The ⁽¹⁾O₂ photosensitization efficiency by nc-Si dispersed in water was confirmed by measurements of the exciton PL of por-Si MPs excited by laser pulses. The relaxation time of the exponential part of the PL transients in the solution without O₂ was τ_ex≈85 μs, which is close to the natural radiative lifetime of excitons confined in nc-Si. The saturation of the solution with gaseous O₂ at a pressure of 760 Torr leads to a decrease in the PL decay time to τ_D≈50 μs. The ratio τ_ex/τ_D≈1.6 is close to the measured PL quenching. These observations indicate that the decrease of the PL lifetime of nc-Si in oxygen-saturated suspensions is caused by the photosensitized generation of ⁽¹⁾O₂ [87].

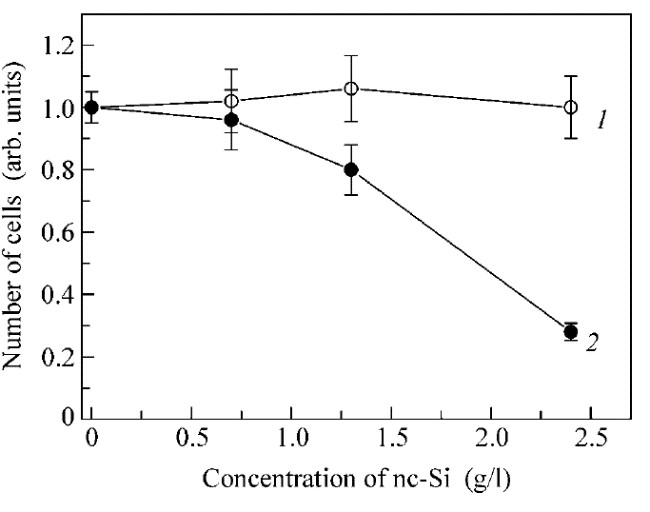
The photosensitized generation of ⁽¹⁾O₂ was confirmed by experiments in vitro, which showed that number of living 3T3 cells (mouse fibroblasts) with added por-Si MPs decreased strongly after photoexcitation as compared to the reference group (see Figure 24). At the same time, the effect of por-Si MPs was almost absent over the entire concentration range in darkness. This fact is concerned with the ⁽¹⁾O₂ generation process under the illumination in the active solution with dispersed nc-Si, because ⁽¹⁾O₂ being strong oxidizing substance results in both killing of cells and the inhibitions of cell proliferation [87]. An analysis of the DNA content of the cells incubated with photoexcited por-Si MPs indicates smaller DNA content is typical for the cell death due to the apoptosis mechanism [88].

Figure 24. Concentration dependence of the relative number of mouse fibroblast cells with added por-Si MPs in darkness (curve 1) and after illumination with white light source for 1 h (curve 2). (Reprinted from Reference [87] by permission from Springer Nature Customer Service Centre GmbH: Springer © 2006).

Mesoporous Si NPs with mean sizes of the order of 100 nm and pore size of 12 nm were used to enhance the photosensitized generation of ⁽¹⁾O₂ with quantum yield ~10% in ethanol and 17% in aqueous medium [89]. Such NPs with concentration of 0.1 mg/mL were added to cancer cell cultures followed with white light illumination that resulted in 45% decrease of cell number [89]. A stronger effect for the cancer cell suppression was observed for microporous Si NPs, which could enter cancer cells by endocytosis mechanism, resulting in ~70% cell death [90]. Photoluminescent NPs prepared from meso- and microporous Si were shown to be efficient both as the photosensitizers of ⁽¹⁾O₂ generation and photoluminescent labels in bioimaging in vitro. The photosensitization ability combined with the PL bioimaging property allow us to consider por-Si NPs as a potential agent for application in as-called cancer theranostics, that is, simultaneously therapy and diagnostics [89,90]. Note, the biological effect of photoexcited nc-Si can be related with both the photosensitized ⁽¹⁾O₂ other active forms of oxygen, for example, superoxide (O^-₂ ion), whose signature was observed as spectral features of the exciton PL quenching at 2.0–2.2 eV [91].

While the results of fundamental studies and in vitro experiments on the ⁽¹⁾O₂ photosensitization by nc-Si seem to be promising, there is a lack of in vivo tests to assess the real potential of nc-Si for PDT applications. Note, the biocompatibility and biodegradability of nc-Si and por-Si NPs [92,93] together with the photosensitization ability are well satisfied to the modern requirements for PDT application [94]. Besides nc-Si prepared from por-Si [87–90] the photosensitizing property was also reported for nc-Si prepared by laser ablation of bulk Si in water [86]. This finding indicates a possible way to obtain nc-Si, which can at as stable and efficient photosensitizers for the cancer theranostics [3].

3.5. Si NPs with Electron Spin Centers as Potential Contrast Agents for ¹H MR

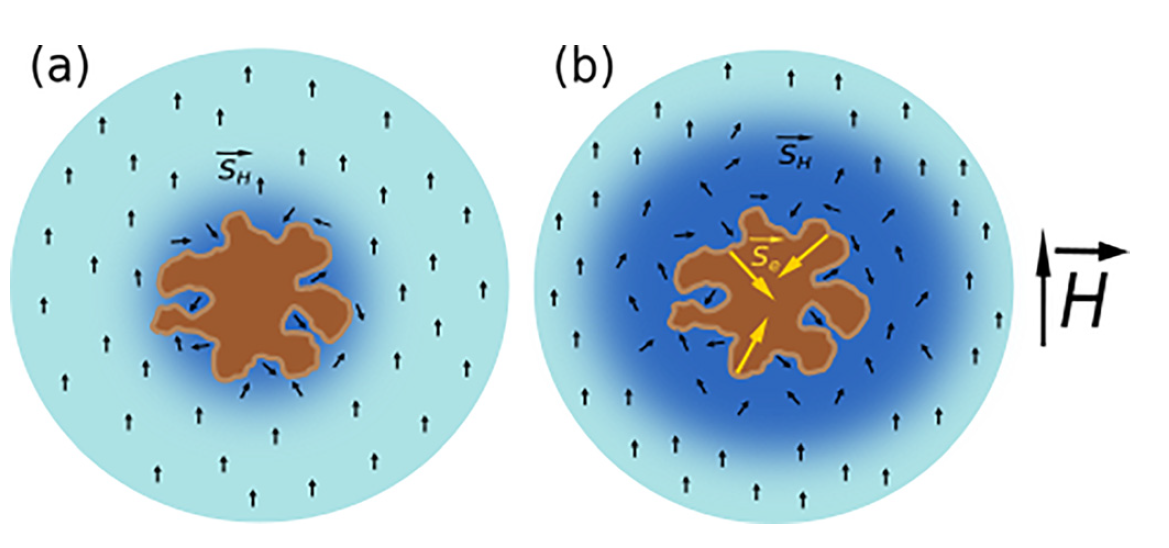
Si NPs with a high number of the electron spin centers can act as contrast agents (CAs) for the conventional biomedical MRI at the proton (¹H) frequency [95]. The MRI contrast property of Si NPs was explained by considering the magnetic dipole-dipole interaction between electron spins on the Si NP’s surfaces and those of surrounding protons [96] as schematically shown in Figure 25. While a solid NP itself can increase the proton spin relaxation (Figure 25a), Si NPs especially prepared from por-Si provide additional opportunities to increase the spin center density due to huge specific surface area of small nc-Si [62]. While por-Si usually contains numerous paramagnetic centers as Si dangling bonds (Si DBs) and their number can be significantly increased by physical and chemical treatments [77]. It was shown that Si NPs prepared from por-Si subjected to thermal annealing (TA) in vacuum could contain a lot of paramagnetic centers, which strongly enhanced the proton spin relaxation of water molecules surrounding those NPs (Figure 25b). It is well known that surface of electrochemically prepared por-Si is passivated by hydrogen atoms [77]. Because the TA treatment induces the hydrogen desorption from the NP’s surface followed by creation of new Si DBs, which can be quantitatively detected by EPR technique [77]. Tailoring of the paramagnetic center number in Si NPs is a possible way to improve their CA properties for MRI applications [96].

Figure 25. (a) Schematic view of the shortening of proton spin relaxation in water (blue regions) nearby a NP (brown spot) without unpaired electron spins; (b) the same scheme for the NP with numerous unpaired electron spins centers on the NP surface. Black and yellow arrows correspond to the proton and electron spins, respectively. (Reprinted from Reference [96] by permission from John Wiley and Sons © 2018).

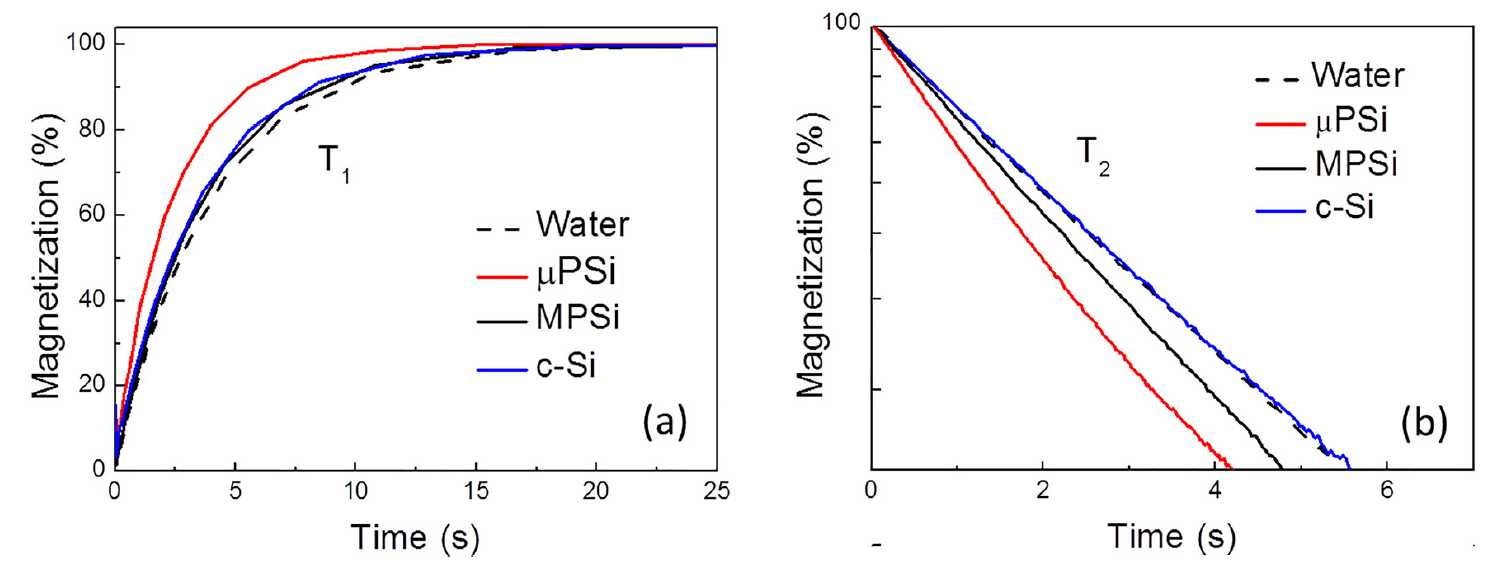
Figure 26 shows typical transients of the longitudinal (left) and transverse (right) proton magnetizations in aqueous suspensions of NPs ( mean size ~100 nm) prepared from mesoporous (MPSi), microporous (µPSi) and from c-Si wafers by using high-energy ball milling of the corresponding bulk samples [96]. The MRI contrasting is caused by shortening of the relaxation times of protons in surrounding water molecules (see Figure 26). The sample of c-Si NPs does not cause significant proton relaxation despite they have high paramagnetic centers concentration. Indeed, the surface area c-Si NPs is rather low and most of the centers are located deeply inside the NPs. NPs prepared from both MPSi and µPSi demonstrate significant T₂ shortening. Pore sizes are different in µPSi (≤ 2nm) and MPSi (2-50 nm) that means a bigger surface area for mPSi and a stronger interaction of water molecules with the surface of NPs.

Figure 26. Transients of (a) longitudinal and (b) transverse proton magnetization of pure water (black dashed line) and aqueous suspensions of Si NPs (1 mg/mL) prepared from c-Si (blue line) MPSi (black line) and μPSi (red line). (Reprinted from Reference [96] by permission from John Wiley and Sons © 2018).

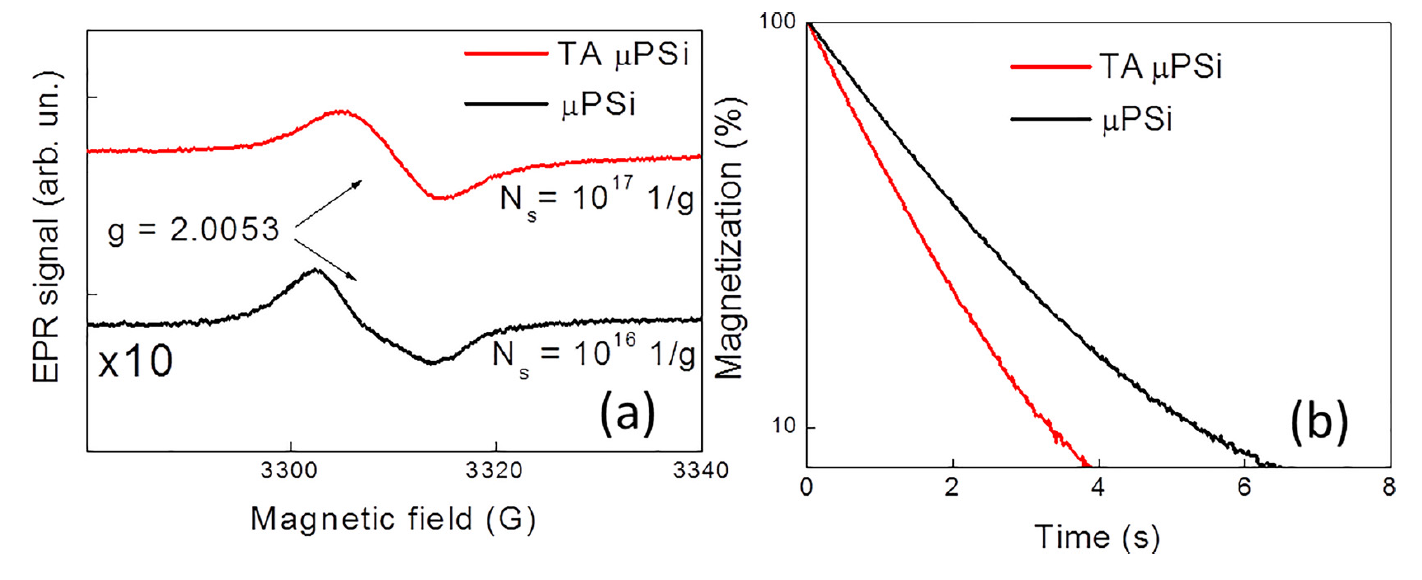
The EPR spectroscopy is used to clarify both the origin of electron spin centers and to measure their concentration in Si NPs after TA. Figure 27a shows EPR spectra of µPSi NPs before and after TA. The both spectra have the effective g-factor of about 2.005, which can be explained by superposition of several types of Si DBs [96], for example, P_b-centers with differently coordinated Si and O atoms [97,98]. The number of Si DBs after TA increases due to thermally induced desorption of hydrogen from the internal surface of µPSi. Despite the concentration of DBs after TA increased by a factor of 10, the T₂ relaxation time decreases only by 3 times (Figure 27b). This discrepancy can be explained by a partial passivation of Si DBs by water molecules [96]. While TA in vacuum can induce a lot of new DBs in por-Si [77], the DB concentration decreases strongly in MPSi after thermal oxidation (TO) in air at 900 °C. This effect is explained by passivation of Si DBs due to formation of a thin layer of the thermal oxide [96].

Figure 27. (a) EPR spectra of as-prepared (black line, the intensity is multiplied by 10) and thermally annealed in vacuum (red line) μPSi NPs. (b) Transients of the transverse proton magnetization in aqueous suspensions of as-prepared (black line) and thermally annealed in vacuum (red line) μPSi NPs. (Reprinted from Reference [96] by permission from John Wiley and Sons © 2018).

The transverse proton relaxation rate induced by Si NPs can be defined as follows [96]:

,               (13)

where T₂^NP is the time of transverse relaxation due to the presence of NPs, T₂ is the measured transverse relaxation time and T₂^W  is the transverse relaxation time in pure water.

The value of R₂ was found to depend almost linearly on concentration of as-prepared MPSi NPs and those after TO. The latter NPs possesed nearly 3 times lower concentration of paramagnetic centers in comparison to as-prepared ones, what caused 3 times lower R₂ in the whole range of the NP concentration [96]. This fact indicates that both types of NPs do not aggregate in highly concentrated suspensions and the pores are still open to ensure access of water molecules that is important for MRI CA application.

Si NP based CAs can be characterized by their specific relaxation efficiency, that is relaxivity, which is defined as the change in relaxation rate after addition of CAs, divided to the concentration of NPs [95,96]. The transverse proton relaxivity can be given by the following expression:

,              (14)

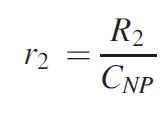
where R₂ is the proton relaxation rate governed by Si NPs, C_NP is the concentration of NPs in aqueous suspension.

The high transverse relaxivity r₂ = 0.5 L/(g×s) for  μPSi NPs after TA correlates with the large number of electron spin centers ~10¹⁷ spin/g [96]. The corresponding MRI relaxivity normalized on the number of Si atoms in NPs is about r₂^Si~ 10^-2 L/(mM×s), which is smaller than that for the standard CAs based on Gd³⁺ ions accounted to 4–6 L/(mM×s) [99] and superparamagnetic iron oxide NPs up to 2×10³ L/(mM×s) [100]. However, similarly to the latter NPs, the relaxivity of Si-based NPs divided on the number of Si DBs r₂^NP~10³ L/(mM×s) and specially designed porous Si NPs with required number of electron spin centers can be considered as potential CAs for biomedical application in MRI [96].

In order to improve the ¹H MRI contrasting property of Si NPs, one can use nanocomposite NPs with iron oxide [101]. Such composite Si NPs were prepared by arc-discharge plasma-assisted method in a closed-cycle inert gas (Ar or N₂) ambient at atmospheric pressure. The process consisted of evaporation of high purity polycrystalline Si powder with addition of metallic iron powder at temperature of about 5500 °C followed with condensation of the vapor mixture in a cooling gas stream to form polycrystalline powder with mean size of nc-Si of about 20–30 nm confirmed by XRD measurements. Despite the relatively small nanocrystal size the prepared NPs after dispersing them in aqueous media exhibited several times larger hydrodynamic sizes about 50-130 nm detected by using a DLS method. This difference can be reletaed to the polycrystalline structure of such NPs or/and their aggregation in aqueous medium [101].

EPR spectra of Si NPs with iron oxide impurities (Figure 28) consist of a broad band with effective g-factor of about 2.1 related to strongly interacting Fe³⁺ ions in γ-Fe₂O₃ (maghemite) [102] and a narrow line with g-factor of 2.0055, which can be assigned to Si DBs as P_b-centers [97]. The larger iron concentration in the samples the stronger broadening of the corresponding EPR band due to increasing the spatially inhomogeneous interactions between Fe³⁺ ions. As for the second line of intrinsic Si DBs they are supposed to be localized in SiO₂ surface coating of the NP surfaces, which was confirmed by X-ray photoelectron spectroscopy and FTIR measurements [101]. Furthermore, HR-TEM images of iron doped Si NPs reveal numerous defects of the crystalline structure as twins and grain boundaries related to the fast cooling rate during their formation in argon flow [103]. Both the iron impurities and intrinsic defects as Si DBs are responsible for the large number of electron spin centers in such NPs [101,103].

Figure 28. EPR spectra of Si NPs with different iron content increasing as 0.004, 0.02 and 0.2 at. % for curves 1, 2 and 3, correspondingly. (Reprinted from Reference [101] by permission from John Wiley and Sons © 2019).

The total concentration of electron spin centers in Si NPs approaches 10¹⁸ spin/g [101] that makes this type of NPs to be efficient for shortening the proton spin relaxation in aqueous media as it was already demonstrated for porous Si NPs [95,96]. In fact, both the longitudinal and transverse relaxation times of protons in aqueous suspensions of plasma-ablated Si NPs were found to be dependent on iron content [101]. The stronger decrease of the transverse proton relaxation was detected for the samples with higher iron content up to 0.2 at%. MRI experiments with phantoms showed that the latter NPs exhibited properties of efficient CAs for the ¹H MRI. The maximal transverse relaxivity accounted 7.3 L/(g×s). The latter value corresponds to the molar relaxivity of  about 200 L/(mM×s) [101], which is close to that reported for CAs based on superparamagnetic iron oxide NPs [100].

The CA property of plasma-ablated Si NPs with iron oxide impurity was confirmed by experiments in vivo [101]. The experiments were carried out with grafted cancer tumor (lung carcinoma 3LL). In vivo MRI visualization of mice with tumor was carried out by using a protocol, which included the following steps: (i) obtaining whole body PD-weighted MRI before injection the NP suspension; (ii) obtaining whole body PD-weighted MRI 20 min after intratumorally injection of 0.5 mL suspension of Si NPs with concentration of 0.5 mg/mL. It was found that tumor area with injected NPs became darker and have more clear boundaries (see Figure 29). The MRI study of the mice for the time period of 24 h after injection of Si NPs showed a decrease of the MRI contrast. This fact can be explained by biodegradation of iron-doped Si NPs similarly to that of pure Si NPs [101].

Figure 29. Transients of the proton magnetization (inset shows the transverse relaxivity vs the iron content), typical TEM image of Si NPs with 0.2 at% of iron impurities and MRI images of cancer tumor before (upper image) and after (down image) injection of such NPs. (Reprinted from Reference [101] by permission from John Wiley and Sons © 2019).

Moreover, aqueous suspensions of Si NPs were explored as efficient sensitizers of electromagnetic radiofrequency (RF) hyperthermia, which is a prospective approach for mild cancer therapy with non-magnetic Si NPs.  The stronger heating rate was reported for iron-doped Si NPs with hydrodynamic size of about 50 nm [101]. The obtained results indicate possible ways for applications of Si-based NPs in the MRI diagnostics and RF therapy of cancer, that is, theranostics. Additional promises in biomedical applications of Si NPs can arise from multinuclear MRI diagnostics by using both the standard ¹H mode and hyperpolarized ²⁹Si NPs as well as other NPs with conventional biomedical nuclei, for example, ¹³C, ¹⁹F and so forth [104].

Besides the MRI diagnostic modality, it was recently demonstrated the possibility to use Si NPs with iron impurities to suppress the cancer tumor growth in vivo [103]. The intratumoral injection and intravenous administration of iron-doped Si NPs resulted in a decrease of the tumor volume by 32% and 23%, respectively. While the intratumoral injection induced the stronger antitumor effect, the observed decrease in tumor volume after intravenous administration confirmed accumulation of Si NPs in the tumor due to as-called enhanced permeability and retention effect, which is well known for various NPs [105]. The antitumor effect of iron-doped Si NPs correlates with increasing the lifetime of laboratory animals. The observed antitumor effect of iron-doped Si NPs can be related to dissolution of Si NPs accumulated in tumor followed with release of iron ions, which induce reactive oxygen species with high toxicity for cancer cells [103].

4. Summary and Outlook

Spin-dependent phenomena in semiconductor NPs are overviewed starting from the basic properties of solid-state semiconductor systems, which depend on preferential orientation of electron and nuclear spins therein, to the recent advances in the development and characterization of semiconductor (mainly, silicon) NPs with spin-dependent properties that are promising for versatile biomedical applications.

A challenging task to control the nuclear-spin polarization in solids has been successfully accomplished in the pioneering work by G. Lampel on the DNP by optical pumping in c-Si. The hyperfine dipolar interaction between the electron and nuclear spins caused an appreciable polarization of the nuclear spins due to the optically induced saturation of the electron spins. Starting from then, the role of the hyperfine interaction was carefully explored to realize the hyperpolarized nuclear states in semiconductor NPs and compound MPs. The hyperpolarization efficiency of ²⁹Si was found to depend on the nuclear relaxation time controlled by the density of electron spins. The nuclear longitudinal relaxation time was shown to shorten with increasing the charge-carrier concentration in semiconductor. The nuclear-spin relaxation in Si NPs underwent a strong shortening with decreasing the mean size of NPs, while surface-passivated Si NPs exhibited the relaxation time from 10² s to 10³ s. In contrast to the nuclear relaxation, the spatial confinement of charge carriers (electrons and holes) in nanostructures significantly increased the electron spin-lattice relaxation time. A transition from itinerant to fully-localized electrons, while inducing hyperfine dephasing, was beneficial in quenching the electron spin-lattice relaxation. The phenomenon of DNP of ²⁹Si in Si NPs and compound MPs was shown to open fascinating prospects for creation of new efficient contrast agents for MRI. The most efficient DNP was achieved for Si MPs, which consisted of hundreds of nanometer-size NPs, what ensured the optimal ratio between nuclear polarization/depolarization as it was confirmed by experiments in vivo.

Besides the nuclear polarization, the electron-spin related phenomena were shown to be very promising for MRI applications. The experimental results confirmed a key role of unpaired electron spins as Si DBs in porous Si MPs and NPs for the enhancement of the proton spin relaxation in aqueous suspensions. The samples of nonporous crystalline Si NPs exhibited a relatively weak decrease of both longitudinal and transverse relaxation times because of low efficiency of the interaction of their unpaired electron spins with proton spins in surrounding water molecules. On the one hand, the thermally oxidized mesoporous Si NPs did not induce a valuable rate of the proton-spin relaxation due to the low density of Si DBs. On the other hand, the vacuum annealed microporous Si NPs exhibited a strong decrease of the relaxation times, especially the transverse one by 2 to 3 times for the NP concentration of the order of 1 mg/mL. The transverse relaxation rate was found to depend nearly linearly on the concentration of porous Si NPs in suspensions ranging from 0.1 to 20 mg/mL. The relaxation rate induced by porous Si NPs was approximately proportional to the number of Si DBs on their surfaces, what indicated a way to enhance the proton relaxation via the interaction with unpaired localized electron spins of Si NPs. The transverse specific relaxation rate (relaxivity) of thermally annealed microporous Si NPs is estimated to be 0.5 L/(g×s) and for plasma-ablated Si NPs with 0.2 at% of iron oxide the corresponding relaxivity is of the order of 10 L/(g×s), which is already promising for MRI applications. The relaxivity of Si NPs can be further improved by using physical and chemical treatments, which will lead to increasing the number of paramagnetic centers in Si NPs that ensures further progress in the design and validation of those NPs as contrast agents for MRI. It is worth noting that both the ¹H MRI contrast properties of Si NPs and their hyperpolarizing properties allow us to consider such NPs as binuclear CAs, which are simultaneously detected at the proton and ²⁹Si frequencies, what is a promising direction in MRI.

In addition to the diagnostic modality of the spin-dependent properties of Si NPs, it was found that the triplet excitons confined in Si NPs of sizes below 10 nm could transfer their energy to molecular oxygen that resulted in generation of highly chemically reactive singlet oxygen promising for the photodynamic therapy of cancer. The energy-transfer process depended on the magnetic field that indicated the spin-related origin of the singlet-oxygen photosensitization. The photosensitizing properties of NPs made from porous Si were tested in experiments with photoinduced destruction of cancer cells in vitro. Further experiments are ongoing to advance Si-NP-based contrast agents for clinical applications in both the MRI diagnostics and the mild therapy of cancer.

 Funding: The work was partially funded by the National Research Nuclear University MEPhI Academic Excellence Project (Contract No. 02.a03.21.0005). V. Yu. T. was funded by the Russian Science Foundation (Project No. 19-72-30012).

 ^{[1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16][17][18][19][20][21][22][23][24][25][26][27][28][29][30][31][32][33][34][35][36][37][38][39][40][41][42][43][44][45][46][47][48][49][50][51][52][53][54][55][56][57][58][59][60][61][62][63][64][65][66][67][68][69][70][71][72][73][74][75][76][77][78][79][80][81][82][83][84][85][86][87][88][89][90][91][92][93][94][95][96][97][98][99][100][101][102][103][104][105]}