
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Constantino Tsallis | + 2792 word(s) | 2792 | 2022-01-25 10:32:51 | | | |
| 2 | Vicky Zhou | + 1 word(s) | 2793 | 2022-01-25 10:56:21 | | | | |
| 3 | Vicky Zhou | + 583 word(s) | 3376 | 2022-02-07 07:45:02 | | | | |
| 4 | Vicky Zhou | -25 word(s) | 3351 | 2022-02-07 07:55:52 | | | | |
| 5 | Vicky Zhou | -11 word(s) | 3340 | 2022-03-10 03:11:58 | | | | |
| 7 | Vicky Zhou | -2340 word(s) | 1000 | 2022-04-13 11:19:58 | | | | |
| 8 | Vicky Zhou | + 1 word(s) | 1001 | 2022-05-07 04:49:58 | | |
Video Upload Options
The concept of entropy constitutes, together with energy, a cornerstone of contemporary physics and related areas. It was originally introduced by Clausius in 1865 along abstract lines focusing on thermodynamical irreversibility of macroscopic physical processes. In the next decade, Boltzmann made the genius connection—further developed by Gibbs—of the entropy with the microscopic world, which led to the formulation of a new and impressively successful physical theory, thereafter named statistical mechanics. The extension to quantum mechanical systems was formalized by von Neumann in 1927, and the connections with the theory of communications and, more widely, with the theory of information were respectively introduced by Shannon in 1948 and Jaynes in 1957. Since then, over fifty new entropic functionals emerged in the scientific and technological literature. The most popular among them are the additive Renyi one introduced in 1961, and the nonadditive one introduced in 1988 as a basis for the generalization of the Boltzmann–Gibbs and related equilibrium and nonequilibrium theories, focusing on natural, artificial and social complex systems. Along such lines, theoretical, experimental, observational and computational efforts, and their connections to nonlinear dynamical systems and the theory of probabilities, are currently under progress. Illustrative applications, in physics and elsewhere, of these recent developments are briefly described in the present synopsis.
Thermodynamics is an empirical physical theory which describes relevant aspects of the behavior of macroscopic systems. In some form or another, all large physical systems are shown to satisfy this theory. It is based on two most relevant concepts, namely energy. The German physicist and mathematician Rudolf Julius Emanuel Clausius (1822–1888) introduced the concept of entropy in 1865 [1][2], along rather abstract lines in fact. He coined the word from the Greek τροπη (trope¯ ), meaning transformation, turning, change. Clausius seemingly appreciated the phonetic and etymological consonance with the word ’energy’ itself, from the Greek ευεργεια (energeia), meaning activity, operation, work. It is generally believed that Clausius denoted the entropy with the letter S in honor of the French scientist Sadi Carnot. For a reversible infinitesimal process, the exact differential quantity dS is related to the differential heat transfer δQreversible through dS = δQreversible /T , T being the absolute temperature. The quantity T-1 plays the role of an integrating factor, which transforms the differential transfer of heat (dependent on the specific path of the physical transformation) into the exact differential quantity of entropy (path-independent). This relation was thereafter generalized by Clausius into its celebrated inequality dS ≥ δQ/T, the equality corresponding to a reversible process. The inequality corresponds to irreversible processes and is directly implied by the so-called Second Principle of Thermodynamics, deeply related to our human perception of the arrow of time.
One decade later, the Austrian physicist and philosopher Ludwig Eduard Boltzmann (1844–1906) made a crucial discovery, namely the connection of the thermodynamic entropy S with the microscopic world [3][4]. The celebrated formula S = k ln W, W being the total number of equally probable microscopic possibilities compatible with our information about the system, is carved in his tombstone in the Central Cemetery of Vienna. Although undoubtedly Boltzmann knew this relation, it appears that he never wrote it in one of his papers. The American physicist, chemist and mathematician Josiah Willard Gibbs (1839–1903) further discussed and extended the physical meaning of this connection [5][6][7]. Their efforts culminated in the formulation of a powerful theory, currently known as statistical mechanics. This very name was, at the time, a deeply controversial matter. Indeed, it juxtaposes the word mechanics—cornerstone of a fully deterministic understanding of Newtonian mechanics—and the word statistics—cornerstone of a probabilistic description, precisely based on non-deterministic concepts. On top of that, there was the contradiction with the Aristotelian view that fluids, e.g., the air, belong to the mineral kingdom of nature, where there is no place for spontaneous motion. In severe variance, Boltzmann’s interpretation of the very concept of temperature was directly related to spontaneous space-time fluctuations of the molecules (‘atoms’) which constitute the fluid itself.
Many important contributions followed, including those by Max Planck, Paul and Tatyana Ehrenfest, and Albert Einstein himself. Moreover, we mention here an important next step concerning entropy, namely its extension to quantum mechanical systems. It was introduced in 1927 [8] by the Hungarian-American mathematician, physicist and computer scientist János Lajos Neumann (John von Neumann; 1903–1957).
The next nontrivial advance was done in 1948 by the American electrical engineer and mathematician Claude Elwood Shannon (1916–2001), who based on the concept of entropy his “Mathematical Theory of Communication” [9][10][11]. This was the seed of what nowadays is ubiquitously referred to as the information theory, within which the American physicist Edwin Thompson Jaynes (1922–1998) introduced the maximal entropy principle, thus establishing the connection with statistical mechanics [12][13]. Along these lines, several generalizations were introduced, the first of them, hereafter noted 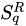 by the Hungarian mathematician Alfréd Rényi (1921–1970) in 1961 [14][15][16][17]. Various others followed in the next few decades within the realm of information theory, cybernetics and other computer-based frames, such as the functionals by Havrda, Charvat [18], Lindhard, Nielsen [19], Sharma, Taneja, Mittal [20][21][22]. During this long maturation period, many important issues have been punctuated. Let us mention, for instance, Jaynes’ “anthropomorphic” conceptualization of entropy [23] (first pointed by E.P. Wigner), and also Landauer’s “Information is physical” [24]. In all cases, the entropy emerges as a measure (a logarithmic measure for the Boltzmann–Gibbs instance) of the number of states of the system that are accessible, or, equivalently, as a measure of our ignorance or uncertainty about the system.
by the Hungarian mathematician Alfréd Rényi (1921–1970) in 1961 [14][15][16][17]. Various others followed in the next few decades within the realm of information theory, cybernetics and other computer-based frames, such as the functionals by Havrda, Charvat [18], Lindhard, Nielsen [19], Sharma, Taneja, Mittal [20][21][22]. During this long maturation period, many important issues have been punctuated. Let us mention, for instance, Jaynes’ “anthropomorphic” conceptualization of entropy [23] (first pointed by E.P. Wigner), and also Landauer’s “Information is physical” [24]. In all cases, the entropy emerges as a measure (a logarithmic measure for the Boltzmann–Gibbs instance) of the number of states of the system that are accessible, or, equivalently, as a measure of our ignorance or uncertainty about the system.
In 1988, the Greek-Argentine-Brazilian physicist Constantino Tsallis proposed the generalization of statistical mechanics itself on the basis of a nonadditive entropy, noted Sq, where the index q is a real number; Sq recovers the Boltzmann–Gibbs (BG) expression for the value q = 1 [25]. This theory is currently referred to as nonextensive statistical mechanics [26]. There was subsequently an explosion of entropic functionals: there are nowadays over fifty such entropies in the available literature. However, very few among them have found neat applications in physics and elsewhere.
References
- Clausius, R. Uber die Wärmeleitung gasförmiger Körper. Ann. Phys. 1865, 125, 353–400.
- Clausius, R. The Mechanical Theory of Heat with Its Applications to the Steam Engine and to Physical Properties of Bodies; John van Voorst, 1 Paternoster Row. MDCCCLXVII: London, UK, 1865.
- Boltzmann, L. Weitere Studien u̇ber das Wȧrmegleichgewicht unter Gas moleku̇len [Further Studies on Thermal Equilibrium Between Gas Molecules]. Wien. Ber. 1872, 66, 275.
- Boltzmann, L. Uber die Beziehung eines allgemeine mechanischen Satzes zum zweiten Haupsatze der Warmetheorie Sitzungsberichte, K. Akademie der Wissenschaften in Wien, Math. Naturwissenschaften 1877, 75, 67–73.
- Gibbs, J.W. Elementary Principles in Statistical Mechanics—Developed with Especial Reference to the Rational Foundation of Thermodynamics; C. Scribner’s Sons: New York, NY, USA, 1902.
- Gibbs, J.W. The collected works. In Thermodynamics; Yale University Press: New Haven, CT, USA, 1948; Volume 1.
- Gibbs, J.W. Elementary Principles in Statistical Mechanics; OX Bow Press: Woodbridge, CT, USA, 1981.
- von Neumann, J. Thermodynamik quantenmechanischer Gesamtheiten. Nachrichten Ges. Wiss. Gott. 1927, 1927, 273–291.
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423.
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656.
- Shannon, C.E. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949.
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630.
- Jaynes, E.T. Information theory and statistical mechanics. II. Phys. Rev. 1957, 108, 171–190.
- Renyi, A. On measures of information and entropy. In Proceedings of the Fourth Berkeley Symposium; University of California Press: Los Angeles, CA, USA, 1961; Volume 1, pp. 547–561.
- Renyi, A. Probability Theory; Dover Publications Inc.: New York, NY, USA, 1970.
- Balatoni, J.; Renyi, A. Remarks on entropy. Publ. Math. Inst. Hung. Acad. Sci. 1956, 1, 9–40.
- Renyi, A. On the dimension and entropy of probability distributions. Acta Math. Acad. Sci. Hung. 1959, 10, 193–215.
- Havrda, J.; Charvat, F. Quantification method of classification processes - Concept of structural α-entropy. Kybernetika 1967, 3, 30–35.
- Lindhard, J.; Nielsen, V. Det Kongelige Danske Videnskabernes Selskab Matematisk-fysiske Meddelelser (Denmark). Stud. Stat. Mech. 1971, 38, 1–42.
- Sharma, B.D.; Mittal, D.P. New non-additive measures of entropy for discrete probability distributions. J. Math. Sci. 1975, 10, 28.
- Sharma, B.D.; Taneja, I.J. Entropy of type (α,β) and other generalized measures in information theory. Metrika 1975, 22, 205.
- Mittal, D.P. On some functional equations concerning entropy, directed divergence and inaccuracy. Metrika 1975, 22, 35.
- Jaynes, E.T. Gibbs vs. Boltzmann entropies. Am. J. Phys. 1965, 33, 391–398.
- Landauer, R. Information is physical. Phys. Today 1991, 44, 23.
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487, [First appeared as preprint in 1987: CBPF-NF-062/87, ISSN 0029–3865, Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro].
- Tsallis, C. Nonextensive Statistical Mechanics—Approaching a Complex World, 1st ed.; Springer: New York, NY, USA, 2009.

