Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Axel Loewe
 + 3161 word(s) 3161 2021-08-05 10:29:23 |
2 update layout and reference
Rita Xu
 -24 word(s) 3137 2021-08-25 04:05:41 | |
3 change the title
Rita Xu
 Meta information modification 3137 2021-08-25 08:31:51 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Loewe, A. Computer Modeling of the Heart. Encyclopedia. Available online: https://encyclopedia.pub/entry/13510 (accessed on 18 April 2024).
Loewe A. Computer Modeling of the Heart. Encyclopedia. Available at: https://encyclopedia.pub/entry/13510. Accessed April 18, 2024.
Loewe, Axel. "Computer Modeling of the Heart" Encyclopedia, https://encyclopedia.pub/entry/13510 (accessed April 18, 2024).
Loewe, A. (2021, August 24). Computer Modeling of the Heart. In Encyclopedia. https://encyclopedia.pub/entry/13510
Loewe, Axel. "Computer Modeling of the Heart." Encyclopedia. Web. 24 August, 2021.
Computer Modeling of the Heart
Edit
This entry is adapted from the peer-reviewed paper 10.3390/hearts2030028

Computer modeling of the electrophysiology of the heart has undergone significant progress. A healthy heart can be modeled starting from the ion channels via the spread of a depolarization wave on a realistic geometry of the human heart up to the potentials on the body surface and the ECG.

in silico electrophysiology electrocardiogram ECG cardiac disease

1. Introduction

This article reviews research aimed at building a bridge between computerized modeling of the electrophysiology of the human heart and the analysis of the electrocardiogram (ECG). Potential applications of computer modeling for better interpretation of the ECG are demonstrated and an outlook for further research is given.
The research field of computerized modeling of the electrophysiology of the heart has reached a mature state. The healthy heart can be replicated in a computer model with various degrees of detail, starting with the ion channels and ending with the spread of a depolarization wave through the atria and the ventricles. Several diseases have been the focus of this research but many open questions remain: modeling can only be as good as our basic understanding of the pathologies of the heart.
On the other hand, after more than 100 years of ECG interpretation, the clinical knowledge about ECG and what it can tell us about cardiac diseases has reached an expert level. Most often, this knowledge is based on personal experience or empirical studies and only coarse attempts are made to relate a decisive feature in the ECG to its pathological origin inside the heart. The classical heart vector is a valuable tool for understanding the general shape of the ECG, but it is not good enough to follow details of the spatial spread of de- and repolarization.
It is astounding that the number of articles where modeling of the heart is extended to the calculation of the ECG and where this is used for better ECG interpretation is limited. Table 1 shows the result of a literature survey.
Table 1. Literature survey of research about modeling of the heart together with the corresponding ECG.
Topic Modeling Challenge References
healthy heart—QRS modeling the Purkinje tree [1][2][3][4][5][6][7][8][9]
healthy heart—T-wave modeling heterogeneity of repolarization [10][11][12][13]
healthy heart—P-wave modeling sinus node excitation and pathways from right to left atrium, anatomical variability [14][15][16][17][18][19][20][21][22]
ischemia and infarction modeling the effect of hyperkalemia, acidosis, hypoxia and cell-to-cell uncoupling [23][24][25][26][27][28][29][30]
ventricular ectopic beats localization with 12-lead ECG [31][32][33][34]
ventricular tachycardia localization of exit points with 12-lead ECG [29][35]
cardiomyopathy modeling typical changes of QRS- and T-wave [36]
bundle branch blocks LBBB and RBBB modeling asynchrony [37][38][39][40]
atrial ectopic beats localization with 12-lead ECG [32][33][34]
atrial tachycardia, flutter modeling all types of flutter [20][41][42][43][44][45][46]
atrial fibrillation and fibrosis modeling fibrosis and its distribution [47][48][49][50][51]
genetic diseases modeling LQT, SQT, Brugada [52][53][54]
imbalance of electrolytes hyper- and hypokalemia and hyper- and hypocalcemia [13][55][56][57][58][59][60]
drug-induced changes effect of various channel blockers [61][62][63]
Methods for calculation of the ECG (and the body surface potential map, BSPM) from the source distribution in the heart have been described in several articles. The main differences between the approaches are (a) the cellular models and their parameters, (b) the method to calculate the spread of depolarization (bidomain, monodomain, eikonal, reaction eikonal) and (c) the method of forward calculation (finite difference, finite element, boundary element methods; homogeneous torso versus different organs considered). The forward problem is obviously related to the inverse problem of ECG as used in ECG imaging (ECGi). Thus, all articles dealing with fast and realistic methods of calculating the lead field matrix that maps the sources in the heart to the body surface ECG are related to the topic of this article but are not discussed in detail.
Published in 2004, the software package ECGSim allows for a fast and easy relation of source patterns on the heart to the corresponding 12-lead ECG. The user can modify local activation times, repolarization times and the slope of the transmembrane voltage [64]. Thus, these source distributions can be realistic or not—no model of excitation spread is running in the background. Meanwhile, advanced software packages to simulate the electrophysiology of the heart are available: openCARP [65][66], acCELLerate [67], FEniCS [68], Chaste [69], propag-5 [70], and LifeV [71]. They all have been verified in an N-version benchmark activity initiated by Niederer [72].
The literature survey yielded several articles that do not focus on a specific disease but rather deal with the general concept of calculating the ECG from computer models of the heart. Lyon et al. gave an outline of a computational pipeline, listed examples of modeling diseases together with the ECG and showed up several applications of modeling in ECG interpretation [73]. Potse suggested a fast method for realistic ECG simulation without oversimplifying the torso model by using a lead-field approach [74]. Building upon this approach, Pezzuto et al. found an even faster method that allows for implementation on a general-purpose graphic processing unit (GPGPU) [75]. Keller et al. investigated the influence of tissue conductivities on the resulting ECG [76]. Schuler et al. [77] found a way to downsample the fine grid necessary for calculating the spread of depolarization for the forward calculation of the ECG—further reducing calculation time. Neic et al. developed a reaction eikonal algorithm that simulates the spread of depolarization very fast and still delivers realistic ECGs [78].
Calculation times for computing the spread of depolarization and repolarization, the lead field matrix and the body surface potentials including the ECG strongly depend on the methods employed: highly detailed cell models versus simplified phenomenological models, high versus low spatial resolutions, etc. They can range from one day down to one second. As an example, the calculation times of the P-waves shown in Figure 1 were 27 h for the full bidomain model and the Courtemanche cell model, 1 h and 24 min for a pseudo-bidomain model and 40 min for a monodomain simulation (heart mesh with 4.7 million elements and 920 k nodes, desktop computer with 12 cores at 1.4 GHz). Fast calculation times are important for the researcher aiming at the identification of new features in the ECG, for creating a training dataset for machine learning and for personalization of a heart model. They are not relevant any more if, for example, a machine learning algorithm is finally used in clinics.
Hearts 02 00028 g001 550
Figure 1. Simulated P-waves of the 12-lead ECG with various atrial shapes, several orientations of the atria inside the torso and a variety of body shapes. The colors represent the total atrial volume in blue, the torso size in red and the orientation angle around the medial-lateral axis in orange [50].

2. Modeling the ECG of a Healthy Heart

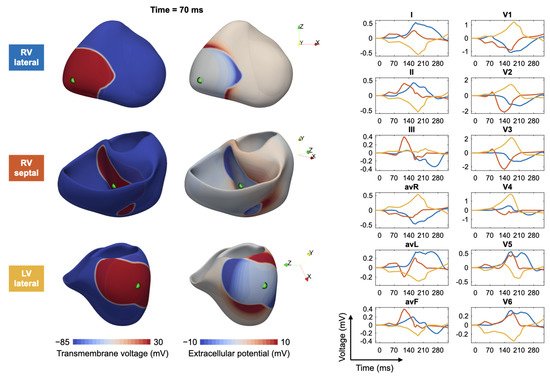
2.1. The QRS Complex and the Purkinje Tree

The morphology of the QRS complex is strongly determined by the topology of the His-Purkinje system in the ventricular subendocardial layer [2]. An earlier approach to fit a Punkinje network model to a measured ECG was published by Keller et al. in 2009 [1]. In total, 744 Purkinje muscle junctions were distributed across the ventricular endocardial surface following specific rules. Other publications followed this scheme and implemented “root points” coupled to thin endocardial layers with very fast conduction [3]. Automatic and reproducible manipulation of root node locations is facilitated by chamber-specific coordinate systems [79][80][81]. Mincholé et al. investigated the impact of anatomical variability on simulated QRS complexes [6]. They found that QRS duration is mainly determined by myocardial volume and not affected by the position of the heart in the torso. The latter influences QRS morphology in the precordial leads, whereas ventricular anatomy dominates in the limb leads. Cranford et al. carried out a sensitivity study: they implemented 1 to 4 “seed stimuli” and up to 384 “regional stimuli” and observed the changes in the QRS complex while changing the number and topology of excitation sites [5]. The topology of four seed stimuli at adapted positions was more relevant than a large number of regional stimuli. Pezzuto et al. were able to reproduce the QRS complex of 11 patients using up to 11 of the earliest activation sites on the endocardium and adapted the conduction velocity in the ventricles and in a fast endocardial layer [7]. Gillette et al. proposed a comprehensive workflow to optimize the positioning of five root disks, timing, and endocardial conduction velocities (10 parameters) to reproduce the QRS complex with a personalized model [8].
The healthy QRS complex can be reproduced faithfully, meaning that adapted heart models show an ECG with high correlation to measured ECGs. This does not prove that the modeled spread of depolarization is the one present in the patient, but it is good to see that there are no inconsistencies. Some relevant questions are: Which parameters in the model are responsible for the natural variability of QRS complexes—both inter- and intra-patient wise [4][6]? Is the heart axis that is visible in the ECG mainly determined by the geometrical axis of the heart or by the properties of the His-Purkinje system? Which simplifications of the thorax model are acceptable and where do we need detailed models?

2.2. The T-Wave and the Repolarization

Modeling the T-wave is a challenging task. If all myocytes in the ventricles would follow the same action potential, the T-wave would have the opposite sign as the R-peak. Heterogeneity is a necessary condition for concordant T-waves. Keller et al. investigated various schemes of heterogeneity of the IKs

repolarization current (transmural, apico-basal, left–right) and found that both transmural and apico-basal gradients can lead to realistic T-waves, whereas a pure left–right heterogeneity creates a notch in the T-wave [11]. Even though the focus of an article of Bukhari et al. was on the changes in the T-wave during dialysis, this article also reported on the heterogeneity that is needed to obtain a realistic T-wave in healthy hearts. They assume a solely transmural dispersion of ion channel conductivities [13]. Xue et al. analyzed how transmural and apico-basal heterogeneities change the morphology of the T-wave. They concluded that mainly apico-basal gradients contribute to a positive T-Wave [10]. The modeled heterogeneity scenarios are informed by experimental cellular data [82]. However, the available data do not allow us to draw definite conclusions and different heterogeneity patterns can lead to the similar T-wave morphologies.

While contraction of the heart happens only after the P-wave and the early QRS complex, it can influence the source distribution during the repolarization. How the contraction of the heart affects the morphology of the simulated T-wave was investigated by Moss et al. They observed an 8% increase in amplitude and a shift of the T-wave peak by 7 ms [12].

2.3. The P-Wave

A review about computerized modeling of the atria including the corresponding ECG was given by Doessel et al. in 2012 [15]. Krueger et al. were the first to set up an atrial model that included realistic fiber orientation [14][83]. They also investigated the influence of atrial heterogeneities on the morphology of the P-wave, created personalized models and compared the ECGs of several patients [16].
The contribution of the left and right atria to the P-wave was analyzed by Loewe et al. [17] and Jacquemet et al. [18]. Even in the last third of the P-wave, one-third of the signal stems from the right atrium [17]. Potse et al. discovered that a jigging morphology of the P-wave, which was observed in computer simulations, was not an artefact but could be observed in a similar way in healthy volunteers when carefully preventing smoothing through filtering or averaging [19]. Loewe et al. investigated the influence of the earliest site of activation in the right atrium (i.e., the sinus node exit site) on the morphology of the P-wave [20] and could demonstrate that small shifts in the earliest excitation site and its proximity to the inter-atrial connections can significantly change the terminal phase of the P-wave. Andlauer et al. dissected the differential effects of atrial dilation and hypertrophy on the morphology of the P-wave [21] and showed that left atrial dilation did not influence P-wave duration significantly, but instead had a strong effect on P-wave amplitude and thus P-wave Terminal Force in lead V1 (PTF-V1).
A literature survey of simulations of the P-wave and in particular of the P-wave in patients suffering from paroxysmal atrial fibrillation (AFib) was published by Filos et al. [43]. All the effects described in the literature that have an influence on the morphology of the P-wave of AFib patients are outlined. Despite the very large number of articles, we conclude that there is still a way to go before these results can be routinely used in clinical practice.
Nagel et al. analyzed the inter- and intra-patient variability of the P-wave in the Physionet ECG database, aiming at the optimization of a simulated database of P-waves [84]. Figure 1 shows several examples of P-waves with various atrial shapes, several orientations of the atria inside the torso and a variety of body shapes.

2.4. Modeling Rhythmic Features and Heart Rate Variability

Modeling of a heart beat most often starts with a stimulation either from an area around the sinus node (atria) or from the model of the Purkinje tree. Modeling of the sinus node is an interesting research topic that goes beyond the scope of this article.
The ECG fluctuates from beat to beat even in the healthy state. Both the RR interval and also the morphology of the P-, QRS- and T-wave are not completely periodic. The fluctuations of the RR interval are well known and analyzed by means of heart rate variability (HRV), as reviewed by Rajendra et al. [85]. HRV is high in normal hearts and low when there is a cardiac problem. The variation in the beat-to-beat RR interval is usually studied in both the time domain and frequency domain. Not many clinicians make use of this measure in daily clinical practice. On the modeling side, only few articles describe simulations of beta-adrenergic and vagal tones on the sinus node [86]. It seems as if there is still a “missing link” between computerized modeling of the heart and HRV interpretation [87].

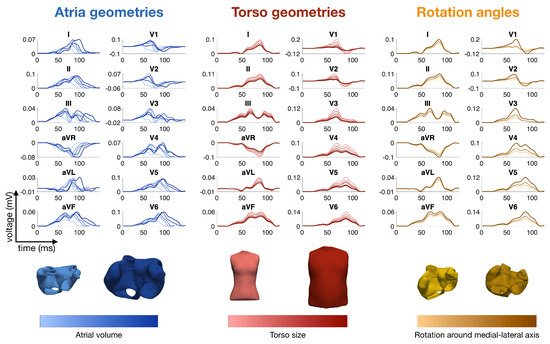
2.5. Modeling Inter- and Intra-Patient Variability

The variety of ECG morphologies observed in a cohort of healthy humans is large. This can be explained by different geometries of the heart [88] , different rotation inside the thorax [6], and different shapes of the torso. Moreover, differences in electrophysiology also contribute to the variability (see, for example, the discussion about the QRS morphology and the Purkinje tree in Section 2.1).
As already mentioned in Section 2.3, Nagel et al. investigated the inter- and intra-patient variability of the P-wave [84]. The beat-to-beat variability of the P-wave in case of atrial fibrillation was investigated by Pezzuto et al. [42]. Already small variations (1 to 5 mm) in the location of the earliest activation site lead to changes in the morphology of the P-wave. This effect was significantly enhanced if slow conducting regions were near the earliest activation site.

3. Modeling Diseases and the Corresponding ECG

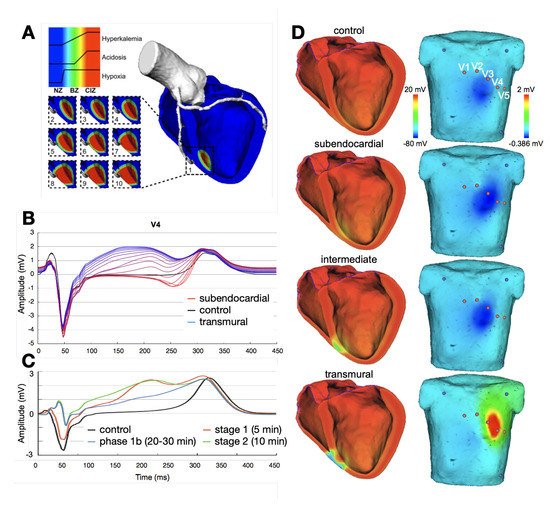
3.1. Ischemia and Infarction

Loewe at al. gave an outline of how computer modeling can support comprehension of cardiac ischemia and discussed the link to the corresponding ECG [28]. Figure 2 shows several examples of ischemic regions together with the corresponding ECG. The parameters of the ten Tusscher–Panfilov cell model which reflect the degree and temporal stage of the occlusion were summarized by Wilhelms et al. [25]. They considered the cellular effects due to hyperkalemia, acidosis and hypoxia as well as due to cellular uncoupling. After clarifying the origin of ST-segment elevation (and depression), they also demonstrated how several ischemic scenarios will not show any ST-segment change [26]. Thus, they were able to explain the large group of non-ST-segment elevation myocardial infarctions (NSTEMI). Potyagaylo et al. showed that these scenarios are not only electrically but also magnetically “silent” [89]. Loewe at al.—using computer modeling—investigated whether additional electrodes, optimized electrode placement or improved analysis of the ST segment could lead to better diagnosis of patients with acute ischemia. They suggest the deviation from baseline at the K-point as being superior to J-point analysis [27].
Hearts 02 00028 g002 550
Figure 2. Examples of ischemic regions with varying transmural extent due to occlusion of the left anterior descending coronary artery and the related levels of hyperkalemia, acidosis, and hypoxia (A). ECG lead V4 for ischemia of varying transmural extent in temporal stage 2 (B) and varying duration of a transmural ischemia (C). Ventricular transmembrane voltage and body surface potential distribution during the action potential plateau (t = 200 ms) for ischemia of varying transmural extent in stage 2 (D). The QRS complex was not optimized in this study. (Images reproduced with permission from [28].)
Ledezma et al. created populations of control and ischemic cell strands and observed the corresponding pseudo-ECGs (which is the voltage between two virtual electrodes at or near to the ends of a tissue strand immersed in an infinite homogeneous volume conductor). Based on these data, they trained an artificial neural network that was able to determine severity (mild or severe) and size of the ischemic region from the pseudo-ECG [30].
All these articles deal with ischemia and “fresh” infarctions (not older than a couple of hours). The modeling of “old” infarction scars seems to be straightforward: the scar areas cannot depolarize, they should be “switched off” during modeling. Basically. the QRS complex will change. In particular, small bridges of viable tissue within a scar area are of interest since they are likely to lead to ventricular tachycardia (VT). Lopez-Perez et al. were able to set up a personalized model of a patient with an old infarction with strong emphasis on modeling border zones. They were able to reproduce the 12-lead ECG of a patient with a history of infarction both in sinus rhythm and during VT [29].
Electrocardiographic imaging of myocardial infarction was the subject of the Challenge of the Computing in Cardiology conference in 2007. BSPMs of patients were provided for the participants. Ghasemi et al. were very successful in finding the location and extent of the infarction using only the heart vector and a very simplified model of the distribution of depolarization during systole [90]. Farina et al. employed a model-based approach to solve the task [23] and also reached very good results; however, based on the full BSPM. Jiang et al. investigated the best electrode arrangements to localize an infarcted area in the heart [24]. A dense set of electrodes including and extending the precordial leads was essential. Optimal results were obtained when using at least 64 electrodes.

3.2. Ventricular Ectopic Beats and Extrasystoles

The localization of ventricular ectopic beats (premature ventricular contractions, PVCs) is a major topic of the inverse problem of ECG. Any knowledge about the site of origin can guide the cardiologist during an ablation procedure and thus shorten the duration of the invasive procedure. Many publications contain chapters on calculating the body surface potential map of ventricular ectopic beats using simulations of the spread of depolarization (see, for example, Potyagaylo et al. [31]). Most of them assume that the individual body shape and cardiac geometry is known, which is, however, not the setting of traditional ECG analysis.
Figure 3 shows, as an example, a fast simulation of the spread of depolarization (transmembrane voltage and epicardial potentials) and the corresponding 12-lead ECG for three different ventricular extrasystoles.
Hearts 02 00028 g003 550
Figure 3. Modeling of ectopic beats and the corresponding ECG: for three different trigger locations in the right ventricle (RV) and left ventricle (LV), the transmembrane voltage (left column), the extracellular potentials (middle column) and corresponding ECGs (right column) are shown. Excitation propagation was computed by solving the anisotropic Eikonal equation.

References

  1. Keller, D.U.J.; Kalayciyan, R.; Dössel, O.; Seemann, G. Fast creation of endocardial stimulation profiles for the realistic simulation of body surface ECGs. In Proceedings of the IFMBE World Congress on Medical Physics and Biomedical Engineering, Munich, Germany, 7–12 September 2009; Volume 25/4, pp. 145–148.
  2. Vigmond, E.J.; Stuyvers, B.D. Modeling our understanding of the His-Purkinje system. Prog. Biophys. Mol. Biol. 2016, 120, 179–188.
  3. Cardone-Noott, L.; Bueno-Orovio, A.; Mincholé, A.; Zemzemi, N.; Rodriguez, B. Human ventricular activation sequence and the simulation of the electrocardiographic QRS complex and its variability in healthy and intraventricular block conditions. EP Eur. 2016, 18, iv4–iv15.
  4. Kahlmann, W.; Poremba, E.; Potyagaylo, D.; Dössel, O.; Loewe, A. Modelling of patient-specific Purkinje activation based on measured ECGs. Curr. Dir. Biomed. Eng. 2017, 3, 171–174.
  5. Cranford, J.P.; O’Hara, T.J.; Villongco, C.T.; Hafez, O.M.; Blake, R.C.; Loscalzo, J.; Fattebert, J.L.; Richards, D.F.; Zhang, X.; Glosli, J.N.; et al. Efficient Computational Modeling of Human Ventricular Activation and Its Electrocardiographic Representation: A Sensitivity Study. Cardiovasc. Eng. Technol. 2018, 9, 447–467.
  6. Mincholé, A.; Zacur, E.; Ariga, R.; Grau, V.; Rodriguez, B. MRI-Based Computational Torso/Biventricular Multiscale Models to Investigate the Impact of Anatomical Variability on the ECG QRS Complex. Front. Physiol. 2019, 10, 1103.
  7. Pezzuto, S.; Prinzen, F.W.; Potse, M.; Maffessanti, F.; Regoli, F.; Caputo, M.L.; Conte, G.; Krause, R.; Auricchio, A. Reconstruction of three-dimensional biventricular activation based on the 12-lead electrocardiogram via patient-specific modelling. EP Eur. 2021, 23, 640–647.
  8. Gillette, K.; Gsell, M.A.; Prassl, A.J.; Karabelas, E.; Reiter, U.; Reiter, G.; Grandits, T.; Peyer, C.; Štern, D.; Urschler, M.; et al. A Framework for the Generation of Digital Twins of Cardiac Electrophysiology from Clinical 12-leads ECGs. Med. Image Anal. 2021, 71, 102080.
  9. Grandits, T.; Effland, A.; Pock, T.; Krause, R.; Plank, G.; Pezzuto, S. GEASI: Geodesic-based Earliest Activation Sites Identification in cardiac models. arXiv 2021, arXiv:2102.09962v1.
  10. Xue, J.; Chen, Y.; Han, X.; Gao, W. Electrocardiographic morphology changes with different type of repolarization dispersions. J. Electrocardiol. 2010, 43, 553–559.
  11. Keller, D.U.J.; Weiss, D.L.; Dossel, O.; Seemann, G. Influence of I(Ks) heterogeneities on the genesis of the T-wave: A computational evaluation. IEEE Trans. Biomed. Eng. 2012, 59, 311–322.
  12. Moss, R.; Moritz Wülfers, E.; Seemann, G. T-Wave Changes Due to Cardiac Deformation Are Dependent on the Temporal Relationship Between Repolarization and Diastolic Phase. Comput. Cardiol. 2018, 45, 1–4.
  13. Bukhari, H.A.; Palmieri, F.; Ramirez, J.; Laguna, P.; Ruiz, J.E.; Ferreira, D.; Potse, M.; Sanchez, C.; Pueyo, E. Characterization of T Wave Amplitude, Duration and Morphology Changes During Hemodialysis: Relationship with Serum Electrolyte Levels and Heart Rate. IEEE Trans. Biomed. Eng. 2020, 1, ahead of print.
  14. Krueger, M.W.; Schmidt, V.; Tobón, C.; Weber, F.M.; Lorenz, C.; Keller, D.U.J.; Barschdorf, H.; Burdumy, M.; Neher, P.; Plank, G.; et al. Modeling atrial fiber orientation in patient-specific geometries: A semi-automatic rule-based approach. In Functional Imaging and Modeling of the Heart 2011; Lecture Notes in Computer Science; Axel, L., Metaxas, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6666, pp. 223–232.
  15. Dössel, O.; Krueger, M.W.; Weber, F.M.; Wilhelms, M.; Seemann, G. Computational modeling of the human atrial anatomy and electrophysiology. Med. Biol. Eng. Comput. 2012, 50, 773–799.
  16. Krueger, M.W.; Dorn, A.; Keller, D.U.J.; Holmqvist, F.; Carlson, J.; Platonov, P.G.; Rhode, K.S.; Razavi, R.; Seemann, G.; Dössel, O. In-silico modeling of atrial repolarization in normal and atrial fibrillation remodeled state. Med. Biol. Eng. Comput. 2013, 51, 1105–1119.
  17. Loewe, A.; Krueger, M.W.; Platonov, P.G.; Holmqvist, F.; Dössel, O.; Seemann, G. Left and Right Atrial Contribution to the P-wave in Realistic Computational Models. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9126, pp. 439–447.
  18. Jacquemet, V. Modeling left and right atrial contributions to the ECG: A dipole-current source approach. Comput. Biol. Med. 2015, 65, 192–199.
  19. Potse, M.; Lankveld, T.A.R.; Zeemering, S.; Dagnelie, P.C.; Stehouwer, C.D.A.; Henry, R.M.; Linnenbank, A.C.; Kuijpers, N.H.L.; Schotten, U. P-wave complexity in normal subjects and computer models. J. Electrocardiol. 2016, 49, 545–553.
  20. Loewe, A.; Krueger, M.W.; Holmqvist, F.; Dössel, O.; Seemann, G.; Platonov, P.G. Influence of the earliest right atrial activation site and its proximity to interatrial connections on P-wave morphology. EP Eur. 2016, 18, iv35–iv43.
  21. Andlauer, R.; Seemann, G.; Baron, L.; Dössel, O.; Kohl, P.; Platonov, P.; Loewe, A. Influence of left atrial size on P-wave morphology: Differential effects of dilation and hypertrophy. EP Eur. 2018, 20, iii36–iii44.
  22. Nagel, C.; Schuler, S.; Dössel, O.; Loewe, A. A bi-atrial statistical shape model for large-scale in silico studies of human atria: Model development and application to ECG simulations. arXiv 2021, arXiv:2102.10838.
  23. Farina, D.; Dössel, O. Model-based approach to the localization of infarction. Comput. Cardiol. 2007, 34, 173–176.
  24. Jiang, Y.; Qian, C.; Hanna, R.; Farina, D.; Dössel, O. Optimization of the electrode positions of multichannel ECG for the reconstruction of ischemic areas by solving the inverse electrocardiographic problem. Int. J. Bioelectromagn. 2009, 11, 27–37.
  25. Wilhelms, M.; Dössel, O.; Seemann, G. Comparing Simulated Electrocardiograms of Different Stages of Acute Cardiac Ischemia. In Proceedings of the International Conference on Functional Imaging and Modeling of the Hear, LNCS, New York, NY, USA, 25–27 May 2011; Volume 6666, pp. 11–19.
  26. Wilhelms, M.; Dössel, O.; Seemann, G. In silico investigation of electrically silent acute cardiac ischemia in the human ventricles. IEEE Trans. Biomed. Eng. 2011, 58, 2961–2964.
  27. Loewe, A.; Schulze, W.H.W.; Jiang, Y.; Wilhelms, M.; Luik, A.; Dössel, O.; Seemann, G. ECG-Based Detection of Early Myocardial Ischemia in a Computational Model: Impact of Additional Electrodes, Optimal Placement, and a New Feature for ST Deviation. BioMed Res. Int. Artic. 2014, 2015, 530352.
  28. Loewe, A.; Wülfers, E.M.; Seemann, G. Cardiac ischemia-insights from computational models. Herzschrittmachertherapie Elektrophysiologie 2018, 29, 48–56.
  29. Lopez-Perez, A.; Sebastian, R.; Izquierdo, M.; Ruiz, R.; Bishop, M.; Ferrero, J.M. Personalized Cardiac Computational Models: From Clinical Data to Simulation of Infarct-Related Ventricular Tachycardia. Front. Physiol. 2019, 10, 580.
  30. Ledezma, C.A.; Zhou, X.; Rodríguez, B.; Tan, P.J.; Díaz-Zuccarini, V. A modeling and machine learning approach to ECG feature engineering for the detection of ischemia using pseudo-ECG. PLoS ONE 2019, 14, e0220294.
  31. Potyagaylo, D.; Chmelevsky, M.; van Dam, P.; Budanova, M.; Zubarev, S.; Treshkur, T.; Lebedev, D. ECG Adapted Fastest Route Algorithm to Localize the Ectopic Excitation Origin in CRT Patients. Front. Physiol. 2019, 10, 183.
  32. Feng, Y.; Roney, C.; Hocini, M.; Niederer, S.; Vigmond, E. Robust Atrial Ectopic Beat Classification From Surface ECG Using Second-Order Blind Source Separation. Comput. Cardiol. 2020, 47.
  33. Yang, T.; Yu, L.; Jin, Q.; Wu, L.; He, B. Localization of Origins of Premature Ventricular Contraction by Means of Convolutional Neural Network From 12-Lead ECG. IEEE Trans. Biomed. Eng. 2018, 65, 1662–1671.
  34. Ferrer-Albero, A.; Godoy, E.J.; Lozano, M.; Martínez-Mateu, L.; Atienza, F.; Saiz, J.; Sebastian, R. Non-invasive localization of atrial ectopic beats by using simulated body surface P-wave integral maps. PLoS ONE 2017, 12, e0181263.
  35. Kania, M.; Coudière, Y.; Cochet, H.; Haissaguerre, M.; Jais, P.; Potse, M. Prediction of the Exit Site of Ventricular Tachycardia Based on Different ECG Lead Systems. Comput. Cardiol. 2017, 44.
  36. Lyon, A.; Bueno-Orovio, A.; Zacur, E.; Ariga, R.; Grau, V.; Neubauer, S.; Watkins, H.; Rodriguez, B.; Mincholé, A. Electrocardiogram phenotypes in hypertrophic cardiomyopathy caused by distinct mechanisms: Apico-basal repolarization gradients vs. Purkinje-myocardial coupling abnormalities. EP Eur. 2018, 20, iii102–iii112.
  37. Potse, M.; Krause, D.; Kroon, W.; Murzilli, R.; Muzzarelli, S.; Regoli, F.; Caiani, E.; Prinzen, F.W.; Krause, R.; Auricchio, A. Patient-specific modelling of cardiac electrophysiology in heart-failure patients. EP Eur. 2014, 16 (Suppl. 4), iv56–iv61.
  38. Nguyen, U.C.; Potse, M.; Regoli, F.; Caputo, M.L.; Conte, G.; Murzilli, R.; Muzzarelli, S.; Moccetti, T.; Caiani, E.G.; Prinzen, F.W.; et al. An in-silico analysis of the effect of heart position and orientation on the ECG morphology and vectorcardiogram parameters in patients with heart failure and intraventricular conduction defects. J. Electrocardiol. 2015, 48, 617–625.
  39. Giffard-Roisin, S.; Fovargue, L.; Webb, J.; Molléro, R.; Lee, J.; Delingette, H.; Ayache, N.; Razavi, R.; Sermesant, M. Estimation of Purkinje Activation from ECG: An Intermittent Left Bundle Branch Block Study. Lect. Notes Comput. Sci. 2017, 10124, 135–142.
  40. Nguyên, U.C.; Potse, M.; Vernooy, K.; Mafi-Rad, M.; Heijman, J.; Caputo, M.L.; Conte, G.; Regoli, F.; Krause, R.; Moccetti, T.; et al. A left bundle branch block activation sequence and ventricular pacing influence voltage amplitudes: An in vivo and in silico study. EP Eur. 2018, 20, iii77–iii86.
  41. Zhou, Z.; Jin, Q.; Yu, L.; Wu, L.; He, B. Noninvasive Imaging of Human Atrial Activation during Atrial Flutter and Normal Rhythm from Body Surface Potential Maps. PLoS ONE 2016, 11, e0163445.
  42. Pezzuto, S.; Gharaviri, A.; Schotten, U.; Potse, M.; Conte, G.; Caputo, M.L.; Regoli, F.; Krause, R.; Auricchio, A. Beat-to-beat P-wave morphological variability in patients with paroxysmal atrial fibrillation: An in silico study. EP Eur. 2018, 20, iii26–iii35.
  43. Filos, D.; Tachmatzidis, D.; Maglaveras, N.; Vassilikos, V.; Chouvarda, I. Understanding the Beat-to-Beat Variations of P-Waves Morphologies in AF Patients During Sinus Rhythm: A Scoping Review of the Atrial Simulation Studies. Front. Physiol. 2019, 10, 742.
  44. Lehrmann, H.; Jadidi, A.S.; Minners, J.; Chen, J.; Müller-Edenborn, B.; Weber, R.; Dössel, O.; Arentz, T.; Loewe, A. Novel Electrocardiographic Criteria for Real-Time Assessment of Anterior Mitral Line Block. JACC Clin. Electrophysiol. 2018, 4, 920–932.
  45. Luongo, G.; Schuler, S.; Luik, A.; Almeida, T.P.; Soriano, D.C.; Dossel, O.; Loewe, A. Non-Invasive Characterization of Atrial Flutter Mechanisms Using Recurrence Quantification Analysis on the ECG: A Computational Study. IEEE Trans. Biomed. Eng. 2021, 68, 914–925.
  46. Luongo, G.; Schuler, S.; Rivolta, M.W.; Dössel, O.; Sassi, R.; Loewe, A. Automatic ECG-based Discrimination of 20 Atrial Flutter Mechanisms: Influence of Atrial and Torso Geometries. Comput. Cardiol. 2020.
  47. Saha, M.; Conte, G.; Caputo, M.L.; Regoli, F.; Krause, R.; Auricchio, A.; Jacquemet, V. Changes in P-wave morphology after pulmonary vein isolation: Insights from computer simulations. Europace 2016, 18, iv23–iv34.
  48. Rodrigo, M.; Climent, A.M.; Liberos, A.; Fernández-Avilés, F.; Berenfeld, O.; Atienza, F.; Guillem, M.S. Highest dominant frequency and rotor positions are robust markers of driver location during noninvasive mapping of atrial fibrillation: A computational study. Heart Rhythm 2017, 14, 1224–1233.
  49. Irakoze, E.; Jacquemet, V. Simulated P wave morphology in the presence of endo-epicardial activation delay. EP Eur. 2018, 20, iii16–iii25.
  50. Nagel, C.; Luongo, G.; Azzolin, L.; Schuler, S.; Dössel, O.; Loewe, A. Non-Invasive and Quantitative Estimation of Left Atrial Fibrosis Based on P Waves of the 12-Lead ECG—A Large-Scale Computational Study Covering Anatomical Variability. J. Clin. Med. 2021, 10, 1797.
  51. Luongo, G.; Azzolin, L.; Schuler, S.; Rivolta, M.W.; Almeida, T.P.; Martínez, J.P.; Soriano, D.C.; Luik, A.; Müller-Edenborn, B.; Jadidi, A.; et al. Machine learning enables noninvasive prediction of atrial fibrillation driver location and acute pulmonary vein ablation success using the 12-lead ECG. Cardiovasc. Digit. Health J. 2021, 2, 126–136.
  52. Seemann, G.; Weiß, D.L.; Sachse, F.B.; Dössel, O. Simulation of the Long-QT Syndrome in a Model of Human Myocardium. Comput. Cardiol. 2003, 30, 287–290.
  53. Weiss, D.L.; Seemann, G.; Sachse, F.B.; Dössel, O. Modelling of the short QT syndrome in a heterogeneous model of the human ventricular wall. EP Eur. 2005, 7s2, 105–117.
  54. Seemann, G.; Alvarez de Eulate, M.; Konrad, N.; Maier, J.; Wilhelms, M.; Keller, D.; Dössel, O.; Scholz, E. Evaluating body surface ECG differences of simulated long-QT syndromes. Comput. Cardiol. 2013, 40, 345–348.
  55. Hernández Mesa, M.; Pilia, N.; Dössel, O.; Severi, S.; Loewe, A. Effects of Serum Calcium Changes on the Cardiac Action Potential and the ECG in a Computational Model. Curr. Dir. Biomed. Eng. 2018, 4, 251–254.
  56. Hernández Mesa, M.; Pilia, N.; Dössel, O.; Loewe, A. Influence of ECG Lead Reduction Techniques for Extracellular Potassium and Calcium Concentration Estimation. Curr. Dir. Biomed. Eng. 2019, 5, 69–72.
  57. Loewe, A.; Lutz, Y.; Nairn, D.; Fabbri, A.; Nagy, N.; Toth, N.; Ye, X.; Fuertinger, D.H.; Genovesi, S.; Kotanko, P.; et al. Hypocalcemia-Induced Slowing of Human Sinus Node Pacemaking. Biophys. J. 2019, 117, 2244–2254.
  58. Pilia, N.; Hernandez Mesa, M.; Dössel, O.; Loewe, A. ECG-based Estimation of Potassium and Calcium Concentrations: Proof of Concept with Simulated Data. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 2610–2613.
  59. Pilia, N.; Severi, S.; Raimann, J.G.; Genovesi, S.; Dössel, O.; Kotanko, P.; Corsi, C.; Loewe, A. Quantification and classification of potassium and calcium disorders with the electrocardiogram: What do clinical studies, modeling, and reconstruction tell us? APL Bioeng. 2020, 4, 041501.
  60. Pilia, N.; Corsi, C.; Severi, S.; Dössel, O.; Loewe, A. Reconstruction of Potassium Concentrations with the ECG on Imbalanced Datasets. arXiv 2020, arXiv:2006.05212.
  61. Wilhelms, M.; Rombach, C.; Scholz, E.P.; Doessel, O.; Seemann, G. Impact of amiodarone and cisapride on simulated human ventricular electrophysiology and electrocardiograms. EP Eur. 2012, 14, v90–v96.
  62. Zemzemi, N.; Bernabeu, M.O.; Saiz, J.; Cooper, J.; Pathmanathan, P.; Mirams, G.R.; Pitt-Francis, J.; Rodriguez, B. Computational assessment of drug-induced effects on the electrocardiogram: from ion channel to body surface potentials. Br. J. Pharmacol. 2013, 168, 718–733.
  63. Zemzemi, N.; Rodriguez, B. Effects of L-type calcium channel and human ether-a-go-go related gene blockers on the electrical activity of the human heart: A simulation study. EP Eur. 2015, 17, 326–333.
  64. Oosterom, A.V.; Oostendorp, T.F. ECGSIM: An interactive tool for studying the genesis of QRST forms. Heart 2004, 90, 165–168.
  65. Plank, G.; Loewe, A.; Neic, A.; Augustin, C.; Huang, Y.L.; Gsell, M.A.; Karabelas, E.; Nothstein, M.; Prassl, A.J.; Sánchez, J.; et al. The openCARP simulation environment for cardiac electrophysiology. Comput. Methods Programs Biomed. 2021, 208, 106223.
  66. Sánchez, J.; Nothstein, M.; Neic, A.; Huang, Y.L.; Prassl, A.J.; Klar, J.; Ulrich, R.; Bach, F.; Zschumme, P.; Selzer, M.; et al. openCARP: An Open Sustainable Framework for In-Silico Cardiac Electrophysiology Research. Comput. Cardiol. 2020, 47.
  67. Seemann, G.; Sachse, F.B.; Karl, M.; Weiss, D.L.; Heuveline, V.; Dössel, O. Framework for modular, flexible and efficient solving the cardiac bidomain equation using PETSc. Math. Ind. 2010, 15, 363–369.
  68. Sundnes, J.; Nielsen, B.F.; Mardal, K.A.; Cai, X.; Lines, G.T.; Tveito, A. On the computational complexity of the bidomain and the monodomain models of electrophysiology. Ann. Biomed. Eng. 2006, 34, 1088–1097.
  69. Cooper, F.; Baker, R.; Bernabeu, M.; Bordas, R.; Bowler, L.; Bueno-Orovio, A.; Byrne, H.; Carapella, V.; Cardone-Noott, L.; Cooper, J.; et al. Chaste: Cancer, Heart and Soft Tissue Environment. J. Open Source Softw. 2020, 5, 1848.
  70. Krause, D.; Potse, M.; Dickopf, T.; Krause, R.; Auricchio, A.; Prinzen, F. Hybrid Parallelization of a Large-Scale Heart Model. Lect. Notes Comput. Sci. 2012, 7174, 120–132.
  71. Quarteroni, A.; Manzoni, A.; Vergara, C. The cardiovascular system: Mathematical modelling, numerical algorithms and clinical applications. Acta Numer. 2017, 26, 365–590.
  72. Niederer, S.A.; Kerfoot, E.; Benson, A.P.; Bernabeu, M.O.; Bernus, O.; Bradley, C.; Cherry, E.M.; Clayton, R.; Fenton, F.H.; Garny, A.; et al. Verification of cardiac tissue electrophysiology simulators using an N-version benchmark. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 4331–4351.
  73. Lyon, A.; Mincholé, A.; Martínez, J.P.; Laguna, P.; Rodriguez, B. Computational techniques for ECG analysis and interpretation in light of their contribution to medical advances. J. R. Soc. Interface 2018, 15, 20170821.
  74. Potse, M. Scalable and Accurate ECG Simulation for Reaction-Diffusion Models of the Human Heart. Front. Physiol. 2018, 9, 370.
  75. Pezzuto, S.; Kal’avský, P.; Potse, M.; Prinzen, F.W.; Auricchio, A.; Krause, R. Evaluation of a Rapid Anisotropic Model for ECG Simulation. Front. Physiol. 2017, 8, 265.
  76. Keller, D.U.J.; Weber, F.M.; Seemann, G.; Dössel, O. Ranking the Influence of Tissue Conductivities on Forward-Calculated ECGs. IEEE Trans. Biomed. Eng. 2010, 57, 1568–1576.
  77. Schuler, S.; Tate, J.D.; Oostendorp, T.F.; MacLeod, R.S.; Dössel, O. Spatial Downsampling of Surface Sources in the Forward Problem of Electrocardiography. In Functional Imaging and Modeling of the Heart; Lecture Notes in Computer Science; Coudière, Y., Ozenne, V., Vigmond, E., Zemzemi, N., Eds.; Springer International Publishing: Berlin, Germany, 2019; Volume 11504, pp. 29–36.
  78. Neic, A.; Campos, F.O.; Prassl, A.J.; Niederer, S.A.; Bishop, M.J.; Vigmond, E.J.; Plank, G. Efficient computation of electrograms and ECGs in human whole heart simulations using a reaction-eikonal model. J. Comput. Phys. 2017, 346, 191–211.
  79. Schuler, S.; Pilia, N.; Potyagaylo, D.; Loewe, A. Cobiveco: Consistent biventricular coordinates for precise and intuitive description of position in the heart—With MATLAB implementation. arXiv 2021, arXiv:2102.02898.
  80. Bayer, J.; Prassl, A.J.; Pashaei, A.; Gomez, J.F.; Frontera, A.; Neic, A.; Plank, G.; Vigmond, E.J. Universal ventricular coordinates: A generic framework for describing position within the heart and transferring data. Med. Image Anal. 2018, 45, 83–93.
  81. Roney, C.H.; Pashaei, A.; Meo, M.; Dubois, R.; Boyle, P.M.; Trayanova, N.A.; Cochet, H.; Niederer, S.A.; Vigmond, E.J. Universal atrial coordinates applied to visualisation, registration and construction of patient specific meshes. Med. Image Anal. 2019, 55, 65–75.
  82. Opthof, T.; Remme, C.A.; Jorge, E.; Noriega, F.; Wiegerinck, R.F.; Tasiam, A.; Beekman, L.; Alvarez-Garcia, J.; Munoz-Guijosa, C.; Coronel, R.; et al. Cardiac activation-repolarization patterns and ion channel expression mapping in intact isolated normal human hearts. Heart Rhythm 2017, 14, 265–272.
  83. Wachter, A.; Loewe, A.; Krueger, M.W.; Dössel, O.; Seemann, G. Mesh structure-independent modeling of patient-specific atrial fiber orientation. Curr. Dir. Biomed. Eng. 2015, 1, 409–412.
  84. Nagel, C.; Pilia, N.; Loewe, A.; Dössel, O. Quantification of Interpatient 12-lead ECG Variabilities within a Healthy Cohort. Curr. Dir. Biomed. Eng. 2020, 6, 493–496.
  85. Rajendra Acharya, U.; Paul Joseph, K.; Kannathal, N.; Lim, C.M.; Suri, J.S. Heart rate variability: A review. Med. Biol. Eng. Comput. 2006, 44, 1031–1051.
  86. Wilders, R.; Hoekstra, M.; van Ginneken, A.C.G.; Verkerk, A.O. Beta-adrenergic modulation of heart rate: Contribution of the slow delayed rectifier K+ current (IKs). Comput. Cardiol. 2010, 37, 629–631.
  87. Dössel, O.; Reumann, M.; Seemann, G.; Weiss, D. The missing link between cardiovascular rhythm control and myocardial cell modeling. Biomed Tech. 2006, 51, 205–209.
  88. Rodero, C.; Strocchi, M.; Marciniak, M.; Longobardi, S.; Whitaker, J.; O’Neill, M.D.; Gillette, K.; Augustin, C.; Plank, G.; Vigmond, E.J.; et al. Linking statistical shape models and simulated function in the healthy adult human heart. PLoS Comput. Biol. 2021, 17, e1008851.
  89. Potyagaylo, D.; Seemann, G.; Schulze, W.; Dössel, O. Magnetocardiography did not uncover electrically silent ischemia in an in-silico study case. Comput. Cardiol. 2015, 42, 1145–1148.
  90. Ghasemi, M. Electrocardiographic imaging of myocardial infarction using heart vector analysis. Comput. Cardiol. 2007.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Cardiac & Cardiovascular Systems
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Axel Loewe
View Times: 541
Entry Collection: Hypertension and Cardiovascular Diseases
Revisions: 3 times (View History)
Update Date: 25 Aug 2021
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback