Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Lin Zhang
 + 1485 word(s) 1485 2021-05-13 08:26:23 |
2 format correct
Lindsay Dong
 + 318 word(s) 1803 2021-06-18 09:44:38 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Zhang, L. Integrated OPAs for Beam Forming/Steering. Encyclopedia. Available online: https://encyclopedia.pub/entry/11007 (accessed on 20 April 2024).
Zhang L. Integrated OPAs for Beam Forming/Steering. Encyclopedia. Available at: https://encyclopedia.pub/entry/11007. Accessed April 20, 2024.
Zhang, Lin. "Integrated OPAs for Beam Forming/Steering" Encyclopedia, https://encyclopedia.pub/entry/11007 (accessed April 20, 2024).
Zhang, L. (2021, June 18). Integrated OPAs for Beam Forming/Steering. In Encyclopedia. https://encyclopedia.pub/entry/11007
Zhang, Lin. "Integrated OPAs for Beam Forming/Steering." Encyclopedia. Web. 18 June, 2021.
Integrated OPAs for Beam Forming/Steering
Edit
This entry is adapted from the peer-reviewed paper 10.3390/app11094017

Integrated optical phased arrays (OPAs) can be used for beam shaping and steering with a small footprint, lightweight, high mechanical stability, low price, and high-yield, benefiting from the mature CMOS-compatible fabrication. 

integrated optical phased arrays beam shaping beam steering

1. Introduction

In recent years, optical phased arrays (OPAs) have attracted a great deal of attention. At optical wavelengths, small diffraction angles for a given aperture size can be achieved, compared with microwave radar systems. Featured by precise and agile free-space beam forming and steering [1][2][3][4][5][6][7][8][9][10][11][12], OPA techniques are highly desirable. However, current commercially available OPA components are mainly based on mechanical control, such as motor-driven rotating collimation stages/mirrors. Mechanical beam steering provides high efficiency and a relatively large scanning angle, through mechanically moving parts such as a gimbal, which can be susceptible to mechanical wear and tear, less stable, and limited in speed [13][14] due to the masses involved. The bulky mechanical steering approach is less preferred as it typically degrades in performance due to acceleration, temperature, vibration, and inertial forces. Additionally, mechanical steering often consumes significant energy. Furthermore, they require a complex assembly and calibration process, causing a greatly high unit cost. More importantly, these mechanical approaches are only capable of steering a single light beam. Arbitrary pointing and rapid steering as needed for advanced communication and sensing applications then become difficult or even incapable [14][15][16][17][18][19].

As one of the promising solutions for the next-generation dynamic beam steering, integrated OPAs simultaneously possess the advantages of being stable, rapid, and precise without relying on any mechanical motion, making them robust and insensitive to external constraints such as accelerations. Some of the integrated OPAs are presented in Figure 1. A wire-bonded device on a chip carrier plugged into a breadboard is presented in Figure 1a. Figure 1b shows a one-dimensional 64-channel chip-scale blue light phased array. A kind of III-V/Si phase-shifter-based OPA is shown in Figure 1c. Figure 1d is the photo of a fabricated OPA chip on a penny. Using an integrated approach, the OPAs can be made very small.

Applsci 11 04017 g001 550

Figure 1. Integrated OPAs. (a) The wire-bonded device on the chip carrier plugged into the breadboard. Reprinted with permission from [20] © The Optical Society. (b) Blue light OPA. Reprinted with permission from [21] © The Optical Society. (c) A set of three 32-channel and one 240-channel OPAs on a coin. Reprinted with permission from the author of [22] published on Arxiv, 2018. (d) A photo of an OPA on a penny. Reprinted with permission from [23] © The Optical Society.

2. Principles

2.1. Fraunhofer Diffraction Model

The Fraunhofer diffraction theory [24] can be used to describe the far-field interference of OPAs, in which scalar field e in the x0y0-plane diffracts to the x1y1-plane at a large distance z0 [13], following the rule below:

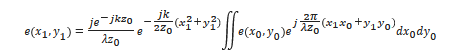
where k is the free-space wave vector. For the N × M OPA presented in Figure 2a, the far field at a certain point r is the far-field pattern of one element, i.e., F (θx, θy), multiplied by the sum of all the phase factors [13]:

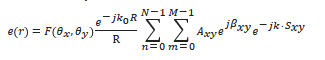
where R = |r|, Axy is the field amplitude, βxy is the relative phase at each element, k0 is the free-space wave vector, and Sxy is the position of the radiating element. θx and θy indicate the angle of x- and y-direction, respectively. For uniform arrays [13], the far field is:

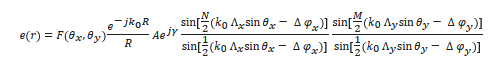
where γ is a phase factor determined by

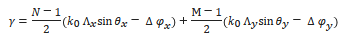
where Λx and Λy are the element spacing along the x- and y-axis, respectively. Δφx and Δφy are the phase differences.

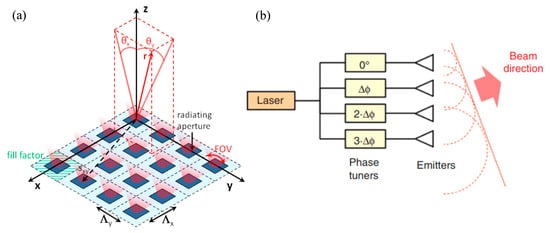
Applsci 11 04017 g002 550

Figure 2. (a) Schematic of an OPA based on WGAs. Reprinted with permission from [13], © Gent University. (b) An OPA based on EF structures. Reproduced from [18] published by De Gruyter, 2016.

In principle, the far-field radiation pattern of OPAs is calculated by the far field of individual antenna multiplied by the array factor [10][25][26]. The far-field pattern can be desirably modulated based on this theory.

2.2. Multi-Slit Diffraction Model

As illustrated in Figure 2b, uniform 1D EF OPAs can be described by the multi-slit diffraction model. The EF OPA is regarded as a rectangular aperture array in the diffraction model. Then the far-field angular intensity distribution [13][26][27] is in the form of:

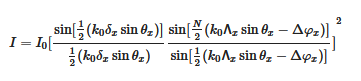
where δx is the element size of the N-element OPA, I0 stands for the unitary peak intensity in the far field of a single element, and θx indicates the angle of x-direction. The identical phase difference of Δφx is applied between adjacent channels placed at a pitch of Λx. The EF OPAs are commonly used to achieve 1D beam forming and steering by phase-shifting between waveguides. As shown in Figure 3a, the first fabricated OPA with a half-wavelength element spacing is used to demonstrate beam steering over a range of 64° by integrated thermo-optic (TO) heaters. The measured intensity of the horizontal cross sections and stitched-together captured images are presented at the top and the bottom [28].

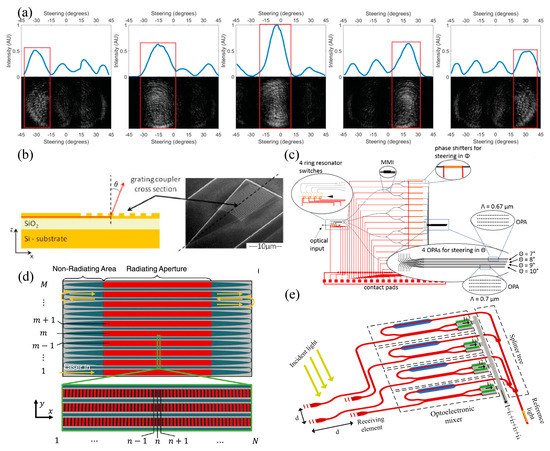
Applsci 11 04017 g003 550

Figure 3. (a) Half-wavelength element spacing OPA with integrated TO heaters for beam steering from left to right. Reproduced from [28] with the permission of AIP Publishing. (b) Schematic view of the cross section of a WGA. Reprinted with permission from [8] © The Optical Society. (c) Schematic image of the proposed 2D beam steering device at a fixed wavelength. Reprinted with permission from [29] © The Optical Society. (d) Schematic of a serpentine OPA. Reprinted with permission from [30] © The Optical Society. (e) A 2 × 2 OPA receiver. Reprinted with permission from [23] © The Optical Society.

2.3. Beam Steering Based on WGAs

Nearly all the proposed 2D OPAs till now depend on WGAs. Not all the 2D OPAs’ far-field patterns are completely formed by phase differences. There are some other steering approaches.

3. Building Blocks

Integrated photonics paves the way for low-cost large-scale OPA chips. As presented in Figure 4, typically, there are four necessary parts in an OPA: laser source, beam splitters, phase shifters, and emitters [12], for efficient light generation, manipulation, and chip-to-free-space transmission. We will discuss each part in detail in this section. Then a brief overview about overlayers and buried oxide (BOX) layers is given. The optimized thicknesses of the overlayers and BOX layers enhance the upward radiation of WGAs.

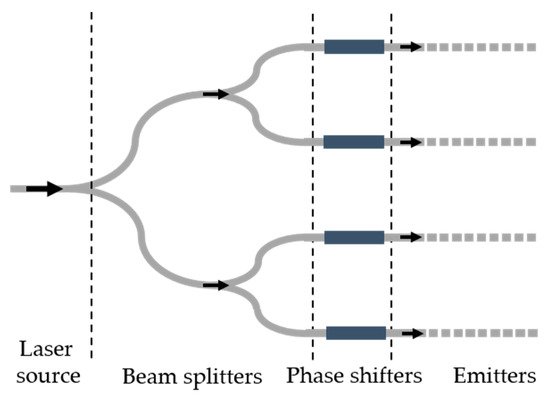
Applsci 11 04017 g004 550

Figure 4. A typical integrated OPA structure.

4. Configurations

In terms of emitter types, OPAs can be sorted into EF OPAs, WGA-based OPAs, and OPAs based on other emitter structures.

4.1. EF OPAs

Typically, EF OPAs can only be tuned by the phase difference between adjacent elements. As presented in Figure 5a, the first experimentally demonstrated aperiodic OPA was implemented on SOI [9]. The 12-channel unequal spaced OPA with a silica (SiO2) overlay and individual TO phase shifters enabled an FOV of 31.9° at 1.55 μm [9].

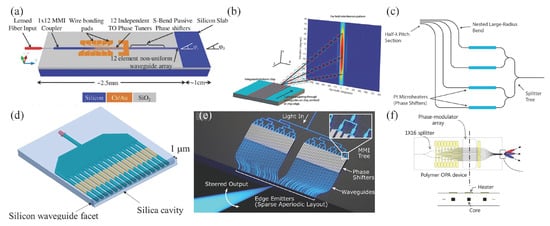
Applsci 11 04017 g007 550

Figure 5. EF OPA structures. (a) A SOI-based EF OPA. Reproduced from [9] with the permission of AIP Publishing. (b) The first demonstrated half-wavelength spacing OPA. Reproduced from [28] with the permission of AIP Publishing. (c) A dispersion-engineered half-wavelength EF OPA with low crosstalk. Reprinted with permission from the author of [31] published on Arxiv, 2018. (d) A SOI-based EF OPA with a SiO2 cavity for envelope tailoring. Reprinted with permission from [26] © The Optical Society. (e) A 1D 64-channel blue OPA with sparse aperiodic spacing. Reprinted with permission from [21] © The Optical Society. (f) Schematic of a 16-channel polymer EF OPA. Reprinted with permission from [32] © The Optical Society.

4.2. WGA-Based OPAs

The first OPA introduced in Si photonics was implemented based on WGA structures, as presented in Figure 6a. The 1D 16-element WGA-based OPA was fabricated on the SOI platform. An FOV of 2.3° × 14.1° was demonstrated with both TO phase modulation and wavelength tuning [7]. A 4 × 4 WGA-based OPA with an FOV of 1.5° was subsequently realized by the same group (Figure 6b). Wavelength tuning based on grating dispersion was exploited to decrease the number of phase controls [8]. The achieved FOV of 1.5° is relatively narrow due to the small fill factor of the OPA, which can be further improved by redesigning OPA with a proper fill factor. An 8 × 8 WGA-based OPA with Si heaters presented in Figure 6c enabled an FOV of 6° × 6° and a beamwidth of 1.6° × 1.6°. Lightly doped Si waveguides, which provided considerable resistances and low optical losses, and heavily doped Si leads were used as heaters to drop most of the heating power on waveguides. Zigzagged Si lead structures were used to increase the heating length and to provide thermal isolations between waveguides and metal contacts. The measured TO efficiency was about 8.5 mW per π phase shift [25].

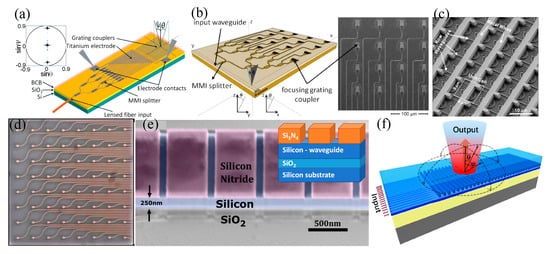
Applsci 11 04017 g008 550

Figure 6. WGA-based OPAs. (a) The first OPA introduced in Si photonics. Reprinted with permission from [7] © The Optical Society. (b) A 4 × 4 WGA-based OPA. Reprinted with permission from [8] © The Optical Society. (c) SEM of a fabricated OPA after dry etching away the dielectric SiO2. Reprinted with permission from [33] © The Optical Society. (d) An 8 × 8 OPA receiver. Reprinted with permission from [23] © The Optical Society. (e) False-colored tilted SEM of an aperiodic Si/Si3N4 grating. Reprinted with permission from [34] © The Optical Society. (f) A high contrast WGA-based OPA with high efficiency and low crosstalk. Reprinted with permission from [35] © The Optical Society.

5. Material Platforms

Integrated OPAs demonstrated on photonics platforms enable low-cost chip-scale applications. In addition to conventional Si platforms, OPAs have been implemented on other photonic integrated platforms. The major platforms of integrated OPAs, which include Si photonics platforms, III/V platforms, and III–V/Si hybrid platforms.

6. Performances

The main evaluation parameters of OPAs, which are FOVs, beamwidths and sidelobe suppression, modulation speeds, power consumption. It is important to note that one of critical factors determining FOVs, beamwidths and sidelobe suppression is the crosstalk and suppression among arrayed waveguide channels, and the efforts paid to reduce it should be reviewed first. For high-performance applications, large-scale OPAs are necessary. The scalability of OPAs will also be discussed. Finally, the calibration of OPAs to compensate for fabrication errors and mitigate crosstalk will be shown.

7. Outlook

More applications can be achieved based on integrated OPAs. Monolithically integrated OPAs take advantage of full integration and small chip sizes. EF OPAs can be used for 1D beam forming and steering. Wavelength-tuned 1D long-WGA-based OPAs with phase modulations decrease steering complexities in 2D steering. Problems of expensive precisely tunable laser sources [11][36] and limited performance [37][38] could be solved. Simplified high-performance on-chip tunable lasers are highly desirable. Large-scale sparse aperiodic 2D OPAs, which have wide FOVs and narrow beamwidths, are promising candidates for high-performance OPA-based applications. Design complexity of large-scale sparse aperiodic 2D OPAs need to be decreased for further applications. A two-chip integrated OPA with a sparse aperiodic aperture might be a promising solution [36].

For applications based on precise beam forming and steering, WGAs with normal direction radiation [37][39] as well as structures with plateau envelops [26][39][40] can be highly desirable Modulation speeds are greatly enhanced by EO phase shifters based on the carrier density changing function. Monolithically integrated LiNbO3 EO phase shifters [41] and contact graphene heaters with high efficiencies and operation speeds, low power consumption [42] can be used for excellent EO modulations. To decrease optical losses of sharp waveguide bends, 45° angle placed antennas may be used to enable optical routing through two sides of the aperture [36]. Fabrication errors need to be carefully treated [43].

References

  1. Wight, D.R.; Heaton, J.M.; Hughes, B.T.; Birbeck, J.C.H.; Hilton, K.P.; Taylor, D.J. Novel phased array optical scanning device implemented using GaAs/AlGaAs technology. Appl. Phys. Lett. 1991, 59, 899–901.
  2. Webb, G.W.; Vernon, W.; Sanchez, M.S.; Rose, S.C.; Angello, S. Optically controlled millimeter wave antenna. In Proceedings of the International Topical Meeting on Microwave Photonics, Melbourne, Australia, 17–19 November 1999; p. 275.
  3. Webb, G.W.; Vernon, W.; Sanchez, M.S.; Rose, S.C.; Angello, S. Novel photonically controlled antenna for MMW communications. In Proceedings of the International Topical Meeting on Microwave Photonics, Oxford, UK, 11–13 September 2000; p. 176.
  4. Igor, V.M.; Oleg, V.M. The brief elementary basics of antenna arrays. In Basic Principles of Fresnel Antenna Arrays, 1st ed.; Springer: Berlin, Germany, 2008; pp. 1–12.
  5. Xiao, F.; Hu, W.; Xu, A. Optical phased-array beam steering controlled by wavelength. Appl. Opt. 2005, 44, 5429–5433.
  6. Hosseini, A.; Kwong, D.; Zhao, Y.; Chen, Y.; Crnogorac, F.; Fabian, R.; Pease, W.; Chen, R.T. Unequally spaced waveguide arrays for silicon nanomembrane-based efficient large angle optical beam steering. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1439–1446.
  7. Acoleyen, K.V.; Bogaerts, W.; Jágerská, J.; Thomas, N.L.; Houdré, R.; Baets, R. Off-chip beam steering with a one-dimensional optical phased array on silicon-on-insulator. Opt. Lett. 2009, 34, 1477–1479.
  8. Acoleyen, K.V.; Rogier, H.; Baets, R. Two-dimensional optical phased array antenna on silicon-on-insulator. Opt. Express 2010, 18, 13655–13660.
  9. Kwong, D.; Hosseini, A.; Zhang, Y.; Chen, R.T. 1 × 12 Unequally spaced waveguide array for actively tuned optical phased array on a silicon nanomembrane. Appl. Phys. Lett. 2011, 99, 051104–051106.
  10. Sun, J.; Timurdogan, E.; Yaacobi, A.; Hosseini, E.S.; Watts, M.R. Large-scale nanophotonic phased array. Nature 2013, 493, 195–199.
  11. Poulton, C.V.; Byrd, M.J.; Russo, P.; Timurdogan, E.; Khandaker, M.; Vermeulen, D.; Watts, M.R. Long-range LiDAR and free-space data communication with high-performance optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 7700108.
  12. Hutchison, D.N.; Sun, J.; Doylend, J.K.; Kumar, R.; Heck, J.; Kim, W.; Phare, C.T.; Feshali, A.; Rong, H. High-resolution aliasing-free optical beam steering. Optica 2016, 3, 887–890.
  13. Acoleyen, K.V. Nanophotonic Beam Steering Elements Using Silicon Technology for Wireless Optical Applications. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2012.
  14. Kim, T.; Bhargava, P.; Poulton, C.V.; Notaros, J.; Yaacobi, A.; Timurdogan, E.; Baiocco, C.; Fahrenkopf, N.; Kruger, S.; Ngai, T.; et al. A single-chip optical phased array in a wafer-scale silicon photonics/CMOS 3D-integration platform. IEEE J. Solid-State Circuits 2019, 54, 3061–3074.
  15. Chang, Y.C.; Miller, S.A.; Phare, C.T.; Shin, M.C.; Zadka, M.; Roberts, S.P.; Stern, B.; Ji, X.; Mohanty, A.; Gordillo, O.A.J.; et al. Scalable low-power silicon photonic platform for all-solid-state beam steering. In Proceedings of the Micro- and Nanotechnology Sensors, Systems, and Applications XI, Baltimore, MD, USA, 13 May 2019; SPIE: Bellingham, WA, USA, 2019; Volume 10982.
  16. Chung, S.W.; Abediasl, H.; Hashemi, H. A monolithically integrated large-scale optical phased array in silicon-on-insulator CMOS. IEEE J. Solid-State Circuits 2018, 53, 275–296.
  17. Poulton, C.V.; Yaacobi, A.; Cole, D.B.; Byrd, M.J.; Raval, M.; Vermeulen, D.; Watts, M.R. Coherent solid-state LiDAR with silicon photonic optical phased arrays. Opt. Lett. 2017, 42, 4091–4094.
  18. Heck, M. Highly integrated optical phased arrays, photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 2017, 6, 93–107.
  19. Luo, X. Engineering Optics 2.0, a Revolution in Optical Theories, Materials, Devices and Systems, 1st ed.; Springer: Singapore, 2019; p. 647.
  20. Kwong, D.; Hosseini, A.; Covey, J.; Zhang, Y.; Xu, X.; Subbaraman, H.; Chen, R.T. On-chip silicon optical phased array for two-dimensional beam steering. Opt. Lett. 2014, 39, 941–944.
  21. Shin, M.C.; Mohanty, A.; Watson, K.; Bhatt, G.R.; Phare, C.T.; Miller, S.A.; Zadka, M.; Lee, B.S.; Ji, X.; Datta, I.; et al. Chip-scale blue light phased array. Opt. Lett. 2020, 45, 1934–1937.
  22. Xie, W.; Komljenovic, T.; Huang, J.; Davenport, M.L.; Bowers, J.E. Dense III-V/Si phase-shifter based optical phased array. arXiv 2019, arXiv:1904.01104.
  23. Fatemi, R.; Abiri, B.; Khachaturian, A.; Hajimiri, A. High sensitivity active flat optics optical phased array receiver with a two-dimensional aperture. Opt. Express 2018, 26, 29983–29999.
  24. Goodman, J.W. Introduction to Fourier Optics, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1996; pp. 74–75.
  25. Sun, J.; Timurdogan, E.; Yaacobi, A.; Su, Z.; Hosseini, E.S.; Cole, D.B.; Watts, M.R. Large-scale silicon photonic circuits for optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 8201115.
  26. Xu, W.; Zhou, L.; Lu, L.; Chen, J. Aliasing-free optical phased array beam-steering with a plateau envelope. Opt. Express 2019, 27, 3354–3368.
  27. Wu, Z.; Jiang, W.; Xia, J.; Huang, Q. Optical phased array antenna with wide steering range using grating array superlattices. In Proceedings of the Sixth International Conference on Optical and Photonic Engineering, Shanghai, China, 24 July 2018; Yu, Y., Zuo, C., Qian, K., Eds.; SPIE: Bellingham, WA, USA, 2018; p. 108272U.
  28. Kossey, M.R.; Rizk, C.; Foster, A.C. End-fire silicon optical phased array with half-wavelength spacing. APL Photonics 2018, 3, 011301.
  29. Tyler, N.A.; Fowler, D.; Malhouitre, S.; Garcia, S.; Grosse, P.; Rabaud, W.; Szelag, B. SiN integrated optical phased arrays for two-dimensional beam steering at a single near-infrared wavelength. Opt. Express 2019, 27, 5851–5858.
  30. Dostart, N.; Zhang, B.; Khilo, A.; Brand, M.; Qubaisi, K.A.; Onural, D.; Feldkhun, D.; Wagner, K.H.; Popović, M.A. Serpentine optical phased arrays for scalable integrated photonic lidar beam steering. Optica 2020, 7, 726–733.
  31. Phare, C.T.; Shin, M.C.; Miller, S.A.; Stern, B.; Lipson, M. Silicon optical phased array with high-efficiency beam formation over 180 degree field of view. arXiv 2018, arXiv:1802.04624.
  32. Kim, S.M.; Park, T.H.; Im, C.S.; Lee, S.S.; Kim, T.; Oh, M.C. Temporal response of polymer waveguide beam scanner with thermo-optic phase-modulator array. Opt. Express 2020, 28, 3768–3778.
  33. Sun, J.; Hosseini, E.; Yaacobi, A.; Cole, D.B.; Leake, G.; Coolbaugh, D.; Watts, M.R. Two-dimensional apodized silicon photonic phased arrays. Opt. Lett. 2014, 39, 367–370.
  34. Zadka, M.; Chang, Y.; Mohanty, A.; Phare, C.T.; Roberts, S.P.; Lipson, M. On-chip platform for a phased array with minimal beam divergence and wide field-of-view. Opt. Express 2018, 26, 2528–2534.
  35. Wang, P.; Luo, G.; Yu, H.; Li, Y.; Wang, M.; Zhou, X.; Chen, W.; Zhang, Y.; Pan, J. Improving the performance of optical antenna for optical phased arrays through high-contrast grating structure on SOI substrate. Opt. Express 2019, 27, 2703–2712.
  36. Fatemi, R.; Khachaturian, A.; Hajimiri, A. A nonuniform sparse 2-D large-FOV optical phased array with a low-power PWM drive. IEEE J. Solid State Circuits 2019, 54, 1200–1215.
  37. Kim, S.H.; You, J.B.; Ha, Y.G.; Kang, G.; Lee, D.S.; Yoon, H.; Yoo, D.E.; Lee, D.W.; Yu, K.; Youn, C.H.; et al. Thermo-optic control of the longitudinal radiation angle in a silicon-based optical phased array. Opt. Lett. 2019, 44, 411–414.
  38. Gao, Y.; Lo, J.C.; Lee, S.; Patel, R.; Zhu, L.; Nee, J.; Tsou, D.; Carney, R.; Sun, J. High-power, narrow-linewidth, miniaturized silicon photonic tunable laser with accurate frequency control. J. Lightwave Technol. 2020, 38, 265–271.
  39. Liu, Y.; Hao, Z.; Wang, L.; Xiong, B.; Sun, C.; Wang, J.; Li, H.; Han, Y.; Luo, Y. A single-chip multi-beam steering optical phased array: Design rules and simulations. Opt. Express 2021, 29, 7049–7059.
  40. Guo, Y.; Guo, Y.; Li, C.; Zhang, L. Bidirectional wide-angle waveguide grating antennas for optical phased arrays. To be submitted.
  41. Wang, C.; Zhang, M.; Chen, X.; Bertrand, M.; Ansari, A.; Chandrasekhar, S.; Winzer, P.; Lončar, M. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 2018, 562, 101–104.
  42. Wang, Y.; Liang, L.; Chen, Y.; Jia, P.; Qin, L.; Liu, Y.; Ning, Y.; Wang, L. Improved performance of optical phased arrays assisted by transparent graphene nanoheaters and air trenches. RSC Adv. 2018, 8, 8442–8449.
  43. Hashemi, H. Monolithic optical phased arrays in silicon. In Proceedings of the 22nd Microoptics Conference (MOC), Tokyo, Japan, 19–22 November 2017.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Optics
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Lin Zhang
View Times: 1.0K
Revisions: 2 times (View History)
Update Date: 18 Jun 2021
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback