- Subjects: Computer Science, Artificial Intelligence
- |
- Contributor:
- Dalibor Martišek
- mapping
- texture
- raytracing
1. Introduction
In computer graphics, ray tracing is a method of graphics rendering that simulates the physical behavior of light. Any physical wave or particle phenomenon with approximately linear motion can be simulated with this technique. Ray tracing is based on recoursive monitoring of a ray or a vawe during its passing through a scene. Various methods may used to simulate the interaction of a beam with scene objects.
In the contribution, there is simulated a multiple ray reflection on balls with applied textures. Fast texturing of balls is described, different ambient, specular and diffuse part of reflection is sumulated using so called Phong illumination model.
2. Direct Mapping of a General Surface
Applying a texture to a general surface is illustrated in Figure 1. Textur is a function which assigns a value of a modulated quantity (color in our case) to a point of plane: ; i.e.
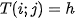 according Figure 1. This texture is applied to a general surface by using so called direct mapping, i. e. function
according Figure 1. This texture is applied to a general surface by using so called direct mapping, i. e. function 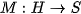 . Composite function
. Composite function 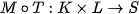 assigns each point from domain
assigns each point from domain  to a segment surface segment
to a segment surface segment 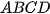 , where
, where
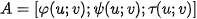
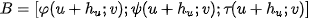
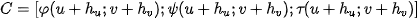
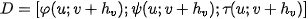
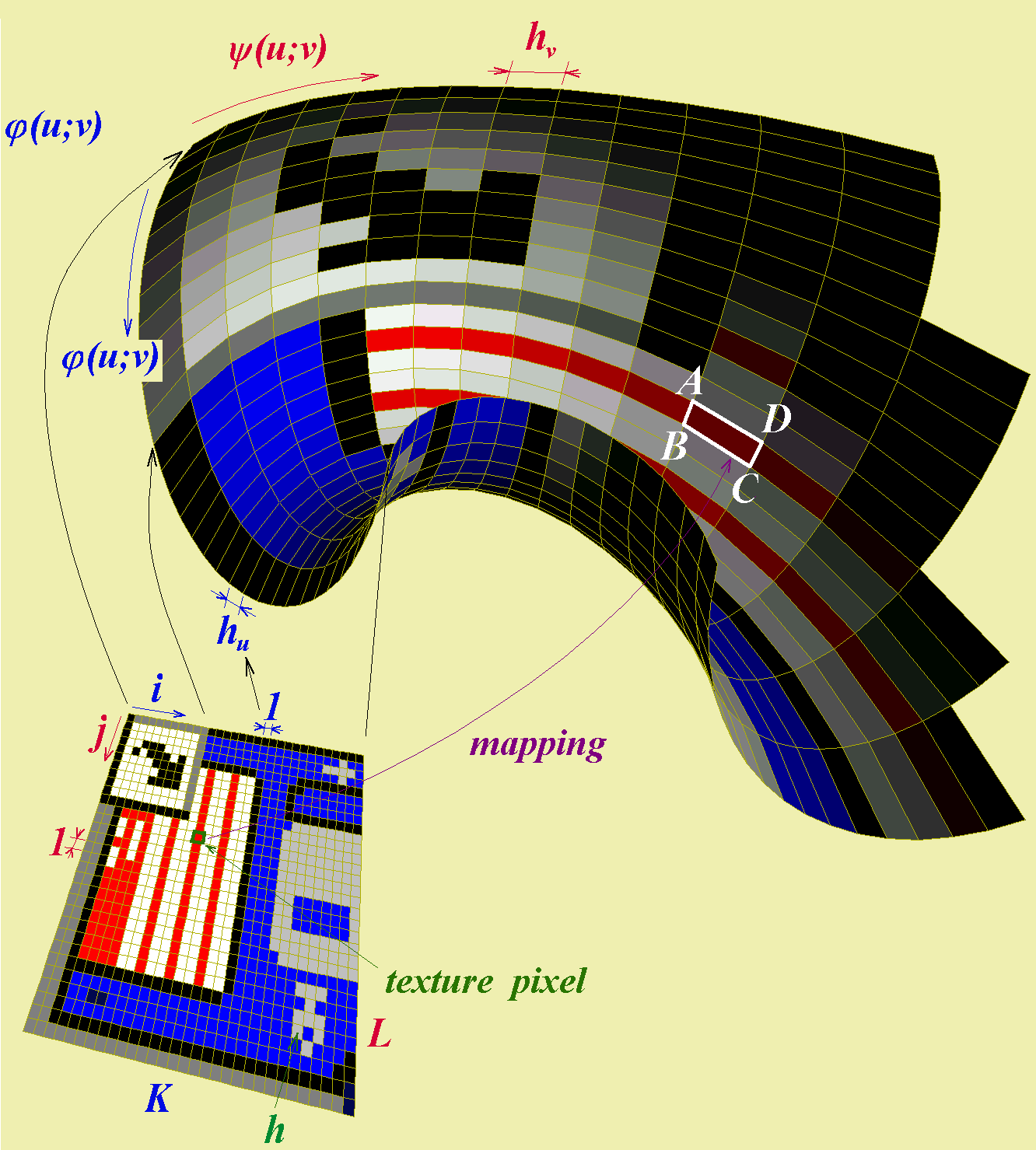
Figure 1. Direct mapping of a general surface.
In Figure 2, a woody torus constructed by direct mapping.

Figure 2. Woody torus constructed using the direct mapping.
3. Inverse mapping of a spherical surface
In direct mapping, the point of texture is assigned to the surface segment and this segment is after it projected to an output window. However, this algorithm is very time-consuming. In case of special surfaces, it is possible to use the inverse action (see Figure 3).
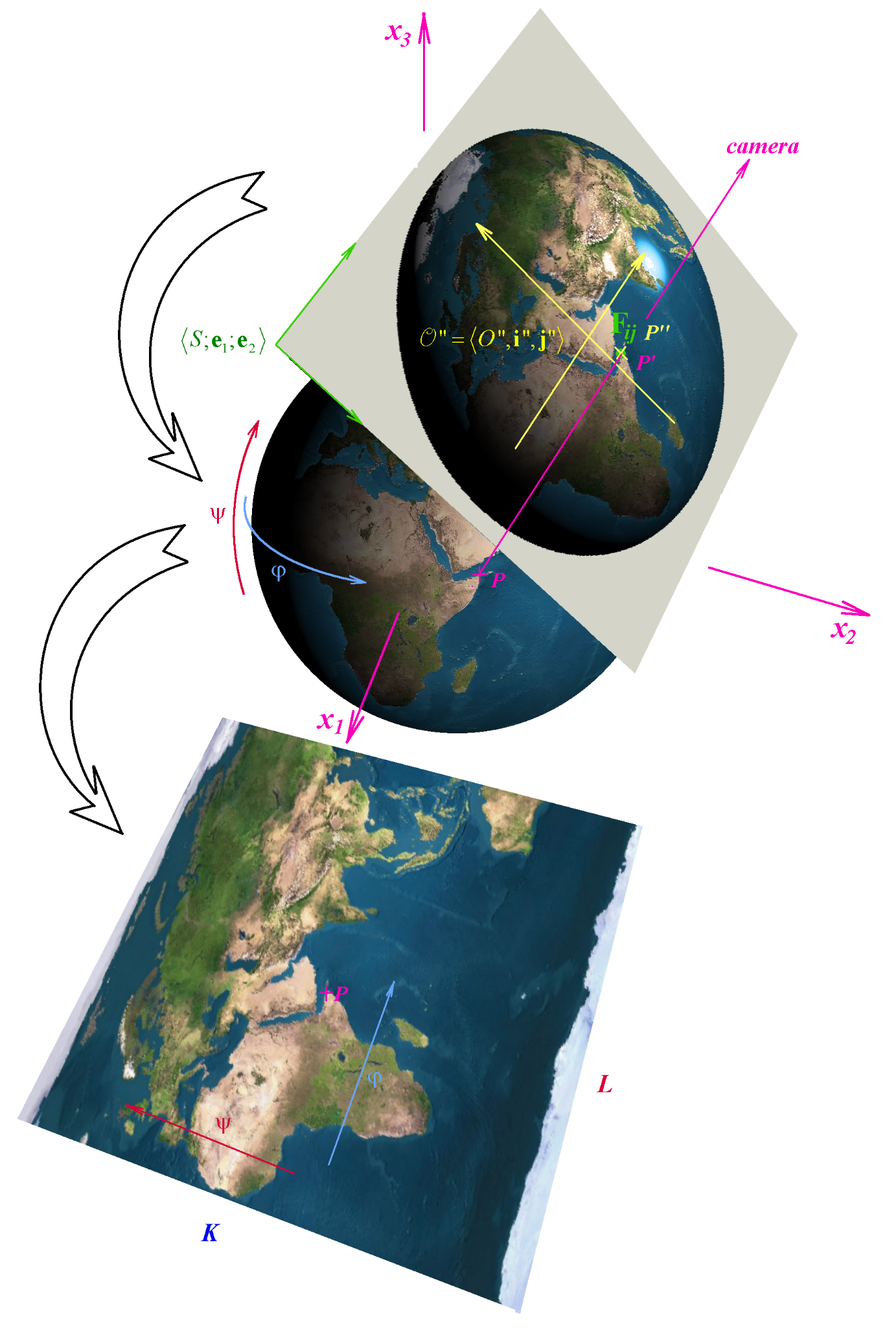
Figure 3. Inverse mapping of a spherical surface.
The projection line is passed through the camera position and the pixel of output device. Its intersection point  with the surface is calculated and, after it, texture color is assigned. Processed pixel of output device is then colored with this color.
with the surface is calculated and, after it, texture color is assigned. Processed pixel of output device is then colored with this color.
Pixel 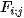 of the output device (see Fig. 3) we identify with the point
of the output device (see Fig. 3) we identify with the point 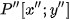 in coordinate system
in coordinate system 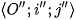 in output device and also with point
in output device and also with point 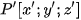 in coordinate system
in coordinate system 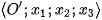 .
.
Calculating intersect 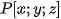 of the line defined by point
of the line defined by point 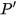 and the camera position with the surface. It its the main complication of this method. This problem leads to system of nonlinear equation which is solvable only by numerical method in generaly. However, in case of spherical surface
and the camera position with the surface. It its the main complication of this method. This problem leads to system of nonlinear equation which is solvable only by numerical method in generaly. However, in case of spherical surface
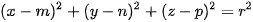
and a straight line
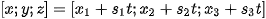
with the unitary directional vector 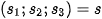 , having
, having
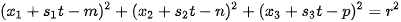
After simple modification and with respect to 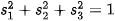 obtaining
obtaining
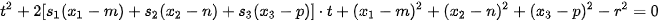
Therefore
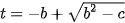
where
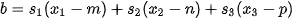
and
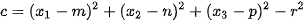
Parameter 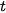 must be positive only in this case and it determine coordinate of the intersection of viewing ray with the sphere. For inverse mapping, it is need to find the corresponding values in parametric representation
must be positive only in this case and it determine coordinate of the intersection of viewing ray with the sphere. For inverse mapping, it is need to find the corresponding values in parametric representation
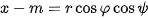
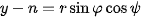
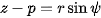
of the spheric surface. Getting
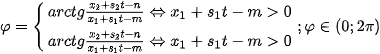
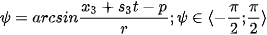
More information can be found in [1].
4. Phong illuminant model
While displaying vector data, we usually work with illumination. Light illuminates a scene (the space displayed) in a certain direction. If a planar optical interface had a microscopically ideal surface then both reflection and refraction would preserve parallelism. However, a real body does not have a totally smooth surface so both reflected and refracted beams have various directions. Asperities have a fractal character and the properties of reflected and refracted beams can be described only approximately. A function which tries to describethis character is called a reflection (refraction).
The first (and the simplest) illumination model for  light sources was published by Bui Tuong Phong [2]. It is an empirical model of local illumination which combines light direction
light sources was published by Bui Tuong Phong [2]. It is an empirical model of local illumination which combines light direction  of
of 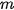 -th light source,
-th light source, 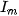 its intensity, normal vector
its intensity, normal vector 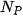 in calculated point
in calculated point 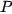 and direction from which point is observed. Furthermore, ambient intensity
and direction from which point is observed. Furthermore, ambient intensity 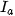 , specular (
, specular (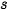 ), diffuse (
), diffuse (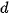 ) and ambient (
) and ambient (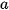 ) part of the reflection and also its „shine“ (
) part of the reflection and also its „shine“ (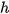 ) is estimated. These parameters gives following equation for illumination intensity
) is estimated. These parameters gives following equation for illumination intensity 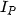 in the surface point
in the surface point 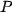 :
:
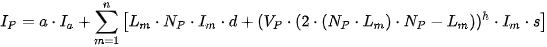
5. Ray tracing
It is possible to achieve a realistic scene by combining illuminant model with so called ray tracing technique. A light ray is sent through each pixel of output window and all optic interactions with group of surfaces and solids are recursively tracked. In Fig. 3, we can see the set of five balls with different optical properties illuminated by three light sources with intensities 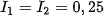 ;
; 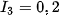 , ambient intensity is
, ambient intensity is 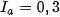 . For the big ball,
. For the big ball, 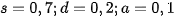 . For the smaller balls (from the left):
. For the smaller balls (from the left): 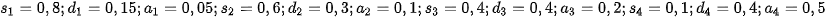 . Ball textures have been constructed using fractal techniques. The same parameters have been used in opening video. More information can be found in [1] (Figure 4).
. Ball textures have been constructed using fractal techniques. The same parameters have been used in opening video. More information can be found in [1] (Figure 4).

Figure 4. Output of the Ray Tracing algorithm where each point of the set has been evaluated by Phong Illumination Model. Recursion depth is five. Software was developed by the author of this entry.
