Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Jerzy Jasielec
 + 4775 word(s) 4775 2021-04-23 06:15:42 |
2 changing latex equations to text
Jerzy Jasielec
 -28 word(s) 4747 2021-04-26 11:51:31 | |
3 format correct
Conner Chen
 Meta information modification 4747 2021-04-29 05:04:02 | |
4 format correct
Conner Chen
 Meta information modification 4747 2021-04-29 05:10:25 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Jasielec, J. Electrodiffusion in Neuroscience and NPP-Equations. Encyclopedia. Available online: https://encyclopedia.pub/entry/9006 (accessed on 02 May 2024).
Jasielec J. Electrodiffusion in Neuroscience and NPP-Equations. Encyclopedia. Available at: https://encyclopedia.pub/entry/9006. Accessed May 02, 2024.
Jasielec, Jerzy. "Electrodiffusion in Neuroscience and NPP-Equations" Encyclopedia, https://encyclopedia.pub/entry/9006 (accessed May 02, 2024).
Jasielec, J. (2021, April 26). Electrodiffusion in Neuroscience and NPP-Equations. In Encyclopedia. https://encyclopedia.pub/entry/9006
Jasielec, Jerzy. "Electrodiffusion in Neuroscience and NPP-Equations." Encyclopedia. Web. 26 April, 2021.
Electrodiffusion in Neuroscience and NPP-Equations
Edit
This entry is adapted from the peer-reviewed paper 10.3390/electrochem2020014

There are two main processes governing the ionic transport, i.e., diffusion—the particle motion caused by a gradient of concentration, and migration—motion of ions caused by a gradient of electrical potential. These two processes are referred to as electrodiffusion. Electrodiffusion of electrolytes serves as a mean for communication in the nervous system. It can directly affect the excitatory transmission in the synaptic cleft. Electrodiffusion maintains the local ions concentration in brain extracellular spaces at heathy levels but may be also involved in the propagation of epileptic seizures during pathological conditions. The accurate interpretation of physiological observations requires better understanding of the underlying electrodiffusion phenomena.The description of electrodiffusion is very often performed using the Nernst–Planck–Poisson (NPP) model. It has been acknowledged that the spatiotemporal dynamics of the ion concentrations in thin dendrites and dendritic spines of nerve cells follow the Nernst–Planck equation, and sub-membrane currents in neuronal membrane have already been successfully described using the NPP model.

electrodiffusion Nernst–Planck–Poisson neuroscience neurons liquid junction potential patch-clamp ionic channels mitochondria

1. The Nernst–Planck–Poisson Model

The Poisson equation describes the electric field occurring due to the movement of ions, i.e., relates the electrical potential, φ, to the concentrations of ions:

 ∇2φ = − Fε ∑izici ,    (1)

where ci represents the concentration of the i-th ion, zi denotes its charge, ε is the dielectric permeability of the medium and F=96485.3 C mol−1 is the Faraday constant. In order to include the information about the external current Iext applied to a system, Poisson equation can be substituted with the Displacement Current equation [1]:

∂E/∂t = Iext − Fε ∑iziJi,   (2)

where the electric field E is directly connected to the gradient of electrical potential, i.e., E = −∇φ.

The Nernst–Planck equation relates the flux of ions Ji to the diffusion (driven by the gradient of concentration, ∇ci), the migration (driven by the gradient of electrical potential, ∇φ), and the convection processes:

 Ji = −Di∇ci − (F/RT)ziDici∇φ + ciυ    (3)

where Di is the diffusion coefficient of the i-th ion, R = 8.31 J mol−1 K−1 is the gas constant, T represents the temperature, and υ is the drift velocity. 

Together with the mass-balance equation:

∂ci/∂t = − ∇Ji,    (4)

they form a set of coupled nonlinear partial differential equations, and with proper initial and boundary conditions, they provide a quantitative description of electrodiffusion phenomena. This set of equations is known as drift-diffusion in computational physics [2][3]; as the Nernst–Planck–Poisson (NPP) [4][5] in electrochemistry and materials engineering, where the role of time-dependent flux is stressed; or as the Poisson–Nernst–Planck (PNP) in biophysics and electrophysiology, where the importance of computing the variable spatial distribution of potential is emphasized [6].

In the end of 19th century, Planck provided the first solution of the NPP equations [7]. He considered one-dimensional diffusion of two monovalent ions through a homogeneous membrane, assuming the occurrence of steady-state (i.e., no changes of concentrations or electric field and constant ionic fluxes across the system). More than a half-century later [8], his solution was extended to describe an arbitrary number of ions of any valence number. These and other analytical solutions [9][10][11] use the electroneutrality assumption. Alternatively, the constant electric field across the membrane can be assumed [12]. It has been shown that the electroneutrality assumption and the constant field hypothesis are the two limiting cases of the Poisson equation [13][14][15].

The electroneutrality is a central principle of the classical electrolyte theory, upon which the key electrochemical and electrophysiological derivations have been based [16]. The NPP problem with the electroneutrality assumption is significantly easier to solve. Although this simplification was historically almost necessary due to the lack of high performing computers, nowadays this attitude cannot be defended, as the access to high computing power is ubiquitous.

By solving the Nernst–Planck equations, we are trying to determine the effect of the electric field, which only arises in the presence of a net charge separation. Therefore, the electroneutrality assumption suffers from a fundamental inherent paradox [17]. Furthermore, the electroneutrality was denounced as unphysical [18], i.e., at finite time it is dynamically inconsistent with the solutions where the Poisson equation is obeyed.

The difficulties with the analytical solution of the NPP problem without the electroneutrality assumption, as well as the search for a more general and widely applicable approach, led the researchers to use the numerical methods. The first time-dependent NPP model using a numerical procedure, namely, an explicit (non-predictive) finite difference method, was developed in 1965 [1]. A decade later, an efficient simulation procedure for multi-component NPP equations using the first fully implicit (predictive) finite difference time scheme was presented by Brumleve and Buck [4]. Their approach to the numerical treatment of NPP has been used in numerous papers in electrochemistry of ion-selective membranes [19][20][21][22][23][24][25][26][27][28][29]. Other numerical methods proposed for the solution of the NPP problem include fast implicit finite difference [30], finite element [31][32][33][34], and network simulation [35][36][37]. The existence of an asymptotic analytical solution [38], found for small voltage-clamp values and for early times, allows testing of the numerical approaches also with respect to temporal dynamics.

The NPP model has been successfully used for the description of a large variety of electrochemical sensors used in potentiometry [23][24][25][26][27][28][29][39] and impedance spectroscopy [4][40][41]. That includes the NPP description of neutral carrier electrodes [42], solid-contact electrodes [43], coated-wire electrodes [44], and ion-selective field effect transistors [44]. Application of NPP in sensors leads to a deeper understanding of sensing mechanisms and underlying electrochemical processes, together with the miniaturization that can lead to the development of more robust and precise electrochemical sensors for in vivo measurements. Particularly interesting is, e.g., the development of biomimetic membranes using the Mg2+/Ca2+ antagonism mechanism [45], mimicking the action of glutamate-gated ion channels in NMDA receptors present in neural tissue [46][47]. The application of NPP for the description of ion sensors will be the topic of another review.

In the field of biophysics, the NPP equations were introduced by Eisenberg [48] in the early 1990s. The numerical method that can be easily transposed in two- or three-dimensional geometry [49], the numerical scheme working in two-dimensional geometry [32], and finally, a lattice-relaxation algorithm able to solve a 3D model [50] allowed the description of physiological systems with various complicated shapes.

Currently, the system of the NPP equations has become multidisciplinary, abundant in many fields of science and technology, e.g., semiconductors [2][3][51], building materials [52][53][54], synthetic and biological charged membranes [55], colloids [56], and electrochemical ion sensors [5]. The NPP allows the optimal scaling of semiconductor properties and device characteristics as devices become smaller [57][58]. The NPP speeds up the technological development, by replacing slow, expensive trial and error experimentation with direct computing [6].

2. The NPP Description of Neurons

Neurons are highly specialized cells and essential cellular elements in the central nervous system. All neurological processes are dependent on complex interactions between single neurons and groups of related neurons. Morphologically, a typical neuron, consists of three regions: (1) the cell body (soma or perikaryon) containing the nucleus and the major cytoplasmic organelles, (2) a variable number of dendrites, and (3) a single axon. At the interface of axon terminals with target cells are the synapses, i.e., specialized zones of contact, which consist of a presynaptic (axonal) element, a narrow synaptic cleft, and a postsynaptic element on a dendrite or soma. The portion of the presynaptic element is the active zone, enriched with ion channels necessary to permit the neurotransmitter release. For a very detailed description of neuron morphology as well as different types of neural cells, see [59].

The NPP equations might serve as a tool for the description of the phenomena occurring during neurotransmitters electrodiffusion [16]. It was used to calculate the reaction rate constant of neurotransmitter acetylcholine (ACh) in the reaction center of the enzyme acetylcholinesterase (AChE) [33][34]. The obtained results showed that the rate coefficient depends on the concentration of the substrate (i.e., change from 2 × 1011 down to 8 × 1010 M−1 min−1 for the substrate concentration change from 1 to 500 mM at an ionic strength of 134 mM), as well as on the ionic-strength of the solution (i.e., it peaks at around 12 × 109 M−1 min−1 at an ionic strength of 134 mM and reduces to about 8 × 109 M−1 min−1 at an ionic strength of 500 mM). A noticeable shift of the peak, located at 0.15 µs for maximum rate coefficient, was found at the physiological ionic strength of 134 mM, which differs from the results of a more idealized Smoluchowski–Poisson–Boltzmann model (peak at 0.31 µs). This suggests that the NPP model is more desirable for the description of the electrostatic-driven diffusion and substrate consumption in this system [33].

The NPP model has also been applied for calculations of glutamate electrodiffusion in synaptic cleft [60]. The results showed that the synaptic currents could significantly accelerate the dispersion of negatively charged neurotransmitter molecules from the cleft and attract the positively charged ones towards the current sinks. Therefore, the shape of the synaptic response strongly depends on the electrodynamic interactions between the charged neurotransmitter molecules and the postsynaptic current. These predictions are well supported by experimental evidence [61].

With the possibility to obtain 3D structures from electron tomography [62] came the opportunity for modelling the systems with complex geometries based on morphologically realistic depictions of cells and organelles relevant to neuroscience. It led to the neurological application of NPP in the description of the node of Ranvier [63], a component in myelinated axons consisting of axonal and glial membranes and small aqueous compartments. Dysfunctions of its nodal complex play an important role in several neurological disorders, such as multiple sclerosis, Charcot–Marie–Tooth disease and Guillain–Barre syndrome. The electrodiffusion in the node of Ranvier is significant since the voltages surrounding individual channels determine channel gating and the response of each channel to the local electrochemical gradient. The NPP results show the accumulation and depletion of ions close to the membrane. The algorithm applied to the node of Ranvier can also be applied for the description of other biophysical processes, such as the generation/transmission of cardiac impulses and synaptic transmission [63].

The synaptic connections are made on dendritic spines, i.e., parts of the neuron’s dendrite that receive input from a single axon at the synapse and are comprised of spine head and spine neck. The strength of the connection between two interacting neurons is reflected by the electric potential change, induced by excitatory current. To investigate the dependence of the electrical properties of spines on their geometry, the NPP modelling was combined with voltage imaging data [64]. Results show that changing the length of the spine neck can regulate the local dendritic voltage and, consequently, contributes to the emergence of an action potential. The correlation between the voltage amplitude and the neck length is confirmed by earlier experimental findings in brain slices [65][66]. This length modulation is complementary to the possible changes in the number of receptors in the synapse, resulting in a long-term modification of the synaptic current during synaptic plasticity [64].

The propagation of the electrical signal in neurons is usually described by cable theory, developed by Goldman, Hodgkin, and Katz [67][68] and successfully used as a framework for studying neuronal conduction. The NPP computation of excitatory postsynaptic potentials shows the limitations of cable theory in cases of thin dendrites or large concentration changes [69]. Also, in the case of small neuronal compartments or dendritic spines, it seems that cable theory may be inadequate, because it assumes spatial and ionic homogeneity [70]. The NPP equations are free from such assumption and allow the more accurate modelling of the constraints that neuronal nanostructures place on the neuronal currents. The application of NPP to dendritic spines results in the following predictions about the influence of geometry on the regulation of electrical current [70]:

  • The voltage inside the spine saturates as the injected current increases.
  • When the spine head is isolated and the current leak through the neck is slow, ions concentrate at the surface of the spine.
  • A large electric field forms at the spine neck–head junction.

The NPP gives important information on the potential profile within the cells of the synaptic circuit and in the intersynaptic space. It relates the electric field inside and outside the cell during the spread of an action potential along an axonal membrane with the complex interaction of ion movements and the evolution of the extracellular signal.

The visual information is translated into electric currents by photoreceptors through changes in their membrane potentials. The NPP was applied for the description of the triad synapse (a type of synapse in the outer plexiform layer formed by a cone, a horizontal cell, and a bipolar cell) in the goldfish retina in order to investigate the importance of ephaptic (electrical) effects [71][72]. These effects were demonstrated by calculating the shift in the current–potential curve for increasingly narrower openings between the cone and the horizontal cell. The NPP results provide convincing evidence that an ephaptic mechanism can produce the feedback effect seen in the experiments. The simulations of the triad synapse also demonstrate the dependence of the feedback on the behavior of the bipolar cell under background illumination [72]. Better understanding of the feedback mechanisms is essential to unravel how visual processing takes place in the retina.

Owing to their close proximity, neurons must have a direct electrodiffusive impact on their neighbors. The neuron environment, consisting of densely packed neurons and neuroglia, has been described using the NPP equations [73]. The results qualitatively and quantitatively agree with the Goldman equation but indicate that there is always a particle flux, even at steady-state.

3. Non-Stationary Liquid Junction Potential

The diffusive currents in extracellular space surrounding a small population of neurons can evoke a non-zero potential gradient, so that potential in soma region is more negative than in the apical region [74]. This diffusion-generated-potential is known as liquid junction potential (LJP), i.e., a potential emerging at a non-selective boundary between two electrolytes. The analysis of the time-dependent LJP response is also important for the practical applications in methods of analytical potentiometry, such as patch-clamp analysis [75] or fully automatic clinical electrolyte analyzers [76][77][78].

The value of LJP is usually calculated using Henderson equation [79][80]. This method is easy to implement and available as free online calculators [81]. However, it has been shown that the Henderson equation is only a special case of NPP [24]. It has also been proven using asymptotic analysis [82] that the Henderson equation is inexact in cases other than liquid junctions of two solutions of common phase but different concentrations, i.e., type 1 in Lingane’s classification [83]. Only for this type of junction does the steady state solution of NPP reduce to the form equivalent to the Henderson equation, consequently, giving the same values. The steady-state solution of NPP allows the validation of the linear concentration profiles assumption and the electroneutrality assumption used in derivation of Henderson equation, showing when the deviations occur [39].

Liquid junction can be described as an imaginary barrier, that separates two solutions of electrolytes connected by the means of a porous plug [84], has a limited width, and possesses the physical characteristics of water. A schematic depiction of the liquid junction system is presented in Figure 1a. This classical approach, developed in the end of 19th century by Nernst [85] and Planck [7] and defined later [86] as constrained liquid junction, has been widely used since [4][18][19][24][39][79][80]. Alternatively, instead of the unphysical barrier, a dynamically relaxing junction of two liquids, in which a diffuse layer continues to expand in a linear semi-infinite space, can be used. This approach, known as free liquid junction, was first presented and described using NPP equations by Hafemann [87]. The dynamics of free liquid junction, as well as the methods of analysis and simulation of liquid junction potentials, have been discussed in more detail in a recent review [88].

 
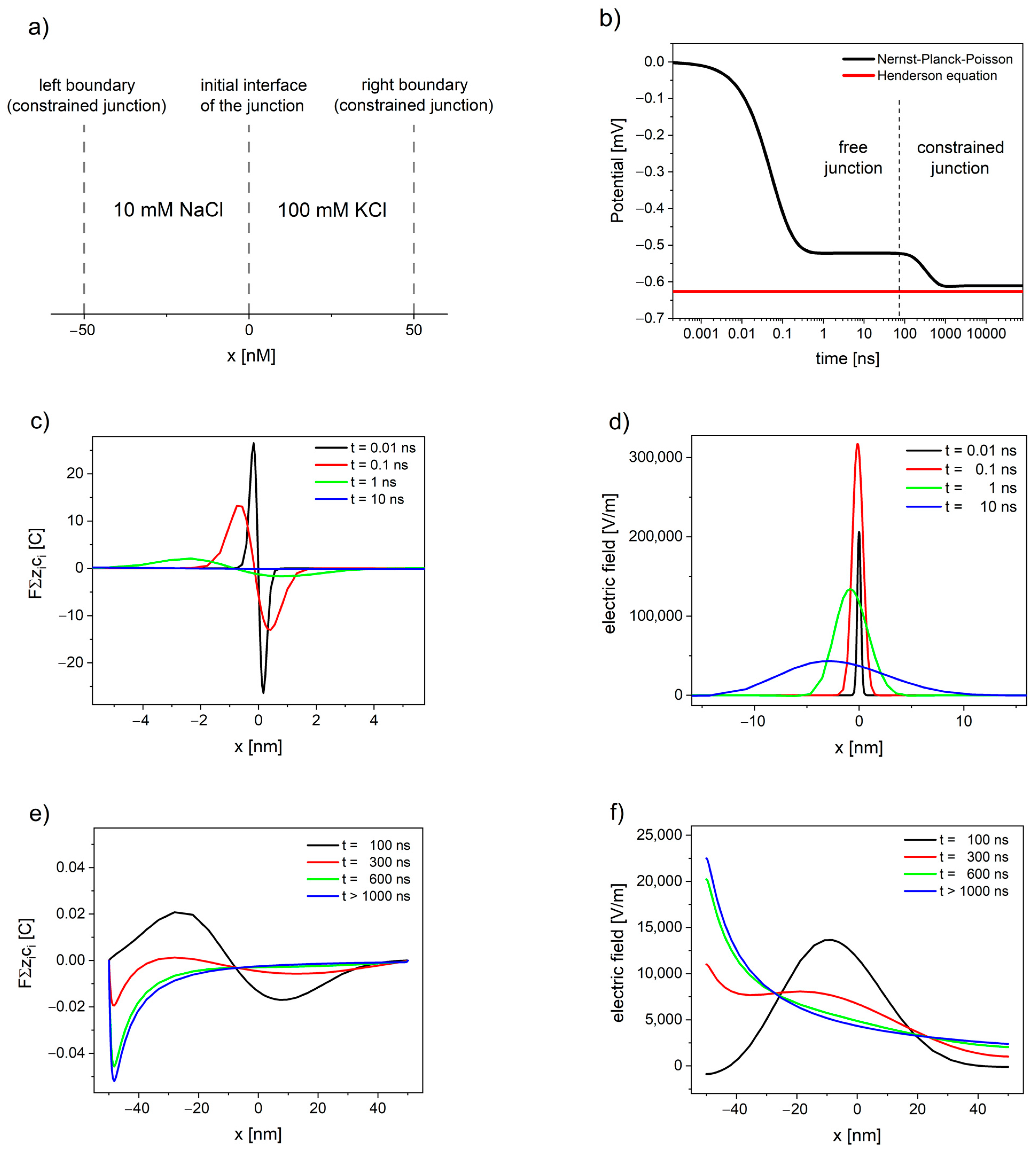
Electrochem 02 00014 g001

Figure 1. The evolution of free and constrained liquid junction potential (LJP) of watery solutions 10 mM NaCl|100 mM KCl calculated using Nernst–Planck–Poisson (NPP) model: (a) schematic depiction of the liquid junction system; (b) the liquid junction potential as a function of time; (c,e) deviation from electroneutrality; and (d,f) the resulting electric field.

 

The NPP system brings the modelling of liquid junction potentials closer to physical relevance, by allowing the simulation of time-dependent potential formation of both free and constrained liquid junction [39]. Figure 1 shows the evolution of liquid junction potential. Initially, the deviation from electroneutrality and the resulting changes in the electric field profiles occurs at the contact between solutions until the value of electric field reaches the maximum. Then, the deviation from electroneutrality and, consequently, the changes in the electric field propagate through the system, while their maximum decreases and shifts away from the initial interface of the junction (see Figure 1c,d). The value of overall electrical potential (area between the electric field and x-axis on Figure 1d) remains constant and corresponds to the value of free LJP. The free liquid junction is not at steady state, and the value of its potential arises as a consequence of the electric field expanding into the solutions.

If the deviation from electroneutrality and the resulting changes in the electric field reach the boundaries of the system, the pseudo-steady state characteristic for free liquid junction is disrupted. The potential changes its value, while the maximum of deviation from electroneutrality and maximum of the electric field shift towards the solution with lower concentration, until the steady state is attained (see Figure 1e,f).

The situation during the continued dialysis and solution mixing, when the interface of junction expands away from the electrode [16], corresponds to free liquid junction; therefore, the value of LJP in this case cannot be correctly estimated based on the Henderson method (the constrained junction approach). Furthermore, the electroneutrality, used by Henderson as assumption, is not fulfilled even at steady state (as shown in Figure 1e). The deviation from the Henderson equation for Lingane’s type 3 junctions ranges from very small (<0.02%) to very significant (>8%) over a very limited range of the diffusion coefficients ratio [89].

4. The NPP Description of Ion Channels

The neuronal compartments, as well as all other types of cells and organelles, are surrounded by phospholipid membranes. Embedded in these membranes are specialized assemblies of proteins, known as ionic channels and pumps—the nanoscopic pathways used to transport ions across the biological membranes [90]. Some types of the ion channels have a selectivity filter, permitting passage of only one type of ions, while others are non-selective, allowing multiple ion species to be transported. The opening and closing of ion channels regulate the communication between cells, the influence of hormones and drugs on the cell function, as well as other electrical activities in the nervous system [91].

The number and density of the ion channels can vary significantly between different types of cells, as well as between different neuronal compartments. The density of sodium channels in soma is quite low with 1 to 5 channels per μm2, while in some axons it can reach 700 to 2000 channels per μm2 [92]. The density of potassium channels varies from 0.5 to 5 channels per μm2 in soma to 240–1100 channels per μm2 in axons [92]. Modifying the density and distribution of ion channels (by natural regulation, spontaneous mutations, or pharmacological intervention) changes the activity pattern of a neuron. The differences in channel density and their influence on neural response have been extensively discussed in several papers [92][93][94][95].

The NPP models used for the description of neuronal compartments, presented in Section 2 of this review [69][63][73][96][97][33][34][64][70][71][72], neglect the effects of ionic channels and the influence of the number, size, and distance between them. Instead, they treat the membrane as an inert and uniform boundary of the considered system and describe it using proper (Dirichlet or Neumann) boundary conditions. Although this approach is justified, allowing much higher computational efficiency, the modeling of individual channels is also of an interest for many researchers.

The NPP found a very wide application in channology [98], i.e., a branch of biophysiology devoted to ion channels. The NPP equations predict quite accurately the current-voltage response of narrow channels over a wide range of salt concentrations in the surrounding solution [99]. The NPP has been applied to explain how the current rectification can be produced by the charges at the channel openings [100][101] and to demonstrate how a channel with ion-specific binding sites can exhibit a lower conductance in a mixture of two types of ions than in the pure solutions of either type [102].

The access resistance (important component of the conductance of ion channel, particularly in wide and short channels) calculated using NPP at the entrance of a circular uncharged pore in neutral membrane [103] is in good agreement with the results of classical Hall’s expression [104], derived from electrostatics. The NPP can be applied also in the situations when Hall’s expression overestimates the access resistance, i.e., for channels embedded in charged membranes [103].

The NPP implementation developed by Nonner and Eisenberg [105][106] has been used in a series of more than 40 papers (see review [107]) to describe the properties of three distinct ion channels: the Cav channels that control the heartbeat, the Nav channels that produce signaling in nervous systems, and the RyR channels that control calcium signaling in nearly all cells, including cardiac and skeletal muscles [108].

Ion channels have been described by a variety of one-dimensional [48][102][109], two-dimensional [110][111], and three-dimensional [50][110][112][113][114] NPP models. The detailed comparison between these models and the experimental responses of simple ionic channels (i.e., gramicidin A channel) shows when the geometrical simplifications are justified. The 2D circularly-symmetric model is especially helpful, because it enables parameter extraction from the experimental data with much more realism than the 1D model and much less computational effort than the 3D model [110].

The NPP can serve as a computationally efficient alternative to other methods available for the description of the individual ionic channels, namely, molecular dynamics (MD) [115][116][117][118] and Brownian dynamics (BD) [119][120]. NPP can be also combined with classical mean density functional theory and Monte Carlo simulations. Such models, summarized in very recent review [121], fill the gap between the really detailed all-atom models studied by MD simulations popular in ion channel studies and mean-field continuum models (such as classical NPP) popular in nanopore studies.

The NPP is probably the simplest form of non-equilibrium theory that takes into account the shape of the channel, the magnitude and the location of charge residues in the channel protein, and different ionic concentrations at two sides of the channels [91]. It is worth mentioning that NPP is considered one of the most idealized models for the description of liquid junction potentials [39] (compared with Henderson equation and Planck formula) and ion channels [121] (compared with more general MD and BD), while at the same time, it is considered a most general model for the description of ion sensors [5] (compared with phase boundary models and diffusion layer models used in potentiometry or with equivalent circuits used in impedance spectroscopy).

The methods for modelling and simulation of ion channels and their application for a variety of channel types have been described in detail in several extensive reviews [91][109][122][123][124][125]. The elucidation of how ion channels work might ultimately help us find the causes of a number of neurological and muscular disorders and potential cures for them [91].

5. Potential Distortions Invisible to Patch-Clamp

The sub-membrane voltage generated through local charge accumulation essentially controls the voltage-dependent activity of membrane proteins [16]. The inhomogeneity in electric fields in the protein and at the lipid-protein interface can result in distortions near their voltage sensor.

The molecular voltage sensor is driven by the electric fields in nanoscopic proximity to the membrane [126][127], i.e., sub-membrane potential V*m. However, in patch-clamp practice, the measured value is the voltage difference between the cell cytoplasm and the bulk of extracellular medium Vm. Sub-membrane electric fields quickly dissipate away from the membrane, therefore, the values of the pipette-measured Vm and the V*m sensed by the receptors and channels may differ [16].

The potential profiles through the ion-selective lipid bilayer calculated using NPP equations (see Figure 2) show that the potential changes extend outside the membrane and consequently cause the potential distortions in neighboring solutions. In the literature, it is either assumed that the electric potential drops pretty much linearly across the lipid bilayer [128] or that a maximum in potential profile occurs inside the membrane [16]. Both of these assumptions are here validated using NPP.

 
Electrochem 02 00014 g002 550

Figure 2. Distortions in transmembrane potential invisible to patch-clamp measurements. Thick black line represents the voltage profile across the system of a cation-selective membrane between two solutions calculated using NPP model. Vm is the transmembrane voltage measured in patch-clamp technique, away from the membrane. V*m is the transmembrane voltage sensed by the channel voltage sensor. Vertical dotted lines represent the approximate sub-membrane locality that primarily affects the channel voltage sensor (assumed at 1 nm distance from the membrane). (a) Concentration of negative charge in the membrane equals 10 nM, (b) concentration of negative charge in the membrane equals 0.

 

Presented NPP results show the dependence of the potential profile on the concentration of the negative charges (anionic sites) inside the lipid bilayer. Near-linear potential drop is observed when the concentration of negative charge in the cation-selective membrane is close in value to the concentration of this cation in the neighboring solutions (see Figure 2a). When the concentration of negative charges is significantly lower, the maximum of the potential occurs (see Figure 2b).

Applying NPP in real geometric structures of biological membranes can quantitatively show the difference between the sub-membrane potential V*m and the patch-clamp readout Vm.

6. Mitochondrial Calcium Transport

Although the brain represents only about 2% of the body weight in an average adult human, it accounts for about 20% of the oxygen and, hence, the energy consumed by the body [129]. The energy (in the form of ATP) is produced in mitochondria through the citric acid cycle and reducing the oxygen by oxidative phosphorylation [90]. This process is accompanied by the influx of calcium ions into the mitochondrial matrix and the precipitation of osmotically inactive amorphous carbonated apatite [130]. Mitochondria can accumulate, store, and release a large amount of calcium ions under a variety of physiological and pathological conditions, such as epilepsy [131], ischemia [132][133], and concussive brain injury [134]. Mitochondrial Ca2+ uptake influences not only energy metabolism [135][136] but also the neural signaling [137][138].

The NPP model has been used to simulate the electrodiffusion of calcium ions through the mitochondrial membrane [139]. In this approach, the mitochondrial membrane is represented by a one-dimensional continuous element where only the maximum inward/outward flux of ions is limited by the channel density. Inside the mitochondrion matrix, the complexation reaction has been introduced by including the reaction terms into the mass balance equations. In cytosol and the mitochondrial matrix, pure Fickian diffusion has been assumed.

The concentration profiles of calcium have been shown in Figure 3. The inclusion of the reaction, occurring inside the mitochondrial matrix in the transport model, allows us to explain the difference between the total matrix concentration of calcium (established to be in the range of 0.5 M to 0.8 M [140][141][142][143][144]) and the free calcium concentration (in the range of 0.17 to 5 μM [145][146][147][148][149][150][151][152]), reported by numerous studies using fluorescent Ca2+ indicators.

 

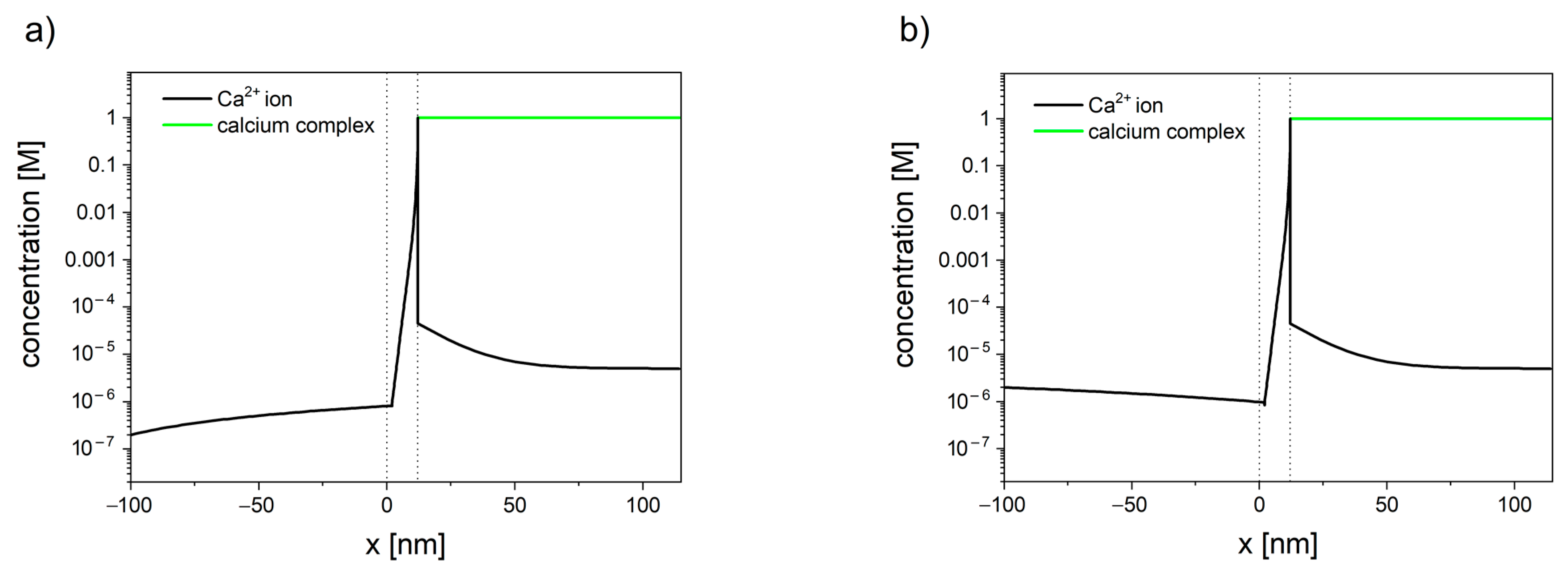
Electrochem 02 00014 g003

Figure 3. Calcium concentration profiles in the system consisted of cytosol (x < 0), mitochondrial membrane (0 < x < 10 nm), and mitochondrial matrix (x > 10 nm). Membrane potential is set to φ = −180 mV. (a) When the concentration of calcium in cytosol is set to 200 nm, the resulting flux is negative (JCa2+ = −2.0 × 10−7), and calcium ions leave the mitochondrion. (b) When the concentration of calcium in the cytosol is set to 2 µM, the resulting flux is positive (JCa2+ = −3.4 × 10−7), and calcium ions enter the mitochondrion.

The presented model [139] can be used as an efficient alternative for single-channel modeling. Despite its simplicity, the model has successfully described the existence of calcium set-point, i.e., the concentration of calcium in cytosis below which calcium stops entering the mitochondrion. For the membrane potential of −180 mV, the set-point was established to be in the range 0.9 µM to 1 µM [139]. The lower the value of the membrane potential, the higher the tendency for calcium to enter the mitochondrion. Furthermore, the concentration profiles inside cytosol have shown the existence of an unstirred layer (see Figure 3), which indicates that the calcium ions enter/leave the membrane faster than it can diffuse from/toward the bulk.

Proper description of calcium electrodiffusion and precipitation of its salts is especially relevant in neural tissue, where calcium signaling occurs, e.g., the concentration of calcium ions in the mitochondria of firing axons have been reported to reach 24 µM [153], comparing with typical values of 1–5 µm [130]. Amorphous carbonated apatite, precipitated as an effect of calcium influx, acts as a pH buffer and, hence, can contribute in maintaining ATP production in ischemic conditions, which delays irreversible damage to heart and brain cells after stroke [130][154]. This calcium salt might also have an auxiliary role in mitigating the effects of oxidative stress [130]. The oxidative stress occurring in neural tissue can lead to cancer [155], but also Parkinson’s, Alzheimer’s, amyothropic lateral sclerosis, and other neurodegenerative diseases [156][157][158]. A better understanding of the calcium electrodiffusion and precipitation of amorphous calcium apatite in mitochondria may, hence, lead to the development of new stroke-protective drugs or improve the neurodegenerative disease prevention.

References

  1. Cohen, H.; Cooley, J. The numerical solution of the time-dependent Nernst-Planck equations. Biophys. J. 1965, 5, 145–162.
  2. Van Roosbroeck, W. Theory of flows of electrons and holes in germanium and other semiconductors. Bell Sys. Tech. J. 1950, 29, 560–607.
  3. Selberherr, S. Analysis and Simulation of Semiconductor Devices; Springer: New York, NY, USA, 1984; pp. 1–293.
  4. Brumleve, T.R.; Buck, R.P. Numerical solution of the Nernst-Planck and Poisson equation system with applications to membrane electrochemistry and solid state physics. J. Electroanal. Chem. 1978, 90, 1–31.
  5. Ivaska, A.; Bobacka, J.; Lewenstam, A. Potentiometric Ion Sensors. Chem. Rev. 2008, 108, 329–351.
  6. Eisenberg, B. Interacting Ions in Biophysics: Real is not Ideal. Biophys. J. 2013, 104, 1849–1866.
  7. Planck, M. Über die Potenzialdifferenz zwischen zwei werdünnten Lösungen binärer Electrolyte. Ann. Phys. Chem. 1890, 40, 561–576.
  8. Schlögl, R. Elektrodiffusion i freier Lösung und geladenen membranen. Z. Phys. Chem. 1954, 1, 305–339.
  9. Helfferich, F.G. Ion. Exchange; McGraw-Hill: New York, NY, USA, 1962; pp. 1–624.
  10. Teorell, T. Transport process and electrical phenomena in ionic membranes. In Progress in Biophysics and Biophysical Chemistry; Butler, J.A.V., Randall, R.T., Eds.; Academic Press: New York, NY, USA, 2016; Volume 3, pp. 305–369.
  11. Conti, F.; Eisenman, G. The non-steady state membrane potential of ion exchangers with fixed sites. Biophys. J. 1965, 5, 247–256.
  12. Mafé, S.; Pellicer, J.; Aguilella, V.M. The Goldman constant field assumption: significance and applicability conditions. Ber. Bunsenges. Phys. Chem. 1986, 90, 476–479.
  13. MacGillivray, A.D. Nernst-Planck equations and the electroneutrality and Donnan equilibrium assumptions. J. Chem. Phys. 1968, 48, 2903–2907.
  14. MacGillivray, A.D.; Hare, D. Applicability of Goldman’s constant field assumption to biological systems. J. Theor. Biol. 1969, 25, 113–126.
  15. Kato, M. Numerical analysis of the Nernst-Planck-Poisson system. J. Theor. Biol. 1995, 177, 299–304.
  16. Savtchenko, L.P.; Poo, M.M.; Rusakov, D.A. Electrodiffusion phenomena in neuroscience: A neglected companion. Nature 2017, 18, 598–612.
  17. Dickinson, E.J.F.; Limon-Petersen, J.G.; Compton, R.G. The electroneutrality approximation in electrochemistry. J. Solid State Electrochem. 2011, 15, 1335–1345.
  18. Perram, J.W.; Stiles, P.J. On the nature of liquid junction and membrane potentials. Phys. Chem. Chem. Phys. 2006, 8, 4200–4213.
  19. Mafé, S.; Pellicer, J.; Aguilella, V.M. Ionic transport and space charge density in electrolytic solutions as described by Nernst-Planck and Poisson equations. J. Phys. Chem. 1986, 90, 6045–6050.
  20. Manzanares, J.A.; Mafé, S.; Pellicer, J. Transport phenomena and asymmetry effects in membranes with asymmetric fixed charge distributions. J. Phys. Chem. 1991, 95, 5620–5624.
  21. Kontturi, A.K.; Kontturi, K.; Mafé, S.; Manzanares, J.A.; Niinikoski, P.; Vouristo, M. Convective diffusion in porous membranes with adsorbed charges. Langmuir 1994, 10, 949–954.
  22. Kontturi, K.; Mafé, S.; Manzanares, J.A.; Pellicer, J.A. New Method for Determining Transport Numbers of Charged Membranes from Convective Diffusion Experiments. J. Electroanal. Chem. Interfacial Electrochem. 1994, 378, 111–116.
  23. Sokalski, T.; Lewenstam, A. Application of Nernst-Planck and Poisson equations for interpretation of liquid junction and membrane potentials in real-time and space domains. Electrochem. Comm. 2001, 3, 107–112.
  24. Sokalski, T.; Lingenfelter, P.; Lewenstam, A. Numerical solution of coupled Nernst-Planck and Poisson equations for liquid junction and ion selective membrane potentials. J. Phys. Chem. B 2003, 107, 2443–2452.
  25. Lingenfelter, P.; Bedlechowicz-Śliwakowska, I.; Sokalski, T.; Maj-Żurawska, M.; Lewenstam, A. Time-dependent phenomena in the potential response of ion-selective electrodes treated by the Nernst-Planck-Poisson model. 1: Intramembrane processes and selectivity. Anal. Chem. 2006, 78, 6783–6791.
  26. Lewenstam, A.; Sokalski, T.; Jasielec, J.; Kucza, W.; Filipek, R.; Wierzba, B.; Danielewski, M. Modelling Non Equilibrium Potentiometry to Understand and Control Selectivity and Detection Limit. ECS Trans. 2009, 19, 219–224.
  27. Jasielec, J.J.; Sokalski, T.; Filipek, R.; Lewenstam, A. Comparison of different approaches to the description of the detection limit of ion-selective electrodes. Electrochim. Acta 2010, 55, 6836–6848.
  28. Szyszkiewicz, K.; Danielewski, M.; Fausek, J.; Jasielec, J.J.; Kucza, W.; Lewenstam, A.; Sokalski, T.; Filipek, R. Breakthrough in modeling of electrodiffusion processes: Continuation and extensions of the classical work of Richard Buck. ECS Trans. 2014, 61, 21–30.
  29. Jasielec, J.J.; Mousavi, Z.; Granholm, K.; Sokalski, T.; Lewenstam, A. Sensitivity and Selectivity of Ion-Selective Electrodes interpreted using the Nernst-Planck-Poisson model (NPP). Anal. Chem. 2018, 90, 9644–9649.
  30. Rudolph, M.J. Digital simulations with the fast implicit finite-difference (FIFD) algorithm. Part 4. Simulation of electrical migration and diffuse double-layer effects. Electroanal. Chem. 1994, 375, 89–99.
  31. Samson, E.; Marchand, J. Numerical solution of the extended Nernst-Planck model. J. Colloid Interface Sci. 1999, 215, 1–8.
  32. Samson, E.; Marchand, J.; Robert, J.-L.; Bournazel, J.-P. Modelling ion diffusion mechanisms in porous media. Int. J. Numer. Meth. Engng. 1999, 46, 2043–2060.
  33. Zhou, Y.C.; Lu, B.Z.; Huber, G.A.; Holst, M.J.; McCammon, J.A. Continuum simulations of acetylcholine consumption by acetylcholinesterase—A Poisson-Nernst-Planck approach. J. Phys. Chem. B 2008, 112, 270–275.
  34. Lu, B.; Holst, M.J.; McCammon, J.A.; Zhou, Y.C. Poisson-Nernst-Planck equations for simulating biomolecular diffusion-reaction processes I: Finite element solutions. J. Comput. Phys. 2010, 229, 6979–6994.
  35. Moya, A.A.; Horno, J. Application of the network simulation method to ionic transport in ion-exchange membranes including diffuse double-layer effects. J. Phys. Chem. B 1999, 103, 10791.
  36. Moleón, J.A.; Moya, A.A. Network simulation of the electrical response of ion-exchange membranes with fixed charge varying linearly with position. J. Electroanal. Chem. 2008, 613, 23–34.
  37. Moleón, J.A.; Moya, A.A. Transient electrical response of ion-exchange membranes with fixed-charge due to ion adsorption. A network simulation approach. J. Electroanal. Chem. 2009, 633, 306–313.
  38. MacGillivray, A.D. Asymptotic Solutions of the Time-Dependent Nernst-Planck Equations. J. Chem. Phys. 1970, 52, 3126–3132.
  39. Jasielec, J.J.; Filipek, R.; Szyszkiewicz, K.; Fausek, J.; Danielewski, M.; Lewenstam, A. Computer simulations of electrodiffusion problems based on Nernst-Planck and Poisson equations. Comp. Mat. Sci. 2012, 63, 75–90.
  40. Grysakowski, B.; Bożek, B.; Danielewski, M. Electro-Diffusion in Multicomponent Ion-Selective Membranes; Numerical Solution of the Coupled Nernst–Planck–Poisson Equations. Defect Diffus. Forum 2008, 273–276, 113–118.
  41. Grysakowski, B.; Jasielec, J.J.; Wierzba, B.; Sokalski, T.; Lewenstam, A.; Danielewski, M. Electrochemical Impedance Spectroscopy (EIS) of Ion Sensors. Direct modelling and inverse problem solving using the Nernst-Planck-Poisson (NPP) model and the HGS(FP) optimization strategy. J. Electroanal. Chem. 2011, 662, 143–149.
  42. Jasielec, J.J.; Sokalski, T.; Filipek, R.; Lewenstam, A. Neutral-Carrier Ion-Selective Electrodes Assessed by Nernst-Planck-Poisson Model. Anal. Chem. 2015, 87, 8665–8672.
  43. Jasielec, J.J.; Lisak, G.; Wagner, M.; Sokalski, T.; Lewenstam, A. Nernst-Planck-Poisson Model for the Qualitative Description of the Behaviour of Solid-Contact Ion-Selective-Electrodes at Low Analyte Concentration. Electroanalysis 2013, 25, 133–140.
  44. Sanders, T.M.; Myers, M.; Asadnia, M.; Umana-Membreno, G.A.; Baker, M.; Fowkes, N.; Parish, G.; Nener, B. Description of ionophore-doped membranes with a blocked interface. Sens. Actuators B 2017, 250, 499–508.
  45. Paczosa-Bator, B.; Stępień, M.; Maj-Żurawska, M.; Lewenstam, A. Biomimetic study of the Ca2+-Mg2+ and K+-Li+ antagonism on biologically active sites: New methodology to study potential dependent ion exchange. Magnes. Res. 2009, 22, 10–20.
  46. Nowak, L.; Bregestovski, P.; Ascher, P.; Herbet, A.; Prochiantz, A. Magnesium gates glutamate-activated channels in mouse central neurons. Nature 1984, 307, 462–465.
  47. Vargas-Caballero, M.; Robinson, H.P.C. Fast and slow voltage-dependent dynamics of magnesium block inthe NMDA receptor: The asymmetric trapping block model. J. Neurosci. 2004, 24, 6171–6180.
  48. Chen, D.P.; Eisenberg, R.S. Poisson-Nernst-Planck (PNP) theory of open ionic channels. Biophys. J. 1993, 64, A22.
  49. Harden, J.L.; Viovy, J.L. Numerical studies of pulsed iontophoresis through model membranes. J. Control. Released 1996, 38, 129–139.
  50. Kurnikova, M.G.; Coalson, R.D.; Graf, P.; Nitzan, A. A lattice relaxation algorithm for 3D Poisson-Nernst-Planck with application to ion transport through the gramicidin A channel. Biophys. J. 1999, 76, 642–656.
  51. McKelvey, J.P. Solid State and Semiconductor Physics; Krieger: Malabar, FL, USA, 1982; pp. 1–504.
  52. Marchand, J.; Gérard, B.; Delagrave, A. Ion transport mechanism in cement-based materials. In Materials Science of Concrete; Skalny, J.P., Ed.; American Ceramic Society: Westerville, OH, USA, 1998; Volume V, pp. 307–400.
  53. Krabbenhøft, K.; Krabbenhøft, J. Application of the Poisson–Nernst–Planck equations to the migration test. Cem. Concr. Res. 2008, 38, 77–88.
  54. Szyszkiewicz, K.; Jasielec, J.J.; Danielewski, M.; Lewenstam, A.; Filipek, R. Modeling of electrodiffusion processes from nano to macro scale. J. Electrochem. Soc. 2017, 164, E3559–E3568.
  55. Lakshminarayanaiah, N. Equations of Membrane Biophysics; Academic Press: New York, NY, USA, 1984.
  56. Probstein, R.F. Physicochemical Hydrodynamics; Butterworth: Stoneham, NA, USA, 1989.
  57. Critchlow, D.L. MOSFET scaling—The driver of VLSI technology. Proc. IEEE 1999, 87, 659–667.
  58. Dennard, R.H.; Gaensslen, F.H.; LeBlanc, A.R. Design of non-implanted MOSFET’s with very small physical dimensions. Proc. IEEE 1999, 87, 668–678.
  59. Hof, P.R.; de Vellis, J.; Nimchinsky, E.A.; Kidd, G.; Claudio, L.; Trapp, B.D. Cellular Components of Nervous Tissue. In Fundamental Neuroscience, 3rd ed.; Squire, L., Berg, D., Bloom, F., du Lac, S., Gosh, A., Spitzer, N., Eds.; Elsevier Science Publishing Co. Inc.: San Diego, CA, USA, 2012; pp. 41–58.
  60. Savtchenko, L.P.; Kulahin, N.; Korogod, S.M.; Rusakov, D.A. Electric fields of synaptic currents could influence diffusion of charged neurotransmitter molecules. Synapse 2004, 51, 270–278.
  61. Sylantyev, S.; Savtchenko, L.P.; Niu, Y.-P.; Ivanov, A.I.; Jensen, T.P.; Kullmann, D.M.; Xiao, M.-Y.; Rusakov, D.A. Electric Fields Due to Synaptic Currents Sharpen Excitatory Transmission. Science 2008, 319, 1845–1849.
  62. Ercius, P.; Alaidi, O.; Rames, M.J.; Ren, G. Electron Tomography: A Three-Dimensional Analytic Tool for Hard and Soft Materials Research. Adv. Mater. 2015, 27, 5638–5663.
  63. Leopre, C.L.; Bartol, T.M.; Coggan, J.S.; Keller, D.X.; Sosinsky, G.E.; Ellisman, M.H.; Sejnowski, T.J. Computational modelling of three dimensional electrodiffusion in biological systems: Application to the node of Ranvier. Biophys. J. 2008, 95, 2624–2635.
  64. Cartailler, J.; Kwon, T.; Yuste, R.; Holcman, D. Deconvolution of voltage sensor time series and electro-diffusion modeling reveal the role of spine geometry in controlling synaptic strength. Neuron 2018, 97, 1–11.
  65. Araya, R.; Jiang, J.; Eisenthal, K.B.; Yuste, R. The spine neck filters membrane potentials. Proc. Natl. Acad. Sci. USA 2006, 103, 17961–17966.
  66. Araya, R.; Vogels, T.P.; Yuste, R. Activity-dependent dendritic spine neck changes are correlated with synaptic strength. Proc. Natl. Acad. Sci. USA 2014, 111, E2895–E2904.
  67. Goldman, D.E. Potential, impedance, and rectification in membranes. J. Gen. Physiol. 1943, 27, 37–60.
  68. Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544.
  69. Qian, N.; Sejnowski, T.J. An electro-diffusion model for computing membrane-potentials and ionic concentrations in branching dendrites, spines and axons. Biol. Cybern. 1989, 62, 1–15.
  70. Holcman, D.; Yuste, R. The new nanophysiology: Regulation of ionic flow in neuronal subcompartments. Nat. Rev. Neurosci. 2015, 16, 685–692.
  71. Gardner, C.L.; Jones, J.R.; Baer, S.M.; Chang, S. Simulation of the ephaptic effect in the cone-horizontal cell synapse of the retina. SIAM J. Appl. Math. 2013, 73, 636–648.
  72. Gardner, C.L.; Jones, J.R.; Baer, S.M.; Crook, S.M. Drift-diffusion simulation of the ephaptic effect in the triad synapse of the retina. J. Comput. Neurosci. 2015, 38, 129–142.
  73. Nanninga, P. A computational neuron model based on Poisson-Nernst-Planck theory. ANZIAM J. 2008, 50, 46–59.
  74. Halnes, G.; Mäki-Marttunen, T.; Keller, D.; Pettersen, K.H.; Andreassen, O.A.; Einevoll, G.T. Effect of Ionic Diffusion on Extracellular Potentials in Neural Tissue. PLoS Comput. Biol. 2016, 12, e1005193.
  75. Neher, E. Correction for liquid junction potentials in patch clamp experiments. Method Enzymol. 1992, 207, 123–131.
  76. Lewenstam, A. Design and pitfalls of ion selective electrodes. Scand. J. Clin. Lab. Investig. Suppl. 1994, 54, 11–19.
  77. Lewenstam, A. Ion-selective electrodes in clinical chemistry: State of the art. Anal. Proc. 1991, 28, 106–109.
  78. Lewenstam, A.; Maj-Żurawska, M.; Hulanicki, A. Application of ion-selective electrodes in clinical analysis. Electroanalysis 1991, 3, 727–734.
  79. Henderson, P. Zur thermodynamik der flüssigkeitsketten. Z. Phys. Chem. 1907, 59, 118–127.
  80. Henderson, P. Zur thermodynamik der flüssigkeitsketten. Z. Phys. Chem. 1908, 63, 325–345.
  81. Jerzy, J. Jasielec Website. Available online: (accessed on 9 December 2020).
  82. Hickman, H.J. The liquid junction potential—The free diffusion junction. Chem. Eng. Sci. 1970, 25, 381–398.
  83. Lingane, J.J. Electroanalytical Chemistry, 2nd ed.; Wiley: New York, NY, USA, 1998.
  84. MacInnes, D.A. The Principles of Electrochemistry, 2nd ed.; Dover Publications: New York, NY, USA, 1961.
  85. Nernst, W.H. Die elektromotorische wirksamkeit der jonen. Z. Phys. Chem. 1889, 4, 129–181.
  86. Guggenheim, E.A. A study of cells with liquid-liquid junctions. J. Am. Chem. Soc. 1930, 52, 1315–1337.
  87. Hafemann, D.R. Charge Separation in Liquid Junctions. J. Phys. Chem. 1965, 69, 4226–4231.
  88. Dickinson, E.J.F.; Freitag, L.; Compton, R.G. Dynamic theory of liquid junction potentials. J. Phys. Chem. B 2010, 114, 187–197.
  89. Ward, K.R.; Dickinson, E.J.F.; Compton, R.G. Dynamic theory of type 3 liquid junctions potentials: Formation of multilayer liquid junctions. J. Phys. Chem. B 2010, 114, 4521–4528.
  90. Nelson, D.L.; Cox, M.M. Lehninger Principles of Biochemistry, 6th ed.; Freeman/Worth: New York, NY, USA, 2012; pp. 690–748.
  91. Chung, S.-H.; Tieleman, D.P. Computational and theoretical approaches to Unraveling the Permeation Dynamics in Biological Nanotubes. In Handbook of Theoretical and Computational Nanotechnology; Rieth, M., Schommers, W., Eds.; American Scientific Publishers: Stevenson Ranch, CA, USA, 2006; Volume 10, pp. 1–54.
  92. Århem, P.; Klement, G.; Blomberg, C. Channel Density Regulation of Firing Patterns in a Cortical Neuron Model. Biophys. J. 2006, 90, 4392–4404.
  93. Zeberg, H.; Blomberg, C.; Århem, P. Ion Channel Density Regulates Switches between Regular and Fast Spiking in Soma but Not in Axons. PLoS Comput. Biol. 2010, 6, e1000753.
  94. Migliore, R.; Lupascu, C.A.; Bologna, L.L.; Romani, A.; Courcol, J.-D.; Antonel, S.; Van Geit, W.A.H.; Thomson, A.M.; Mercer, A.; Lange, S.; et al. The physiological variability of channel density in hippocampal CA1 pyramidal cells and interneurons explored using a unified data-driven modeling workflow. PLoS Comput. Biol. 2018, 14, e1006423.
  95. Motipally, S.I.; Allen, K.M.; Williamson, D.K.; Marsat, G. Differences in Sodium Channel Densities in the Apical Dendrites of Pyramidal Cells of the Electrosensory Lateral Line Lobe. Front. Neural Circuits 2019, 13, 41.
  96. Mori, Y.; Peskin, C.S.A. A numerical method for cellular electrophysiology based on the electrodiffusion equations with internal boundary conditions at membranes. Commun. Appl. Math. Comput. Sci. 2009, 4, 85–134.
  97. Pods, J.; Schönke, J.; Bastian, P. Electrodiffusion model of neurons and extracellular space using the Poisson-Nernst-Planck equations—Numerical simnulation of intra- and extracellular potential for an axon model. Biophys. J. 2013, 105, 242–254.
  98. Eisenberg, R.S. Channels are enzymes. J. Memb. Biol. 1990, 115, 1–12.
  99. Schuss, Z.; Nadler, B.; Eisenberg, R.S. Derivation of Poisson and Nernst-Planck equations in a bath and channel from a molecular model. Phys. Rev. E 2001, 64, 036116.
  100. Chen, D.; Lear, J.; Eisenberg, B. Permeation through an open channel: Poisson-Nernst-Planck theory of a synthetic ionic channel. Biophys. J. 1997, 72, 97–116.
  101. Woolley, G.A.; Biggin, P.C.; Schultz, A.; Lien, L.; Jaikaran, D.; Breed, J.; Crowhurst, K.; Sansom, M.S. Intrinsic rectifiction of ion flux in alamethicin channels: Studies with an alamethicin dimer. Biophys. J. 1997, 73, 770–778.
  102. Nonner, W.; Chen, D.; Eisenberg, B. Anomalous mole fraction effect, electrostatics and binding in ionic channels. Biophys. J. 1998, 74, 2327–2334.
  103. Aquilella-Arzo, M.; Aguilella, V.M.; Eisenberg, R.S. Computing numerically the access resistance of a pore. Eur. Biophys. J. 2005, 34, 314–322.
  104. Hall, J.E. Access resistance of a small circular pore. J. Gen. Phys. 1975, 66, 531–532.
  105. Nonner, W.; Eisenberg, B. Ion Permeation and glutamate residues linked by Poisson-Nernst-Planck theory in L-type calcium channels. Biophys. J. 1998, 75, 1287–1305.
  106. Nonner, W.; Catacuzzeno, L.; Eisenberg, B. Binding and selectivity in L-type Ca channels. Biophys. J. 2000, 79, 1976–1992.
  107. Eisenberg, B. Crowded Charges in Ion Channels. In Advances in Chemical Physics; Rice, S., Ed.; John Wiley & Sons: New York, NY, USA, 2011; pp. 77–223.
  108. Eisenberg, B. Ionic interactions are everywhere. Physiology 2013, 28, 28–38.
  109. Maffeo, C.; Bhattacharya, S.; Yoo, J.; Wells, D.; Aksimentiev, A. Modelling and simulation of Ion Channels. Chem. Rev. 2012, 112, 6250–6284.
  110. Hollerbach, U.; Chen, D.-P.; Eisenberg, R.S. Two- and three- dimensional Poisson-Nernst-Planck simulations of current flow through Gramicidin A channel. J. Sci. Comp. 2001, 16, 373–409.
  111. Valent, I.; Petrovič, P.; Neogrády, P.; Schreiber, I.; Marek, M. Electrodiffusion kinetics of ionic transport in a siple membrane channel. J. Phys. Chem. 2013, 117, 14283–14293.
  112. Cárdenas, A.E.; Coalson, R.D.; Kurnikova, M.G. Three-dimensional Poisson-Nernst-Planck theory studies: Influence of membrane electrostatics on gramicidin A channel conductance. Biophys. J. 2000, 79, 80–93.
  113. Koumanov, A.; Zachariae, U.; Engelhardt, H.; Karshikoff, A. Improved 3D continuum calculations of ion flux through membrane channels. Eur. Biophys. J. 2003, 32, 689–702.
  114. Van der Straaten, T.A.; Tang, J.M.; Ravaioli, U.; Eisenberg, R.S.; Aluru, N.R. Simulating ion permeation through the ompF porin ion channel using three-dimensional drift-diffusion theory. J. Comput. Electron. 2003, 2, 29–47.
  115. Roux, B. The membrane potential and its representation by a constant electric field in computer simulations. Biophys. J. 2008, 95, 4205–4216.
  116. Kutzner, C.; Grubmuller, H.; de Groot, B.L.; Zachariae, U. Computational electrophysiology: The molecular dynamics of ion channel permeation and selectivity in atomistic detail. Biophys. J. 2011, 101, 809–817.
  117. Jensen, M.; Borhani, W.; Lindorff-Larsen, K.; Maragakis, P.; Jogini, V.; Eastwood, M.P.; Dror, R.O.; Shaw, D.E. Principles of conduction and hydrophobic gating in K+ channels. Proc. Natl. Acad. Sci. USA 2010, 107, 5833–5838.
  118. Bidon-Chanal, A.; Krammer, E.-M.; Blot, D.; Pebay-Peyroula, E.; Chipot, C.; Ravaud, S.; Dehez, F. How do membrane transporters sense pH? The case of mitochondrial ADP-ATP carrier. J. Phys. Chem. Lett. 2013, 4, 3787–3791.
  119. Roux, B.; Allen, T.; Berneche, S.; Im, W. Theoretical and computational models of biological ion channels. Q. Rev. Biophys. 2004, 37, 15–103.
  120. Krammer, E.-M.; Homblé, F.; Prévost, M. Molecular origin of VDAC selectivity towards inorganic ions: A combined molecular and Brownian dynamics study. Biochem. Biophys. Acta 2013, 1828, 1284–1292.
  121. Boda, D.; Valiskó, M.; Gillespie, D. Modeling the Device Behavior of Biological and Synthetic Nanopores with Reduced Models. Entropy 2020, 22, 1259.
  122. Miękisz, J.; Gomułkiewicz, J.; Miękisz, S. Mathematical models of ion transport through cell membrane channels. Math. Appl. 2014, 42, 39–62.
  123. Kuyucak, S.; Andersen, O.S.; Chung, S.-H. Models of permeation in ion channels. Rep. Prog. Phys. 2001, 64, 1427–1472.
  124. Corry, B.; Chung, S.-H. Mechanism of valence selectivity in biological ion channels. Cell Mol. Life Sci. 2006, 63, 301–315.
  125. Liu, J.-L.; Eisenberg, B. Molecular Mean-Field Theory of Ionic Solutions: A Poisson-Nernst-Planck-Bikerman Model. Entropy 2020, 22, 550.
  126. Bezanilla, F. The voltage sensor in voltage-dependent ion channels. Physiol. Rev. 2000, 80, 555–592.
  127. Catteral, W.A. Ion channel voltage sensors: Structure, function, and pathophysiology. Neuron 2010, 67, 915–928.
  128. Tombola, F.; Pathak, M.M.; Isacoff, E.Y. How does voltage open an ion channel? Annu. Rev. Cell. Dev. Biol. 2006, 22, 23–52.
  129. Clarke, D.D.; Sokoloff, L. Circulation and energy metabolism of the brain. In Basic Neurochemistry: Molecular, Cellular, and Medical Aspects, 6th ed.; Siegel, G.J., Agranoff, B.W., Albers, R.W., Fisher, S.K., Uhler, M.D., Eds.; Lippincott-Raven: New York, NY, USA, 1999; pp. 637–669.
  130. Jasielec, J.J.; Filipek, R.; Dołowy, K.; Lewenstam, A. Precipitation of Inorganic Salts in Mitochondrial Matrix. Membranes 2020, 10, 81.
  131. Griffiths, T.; Evans, M.C.; Meldrum, B.S. Intracellular sites of early calcium accumulation in the rat hippocampus during status epilepticus. Neurosci. Lett. 1982, 30, 329–334.
  132. Erecińska, M.; Silver, I.A. Relationships between ions and energy metabolism: Celebral calcium movements during ischemia and subsequent recovery. Can. J. Physiol. Pharmacol. 1992, 70, S190–S193.
  133. Zaidan, E.; Sims, N.R. The calcium content of mitochondria from brain subregions following short-term forebrain ischemia and recirculation in the rat. J. Neurochem. 1994, 63, 1812–1819.
  134. Fineman, I.; Hovda, D.A.; Smith, M.; Yoshino, A.; Becker, D.P. Concussive brain injury is associated with a prolonged accumulation of calcium: A 45Ca autoradiographic study. Brain Res. 1993, 624, 94–102.
  135. Sparagna, G.C.; Gunter, K.K.; Sheu, S.S.; Gunter, T.E. Mitochondrial calcium uptake from physiological-type pulses of calcium. A description of the rapid uptake mode. J. Biol. Chem. 1995, 270, 27510–27515.
  136. Williams, G.S.; Boyman, L.; Chikando, A.C.; Khairallah, R.J.; Lederer, W.J. Mitochondrial calcium uptake. Proc. Natl. Acad. Sci. USA 2013, 110, 10479–10486.
  137. McCormack, J.G.; Denton, R.M. The role of mitochondrial Ca2+ transport and matrix Ca2+ in signal transduction in mammalian tissues. Biochim. Biophys. Acta 1990, 1018, 287–291.
  138. Kannurpatti, S.S.; Sanganahalli, B.G.; Herman, P.; Hyder, F. Role of mitochondrial calcium uptake homeostasis on resting-state fMRI brain networks. NMR Biomed. 2015, 28, 1579–1588.
  139. Jasielec, J.J.; Filipek, R.; Szyszkiewicz, K.; Sokalski, T.; Lewenstam, A. Continuous Modeling of Calcium Transport through Biological Membranes. J. Mater. Eng. Perform. 2016, 25, 3285–3290.
  140. Lehninger, A.L.; Rossi, C.S.; Greenawalt, J.W. Respiration-dependent accumulation of inorganic phosphate and Ca ions by rat liver mitochondria. Biochem. Biophys. Res. Commun. 1963, 10, 444–448.
  141. Lehninger, A.L. Mitochondria and calcium ion transport. Biochem. J. 1970, 119, 129–138.
  142. Rossi, C.S.; Lehninger, A.L. Stoichiometric relationships between accumulation of ions by mitochondria and the energy-coupling sites in the respiratory chain. Biochem. Z. 1963, 338, 698–713.
  143. Rossi, C.S.; Lehninger, A.L. Stoichiometry of respiratory stimulation, accumulation of Ca2+ and phosphate and oxidative phosphorylation in rat liver mitochondria. J. Biol. Chem. 1964, 239, 3971–3980.
  144. Lehninger, A.L.; Carafoli, E.; Rossi, C.S. Energy-linked ion movements in mitochondrial systems. Adv. Enzymol. Relat. Areas Mol. Biol. 1967, 29, 259–320.
  145. Arnaudeau, S.; Kelley, W.L.; Walsh, J.V.; Demaurex, N. Mitochondria recycle Ca2+ to the endoplasmic reticulum and prevent the depletion of neighboring endoplasmic reticulum regions. J. Biol. Chem. 2001, 276, 29430–29439.
  146. Brandenburger, Y.; Kennedy, E.D.; Python, C.P.; Rossier, M.F.; Vallotton, M.B.; Wollheim, C.B.; Capponi, A.M. Possible role for mitochondrial calcium in angiotensin II- and potassium-stimulated steroidogenesis in bovine adrenal glomerulosa cells. Endocrinology 1996, 137, 5544–5551.
  147. Schreur, J.H.; Figueredo, V.M.; Miyamae, M.; Shames, D.M.; Baker, A.J.; Camacho, S.A. Cytosolic and mitochondrial [Ca2+] in whole hearts using indo-1 acetoxymethyl ester: Effects of high extracellular Ca2+. Biophys. J. 1996, 70, 2571–2580.
  148. Miyata, H.; Silverman, H.S.; Sollott, S.J.; Lakatta, E.G.; Stern, M.D.; Hansford, R.G. Measurement of mitochondrial free Ca2+ concentration in living single rat cardiac myocytes. Am. J. Physiol. 1991, 261, H1123–H1134.
  149. Moreno-Sanchez, R.; Hansford, R.G. Dependence of cardiac mitochondrial pyruvate dehydrogenase activity on intramitochondrial free Ca2+ concentration. Biochem. J. 1988, 256, 403–412.
  150. Allen, S.P.; Stone, D.; McCormack, J.G. The loading of fura-2 into mitochondria in the intact perfused rat heart and its use to estimate matrix Ca2+ under various conditions. J. Mol. Cell. Cardiol. 1992, 24, 765–773.
  151. Lukács, G.L.; Kapus, A. Measurement of the matrix free Ca2+ concentration in heart mitochondria by entrapped fura-2 and quin2. Biochem. J. 1987, 248, 609–613.
  152. Davis, M.H.; Altschuld, R.A.; Jung, D.W.; Brierley, G.P. Estimation of intramitochondrial pCa and pH by fura-2 and 2,7 biscarboxyethyl-5(6)-carboxyfluorescein (BCECF) fluorescence. Biochem. Biophys. Res. Commun. 1987, 149, 40–45.
  153. Ivannikov, M.V.; Macleod, G.T. Mitochondrial free Ca2+ levels and their effects on energy metabolism in Drosophila motor nerve terminals. Biophys. J. 2013, 104, 2353–2361.
  154. Dołowy, K. Calcium phosphate buffer formed in the mitochondrial matrix during preconditioning supports ∆pH formation and ischemic ATP production and prolongs cell survival—A hypothesis. Mitochondrion 2019, 47, 210–217.
  155. Liou, G.Y.; Storz, P. Reactive oxygen species in cancer. Free Radic. Res. 2010, 44, 479–496.
  156. Simonian, N.A.; Coyle, J.T. Oxidative Stress in Neurodegenerative Diseases. Ann. Rev. Pharmacol. Toxicol. 1996, 36, 83–106.
  157. Barnham, K.J.; Masters, C.L.; Bush, A.I. Neurodegenerative diseases and oxidatives stress. Nat. Rev. Drug Discov. 2004, 3, 205–214.
  158. Rao, A.V.; Balachandran, B. Role of oxidative stress and antioxidants in neurodegenerative diseases. Nutr. Neurosci. 2002, 5, 291–309.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Electrochemistry; Biochemistry & Molecular Biology; Neurosciences
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Jerzy Jasielec
View Times: 1.4K
Revisions: 4 times (View History)
Update Date: 29 Apr 2021
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback