Encyclopedia
Please note this is an old version of this entry, which may differ significantly from the current revision.
There are two main processes governing the ionic transport, i.e., diffusion—the particle motion caused by a gradient of concentration, and migration—motion of ions caused by a gradient of electrical potential. These two processes are referred to as electrodiffusion. Electrodiffusion of electrolytes serves as a mean for communication in the nervous system. It can directly affect the excitatory transmission in the synaptic cleft. Electrodiffusion maintains the local ions concentration in brain extracellular spaces at heathy levels but may be also involved in the propagation of epileptic seizures during pathological conditions. The accurate interpretation of physiological observations requires better understanding of the underlying electrodiffusion phenomena.The description of electrodiffusion is very often performed using the Nernst–Planck–Poisson (NPP) model. It has been acknowledged that the spatiotemporal dynamics of the ion concentrations in thin dendrites and dendritic spines of nerve cells follow the Nernst–Planck equation, and sub-membrane currents in neuronal membrane have already been successfully described using the NPP model.
- electrodiffusion
- Nernst–Planck–Poisson
- neuroscience
- neurons
- liquid junction potential
- patch-clamp
- ionic channels
- mitochondria
1. The Nernst–Planck–Poisson Model
The Poisson equation describes the electric field occurring due to the movement of ions, i.e., relates the electrical potential, φ, to the concentrations of ions:
where ci represents the concentration of the i-th ion, zi denotes its charge, ε is the dielectric permeability of the medium and F=96485.3 C mol−1 is the Faraday constant. In order to include the information about the external current Iext applied to a system, Poisson equation can be substituted with the Displacement Current equation [10]:
where the electric field E is directly connected to the gradient of electrical potential, i.e., E = −∇φ.
∇2φ = − Fε ∑izici , (1)
∂E/∂t = Iext − Fε ∑iziJi, (2)
The Nernst–Planck equation relates the flux of ions Ji to the diffusion (driven by the gradient of concentration, ∇ci), the migration (driven by the gradient of electrical potential, ∇φ), and the convection processes:
where Di is the diffusion coefficient of the i-th ion, R = 8.31 J mol−1 K−1 is the gas constant, T represents the temperature, and υ is the drift velocity.
Ji = −Di∇ci − (F/RT)ziDici∇φ + ciυ (3)
Together with the mass-balance equation:
they form a set of coupled nonlinear partial differential equations, and with proper initial and boundary conditions, they provide a quantitative description of electrodiffusion phenomena. This set of equations is known as drift-diffusion in computational physics [11,12]; as the Nernst–Planck–Poisson (NPP) [13,14] in electrochemistry and materials engineering, where the role of time-dependent flux is stressed; or as the Poisson–Nernst–Planck (PNP) in biophysics and electrophysiology, where the importance of computing the variable spatial distribution of potential is emphasized [15].
∂ci/∂t = − ∇Ji, (4)
In the end of 19th century, Planck provided the first solution of the NPP equations [16]. He considered one-dimensional diffusion of two monovalent ions through a homogeneous membrane, assuming the occurrence of steady-state (i.e., no changes of concentrations or electric field and constant ionic fluxes across the system). More than a half-century later [17], his solution was extended to describe an arbitrary number of ions of any valence number. These and other analytical solutions [18,19,20] use the electroneutrality assumption. Alternatively, the constant electric field across the membrane can be assumed [21]. It has been shown that the electroneutrality assumption and the constant field hypothesis are the two limiting cases of the Poisson equation [22,23,24].
The electroneutrality is a central principle of the classical electrolyte theory, upon which the key electrochemical and electrophysiological derivations have been based [1]. The NPP problem with the electroneutrality assumption is significantly easier to solve. Although this simplification was historically almost necessary due to the lack of high performing computers, nowadays this attitude cannot be defended, as the access to high computing power is ubiquitous.
By solving the Nernst–Planck equations, we are trying to determine the effect of the electric field, which only arises in the presence of a net charge separation. Therefore, the electroneutrality assumption suffers from a fundamental inherent paradox [25]. Furthermore, the electroneutrality was denounced as unphysical [26], i.e., at finite time it is dynamically inconsistent with the solutions where the Poisson equation is obeyed.
The difficulties with the analytical solution of the NPP problem without the electroneutrality assumption, as well as the search for a more general and widely applicable approach, led the researchers to use the numerical methods. The first time-dependent NPP model using a numerical procedure, namely, an explicit (non-predictive) finite difference method, was developed in 1965 [10]. A decade later, an efficient simulation procedure for multi-component NPP equations using the first fully implicit (predictive) finite difference time scheme was presented by Brumleve and Buck [13]. Their approach to the numerical treatment of NPP has been used in numerous papers in electrochemistry of ion-selective membranes [27,28,29,30,31,32,33,34,35,36,37]. Other numerical methods proposed for the solution of the NPP problem include fast implicit finite difference [38], finite element [39,40,41,42], and network simulation [43,44,45]. The existence of an asymptotic analytical solution [46], found for small voltage-clamp values and for early times, allows testing of the numerical approaches also with respect to temporal dynamics.
The NPP model has been successfully used for the description of a large variety of electrochemical sensors used in potentiometry [31,32,33,34,35,36,37,47] and impedance spectroscopy [13,48,49]. That includes the NPP description of neutral carrier electrodes [50], solid-contact electrodes [51], coated-wire electrodes [52], and ion-selective field effect transistors [52]. Application of NPP in sensors leads to a deeper understanding of sensing mechanisms and underlying electrochemical processes, together with the miniaturization that can lead to the development of more robust and precise electrochemical sensors for in vivo measurements. Particularly interesting is, e.g., the development of biomimetic membranes using the Mg2+/Ca2+ antagonism mechanism [53], mimicking the action of glutamate-gated ion channels in NMDA receptors present in neural tissue [54,55]. The application of NPP for the description of ion sensors will be the topic of another review.
In the field of biophysics, the NPP equations were introduced by Eisenberg [56] in the early 1990s. The numerical method that can be easily transposed in two- or three-dimensional geometry [57], the numerical scheme working in two-dimensional geometry [40], and finally, a lattice-relaxation algorithm able to solve a 3D model [58] allowed the description of physiological systems with various complicated shapes.
Currently, the system of the NPP equations has become multidisciplinary, abundant in many fields of science and technology, e.g., semiconductors [11,12,59], building materials [60,61,62], synthetic and biological charged membranes [63], colloids [64], and electrochemical ion sensors [14]. The NPP allows the optimal scaling of semiconductor properties and device characteristics as devices become smaller [65,66]. The NPP speeds up the technological development, by replacing slow, expensive trial and error experimentation with direct computing [15].
2. The NPP Description of Neurons
Neurons are highly specialized cells and essential cellular elements in the central nervous system. All neurological processes are dependent on complex interactions between single neurons and groups of related neurons. Morphologically, a typical neuron, consists of three regions: (1) the cell body (soma or perikaryon) containing the nucleus and the major cytoplasmic organelles, (2) a variable number of dendrites, and (3) a single axon. At the interface of axon terminals with target cells are the synapses, i.e., specialized zones of contact, which consist of a presynaptic (axonal) element, a narrow synaptic cleft, and a postsynaptic element on a dendrite or soma. The portion of the presynaptic element is the active zone, enriched with ion channels necessary to permit the neurotransmitter release. For a very detailed description of neuron morphology as well as different types of neural cells, see [69].
The NPP equations might serve as a tool for the description of the phenomena occurring during neurotransmitters electrodiffusion [1]. It was used to calculate the reaction rate constant of neurotransmitter acetylcholine (ACh) in the reaction center of the enzyme acetylcholinesterase (AChE) [41,42]. The obtained results showed that the rate coefficient depends on the concentration of the substrate (i.e., change from 2 × 1011 down to 8 × 1010 M−1 min−1 for the substrate concentration change from 1 to 500 mM at an ionic strength of 134 mM), as well as on the ionic-strength of the solution (i.e., it peaks at around 12 × 109 M−1 min−1 at an ionic strength of 134 mM and reduces to about 8 × 109 M−1 min−1 at an ionic strength of 500 mM). A noticeable shift of the peak, located at 0.15 µs for maximum rate coefficient, was found at the physiological ionic strength of 134 mM, which differs from the results of a more idealized Smoluchowski–Poisson–Boltzmann model (peak at 0.31 µs). This suggests that the NPP model is more desirable for the description of the electrostatic-driven diffusion and substrate consumption in this system [41].
The NPP model has also been applied for calculations of glutamate electrodiffusion in synaptic cleft [70]. The results showed that the synaptic currents could significantly accelerate the dispersion of negatively charged neurotransmitter molecules from the cleft and attract the positively charged ones towards the current sinks. Therefore, the shape of the synaptic response strongly depends on the electrodynamic interactions between the charged neurotransmitter molecules and the postsynaptic current. These predictions are well supported by experimental evidence [2].
With the possibility to obtain 3D structures from electron tomography [71] came the opportunity for modelling the systems with complex geometries based on morphologically realistic depictions of cells and organelles relevant to neuroscience. It led to the neurological application of NPP in the description of the node of Ranvier [6], a component in myelinated axons consisting of axonal and glial membranes and small aqueous compartments. Dysfunctions of its nodal complex play an important role in several neurological disorders, such as multiple sclerosis, Charcot–Marie–Tooth disease and Guillain–Barre syndrome. The electrodiffusion in the node of Ranvier is significant since the voltages surrounding individual channels determine channel gating and the response of each channel to the local electrochemical gradient. The NPP results show the accumulation and depletion of ions close to the membrane. The algorithm applied to the node of Ranvier can also be applied for the description of other biophysical processes, such as the generation/transmission of cardiac impulses and synaptic transmission [6].
The synaptic connections are made on dendritic spines, i.e., parts of the neuron’s dendrite that receive input from a single axon at the synapse and are comprised of spine head and spine neck. The strength of the connection between two interacting neurons is reflected by the electric potential change, induced by excitatory current. To investigate the dependence of the electrical properties of spines on their geometry, the NPP modelling was combined with voltage imaging data [72]. Results show that changing the length of the spine neck can regulate the local dendritic voltage and, consequently, contributes to the emergence of an action potential. The correlation between the voltage amplitude and the neck length is confirmed by earlier experimental findings in brain slices [73,74]. This length modulation is complementary to the possible changes in the number of receptors in the synapse, resulting in a long-term modification of the synaptic current during synaptic plasticity [72].
The propagation of the electrical signal in neurons is usually described by cable theory, developed by Goldman, Hodgkin, and Katz [75,76] and successfully used as a framework for studying neuronal conduction. The NPP computation of excitatory postsynaptic potentials shows the limitations of cable theory in cases of thin dendrites or large concentration changes [5]. Also, in the case of small neuronal compartments or dendritic spines, it seems that cable theory may be inadequate, because it assumes spatial and ionic homogeneity [77]. The NPP equations are free from such assumption and allow the more accurate modelling of the constraints that neuronal nanostructures place on the neuronal currents. The application of NPP to dendritic spines results in the following predictions about the influence of geometry on the regulation of electrical current [77]:
-
The voltage inside the spine saturates as the injected current increases.
-
When the spine head is isolated and the current leak through the neck is slow, ions concentrate at the surface of the spine.
-
A large electric field forms at the spine neck–head junction.
The NPP gives important information on the potential profile within the cells of the synaptic circuit and in the intersynaptic space. It relates the electric field inside and outside the cell during the spread of an action potential along an axonal membrane with the complex interaction of ion movements and the evolution of the extracellular signal.
The visual information is translated into electric currents by photoreceptors through changes in their membrane potentials. The NPP was applied for the description of the triad synapse (a type of synapse in the outer plexiform layer formed by a cone, a horizontal cell, and a bipolar cell) in the goldfish retina in order to investigate the importance of ephaptic (electrical) effects [78,79]. These effects were demonstrated by calculating the shift in the current–potential curve for increasingly narrower openings between the cone and the horizontal cell. The NPP results provide convincing evidence that an ephaptic mechanism can produce the feedback effect seen in the experiments. The simulations of the triad synapse also demonstrate the dependence of the feedback on the behavior of the bipolar cell under background illumination [79]. Better understanding of the feedback mechanisms is essential to unravel how visual processing takes place in the retina.
Owing to their close proximity, neurons must have a direct electrodiffusive impact on their neighbors. The neuron environment, consisting of densely packed neurons and neuroglia, has been described using the NPP equations [7]. The results qualitatively and quantitatively agree with the Goldman equation but indicate that there is always a particle flux, even at steady-state.
3. Non-Stationary Liquid Junction Potential
The diffusive currents in extracellular space surrounding a small population of neurons can evoke a non-zero potential gradient, so that potential in soma region is more negative than in the apical region [80]. This diffusion-generated-potential is known as liquid junction potential (LJP), i.e., a potential emerging at a non-selective boundary between two electrolytes. The analysis of the time-dependent LJP response is also important for the practical applications in methods of analytical potentiometry, such as patch-clamp analysis [81] or fully automatic clinical electrolyte analyzers [82,83,84].
The value of LJP is usually calculated using Henderson equation [85,86]. This method is easy to implement and available as free online calculators [87]. However, it has been shown that the Henderson equation is only a special case of NPP [32]. It has also been proven using asymptotic analysis [88] that the Henderson equation is inexact in cases other than liquid junctions of two solutions of common phase but different concentrations, i.e., type 1 in Lingane’s classification [89]. Only for this type of junction does the steady state solution of NPP reduce to the form equivalent to the Henderson equation, consequently, giving the same values. The steady-state solution of NPP allows the validation of the linear concentration profiles assumption and the electroneutrality assumption used in derivation of Henderson equation, showing when the deviations occur [47].
Liquid junction can be described as an imaginary barrier, that separates two solutions of electrolytes connected by the means of a porous plug [90], has a limited width, and possesses the physical characteristics of water. A schematic depiction of the liquid junction system is presented in Figure 1a. This classical approach, developed in the end of 19th century by Nernst [91] and Planck [16] and defined later [92] as constrained liquid junction, has been widely used since [13,26,27,32,47,85,86]. Alternatively, instead of the unphysical barrier, a dynamically relaxing junction of two liquids, in which a diffuse layer continues to expand in a linear semi-infinite space, can be used. This approach, known as free liquid junction, was first presented and described using NPP equations by Hafemann [93]. The dynamics of free liquid junction, as well as the methods of analysis and simulation of liquid junction potentials, have been discussed in more detail in a recent review [94].
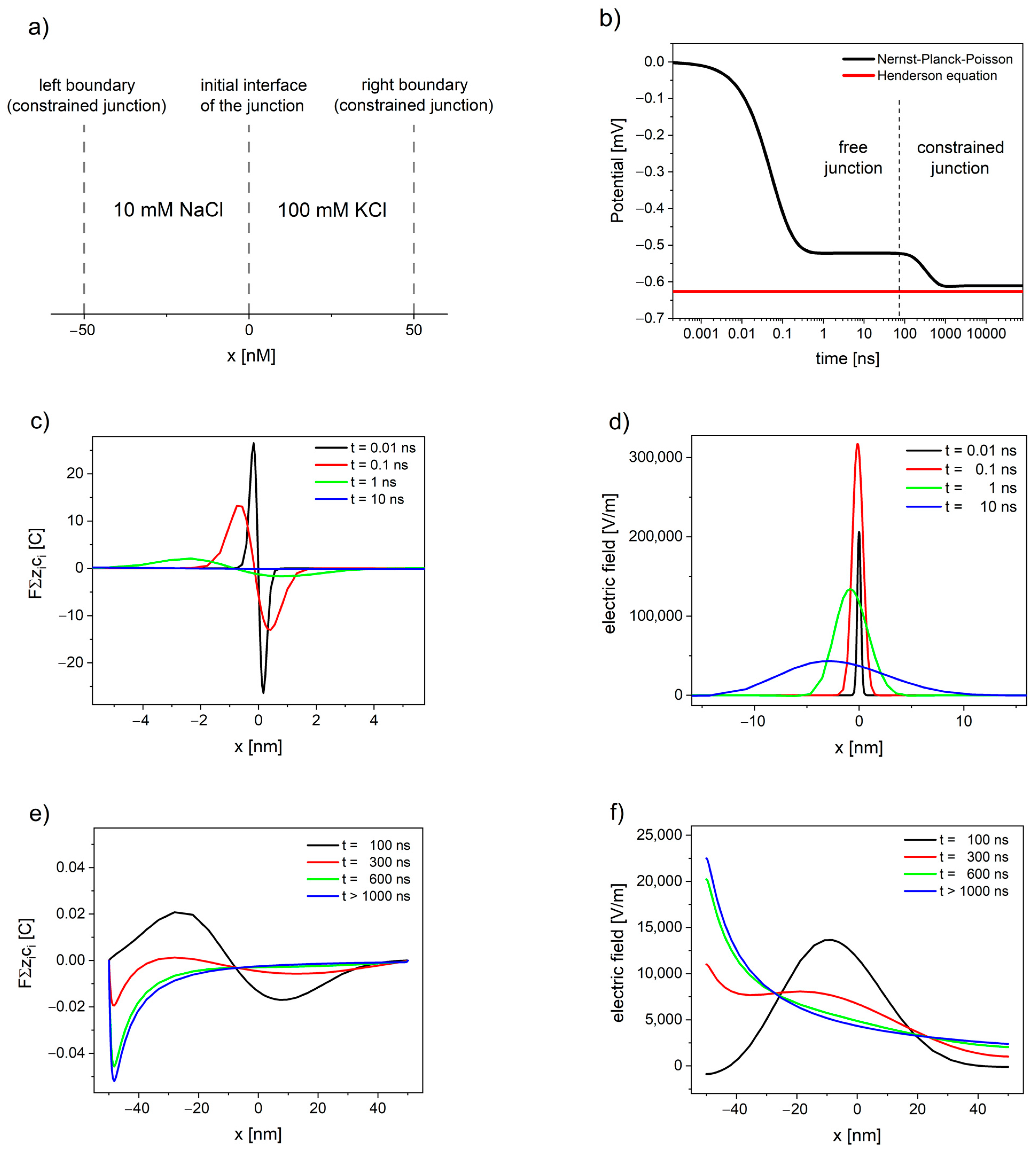
Figure 1. The evolution of free and constrained liquid junction potential (LJP) of watery solutions 10 mM NaCl|100 mM KCl calculated using Nernst–Planck–Poisson (NPP) model: (a) schematic depiction of the liquid junction system; (b) the liquid junction potential as a function of time; (c,e) deviation from electroneutrality; and (d,f) the resulting electric field.
The NPP system brings the modelling of liquid junction potentials closer to physical relevance, by allowing the simulation of time-dependent potential formation of both free and constrained liquid junction [47]. Figure 1 shows the evolution of liquid junction potential. Initially, the deviation from electroneutrality and the resulting changes in the electric field profiles occurs at the contact between solutions until the value of electric field reaches the maximum. Then, the deviation from electroneutrality and, consequently, the changes in the electric field propagate through the system, while their maximum decreases and shifts away from the initial interface of the junction (see Figure 1c,d). The value of overall electrical potential (area between the electric field and x-axis on Figure 1d) remains constant and corresponds to the value of free LJP. The free liquid junction is not at steady state, and the value of its potential arises as a consequence of the electric field expanding into the solutions.
If the deviation from electroneutrality and the resulting changes in the electric field reach the boundaries of the system, the pseudo-steady state characteristic for free liquid junction is disrupted. The potential changes its value, while the maximum of deviation from electroneutrality and maximum of the electric field shift towards the solution with lower concentration, until the steady state is attained (see Figure 1e,f).
The situation during the continued dialysis and solution mixing, when the interface of junction expands away from the electrode [1], corresponds to free liquid junction; therefore, the value of LJP in this case cannot be correctly estimated based on the Henderson method (the constrained junction approach). Furthermore, the electroneutrality, used by Henderson as assumption, is not fulfilled even at steady state (as shown in Figure 1e). The deviation from the Henderson equation for Lingane’s type 3 junctions ranges from very small (<0.02%) to very significant (>8%) over a very limited range of the diffusion coefficients ratio [95].
4. The NPP Description of Ion Channels
The neuronal compartments, as well as all other types of cells and organelles, are surrounded by phospholipid membranes. Embedded in these membranes are specialized assemblies of proteins, known as ionic channels and pumps—the nanoscopic pathways used to transport ions across the biological membranes [96]. Some types of the ion channels have a selectivity filter, permitting passage of only one type of ions, while others are non-selective, allowing multiple ion species to be transported. The opening and closing of ion channels regulate the communication between cells, the influence of hormones and drugs on the cell function, as well as other electrical activities in the nervous system [97].
The number and density of the ion channels can vary significantly between different types of cells, as well as between different neuronal compartments. The density of sodium channels in soma is quite low with 1 to 5 channels per μm2, while in some axons it can reach 700 to 2000 channels per μm2 [98]. The density of potassium channels varies from 0.5 to 5 channels per μm2 in soma to 240–1100 channels per μm2 in axons [98]. Modifying the density and distribution of ion channels (by natural regulation, spontaneous mutations, or pharmacological intervention) changes the activity pattern of a neuron. The differences in channel density and their influence on neural response have been extensively discussed in several papers [98,99,100,101].
The NPP models used for the description of neuronal compartments, presented in Section 2 of this review [5,6,7,8,9,41,42,72,77,78,79], neglect the effects of ionic channels and the influence of the number, size, and distance between them. Instead, they treat the membrane as an inert and uniform boundary of the considered system and describe it using proper (Dirichlet or Neumann) boundary conditions. Although this approach is justified, allowing much higher computational efficiency, the modeling of individual channels is also of an interest for many researchers.
The NPP found a very wide application in channology [102], i.e., a branch of biophysiology devoted to ion channels. The NPP equations predict quite accurately the current-voltage response of narrow channels over a wide range of salt concentrations in the surrounding solution [103]. The NPP has been applied to explain how the current rectification can be produced by the charges at the channel openings [104,105] and to demonstrate how a channel with ion-specific binding sites can exhibit a lower conductance in a mixture of two types of ions than in the pure solutions of either type [106].
The access resistance (important component of the conductance of ion channel, particularly in wide and short channels) calculated using NPP at the entrance of a circular uncharged pore in neutral membrane [107] is in good agreement with the results of classical Hall’s expression [108], derived from electrostatics. The NPP can be applied also in the situations when Hall’s expression overestimates the access resistance, i.e., for channels embedded in charged membranes [107].
The NPP implementation developed by Nonner and Eisenberg [109,110] has been used in a series of more than 40 papers (see review [111]) to describe the properties of three distinct ion channels: the Cav channels that control the heartbeat, the Nav channels that produce signaling in nervous systems, and the RyR channels that control calcium signaling in nearly all cells, including cardiac and skeletal muscles [112].
Ion channels have been described by a variety of one-dimensional [56,106,113], two-dimensional [114,115], and three-dimensional [58,114,116,117,118] NPP models. The detailed comparison between these models and the experimental responses of simple ionic channels (i.e., gramicidin A channel) shows when the geometrical simplifications are justified. The 2D circularly-symmetric model is especially helpful, because it enables parameter extraction from the experimental data with much more realism than the 1D model and much less computational effort than the 3D model [114].
The NPP can serve as a computationally efficient alternative to other methods available for the description of the individual ionic channels, namely, molecular dynamics (MD) [119,120,121,122] and Brownian dynamics (BD) [123,124]. NPP can be also combined with classical mean density functional theory and Monte Carlo simulations. Such models, summarized in very recent review [125], fill the gap between the really detailed all-atom models studied by MD simulations popular in ion channel studies and mean-field continuum models (such as classical NPP) popular in nanopore studies.
The NPP is probably the simplest form of non-equilibrium theory that takes into account the shape of the channel, the magnitude and the location of charge residues in the channel protein, and different ionic concentrations at two sides of the channels [97]. It is worth mentioning that NPP is considered one of the most idealized models for the description of liquid junction potentials [47] (compared with Henderson equation and Planck formula) and ion channels [125] (compared with more general MD and BD), while at the same time, it is considered a most general model for the description of ion sensors [14] (compared with phase boundary models and diffusion layer models used in potentiometry or with equivalent circuits used in impedance spectroscopy).
The methods for modelling and simulation of ion channels and their application for a variety of channel types have been described in detail in several extensive reviews [97,113,126,127,128,129]. The elucidation of how ion channels work might ultimately help us find the causes of a number of neurological and muscular disorders and potential cures for them [97].
5. Potential Distortions Invisible to Patch-Clamp
The sub-membrane voltage generated through local charge accumulation essentially controls the voltage-dependent activity of membrane proteins [1]. The inhomogeneity in electric fields in the protein and at the lipid-protein interface can result in distortions near their voltage sensor.
The molecular voltage sensor is driven by the electric fields in nanoscopic proximity to the membrane [130,131], i.e., sub-membrane potential V*m. However, in patch-clamp practice, the measured value is the voltage difference between the cell cytoplasm and the bulk of extracellular medium Vm. Sub-membrane electric fields quickly dissipate away from the membrane, therefore, the values of the pipette-measured Vm and the V*m sensed by the receptors and channels may differ [1].
The potential profiles through the ion-selective lipid bilayer calculated using NPP equations (see Figure 2) show that the potential changes extend outside the membrane and consequently cause the potential distortions in neighboring solutions. In the literature, it is either assumed that the electric potential drops pretty much linearly across the lipid bilayer [132] or that a maximum in potential profile occurs inside the membrane [1]. Both of these assumptions are here validated using NPP.
Figure 2. Distortions in transmembrane potential invisible to patch-clamp measurements. Thick black line represents the voltage profile across the system of a cation-selective membrane between two solutions calculated using NPP model. Vm is the transmembrane voltage measured in patch-clamp technique, away from the membrane. V*m is the transmembrane voltage sensed by the channel voltage sensor. Vertical dotted lines represent the approximate sub-membrane locality that primarily affects the channel voltage sensor (assumed at 1 nm distance from the membrane). (a) Concentration of negative charge in the membrane equals 10 nM, (b) concentration of negative charge in the membrane equals 0.
Presented NPP results show the dependence of the potential profile on the concentration of the negative charges (anionic sites) inside the lipid bilayer. Near-linear potential drop is observed when the concentration of negative charge in the cation-selective membrane is close in value to the concentration of this cation in the neighboring solutions (see Figure 2a). When the concentration of negative charges is significantly lower, the maximum of the potential occurs (see Figure 2b).
Applying NPP in real geometric structures of biological membranes can quantitatively show the difference between the sub-membrane potential V*m and the patch-clamp readout Vm.
6. Mitochondrial Calcium Transport
Although the brain represents only about 2% of the body weight in an average adult human, it accounts for about 20% of the oxygen and, hence, the energy consumed by the body [133]. The energy (in the form of ATP) is produced in mitochondria through the citric acid cycle and reducing the oxygen by oxidative phosphorylation [96]. This process is accompanied by the influx of calcium ions into the mitochondrial matrix and the precipitation of osmotically inactive amorphous carbonated apatite [134]. Mitochondria can accumulate, store, and release a large amount of calcium ions under a variety of physiological and pathological conditions, such as epilepsy [135], ischemia [136,137], and concussive brain injury [138]. Mitochondrial Ca2+ uptake influences not only energy metabolism [139,140] but also the neural signaling [141,142].
The NPP model has been used to simulate the electrodiffusion of calcium ions through the mitochondrial membrane [143]. In this approach, the mitochondrial membrane is represented by a one-dimensional continuous element where only the maximum inward/outward flux of ions is limited by the channel density. Inside the mitochondrion matrix, the complexation reaction has been introduced by including the reaction terms into the mass balance equations. In cytosol and the mitochondrial matrix, pure Fickian diffusion has been assumed.
The concentration profiles of calcium have been shown in Figure 3. The inclusion of the reaction, occurring inside the mitochondrial matrix in the transport model, allows us to explain the difference between the total matrix concentration of calcium (established to be in the range of 0.5 M to 0.8 M [144,145,146,147,148]) and the free calcium concentration (in the range of 0.17 to 5 μM [149,150,151,152,153,154,155,156]), reported by numerous studies using fluorescent Ca2+ indicators.
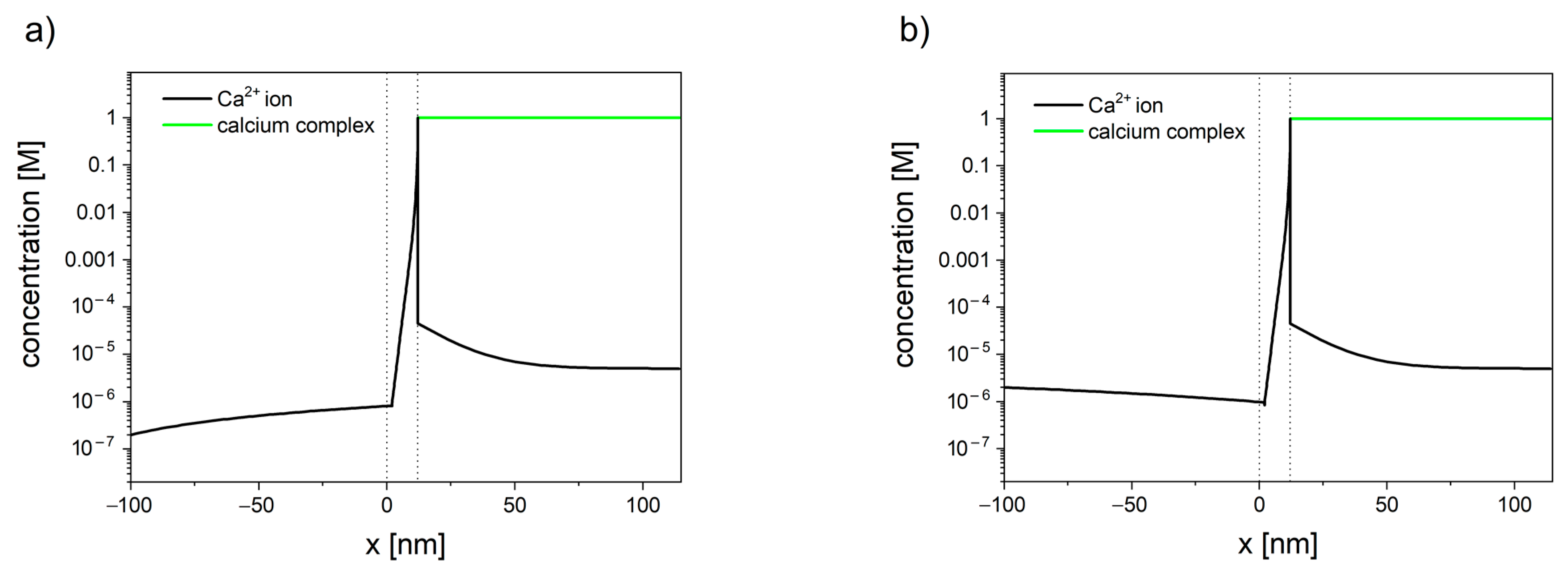
Figure 3. Calcium concentration profiles in the system consisted of cytosol (x < 0), mitochondrial membrane (0 < x < 10 nm), and mitochondrial matrix (x > 10 nm). Membrane potential is set to φ = −180 mV. (a) When the concentration of calcium in cytosol is set to 200 nm, the resulting flux is negative (JCa2+ = −2.0 × 10−7), and calcium ions leave the mitochondrion. (b) When the concentration of calcium in the cytosol is set to 2 µM, the resulting flux is positive (JCa2+ = −3.4 × 10−7), and calcium ions enter the mitochondrion.
The presented model [143] can be used as an efficient alternative for single-channel modeling. Despite its simplicity, the model has successfully described the existence of calcium set-point, i.e., the concentration of calcium in cytosis below which calcium stops entering the mitochondrion. For the membrane potential of −180 mV, the set-point was established to be in the range 0.9 µM to 1 µM [143]. The lower the value of the membrane potential, the higher the tendency for calcium to enter the mitochondrion. Furthermore, the concentration profiles inside cytosol have shown the existence of an unstirred layer (see Figure 3), which indicates that the calcium ions enter/leave the membrane faster than it can diffuse from/toward the bulk.
Proper description of calcium electrodiffusion and precipitation of its salts is especially relevant in neural tissue, where calcium signaling occurs, e.g., the concentration of calcium ions in the mitochondria of firing axons have been reported to reach 24 µM [157], comparing with typical values of 1–5 µm [134]. Amorphous carbonated apatite, precipitated as an effect of calcium influx, acts as a pH buffer and, hence, can contribute in maintaining ATP production in ischemic conditions, which delays irreversible damage to heart and brain cells after stroke [134,158]. This calcium salt might also have an auxiliary role in mitigating the effects of oxidative stress [134]. The oxidative stress occurring in neural tissue can lead to cancer [159], but also Parkinson’s, Alzheimer’s, amyothropic lateral sclerosis, and other neurodegenerative diseases [160,161,162]. A better understanding of the calcium electrodiffusion and precipitation of amorphous calcium apatite in mitochondria may, hence, lead to the development of new stroke-protective drugs or improve the neurodegenerative disease prevention.
This entry is adapted from the peer-reviewed paper 10.3390/electrochem2020014
This entry is offline, you can click here to edit this entry!
