Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Gangqiang Zhang
 + 1741 word(s) 1741 2021-03-15 09:41:14 |
2 update layout and reference
Rita Xu
 Meta information modification 1741 2021-03-24 11:15:24 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Zhang, G. Machine Learning-Based Fusion Model. Encyclopedia. Available online: https://encyclopedia.pub/entry/8220 (accessed on 16 November 2024).
Zhang G. Machine Learning-Based Fusion Model. Encyclopedia. Available at: https://encyclopedia.pub/entry/8220. Accessed November 16, 2024.
Zhang, Gangqiang. "Machine Learning-Based Fusion Model" Encyclopedia, https://encyclopedia.pub/entry/8220 (accessed November 16, 2024).
Zhang, G. (2021, March 24). Machine Learning-Based Fusion Model. In Encyclopedia. https://encyclopedia.pub/entry/8220
Zhang, Gangqiang. "Machine Learning-Based Fusion Model." Encyclopedia. Web. 24 March, 2021.
Machine Learning-Based Fusion Model
Edit
This entry is adapted from the peer-reviewed paper 10.3390/s21010046

The launch of GRACE satellites has provided a new avenue for studying the terrestrial water storage anomalies (TWSA) with unprecedented accuracy. However, the coarse spatial resolution greatly limits its application in hydrology researches on local scales. To overcome this limitation, this study develops a machine learning-based fusion model to obtain high-resolution (0.25°) groundwater level anomalies (GWLA) by integrating GRACE observations in the North China Plain. 

machine learning-based fusion model GRACE gradient boosting decision tree groundwater level anomalies statistical downscaling North China Plain

1.Introduction

As a significant supply source of freshwater resources, groundwater plays a crucial role in social production and human life [1][2]. Globally, it provides drinking water for approximately two billion people [3] and irrigation for roughly 40% of areas equipped for irrigation [4]. Due to extreme climate episodes and anthropogenic actives (e.g., drought and overuse of irrigation water), groundwater resources are seriously over-exploited in some typical regions [5][6], leading to a series of environmental issues, such as land subsidence and seawater intrusion [7][8]. Therefore, understanding the dynamics changes in groundwater is necessary for the effective utilization and sustainable management of water resources [2][9].

The traditional method to monitor groundwater levels is based on ground-based measurements [10][11]. However, it is not applicable to large-scale and remote regions restricted by national policies, limited stations, and instrument accuracy. The Gravity Recovery and Climate Experiment (GRACE) satellites, successfully launched in March 2002 [12], provides a kind of new method for monitoring the global time-variable gravity field with unprecedented accuracy [13]. Additionally, it can provide continuous terrestrial water storage anomalies (TWSA) and cover most parts of the world, which is especially beneficial for areas lacking ground-based measurements. By integrating auxiliary information from hydrological models, groundwater storage anomalies (GWSA) can be further isolated from GRACE observations. Previous studies have demonstrated that GRACE missions show great potential in various fields, e.g., detection of terrestrial water storage [14][15][16] and groundwater storage [17][18]. Swenson et al. [14] derived region-scale water storage by applying averaging kernels to a realistic synthetic GRACE gravity signal within North American river basins. Results indicated that the accuracy might be better than 1 cm for regions with 400,000 km2 or larger areas. Rodell et al. [17] simulated groundwater storage based on GRACE and hydrological modeling system, and the results showed that it was being depleted at a mean rate of 4.0 ± 1.0 cm/yr equivalent height of water over the Indian states of Rajasthan, Punjab and Haryana (including Delhi).

Although remarkable achievements have been made in large-scale areas, the application of GRACE observations in local areas is very limited due to the coarse spatial resolution (~200,000 km2) [19]. Consequently, some downscaling methods have been proposed for providing high-resolution GRACE products, which are mainly divided into two categories: dynamic downscaling and statistical downscaling [20][21], respectively. Normally, dynamic downscaling tends to achieve regional downscaling by using the initial boundary conditions of global climate models [22][23] directly. For example, Eicker et al. [24] assimilated GRACE-derived TWSA into the WaterGAP Global Hydrology Model by introducing a new Kalman filter method, which can provide reasonable results in the Mississippi river basin. Although data assimilation methods remain consistent in the physical process, some shortcomings still require to be considered [25]. The implementation of data assimilation is relatively complicated [26], and its accuracy is subject to the full error covariance matrix of GRACE observations and hydrological models [27][28].

Compared to dynamic downscaling, statistical downscaling usually establishes the linear or non-linear relationships between input and target variables, aiming to produce local-scale information [29][30]. Initially, linear regression models are employed to downscale GRACE products [31][32][33]. For example, Ning et al. [31] achieved the downscaling of GRACE data in parts of Yunnan by constructing an empirical regression model based on the water balance equation, and the results indicated the feasibility for downscaling GRACE data. Yin et al. [33] proposed a new statistical downscaling algorithm by building the relationship between multi-source evapotranspiration (ET) products and GWSA in the North China Plain, which obtained desirable downscaled results but limited by the strong correlation between TWS and ET. Practically, the relationships between predictor and predictand tend to be non-linear rather than linear. The development of machine learning algorithms provides effective measures to quantify the complicated relationship by constructing non-linear models. Artificial neural networks (ANNs) have the capabilities of simulating complex hydrological characteristics to an arbitrary degree of accuracy [34][35]. This makes ANN becomes an attractive measure in the downscaling researches, which have been applied to some typical regions, e.g., the Northern High Plains [36], California’s Central Valley [34], and the Lower Peninsula of Michigan [26]. Similarly, some tree-based machine learning algorithms (e.g., random forest (RF) and gradient boosting decision tree (GBDT)) become popular in regression tasks with the advantages of simplicity and effectiveness. The RF algorithm has been utilized to downscale GRACE observations and obtained satisfactory results in some areas [37][38]. As a kind of ensemble machine learning algorithm, GBDT performs well in constructing non-linear regression models, which is often employed to forecast ET [39] and urban flood [40][41], but rarely in GWLA. Furthermore, the multi-stage machine learning algorithm may have more powerful expressive performance than a single algorithm in downscaling GRACE products. For example, Seyoum et al. [42] designed a two-layer boosted regression trees (BRT) model by utilizing GRACE data and hydrological variables in a glacial aquifer system of the United States, which can predict groundwater level anomalies (GWLA) with a high spatial resolution.

2. Study Area and Data

2.1. Study Area

The North China Plain, located in the eastern coastal region of China, lies between latitude 35° N–41° N and longitude 113° E–120° E (Figure 1). It is one of the three great plains in China, covering an area of approximately 140,000 km2 [43]. The NCP is a central agricultural area in China, which produces about one-fourth of the country’s total grain yield [10]. The main crops include winter wheat and summer maize, and the NCP supplies more than 50% of the wheat and approximately 33% of the maize production in China [44].

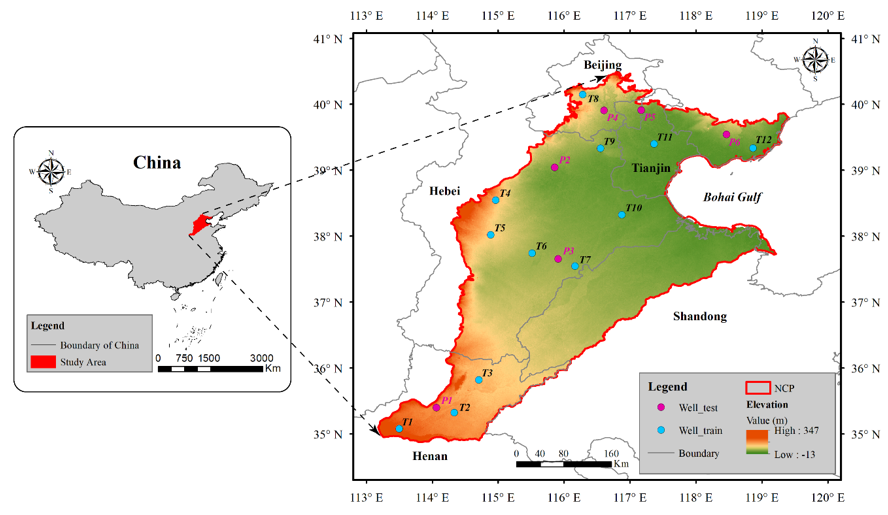
Figure 1. Location and digital elevation model map of the NCP. The blue and magenta dots represent the training and testing wells, respectively.

The NCP belongs to a continental monsoon climate with an annual average temperature between 8 and 15 °C [33][45]. The annual precipitation, most of which occurs during the growth period of summer maize, ranges from 500 to 600 mm, and annual evaporation is 900–1400 mm [46][47]. The NCP contains a shallow unconfined aquifer (40–60 m) and three confined aquifers of different depths (120–170 m, 250–360 m, and 400–600 m) [48].

2.2. Data

The fusion model, proposed in this study, is designed based on the water balance principle and machine learning methods (i.e., multiple linear regression and GBDT). Several datasets (terrestrial water storage anomalies, precipitation, runoff, evapotranspiration, soil moisture, snow water equivalent, and groundwater level) are chosen to owe to their close relationship with groundwater storage changes, as shown in Figure 2.

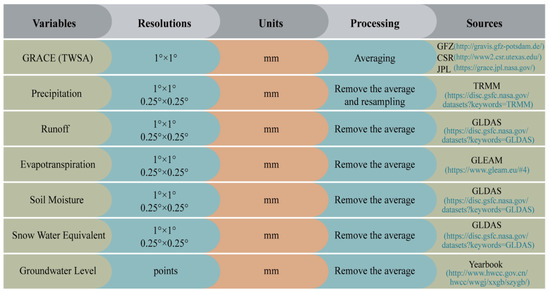
传感器21 00046 g002 550

Figure 2. Summary of variable information (resolutions, units, processing, and sources) employed in the fusion model.

Specifically, some variables should be resampled from 0.25° to 1° for matching the spatial availability of GRACE products, and the study period covers from January 2005 to December 2014, with a total of 120 months. The schematic diagram of the water balance principle is shown in Figure 3.

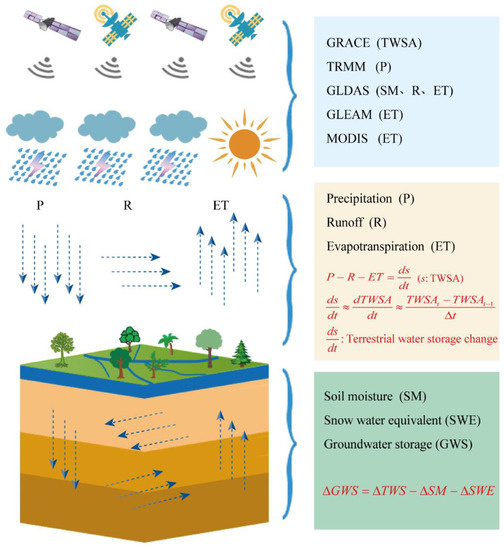
传感器21 00046 g003 550

Figure 3. Sketch map of the water cycle.

2.2.1. GRACE TWSA

The GRACE gravity satellites, jointly developed by NASA (National Aeronautics and Space Administration) and DLR (German Aerospace Center), were launched in 2002 and successfully completed its missions in 2017 [13]. They were designed to track global mass changes or gravity variations using the K-band ranging system and low-low satellite tracking satellite mode [13][49]. In this study, GRACE observations are provided by the Jet Propulsion Laboratory (JPL), Center for Space Research (CSR), and GeoForschungsZentrum Potsdam (GFZ), respectively. The gridded-gain factors are utilized to reduce the leakage error [50], which are available at [51]. Some discrepancies exist among these three solutions due to different processing strategies and tuning parameters [52]. Therefore, we utilize the ensemble average of different solutions as the representative TWS estimates in the following discussion.

2.2.2. TRMM Precipitation

The Tropical Rainfall Measurement Mission (TRMM) is a joint project of NASA and Japan Aerospace Exploration Agency (JAXA), aiming to analyze the impact of rainfall data on weather and climate [53]. The monthly precipitation products (2003–2015) used in this study are the TRMM 3b43 with the spatial resolution of 0.25° × 0.25°. The dataset can be obtained from the Goddard Earth Sciences Data and Information Services Center (GES DISC) [54]. Previous studies [16] have demonstrated that TRMM data match well with gauged stations compared to other remotes sensing products, thus utilized in this study.

2.2.3. GLDAS Data

The Global Land Data Assimilation System (GLDAS) is developed by the Goddard Space Flight Center (GSFC). The primary goal of the GLDAS is to ingest satellite- and ground-based observational data products, using advanced land surface modeling and data assimilation techniques, in order to generate optimal fields of land surface states and fluxes [55]. Up to now, there have been four land surface models (LSM), namely Mosaic [56], Community Land Model (CLM) [57], Noah [58], and Variable Infiltration Capacity (VIC) [59], respectively. The Noah model is selected to provide some water-budget variables, including runoff (R), soil moisture (SM), and snow water equivalent (SWE). The runoff includes surface runoff and underground runoff, and soil moisture is the sum of four soil water layers. The datasets from the Noah model include two kinds of temporal resolutions (3-h and monthly scale) and spatial resolutions (0.25° × 0.25° and 1° × 1°). Monthly datasets are chosen in this study, with the resolutions of 0.25° and 1°, which are available at [60].

2.2.4. GLEAM Product

GLEAM (Global Land Evaporation Amsterdam Model) is a set of algorithms dedicated to estimating global evapotranspiration by combining satellite observations and the Priestley and Taylor equation [61]. It has been continuously revised and updated since 2011, and the third version of the model was released in 2017 [62]. The latest version GLEAM v3.3 contains two kinds of data sets (v3.3a and v3.3b), differing in their forcing and temporal coverage [63]. In this study, the GLEAM v3.3a is employed to provide monthly estimates in evapotranspiration, spanning the 36 years from 1980 to 2018.

2.2.5. Groundwater Level

Monthly groundwater level, collected from the Haihe River Basin Water Resources Bulletin [64], is used to validate the accuracy of the downscaled TWSA and predicted water level. Groundwater monitoring wells are unevenly distributed across the NCP, and there are abnormal jumps, data gaps, and outliers in some wells. Therefore, the collected data require pre-processing as follows: (1) ignore the wells with more missing months and obvious errors; (2) aggregate the groundwater level to pixels values on 0.25° cells by using the simple average of groundwater observations within the pixel; (3) remove the mean value to obtain the groundwater level anomalies data. A total of 18 wells are selected for this study (Figure 1), and 12 wells are used to train the downscaled model, while the remaining 6 wells are used to test the performance of models.

References

  1. Aeschbach-Hertig, W.; Gleeson, T. Regional strategies for the accelerating global problem of groundwater depletion. Nat. Geosci. 2012, 5, 853–861, doi:10.1038/ngeo1617.
  2. Gleeson, T.; Cuthbert, M.; Ferguson, G.; Perrone, D. Global groundwater sustainability, resources, and systems in the An-thropocene. Annu. Rev. Earth Pl. Sc. 2020, 48, 431–463, doi:10.1146/annurev-earth-071719-055251.
  3. Morris, B.L.; Lawrence, A.R.L.; Chilton, P.J.C.; Adams, B.; Calow, R.C.; Klinck, B.A. Groundwater and Its Susceptibility to Deg-radation: A Global Assessment of the Problem and Options for Management; UNEP Early Warning & Assessment Report Series RS. 03-3; UNEP: Nairobi, Kenya, 2003.
  4. Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sc. 2010, 14, 1863–1880, doi:10.5194/hess-14-1863-2010.
  5. Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Change. 2013, 3, 322–329, doi:10.1038/nclimate1744.
  6. Wu, W.; Lo, M.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.F.; Ducharne, A.; Yang, Z. Divergent effects of climate change on future groundwater availability in key mid-latitude aquifers. Nat. Commun. 2020, 11, 3710, doi:10.1038/s41467-020-17581-y.
  7. Bierkens, M.F.P.; Wada, Y. Non-renewable groundwater use and groundwater depletion: A review. Environ. Res. Lett. 2019, 14, 063002, doi:10.1088/1748-9326/ab1a5f.
  8. Lall, U.; Josset, L.; Russo, T. A snapshot of the world's groundwater challenges. Annu. Rev. Env. Resour. 2020, 45, 1–24, doi:10.1146/annurev-environ-102017-025800.
  9. Yin, W.; Li, T.; Zheng, W.; Hu, L.; Han, S.; Tangdamrongsub, N.; Šprlák, M.; Huang, Z. Improving regional groundwater storage estimates from GRACE and global hydrological models over Tasmania, Australia. Hydrogeol. J. 2020, 28, 1809–1825, doi:10.1007/s10040-020-02157-3.
  10. Feng, W.; Shum, C.; Zhong, M.; Pan, Y. Groundwater storage changes in China from satellite gravity: An overview. Remote Sens. 2018, 10, 674, doi:10.3390/rs10050674.
  11. Zhang, M.; Hu, L.; Yao, L.; Yin, W. Surrogate Models for Sub-Region Groundwater Management in the Beijing Plain, China. Water 2017, 9, 766, doi:10.3390/w9100766.
  12. Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the earth system. Science 2004, 305, 503–505, doi:10.1126/science.1099192.
  13. Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607, doi:10.1029/2004GL019920.
  14. Swenson, S.; Wahr, J.; Milly, P.C.D. Estimated accuracies of regional water storage variations inferred from the Gravity Re-covery and Climate Experiment (GRACE). Water Resour. Res. 2003, 39, W1223, doi:10.1029/2002WR001808.
  15. Zhong, Y.; Zhong, M.; Mao, Y.; Ji, B. Evaluation of Evapotranspiration for Exorheic Catchments of China during the GRACE Era: From a Water Balance Perspective. Remote Sens. 2020, 12, 511, doi:10.3390/rs12030511.
  16. Yin, W.; Han, S.; Zheng, W.; Yeo, I.; Hu, L.; Tangdamrongsub, N.; Ghobadi-Far, K. Improved water storage estimates within the North China Plain by assimilating GRACE data into the CABLE model. J. Hydrol. 2020, 590, 125348, doi:10.1016/j.jhydrol.2020.125348.
  17. Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002, doi:10.1038/nature08238.
  18. Yin, W.; Hu, L.; Jiao, J.J.; Lo Russo, S. Evaluation of groundwater storage variations in Northern China Using GRACE Data. Geofluids 2017, 2017, 8254824, doi:10.1155/2017/8254824.
  19. Famiglietti, J.S.; Rodell, M. Water in the balance. Science 2013, 340, 1300–1301, doi:10.1126/science.1236460.
  20. Wilby, R.L.; Wigley, T.M.L. Downscaling general circulation model output: A review of methods and limitations. Prog. Phys. Geogr Earth Environ. 1997, 21, 530–548, doi:10.1177/030913339702100403.
  21. Tang, J.; Niu, X.; Wang, S.; Gao, H.; Wang, X.; Wu, J. Statistical downscaling and dynamical downscaling of regional climate in China: Present climate evaluations and future climate projections. J. Geophys. Res. Atmos. 2016, 121, 2110–2129, doi:10.1002/2015JD023977.
  22. Giorgi, F. Simulation of regional climate using a limited area model nested in a general circulation model. J. Climate. 1990, 3, 941–963, doi:10.1175/1520-0442(1990)003<0941:SORCUA>2.0.CO;2.
  23. Xu, Z.; Han, Y.; Yang, Z. Dynamical downscaling of regional climate: A review of methods and limitations. Sci. China Earth Sci. 2018, 62, 365–375, doi:10.1007/s11430-018-9261-5.
  24. Eicker, A.; Schumacher, M.; Kusche, J.; Döll, P.; Schmied, H.M. Calibration/Data assimilation approach for integrating GRACE data into the WaterGAP Global Hydrology Model (WGHM) using an Ensemble Kalman Filter: First results. Surv. Geophys. 2014, 35, 1285–1309, doi:10.1007/s10712-014-9309-8.
  25. Forootan, E.; Rietbroek, R.; Kusche, J.; Sharifi, M.A.; Awange, J.L.; Schmidt, M.; Omondi, P.; Famiglietti, J. Separation of large scale water storage patterns over Iran using GRACE, altimetry and hydrological data. Remote Sens. Environ. 2014, 140, 580–595, doi:10.1016/j.rse.2013.09.025.
  26. Sahour, H.; Sultan, M.; Vazifedan, M.; Abdelmohsen, K.; Karki, S.; Yellich, J.A.; Gebremichael, E.; Alshehri, F.; Elbayoumi, T.M. Statistical applications to downscale GRACE-derived terrestrial water storage data and to fill temporal gaps. Remote Sens. 2020, 12, 533, doi:10.3390/rs12030533.
  27. Nie, W.; Zaitchik, B.F.; Rodell, M.; Kumar, S.V.; Arsenault, K.R.; Li, B.; Getirana, A. Assimilating GRACE into a land surface model in the presence of an irrigation‐induced groundwater trend. Water Resour. Res. 2019, 55, 11274–11294, doi:10.1029/2019WR025363.
  28. Khaki, M.; Schumacher, M.; Forootan, E.; Kuhn, M.; Awange, J.L.; van Dijk, A.I.J.M. Accounting for spatial correlation errors in the assimilation of GRACE into hydrological models through localization. Adv. Water Resour. 2017, 108, 99–112, doi:10.1016/j.advwatres.2017.07.024.
  29. Wilby, R.L.; Wigley, T.M.L.; Conway, D.; Jones, P.D.; Hewitson, B.C.; Main, J.; Wilks, D.S. Statistical downscaling of general circulation model output: A comparison of methods. Water Resour. Res. 1998, 34, 2995–3008, doi:10.1029/98WR02577.
  30. Gutiérrez, J.M.; San-Martín, D.; Brands, S.; Manzanas, R.; Herrera, S. Reassessing statistical downscaling techniques for their robust application under climate change conditions. J. Climate. 2013, 26, 171–188, doi:10.1175/JCLI-D-11-00687.1.
  31. Ning, S.; ISHIDAIRA, H.; WANG, J. Statistical downscaling of GRACE-derived terrestrial water storage using satellite and GLDAS products. J. Jpn. Soc. Civ. Eng. Ser. B1 Hydraul. Eng. 2014, 70, 133–138, doi:10.2208/jscejhe.70.I_133.
  32. Wan, Z.; Zhang, K.; Xue, X.; Hong, Z.; Hong, Y.; Gourley, J.J. Water balance-based actual evapotranspiration reconstruction from ground and satellite observations over the conterminous United States. Water Resour. Res. 2015, 51, 6485–6499, doi:10.1002/2015WR017311.
  33. Yin, W.; Hu, L.; Zhang, M.; Wang, J.; Han, S. Statistical downscaling of GRACE-derived groundwater storage using ET data in the North China Plain. J. Geophys. Res. Atmos. 2018, 123, 5973–5987, doi:10.1029/2017JD027468.
  34. Miro, M.; Famiglietti, J. Downscaling GRACE remote sensing datasets to high-resolution groundwater storage change maps of California’s Central Valley. Remote Sens. 2018, 10, 143, doi:10.3390/rs10010143.
  35. Kumar, P.S.; Praveen, T.V.; Prasad, M.A. Artificial neural network model for rainfall-runoff—A case study. Int. J. Hybrid Inf. Technol. 2016, 9, 263–272, doi:10.14257/ijhit.2016.9.3.24.
  36. Seyoum, W.M.; Milewski, A.M. Improved methods for estimating local terrestrial water dynamics from GRACE in the Northern High Plains. Adv. Water Resour. 2017, 110, 279–290.
  37. Chen, L.; He, Q.; Liu, K.; Li, J.; Jing, C. Downscaling of GRACE-derived groundwater storage based on the random forest model. Remote Sens. 2019, 11, 2979, doi:10.3390/rs11242979.
  38. Rahaman, M.; Thakur, B.; Kalra, A.; Li, R.; Maheshwari, P. Estimating high-resolution groundwater storage from GRACE: A random forest approach. Environments 2019, 6, 63, doi:10.3390/environments6060063.
  39. Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agr. Forest Meteorol. 2018, 263, 225–241.
  40. Wu, Z.; Zhou, Y.; Wang, H. Real-Time Prediction of the Water Accumulation Process of Urban Stormy Accumulation Points Based on Deep Learning. IEEE Access 2020, 8, 151938–151951, doi:10.1109/ACCESS.2020.3017277.
  41. Wu, Z.; Zhou, Y.; Wang, H.; Jiang, Z. Depth prediction of urban flood under different rainfall return periods based on deep learning and data warehouse. Sci. Total Environ. 2020, 716, 137077, doi:10.1016/j.scitotenv.2020.137077.
  42. Seyoum, W.; Kwon, D.; Milewski, A. Downscaling GRACE TWSA data into high-resolution groundwater level anomaly using machine learning-based models in a glacial aquifer system. Remote Sens. 2019, 11, 824, doi:10.3390/rs11070824.
  43. Zheng, L.; Pan, Y.; Gong, H.; Huang, Z.; Zhang, C. Comparing Groundwater Storage Changes in Two Main Grain Producing Areas in China: Implications for Sustainable Agricultural Water Resources Management. Remote Sens. 2020, 12, 2151, doi:10.3390/rs12132151.
  44. Wang, J.; Wang, E.; Yang, X.; Zhang, F.; Yin, H. Increased yield potential of wheat-maize cropping system in the North China Plain by climate change adaptation. Climatic Change. 2012, 113, 825–840, doi:10.1007/s10584-011-0385-1.
  45. Guo, H.; Zhang, Z.; Cheng, G.; Li, W.; Li, T.; Jiao, J.J. Groundwater-derived land subsidence in the North China Plain. Environ. Earth Sci. 2015, 74, 1415–1427, doi:10.1007/s12665-015-4131-2.
  46. Liu, C.; Yu, J.; Eloise, K. Groundwater exploitation and its impact on the environment in the North China Plain. Water Int. 2001, 26, 265–272, doi:10.1080/02508060108686913.
  47. Feng, W.; Zhong, M.; Lemoine, J.; Biancale, R.; Hsu, H.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118, doi:10.1002/wrcr.20192.
  48. Sakura, Y.; Tang, C.; Yoshioka, R.; Ishiashi, H. Intensive Use of Groundwater in Some Areas of China and Japan. Intensive Use of Groundwater: Challenges and Opportunities; CRC Press: Boca Raton, FL, USA, 2003.
  49. Feng, W. GRAMAT: A comprehensive Matlab toolbox for estimating global mass variations from GRACE satellite data. Earth Sci. Inform. 2019, 12, 389–404, doi:10.1007/s12145-018-0368-0.
  50. Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, W4531, doi:10.1029/2011WR011453.
  51. Monthly Mass Grids Land. Available online: https://grace.jpl.nasa.gov/data/get-data/monthly-mass-grids-land/(accessed on 8 December 2020).
  52. Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397, doi:10.1002/2013GL058632.
  53. Kummerow, C.; Simpson, J.; Thiele, O.; Barnes, W.; Chang, A.T.C.; Stocker, E.; Adler, R.F.; Hou, A.; Kakar, R.; Wentz, F.; et al. The status of the Tropical Rainfall Measuring Mission (TRMM) after two years in Orbit. J. Appl. Meteorol. 2000, 39, 1965–1982, doi:10.1175/1520-0450(2001)040<1965:TSOTTR>2.0.CO;2.
  54. NASA Dataset. Available online: https://disc.gsfc.nasa.gov/datasets?keywords=TRMM (accessed on 8 December 2020).
  55. Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. B. Am. Meteorol. Soc. 2004, 85, 381–394, doi:10.1175/BAMS-85-3-381.
  56. Koster, R.D.; Suarez, M.J.; Heiser, M. Variance and Predictability of Precipitation at Seasonal-to-Interannual Timescales. J. Hydrometeorol. 2000, 1, 26–46, doi:10.1175/1525-7541(2000)001<0026:VAPOPA>2.0.CO;2.
  57. Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G.; et al. The Common Land Model. B. Am. Meteorol. Soc. 2003, 84, 1013–1024, doi:10.1175/BAMS-84-8-1013.
  58. Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.; Koren, V.; Duan, Q.Y.; Ek, M.; Betts, A. Modeling of land surface evapo-ration by four schemes and comparison with FIFE observations. J. Geophys. Res. Atmos. 1996, 101, 7251–7268, doi:10.1029/95jd02165.
  59. Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. 1994, 99, 14415–14428, doi:10.1029/94jd00483.
  60. NASA Dataset. Available online: https://disc.gsfc.nasa.gov/datasets?keywords=GLDAS (accessed on 8 December 2020).
  61. Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469, doi:10.5194/hess-15-453-2011.
  62. Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925, doi:10.5194/gmd-10-1903-2017.
  63. Gleam dataset. Available online: https://www.gleam.eu/#datasets (accessed on 8 December 2020).
  64. HWCC. Available online: http://www.hwcc.gov.cn/hwcc/wwgj/xxgb/szygb/(accessed on 8 December 2020).
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Electrical & Electronic
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Gangqiang Zhang
View Times: 1.6K
Entry Collection: Remote Sensing Data Fusion
Revisions: 2 times (View History)
Update Date: 25 Mar 2021
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback