
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Szymon Łukaszyk | -- | 435 | 2024-08-27 15:33:10 | | | |
| 2 | Jason Zhu | + 1 word(s) | 436 | 2024-08-29 03:53:47 | | | | |
| 3 | Szymon Łukaszyk | Meta information modification | 463 | 2024-08-29 19:45:02 | | | | |
| 4 | Catherine Yang | -1 word(s) | 462 | 2024-10-31 03:14:51 | | | | |
| 5 | Szymon Łukaszyk | Meta information modification | 462 | 2024-11-11 09:50:19 | | | | |
| 6 | Szymon Łukaszyk | + 12 word(s) | 474 | 2024-11-11 09:53:46 | | | | |
| 7 | Szymon Łukaszyk | Meta information modification | 474 | 2024-11-11 09:56:46 | | | | |
| 8 | Szymon Łukaszyk | + 15 word(s) | 489 | 2024-11-11 10:14:09 | | | | |
| 9 | Szymon Łukaszyk | -30 word(s) | 459 | 2025-12-27 18:56:02 | | |
Video Upload Options
Assembly theory is a framework for quantifying selection, evolution, and complexity. It, therefore, spans various scientific disciplines, including physics, chemistry, biology, and information theory. Assembly theory is rooted in the assembly of an object from a set of basic building units, forming an initial assembly pool and from subunits that entered the assembly pool in previous assembly steps. Hence, the object is defined not as a set of point particles but by the history of its assembly, where the assembly index is the smallest number of steps required to assemble the object.
Assembly theory was formulated in 2017[1], introducing the concept of assembly index (initially called "pathway complexity") of an object as the smallest number of steps required to assemble this object from a set of basic building units, forming an initial assembly pool and from subunits that entered the assembly pool in previous assembly steps. The assembly index is, therefore, a measure of the complexity of the object, which is computable[5], unlike Kolmogorov complexity, for example, and captures the structural information about the object, unlike Shannon entropy. The theoretical background for the theory was researched[5] based on directed multigraphs showing that the assembly index of an object is computable for all finite objects.
Consider two binary strings C = [01010101] and D = [00010111] and the initial assembly pool containing two bits 0 and 1. Both strings have the same length N = 8 and the same Shannon entropy H(C) = H(D) = log2(2) = 1. However, the assembly index of the first string is a(C) = 3 (In step 1, assemble "01" and put it into the assembly pool, in step 2 assemble "01" with "01" taken from the assembly pool and put "0101" into the assembly pool, and in step 3 assemble "0101" assembled in the second step with "0101" taken from the assembly pool), while the assembly index of the second string is a(D) = 6, since only the substring "01" can be reused from the assembly pool[8].
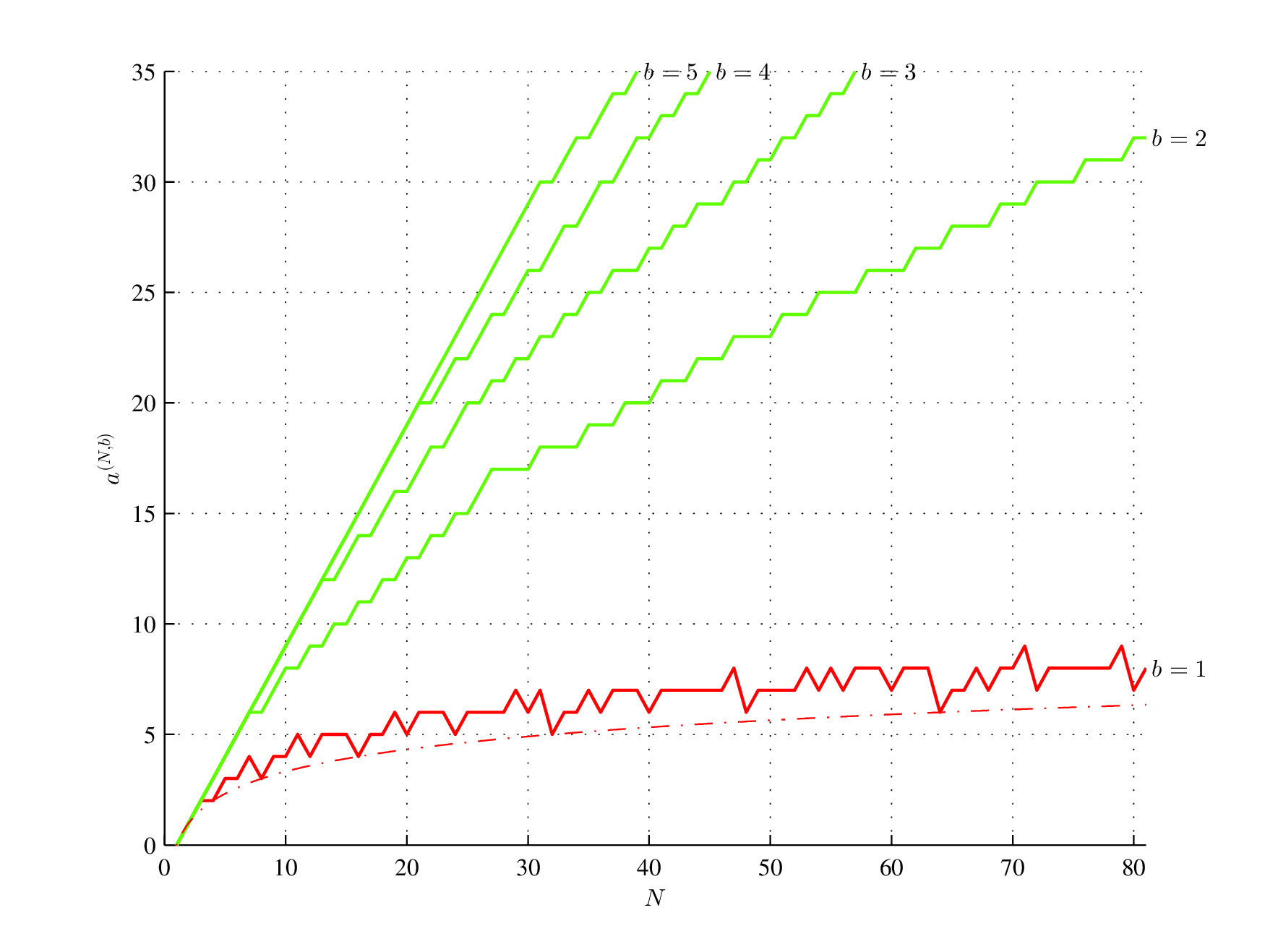
Minimum (red; log2(N), red, dash-dot) and maximum (green) assembly index for 1 ≤ b ≤ 5 and 0 < N ≤ 81. N is the string length; b is the alphabet size.
Basic building units depend on a particular application of the assembly theory. In chemistry, it has found applications in drug discovery[3]. Furthermore, the theoretical value of the assembly index of a molecule, where the initial assembly pool contains chemical bonds, can be experimentally confirmed using tandem mass spectrometry, nuclear magnetic resonance, or infrared spectroscopy[4][7]. Therefore, the assembly index is the universal threshold between abiotic and biotic molecules and a robust, simple biosignature for distinguishing random, abiotic objects from biologically or technologically assembled ones, as only biotic samples can have an assembly index above 15. The more complex a given object, the less likely an identical copy can exist without some information-driven mechanism that generates that object[6].
References
- Stuart M. Marshall; Alastair R. G. Murray; Leroy Cronin; A probabilistic framework for identifying biosignatures using Pathway Complexity. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci.. 2017, 375, 20160342.
- Sara Imari Walker; Leroy Cronin; Alexa Drew; Shawn Domagal-Goldman; Theresa Fisher; Michael Line . Probabilistic Biosignature Frameworks; Victoria Meadows; Giada Arney; Britney Schmidt; David J. Des Marais, , Eds.; University of Arizona: Tucson, AZ, United States, 2019; pp. 1-1.
- Yu Liu; Cole Mathis; Michał Dariusz Bajczyk; Stuart M. Marshall; Liam Wilbraham; Leroy Cronin; Exploring and mapping chemical space with molecular assembly trees. Sci. Adv.. 2021, 7, eabj2465.
- Stuart M. Marshall; Cole Mathis; Emma Carrick; Graham Keenan; Geoffrey J. T. Cooper; Heather Graham; Matthew Craven; Piotr S. Gromski; Douglas G. Moore; Sara. I. Walker; Leroy Cronin; Identifying molecules as biosignatures with assembly theory and mass spectrometry. Nat. Commun.. 2021, 12, 1-9.
- Stuart M. Marshall; Douglas G. Moore; Alastair R. G. Murray; Sara I. Walker; Leroy Cronin; Formalising the Pathways to Life Using Assembly Spaces. Entropy. 2022, 24, 884.
- Abhishek Sharma; Dániel Czégel; Michael Lachmann; Christopher P. Kempes; Sara I. Walker; Leroy Cronin; Assembly theory explains and quantifies selection and evolution. Nat.. 2023, 622, 321-328.
- Michael Jirasek; Abhishek Sharma; Jessica R. Bame; S. Hessam M. Mehr; Nicola Bell; Stuart M. Marshall; Cole Mathis; Alasdair MacLeod; Geoffrey J. T. Cooper; Marcel Swart; Rosa Mollfulleda; Leroy Cronin; Investigating and Quantifying Molecular Complexity Using Assembly Theory and Spectroscopy. ACS Central Sci.. 2024, 10, 1054-1064.
- Szymon Łukaszyk; Wawrzyniec Bieniawski; Assembly Theory of Binary Messages. Math.. 2024, 12, 1600.




