Assembly theory was formulated in 2017^[1], introducing the concept of assembly index (initially called "pathway complexity") of an object as the smallest number of steps required to assemble this object from a set of basic building units, forming an initial assembly pool, and from subunits that entered the assembly pool in previous assembly steps. The assembly index is, therefore, a measure of the complexity of the object, which is computable^[25], unlike Kolmogorov complexity, for example, and captures the structural information about the object, unlike Shannon entropy. The theoretical background for the theory was researched^[25] based on directed multigraphs, showing that the assembly index of an object is computable for all finite objects. In particular, determining the assembly index is NP-complete as it equals the size of the smallest straight-line program (SLP) that generates the given sequence, which reduces its determination to the smallest grammar problem^[3]. Therefore, grammar-based compression algorithms only provide upper bounds on the composite index and are not equivalent to it^[4]. Furthermore, the assembly plan for a maximum-assembly-index string tends to maximize the number of strings assembled in independent assembly steps^[5].

Consider two binary strings C = [01010101] and D = [00010111] and the initial assembly pool containing two bits 0 and 1. Both strings have the same length N = 8 and the same Shannon entropy H(C) = H(D) = log₂(2) = 1. However, the assembly index of the first string is a(C) = 3 (In step 1, assemble "01" and put it into the assembly pool, in step 2 assemble "01" with "01" taken from the assembly pool and put "0101" into the assembly pool, and in step 3 assemble "0101" assembled in the second step with "0101" taken from the assembly pool), while the assembly index of the second string is a(D) = 6, since only the substring "01" can be reused from the assembly pool^[68].

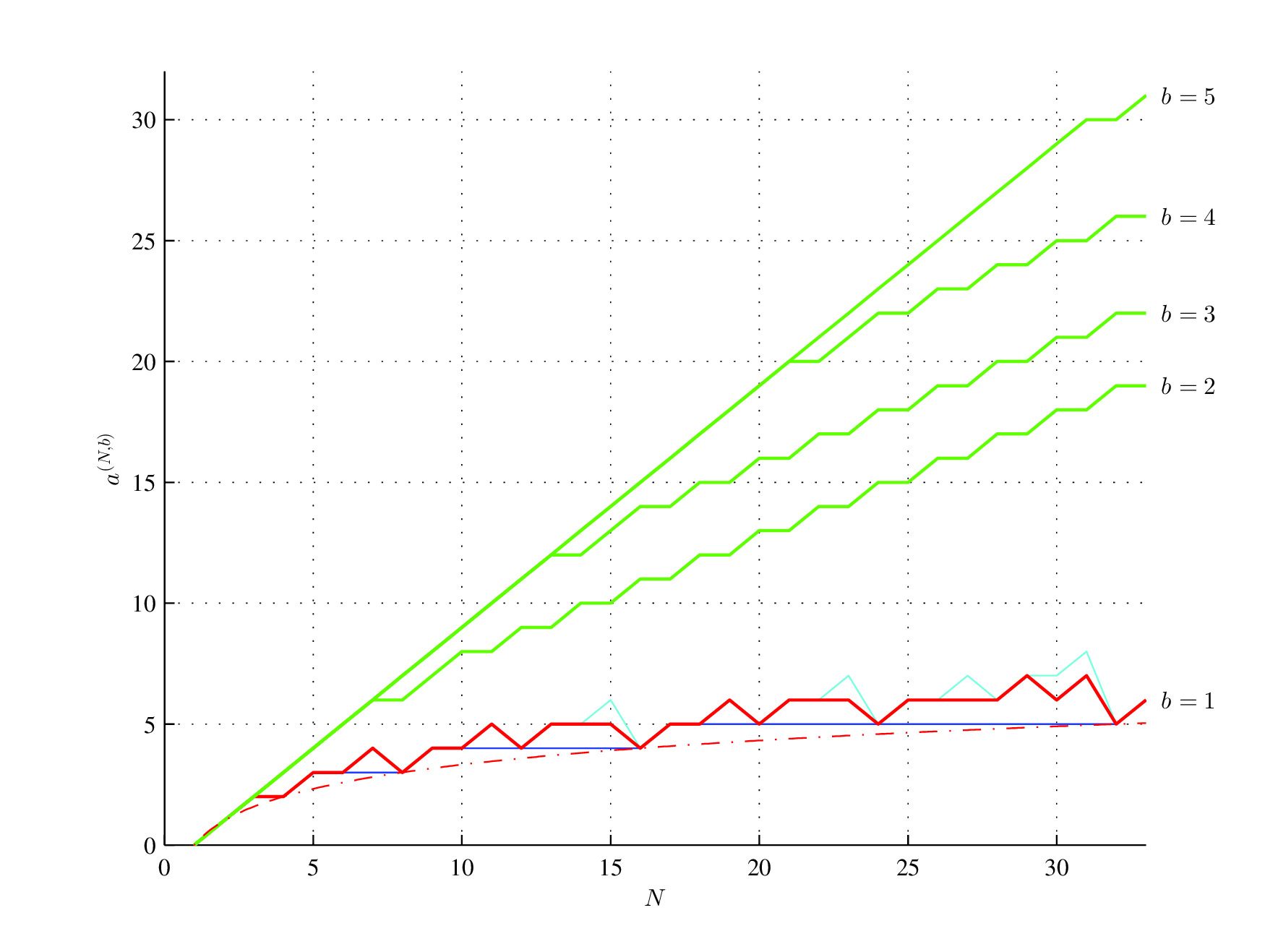
M

Lower assembly inimdex boum (red;nd (OEIS A003313, red), log2(N), (red, dash-dot) and , lower assembly depth bound of maximum (green) assembly index for thstrings for b>1 (blue),

OEIS A014701 sequence (cyalphabet sizesn), and upper assembly index bounds (green) b ∈for {1,2,3,4,5} ≤ b ≤ 4 and 0 < N ≤ 33.

Basic building units depend on a particular application of the assembly theory. In chemistry, it has found applications in drug discovery^[73]. Furthermore, the theoretical value of the assembly index of a molecule, where the initial assembly pool contains chemical bonds, can be experimentally confirmed using tandem mass spectrometry, nuclear magnetic resonance, or infrared spectroscopy^[84][97]. Therefore, the assembly index is the universal threshold between abiotic and biotic molecules and a robust, and simple biosignature^[1][2] ftor distinguishing random, abiotic objects from biologically or technologically assembled ones, as only biotic samples can have an  molecular assembly index above 15. The more complex a given object, the less likely an identical copy can exist without some information-driven mechanism that generates that object^[10].

A discrete Dirichlet energy of the pathway depths can be assigned to the assembly space and splits into the size of the space and a secondary energy charging each assembly step with the square of the depth difference between the two subunits it joins. The assembly index, the assembly depth, and the Dirichlet energy are mutually independent: the shortest unary string for which an extra step beyond the assembly index lowers the energy has length 13, and the shortest for which minimum energy and minimum depth are attained by different plans has length 25^[11].

An ensemble of objects can be co-assembled within a single joint assembly space, and this can be done in three non-equivalent ways: keeping every object at its own assembly index with one formation history per subunit, keeping it while admitting several histories of the same subunit, or minimizing the whole space at the cost of assembling some object non-optimally. Their sizes can all differ, while their computational costs always do — collective minimization is NP-complete, whereas the other two are NP-hard and lie in the second level of the polynomial hierarchy. For some ensembles, the first of the three is impossible altogether, so the plurality of copies that assembly theory records as an observation becomes a structural requirement — copies of the same object differing only by their formation history^[116].