Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Honghong Wang
 -- 3629 2024-03-05 13:03:06 |
2 format correct
Mona Zou
+ 1 word(s) 3630 2024-03-06 09:49:51 | |
3 format correct
Mona Zou
-12 word(s) 3618 2024-03-11 09:10:56 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Wang, H.; Mao, Y.; Du, J. Continuum Robots and Magnetic Soft Robots. Encyclopedia. Available online: https://encyclopedia.pub/entry/55874 (accessed on 03 May 2024).
Wang H, Mao Y, Du J. Continuum Robots and Magnetic Soft Robots. Encyclopedia. Available at: https://encyclopedia.pub/entry/55874. Accessed May 03, 2024.
Wang, Honghong, Yi Mao, Jingli Du. "Continuum Robots and Magnetic Soft Robots" Encyclopedia, https://encyclopedia.pub/entry/55874 (accessed May 03, 2024).
Wang, H., Mao, Y., & Du, J. (2024, March 05). Continuum Robots and Magnetic Soft Robots. In Encyclopedia. https://encyclopedia.pub/entry/55874
Wang, Honghong, et al. "Continuum Robots and Magnetic Soft Robots." Encyclopedia. Web. 05 March, 2024.
Continuum Robots and Magnetic Soft Robots
Edit
This entry is adapted from the peer-reviewed paper 10.3390/mi15030313

Magnetic soft robots, as an innovative branch of the soft robotics discipline, are eye-catching because of their excellent controllability and high flexibility under the control of magnetic fields. Thanks to the properties of magnetic materials, this type of robot can be manufactured into extremely fine micro guide wires, making it particularly applicable in fields such as minimally invasive pipeline interventional treatment or interventional laser surgery. Although magnetic soft robots and continuum robots belong to the same category of soft robots, they show obvious differences and complementarities in design concepts, application scenarios, and technical implementation. Especially from the perspective of structural size, continuum robots have encountered certain challenges in miniaturization, and magnetic soft robots can be regarded as an important expansion and deepening of continuum robots in terms of size reduction.

soft robots magnetic soft robots continuum robots interdisciplinary challenges medical robots

1. Continuum Robots

The researchers elucidate the modeling methodologies of continuum and magnetic soft robots through illustrative diagrams and mathematical expressions. This includes exploring principles, data, and hybrid modeling techniques and simplifying the complexity of interdisciplinary integration.

1.1. Principle Modeling

Modeling continuum robots is a multifaceted and multi-dimensional challenge. From the perspective of handling the unit structural form, continuum robot modeling can be primarily categorized into several approaches: Cosserat rod theory [1][2][3][4] for micropolar bodies, piecewise constant curvature (PCC) models [5], arc segment models [6], geometrically finite element methods [7], and modal methods [8][9]. Micropolar and finite element approaches are more suited for describing complex nonlinear deformations in continuum robots. At the same time, PCC and arc segment models are better tailored for rapid calculation and control in engineering applications of continuum robots.
Although the Cosserat rod approach, PCC, arc segment models, and modal methods differ in their names and forms of representation, they essentially serve as distinct simplification methods for addressing the same problem. Viewed from the perspectives of group theory and topology [10][11][12], these methods all aim to describe the position and orientation of continuum robots at specific points. Consequently, the kinematic description of continuum robots is fundamentally consistent with that of rigid robots. The particular expressions are as follows:

In the context of continuum robot modeling, 𝒈∈𝑆𝐸(3) encompasses both the position 𝐩(𝑋,𝑡) and orientation 𝐑(𝑋,𝑡). Precisely depicting the robot’s orientation, including its position and direction, is undoubtedly a central aspect of modeling. Various orientation representation methods, such as rotation matrices, Euler angles, unit quaternions, screw theory [13], and Plücker coordinates, each possess their distinct advantages, limitations, and applicability [14]. The actual choice depends on multiple factors, including the complexity of the application environment and available computational resources. These representation methods can be interconverted through mathematical transformations in certain intricate application scenarios, offering enhanced flexibility. A common method of orientation conversion is presented below:

Although rotation matrices are excellent for their intuitiveness, they can be computationally and storage-intensive, which may become a limiting factor in applications of continuum robots requiring real-time control and dynamic simulation. In contrast, Euler angles are easy to understand and implement, but can introduce unnecessary restrictions and complexities in describing complex orientation changes due to the gimbal lock issue. Unit quaternions and screw theory [15][16], within the mathematical framework of Lie groups and Lie algebras, offer more precise and efficient methods for describing the complex motions and configurations of continuum and magnetic soft robots. Lie groups and Lie algebras facilitate a lossless mapping from nonlinear to linear, providing profound and refined mathematical insights into this problem.
From an interdisciplinary perspective, selecting an appropriate method for orientation representation involves a decision-making process that spans multiple dimensions and levels. This decision affects the accuracy and complexity of the model and significantly influences the design of subsequent control algorithms and the optimization of the overall system. Therefore, when making this decision, it is imperative to consider various technical and application factors comprehensively. This interdisciplinary and multi-faceted approach not only aids in advancing fundamental research in continuum robots, but also provides solid theoretical support for their application in various practical scenarios.
In the discussion above, the researchers have detailed the rigid description of robot kinematics. However, given the significant compliance and adaptability of continuum robots, constructing their nonlinear dynamic equations necessitates particular attention to accurately handling the constitutive relations of compliance. In this context, Poincaré’s new dynamics equations provide a critical theoretical framework [17]. Following the criterion of continuity for partial derivatives, ∂𝑡∂𝑋=∂𝑋∂𝑡, the researchers can derive the compatibility equations for continuum robots:

The researchers have ad𝝃𝜼=[𝝃,𝜼]=𝝃𝜼−𝜼𝝃. Observing equations from a temporal or spatial perspective reveals that the velocity field variable 𝜼 can be expressed as the strain field variable 𝝃, independent of time t. Building upon Equation (3), it is essential to establish the relationship between strain 𝝃 and the generalized coordinates 𝒒. Solid mechanics [18] provides the theoretical underpinning for this relationship. The relationship of the generalized coordinates 𝒒 can be represented as follows:

where 𝝫(𝑋) is the basis function. To capture the dynamic behavior of continuum robots in complex environments and under the influence of various forces, the kinematic model of continuum robots can be described using the Euler–Lagrange equation or Hamiltonian equation, based on the generalized coordinates 𝒒. This kinematic model can be represented as:


In this context, 𝑴(𝒒) represents the mass matrix, 𝑪(𝒒,𝒒˙) denotes the Coriolis term, 𝑮(𝒒) signifies the gravitational term, and 𝝉R is the input torque. Equation (5) establishes a more general dynamic equation for continuum robots. To delve deeper into the analysis and synthesis of continuum robots, it is imperative to transform their dynamic model Equation (5) into a first-order Hamiltonian form. This transformation is beneficial for comprehending the fundamental characteristics of the system, but also serves as a powerful mathematical tool for further control and optimization endeavors.

In the realm of multibody dynamics modeling, the process is often complex. Specifically, for tendon-driven, multi-rod-driven, and magnetic drive continuum and magnetic soft robots, it becomes necessary to incorporate the descriptions of tendons, rods, or magnetic fields, and establish their relationships with the generalized coordinates. Furthermore, additional elements may need to be considered to develop a more comprehensive dynamical model. For instance, tendons [19], multi-rod [20] and magnetic [21] elements. Sometimes, introducing Lagrangian multipliers, as suggested in [22], is required to accurately describe these interactions in the model. An interdisciplinary and multifaceted approach is often necessary for more complex scenarios, considering various factors such as environmental constraints, as detailed in [23]. It is important to note that even with a comprehensive model, there are inherent assumptions and limitations. For instance, some models might assume material homogeneity or overlook nonlinear factors like friction and air resistance. Therefore, understanding the assumptions and limitations of these models is crucial when applying them in practical scenarios.

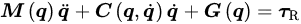
1.2. Data Modeling

Traditional rigid robots have been primarily utilized in factory settings, focusing on executing single, predefined tasks. Precise mathematical models are often one of the best options for these applications. However, as the tasks and environments for robotic applications become more complex, researchers have attempted to develop more intricate models. Yet, this approach significantly increases computational costs. In practical applications, compromises often need to be made, followed by optimization through control algorithms, which may not fully leverage the potential of modeling techniques. The challenge of modeling and controlling compliant continuum robots designed to operate in complex environments is substantial. Initially, the focus was primarily on developing models based on various assumptions.
With the ascent of deep learning [24][25][26] and artificial intelligence [27], data-driven models have garnered widespread attention across multiple domains, including robotics [28][29][30]. These models are increasingly being integrated into robotic modeling processes. Soft robots have notably adopted these advanced technologies, achieving significant breakthroughs [31][32][33]. This trend has also captivated researchers in continuum robots, a field grappling with nonlinear modeling challenges, spurring extensive research into data-driven modeling methodologies for continuum robots [34][35][36]. Data-driven modeling relies heavily on collecting and preprocessing high-quality data and selecting features and models carefully. In the context of continuum robotics, data acquisition predominantly depends on sensor data [37][38] (such as position, shape, flexibility, and bending), control signals, external databases or systems [39] (like SOFA [40], Sorosim [41], and SimSOFT [42]), nonlinear experimental data [43], simulation data [44][45][46], particular environmental factors, and expert input.
In data-driven modeling, particularly in the application to continuum robots, subsequent steps and corresponding challenges arise once data collection is completed. These steps include data preprocessing [47][48], feature engineering [49][50], model selection [51][52], model training [53], model validation [54] and, ultimately, model deployment [55]. For instance, challenges such as addressing missing and outlier values often arise during the data preprocessing stage, which is typically complex and prone to errors. Feature selection and engineering require an in-depth analysis of the raw data to identify the most relevant features. Meanwhile, during the model selection and training phases, the researchers encounter the intricate task of choosing the most suitable model for the problem and fine-tuning its parameters.
Research and practice have adopted various effective strategies to address complex issues. During the data preprocessing stage, statistical methods and professional cleaning tools are employed [56]. Machine learning assesses feature importance and conducts correlation and causality analyses for feature selection. Model selection and training heavily rely on cross-validation and grid search techniques. Regularization or ensemble methods are utilized during the model validation phase to prevent overfitting. Finally, model deployment involves A/B testing to verify real-world utility and performance monitoring to ensure stability. Data-driven modeling, especially in applying continuum robots, confronts various challenges. These include, but are not limited to, data quality, high dimensionality and sparsity, imbalanced datasets, and the optimization of model hyperparameters. Furthermore, computational resource limitations and model interpretability must also be considered. Specific techniques and approaches must be employed to ensure the effectiveness and reliability of the models.
Various machine-learning models have been successfully employed in various application scenarios of continuum robots. These models include neural networks [57][58][59], reinforcement learning [60], support vector machines [61], and a myriad of combined strategies [62]. They have demonstrated exceptional performance in trajectory prediction, action recognition, and fault detection. Moreover, statistical models like Bayesian networks and Gaussian processes have also played a role in estimating the state and parameters of robots.
However, it is noteworthy that in the application of continuum robots, the interpretability of models [63][64][65] holds importance. This is especially evident in critical application scenarios such as medical surgery, where understanding the logic behind model predictions enhances user trust in the model and is also a critical factor in ensuring operational safety. Yet, deep learning models are often perceived as ’black boxes’ with complex internal logic to decipher. This challenge extends beyond technical aspects, encompassing ethical, social, and legal dimensions, suggesting that a comprehensive solution may involve a broader range of disciplines.
An interdisciplinary perspective, particularly from fields such as computer science, ethics in artificial intelligence, and psychology, offers new directions and methodologies for addressing the issue of model interpretability [66][67][68]. Integrating concepts like attention mechanisms [69] and local interpretable models can uncover the rationale behind model decisions [70]. This not only enhances the credibility of models in applications such as continuum robots, but also takes into account the ethical and social responsibilities of the models. In applying continuum robots, data-driven modeling is pivotal in solving technical challenges and opens new avenues for interdisciplinary research and collaboration. This contributes not only to the expansion of application horizons, but also provides new perspectives and tools at both theoretical and practical levels for addressing complex problems in the real world.

1.3. Hybrid Modeling

Principle modeling typically focuses on deriving fundamental equations of robot kinematics from basic physical principles. Still, such models often necessitate simplifications or assumptions in dealing with complex factors, such as friction and nonlinear responses. Conversely, data-driven modeling relies on extensive information collected from experimental data or real-world operations, fitting or interpreting these data through machine learning or statistical methods. Yet, it may lack a profound understanding of the underlying physical processes. Hybrid modeling [71][72] aims to synthesize the strengths of both approaches, thereby achieving a more comprehensive and accurate representation of intelligent system behavior.
Hybrid modeling represents a multi-scientific amalgamated modeling strategy [73], integrating diverse modeling methodologies and data sources [74][75]. This includes, but is not limited to, physically based models, data-driven models, statistical models, heuristic algorithms, and expert knowledge. The strategy aims to achieve comprehensive and precise description and control of complex, uncertain, and nonlinear systems by amalgamating various sources of information. The framework is applicable in the narrow sense of combining physical and data models and in a broader context of blending interdisciplinary modeling approaches [76]. Hybrid modeling in continuum robots primarily focuses on incorporating data-driven elements into physical models, particularly in the aspect of control algorithms [77]. Although the efficacy of this hybrid method has been notably enhanced with the continuous advancement of principle models and data science technologies [78], the significant compliant nonlinearity characteristics of continuum robots and the complexity of their operating environments necessitate and urge the expansion of the application scope and perspective of hybrid modeling.
Hybrid modeling has been extensively researched across various disciplines [72][79][80][81][82]. For the first time, the researchers explore the hybrid modeling of continuum robots from both vertical and horizontal perspectives. A key element in the vertical approach is determining how to allocate weights to theoretical and data models appropriately, a process often dynamic and dependent on the environment. In scenarios with insufficient experimental data or low data quality, theoretical modeling is usually given greater weight, leveraging existing physical knowledge and mathematical theories for more reliable predictions. Conversely, when data are abundant and reliable, data models may receive higher weighting to capture complex environments’ impacts or nonlinear factors’ impacts more accurately. Additionally, in the framework of hybrid modeling, the horizontal integration strategy is also crucial, involving the combination of different types or sources of models on the same level [83][84][85][86]. For example, a continuum robot may possess multiple degrees of motion and sensory modules, each capable of being modeled theoretically and through data independently. Horizontal integration then addresses how to amalgamate these independent or partially overlapping models into a unified, more comprehensive model.
The hybrid modeling approach may increase the complexity and computational cost of the model while also complicating the model validation process. Ensuring that theoretical and data models are based on consistent assumptions and datasets to maintain data consistency presents a challenge [80][87]. Dynamically adjusting model weights can enhance adaptability, but may also impact model performance. Additionally, in an interdisciplinary environment, model interpretability should not be overlooked [88]. Resolving potential disciplinary contradictions or conflicts is a complex yet necessary task. Hybrid modeling provides a possible theoretical framework for continuum robots and extends to a more interdisciplinary domain. Within the broader context of interdisciplinary research, hybrid modeling could emerge as a diversified framework, accommodating knowledge and methodologies from various fields ranging from physics and material science to computer science, robotics, and statistics. This not only accelerates the flow of information and exchange of knowledge between disciplines, but also enriches the interdimensionality and accuracy of the models. More importantly, such interdisciplinary collaboration implies a multi-faceted examination of model assumptions and limitations, enhancing the model’s reliability and adaptability.

2. Magnetic Soft Robots

While continuum robots focus on millimeter-scale or more oversized dimensions, magnetic soft robots can extend to the nanoscale. However, ignoring the quantum effects of microscopic physical phenomena becomes challenging at the nanoscale. Therefore, the influences of different forms of magnetic fields and quantum effects are equally important to consider.

2.1. Uniform Magnetic Field

The uniform magnetic field is essential for its stable control environment in magnetic soft robots. This stability simplifies experimental design and ensures predictability and repeatability in wide-ranging applications, highlighting the need for advanced modeling to leverage its unique benefits effectively. For the magnetic soft robots described in Equation (5), the primary source of actuation has shifted from mechanical drive to the torque exerted by magnetic moments. This transition simplifies the model and opens new possibilities for precise control. Specifically, based on the existing continuum robot dynamics models, the researchers can construct a more comprehensive and unified theoretical framework for magnetic soft robots in uniform magnetic fields by introducing magnetic moments as the main source of actuation [21][89][90]. For instance, the interaction between the magnetic moment 𝒎 and a uniform magnetic field 𝑩 can be described by the following mathematical expression involving magnetic field strength, current density, and other physical parameters:

The magnetic moment term in Equation (7) needs to be incorporated into Equation (5) to successfully construct the dynamic model of filamentous magnetic soft robots. This model increases the complexity and comprehensiveness of the original dynamics model, and opens new possibilities for precise control and optimization. Further information on the construction of filamentous magnetic soft robots can be found in the related literature [91][92][93][94].

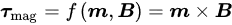
2.2. Non-Uniform Magnetic Field

Despite the preference for uniform magnetic fields due to their simplicity in modeling and predictability in operational contexts, such as in the case of filamentous magnetic soft robots [95], non-uniform magnetic fields have demonstrated undeniable advantages in specific specialized medical applications. Specifically, non-uniform magnetic fields offer enhanced capabilities for localized and adaptive manipulation, making them particularly suitable for interventions in complex and deep-seated tissue structures, such as aortic treatment [96], cancer therapy [97][98][99], neuro intervention [100], intravascular surgery [101][102], and endoscopic procedures [103], etc. [104]. These unique advantages underscore the critical importance of non-uniform magnetic field modeling in medical scenarios requiring high precision and flexibility in deploying soft magnetic robots.
In a uniform magnetic field, since the net magnetic force is zero, our discussion primarily focuses on the influence of the magnetic torque. However, when transitioning to a non-uniform magnetic field, the situation becomes more complex. In such environments, microrobots are influenced not only by magnetic torque but also by magnetic forces. This can be expressed by the following equation, which demonstrates that:

Although the hybrid Equation (8) increases the complexity of the model, it also expands our capability to control magnetic soft robots in various application scenarios precisely. Furthermore, fluid resistance becomes an indispensable dynamic factor in scenarios involving fluid mediums, such as operations within blood vessels or body cavities, especially in applications involving the manipulation of microrobots in fluid mediums. The following equation can represent this resistance:

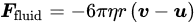
With a viscosity of 𝜂, 𝒖 is the fluid velocity and 𝒗 is the velocity of the robot in the fluid, and r is the approximate radius of the robot. Considering fluid resistance makes the multiphysics model more aligned with real-world applications and provides rich content for subsequent in-depth analysis and understanding. The net external force generated by the magnetic field and fluid resistance is reflected in the acceleration 𝑑2𝒙𝑑𝑡2 of the robot’s center of mass. The latter describes the robot’s angular acceleration 𝑑2𝜃𝑑𝑡2 around its center of mass, which is determined by the total external torque 𝜏 applied. These two equations provide us with a complete and in-depth perspective for understanding and analyzing the dynamic behavior of robots in complex multiphysics fields. Therefore, the motion equation and rotational dynamics of the robot are, respectively, given by:

 
It should be noted that fluid resistance, the mass matrix, and the Coriolis terms remain constant in both models. However, the researchers often face more complex magnetic field environments in practical applications. These environments may not only be non-uniform, but may also involve the combined effects of multiple magnetic fields. More importantly, in actual surgical applications, it is necessary to consider problems faced by interdisciplinary, such as biofilms [105] and infections related to catheters [106][107]. Although the literature [108] proposes a strategy for preventing biological infections, it still confronts multiple challenges [109]. Therefore, realizing the application of magnetic soft robots in the medical field requires interdisciplinary collaboration and integration.

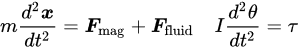
2.3. Quantum Effects

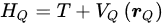
At the micro and nano scales, modeling magnetic soft robots particularly requires further consideration of aspects such as quantum effects and molecular dynamics, as these factors may play a significant role at this scale [110]. For instance, quantum effects could influence the electromagnetic properties of materials [111][112]. Therefore, it is necessary to select a quantum mechanical model to describe these phenomena in addition to the dynamic description provided by Equation (10). This could include models like Density Functional Theory [113][114] (DFT) or Hartree–Fock [115][116], among others. This model is typically defined by a Hamiltonian 𝐻𝑄:

where T represents the kinetic energy term and 𝑉𝑄(𝒓𝑄) is the quantum potential energy. The system’s ground state or several low-excited states are found by solving the Schrödinger equation or other quantum equations corresponding to the Hamiltonian 𝐻𝑄. Subsequently, the quantum correction force 𝑭𝑄 is calculated, which is typically the gradient of the quantum potential energy 𝑉𝑄 concerning the coordinates 𝒓𝑄:


This approach of introducing quantum effects through quantum correction forces offers the advantages of simplicity and broad applicability. Still, it also has the drawbacks of limited accuracy and the potential for increased computational burden. Finally, it is worth noting that in addition to quantum correction forces, path integral molecular dynamics (PIMD) can be used for a careful consideration of quantum effects [117][118]. PIMD represents a more exhaustive yet complex method, typically employed in systems where precise consideration of quantum effects is necessary.
The complex response characteristics of magnetic soft robots in nonlinear magnetic fields increase the difficulty of data modeling, rendering traditional linear models inadequate. Nonlinear models or deep learning algorithms are necessary to capture these relationships [119]. Modeling of magnetic soft robots must address time dependency, potentially utilizing networks with memory capabilities such as RNNs or LSTMs. Three-dimensional operations and complex magnetic fields pose challenges for data collection, necessitating specialized sensors or computer vision techniques. Data modeling [120][121][122] and hybrid modeling offers multiple options for magnetic soft robots, in contrast to the mature technologies of continuum robots. Researchers should draw on continuum robot strategies, emphasizing the integration of precise models, advanced algorithms, and sensing technologies while focusing on interdisciplinary biocompatibility studies in biological environments.
Data modeling for magnetic soft robots poses more significant challenges than traditional continuum robots, necessitating the management of more complex issues such as data sparsity imbalance and ensuring model interpretability and safety. Models must accurately capture nonlinear magnetic responses and maintain reliability in dynamic environments. This requires integrating data science and physics knowledge, advanced deep learning, and physical models to ensure accuracy in their three-dimensional operations and complex magnetic field responses. Therefore, interdisciplinary hybridization and combining theoretical and practical data are crucial in developing magnetic soft robots.

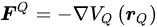
References

  1. Rubin, M.; Rubin, M. Cosserat Theories: Shells, Rods and Points; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–480.
  2. Renda, F.; Boyer, F.; Dias, J.; Seneviratne, L. Discrete cosserat approach for multisection soft manipulator dynamics. IEEE Trans. Robot. 2018, 34, 1518–1533.
  3. Zhang, X.; Naughton, N.; Parthasarathy, T.; Gazzola, M. Friction modulation in limbless, three-dimensional gaits and heterogeneous terrains. Nat. Commun. 2021, 12, 6076.
  4. Zhang, X.; Chan, F.K.; Parthasarathy, T.; Gazzola, M. Modeling and simulation of complex dynamic musculoskeletal architectures. Nat. Commun. 2019, 10, 4825.
  5. Webster, R.J., III; Jones, B.A. Design and kinematic modeling of constant curvature continuum robots: A review. Int. J. Robot. Res. 2010, 29, 1661–1683.
  6. Hasanzadeh, S.; Janabi-Sharifi, F. An efficient static analysis of continuum robots. J. Mech. Robot. 2014, 6, 031011.
  7. Li, X.; Yu, W.; Baghaee, M.; Cao, C.; Chen, D.; Liu, J.; Yuan, H. Geometrically exact finite element formulation for tendon-driven continuum robots. Acta Mech. Solida Sin. 2022, 35, 552–570.
  8. Godage, I.S.; Branson, D.T.; Guglielmino, E.; Medrano-Cerda, G.A.; Caldwell, D.G. Dynamics for biomimetic continuum arms: A modal approach. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7–11 December 2011; pp. 104–109.
  9. Yang, J.; Peng, H.; Zhou, W.; Zhang, J.; Wu, Z. A modular approach for dynamic modeling of multisegment continuum robots. Mech. Mach. Theory 2021, 165, 104429.
  10. Dickson, L.E. Modern Algebraic Theories; BH Sanborn & Company: Denver, CO, USA, 1926.
  11. Robinson, D.J. A Course in the Theory of Groups; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 80.
  12. Armstrong, M.A. Groups and Symmetry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1997.
  13. Dai, J. Geometrical Foundations and Screw Algebra for Mechanisms and Robotics; Springer: Berlin/Heidelberg, Germany, 2014.
  14. Siciliano, B.; Khatib, O.; Kröger, T. Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 200.
  15. Murray, R.M.; Li, Z.; Sastry, S.S. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 1994.
  16. Lynch, K.M.; Park, F.C. Modern Robotics; Cambridge University Press: Cambridge, UK, 2017.
  17. Poincaré, H. Sur une forme nouvelle des équations de la mécanique. CR Acad. Sci. 1901, 132, 369–371.
  18. Dym, C.L.; Shames, I.H. Solid Mechanics; Springer: Berlin/Heidelberg, Germany, 1973.
  19. Till, J.; Aloi, V.; Rucker, C. Real-time dynamics of soft and continuum robots based on Cosserat rod models. Int. J. Robot. Res. 2019, 38, 723–746.
  20. Wu, G.; Shi, G. Design, modeling, and workspace analysis of an extensible rod-driven parallel continuum robot. Mech. Mach. Theory 2022, 172, 104798.
  21. Edelmann, J.; Petruska, A.J.; Nelson, B.J. Magnetic control of continuum devices. Int. J. Robot. Res. 2017, 36, 68–85.
  22. Hesch, C.; Glas, S.; Schuß, S. Space-time multibody dynamics. Multibody Syst. Dyn. 2023, 1–20.
  23. Chen, P.; Liu, Y.; Yuan, T.; Shi, W. Modeling of continuum robots with environmental constraints. In Engineering with Computers; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–14.
  24. McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133.
  25. Kelley, H.J. Gradient theory of optimal flight paths. Ars J. 1960, 30, 947–954.
  26. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9.
  27. Littman, M.L.; Ajunwa, I.; Berger, G.; Boutilier, C.; Currie, M.; Doshi-Velez, F.; Hadfield, G.; Horowitz, M.C.; Isbell, C.; Kitano, H.; et al. Gathering strength, gathering storms: The one hundred year study on artificial intelligence (AI100) 2021 study panel report. arXiv 2022, arXiv:2210.15767.
  28. Soori, M.; Arezoo, B.; Dastres, R. Artificial intelligence, machine learning and deep learning in advanced robotics, A review. Cogn. Robot. 2023, 3, 54–70.
  29. Morales, E.F.; Murrieta-Cid, R.; Becerra, I.; Esquivel-Basaldua, M.A. A survey on deep learning and deep reinforcement learning in robotics with a tutorial on deep reinforcement learning. Intell. Serv. Robot. 2021, 14, 773–805.
  30. Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589.
  31. Jumet, B.; Bell, M.D.; Sanchez, V.; Preston, D.J. A data-driven review of soft robotics. Adv. Intell. Syst. 2022, 4, 2100163.
  32. Bhagat, S.; Banerjee, H.; Ho Tse, Z.T.; Ren, H. Deep reinforcement learning for soft, flexible robots: Brief review with impending challenges. Robotics 2019, 8, 4.
  33. Kim, D.; Kim, S.H.; Kim, T.; Kang, B.B.; Lee, M.; Park, W.; Ku, S.; Kim, D.; Kwon, J.; Lee, H.; et al. Review of machine learning methods in soft robotics. PLoS ONE 2021, 16, e0246102.
  34. George Thuruthel, T.; Ansari, Y.; Falotico, E.; Laschi, C. Control strategies for soft robotic manipulators: A survey. Soft Robot. 2018, 5, 149–163.
  35. Sahoo, A.R.; Chakraborty, P. A Study on Position Control of a Continuum Arm Using MAML (Model-Agnostic Meta-Learning) for Adapting Different Loading Conditions. IEEE Access 2022, 10, 14980–14992.
  36. Wei, D.; Zhou, J.; Zhu, Y.; Ma, J.; Ma, S. Axis-space framework for cable-driven soft continuum robot control via reinforcement learning. Commun. Eng. 2023, 2, 61.
  37. Reiter, A.; Goldman, R.E.; Bajo, A.; Iliopoulos, K.; Simaan, N.; Allen, P.K. A learning algorithm for visual pose estimation of continuum robots. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 2390–2396.
  38. Thuruthel, T.G.; Shih, B.; Laschi, C.; Tolley, M.T. Soft robot perception using embedded soft sensors and recurrent neural networks. Sci. Robot. 2019, 4, eaav1488.
  39. Schegg, P.; Duriez, C. Review on generic methods for mechanical modeling, simulation and control of soft robots. PLoS ONE 2022, 17, e0251059.
  40. Largilliere, F.; Verona, V.; Coevoet, E.; Sanz-Lopez, M.; Dequidt, J.; Duriez, C. Real-time control of soft-robots using asynchronous finite element modeling. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2550–2555.
  41. Mathew, A.T.; Hmida, I.M.B.; Armanini, C.; Boyer, F.; Renda, F. Sorosim: A matlab toolbox for hybrid rigid-soft robots based on the geometric variable-strain approach. IEEE Robot. Autom. Mag. 2022, 30, 106–122.
  42. Grazioso, S.; Di Gironimo, G.; Siciliano, B. A geometrically exact model for soft continuum robots: The finite element deformation space formulation. Soft Robot. 2019, 6, 790–811.
  43. Wu, Q.; Gu, Y.; Li, Y.; Zhang, B.; Chepinskiy, S.A.; Wang, J.; Zhilenkov, A.A.; Krasnov, A.Y.; Chernyi, S. Position control of cable-driven robotic soft arm based on deep reinforcement learning. Information 2020, 11, 310.
  44. Giorelli, M.; Renda, F.; Calisti, M.; Arienti, A.; Ferri, G.; Laschi, C. Neural network and jacobian method for solving the inverse statics of a cable-driven soft arm with nonconstant curvature. IEEE Trans. Robot. 2015, 31, 823–834.
  45. Thuruthel, T.G.; Falotico, E.; Renda, F.; Laschi, C. Learning dynamic models for open loop predictive control of soft robotic manipulators. Bioinspiration Biomimetics 2017, 12, 066003.
  46. Lee, K.H.; Fu, D.K.; Leong, M.C.; Chow, M.; Fu, H.C.; Althoefer, K.; Sze, K.Y.; Yeung, C.K.; Kwok, K.W. Nonparametric online learning control for soft continuum robot: An enabling technique for effective endoscopic navigation. Soft Robot. 2017, 4, 324–337.
  47. Zheng, A.; Casari, A. Feature Engineering for Machine Learning: Principles and Techniques for Data Scientists; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018.
  48. Felix, E.A.; Lee, S.P. Systematic literature review of preprocessing techniques for imbalanced data. IET Softw. 2019, 13, 479–496.
  49. Kuhn, M.; Johnson, K. Feature Engineering and Selection: A Practical Approach for Predictive Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019.
  50. Khurana, U.; Samulowitz, H.; Turaga, D. Feature engineering for predictive modeling using reinforcement learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32.
  51. Anderson, D.; Burnham, K. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: Cham, Switzerland, 2004; Volume 63, pp. 1–488.
  52. Clarke, B. Comparing Bayes model averaging and stacking when model approximation error cannot be ignored. J. Mach. Learn. Res. 2003, 4, 683–712.
  53. Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016.
  54. Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2.
  55. Singh, P. Deploy Machine Learning Models to Production; Springer: Cham, Switzerland, 2021.
  56. Van der Loo, M.; De Jonge, E. Statistical Data Cleaning with Applications in R; John Wiley & Sons: Hoboken, NJ, USA, 2018.
  57. Tan, N.; Yu, P.; Zhang, X.; Wang, T. Model-free motion control of continuum robots based on a zeroing neurodynamic approach. Neural Netw. 2021, 133, 21–31.
  58. Tariverdi, A.; Venkiteswaran, V.K.; Richter, M.; Elle, O.J.; Tørresen, J.; Mathiassen, K.; Misra, S.; Martinsen, Ø.G. A recurrent neural-network-based real-time dynamic model for soft continuum manipulators. Front. Robot. AI 2021, 8, 631303.
  59. Tan, N.; Yu, P.; Zhong, Z.; Zhang, Y. Data-Driven Control for Continuum Robots Based on Discrete Zeroing Neural Networks. IEEE Trans. Ind. Inform. 2022, 19, 7088–7098.
  60. Youssef, S.M.; Soliman, M.; Saleh, M.A.; Elsayed, A.H.; Radwan, A.G. Design and control of soft biomimetic pangasius fish robot using fin ray effect and reinforcement learning. Sci. Rep. 2022, 12, 21861.
  61. Goldman, R.E.; Bajo, A.; Simaan, N. Compliant motion control for multisegment continuum robots with actuation force sensing. IEEE Trans. Robot. 2014, 30, 890–902.
  62. Ji, G.; Yan, J.; Du, J.; Yan, W.; Chen, J.; Lu, Y.; Rojas, J.; Cheng, S.S. Towards safe control of continuum manipulator using shielded multiagent reinforcement learning. IEEE Robot. Autom. Lett. 2021, 6, 7461–7468.
  63. Molnar, C. Interpretable Machine Learning; Lulu.com: Morrisville, NC, USA, 2020.
  64. Tsang, W.K.; Benoit, D.F. Interpretability and Explainability in Machine Learning. In Living Beyond Data: Toward Sustainable Value Creation; Springer: Berlin/Heidelberg, Germany, 2022; pp. 89–100.
  65. Hall, P.; Gill, N. An Introduction to Machine Learning Interpretability; O’Reilly Media, Incorporated: Sebastopol, CA, USA, 2019.
  66. Amann, J.; Blasimme, A.; Vayena, E.; Frey, D.; Madai, V.I.; Consortium, P. Explainability for artificial intelligence in healthcare: A multidisciplinary perspective. BMC Med. Inform. Decis. Mak. 2020, 20, 1–9.
  67. Dwivedi, Y.K.; Hughes, L.; Ismagilova, E.; Aarts, G.; Coombs, C.; Crick, T.; Duan, Y.; Dwivedi, R.; Edwards, J.; Eirug, A.; et al. Artificial Intelligence (AI): Multidisciplinary perspectives on emerging challenges, opportunities, and agenda for research, practice and policy. Int. J. Inf. Manag. 2021, 57, 101994.
  68. Xu, Q.; Xie, W.; Liao, B.; Hu, C.; Qin, L.; Yang, Z.; Xiong, H.; Lyu, Y.; Zhou, Y.; Luo, A.; et al. Interpretability of Clinical Decision Support Systems Based on Artificial Intelligence from Technological and Medical Perspective: A Systematic Review. J. Healthc. Eng. 2023, 2023, 9919269.
  69. Chen, P.; Dong, W.; Wang, J.; Lu, X.; Kaymak, U.; Huang, Z. Interpretable clinical prediction via attention-based neural network. BMC Med. Inform. Decis. Mak. 2020, 20, 1–9.
  70. Van der Velden, B.H.; Kuijf, H.J.; Gilhuijs, K.G.; Viergever, M.A. Explainable artificial intelligence (XAI) in deep learning-based medical image analysis. Med. Image Anal. 2022, 79, 102470.
  71. Zhang, J.; Petersen, S.D.; Radivojevic, T.; Ramirez, A.; Pérez-Manríquez, A.; Abeliuk, E.; Sánchez, B.J.; Costello, Z.; Chen, Y.; Fero, M.J.; et al. Combining mechanistic and machine learning models for predictive engineering and optimization of tryptophan metabolism. Nat. Commun. 2020, 11, 4880.
  72. Gettelman, A.; Geer, A.J.; Forbes, R.M.; Carmichael, G.R.; Feingold, G.; Posselt, D.J.; Stephens, G.L.; van den Heever, S.C.; Varble, A.C.; Zuidema, P. The future of Earth system prediction: Advances in model-data fusion. Sci. Adv. 2022, 8, eabn3488.
  73. Yang, S.; Navarathna, P.; Ghosh, S.; Bequette, B.W. Hybrid modeling in the era of smart manufacturing. Comput. Chem. Eng. 2020, 140, 106874.
  74. Zhou, T.; Gani, R.; Sundmacher, K. Hybrid data-driven and mechanistic modeling approaches for multiscale material and process design. Engineering 2021, 7, 1231–1238.
  75. Zhang, H.; Qi, Q.; Ji, W.; Tao, F. An update method for digital twin multi-dimension models. Robot. Comput. Integr. Manuf. 2023, 80, 102481.
  76. Xiang, L.; Xunbo, L.; Liang, C. Multi-disciplinary modeling and collaborative simulation of multi-robot systems based on HLA. In Proceedings of the 2007 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 15–18 December 2007; pp. 553–558.
  77. Braganza, D.; Dawson, D.M.; Walker, I.D.; Nath, N. A neural network controller for continuum robots. IEEE Trans. Robot. 2007, 23, 1270–1277.
  78. Thuruthel, T.G.; Falotico, E.; Renda, F.; Laschi, C. Model-based reinforcement learning for closed-loop dynamic control of soft robotic manipulators. IEEE Trans. Robot. 2018, 35, 124–134.
  79. Lu, Y.; Yang, B.; Mo, Y. Two-timescale mechanism-and-data-driven control for aggressive driving of autonomous cars. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 7874–7879.
  80. Tsopanoglou, A.; del Val, I.J. Moving towards an era of hybrid modelling: Advantages and challenges of coupling mechanistic and data-driven models for upstream pharmaceutical bioprocesses. Curr. Opin. Chem. Eng. 2021, 32, 100691.
  81. Arcomano, T.; Szunyogh, I.; Wikner, A.; Pathak, J.; Hunt, B.R.; Ott, E. A hybrid approach to atmospheric modeling that combines machine learning with a physics-based numerical model. J. Adv. Model. Earth Syst. 2022, 14, e2021MS002712.
  82. Lee, D.; Jayaraman, A.; Kwon, J.S.I. A Hybrid Mechanistic Data-Driven Approach for Modeling Uncertain Intracellular Signaling Pathways. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 1903–1908.
  83. Hammes-Schiffer, S.; Galli, G. Integration of theory and experiment in the modelling of heterogeneous electrocatalysis. Nat. Energy 2021, 6, 700–705.
  84. Ellis, J.; Jacobs, M.; Dijkstra, J.; van Laar, H.; Cant, J.; Tulpan, D.; Ferguson, N. Synergy between mechanistic modelling and data-driven models for modern animal production systems in the era of big data. Animal 2020, 14, s223–s237.
  85. Sansana, J.; Joswiak, M.N.; Castillo, I.; Wang, Z.; Rendall, R.; Chiang, L.H.; Reis, M.S. Recent trends on hybrid modeling for Industry 4.0. Comput. Chem. Eng. 2021, 151, 107365.
  86. Kurz, S.; De Gersem, H.; Galetzka, A.; Klaedtke, A.; Liebsch, M.; Loukrezis, D.; Russenschuck, S.; Schmidt, M. Hybrid modeling: Towards the next level of scientific computing in engineering. J. Math. Ind. 2022, 12, 1–12.
  87. Mahanty, B. Hybrid modeling in bioprocess dynamics: Structural variabilities, implementation strategies, and practical challenges. Biotechnol. Bioeng. 2023, 120, 2072–2091.
  88. Wang, J.; Li, Y.; Gao, R.X.; Zhang, F. Hybrid physics-based and data-driven models for smart manufacturing: Modelling, simulation, and explainability. J. Manuf. Syst. 2022, 63, 381–391.
  89. Kratchman, L.B.; Bruns, T.L.; Abbott, J.J.; Webster, R.J. Guiding elastic rods with a robot-manipulated magnet for medical applications. IEEE Trans. Robot. 2016, 33, 227–233.
  90. Fu, S.; Chen, B.; Li, D.; Han, J.; Xu, S.; Wang, S.; Huang, C.; Qiu, M.; Cheng, S.; Wu, X.; et al. A Magnetically Controlled Guidewire Robot System with Steering and Propulsion Capabilities for Vascular Interventional Surgery. Adv. Intell. Syst. 2023, 5, 2300267.
  91. Wang, L.; Kim, Y.; Guo, C.F.; Zhao, X. Hard-magnetic elastica. J. Mech. Phys. Solids 2020, 142, 104045.
  92. Sano, T.G.; Pezzulla, M.; Reis, P.M. A Kirchhoff-like theory for hard magnetic rods under geometrically nonlinear deformation in three dimensions. J. Mech. Phys. Solids 2022, 160, 104739.
  93. Huang, W.; Liu, M.; Hsia, K.J. A discrete model for the geometrically nonlinear mechanics of hard-magnetic slender structures. Extrem. Mech. Lett. 2023, 59, 101977.
  94. Li, X.; Yu, W.; Liu, J.; Zhu, X.; Wang, H.; Sun, X.; Liu, J.; Yuan, H. A mechanics model of hard-magnetic soft rod with deformable cross-section under three-dimensional large deformation. Int. J. Solids Struct. 2023, 279, 112344.
  95. Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic soft continuum robots. Sci. Robot. 2019, 4, eaax7329.
  96. Richter, M.; Kaya, M.; Sikorski, J.; Abelmann, L.; Venkiteswaran, V.K.; Misra, S. Magnetic Soft Helical Manipulators with Local Dipole Interactions for Flexibility and Forces. Soft Robot. 2023, 10, 647–659.
  97. Gavilán, H.; Avugadda, S.K.; Fernández-Cabada, T.; Soni, N.; Cassani, M.; Mai, B.T.; Chantrell, R.; Pellegrino, T. Magnetic nanoparticles and clusters for magnetic hyperthermia: Optimizing their heat performance and developing combinatorial therapies to tackle cancer. Chem. Soc. Rev. 2021, 50, 11614–11667.
  98. Gavilán, H.; Rizzo, G.M.; Silvestri, N.; Mai, B.T.; Pellegrino, T. Scale-up approach for the preparation of magnetic ferrite nanocubes and other shapes with benchmark performance for magnetic hyperthermia applications. Nat. Protoc. 2023, 18, 783–809.
  99. Lee, J.H.; Jang, J.t.; Choi, J.s.; Moon, S.H.; Noh, S.h.; Kim, J.w.; Kim, J.G.; Kim, I.S.; Park, K.I.; Cheon, J. Exchange-coupled magnetic nanoparticles for efficient heat induction. Nat. Nanotechnol. 2011, 6, 418–422.
  100. Kim, Y.; Genevriere, E.; Harker, P.; Choe, J.; Balicki, M.; Patel, A.B.; Zhao, X. Telerobotically Controlled Magnetic Soft Continuum Robots for Neurovascular Interventions. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 9600–9606.
  101. Liu, Y.; Mohanraj, T.G.; Rajebi, M.R.; Zhou, L.; Alambeigi, F. Multiphysical analytical modeling and design of a magnetically steerable robotic catheter for treatment of peripheral artery disease. IEEE/ASME Trans. Mechatronics 2022, 27, 1873–1881.
  102. Lu, K.; Zhou, C.; Li, Z.; Liu, Y.; Wang, F.; Xuan, L.; Wang, X. Multi-level magnetic microrobot delivery strategy within a hierarchical vascularized organ-on-a-chip. Lab Chip 2024, 24, 446–459.
  103. Pittiglio, G.; Lloyd, P.; da Veiga, T.; Onaizah, O.; Pompili, C.; Chandler, J.H.; Valdastri, P. Patient-specific magnetic catheters for atraumatic autonomous endoscopy. Soft Robot. 2022, 9, 1120–1133.
  104. Thomas, T.L.; Sikorski, J.; Ananthasuresh, G.; Venkiteswaran, V.K.; Misra, S. Design, sensing, and control of a magnetic compliant continuum manipulator. IEEE Trans. Med. Robot. Bionics 2022, 4, 910–921.
  105. Flemming, H.C.; Wingender, J. The biofilm matrix. Nat. Rev. Microbiol. 2010, 8, 623–633.
  106. Faustino, C.M.; Lemos, S.M.; Monge, N.; Ribeiro, I.A. A scope at antifouling strategies to prevent catheter-associated infections. Adv. Colloid Interface Sci. 2020, 284, 102230.
  107. Rajaramon, S.; Shanmugam, K.; Dandela, R.; Solomon, A.P. Emerging evidence-based innovative approaches to control catheter-associated urinary tract infection: A review. Front. Cell. Infect. Microbiol. 2023, 13, 1134433.
  108. Baburova, P.I.; Kladko, D.V.; Lokteva, A.; Pozhitkova, A.; Rumyantceva, V.; Rumyantceva, V.; Pankov, I.V.; Taskaev, S.; Vinogradov, V.V. Magnetic Soft Robot for Minimally Invasive Urethral Catheter Biofilm Eradication. ACS Nano 2023, 17, 20925–20938.
  109. Koo, H.; Allan, R.N.; Howlin, R.P.; Stoodley, P.; Hall-Stoodley, L. Targeting microbial biofilms: Current and prospective therapeutic strategies. Nat. Rev. Microbiol. 2017, 15, 740–755.
  110. Cava, R.; de Leon, N.; Xie, W. Introduction: Quantum Materials. Chem. Rev. 2021, 121, 2777–2779.
  111. Tokura, Y.; Kawasaki, M.; Nagaosa, N. Emergent functions of quantum materials. Nat. Phys. 2017, 13, 1056–1068.
  112. Shulga, K.; Il’ichev, E.; Fistul, M.V.; Besedin, I.; Butz, S.; Astafiev, O.; Hübner, U.; Ustinov, A.V. Magnetically induced transparency of a quantum metamaterial composed of twin flux qubits. Nat. Commun. 2018, 9, 150.
  113. Zunger, A. Bridging the gap between density functional theory and quantum materials. Nat. Comput. Sci. 2022, 2, 529–532.
  114. Thomas, L.H. The calculation of atomic fields. Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1927; Volume 23, pp. 542–548.
  115. Hartree, D.R. The wave mechanics of an atom with a non-Coulomb central field. Part I. Theory and methods. In Proceedings of the Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1928; Volume 24, pp. 89–110.
  116. Jones, M.A.; Vallury, H.J.; Hill, C.D.; Hollenberg, L.C. Chemistry beyond the Hartree–Fock energy via quantum computed moments. Sci. Rep. 2022, 12, 8985.
  117. Sauceda, H.E.; Gálvez-González, L.E.; Chmiela, S.; Paz-Borbón, L.O.; Müller, K.R.; Tkatchenko, A. BIGDML—Towards accurate quantum machine learning force fields for materials. Nat. Commun. 2022, 13, 3733.
  118. Bocus, M.; Goeminne, R.; Lamaire, A.; Cools-Ceuppens, M.; Verstraelen, T.; Van Speybroeck, V. Nuclear quantum effects on zeolite proton hopping kinetics explored with machine learning potentials and path integral molecular dynamics. Nat. Commun. 2023, 14, 1008.
  119. Wang, X.; Mao, G.; Ge, J.; Drack, M.; Cañón Bermúdez, G.S.; Wirthl, D.; Illing, R.; Kosub, T.; Bischoff, L.; Wang, C.; et al. Untethered and ultrafast soft-bodied robots. Commun. Mater. 2020, 1, 67.
  120. Ni, Y.; Sun, Y.; Zhang, H.; Li, X.; Zhang, S.; Li, M. Data-Driven Navigation of Ferromagnetic Soft Continuum Robots Based on Machine Learning. Adv. Intell. Syst. 2023, 5, 2200167.
  121. Liu, Z.; Wang, S.; Feng, F.; Xie, L. A magnetorheological fluid based force feedback master robot for vascular interventional surgery. J. Intell. Robot. Syst. 2022, 106, 20.
  122. Yao, J.; Cao, Q.; Ju, Y.; Sun, Y.; Liu, R.; Han, X.; Li, L. Adaptive actuation of magnetic soft robots using deep reinforcement learning. Adv. Intell. Syst. 2023, 5, 2200339.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Biomedical
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Honghong Wang
,
Yi Mao
,
Jingli Du
View Times: 72
Revisions: 3 times (View History)
Update Date: 11 Mar 2024
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback