Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Kefeng Li
 -- 3078 2024-02-01 05:03:33 |
2 Reference format revised.
Lindsay Dong
 Meta information modification 3078 2024-02-02 07:33:43 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Meng, W.; Pan, H.; Sha, Y.; Zhai, X.; Xing, A.; Lingampelly, S.S.; Sripathi, S.R.; Wang, Y.; Li, K. Role of Metabolic Connectome in Complex Diseases. Encyclopedia. Available online: https://encyclopedia.pub/entry/54624 (accessed on 19 May 2024).
Meng W, Pan H, Sha Y, Zhai X, Xing A, Lingampelly SS, et al. Role of Metabolic Connectome in Complex Diseases. Encyclopedia. Available at: https://encyclopedia.pub/entry/54624. Accessed May 19, 2024.
Meng, Weiyu, Hongxin Pan, Yuyang Sha, Xiaobing Zhai, Abao Xing, Sai Sachin Lingampelly, Srinivasa R. Sripathi, Yuefei Wang, Kefeng Li. "Role of Metabolic Connectome in Complex Diseases" Encyclopedia, https://encyclopedia.pub/entry/54624 (accessed May 19, 2024).
Meng, W., Pan, H., Sha, Y., Zhai, X., Xing, A., Lingampelly, S.S., Sripathi, S.R., Wang, Y., & Li, K. (2024, February 01). Role of Metabolic Connectome in Complex Diseases. In Encyclopedia. https://encyclopedia.pub/entry/54624
Meng, Weiyu, et al. "Role of Metabolic Connectome in Complex Diseases." Encyclopedia. Web. 01 February, 2024.
Role of Metabolic Connectome in Complex Diseases
Edit
This entry is adapted from the peer-reviewed paper 10.3390/metabo14020093

The interconnectivity of advanced biological systems is essential for their proper functioning. In modern connectomics, biological entities such as proteins, genes, RNA, DNA, and metabolites are often represented as nodes, while the physical, biochemical, or functional interactions between them are represented as edges. Among these entities, metabolites are particularly significant as they exhibit a closer relationship to an organism’s phenotype compared to genes or proteins. Moreover, the metabolome has the ability to amplify small proteomic and transcriptomic changes, even those from minor genomic changes. Metabolic networks, which consist of complex systems comprising hundreds of metabolites and their interactions, play a critical role in biological research by mediating energy conversion and chemical reactions within cells. 

metabolic connectome network models disease diagnosis drug discovery

1. Introduction

Biological networks are widely used as graphical representations to describe and analyze biological systems. In these networks, graphs are used to represent biological entities, such as proteins, genes, RNA, DNA, and metabolites, as nodes. The edges of the network correspond to the physical, biochemical, or functional interactions between these entities [1]. Through analysis of these biological networks, the interrelationships between different biological entities can be revealed, including protein–protein, protein–DNA, protein–metabolite, and other associations. This allows the networks to capture the basic characteristics of biological systems and reveal the information patterns within them [2].
In order to deeply understand and quantify the characteristics and behaviors of biological networks, researchers utilize a series of evaluation indicators (Figure 1). Indicators such as node degree, clustering coefficient, average shortest path length, and centrality are widely used to measure the degree of node connection, community structure, global connectivity, and node importance in networks [3][4]. Small-world properties describe the global structure of networks [5]. Additionally, modularity identifies functional modules and subnetworks, providing comprehensive evaluation for deeper understanding of biological system structure and function [6][7][8].
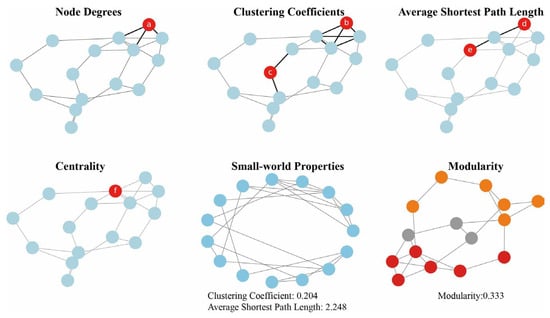
Metabolites 14 00093 g001
Figure 1. Network properties. In this example, node ‘a’ has a degree of 3. Node ‘b’ has a clustering coefficient of 1, and node ‘c’ has a clustering coefficient of 0. The average shortest path length between nodes ‘d’ and ‘e’ is two steps, passing through one intermediate node. Node ‘f’ contributes significantly to the centrality because it has a relatively large number of edges connecting it to other nodes. The small-world properties are measured by calculating the clustering coefficient and the average shortest path length. Each module in the modularity is represented by a different color.
Currently, biological networks are classified based on different features and purposes. For example, protein–protein interaction networks describe protein interactions [9], gene regulatory networks reveal complex gene expression regulation mechanisms [10], and metabolic networks graphically represent metabolic processes [11]. Brain networks describe neuron and synapse interactions [12], while social networks represent social relationships between individuals [13]. Among these, metabolic networks have high plasticity and complexity as the basis of life activities and information transmission within organisms. They are complex network structures composed of interactions among multiple biological entities [11][14]. Metabolic networks are crucial in biological research to understand the complexity of biological systems and reveal interactions and regulatory relationships among different entities.

2. Construction Methods of Metabolic Networks

Metabolic networks can be represented by various types of relationships, including statistical correlations, causal relationships, biochemical reactions, and chemical structural similarities [14][15]. Statistical correlations and causal relationships are used to describe the relationships between molecules [16][17], while biochemical reactions and chemical structural similarities describe the interactions between molecules [18][19]. By constructing networks using these different relationship types, algorithms from network theory can be applied to metabolic networks to gain a more comprehensive understanding of metabolic processes [2]. The codes for constructing metabolic networks are provided in Table 1.
Table 1. Codes for metabolic networks.
Metabolic Network Method/Model Language Source
Correlation-based Pearson correlation And Spearman rank correlation Python https://github.com/aishapectyo/Correlations-Pearson-Spearman (accessed on 28 November 2023)
Distance correlation [20] Python https://github.com/vnmabus/dcor (accessed on 28 November 2023)
Gaussian graphical model R https://github.com/donaldRwilliams/BGGM (accessed on 28 November 2023)
Causal-based Causal inference model [21] Python https://github.com/BiomedSciAI/causallib (accessed on 28 November 2023)
Structural equation model R https://github.com/yrosseel/lavaan (accessed on 28 November 2023)
Dynamic causal model Python https://github.com/tmdemelo/pydcm (accessed on 28 November 2023)
Pathway-based Pathway Python https://github.com/iseekwonderful/PyPathway (accessed on 28 November 2023)
Chemical structure similarity-based Chemical structure similarity Python https://github.com/labsyspharm/lsp-cheminformatics (accessed on 28 November 2023)

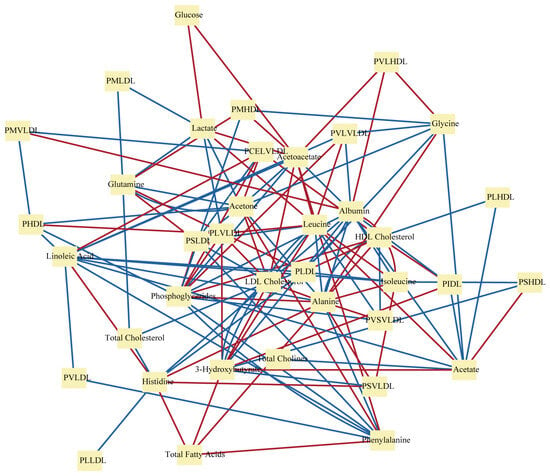
2.1. Correlation-Based Metabolic Network

Correlation-based metabolic networks are widely used in metabolic research. These networks use the correlations among metabolites to establish connectivity relationships, simplifying multidimensional data while preserving most interpretive information (Figure 2) [22]. This method reveals coordinated behaviors between biological components and allows an analysis of network properties to better understand metabolite interactions and identify key metabolites in pathways [23][24]. Furthermore, correlation-based networks can also be applied to study metabolic disease pathogenesis and discover new treatments [22][25].
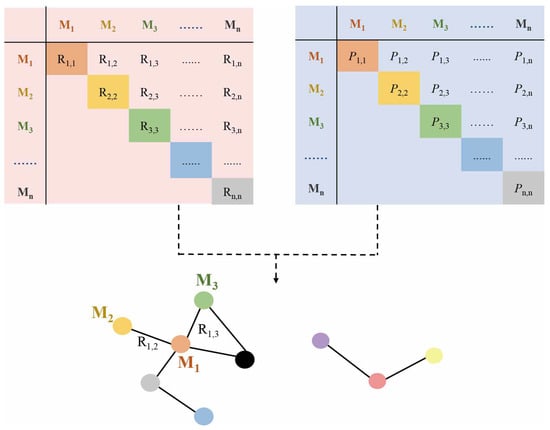
Metabolites 14 00093 g002
Figure 2. Creating metabolic network based on correlation analysis. Correlation-based metabolic networks use correlations among metabolites to establish connectivity relationships and simplify multidimensional data. R: correlation value; P: p-value; M: metabolite.
In a correlation network, the correlation value ranges from −1 to 1, with 1 representing a positive correlation, −1 representing a negative correlation, and 0 representing no linear correlation. The closer the correlation coefficient is to −1 or 1, the stronger the correlation, while values closer to 0 indicate a weak or no linear relationship. If the correlation value of two metabolites reaches a set threshold, a connection is established between them [26]. Methods to calculate metabolite correlations include Pearson correlation, Spearman rank correlation, distance correlation, and Gaussian graphical models [27][28][29]. Pearson correlation measures linear relationships, while Spearman rank and distance correlations assess monotonic relationships [27][29][30]. The Pearson correlation coefficients are obtained by calculating the covariance between variables divided by their standard deviations. The Spearman rank correlation coefficient sorts the values of the variables, then calculates the rank difference after sorting, and obtains it by dividing the covariance of the rank difference by the standard deviation. The distance correlation is obtained by calculating the distance covariance among variables divided by their respective standard deviations. 
However, due to the stringent metabolic control and extended reaction sequences present in metabolic networks, the use of Pearson correlation and Spearman rank correlation often results in highly interconnected and dense networks, complicating network analysis and interpretation [14]. Gaussian graphical models calculate partial instead of total correlations, correcting indirect effects to better reveal correlations in complex metabolism [31][32]. Importantly, observed correlations may be due to common influencing factors and do not necessarily represent direct causal relationships.

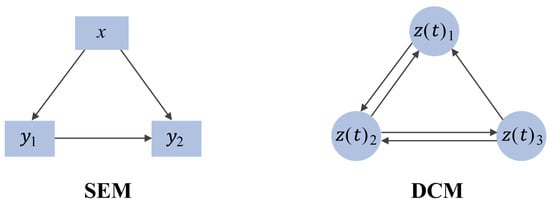
2.2. Causal-Based Metabolic Network

Causal relationship-based metabolic networks are complex biological networks that help us to understand the operating mechanisms of biological systems by revealing the interactions and effects between metabolites. Causal networks are graph models representing causal relationships, comprising variables and the causal relationships between them. The objective in constructing a causal network is to infer causal relationships between variables from observational data to better understand and predict system behavior [33][34]. The network consists of nodes, representing variables like genes, metabolites, and biological processes, and edges, representing causal relationships between variables that can be direct or indirect. A key feature of causal networks is discoverability, making them suitable for processing large-scale data with a limited understanding of interconnectivity [15].
Statistical methods using causal inference and discovery techniques are widely used in constructing causal networks to detect causal relationships between variables [35]. The causal inference model is a statistical framework used to infer causal relationships through observational data. This model applies statistical and causal inference principles, analyzing correlation, causal direction, and mechanisms to infer causal relationships [36].
In addition, structural equation modeling (SEM) and dynamic causal modeling (DCM) are also methods for causal inference (Figure 3) [35][37][38]. SEM is a multivariate statistical model that infers causal relationships among variables by modeling the relationship between observed variables and latent constructs, based on the covariance or correlation coefficient matrix [37][39]. Variables are manifest or latent. Manifest variables are directly measurable, while latent are indirect [40][41]. SEM can analyze direct and indirect effects among multiple variables, as well as relationships between variables and latent constructs [42][43].
Metabolites 14 00093 g003
Figure 3. Structural equation model (SEM) and dynamic causal model (DCM). Among them, 𝑥 represents the independent variable, 𝑦 represents the dependent variables, and 𝑧(𝑡) represents the concentration of metabolites at time t.

2.3. Pathway-Based Metabolic Network

Pathway-based metabolic networks describe the interactions between biochemical reactions. These enzymatic reactions form the foundation of metabolic reactions within organisms, facilitating the synthesis, decomposition, and transformation of metabolites. Metabolites, including proteins, nucleic acids, sugars, lipids, and more, are chemical substances present within an organism. The complex metabolic network is formed by the biochemical reactions between these metabolites, interacting to maintain normal life functions (Figure 4) [44]. To better understand and utilize metabolic networks, it is necessary to select appropriate databases for data, prune networks for analysis, use algorithms to identify pathways, and develop computational methods to optimize pathways.
Metabolites 14 00093 g004
Figure 4. The metabolic network linking metabolic pathways and metabolites. Among them, blue represents negative correlation, and red represents positive correlation.
In designing metabolic pathways, database representation methods are used to describe the relationships between chemical reactions and metabolites. The two common methods are graph and stoichiometric matrix representations. Graph representations show topological connectivity using nodes for metabolites and edges for reactions. This visual representation intuitively displays topological and pathway structure, aiding understanding and analyzing pathway composition and function. Common graph-based databases include KEGG [45] and MetaCyc [46]. Stoichiometric matrices numerically describe quantitative stoichiometries between reactions and metabolites in rows and columns. This provides comprehensive quantitative information about their design, including reaction directionality, rates, and metabolite proportions. Common matrix-based databases include BiGG [47] and ModelSEED [48].
Network pruning is a commonly used technique to simplify complex metabolic networks during pathway design. This technique reduces complexity by removing irrelevant reactions or metabolites, thereby improving computational efficiency and design accuracy [49]. The goal is to remove components that do not significantly impact overall pathway performance, reducing computational and optimization complexity.

2.4. Metabolic Network Based on Chemical Structure Similarity

Chemical structural similarity is a method of comparing and matching chemical molecules based on their structural characteristics. By comparing the structural features among compounds, the degree of similarity between them can be measured [50]. Metabolites with high similarity are often linked together, indicating that they may participate in similar metabolic reactions or pathways. The chemical and structural similarities among metabolites can then be converted into edges in the network to construct a metabolic network that reflects these similarity relationships (Figure 5) [51]. This network can reveal collections of metabolites with similar chemical structures, elucidating their functions and interactions in metabolic pathways.
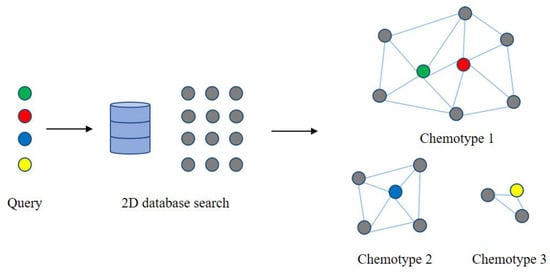
Metabolites 14 00093 g005
Figure 5. Chemical similarity networks. The reference compounds are identified from the bioactivity database using 2D similarity fingerprints of the query ligands. Then, the identified compounds are further clustered into chemical similarity subnetworks based on representative chemotypes. Among them, the colored nodes represent query ligands, and the gray nodes represent reference compounds.
Chemical structure descriptors play a key role in constructing metabolic networks. Chemical structure descriptors are numerical representation methods used to describe the structural characteristics of compounds [52]. Commonly used chemical structure descriptors include 2D and 3D chemical fingerprints [53]. Two-dimensional chemical fingerprints are feature vectors generated based on the 2D structural information of compounds, incorporating characteristics of compound connectivity, atomic type, and ring structure. These can be used to calculate the similarity among compounds and screen chemical libraries [54]. The Tanimoto index calculates shared features between 2D fingerprints to quantify similarity on a 0 to 1 scale, where values nearer 1 indicate higher similarity [54][55].
Three-dimensional chemical fingerprints are feature vectors generated based on the three-dimensional structural information of compounds, taking into account conformations, shape, charge distribution, and other 3D characteristics By calculating the 3D chemical fingerprint similarities among compounds, their structural similarity can be evaluated [56]. Euclidean distance evaluates the differences between 3D fingerprint vectors and is used to assess structural similarity, where less distance means more similarity [57].

3. Application of Metabolic Network

Metabolites are more closely related to an organism’s phenotype than genes and proteins. Moreover, the metabolome serves to amplify potentially immeasurably small changes in the proteome and transcriptome, even those derived from minor changes in the genome. The health and disease states of the body can be more meaningfully characterized by the metabolic state of the human cells, tissues, organs, and the organism as a whole [58]. Abnormal metabolism either causes or results from complex diseases like hypertension, diabetes, cancer, and heart disease. Thus, adequately understanding human metabolism and metabolic interactions is a necessary step towards efficiently treating and diagnosing these complex diseases. However, metabolism involves countless individual reactions that are highly interconnected through shared metabolites [59]. Developing and applying metabolic networks plays a significant role in medical research, especially in elucidating disease pathogenesis, prediction, diagnosis, and drug discovery.
A metabolic network is a complex system of hundreds of metabolites and their interactions involved in energy conversion and chemical reactions within cells [60]. Exploring the function and structure of metabolic networks can provide insight into metabolic abnormalities and signaling transduction disorders in disease, and further revealing the strong link between disease and metabolism [61]. Systems biology and computational biology approaches are used to construct and model metabolic networks in analyzing them [62][63]. This elucidates pathway and interaction complexity, regulatory mechanisms between metabolites, and the rapid spread of single-node perturbations across the tightly regulated, simultaneous network [64][65].

3.1. Metabolic Networks in Disease Mechanisms

Firstly, a strategy to compare metabolic networks in disease states and normal states followed by identifying changes in disease-related metabolic pathways is an essential way for discovering and confirming disease-specific metabolic abnormalities. These changes may include the depletion or accumulation of metabolites, alterations in enzyme activity, and the remodeling of metabolic pathways. Gaining a deeper understanding of these abnormalities can shed light on the pathogenesis of the disease.
Metabolic networks represent cellular metabolism through lists of reactions occurring in cells [66]. These reactions have been associated with particular cellular compartments and further grouped into pathways. Certain metabolic pathways may play crucial roles in particular diseases or physiological states, and regulating metabolic pathways is essential for maintaining normal physiological states [67]. Metabolic networks integrate metabolomics and pathway databases. Network topology and metabolite flow analysis identify pathways and regulation implicated in pathogenesis, such as abnormal glycolytic pathways in tumor cells [68][69]. 
Moreover, metabolites can be passed between compartments (e.g., mitochondria or cytoplasm) through transport reactions, thereby acting as signaling molecules involved in regulating pathological and physiological processes in cells [70]. The close interaction between metabolic networks and signal transduction networks can help reveal how metabolic abnormalities affect signal transduction and further understand the pathogenesis of diseases [71].
Metabolic network analysis also provides a considerable tool for personalized medicine. By integrating clinical, genomic, and network data, one can predict drug responses and guide individualized treatment. This improves effectiveness and reduces side effects. Type 2 diabetes mellitus (T2DM) is recognized as one of the main threats to human health in the 21st century, emerging as a complex metabolic disease [72][73][74].
The establishment and simulation of a metabolic network model can be beneficial to understand the pathogenesis of diseases. Multi-omics data integration has built dynamic models simulating pathway and metabolite changes in disease [75]. These models may predict disease progression, assess therapeutic efficacy, and further inform drug development. 

3.2. Metabolic Networks in Disease Prediction and Diagnosis

Metabolic networks have great potential in disease prediction and diagnosis. Metabolic network analysis can identify changes in metabolite concentrations, metabolic pathways, or metabolic enzymes that are associated with specific diseases. Biomarkers refer to biochemical indicators, which can signify possible changes in the function or structure of cells, tissues, organs, and systems. They are discriminant features related to the onset and progression of disease [76]. Metabolites have long been used as biomarkers in blood or urine to diagnose disease. Metabolic biomarkers refer to metabolites or combinations of metabolites associated with a particular disease. By comparing the metabolic profiles of diseased and healthy groups, metabolite pairs that change during disease onset and progression can be identified. These can elucidate pathogenesis and serve as early diagnosis biomarkers or for evaluating treatment efficacy [77].
Chang et al. [76] constructed sex-specific and apolipoprotein E (APOE)-specific metabolic networks. They proposed patient-specific biomarkers predictive of disease state and significantly associated with cognitive function. Based on computational network modeling, they integrated cognitive assessments and metabolomic profiling to confirm targeted precision therapeutics for Alzheimer’s disease (AD) patient subgroups. Recently, a bi-random walks method predicted disease–metabolite associations by executing the algorithm on reconstructed networks [78].
Furthermore, metabolic network analysis can predict disease progression. By analyzing dynamic changes in metabolic network models, researchers can simulate disease progression and predict the progression rate and possible outcomes [79]. This elucidates disease occurrence mechanisms and provides important guidance for disease treatment and intervention.
Metabolic network analysis plays an important role in cancer research. Tumors reprogram biochemical pathways to promote unregulated cell growth and survival [80]. Metabolic network facilitates the discovery of specific metabolic dependencies that arise in cancers [81]. The complex interrelationships between oncogenes, gene expression, and metabolism offer the potential to discover novel biomarkers and drug targets with therapeutic and prognostic value.

3.3. Drug Discovery and Disease Treatment

In addition, metabolic network analysis has become an invaluable tool for drug discovery and development. Studying metabolic networks allows researchers to predict a drug’s mechanism of action and metabolic fate [82]. Advances in systems biology enable the prediction of functional effects of system perturbations using large-scale network models. The topological features of metabolic networks confer flexibility and robustness to complex biosystems. And in general, they may explain why many drug candidates are ineffective and why unexpected severe side effects happen [83]. Understanding these network properties is essential for rational drug design to improve efficacy and reduce adverse effects. Metabolic network models have been applied to simulate drug treatment and predict side effects.
Another advantage of metabolic network analysis is the ability to narrow down putative drug targets for in vitro validation, reducing reliance on expensive and time-consuming experimental approaches [84]. By analyzing crucial nodes and regulatory pathways in metabolic networks, key molecules in disease processes can be identified as potential therapeutic targets or lead compounds. These may include important metabolic regulators, bottleneck enzymes, and transporters, or disease-associated metabolites. Recent years, modeling cancer metabolism has been widely used in metabolic networks [85]. Tissue-specific and generic models have allowed prediction of drug targets in cancers [86][87]. Comparing healthy metabolic networks and cancer networks reveal cancer-specific features which could be potential pan-cancer targets [88]. 

4. Conclusions

In summary, further advancement in metabolic network analysis will require a multifaceted research effort. As technology continues to progress and in-depth studies elucidate the complexities of metabolic systems, metabolic network models can be expected to improve dramatically. Ongoing refinements in areas such as individualized network construction, the integration of diverse omics data, and the elucidation of shared network dysregulation among diseases will ultimately enhance the utility of metabolic networks across a wide range of biomedical applications. The future is promising for metabolic network analysis to fulfill its potential in accelerating disease prediction, diagnosis, prognosis, and precise treatment.

References

  1. Assenov, Y.; Ramirez, F.; Schelhorn, S.E.; Lengauer, T.; Albrecht, M. Computing topological parameters of biological networks. Bioinformatics 2008, 24, 282–284.
  2. Muzio, G.; O’Bray, L.; Borgwardt, K. Biological network analysis with deep learning. Brief. Bioinform. 2021, 22, 1515–1530.
  3. Klein, C.; Marino, A.; Sagot, M.F.; Vieira Milreu, P.; Brilli, M. Structural and dynamical analysis of biological networks. Brief. Funct. Genom. 2012, 11, 420–433.
  4. Mengiste, S.A.; Aertsen, A.; Kumar, A. Relevance of network topology for the dynamics of biological neuronal networks. bioRxiv 2021.
  5. May, R.M. Network structure and the biology of populations. Trends Ecol. Evol. 2006, 21, 394–399.
  6. Melo, D.; Porto, A.; Cheverud, J.M.; Marroig, G. Modularity: Genes, development and evolution. Annu. Rev. Ecol. Evol. Syst. 2016, 47, 463–486.
  7. Lorenz, D.M.; Jeng, A.; Deem, M.W. The emergence of modularity in biological systems. Phys. Life Rev. 2011, 8, 129–160.
  8. Lee, U.; Mashour, G.A. Role of Network Science in the Study of Anesthetic State Transitions. Anesthesiology 2018, 129, 1029–1044.
  9. De Las Rivas, J.; Fontanillo, C. Protein-protein interactions essentials: Key concepts to building and analyzing interactome networks. PLoS Comput. Biol. 2010, 6, e1000807.
  10. Wu, M.; Su, R.Q.; Li, X.; Ellis, T.; Lai, Y.C.; Wang, X. Engineering of regulated stochastic cell fate determination. Proc. Natl. Acad. Sci. USA 2013, 110, 10610–10615.
  11. Folger, O.; Jerby, L.; Frezza, C.; Gottlieb, E.; Ruppin, E.; Shlomi, T. Predicting selective drug targets in cancer through metabolic networks. Mol. Syst. Biol. 2011, 7, 501.
  12. Park, H.J.; Friston, K. Structural and functional brain networks: From connections to cognition. Science 2013, 342, 1238411.
  13. Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826.
  14. Amara, A.; Frainay, C.; Jourdan, F.; Naake, T.; Neumann, S.; Novoa-Del-Toro, E.M.; Salek, R.M.; Salzer, L.; Scharfenberg, S.; Witting, M. Networks and Graphs Discovery in Metabolomics Data Analysis and Interpretation. Front. Mol. Biosci. 2022, 9, 841373.
  15. Yazdani, A.; Yazdani, A.; Mendez-Giraldez, R.; Samiei, A.; Kosorok, M.R.; Schaid, D.J. From classical mendelian randomization to causal networks for systematic integration of multi-omics. Front. Genet. 2022, 13, 990486.
  16. Ness, R.O.; Sachs, K.; Vitek, O. From Correlation to Causality: Statistical Approaches to Learning Regulatory Relationships in Large-Scale Biomolecular Investigations. J. Proteome Res. 2016, 15, 683–690.
  17. Rohrer, J.M. Thinking Clearly About Correlations and Causation: Graphical Causal Models for Observational Data. Adv. Methods Pract. Psychol. Sci. 2018, 1, 27–42.
  18. Hattori, M.; Okuno, Y.; Goto, S.; Kanehisa, M. Development of a chemical structure comparison method for integrated analysis of chemical and genomic information in the metabolic pathways. J. Am. Chem. Soc. 2003, 125, 11853–11865.
  19. Holliday, G.L.; Andreini, C.; Fischer, J.D.; Rahman, S.A.; Almonacid, D.E.; Williams, S.T.; Pearson, W.R. MACiE: Exploring the diversity of biochemical reactions. Nucleic Acids Res. 2012, 40, D783–D789.
  20. Ramos-Carreño, C.; Torrecilla, J.L. dcor: Distance correlation and energy statistics in Python. SoftwareX 2023, 22, 101326.
  21. Shimoni, Y.; Karavani, E.; Ravid, S.; Bak, P.; Ng, T.H.M.; Alford, S.H.; Meade, D.; Goldschmidt, Y. An Evaluation Toolkit to Guide Model Selection and Cohort Definition in Causal Inference. arXiv 2019, arXiv:1906.00442.
  22. Batushansky, A.; Toubiana, D.; Fait, A. Correlation-Based Network Generation, Visualization, and Analysis as a Powerful Tool in Biological Studies: A Case Study in Cancer Cell Metabolism. Biomed. Res. Int. 2016, 2016, 8313272.
  23. Nishihara, R.; Glass, K.; Mima, K.; Hamada, T.; Nowak, J.A.; Qian, Z.R.; Kraft, P.; Giovannucci, E.L.; Fuchs, C.S.; Chan, A.T.; et al. Biomarker correlation network in colorectal carcinoma by tumor anatomic location. BMC Bioinform. 2017, 18, 304.
  24. Kotze, H.L.; Armitage, E.G.; Sharkey, K.J.; Allwood, J.W.; Dunn, W.B.; Williams, K.J.; Goodacre, R. A novel untargeted metabolomics correlation-based network analysis incorporating human metabolic reconstructions. BMC Syst. Biol. 2013, 7, 107.
  25. Chen, P.Y.; Cripps, A.W.; West, N.P.; Cox, A.J.; Zhang, P. A correlation-based network for biomarker discovery in obesity with metabolic syndrome. BMC Bioinform. 2019, 20, 477.
  26. Jahagirdar, S.; Suarez-Diez, M.; Saccenti, E. Simulation and Reconstruction of Metabolite-Metabolite Association Networks Using a Metabolic Dynamic Model and Correlation Based Algorithms. J. Proteome Res. 2019, 18, 1099–1113.
  27. de Siqueira Santos, S.; Takahashi, D.Y.; Nakata, A.; Fujita, A. A comparative study of statistical methods used to identify dependencies between gene expression signals. Brief. Bioinform. 2014, 15, 906–918.
  28. Aguilera-Mendoza, L.; Marrero-Ponce, Y.; Garcia-Jacas, C.R.; Chavez, E.; Beltran, J.A.; Guillen-Ramirez, H.A.; Brizuela, C.A. Automatic construction of molecular similarity networks for visual graph mining in chemical space of bioactive peptides: An unsupervised learning approach. Sci. Rep. 2020, 10, 18074.
  29. Kumari, S.; Nie, J.; Chen, H.S.; Ma, H.; Stewart, R.; Li, X.; Lu, M.Z.; Taylor, W.M.; Wei, H. Evaluation of gene association methods for coexpression network construction and biological knowledge discovery. PLoS ONE 2012, 7, e50411.
  30. Allen, E.; Moing, A.; Ebbels, T.M.; Maucourt, M.; Tomos, A.D.; Rolin, D.; Hooks, M.A. Correlation Network Analysis reveals a sequential reorganization of metabolic and transcriptional states during germination and gene-metabolite relationships in developing seedlings of Arabidopsis. BMC Syst. Biol. 2010, 4, 62.
  31. Dyrba, M.; Mohammadi, R.; Grothe, M.J.; Kirste, T.; Teipel, S.J. Gaussian Graphical Models Reveal Inter-Modal and Inter-Regional Conditional Dependencies of Brain Alterations in Alzheimer’s Disease. Front. Aging Neurosci. 2020, 12, 99.
  32. Krumsiek, J.; Suhre, K.; Illig, T.; Adamski, J.; Theis, F.J. Gaussian graphical modeling reconstructs pathway reactions from high-throughput metabolomics data. BMC Syst. Biol. 2011, 5, 21.
  33. Hackett, S.R.; Baltz, E.A.; Coram, M.; Wranik, B.J.; Kim, G.; Baker, A.; Fan, M.; Hendrickson, D.G.; Berndl, M.; McIsaac, R.S. Learning causal networks using inducible transcription factors and transcriptome-wide time series. Mol. Syst. Biol. 2020, 16, e9174.
  34. Perfetto, L.; Briganti, L.; Calderone, A.; Perpetuini, A.C.; Lannuccelli, M.; Langone, F.; Licata, L.; Marinkovic, M.; Mattioni, A.; Pavlidou, T.; et al. SIGNOR: A database of causal relationships between biological entities. Nucleic Acids Res. 2016, 44, D548–D554.
  35. Yao, L.Y.; Chu, Z.X.; Li, S.; Li, Y.L.; Gao, J.; Zhang, A.D. A Survey on Causal Inference. ACM Trans. Knowl. Discov. Data 2021, 15, 74.
  36. Nogueira, A.R.; Pugnana, A.; Ruggieri, S.; Pedreschi, D.; Gama, J. Methods and tools for causal discovery and causal inference. Wiley Interdiscip. Rev.-Data Min. Knowl. Discov. 2022, 12, e1449.
  37. Rosa, G.J.; Valente, B.D.; de los Campos, G.; Wu, X.L.; Gianola, D.; Silva, M.A. Inferring causal phenotype networks using structural equation models. Genet. Sel. Evol. 2011, 43, 6.
  38. Friston, K. Dynamic causal modeling and Granger causality Comments on: The identification of interacting networks in the brain using fMRI: Model selection, causality and deconvolution. Neuroimage 2011, 58, 303–305, author reply 310–311.
  39. Peters, J.; Janzing, D.; Schölkopf, B. Causal inference on time series using restricted structural equation models. Adv. Neural Inf. Process. Syst. 2013, 26, 154–162.
  40. Rose, N.; Wagner, W.; Mayer, A.; Nagengast, B. Model-Based Manifest and Latent Composite Scores in Structural Equation Models. Collabra Psychol. 2019, 5, 9.
  41. Bollen, K.A.; Hoyle, R.H. Latent variables in structural equation modeling. In Handbook of Structural Equation Modeling; Hoyle, R.H., Ed.; Guilford Press: New York, NY, USA, 2012; pp. 56–67.
  42. Yuan, K.-H.; Kouros, C.D.; Kelley, K. Diagnosis for covariance structure models by analyzing the path. Struct. Equ. Model. A Multidiscip. J. 2008, 15, 564–602.
  43. Friston, K.J. Functional and effective connectivity: A review. Brain Connect. 2011, 1, 13–36.
  44. Wang, J.; Sun, Y.; Teng, S.; Li, K. Prediction of sepsis mortality using metabolite biomarkers in the blood: A meta-analysis of death-related pathways and prospective validation. BMC Med. 2020, 18, 83.
  45. Kanehisa, M.; Furumichi, M.; Tanabe, M.; Sato, Y.; Morishima, K. KEGG: New perspectives on genomes, pathways, diseases and drugs. Nucleic Acids Res. 2017, 45, D353–D361.
  46. Caspi, R.; Billington, R.; Ferrer, L.; Foerster, H.; Fulcher, C.A.; Keseler, I.M.; Kothari, A.; Krummenacker, M.; Latendresse, M.; Mueller, L.A.; et al. The MetaCyc database of metabolic pathways and enzymes and the BioCyc collection of pathway/genome databases. Nucleic Acids Res. 2016, 44, D471–D480.
  47. King, Z.A.; Lu, J.; Drager, A.; Miller, P.; Federowicz, S.; Lerman, J.A.; Ebrahim, A.; Palsson, B.O.; Lewis, N.E. BiGG Models: A platform for integrating, standardizing and sharing genome-scale models. Nucleic Acids Res. 2016, 44, D515–D522.
  48. Henry, C.S.; DeJongh, M.; Best, A.A.; Frybarger, P.M.; Linsay, B.; Stevens, R.L. High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat. Biotechnol. 2010, 28, 977–982.
  49. Wang, L.; Dash, S.; Ng, C.Y.; Maranas, C.D. A review of computational tools for design and reconstruction of metabolic pathways. Synth. Syst. Biotechnol. 2017, 2, 243–252.
  50. Yamanishi, Y.; Araki, M.; Gutteridge, A.; Honda, W.; Kanehisa, M. Prediction of drug-target interaction networks from the integration of chemical and genomic spaces. Bioinformatics 2008, 24, i232–i240.
  51. Lo, Y.-C.; Torres, J.Z. Chemical similarity networks for drug discovery. Spec. Top. Drug Discov. 2016, 1, 53–70.
  52. Wale, N.; Watson, I.A.; Karypis, G. Comparison of descriptor spaces for chemical compound retrieval and classification. Knowl. Inf. Syst. 2008, 14, 347–375.
  53. Hu, G.; Kuang, G.; Xiao, W.; Li, W.; Liu, G.; Tang, Y. Performance evaluation of 2D fingerprint and 3D shape similarity methods in virtual screening. J. Chem. Inf. Model. 2012, 52, 1103–1113.
  54. Willett, P. Similarity searching using 2D structural fingerprints. Methods Mol. Biol. 2011, 672, 133–158.
  55. Bajusz, D.; Rácz, A.; Héberger, K. Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations? J. Cheminformatics 2015, 7, 20.
  56. Lo, Y.C.; Rensi, S.E.; Torng, W.; Altman, R.B. Machine learning in chemoinformatics and drug discovery. Drug Discov. Today 2018, 23, 1538–1546.
  57. Willett, P. Similarity-based data mining in files of two-dimensional chemical structures using fingerprint measures of molecular resemblance. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 241–251.
  58. Ma, H.; Goryanin, I. Human metabolic network reconstruction and its impact on drug discovery and development. Drug Discov. Today 2008, 13, 402–408.
  59. Li, K.; Bertrand, K.; Naviaux, J.C.; Monk, J.M.; Wells, A.; Wang, L.; Lingampelly, S.S.; Naviaux, R.K.; Chambers, C. Metabolomic and exposomic biomarkers of risk of future neurodevelopmental delay in human milk. Pediatr. Res. 2023, 93, 1710–1720.
  60. Judge, A.; Dodd, M.S. Metabolism. Essays Biochem. 2020, 64, 607–647.
  61. Dräger, A.; Planatscher, H. Metabolic Networks. In Encyclopedia of Systems Biology; Dubitzky, W., Wolkenhauer, O., Cho, K.-H., Yokota, H., Eds.; Springer: New York, NY, USA, 2013; pp. 1249–1251.
  62. Waller, T.C.; Berg, J.A.; Lex, A.; Chapman, B.E.; Rutter, J. Compartment and hub definitions tune metabolic networks for metabolomic interpretations. GigaScience 2020, 9, giz137.
  63. Theorell, A.; Stelling, J. Metabolic networks, microbial consortia, and analogies to smart grids. Proc. IEEE 2022, 110, 541–556.
  64. Burke, P.E.P.; Campos, C.B.L.; Costa, L.D.F.; Quiles, M.G. A biochemical network modeling of a whole-cell. Sci. Rep. 2020, 10, 13303.
  65. Frainay, C.; Jourdan, F. Computational methods to identify metabolic sub-networks based on metabolomic profiles. Brief. Bioinform. 2017, 18, 43–56.
  66. Väremo, L.; Nookaew, I.; Nielsen, J. Novel insights into obesity and diabetes through genome-scale metabolic modeling. Front. Physiol. 2013, 4, 92.
  67. Faust, K.; Croes, D.; van Helden, J. Prediction of metabolic pathways from genome-scale metabolic networks. Biosystems 2011, 105, 109–121.
  68. Hecht, F. On the origins of cancer genetics and cytogenetics. Cancer Genet. Cytogenet. 1987, 29, 187–190.
  69. Bintener, T.; Pacheco, M.P.; Sauter, T. Towards the routine use of in silico screenings for drug discovery using metabolic modelling. Biochem. Soc. Trans. 2020, 48, 955–969.
  70. Beguerisse-Díaz, M.; Bosque, G.; Oyarzún, D.; Picó, J.; Barahona, M. Flux-dependent graphs for metabolic networks. NPJ Syst. Biol. Appl. 2018, 4, 32.
  71. Tomar, N.; De, R.K. Comparing methods for metabolic network analysis and an application to metabolic engineering. Gene 2013, 521, 1–14.
  72. Zelezniak, A.; Pers, T.H.; Soares, S.; Patti, M.E.; Patil, K.R. Metabolic network topology reveals transcriptional regulatory signatures of type 2 diabetes. PLoS Comput. Biol. 2010, 6, e1000729.
  73. Zimmet, P.; Alberti, K.G.; Shaw, J. Global and societal implications of the diabetes epidemic. Nature 2001, 414, 782–787.
  74. Hameed, I.; Masoodi, S.R.; Mir, S.A.; Nabi, M.; Ghazanfar, K.; Ganai, B.A. Type 2 diabetes mellitus: From a metabolic disorder to an inflammatory condition. World J. Diabetes 2015, 6, 598–612.
  75. Lee, M.H.; Hwang, Y.H.; Yun, C.S.; Han, B.S.; Kim, D.Y. Altered small-world property of a dynamic metabolic network in murine left hippocampus after exposure to acute stress. Sci. Rep. 2022, 12, 3885.
  76. Wei, P.J.; Ma, W.; Li, Y.; Su, Y. Disease biomarker identification based on sample network optimization. Methods 2023, 213, 42–49.
  77. Hu, Y.; Zhao, T.; Zhang, N.; Zang, T.; Zhang, J.; Cheng, L. Identifying diseases-related metabolites using random walk. BMC Bioinform. 2018, 19, 116.
  78. Lei, X.; Tie, J. Prediction of disease-related metabolites using bi-random walks. PLoS ONE 2019, 14, e0225380.
  79. Baumgartner, C.; Spath-Blass, V.; Niederkofler, V.; Bergmoser, K.; Langthaler, S.; Lassnig, A.; Rienmüller, T.; Baumgartner, D.; Asnani, A.; Gerszten, R.E. A novel network-based approach for discovering dynamic metabolic biomarkers in cardiovascular disease. PLoS ONE 2018, 13, e0208953.
  80. Kerk, S.A.; Papagiannakopoulos, T.; Shah, Y.M.; Lyssiotis, C.A. Metabolic networks in mutant KRAS-driven tumours: Tissue specificities and the microenvironment. Nat. Rev. Cancer 2021, 21, 510–525.
  81. Hiller, K.; Metallo, C.M. Profiling metabolic networks to study cancer metabolism. Curr. Opin. Biotechnol. 2013, 24, 60–68.
  82. Kell, D.B.; Goodacre, R. Metabolomics and systems pharmacology: Why and how to model the human metabolic network for drug discovery. Drug Discov. Today 2014, 19, 171–182.
  83. Shaked, I.; Oberhardt, M.A.; Atias, N.; Sharan, R.; Ruppin, E. Metabolic Network Prediction of Drug Side Effects. Cell Syst. 2016, 2, 209–213.
  84. Karta, J.; Bossicard, Y.; Kotzamanis, K.; Dolznig, H.; Letellier, E. Mapping the Metabolic Networks of Tumor Cells and Cancer-Associated Fibroblasts. Cells 2021, 10, 304.
  85. Fouladiha, H.; Marashi, S.A. Biomedical applications of cell- and tissue-specific metabolic network models. J. Biomed. Inform. 2017, 68, 35–49.
  86. Lewis, N.E.; Abdel-Haleem, A.M. The evolution of genome-scale models of cancer metabolism. Front. Physiol. 2013, 4, 237.
  87. Di Filippo, M.; Colombo, R.; Damiani, C.; Pescini, D.; Gaglio, D.; Vanoni, M.; Alberghina, L.; Mauri, G. Zooming-in on cancer metabolic rewiring with tissue specific constraint-based models. Comput. Biol. Chem. 2016, 62, 60–69.
  88. Agren, R.; Bordel, S.; Mardinoglu, A.; Pornputtapong, N.; Nookaew, I.; Nielsen, J. Reconstruction of genome-scale active metabolic networks for 69 human cell types and 16 cancer types using INIT. PLoS Comput. Biol. 2012, 8, e1002518.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Medical Informatics
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Weiyu Meng
,
Hongxin Pan
,
Yuyang Sha
,
Xiaobing Zhai
,
Abao Xing
,
Sai Sachin Lingampelly
,
Srinivasa R. Sripathi
,
Yuefei Wang
,
Kefeng Li
View Times: 128
Revisions: 2 times (View History)
Update Date: 02 Feb 2024
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback