
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Yuehai Zhou | -- | 4786 | 2023-12-19 08:54:46 | | | |
| 2 | Sirius Huang | -4 word(s) | 4782 | 2023-12-21 09:14:34 | | |
Video Upload Options
Due to the simultaneous existence of severe difficulties caused by multi-path, Doppler, and environmental noise caused by underwater acoustic channels, designing a stable and reliable underwater acoustic communication system (UWACS) is a challenging task. In addition to channel estimation and equalization, the technique of channel codes, which is capable of approaching Shannon’s capacity at a low encoding and decoding complexity, offers an efficient and reliable solution to improve the performance of the UWACS and thus draws extensive attention from the research community.
1. Introduction
2. BCH and RS Codes
are encoded into a code word of length 𝑁 with a polynomial in the Galois field. The specific relationship can be expressed as:
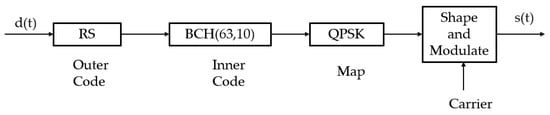
where the positive integers 𝑚≥3, 𝑡<2𝑚−1, and 𝑡 denote the number of codewords that can be corrected. It generally employs the bounded distance Berlekamp decoding algorithm. Due to the coding and decoding algorithm’s low complexity and the maximum–minimum distance property to avoid its error leveling problem at low error bit rates, it can be employed in systems with limited power consumption. In 1993, Widmer et al. [2] used a BCH-coded UWACS with 28 check bits added to the message bits to offer extremely reliable communications with an error bit rate of 0.013% in deep water, shallow water, convergence zones, and surface pipeline environments. This guided further development of the system’s error correction capabilities based on BCH codes. In 1999, LR LeBlanc [3] proposed a BCH-coded chirp frequency-shift keying (CFSK) modem for shallow sea UWAC, with BERs of 7×10−3 and 2×10−2 at about a 90 m communication distance and SNR of 46 dB and 44 dB, respectively, the feasibility of the BCH code in implementing the UWAC hardware system was verified. In 2001, Stojanovic M et al. [4] employed BCH (63, 10) as an inner code for concatenated RS-BCH-coded multiuser UWAC, as illustrated in Figure 1. The excellent performance of the four mobile users transmitting in severely reverberant environments with a bandwidth expansion factor of seven was verified.
3. Convolutional Codes

4. Turbo Codes
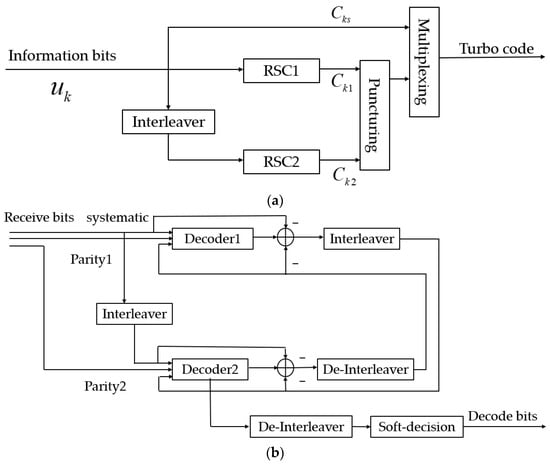
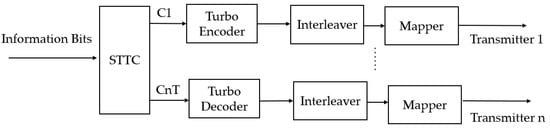
where 𝑢˜𝑘 is the decoded bit, and 𝐿𝑎(𝑢˜𝑘) is its log likelihood ratio; the soft decision decoded output is the basis of the iterative equalization for the UWAC receiver. In 2001, Proakis J G. et al. proposed a turbo-coded DFE modem. They demonstrated that the joint decision feedback equalization and turbo decoding are more robust than the turbo equalizer in an UWA sparse channel scenario, thus verifying the feasibility of the turbo code in an UWACS [38]. In 2005, Huang J et al. employed a coded OFDM system with a 1/2 code rate turbo code, which achieved data rates of 9 kbps and 2.8 kbps with BERs lower than 10−4 at distances of 5 km and 10 km, respectively [39]. As shown in Figure 7, in 2007, Roy S et al. proposed layered space–time coding with a wide range code rates of turbo codes, achieving very high spectral efficiencies in a system with many transmit antennas [40].
5. LDPC Codes
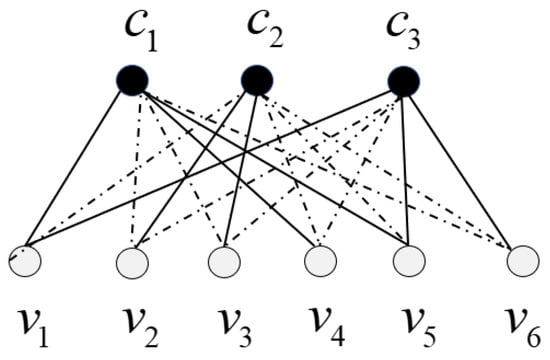
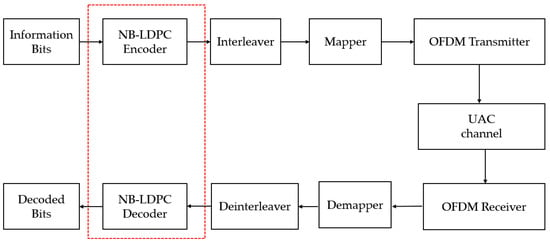
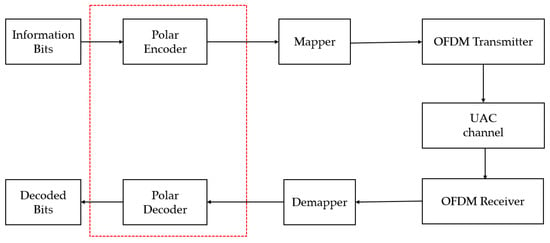
6. Polar Codes
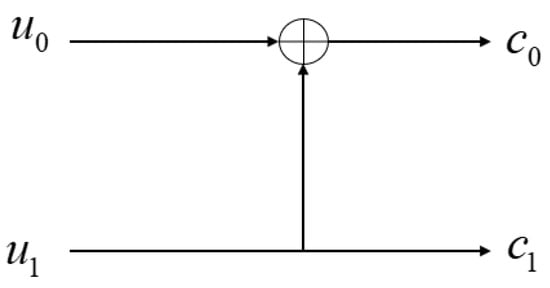
can be obtained using 𝑛 Kronecker products of the basic element as follows:
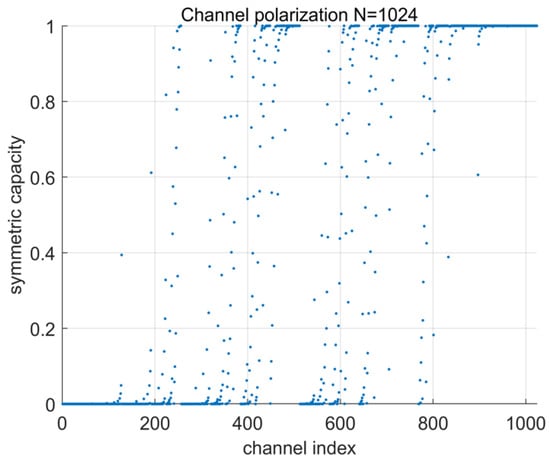
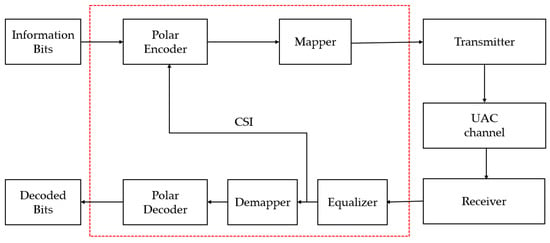
where 𝐵 is the bit reversal permutation matrix. After constructing code 𝐶, it is necessary to determine the index of the information and frozen bits. Usually, there are Bhattacharyya parameter, Gaussian approximation, density evolution, Monte Carlo [69], polarization weight (PW), etc., methods available. It is worth mentioning that Huawei proposed the PW, a sub-channel reliability assessment method independent of channel characteristics, which is suitable for constructing polar codes for dynamic UWA channels [70]. In polar code decoding with successive cancellation (SC) decoding, which requires sufficiently large code lengths, the block error probability decays exponentially in the square root of the code length. The recursive nature of the SC decoding may impose a large latency depending on the implementation. A major improvement in decoding performance can be achieved using successive cancellation list (SCL) decoding, which keeps a list of most likely decoding paths at all times, unlike the SC decoder, which only keeps one decoding path; that is, it performs a symbol-wise hard decision at each decoding stage. A significant improvement to SCL is the cyclic redundancy check (CRC)-aided SCL (CA-SCL), where the message is encoded with a CRC and then polar coded [71]. So far, CRC-SCL is currently the outstanding decoding method for polar codes.
References
- Gorenstein, D.; Zierler, N. A class of error-correcting codes in pm symbols. J. Soc. Ind. Appl. Math. 1961, 9, 207–214.
- Widmer, H.P.; Lev, E.; Costabile, J.J. Demonstration of a Low-Frequency, Long-Range Acoustic Communications System. Johns Hopkins APL Tech. Dig. 1993, 14, 174.
- LeBlanc, L.R.; Beaujean, P.P.; Singer, M.; Boubli, C.; Strutt, G.T. Chirp FSK modem for high reliability communication in shallow water. In Proceedings of the Oceans’ 99. MTS/IEEE. Riding the Crest into the 21st Century. Conference and Exhibition. Conference Proceedings (IEEE Cat. No. 99CH37008), Seattle, WA, USA, 13–16 September 1999; Volume 1, pp. 222–227.
- Stojanovic, M.; Freitag, L. Multiuser undersea acoustic communications in the presence of multipath propagation. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference Proceedings (IEEE Cat. No. 01CH37295), Honolulu, HI, USA, 5–8 November 2001; Volume 4, pp. 2165–2169.
- Guo, S.; Zhao, Z.; Pan, Q. A CDMA acoustic communication system for multiple underwater robots. In Proceedings of the 2008 IEEE International Conference on Robotics and Biomimetics, Bangkok, Thailand, 22–25 February 2009; pp. 1522–1526.
- Pompili, D.; Akyildiz, I.F. A multimedia cross-layer protocol for underwater acoustic sensor networks. IEEE Trans. Wirel. Commun. 2010, 9, 2924–2933.
- Huang, Y.; Zhou, S.; Shi, Z.; Lai, L. Channel frequency response-based secret key generation in underwater acoustic systems. IEEE Trans. Wirel. Commun. 2016, 15, 5875–5888.
- Barreto, G.; Simão, D.H.; Pellenz, M.E.; Souza, R.D.; Jamhour, E.; Penna, M.C.; Brante, G.; Chang, B.S. Energy-efficient channel coding strategy for underwater acoustic networks. Sensors 2017, 17, 728.
- Niemann, E.; Nicolaides, K.; Dhuness, K. A prototype broadband acoustic underwater data communication system for high data rates. In Proceedings of the OCEANS 2021, San Diego, CA, USA, 20–23 September 2021; pp. 1–6.
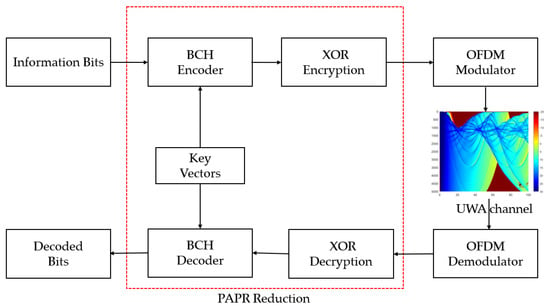
- Murad, M.; Tasadduq, I.A.; Otero, P. Ciphered BCH Codes for PAPR Reduction in the OFDM in Underwater Acoustic Channels. J. Mar. Sci. Eng. 2022, 10, 91.
- Reed-Solomon Codes and Their Applications; John Wiley & Sons: Hoboken, NJ, USA, 1999.
- Trubuil, J.; Goalic, A.; Beuzelin, N. Synchronization and channel coding in shallow water acoustic communication. In Proceedings of the OCEANS 2008, Quebec, QC, Canada, 15–18 September 2008; pp. 1–5.
- Goalic, A.; Trubuil, J.; Laot, C.; Beuzelin, N. Underwater acoustic communication using Reed Solomon Block Turbo Codes channel coding to transmit images and speech. In Proceedings of the OCEANS 2010 MTS/IEEE SEATTLE, Seattle, WA, USA, 20–23 September 2010; pp. 1–6.
- Nie, X.; Xu, W.; Zheng, J. Time reversal acoustic communication with concatenated reed-solomon code. In Proceedings of the 2012 Oceans-Yeosu, Yeosu, Republic of Korea, 21–24 May 2012; pp. 1–4.
- Esmaiel, H.; Jiang, D. Image transmission over underwater acoustic environment using OFDM technique with HQAM mapper. In Proceedings of the 2013 IEEE Third International Conference on Information Science and Technology (ICIST), Yangzhou, China, 23–25 March 2013; pp. 1596–1601.
- Diamant, R.; Lampe, L. Adaptive error-correction coding scheme for underwater acoustic communication networks. IEEE J. Ocean. Eng. 2014, 40, 104–114.
- Khanai, R.; Shahapur, S.S.; Torse, D. Performance analysis of underwater acoustic communication using IDMA-OFDM-MIMO with Reed Solomon and turbo code. Int. J. Comput. Netw. Inf. Secur. 2018, 10, 41–46.
- Sklivanitis, G.; Pelekanakis, K.; Yıldırım, S.A.; Petroccia, R.; Alves, J.; Pados, D.A. Physical layer security against an informed eavesdropper in underwater acoustic channels: Reconciliation and privacy amplification. In Proceedings of the 2021 Fifth Underwater Communications and Networking Conference (UComms), Lerici, Italy, 31 August–2 September 2021; pp. 1–5.
- Viterbi, A. Convolutional codes and their performance in communication systems. IEEE Trans. Commun. Technol. 1971, 19, 751–772.
- Moon, T.K. Error Correction Coding: Mathematical Methods and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2020.
- Catipovic, J.; Deffenbaugh, M.; Freitag, L.; Frye, D. An acoustic telemetry system for deep ocean mooring data acquisition and control. In Proceedings of the Oceans, Seattle, WA, USA, 18–21 September 1989; Volume 3, pp. 887–892.
- Catipovic, J.A.; Baggeroer, A.B. Performance of sequential decoding of convolutional codes over fully fading ocean acoustic channels. IEEE J. Ocean. Eng. 1990, 15, 1–7.
- Lam, W.K.; Ormondroyd, R.F. A coherent COFDM modulation system for a time-varying frequency-selective underwater acoustic channel. In Proceedings of the Seventh International Conference on Electronic Engineering in Oceanography—Technology Transfer from Research to Industry, Southampton, UK, 23–25 June 1997.
- Stojanovic, M.; Proarkis, J.G.; Rice, J.A.; Rice, J.A.; Green, M.D. Spread spectrum underwater acoustic telemetry. In Proceedings of the IEEE Oceanic Engineering Society. OCEANS’98. Conference Proceedings (Cat. No. 98CH36259), Nice, France, 28 September–1 October 1998; Volume 2, pp. 650–654.
- Zhu, W.-Q.; Wang, C.-H.; Pan, F.; Zhu, M.; Wang, R.; Zhang, X.-J.; Dai, Y.-M. Underwater acoustic communication system of AUV. In Proceedings of the IEEE Oceanic Engineering Society. OCEANS’98. Conference Proceedings (Cat. No. 98CH36259), Nice, France, 28 September–1 October 1998; Volume 1, pp. 477–481.
- Blackmon, F.; Sozer, E.; Murandian, M.; Proakis, J.; Salehi, M. Performance comparison of iterative/integral equalizer/decoder structures for underwater acoustic channels. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference Proceedings (IEEE Cat. No. 01CH37295), Honolulu, HI, USA, 5–8 November 2001; Volume 4, pp. 2191–2200.
- Park, J.; Seo, C.; Park, K.C.; Yoon, J.R. Effectiveness of convolutional code in multipath underwater acoustic channel. Jpn. J. Appl. Phys. 2013, 52, 07HG01.
- de Souza, F.; Souza, R.; Brante, G.; Pellenz, M.; Rosas, F.; Chang, B. Code rate optimization for energy efficient delay constrained underwater acoustic communications. In Proceedings of the OCEANS 2015-Genova, Genova, Italy, 18–21 May 2015; pp. 1–4.
- de Souza, F.; Souza, R.; Brante, G.; Souza, R.D.; Pellenz, M.E.; Rosas, F. Optimizing the number of hops and retransmissions for energy efficient multi-hop underwater acoustic communications. IEEE Sens. J. 2016, 16, 3927–3938.
- Behgam, M.; Zheng, Y.R.; Liu, Z. Coding for short messages in multipath underwater acoustic communication channels. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018; pp. 1–5.
- Lee, H.S.; Jung, J.W.; Baek, C.U.; Lee, A.H.; Kim, W.J. Adaptive modulation and coding for underwater acoustic communication. In Proceedings of the 2019 Eleventh International Conference on Ubiquitous and Future Networks (ICUFN), Zagreb, Croatia, 2–5 July 2019; pp. 54–56.
- Wu, F.Y.; Tian, T.; Su, B.X.; Song, Y.C. Hadamard–Viterbi Joint Soft Decoding for MFSK Underwater Acoustic Communications. Remote Sens. 2022, 14, 6038.
- Wang, J.; Zhang, S.; Luo, P.; Zhao, X. A Strong Security Key Agreement Scheme for Underwater Acoustic Networks. In Proceedings of the International Conference on Innovative Computing, Singapore, 1–3 February 2023; Springer Nature Singapore: Singapore, 2023; pp. 666–677.
- Berrou, C.; Glavieux, A.; Thitimajshima, P. Near Shannon limit error-correcting coding and decoding: Turbo-codes. 1. In Proceedings of the ICC’93-IEEE International Conference on Communications, Geneva, Switzerland, 23–26 May 1993; Volume 2, pp. 1064–1070.
- Tuchler, M.; Koetter, R.; Singer, A.C. Turbo equalization: Principles and new results. IEEE Trans. Commun. 2002, 50, 754–767.
- Zheng, Y.R.; Wu, J.; Xiao, C. Turbo equalization for single-carrier underwater acoustic communications. IEEE Commun.-Tions Mag. 2015, 53, 79–87.
- Jasim, S.; Abbas, A. Performance of turbo code with different parameters. J. Univ. Babylon 2017, 25, 1684–1692.
- Sozer, E.M.; Proakis, J.G.; Blackmon, F. Iterative equalization and decoding techniques for shallow water acoustic channels. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference Proceedings (IEEE Cat. No. 01CH37295), Honolulu, HI, USA, 5–8 November 2001; Volume 4, pp. 2201–2208.
- Huang, J.; Sun, J.; He, C.; Sheng, X.H.; Zhang, Q.F. High-speed underwater acoustic communication based on OFDM. In Proceedings of the 2005 IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Beijing, China, 8–12 August 2005; Volume 2, pp. 1135–1138.
- Roy, S.; Duman, T.M.; McDonald, V.; Proakis, J.G. High-rate communication for underwater acoustic channels using multiple transmitters and space–time coding: Receiver structures and experimental results. IEEE J. Ocean. Eng. 2007, 32, 663–688.
- Xu, X.; Qiao, G.; Su, J.; Su, J.; Hu, P.; Sang, E. Study on turbo code for multicarrier underwater acoustic communication. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2008; pp. 1–4.
- Labrador, Y.; Karimi, M.; Pan, D.; Miller, J. Modulation and error correction in the underwater acoustic communication channel. Int. J. Comput. Sci. Netw. Secur. 2009, 9, 123–130.
- Iruthayanathan, N.; Vishvaksenan, K.S.; Rajendran, V.; Mohankumar, S. Performance analysis of turbo-coded MIMO–OFDM system for underwater communication. Comput. Electr. Eng. 2015, 43, 1–8.
- Bocus, M.J.; Agrafiotis, D.; Doufexi, A. Non-orthogonal multiple access (NOMA) for underwater acoustic communication. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–5.
- Bocus, M.J.; Doufexi, A.; Agrafiotis, D. Performance of OFDM-based massive MIMO OTFS systems for underwater acoustic communication. IET Commun. 2020, 14, 588–593.
- Minaeva, O.N.; Miroshnikova, N.E.; Sattarova, A.I. Research of the Convolutional and Product Turbo Codes Characteristics in Conditions of Underwater Channel. In Proceedings of the 2022 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russian, 15–17 March 2022; pp. 1–5.
- Yang, Y.; Li, Y. Research and Implementation of Turbo Coding Technology in High-Speed Underwater Acoustic OFDM Communication. J. Robot. 2022, 2022, 2576303.
- Jeong, H.W.; Jung, J.W.; Kim, I.S. Non-coherent turbo coded frequency shift keying for reliable covert underwater acoustic communications. J. Acoust. Soc. Am. 2022, 151, A235.
- Thorpe, J. Low-density parity-check (LDPC) codes constructed from protographs. IPN Prog. Rep. 2003, 42, 42–154.
- Richardson, T.; Kudekar, S. Design of low-density parity check codes for 5G new radio. IEEE Commun. Mag. 2018, 56, 28–34.
- Richardson, T.J.; Urbanke, R.L. Efficient encoding of low-density parity-check codes. IEEE Trans. Inf. Theory 2001, 47, 638–656.
- Kou, Y.; Lin, S.; Fossorier, M.P.C. Low-density parity-check codes based on finite geometries: A rediscovery and new results. IEEE Trans. Inf. Theory 2001, 47, 2711–2736.
- Li, Z.; Chen, L.; Zeng, L.; Fong, W.H. Efficient encoding of quasi-cyclic low-density parity-check codes. IEEE Trans. Commun. 2006, 54, 71–81.
- Dehghan, A.; Banihashemi, A.H. On the Tanner graph cycle distribution of random LDPC, random protograph-based LDPC, and random quasi-cyclic LDPC code ensembles. IEEE Trans. Inf. Theory 2018, 64, 4438–4451.
- Chen, J.; Fossorier, M.P.C. Density evolution for two improved BP-based decoding algorithms of LDPC codes. IEEE Commun. Lett. 2002, 6, 208–210.
- Li, B.; Zhou, S.; Stojanovic, M.; Freitag, L.; Huang, J.; Willett, P. MIMO-OFDM over An Underwater Acoustic Channel. In Proceedings of the OCEANS 2007, Vancouver, BC, Canada, 29 September–4 October 2007; pp. 1–6.
- Huang, J.; Zhou, S.; Willett, P. Nonbinary LDPC coding for multicarrier underwater acoustic communication. IEEE J. Sel. Areas Commun. 2008, 26, 1684–1696.
- Chen, Y.; Xu, X.; Zhang, L. Performance analysis of LDPC codes over shallow water acoustic channels. In Proceedings of the 2009 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 24–26 September 2009; pp. 1–4.
- Kang, T.; Iltis, R.A. Iterative carrier frequency offset and channel estimation for underwater acoustic OFDM systems. IEEE J. Sel. Areas Commun. 2008, 26, 1650–1661.
- Qi, X.-K.; Li, Y.; Huang, H.-N. Construction of Reversible QC-LDPC Codes and Its Performance in Underwater Acoustic Communication System. J. Electron. Inf. Technol. 2013, 34, 1986–1992.
- Tao, J.; Zheng, Y.R. Turbo detection for MIMO–OFDM underwater acoustic communications. Int. J. Wirel. Inf. Netw. 2013, 20, 27–38.
- Chen, Y.; Wang, Z.; Wan, L.; Zhou, S.; Xu, X. OFDM-modulated dynamic coded cooperation in underwater acoustic channels. IEEE J. Ocean. Eng. 2014, 40, 159–168.
- Liu, S.; Song, A. Optimization of LDPC codes over the underwater acoustic channel. Int. J. Distrib. Sens. Netw. 2016, 12, 8906985.
- Li, D.; Wu, Y.; Zhu, M. Nonbinary LDPC code for noncoherent underwater acoustic communication under non-Gaussian noise. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–6.
- Padala, S.K.; D’Souza, J. Performance of spatially coupled LDPC codes over underwater acoustic communication channel. In Proceedings of the 2020 National Conference on Communications (NCC), Kharagpur, India, 21–23 February 2020; pp. 1–5.
- Wei, X.F.; Chen, J. Performance Simulation of Underwater Acoustic Spread Spectrum Communication Based on LDPC Code. In Proceedings of the Journal of Physics: Conference Series. IOP Publ. 2021, 1873, 012018.
- Zhao, Z.; Sun, Z. Short-Block-Length Low-Density Parity-Check Codes-Based Underwater Acoustic Spread-Spectrum Communication System. Electronics 2023, 12, 3884.
- Arikan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073.
- Vangala, H.; Viterbo, E.; Hong, Y. A comparative study of polar code constructions for the AWGN channel. arXiv 2015, arXiv:1501.02473.
- He, G.; Belfiore, J.C.; Land, I.; Yang, G.; Liu, X.; Chen, Y.; Li, R.; Wang, J.; Ge, Y.; Zhang, R. Beta-expansion: A theoretical framework for fast and recursive construction of polar codes. In Proceedings of the GLOBECOM 2017–2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6.
- Niu, K.; Chen, K. CRC-aided decoding of polar codes. IEEE Commun. Lett. 2012, 16, 1668–1671.
- Qiao, G.; Xing, S.; Zhou, F. A multi-user detection scheme based on polar code construction in downlink underwater acoustic OFDM communication system. IEEE Access 2019, 7, 65973–65981.
- Zhai, Y.; Li, J.; Feng, H. Research on Polar coding application for underwater acoustic OFDM communication system. In Proceedings of the 2020 IEEE 6th International Conference on Computer and Communications (ICCC), Chengdu, China, 11–14 December 2020; pp. 322–328.
- Falk, M.; Bauch, G.; Nissen, I. On channel codes for short underwater messages. Information 2020, 11, 58.
- Zhou, C.; Cao, H.; Li, Q. Joint coding of underwater acoustic communication source channel based on polar code. In Proceedings of the International Conference on Network Communication and Information Security (ICNCIS 2021), Sanya, China, 3–5 December 2021; Volume 12175, pp. 19–23.
- Yushuang, Z.; Haihong, F.; Jilong, L.I.; Feng, H. Polar code construction method for the polar coded modulation orthogonal frequency division multiplexing underwater acoustic communication. Tech. Acoust. 2023, 48, 482–495.
- Chen, R.; Wu, W.; Zeng, Q.; Liu, S. Construction and application of polar codes in OFDM underwater acoustic communication. Appl. Acoust. 2023, 211, 109473.
- Liu, F.; Wu, Q.; Li, C.; Chen, F.; Xu, Y. Polar coding aided by adaptive channel equalization for underwater acoustic communication. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences. 2023, Volume 106, pp. 83–87. Available online: https://search.ieice.org/bin/summary.php?id=e106-a_1_83 (accessed on 26 October 2023).
- Yang, X.; Zhou, Y.; Wang, R.; Tong, F. Research and Implementation on a Real-time OSDM MODEM for Underwater Acoustic Communications. IEEE Sens. J. 2023, 23, 18434–18448.




