AutoML with Bayesian Optimizations for Big Data Management

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Aristeidis Karras	--	2520	2023-11-03 09:34:08	\|
2	format correct	Catherine Yang	-1 word(s)	2519	2023-11-03 09:44:47	\|

This entry is adapted from the peer-reviewed paper 10.3390/info14040223

The field of automated machine learning (AutoML) has gained significant attention in recent years due to its ability to automate the process of building and optimizing machine learning models.

big data management stochastic data engineering automated machine learning

1. Introduction

Automated Machine Learning (AutoML) can be applied to Big Data processing, management, and systems in several ways. One way is by using AutoML to automatically optimize the performance of machine learning models on large datasets. This can include selecting the most appropriate algorithm, tuning hyperparameters, and selecting features. Another way is to use AutoML to automate the process of building and deploying machine learning models in a big data environment. For example, AutoML can be used to automatically scale and distribute models across a cluster of machines or to automatically select the best storage and processing options for a given dataset. Additionally, AutoML can also be used for automating feature engineering on big data. This can help to reduce the time and effort required to prepare large datasets for machine learning. Automated Machine Learning (AutoML) refers to the process of automating the entire machine learning pipeline, from data preprocessing to model selection, training, and deployment. There are several techniques used in AutoML to achieve this automation. Some of the most common techniques include:

Hyperparameter tuning: This involves automatically searching for the best combination of hyperparameters for a given machine-learning model. This can be done using techniques such as grid search, random search, or Bayesian optimization.
Feature selection and engineering: AutoML can be used to automatically select the most relevant features for a given dataset and to perform feature engineering tasks such as scaling, normalization, and dimensionality reduction.
Model selection: AutoML can be used to automatically select the best machine learning model for a given dataset. This can be done by comparing the performance of different models on the dataset, or by using techniques such as ensembling or stacking to combine the predictions of multiple models.
Neural Architecture Search (NAS): This is a subfield of AutoML that aims to automate the design of neural network architectures. The goal is to find the best neural network architecture for a given task and dataset ^[1]^[2]^[3]^[4].
Automated Deployment: AutoML can be used to automate the process of deploying machine learning models into production. This can include tasks such as model versioning, monitoring, and scaling.

Overall, the goal of AutoML is to make the process of building and deploying machine learning models faster, easier, and more accessible to non-experts by automating many of the time-consuming and tedious tasks involved in the machine learning pipeline.

2. Automated Machine Learning in Industry

Machine learning has become more widely applied in several industries in recent years. Businesses may be more proactive and boost productivity by using industrial applications like defect detection ^[5] and predictive maintenance ^[6]^[7]. Patient data have aided in the treatment of complex diseases like multiple sclerosis and helped doctors choose the most suitable drug in the healthcare industry, to reference ^[8]. In the insurance and banking sectors, it is feasible to forecast the risks involved with loan applications ^[9] and claims processing ^[10]^[11], allowing for the automatic identification of fraudulent behaviours. Last but not least, improvements in sales and revenue forecasts support supply chain optimization, according to ^[12].

It takes time and is prone to errors to manually build these actionable machine learning models that may have economic value. Instead, the performance of several models should be assessed while considering diverse methods, hyperparameter tuning, and feature selection into consideration. An ideal option for automation is this incredibly iterative process. The data scientist may now focus on more creative tasks thanks to AutoML, which frees them up from this tedious task and increases the value of the business. By using fast prototyping, new business cases may be found, assessed, and validated.

In the real world, AutoML could provide many insights. Early feedback on the data’s appropriateness for anticipating the given target may come by running a variety of models on the input data. There may be an indication of insufficient predictive power in the data if there are several models built using a wide range of methodologies and they perform similarly to the baseline. In theory, however, reliable models will be produced, giving the data scientist the choice of using the best model that was generated or building an ensemble of several models ^[13]. The optimization of the feature set via AutoML has a by-product, too: A feature relevance estimate based on the characteristics used as model inputs may be produced via statistical analysis of model quality.

3. Feature Engineering and Selection

Researchers have been driven to automate various steps in the machine learning pipeline as a result of the problem of manual hyperparameter tuning ^[14], including feature engineering ^[15], meta-learning ^[16], architecture search ^[17], and full Combined Model Selection and Hyperparameter optimization ^[18].

Feature engineering: The research discusses the challenges associated with representation learning, feature preprocessing, and selecting the best discriminating features for a given classification or regression task. Gaudel and Sebag ^[19] approach feature engineering as a single-player game and train a reinforcement learning-based agent to select the most beneficial traits. To do this, they first model the feature selection problem as a Markov Decision Process (MDP). They also imply a connection between a reward and the eventual status generalization error. The agent develops a tactic that reduces the overall generalization error. Overall, Gaudel’s and Sebag’s approaches to feature engineering using reinforcement learning show promise in improving the performance of classification and regression models by selecting the most informative features.

To find the most discriminating features, Explorekit ^[20] not only selects the features repeatedly but also creates new candidate features. Katz et al. create unary features by using a single feature with normalization and discrimination operations. They not only combine two or more features to create new candidates, but they also use meta-features collected from the datasets and candidates to train a feature rank estimator. The feature with the highest rank that improves classification accuracy beyond a certain threshold is added to the selected feature set in each cycle.

The Learning Feature Engineering (LFE) approach is a technique aimed at reducing the computational cost associated with iterative feature selection procedures by learning from previous trials the effectiveness of different modifications. The primary objective of the LFE approach is to derive a discriminant feature representation that can improve the performance of classification or regression models. Learning Feature Engineering (LFE) ^[21] learns from previous trials the efficacy of a modification in order to minimize the computing cost of iterative feature selection procedures. A discriminant feature representation is calculated after mapping the original feature space with the best transformation.

An automated feature selection method based on regression is called AutoLearn ^[22]. Filtering the initial features and eliminating those that offer little information gain is the first step of the recommended method. Then feature pairs are filtered based on distance correlation to remove dependent pairings. The new features are developed based on the remaining pairs using ridge regression. The best characteristics are those that provide the most stability and knowledge gain, according to ^[23]. Gene expression data is one of the datasets with which AutoLearn has been used.

4. Meta-Learning

By employing metadata about the problem at hand, such as the dataset and the available algorithms and their settings, meta-learning techniques try to improve the performance of an AutoML system. The field is often applied to itself by employing machine learning techniques to acquire and analyze this metainformation. The performance statistics of straightforward algorithms frequently make up the metadata cited in ^[24], which is the metadata connected with datasets.

The goal of prediction of the learning curve is to develop a model that forecasts how much a learner’s performance will improve with further training time ^[25]. Another approach to this idea is to make an attempt to predict how long an algorithm ^[26] will take to execute. It has occasionally been helpful to predict a ranking of the available algorithms rather than forecasting absolute performance outcomes ^[27].

In the context of neural networks, meta-learners try to improve the optimizer of a deep or shallow (convolutional) neural network (CNN) by automatically adjusting hyper-parameters to reach a minimum as rapidly as is practical. The best hyperparameters for optimizing neural networks are found in ^[28], utilizing gradients and a Long Short-Term Memory network ^[29]^[30]. Similar to how Chen et al. ^[31] train an optimizer for fundamental synthetic functions like Gaussian Processes. They demonstrate how the optimizer may be used to solve a wide range of black-box problems. For instance, without accessing the gradients of the loss function relative to the hyperparameters, the trained optimizer is used to change the hyperparameters of a Support Vector Machine ^[32].

5. Neural Architecture Search (NAS)

The design search literature investigates methods for robotically choosing neural network architectures without human involvement. Neural Architecture Search by Hill-climbing (NASH) is recommended by Elsken et al. ^[33] utilizing the local search. The method starts with a high-performance convolutional architecture that has been trained, if possible (parent). The original parent network is then randomly subjected to two types of network morphisms (transformations) in order to produce children with either a deeper or broader design. The young architects are instructed, and the one who performs best moves on to the next level. The process repeats until the validation’s accuracy reaches its maximum. Real et al. ^[34] indicate an evolutionary architecture search based on pairwise comparisons within the population. The algorithm starts with an initial population as parents, and each network goes through random mutations such as adding and removing convolutional layers and skipping connections to produce offspring. The winning parent and offspring then perform a pairwise comparison, with the losing parent and offspring being removed.

He et al. ^[35] search automatically for compressing a given CNN for mobile and embedded applications, in contrast to evolutionary approaches, which ask for bigger and more exact structures. Their AutoML for Model Compression (AMC) method directs a reinforcement learning agent to evaluate each layer’s sparsity ratio and compress each layer one at a time. The issue of combined model selection and hyperparameter optimization, which can be resolved by combining the aforementioned building pieces, is the main focus of this work. Ultimately, a thorough solution determines the best machine-learning pipeline for unprocessed (raw) feature vectors in the shortest time possible for a fixed quantity of computer resources. This has led to a number of Automated Machine Learning (AutoML) contests since 2015 ^[36]. To obtain excellent performance on unseen test data, a complete pipeline includes data cleaning, feature engineering (selection and construction), model selection, hyperparameter optimization, and finally the building of an ensemble of the best-trained models. A challenging challenge is optimizing the entire machine learning pipeline, which is not necessarily differentiable end-to-end, and many methods and procedures have been investigated.

6. The CASH Problem

Theorem 1 (CASH Problem).

Given a machine learning model f and a dataset D, find the set of hyperparameters H that minimizes the expected loss

L (f_{H} (D))

, where L is a loss function that measures the performance of the model on the dataset. Formally, it can be written as:

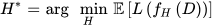where

H^{*}

is the optimal set of hyperparameters, and the expectation is taken over all possible datasets that could be generated from the underlying data distribution.

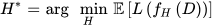
The CASH problem is inherently difficult due to several factors. Firstly, the space of possible hyperparameters H for a machine learning model can be extremely large and complex, leading to a combinatorial explosion in the number of possible configurations to evaluate. Secondly, the optimal hyperparameters can be highly dependent on the specific dataset D and the task at hand, making it difficult to find a “one-size-fits-all” set of hyperparameters. In addition, evaluating the loss function L can be computationally expensive, especially when dealing with large and complex models or datasets. This can limit the number of possible hyperparameter configurations that can be evaluated, making it difficult to exhaustively search the space of possible hyperparameters.

7. Optimization Techniques

The most noteworthy example of the numerous techniques for optimizing hyperparameters is Bayesian optimization ^[37], which is a crucial step towards resolving the CASH problem as a whole. Building a model of projected loss and variance for each input is the goal. The model (or current belief) is updated using posteriori data following each optimization step (hence the name Bayesian). A defined acquisition function trades off locations with low predicted loss (exploitation) with those with significant variance to decide where to sample the next real loss (exploration). Although Random Forests have been used to model the loss surface of the hyperparameters as a Gaussian distribution in Sequential Model-based optimization for general Algorithm Configuration (SMAC) ^[38] and the Tree-structured Parzen Estimator ^[39], Gaussian Processes are typically the preferred model in Bayesian optimization.

Model-free techniques include Successive Halving ^[40], developed on Hyperband ^[14] exploits the progress of real-time optimization to eliminate a collection of competing hyperparameter configurations throughout the course of a whole optimization run, maybe with several restarts. Evolutionary strategies, which also permit perturbations of the individual configurations during training ^[41], are a modest modification of this. Multiple iterations of the optimizer may be unrolled in the particular situation when both the optimize and the optimizer are differentiable, and an update for the hyperparameters can be calculated using gradient descent and backpropagation ^[42].

8. Tiny Machine Learning

Additionally, there has been a growing interest in the field of Tiny Machine Learning (TinyML), which focuses on implementing machine learning algorithms on resource-constrained devices such as IoT sensors and edge devices. The researchers proposed an intelligent microprocessor integrating TinyML in Smart Hotels for rapid accident prevention ^[43]. Moreover, the researchers have conducted a comprehensive survey on the state-of-the-art techniques and challenges in the field of Automated Machine Learning for TinyML ^[44]. The survey provides an overview of the various approaches used for model compression, acceleration, and quantization and their trade-offs. It also highlights the challenges and future research directions in this field.

9. AutoML

Overall, AutoML is an active area of research, aimed at automating the process of model selection, hyperparameter optimization, and feature engineering. Nagarajah and Poravi ^[45] provided a comprehensive review of AutoML systems and highlighted their advantages and limitations. Bahri et al. ^[46] presented a state-of-the-art review of AutoML with a focus on anomaly detection, challenges, and research directions. Remeseiro and Bolon-Canedo ^[47] reviewed feature selection methods in medical applications. Isabona et al. ^[48] proposed a machine learning-based boosted regression ensemble combined with hyperparameter tuning for optimal adaptive learning. Guo et al. ^[49] presented a federated hyperparameter optimization approach for multi-institutional medical image segmentation. Li et al. ^[50] proposed Hyper-Tune, an efficient hyperparameter tuning framework. Passos and Mishra ^[51] provided a tutorial on automatic hyperparameter tuning of deep spectral modeling for regression and classification tasks. Yu and Zhu ^[52] reviewed hyperparameter optimization algorithms and their applications. Bischl et al. ^[53] provided an overview of the foundations, algorithms, best practices, and open challenges of hyperparameter optimization. Sipper ^[54] conducted a large-scale study of hyperparameter tuning for machine learning algorithms. Giotopoulos et al. ^[55] presented a neuro-fuzzy employee ranking system in the public sector that incorporates machine learning techniques.

Although each of the preceding works has a lot to contribute to the field, they do not incorporate many different parameters or methods as proposed here. Therefore, the contribution of this work is effective hyperparameter optimization and training using various datasets, methods, and sampling schemes for accelerating training in large datasets.

References

Kang, J.S.; Kang, J.; Kim, J.J.; Jeon, K.W.; Chung, H.J.; Park, B.H. Neural Architecture Search Survey: A Computer Vision Perspective. Sensors 2023, 23, 1713.
Baymurzina, D.; Golikov, E.; Burtsev, M. A review of neural architecture search. Neurocomputing 2022, 474, 82–93.
Lindauer, M.; Hutter, F. Best Practices for Scientific Research on Neural Architecture Search. J. Mach. Learn. Res. 2020, 21, 9820–9837.
Jin, H.; Song, Q.; Hu, X. Auto-Keras: An Efficient Neural Architecture Search System. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD ’19), Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 1946–1956.
Figueiredo, E.; Park, G.; Farrar, C.R.; Worden, K.; Figueiras, J. Machine learning algorithms for damage detection under operational and environmental variability. Struct. Health Monit. 2011, 10, 559–572.
Susto, G.A.; Schirru, A.; Pampuri, S.; McLoone, S.; Beghi, A. Machine learning for predictive maintenance: A multiple classifier approach. IEEE Trans. Ind. Inform. 2014, 11, 812–820.
Li, H.; Parikh, D.; He, Q.; Qian, B.; Li, Z.; Fang, D.; Hampapur, A. Improving rail network velocity: A machine learning approach to predictive maintenance. Transp. Res. Part Emerg. Technol. 2014, 45, 17–26.
Stühler, E.; Braune, S.; Lionetto, F.; Heer, Y.; Jules, E.; Westermann, C.; Bergmann, A.; van Hövell, P. Framework for personalized prediction of treatment response in relapsing remitting multiple sclerosis. BMC Med. Res. Methodol. 2020, 20, 24.
Handzic, M.; Tjandrawibawa, F.; Yeo, J. How neural networks can help loan officers to make better informed application decisions. Informing Sci. 2003, 6, 97–109.
Viaene, S.; Dedene, G.; Derrig, R.A. Auto claim fraud detection using Bayesian learning neural networks. Expert Syst. Appl. 2005, 29, 653–666.
Pérez, J.M.; Muguerza, J.; Arbelaitz, O.; Gurrutxaga, I.; Martín, J.I. Consolidated tree classifier learning in a car insurance fraud detection domain with class imbalance. In Proceedings of the International Conference on Pattern Recognition and Image Analysis, Bath, UK, 23–25 August 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 381–389.
Tsoumakas, G. A survey of machine learning techniques for food sales prediction. Artif. Intell. Rev. 2019, 52, 441–447.
Karras, C.; Karras, A.; Tsolis, D.; Avlonitis, M.; Sioutas, S. A Hybrid Ensemble Deep Learning Approach for Emotion Classification. In Proceedings of the 2022 IEEE International Conference on Big Data (Big Data), Atlanta, GA, USA, 17–20 December 2022; pp. 3881–3890.
Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816.
Duan, J.; Zeng, Z.; Oprea, A.; Vasudevan, S. Automated generation and selection of interpretable features for enterprise security. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 1258–1265.
Andrychowicz, M.; Denil, M.; Gómez, S.; Hoffman, M.W.; Pfau, D.; Schaul, T.; Shillingford, B.; de Freitas, N. Learning to learn by gradient descent by gradient descent. In Advances in Neural Information Processing Systems; Lee, D., Sugiyama, M., Luxburg, U., Guyon, I., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2016; Volume 29.
Zoph, B.; Le, Q.V. Neural architecture search with reinforcement learning. arXiv 2016, arXiv:1611.01578.
Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.; Blum, M.; Hutter, F. Efficient and robust automated machine learning. Adv. Neural Inf. Process. Syst. 2015, 28.
Gaudel, R.; Sebag, M. Feature selection as a one-player game. In Proceedings of the International Conference on Machine Learning, Haifa, Israel, 21–25 June 2010; pp. 359–366.
Katz, G.; Shin, E.C.R.; Song, D. Explorekit: Automatic feature generation and selection. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 979–984.
Nargesian, F.; Samulowitz, H.; Khurana, U.; Khalil, E.B.; Turaga, D.S. Learning Feature Engineering for Classification. In Proceedings of the IJCAI, Melbourne, Australia, 19–25 August 2017; pp. 2529–2535.
Kaul, A.; Maheshwary, S.; Pudi, V. Autolearn—Automated feature generation and selection. In Proceedings of the 2017 IEEE International Conference on data mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 217–226.
Meinshausen, N.; Bühlmann, P. Stability selection. J. R. Stat. Soc. Ser. (Stat. Methodol.) 2010, 72, 417–473.
Pfahringer, B.; Bensusan, H.; Giraud-Carrier, C.G. Meta-Learning by Landmarking Various Learning Algorithms. In Proceedings of the ICML, Stanford, CA, USA, 29 June–2 July 2000; pp. 743–750.
Klein, A.; Falkner, S.; Springenberg, J.T.; Hutter, F. Learning Curve Prediction with Bayesian Neural Networks. In Proceedings of the ICLR, Toulon, France, 24–26 April 2017.
Eggensperger, K.; Lindauer, M.; Hutter, F. Neural networks for predicting algorithm runtime distributions. arXiv 2017, arXiv:1709.07615.
Brazdil, P.B.; Soares, C. A comparison of ranking methods for classification algorithm selection. In Proceedings of the European Conference on Machine Learning, Barcelona, Spain, 31 May–2 June 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 63–75.
Andrychowicz, M.; Denil, M.; Gomez, S.; Hoffman, M.W.; Pfau, D.; Schaul, T.; Shillingford, B.; De Freitas, N. Learning to learn by gradient descent by gradient descent. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016.
Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780.
Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45.
Chen, Y.; Hoffman, M.W.; Colmenarejo, S.G.; Denil, M.; Lillicrap, T.P.; Botvinick, M.; Freitas, N. Learning to learn without gradient descent by gradient descent. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 748–756.
Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297.
Elsken, T.; Metzen, J.H.; Hutter, F. Simple and efficient architecture search for convolutional neural networks. arXiv 2017, arXiv:1711.04528.
Real, E.; Moore, S.; Selle, A.; Saxena, S.; Suematsu, Y.L.; Tan, J.; Le, Q.V.; Kurakin, A. Large-scale evolution of image classifiers. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 2902–2911.
He, Y.; Lin, J.; Liu, Z.; Wang, H.; Li, L.J.; Han, S. Amc: Automl for model compression and acceleration on mobile devices. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 784–800.
Guyon, I.; Sun-Hosoya, L.; Boullé, M.; Escalante, H.J.; Escalera, S.; Liu, Z.; Jajetic, D.; Ray, B.; Saeed, M.; Sebag, M.; et al. Analysis of the automl challenge series. Autom. Mach. Learn. 2019, 177–219.
Brochu, E.; Cora, V.M.; De Freitas, N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. arXiv 2010, arXiv:1012.2599.
Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Proceedings of the International Conference on Learning and Intelligent Optimization, Rome, Italy, 17–21 January 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 507–523.
Feurer, M.; Springenberg, J.; Hutter, F. Initializing Bayesian Hyperparameter Optimization via Meta-Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29.
Jamieson, K.; Talwalkar, A. Non-stochastic best arm identification and hyperparameter optimization. In Proceedings of the Artificial Intelligence and Statistics, PMLR, Cadiz, Spain, 9–11 May 2016; pp. 240–248.
Jaderberg, M.; Dalibard, V.; Osindero, S.; Czarnecki, W.M.; Donahue, J.; Razavi, A.; Vinyals, O.; Green, T.; Dunning, I.; Simonyan, K.; et al. Population based training of neural networks. arXiv 2017, arXiv:1711.09846.
Maclaurin, D.; Duvenaud, D.; Adams, R. Gradient-based hyperparameter optimization through reversible learning. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 2113–2122.
Zacharia, A.; Zacharia, D.; Karras, A.; Karras, C.; Giannoukou, I.; Giotopoulos, K.C.; Sioutas, S. An Intelligent Microprocessor Integrating TinyML in Smart Hotels for Rapid Accident Prevention. In Proceedings of the 2022 7th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Ioannina, Greece, 23–25 September 2022; pp. 1–7.
Schizas, N.; Karras, A.; Karras, C.; Sioutas, S. TinyML for Ultra-Low Power AI and Large Scale IoT Deployments: A Systematic Review. Future Internet 2022, 14, 363.
Nagarajah, T.; Poravi, G. A Review on Automated Machine Learning (AutoML) Systems. In Proceedings of the 2019 IEEE 5th International Conference for Convergence in Technology (I2CT), Bombay, India, 29–31 March 2019; pp. 1–6.
Bahri, M.; Salutari, F.; Putina, A.; Sozio, M. Automl: State of the art with a focus on anomaly detection, challenges, and research directions. Int. J. Data Sci. Anal. 2022, 14, 113–126.
Remeseiro, B.; Bolon-Canedo, V. A review of feature selection methods in medical applications. Comput. Biol. Med. 2019, 112, 103375.
Isabona, J.; Imoize, A.L.; Kim, Y. Machine Learning-Based Boosted Regression Ensemble Combined with Hyperparameter Tuning for Optimal Adaptive Learning. Sensors 2022, 22, 3776.
Guo, P.; Yang, D.; Hatamizadeh, A.; Xu, A.; Xu, Z.; Li, W.; Zhao, C.; Xu, D.; Harmon, S.; Turkbey, E.; et al. Auto-FedRL: Federated Hyperparameter Optimization for Multi-institutional Medical Image Segmentation. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer Nature Switzerland: Cham, Switzerland, 2022; pp. 437–455.
Li, Y.; Shen, Y.; Jiang, H.; Zhang, W.; Li, J.; Liu, J.; Zhang, C.; Cui, B. Hyper-Tune: Towards Efficient Hyper-parameter Tuning at Scale. arXiv 2022, arXiv:2201.06834.
Passos, D.; Mishra, P. A tutorial on automatic hyperparameter tuning of deep spectral modelling for regression and classification tasks. Chemom. Intell. Lab. Syst. 2022, 223, 104520.
Yu, T.; Zhu, H. Hyper-parameter optimization: A review of algorithms and applications. arXiv 2020, arXiv:2003.05689.
Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.L.; et al. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2021, 13, e1484.
Sipper, M. High Per Parameter: A Large-Scale Study of Hyperparameter Tuning for Machine Learning Algorithms. Algorithms 2022, 15, 315.
Giotopoulos, K.C.; Michalopoulos, D.; Karras, A.; Karras, C.; Sioutas, S. Modelling and Analysis of Neuro Fuzzy Employee Ranking System in the Public Sector. Algorithms 2023, 16, 151.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Computer Science, Artificial Intelligence

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Markos Avlonitis

View Times: 292

Update Date: 03 Nov 2023

Table of Contents

Video Upload Options

Confirm