Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Cheng Yang | -- | 3953 | 2023-08-23 12:56:25 | | | |
| 2 | Jason Zhu | -11 word(s) | 3942 | 2023-08-24 03:48:28 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Yang, C.; Sun, Y.; Zou, Y.; Zheng, F.; Liu, S.; Zhao, B.; Wu, M.; Cui, H. Problem Formulation in Distribution Network. Encyclopedia. Available online: https://encyclopedia.pub/entry/48371 (accessed on 07 February 2026).
Yang C, Sun Y, Zou Y, Zheng F, Liu S, Zhao B, et al. Problem Formulation in Distribution Network. Encyclopedia. Available at: https://encyclopedia.pub/entry/48371. Accessed February 07, 2026.
Yang, Cheng, Yupeng Sun, Yujie Zou, Fei Zheng, Shuangyu Liu, Bochao Zhao, Ming Wu, Haoyang Cui. "Problem Formulation in Distribution Network" Encyclopedia, https://encyclopedia.pub/entry/48371 (accessed February 07, 2026).
Yang, C., Sun, Y., Zou, Y., Zheng, F., Liu, S., Zhao, B., Wu, M., & Cui, H. (2023, August 23). Problem Formulation in Distribution Network. In Encyclopedia. https://encyclopedia.pub/entry/48371
Yang, Cheng, et al. "Problem Formulation in Distribution Network." Encyclopedia. Web. 23 August, 2023.
Copy Citation
Distributed generators (DGs) have a high penetration rate in distribution networks (DNs). Understanding their impact on a DN is essential for achieving optimal power flow (OPF). Various DG models, such as stochastic and forecasting models, have been established and are used for OPF. While conventional OPF aims to minimize operational costs or power loss, the “Dual-Carbon” target has led to the inclusion of carbon emission reduction objectives. Additionally, state-of-the-art optimization techniques such as machine learning (ML) are being employed for OPF.
optimal power flow
distributed generators
distribution network
1. Introduction
The proportion of DGs connected to DNs has increased significantly due to the implementation of the “Dual-Carbon” strategy. DGs, which typically consist of photovoltaic cells (PVs) and wind turbines (WTs), offer clean and renewable energy. However, the output from these DGs is often intermittent, resulting in challenges for grid stability. To address these challenges, a battery energy storage system (BESS) is commonly used to smooth out the output curve. The integration of DGs has transformed the traditional DN model from a passive energy receiver into an active network that participates in energy exchange. The energy exchange of DGs is typically achieved through power routers (PRs). OPF is a common technique used to reduce network loss and the cost of DN [1][2]. The objective of OPF is to minimize system losses and to allocate power rationally among different nodes while ensuring system safety and stability. In addition to these objectives, carbon emissions [3] are also considered as optimization targets.
To achieve OPF with DGs, understanding their impact on DNs is of utmost importance. Ref. [4] investigated the relationship between nodal voltage and the placement of DGs. Two types of DG models, namely stochastic and forecasting, were established to account for their uncertainty. Additionally, the combination of OPF with the electricity market is a hot topic, with recent studies, as seen in references [5][6][7], establishing a demand response (DR) model for calculating locational marginal prices (LMP) and scheduling DG output.
The power flow model, which is the basis of the OPF problem, is also reviewed. The model can be categorized into conventional nonlinear and linear approximation models. The conventional model can reflect the power flow distribution directly, but its nonlinear nature makes it less desirable for calculations. Linear models, on the other hand, can speed up the calculation process but may lose some accuracy. In addition, new component models have been added to the equality and inequality of the model to reflect the new components in DNs.
After defining the basic problem of OPF, various methods for solving the OPF problem are reviewed. However, changes and uncertainties in energy demand, energy flow, and load changes in active distribution networks (ADNs) can lead to voltage offset, frequency dislocation, and power losses at various nodes in the network. As a result, the scheduling and optimization of ADNs can be complex. To address these challenges, it is necessary to optimize the energy distribution and load control of ADNs through an optimal power flow analysis.
Mathematical optimization methods for solving the OPF problem include conventional OPF, Alternating Direction Method of Multipliers (ADMM), Mixed Integer Linear Programming (MILP), Semi-Definite Programming (SDP), Second-Order Conic Programming (SOCP), Quadratic Programming (QP), and others. While mathematical optimization methods can provide rapid convergence and are easy to implement, they may require significant computation resources. The primary concept behind mathematical optimization is to transform the original non-convex OPF model into convex models, thus improving the accuracy and convergence time of the model.
Heuristic optimization methods for solving the OPF problem include Sunflower Optimization (SFO), Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and others. Heuristic optimization methods can handle non-convex and nonlinear problems, but they may not guarantee convergence or optimality and may depend on random factors. These methods reveal the design principles of optimization algorithms by understanding the behavior, function, experience, rules, and mechanisms of action in biological, physical, chemical, social, artistic, and other systems or domains. Under the guidance of specific problem characteristics, the corresponding feature models are refined to design intelligent iterative search-type optimization algorithms.
To the best knowledge of the authors, there is no previous review that extensively covers problem formulation and optimization methods for the OPF problem. Refs. [8][9][10][11][12][13][14] have reviewed optimization methods to solve OPF problem, Ref. [12] has reviewed heuristic and conventional algorithms in the DN while introducing some basic principles of OPF; Ref. [8] focused on the mathematical model of OPF, but has not considered other methods or modeling of new models in DN. In their articles, Refs. [13][14] individually reviewed the ADMM and heuristic methods for OPF. However, it is important to note that these reviews do not encompass the entirety of available optimization methods for OPF. Refs. [9][10] mainly focused on the problem formulation and the benefits of different methods but only presented a table for the drawbacks without providing a detailed explanation of how the algorithms work. On the other hand, Ref. [11] explained and analyzed some of the methods through case studies but included only a few methods and only in a certain network.
2. Problem Formulation
In general, distribution networks comprise loads, power lines, transformers, and DGs. However, the widespread deployment of DGs such as PV and WT, in addition to the use of various new smart meter technologies, has played a crucial role in transforming distribution networks. As a result, the nature of the distribution network has significantly changed.
2.1. Impact of DG in DN
When DGs are connected to DNs, they typically have an impact on nodal voltage and power loss in the network. A comparison of DNs before and after any DGs are connected to the DN is shown in Figure 1 and Figure 2.
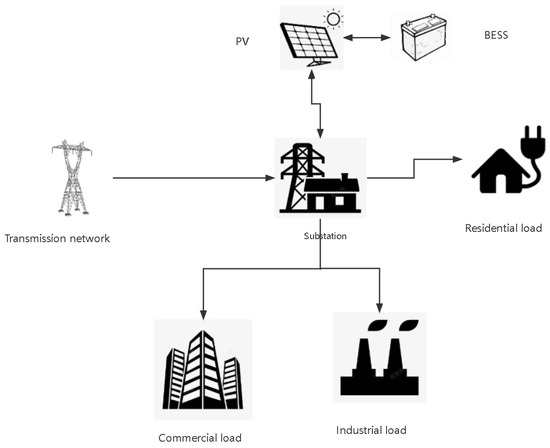
Figure 1. DN with DGs.
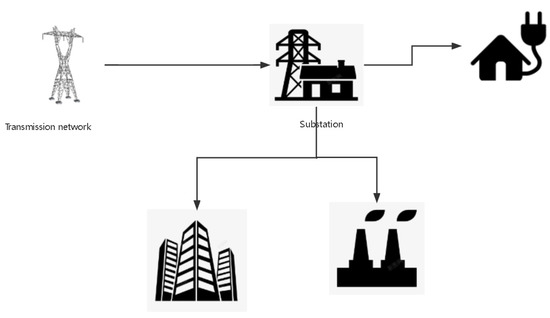
Figure 2. DN without DGs.
In [4], the influence mechanism of DGs on reactive power and voltage characteristics of DNs was explained. Additionally, Ref. [15] showed that the placement of loads in different positions can have varying impacts on voltage stability. Loads located too close to the substation can cause the voltage to be too high and can overload the load, while loads located too close to the end of the line can cause the voltage to be too low and can create an unstable power supply.
To determine the optimal placement of DGs, Ref. [16] evaluated the impact of solar PV systems on the reliability of power distribution systems using various methods. They used energy not supplied (ENS) as the primary indicator to evaluate the impact. The results revealed that distributed solar PV input significantly affects the ENS value, and the ENS value was reduced by 50% when the capacity factor of the solar PV system was equal to one. The researchers also assessed the impact of installing solar PV systems under different conditions and further evaluated the improvement in grid reliability by adding energy storage facilities.
In [17], the impact of integrating squirrel cage induction generator (SCIG) WTs at different positions on the power system was investigated. The study concluded that integrating SCIG WTs into the power system can achieve better voltage and can reduce power losses. However, voltage stability issues may arise when SCIG WTs are integrated into the power system at certain positions.
2.2. Generator Modeling
Due to the uncertainty aspect of PVs and WTs, the uncertainty of DGs can be addressed in the following ways: stochastic and forecasting models. A brief summary of the two models is expressed in Figure 3.
Figure 3. Brief summary of DG models.
2.2.1. Stochastic Model
The output of DGs is a stochastic event and, hence, can be expressed by a set of random variables. This uncertainty arises from various factors such as weather conditions, load variations, and system disturbances. In their research, Ref. [18] addressed the uncertainty of power outputs of DGs based on probability. They proposed a probabilistic approach to model the output fluctuations of DGs within a certain range. They noted that the output of DGs fluctuates within a range, and thus, they proposed a probabilistic approach to model the uncertainty.
Similarly, in their study, Ref. [19] expressed uncertainty via a range of random variables, which were observed over a specified time interval. The goal of these approaches is to effectively capture the uncertainty associated with the output of DGs, thereby supporting the optimization of power system operations.
Stochastic models offer several advantages in the evaluation of the reliability and stability aspects of photovoltaic systems. By analyzing probability distributions, these models facilitate the identification and resolution of potential issues. Moreover, they consider uncertainties associated with DGs, effectively incorporating risk factors into system design and planning. This integration enhances the reliability of decision-making processes. Furthermore, stochastic models are particularly well suited for long-term planning purposes. Leveraging historical data, these models can forecast and evaluate future power generation over extended time periods, providing valuable guidance for system design and investment decisions.
However, stochastic models also have certain limitations. They heavily rely on the quality and reliability of available data, making them highly dependent on data quality. Insufficient or inaccurate data can adversely impact the accuracy and efficacy of probability models, potentially leading to flawed results and incorrect applications. Furthermore, stochastic models prove inadequate in handling short-term fluctuations and exceptional cases. Due to their inherent characteristics, these models encounter challenges in effectively addressing short-term power generation variations and individual anomalous situations. Consequently, these limitations can introduce forecasting biases and should be carefully considered when utilizing stochastic models in practice.
2.2.2. Forecasting Model
Utilizing the relation between weather conditions and output, it is possible to establish a mathematical function to estimate the DG output. Ref. [5] estimated the output of DG by using the weather conditions. The active power output of a PV module was determined based on the input solar irradiance and ambient temperature. The equation was used in the paper to generate an active power curve that corresponds to the solar irradiance and ambient temperature data entered [20]. The commonly used PV power prediction formula calculates the predicted PV power (𝑃𝑉) based on weather conditions such as solar radiation intensity (G) and PV panel temperature (T). The formula is as follows:
𝑃𝑉(𝑡)=𝐴×𝐺(𝑡)×(1−𝛽×(𝑇(𝑡)−𝑇𝑟𝑒𝑓))
The commonly used wind turbine power prediction formula calculates the predicted wind turbine power P based on weather conditions such as wind speed (V), air density (𝜌), and the rated power of the turbine (𝑃𝑟𝑎𝑡𝑒𝑑). The formula is as follows:
𝑃=0.5×𝜌×𝐴×𝐶𝑝×𝑉3
Forecasting models offer several advantages in the context of DGs. These models leverage advanced algorithms and real-time data to provide accurate short-term predictions, enabling informed decision-making in electricity market operations and real-time dispatch. By considering multiple influencing factors such as weather conditions, seasons, and system parameters, forecasting models enhance the accuracy and reliability of predictions. Additionally, these models support intelligent operation and optimization, providing decision support for power plant operations to optimize generation scheduling and to improve energy utilization efficiency.
However, forecasting models also have certain limitations that should be taken into account. They require high-quality and timely input data to ensure accuracy and reliability. Particularly, accurate weather data and real-time operational data are crucial for achieving optimal performance. Moreover, the establishment and maintenance of high-quality forecasting models involve substantial costs. These costs include the acquisition of extensive data, the implementation of complex algorithms, and the allocation of appropriate computational resources. Therefore, cost-related challenges can arise in the development and maintenance phases. Finally, forecasting models are unable to account for future uncertainties, such as unforeseen weather events. While they provide accurate short-term predictions, unexpected uncertainties in the future cannot be accurately predicted using these models.
2.3. Demand Response
DR is a mechanism by which power users receive direct notifications or price increase signals from the power supplier to induce load reduction when the wholesale market price of electricity rises or the system reliability is threatened. This allows users to modify their inherent electricity consumption habits and to reduce or shift their electricity load over a certain period in response to the power supply, ensuring the stability of the power grid and suppressing short-term behavior of electricity price increases.
In [5][6][7], the commonly used model for the OPF problem was the electricity elasticity model, which changes the price of electricity for consumers. The article [5] provided an implementation of electricity elasticity in a DR model. The DR model assumes that multiple consumers are connected to each node and that their loads are classified as either flexible or non-flexible.
Another approach presented in [6] used electricity prices to build a DR model that modifies the load curve to obtain an equivalent daily load curve. The model considers the elasticity coefficient of the electricity price, which measures the sensitivity of electricity demand to price changes. The elasticity coefficient matrix was used to model user demand response behavior, ensuring that electricity demand in each period is related not only to the current price but also to the electricity price of other periods. This approach is particularly effective when Time-of-Use (TOU) rates are adopted.
Finally, the paper [7] proposed a combination of DR and OPF problems, the former being combined with LMP through a Lagrangian function in the latter. This approach optimizes load management by ensuring that LMP reflects the real cost of operating the power system while optimizing the use of flexible loads.
2.4. Power Flow Model
Power flow calculations, which involve solving complex equations and handling large-scale networks, often require significant computational time and resources. Ref. [21] introduced a general power flow calculation method for DN with DGs and voltage regulators. The power line can be represented by the 𝜋 model. Transformers can be represented by admittance matrices, while the load can be represented by a vector. The voltage output of a step-voltage regulator can be described using a function of tap, and the impedance and voltage drop of a compensator can be computed using the ratio of the voltage transformer and current transformer and the impedance of the line. A brief summary of the power flow models is expressed in Figure 4.
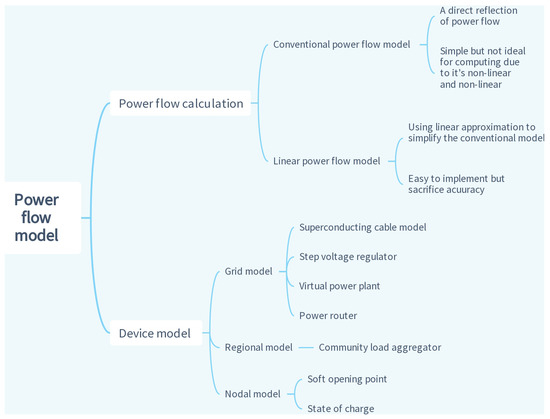
Figure 4. Brief summary of power flow models.
In [11], the Backward/Forward Sweep (BFS) method, a well-established and highly regarded power flow calculation algorithm, was shown to be a popular choice for accurately evaluating power flows in distribution networks. This method was used to calculate the power flow in the network. In [22], the Bus Injection Model (BIM) was discussed, which is used for analysis and optimization using nodal variables such as voltages, current, and power injections. This model does not directly deal with power flows on individual branches.
Based on the conventional power flow model, several approximation models have been established. The simplest approximation is to ignore some nonlinear factors in power flow calculations. In [1], a linearized power flow model was introduced, which assumes the network to be lossless. In [23], a linearized model was proposed that assumes the voltage drop to be small and uses per-unit (p.u.) values to replace real values. The model also introduces loss factors for distribution systems, which linearizes and divides the distribution grid into a few sub-areas to improve accuracy and efficiency. In [24], the Zero-Inflated Poisson (ZIP) model was combined with the current injection method to linearize the four-wire system. In [25], two linearizations based on polar coordinates were mentioned. The first approximation considers the phase angle deviation caused by impedance to be small, making sin 𝜃 0 and cos 𝜃 1 [26]. The second approximation is based on the same assumption; [27] proposed a novel power flow model, the decoupled linearized power flow model, which is state-independent and highly accurate in voltage magnitude.
Another approach to obtain linear equations is to use other methods for linearization. In [28], an approximate model for the power flow problem in three-phase unbalanced ADNs was proposed based on the Wirtinger model. In [29], a linearization method for three-phase unbalanced power systems was proposed. The method linearizes the magnitude and phase of voltage on the complex plane by representing small perturbations in voltage amplitude and phase as complex numbers and by performing a Taylor series expansion on the complex numbers to approximate the voltage changes. In [25], Taylor expansion was used for DC networks. Certain variables, such as voltage magnitude or voltage squares, are treated as independent variables, and the power flow equations are expressed using these variables to obtain linear formulas.
Similarly, Ref. [7] used first-order Taylor expansion for power loss linearization. Ref. [30] used a linearized Euclidean norm for branch current magnitudes and nodal voltages. The voltage angle range was limited for better accuracy, and an approximation of DG power injection was acquired via first-order expansion of the estimated value. In [23][31], a linearized power flow model was proposed. The model was linearized based on the loss factor-based linearization method, which is commonly used in most electricity markets in the U.S. The losses are naturally quadratic and cannot be linearized using a cold start in a non-iterative manner. Therefore, the loss factor-based linearization method was used to facilitate the fully linear formulation of the network model. The losses were linearized based on a base case system operating condition.
The conventional power flow calculation model offers high accuracy and reliability, making it suitable for various scales and types of power systems. However, it is limited by its high computational complexity and stringent data requirements, making it unsuitable for real-time calculations. Conversely, the approximate power flow calculation model provides fast computation speeds and is applicable for real-time calculations.
Considering different scenarios, some devices are used for optimization, these devices need to be modeled and added to the power flow model:
-
Various models have been proposed from the grid perspective to enhance and optimize power system operations. These models include the superconducting cable model, voltage regulator model, flexible loop converter, and energy router model. Each model serves a specific purpose, such as improving transmission efficiency, voltage regulation, and interconnection between microgrids. In [32], the zero-resistance characteristic of superconducting material was considered, and the superconducting magnet parameters were introduced to reflect the superconducting properties. The modeling of the superconducting cable was constructed using a nonlinear inductance, current source, and leakage resistance to model the cable as an element within the circuit analysis. Voltage regulators play a crucial role in maintaining stable power transmission by adjusting the voltage levels of transformers. These devices ensure that voltage remains within the desired range, mitigating potential issues associated with voltage fluctuations. The power flow calculation method proposed in [21] considers the influence of distributed generation and voltage regulators. The method adds the power equation of distributed generation to the power flow equation of the system and uses the three-phase power injection method in the calculation, which overcomes the convergence problem that traditional power flow calculation methods face. In [33], the modeling of step voltage regulators (svrs) was achieved by assuming that the svr is an ideal component and by modeling it as a three-phase element. The series impedance of the single-phase autotransformer of the svr wes assumed to be zero. The Virtual Power Plant (VPP) model was proposed in [34], which allows for the integration of distributed energy resources as a virtual unit and can participate in the energy market. To interconnect microgrids, power routers must be used. In [35], a stable model for PRs was proposed based on the steady-state power flow calculation model. The line structure in the hybrid AC/DC distribution system based on PR is divided into eight types according to the bus type at both ends of the line and the line type. The power transaction between microgrids relies on energy routers, as proposed by [36]. The energy router is modeled using the port-bus incidence matrix by expressing the energy router using nodal currents and by applying constraints such as Kirchhoff’s current law (KCL) and Kirchhoff’s voltage law (KVL) before embedding it into the existing power system power flow model.
-
The flexible closed-loop converter, constructed using power electronic devices, can achieve DC transmission and can solve the impact of closing AC load loop on the power grid, providing ideas for the closed-loop control of distribution networks. According to [37], there are four operational modes for the flexible closed-loop converter: closed-loop operation mode, power flow transfer mode, circulating current limiting mode, and power flow control mode. The power flow transfer and power flow control modes involve solving the power flow equations. In the power flow transfer mode, when a line of a substation fails or stops operating due to maintenance, the closed-loop controller transfers the remaining load to another line. In the power flow control mode, the closed-loop controller outputs adjustable voltage amplitudes and phases according to the power demand of the secondary power supply line, such as load balancing and minimum line loss, and inserts it into the line for the control of four-quadrant power flow.
-
From the regional perspective, a Community Load Aggregator (CLA) is established. In some studies, a whole residential area is considered to be a node. Ref. [38] established the CLA model by integrating and modeling the residential load, electric vehicle load, and communication load in a community. The model is divided into static and dynamic loads, where static loads refer to the residential and communication loads that have relatively stable characteristics, while dynamic loads refer to the electric vehicle load, which has significant time-varying characteristics and requires optimized scheduling strategies.
-
For a single node, the Soft Opening Point (SOP) model and the State of Charge (SOC) model are established. Ref. [39] modeled SOP and estimated the loss of SOP with the least square estimator. To describe the status of energy storage of a single nodal DG, Ref. [40] used SOC. The formula was used to determine the SOC of a battery based on the battery’s charging and discharging power, charging and discharging efficiency, rated capacity, and calculation time interval.
2.5. Objective Function
There are two main types of objective functions with constraints: one considers network loss, while the other also considers the cost of generators and node voltages.
In [29], the objective function was set as the minimization of power loss after deploying DGs in a distribution network. In [41], the objective function was adjusted to include power loss as a Lagrangian function for ADMM. In [2], power transfer distribution factors (PTDFs) were introduced to calculate the estimated contributions of changes in power output from each generator to each flow into the corresponding transmission line/interface based on the topology of the power system’s transmission network. This approach is used to establish mathematical relationships between characteristics such as line resistance and node stress, representing the interconnectivity and power transfer capacity between nodes and lines. In [34], the objective function was set as the Source–Load–Storage Matching Index, which aims to allocate distributed energy resources (DERs) to support the grid’s load demand while minimizing the economic cost. In [23][42], not only power loss but also the LMPs were considered for pricing. The LMPs reflect the power production and demand characteristics of the network, and the pricing information can provide economic incentives to encourage optimal utilization of resources.
In addition to traditional objectives such as power loss and cost, carbon emission is also being considered in power system optimization due to the “Dual-Carbon” policy. For example, in [43], an electrothermal model for thermal loads in DNs was established, and a carbon dioxide emission cost was put into consideration when optimizing, in addition to the general loss and cost functions. Similarly, in [44], the effect of temperature on transmission line load was considered, and the goal was to reduce power flow losses accordingly. In [3], the carbon dioxide generated when renewable generators cannot supply the loads was considered as a goal when optimizing. In [45], security was also introduced as one of the objectives of power system optimization.
References
- Sadnan, R.; Dubey, A. Learning optimal power flow solutions using linearized models in power distribution systems. In Proceedings of the 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Fort Lauderdale, FL, USA, 20–25 June 2021; pp. 1586–1590.
- Farfan-Ramirez, S.; Gutierrez-Alcaraz, G.; Perez-Hernandez, G. Two lossy multi-period optimal power flow formulations with renewable energy and storage. In Proceedings of the 2018 North American Power Symposium (NAPS), Fargo, ND, USA, 9–11 September 2018; pp. 1–6.
- Zheng, P.; Cheng, N.; Huang, X. Carbon reduction assessment of electric vehicle aggregation participating in distribution network dispatching based on v2g technology. In Proceedings of the 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 27–30 October 2022; pp. 1563–1568.
- Ma, T.; Zhang, T. Research on reactive power and voltage characteristics analysis and reactive power configuration strategy of active distribution network. In Proceedings of the 2019 12th International Conference on Intelligent Computation Technology and Automation (ICICTA), Xiangtian, China, 19–27 August 2019; pp. 108–111.
- Verma, R.; Padhy, N.P. Optimal power flow based dr in active distribution network with reactive power control. IEEE Syst. J. 2022, 16, 3522–3530.
- Oi, L.; Wu, K.; Wang, Y.; Jing, X.; Cui, C.; Zhao, R. Research on dynamic optimized operation strategy of distribution network considering demand response. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 901–906.
- Vaishya, S.R.; Abhyankar, A.R.; Kumar, P. A novel loss sensitivity based linearized opf and lmp calculations for active balanced distribution networks. IEEE Syst. J. 2023, 17, 1340–1351.
- Shah, C.; Wies, R. Algorithms for optimal power flow in isolated distribution networks using different battery energy storage models. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5.
- Veeraganti, S.D.; Mohammed Imran, A. Optimal placement and sizing of dg and d-statcom in a distribution system: A review. In Proceedings of the 2022 International Virtual Conference on Power Engineering Computing and Control: Developments in Electric Vehicles and Energy Sector for Sustainable Future (PECCON), Chennai, India, 5–6 May 2022; pp. 1–13.
- Verma, A.; Thakur, R. A review on methods for optimal placement of distributed generation in distribution network. In Proceedings of the 2022 Interdisciplinary Research in Technology and Management (IRTM), Kolkata, India, 24–26 February 2022; pp. 1–8.
- Mylonas, C.; Karagiannopoulos, S.; Aristidou, P.; Shchetinin, D.; Hug, G. Comparison of optimal power flow formulations in active distribution grids. In Proceedings of the 12th Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2020), Paphos, Cyprus, 9–12 November 2020; Volume 2020, pp. 378–383.
- Charles, P.; Mehazzem, F.; Soubdhan, T. A review on optimal power flow problems: Conventional and metaheuristic solutions. In Proceedings of the 2020 2nd International Conference on Smart Power & Internet Energy Systems (SPIES), Bangkok, Thailand, 5 July 2020; pp. 577–582.
- Papadimitrakis, M.; Giamarelos, N.; Stogiannos, M.; Zois, E.; Livanos, N.; Alexandridis, A. Metaheuristic search in smart grid: A review with emphasis on planning, scheduling and power flow optimization applications. Renew. Sustain. Energy Rev. 2021, 145, 111072.
- Maneesha, A.; Swarup, K. A survey on applications of Alternating Direction Method of Multipliers in smart power grids. Renew. Sustain. Energy Rev. 2021, 152, 111687.
- Shin, B.H.; Oh, G.D.; Kim, S.C.; Jung, K.H. Power flow and economics analysis for rmu-based low-voltage distribution networks operation. In Proceedings of the CIRED 2021—The 26th International Conference and Exhibition on Electricity Distribution, Online, 20–23 September 2021; Volume 2021, pp. 2432–2436.
- Meegoda, M.; Balasooriya, B.; Dharmapriya, E.; Kumara, J.; Amarasinghe, P.A.G.M.; Abeygunawardane, S.K. Impact of solar PV systems on the reliability of power distribution systems. In Proceedings of the 2020 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 28–30 July 2020; pp. 560–565.
- Fernández, J.; Grijalva, S. Implicit reactive power flow representation to support distribution system der energy scheduling. In Proceedings of the 2022 North American Power Symposium (NAPS), Salt Lake City, UT, USA, 9–11 October 2022; pp. 1–5.
- Huang, H.; Zhou, M.; Zhang, S.; Zhang, L.; Li, G.; Sun, Y. Exploiting the operational flexibility of wind integrated hybrid AC/DC power systems. IEEE Trans. Power Syst. 2021, 36, 818–826.
- Li, B.; Zhang, X.; Wang, K.; Zhang, Y.; Zhu, Z.; Liu, J. Cooperative optimal scheduling of interconnected transmission-distribution-micro power system. In Proceedings of the 2022 12th International Conference on Power, Energy and Electrical Engineering (CPEEE), Scopus Shiga, Japan, 25–27 February 2022; pp. 215–219.
- Ammar, M.; Sharaf, A.M. Optimized use of pv distributed generation in voltage regulation: A probabilistic formulation. IEEE Trans. Ind. Inform. 2019, 15, 247–256.
- Zhu, L.; Chen, S.; Mo, W.; Wang, Y.; Li, G.; Chen, G. Power flow calculation for distribution network with distributed generations and voltage regulators. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 662–667.
- Biswas, B.D.; Kamalasadan, S. Alternative sdp relaxed optimal power flow formulation for radial distribution networks. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 2–5 January 2022; pp. 1–6.
- Yuan, H.; Li, F.; Wei, Y.; Zhu, J. Novel linearized power flow and linearized opf models for active distribution networks with application in distribution lmp. IEEE Trans. Smart Grid 2018, 9, 438–448.
- Heidari-Akhijahani, A.; Safdarian, A.; Vrakopoulou, M. A linear ac power flow model for unbalanced multi-phase distribution networks based on current injection equations. IEEE Trans. Power Syst. 2021, 36, 3806–3809.
- Campos, A.C.D.; Pinto, R.S.; Filho, M.O.D.L.; Unsihuay-Vila, C. A linear AC three-phase optimal power flow model for active distribution networks and microgrids. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Lima, Peru, 15–17 September 2021; pp. 1–5.
- Li, H.; Yan, X.; Yan, J.; Zhang, A.; Zhang, F. A three-phase unbalanced linear power flow solution with pv bus and zip load. IEEE Access 2019, 7, 138879–138889.
- Yang, J.; Zhang, N.; Kang, C.; Xia, Q. A state-independent linear power flow model with accurate estimation of voltage magnitude. IEEE Trans. Power Syst. 2017, 32, 3607–3617.
- Sepúlveda, S.; Ruíz, A.G.; Mora-Flórez, J.J. Optimal power flow for three-phase unbalanced active distribution networks with delta connections. In Proceedings of the 2022 IEEE ANDESCON, Barranquilla, Colombia, 16–19 November 2022; pp. 1–6.
- Feng, K.; Wu, Z.; Li, P.; Hu, M. Optimal active and reactive power coordinated dispatch in unbalanced distribution networks. In Proceedings of the 2020 International Conference on Smart Grids and Energy Systems (SGES), Perth, Australia, 23–26 November 2020; pp. 385–389.
- Giraldo, J.S.; Vergara, P.P.; López, J.C.; Nguyen, P.H.; Paterakis, N.G. A novel linear optimal power flow model for three-phase electrical distribution systems. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020; pp. 1–6.
- Yang, Z.; Zhong, H.; Bose, A.; Zheng, T.; Xia, Q.; Kang, C. A linearized opf model with reactive power and voltage magnitude: A pathway to improve the mw-only dc opf. IEEE Trans. Power Syst. 2018, 33, 1734–1745.
- Zhang, Z.; Cheng, R.; He, X.; Huang, J.; Zhang, Z.; Zhang, A.; Ren, L. Research on optimal power flow control of closed-loop distribution network with superconducting cable. In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 28–30 March 2020; pp. 555–559.
- Bazrafshan, M.; Gatsis, N.; Zhu, H. Optimal power flow with step-voltage regulators in multi-phase distribution networks. IEEE Trans. Power Syst. 2019, 34, 4228–4239.
- Wang, J.; Du, W.; Yang, D.; Liu, G.; Chen, H. An optimal scheduling method of virtual power plant cluster considering generation-grid-load-storage coordination. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 8–11 April 2021; pp. 1048–1052.
- Li, P.; Sheng, W.; Duan, Q. Optimal power flow calculation method for AC/DC hybrid distribution network based on power router. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 8–11 April 2021; pp. 1694–1699.
- Miao, J.; Zhang, N.; Kang, C.; Wang, J.; Wang, Y.; Xia, Q. Steady-state power flow model of energy router embedded ac network and its application in optimizing power system operation. IEEE Trans. Smart Grid 2018, 9, 4828–4837.
- Zhang, Y.; Mao, Z.; Liu, J.; Xu, H. Research on optimal power flow by interior point method for ac distribution network with flexible loop converters. In Proceedings of the 2022 7th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 23–26 September 2022; pp. 257–263.
- Wang, H.; Li, Y.; Shi, S.; Zhou, Y.; Lei, T.; Feng, D.; Fang, C.; Liu, Z. Optimal power scheduling strategy in residential distribution network based on multi-dimensional network integration. In Proceedings of the 2021 Power System and Green Energy Conference (PSGEC), Shanghai, China, 13–16 May 2021; pp. 85–90.
- Ivic, D.R.; Stefanov, P.C. An extended control strategy for weakly meshed distribution networks with soft open points and distributed generation. IEEE Access 2021, 9, 137886–137901.
- Chen, Y.; Zhao, W.; Hou, H.; Yuan, Z.; Xu, I. Research on optimal dispatching strategy of multi-terminal dc distribution network. In Proceedings of the 2022 China International Conference on Electricity Distribution (CICED), Changsha, China, 7–8 September 2022; pp. 525–529.
- Mhanna, S.; Verbič, G.; Chapman, A.C. Adaptive admm for distributed AC optimal power flow. IEEE Trans. Power Syst. 2019, 34, 2025–2035.
- Wei, W.; Wang, J.; Wu, L. Distribution optimal power flow with real-time price elasticity. IEEE Trans. Power Syst. 2018, 33, 1097–1098.
- Zhao, Z.; Wang, Z.; Hao, J.; Wang, S.; Wang, X.; Xie, H.; Li, X. A multi-objective power flow optimization model of electric and thermal distribution network using the power flow method. In Proceedings of the 2022 9th International Forum on Electrical Engineering and Automation (IFEEA), Zhuhai, China, 4–6 November 2022; pp. 687–690.
- Picanco, A.F.; Oliveira, A.P. Reactive optimal power flow in the temperature-dependent power flow using interior point method with artificial neural network. In Proceedings of the Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2018), Dubrovnik, Croatia, 12–15 November 2018; pp. 1–6.
- Anthony, I.O.; Mokryani, G.; Zubo, R.H.; Ezechukwu, O.A.; Ivry, P. Distribution network reconfiguration considering security-constraint and multi-dg configurations. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Torino, Italy, 1–4 September 2020; pp. 1–6.
More
Information
Subjects:
Engineering, Electrical & Electronic
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
639
Revisions:
2 times
(View History)
Update Date:
24 Aug 2023
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




