
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Farzad Kiani | -- | 1527 | 2023-05-25 15:19:07 | | | |
| 2 | Camila Xu | Meta information modification | 1527 | 2023-05-26 03:08:14 | | | | |
| 3 | Farzad Kiani | + 24 word(s) | 1551 | 2023-08-07 18:57:17 | | |
Video Upload Options
The concept of chaos has been applied extensively in various applications with the growth of nonlinear dynamical systems that are highly sensitive to the initial state. Chaos-based algorithms can generate a large number of different search points in a short time, which can help explore the optimization area more efficiently and quickly than traditional optimization algorithms. In this regard, a new method named CSCSO is proposed to improve the shortcomings of the recently proposed Sand Cat Swarm Optimization (SCSO) algorithm with this chaos theory. This algorithm has also been tested in engineering and social science-based constrained problems. Especially in social sciences, it solves basic problems with this kind of artificial intelligence-based mechanism instead of traditional methods such as questionnaires and fieldresearch.
1. Introduction
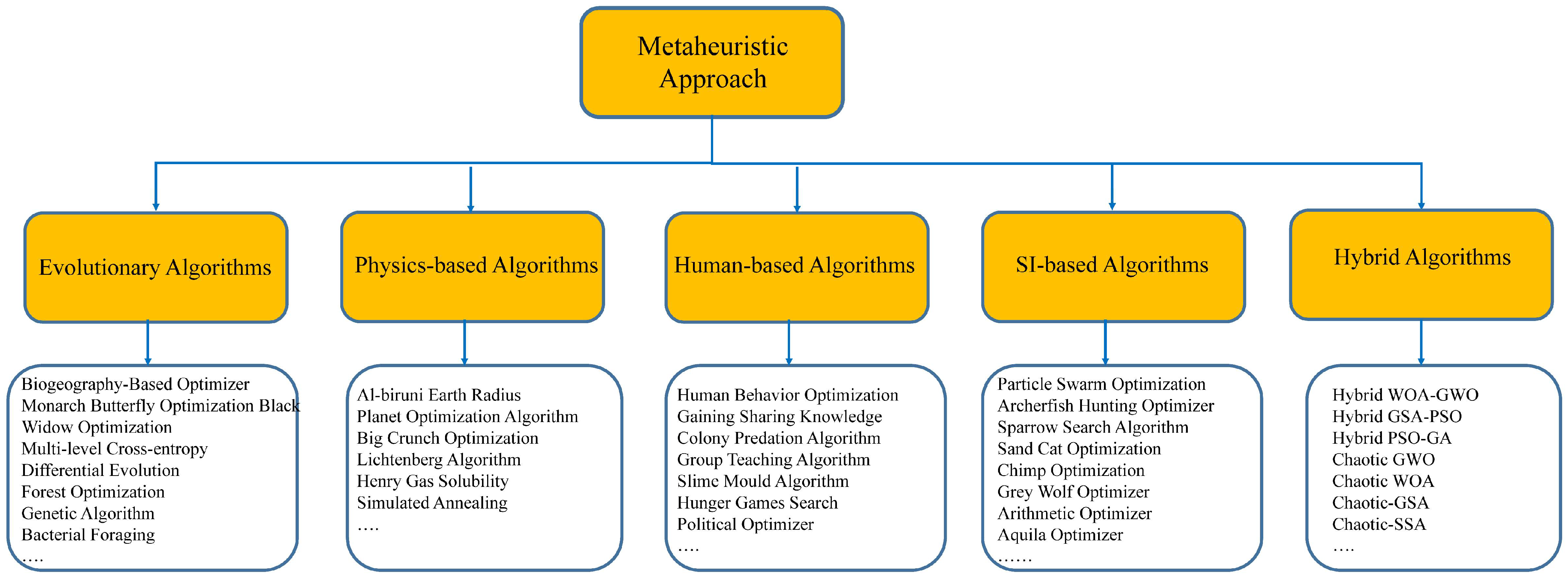
2. The Analysis of Chaos-Based Metaheuristic Methods
References
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl. Based Syst. 2023, 262, 136.
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm, Computer Methods. Appl. Mech. Eng. 2021, 376, 113609.
- Kiani, F.; Anka, F.A.; Erenel, F. PSCSO: Enhanced Sand Cat Swarm Optimization Inspired by the Political System to Solve Complex Problems. Adv. Eng. Softw. 2023, 178, 103423.
- Kalinin, K.P.; Berloff, N.G. Computational complexity continuum within using formulation of NP problems. Nat. Commun. Phys. 2022, 5, 20.
- Kumar, S.; Yildiz, B.S.; Mehta, P.; Panagant, N.; Sait, S.M.; Mirjalili, S.; Yildiz, A.R. Chaotic marine predators algorithm for global optimization of real-world engineering problems. Knowl. Based Syst. 2023, 261, 110192.
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82.
- Ghasemi, M.; Kadkhoda Mohammadi, S.; Zare, M.; Mirjalili, S.; Gil, M.; Hemmati, R. A new firefly algorithm with improved global exploration and convergence with application to engineering optimization. Decis. Anal. J. 2022, 5, 100125.
- Nematzadeh, S.; Kiani, F.; Torkamanian-Afshar, M.; Aydin, N. Tuning hyperparameters of machine learning algorithms and deep neural networks using metaheuristics: A bioinformatics study on biomedical and biological cases. Comput. Biol. Chem. 2022, 97, 107619.
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 2021, 1–25.
- Osuna-Enciso, V.; Cuevas, E.; Castañeda, B.M. A diversity metric for population-based metaheuristic algorithms. Inf. Sci. 2022, 586, 192–208.
- Agushaka, J.O.; Ezugwu, A.E. Initialisation Approaches for Population-Based Metaheuristic Algorithms: A Comprehensive Review. Appl. Sci. 2022, 12, 896.
- Gezici, H.; Livatyali, H. Chaotic Harris hawks optimization algorithm. J. Comput. Des. Eng. 2022, 9, 216–245.
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73.
- He, Y.; Zhang, F.; Mirjalili, S.; Zhang, T. Novel binary differential evolution algorithm based on Taper-shaped transfer functions for binary optimization problems. Swarm Evol. Comput. 2022, 69, 101022.
- Bao, C.; Gao, D.; Gu, W.; Xu, L.; Goodman, L. A new adaptive decomposition-based evolutionary algorithm for multi- and many-objective optimization. Expert Syst. Appl. 2023, 213, 119080.
- Hayyolalam, V.; Pourhaji Kazem, A.A. Black Widow Optimization Algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249.
- El-Kenawy, E.M.; Abdelhamid AIbrahim, A.; Mirjalili, S. Al-biruni earth radius (ber) metaheuristic search optimization algorithm. Comput. Syst. Sci. Eng. 2023, 45, 1917–1934.
- Sang-To, T.; Hoang-Le, M.; Wahab, M.A. An efficient Planet Optimization Algorithm for solving engineering problems. Sci. Rep. 2022, 12, 8362.
- Ahmadianfar, I.; Heidari, A.; Gandomi, A.H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta Method. Expert Syst. Appl. 2021, 181, 115079.
- Ahmadi, S.A. Human behavior-based optimization: A novel metaheuristic approach to solve complex optimization problems. Neural Comput. Appl. 2017, 28, 233–244.
- Dehghani, M.; Trojovská, E.; Trojovský, P.A. new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process. Sci. Rep. 2022, 12, 9924.
- Askari, Q.; Younas, I.; Saeed, M. Political Optimizer: A novel socio-inspired meta-heuristic for global optimization. Knowl.-Based Syst. 2020, 195, 1–25.
- Sindhiya, R.; Perumal, B.; Pallikonda, M. A hybrid deep learning based brain tumor classification and segmentation by stationary wavelet packet transform and adaptive kernel fuzzy c means clustering. Adv. Eng. Softw. 2022, 170, 103146.
- Seyyedabbasi, A.; Kiani, F. I-GWO and Ex-GWO: Improved algorithms of the Grey Wolf Optimizer to solve global optimization problems. Eng. Comput. 2021, 37, 509–532.
- Zitouni, F.; Harous, S.; Belkeram, A.; Hammou, L.E.B. The Archerfish Hunting Optimizer: A Novel Metaheuristic Algorithm for Global Optimization. Arab J. Sci. Eng. 2022, 47, 2513–2553.
- Saremi, S.; Mirjalili, S.; Lewis, A. Biogeography-based optimization with chaos. Neural Comput. Appl. 2014, 25, 1077–1097.
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250.
- Kohli, M.; Arora, S. Chaotic grey wolf optimization algorithm for constrained optimization problems. J. Comput. Des. Eng. 2018, 5, 458–472.
- Amirteimoori, A.; Mahdavi, I.; Solimanpur, M.; Ali, S.S.; Tirkolaee, E.B. A parallel hybrid PSO-GA algorithm for the flexible flow-shop scheduling with transportation. Comput. Ind. Eng. 2022, 173, 1–16.
- Naik, A. Chaotic Social Group Optimization for Structural Engineering Design Problems. J. Bionic Eng. 2023, 2023, 1–26.
- Kiani, F.; Seyyedabbasi, A.; Mahouti, P. Optimal characterization of a microwave transistor using grey wolf algorithms. Analog. Integr. Circ. Sig. Process 2021, 109, 599–609.
- Sharma, V.; Tripathi, A.K. A systematic review of meta-heuristic algorithms in IoT based application. Array 2022, 14, 100164.
- Anka, F.; Seyyedabbasi, A. Metaheuristic Algorithms in IoT: Optimized Edge Node Localization. In Engineering Applications of Modern Metaheuristics. Studies in Computational Intelligence; Akan, T., Anter, A.M., Etaner-Uyar, A.Ş., Oliva, D., Eds.; Springer: Cham, Switzerland, 2023; Volume 1069.
- Kiani, F.; Seyyedabbasi, A.; Nematzadeh, S. Improving the performance of hierarchical wireless sensor networks using the metaheuristic algorithms: Efficient cluster head selection. Sens. Rev. 2021, 41, 368–381.
- Babaeinesami, A.; Tohidi, H.; Ghasemi, P.; Goodarzian, F.; Tirkolaee, E.B. A closed-loop supply chain configuration considering environmental impacts: A self-adaptive NSGA-II algorithm. Appl. Intell. 2022, 52, 13478–13496.
- Wang, G.G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014.
- MiarNaeimi, F.; Azizyan, G.; Rashki, M. Multi-level cross entropy optimizer (MCEO): An evolutionary optimization algorithm for engineering problems. Eng. Comput. 2018, 34, 719–739.
- Ghaemi, M.; Feizi-Derakhshi, M. Forest Optimization Algorithm. Expert Syst. Appl. 2014, 41, 6676–6687.
- Guo, C. A survey of bacterial foraging optimization. Neurocomputing 2021, 452, 728–746.
- Kaveh, A.; Bakhshpoori, T. Big Bang-Big Crunch Algorithm. In Metaheuristics: Outlines, MATLAB Codes and Examples; Springer: Cham, Switzerland, 2019.
- Pereira, J.L.J.; Francisco, M.B.; Diniz, C.A.; Oliver, G.A.; Cunha, S.S., Jr.; Gomes, G.F. Lichtenberg algorithm: A novel hybrid physics-based meta-heuristic for global optimization. Expert Syst. Appl. 2021, 170, 114522.
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667.
- Mohamed, A.; Emam, A.; Zoheir, B. SAM-HIT: A Simulated Annealing Multispectral to Hyperspectral Imagery Data Transformation. Remote Sens. 2023, 15, 1154.
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K. Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cyber. 2020, 11, 1501–1529.
- Tu, J.; Chen, H.; Wang, M.; Gandomi, A.H. The Colony Predation Algorithm. J. Bionic. Eng. 2021, 18, 674–710.
- Zhang YJin, Z. Group teaching optimization algorithm: A novel metaheuristic method for solving global optimization problems. Expert Syst. Appl. 2020, 148, 113246.
- Yang, Y. Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021, 177, 114864.
- Li, S.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323.
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948.
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in Sparrow Search Algorithm: A Comprehensive Survey. Arch. Comput. Methods Eng. 2023, 30, 427–455.
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338.
- Mohammed, H.; Rashid, T. A novel hybrid GWO with WOA for global numerical optimization and solving pressure vessel design. Neural Comput. Appl. 2020, 32, 14701–14718.
- Patel, S.K.; Pandey, A.K.; Roshan, R.; Singh, U.K. Application of PSO and GSA Hybrid Optimization Method for 1-D Inversion of Magnetotelluric Data. In Proceedings of the International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Odisha, India, 3–5 October 2016; pp. 1908–1911.
- Wang, W.; Liu, F.; Wang, W.; Cheng, M. The Chaotic Time Series Prediction Method Based on Sparrow Search Algorithm Optimization. In Proceeding of the 2nd International Conference on Intelligent Computing and Human-Computer Interaction (ICHCI), Shenyang, China, 17–19 December 2021.
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61.
- Mirjalili, S.; Gandomi, A.H. Chaotic gravitational constants for the gravitational search algorithm. Appl. Soft Comput. 2017, 53, 407–419.
- Kaur, G.; Arora, S. (2018). Chaotic whale optimization algorithm. J. Comput. Des. Eng. 2018, 5, 275–284.
- Yang, D.X.; Li, G.; Cheng, G.D. On the efficiency of chaos optimization algorithms for global optimization. Chaos Solitons Fractals 2007, 34, 1366–1375.
- Secui, D.C. A modified Symbiotic Organisms Search algorithm for large scale economic dispatch problem with valve-point effects. Energy 2016, 113, 366–384.
- Rezaee Jordehi, A. A chaotic-based big bang–big crunch algorithm for solving global optimisation problems. Neural Comput. Appl. 2014, 25, 1329–1335.
- Erol, O.K.; Eksin, I. A new optimization method: Big bang-big crunch. Adv. Eng. Softw. 2006, 37, 106–111.
- Wang, G.G.; Deb, S.; Gandomi, A.H.; Zhang, Z.; Alavi, A.H. Chaotic cuckoo search. Soft Comput. 2016, 20, 3349–3362.
- Wang GGGandomi, A.H.; Alavi, A.H. A chaotic particle-swarm krill herd algorithm for global numerical optimization. Kybernetes 2013, 42, 962–978.
- Saremi, S.; Mirjalili, S.M.; Mirjalili, S. Chaotic krill herd optimization algorithm. Procedia Technol. 2014, 12, 180–185.
- Cheng, C.T.; Wang, W.C.; Xu, D.M.; Chau, K.W. Optimizing hydropower reservoir operation using hybrid genetic algorithm and chaos. Water Resour. Manag. 2008, 22, 895–909.
- Qiao, W.; Yang, Z. Modified dolphin swarm algorithm based on chaotic maps for solving high-dimensional function optimization problems. IEEE Access 2019, 7, 110472–110486.
- Wu, T.Q.; Yao, M.; Yang, J.H. Dolphin swarm algorithm. Front. Inf. Technol. Electron. Eng. 2016, 17, 717–729.
- Tian, Y.; Jiang, P. Optimization of Tool Motion Trajectories for Pocket Milling Using a Chaos and Colony Algorithm. In Proceeding of the 10th IEEE International Conference on Computer-Aided Design and Computer Graphics, Beijing, China, 15–18 October 2007; pp. 389–394.





