Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Shahid Hussain | -- | 2080 | 2023-05-17 15:38:18 | | | |
| 2 | Jessie Wu | + 51 word(s) | 2131 | 2023-05-18 07:17:30 | | | | |
| 3 | Jessie Wu | Meta information modification | 2131 | 2023-05-18 07:17:42 | | | | |
| 4 | Jessie Wu | + 2 word(s) | 2133 | 2023-05-18 07:19:44 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Hussain, S.; Kallaste, A.; Vaimann, T. Optimization of Additive Manufacturing Electrical Machines. Encyclopedia. Available online: https://encyclopedia.pub/entry/44444 (accessed on 07 February 2026).
Hussain S, Kallaste A, Vaimann T. Optimization of Additive Manufacturing Electrical Machines. Encyclopedia. Available at: https://encyclopedia.pub/entry/44444. Accessed February 07, 2026.
Hussain, Shahid, Ants Kallaste, Toomas Vaimann. "Optimization of Additive Manufacturing Electrical Machines" Encyclopedia, https://encyclopedia.pub/entry/44444 (accessed February 07, 2026).
Hussain, S., Kallaste, A., & Vaimann, T. (2023, May 17). Optimization of Additive Manufacturing Electrical Machines. In Encyclopedia. https://encyclopedia.pub/entry/44444
Hussain, Shahid, et al. "Optimization of Additive Manufacturing Electrical Machines." Encyclopedia. Web. 17 May, 2023.
Copy Citation
Optimization in electrical machine design refers to the process of making improvements to the design of an electrical machine in order to maximize its performance and/or cost-effectiveness. To examine and optimize several aspects of the machine, including various parameters such as the shape of the machine, mathematical models and algorithms are often used.
additive manufacturing
topology optimization
level set
flux
1. Introduction
Generally, optimization techniques can be classified as deterministic and stochastic optimization. Deterministic optimization techniques, such as gradient-based methods, use a specific mathematical formula to find the optimal solution. They are fast and reliable but may be trapped in a local minimum while stochastic optimization techniques, such as genetic algorithms and particle swarm optimization use random processes to explore the solution space. They are less likely to get trapped in a local minimum but may be slower and less reliable [1]. The choice of method depends on the specific problem and requirements of the application.
Moreover, commonly used machine geometry templates and mathematical models for optimization are used to shape magnetic structures in electrical machines. These methods are well established and have been used for many years in the design and optimization of electrical machines. The use of these methods can make the design process more efficient and manageable, but it also restricts the design options to the predefined parameters, limiting the possible shapes and forms that can be generated. On the other hand, topology optimization (TO) is a more recent technique that involves the optimization of the overall layout and structure of the magnetic components in an electrical machine, rather than just the shape of individual components. For example, in the design of electrical machines, flux barriers inside the rotor or stator design spaces can be added and optimized for performance improvement. If the geometry optimization is utilized for the flux barriers, it increases the optimization variables and is not flexible to get the optimal shape [2][3][4][5]. Nevertheless, the TO approach can lead to more efficient and lightweight designs, but it is generally more computationally intensive and requires specialized software [6][7][8]. The integration of TO and AM is demonstrated in the flowchart depicted in Figure 1.
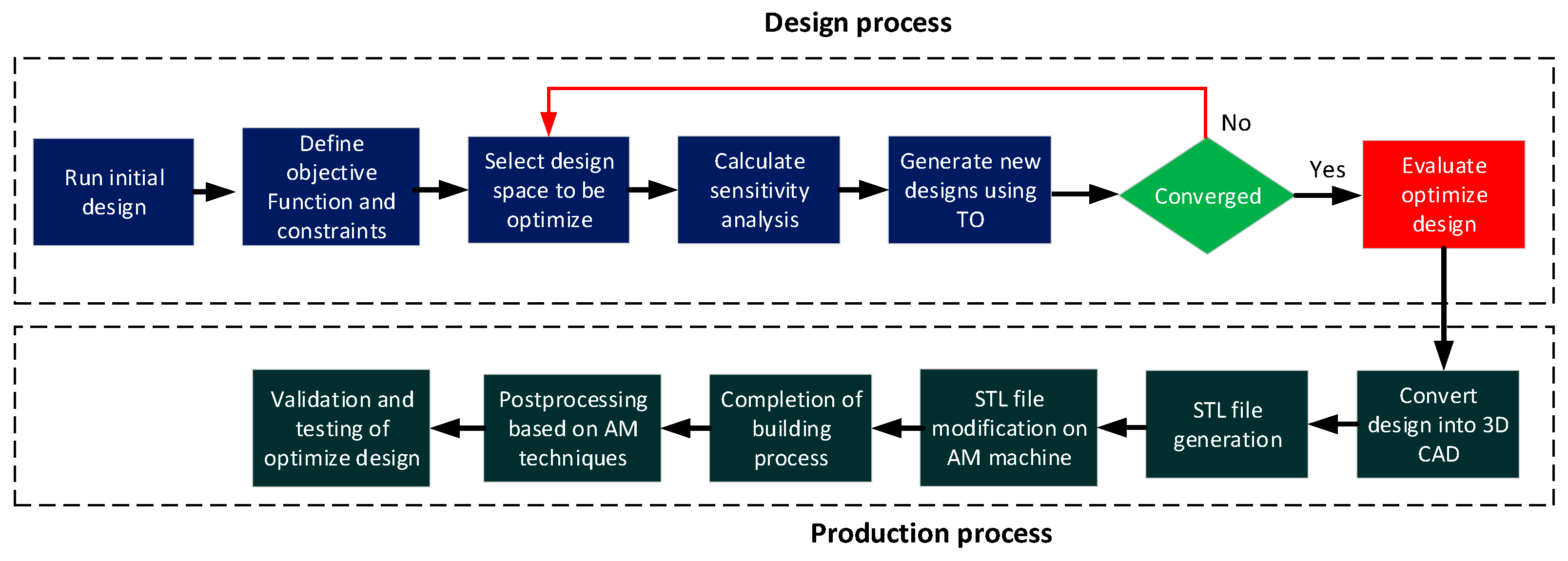
Figure 1. Steps involved for the TO and AM integration.
2. Topology Optimization of Reluctance Machines
The main objective of most TO studies for electric machines is to improve torque density and optimize the torque profile or cogging torque by adjusting the material distribution in the rotor. This can be achieved by using advanced optimization techniques and algorithms to find the optimal distribution of material in the rotor that results in the highest torque density or the desired torque profile [9]. Additionally, reluctance machines such as synchronous reluctance and switch reluctance machines have a simple construction compared to other types of electric machines, which makes them a good candidate for TO [9][10][11][12][13]. Despite receiving less attention, the TO of electric machine stator design has been reported in [14][15]. Different TO methods have been developed in the field of electrical machines during the last few years and these techniques may be broadly categorized into three groups: (i) the ON–OFF method, (ii) the Level set method, and (iii) the Material density method.
2.1. ON–OFF Method
The ON–OFF-based TO technique divides the design space into smaller cells and assigns each cell as either air (OFF) or iron (ON) through a discretization process using triangular or rectangular mesh structure [16]. This technique can be combined with various numerical optimization methods, such as evolutionary and gradient-based algorithms, to find approximate optimal solutions. In [17][18][19][20], evolutionary-based methods that do not require gradient information have been used. However, it may result in complex and non-intuitive shapes with isolated or disconnected regions of material, as shown in Figure 2a. This can lead to difficulties in fabrication or reduced performance of the final design. To overcome this issue, the author in [21][22][23][24] proposed the ON–OFF method with an immune algorithm to optimize the rotor of SRM, in which the filtering process is introduced to obtain the feasible shapes and improve the torque property as shown in Figure 2b.
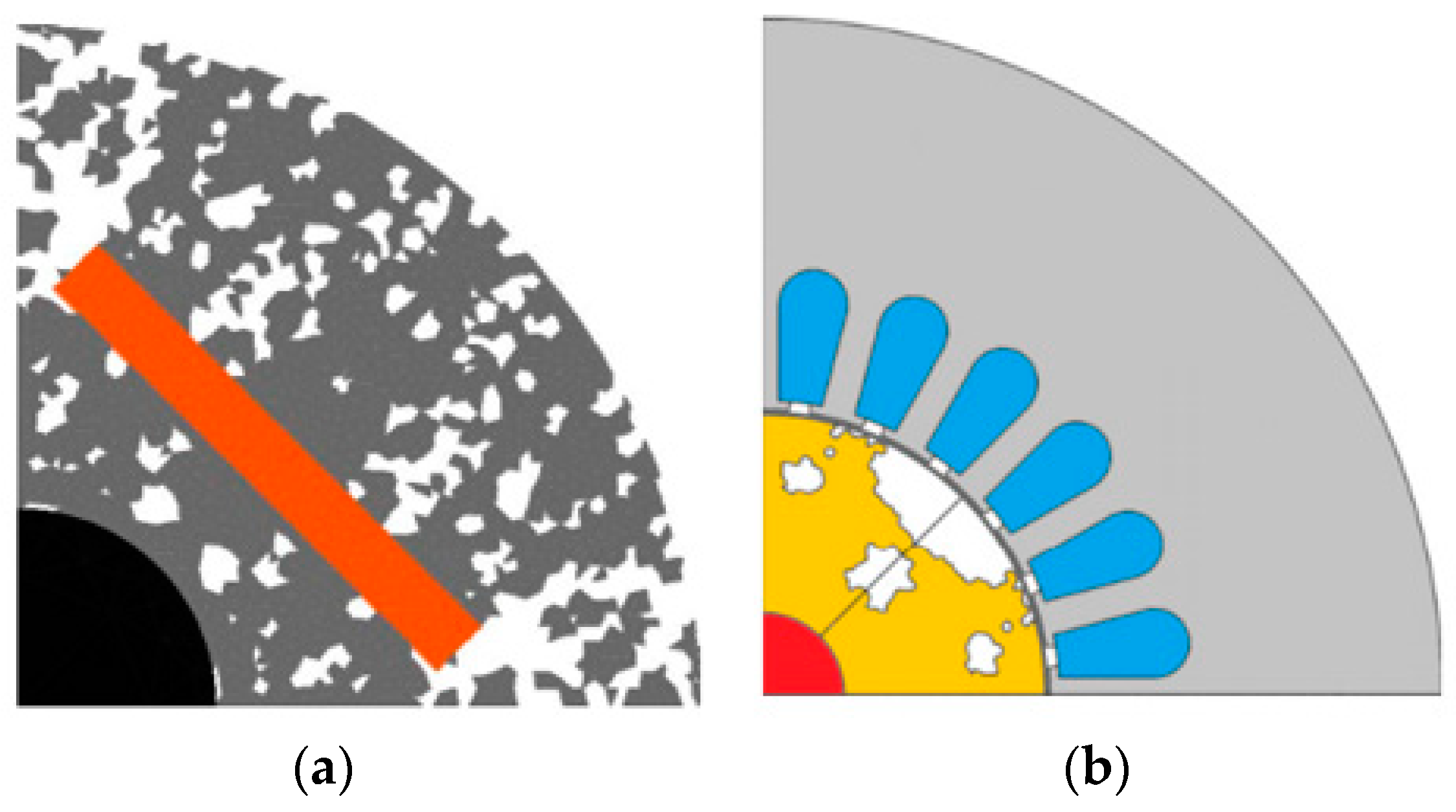
Figure 2. ON–OFF TO results: (a) without filter; (b) with filter using immune algorithm.
In [5][25], ON–OFF-based normalized Gaussian network (NGNet) is presented to improve the torque density and reduce the iron losses. The output of the NGNet is determined by:
where is the Gaussian function, and are the weight coefficient and normalized function, respectively. represents the number of Gaussian functions and i, j is the number of cells. The state of the cells can be determined by:
The material is configured to iron when the cell is in the on state, whereas it is configured to air when the cell is in the off state. Three different optimization problems were studied to improve the performance of the machine: (i) maximize torque; (ii) minimize iron losses with constraint of average torque; (iii) maximize average torque with constraint of iron losses. Furthermore, the Gaussian function distribution and the optimized design is shown in Figure 3a. There should be a tradeoff between the average torque and the iron losses because the wider rotor surface increases the torque, but also, the latter should be made smaller to reduce the iron losses. Another filtering technique, Gabor filter combined with ON–OFF method based on NGNet, is presented in [26]. The authors concluded that the proposed filter provided lower torque ripples as compared to the conventional NGNet, and the optimized design using filter gives the thinner flux barriers as depicted in Figure 3b. The main disadvantage of the abovementioned methods is the high computational cost because the FEA computation is needed at each generation [27].
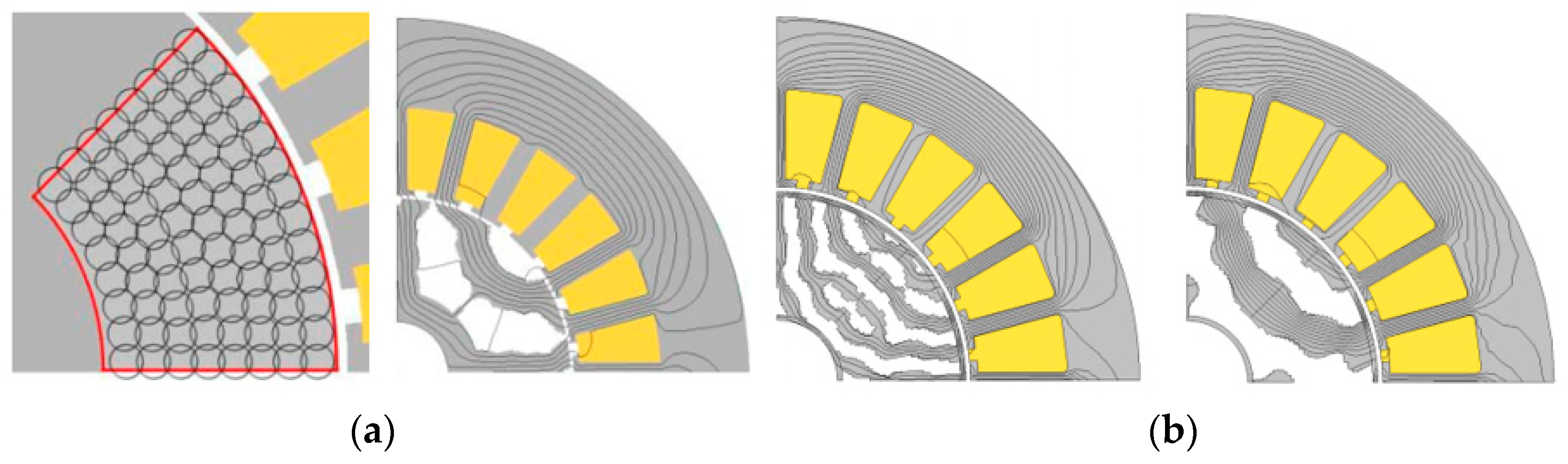
Figure 3. (a) Gaussian function distribution and optimized resulted shape; (b) Gabor filter and without filter [26].
The gradient based ON–OFF TO solves the problem of high computational cost but has the probability that it may stop on a local optimal solution. In [28], the gradient-based TO are applied to a 6/14 SRM to enhance the dynamic torque of the machine. The stator tooth is selected for the design space of the TO, then utilizes the method of adjoint gradients with respect to the material properties to optimize the material distribution for the reduction of torque ripples. The main drawback of this method is the difficulty in the evaluation of the non-differentiable functions [5].
2.2. Level Set Method
The level set method uses an implicit function known as the “level set function” to handle interfaces and shapes numerically. The level set method was first introduced in [29] for the purpose of using it in TO to represent material boundaries. They demonstrated that this method can be used to design a cantilever beam with distinct boundaries without being dependent on a mesh or grayscale elements. Furthermore, the level set technique, which is based on gradients, produces a solution that is more practical for the given problem but lower convergence rate. In the level set TO, the material boundaries are shown in Figure 4a and computationally it can be defined as [30]:
The objective of level set topology optimization is to find the optimal distribution of material in a design space to meet specific design objectives, by determining the value of at each location . In [31], the rotor of the synchronous reluctance machine was optimized using the level set method combined with the continuum sensitivity analysis. The objective function of the problem was to improve the torque of the machine by redistributing the magnetic material throughout the rotor design. The torque ripples profile of 8/6 pole SRM is enhanced by using the level set method, and sensitivity analysis having the adjoint variable method is utilized in [32]. In the optimized design, the average torque is improved by 12% with also the reduction in the torque ripples. The initial and optimized model with the torque waveform comparison is shown in Figure 4b. For reducing the iron losses and improving the torque of the synchronous reluctance machine, the level set method with sensitivity analysis of adjoint variable method is employed [33].
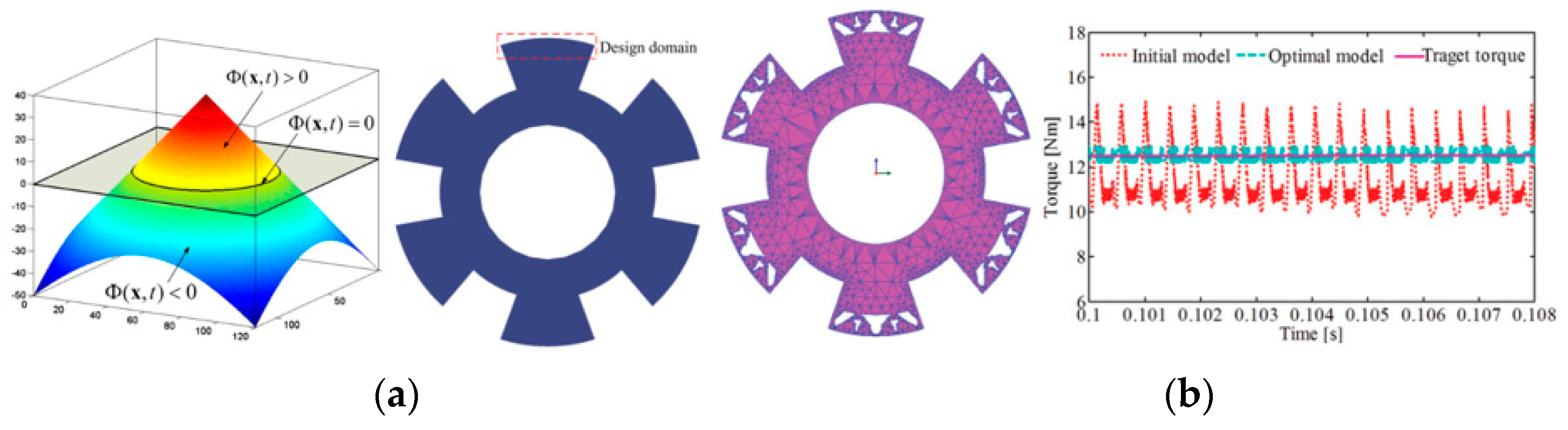

Figure 4. Level set TO: (a) Different domain of level set method [32]; (b) Initial and optimized model with torque waveform.
Additionally, this technique does not need the creation of intermediary materials or rely on the mesh that is used to discretize the design domain [34]. The level set approach for TO of EM devices has become quite well-liked as a result of these benefits [35]. However, this approach has certain limitations, including the need for an initial definition for the level set representation, convergence to local optima, and difficulties in computing the form gradients necessary to develop the interface [36].
2.3. Material Density Method
The density method is a technique that was originally developed for solid mechanics TO [37]. It is a simple method that has recently gained popularity for electromagnetic TO, even for multi-material problems. This method is based on the idea of using a density function to represent the material distribution in the design domain, then using optimization algorithms to find the optimal density distribution that satisfies certain design constraints and objectives. This method has been found to be effective for a wide range of electromagnetic optimization problems and has been applied to a variety of different types of electromagnetic structures [12][15][38][39][40][41]. It is based on interpolation, filtering, and projection schemes, and originally used the simple power-law as the material penalization function. This leads to the SIMP (Solid Isotropic Material with Penalization) approach [42]. A schematic flowchart of procedures in the material density method is presented in Figure 5.
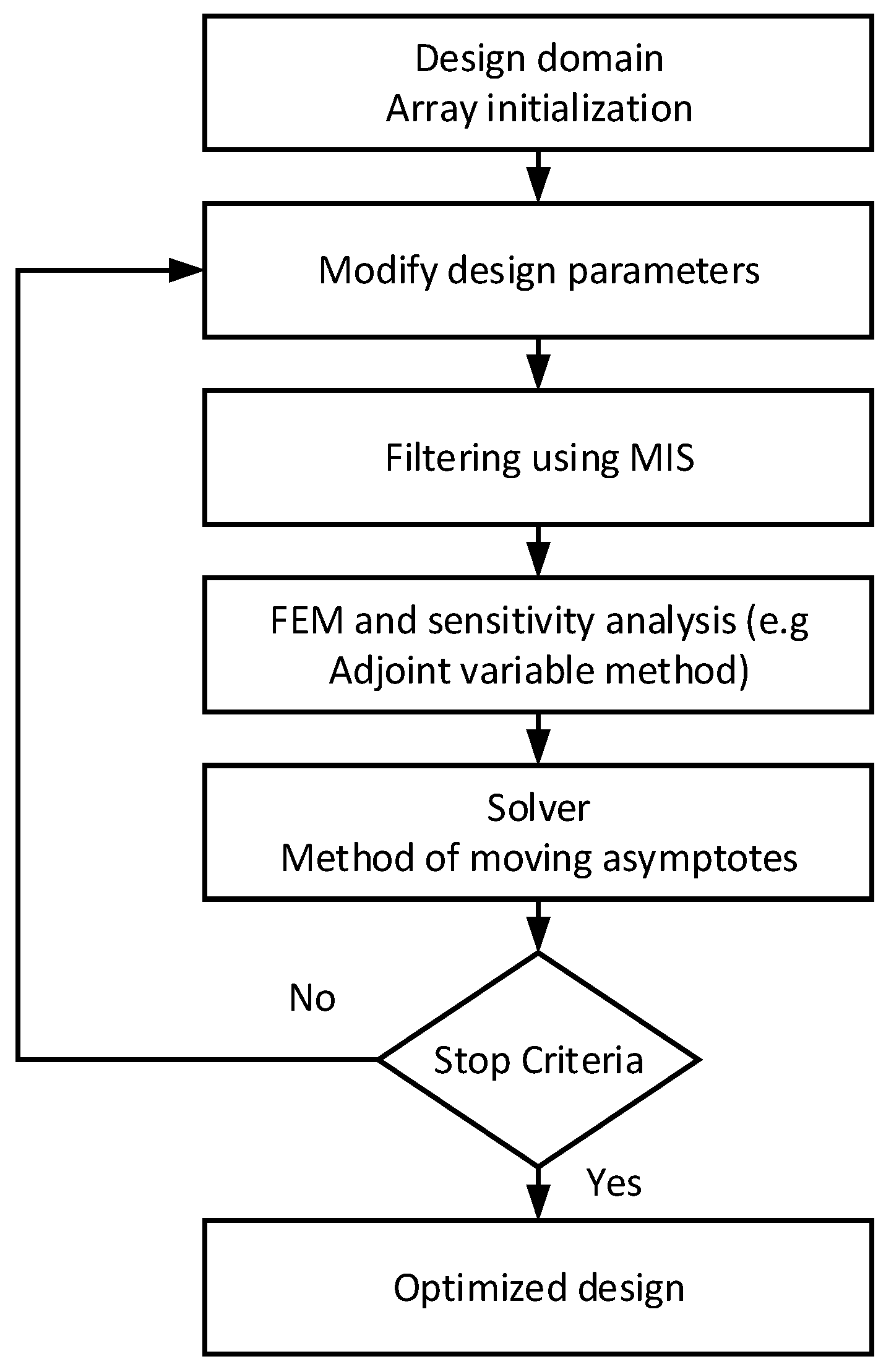
Figure 5. Flowchart of the TO using the material density-based method.
By solving the magnetic flux density and integrating the Maxwell tensor stress using (5) to determine torque, the material density approach is used to optimize the 8/6 pole rotor of the SRM [43].
The objective of the optimization problem is to determine the function density and is defined as:
where and represents the ferromagnetic region and air region, respectively. In the material density method, the gives the values between 0 and 1 but practically, the distribution of the material is either 0 or 1, due to which the discontinuity exists in the final shape. To make the material distribution feasible, the magnetic reluctivity is defined by the smooth heaviside function [44]:
where hℎ represents the one half of the transition width between and . The magnetic reluctivity is defined as:
where is the magnetic reluctivity and is a function of the mgnetic flux density and , is the reluctivity of the element and reluctivity of air, respectively. The penalization coefficient is represented by the variable . By choosing the proper value of , the gray elements can be eliminated. In [45], the material density-based TO was utilized for the torque ripple minimization and the design space include the stator teeth and rotor poles. The optimized design showed a significant amount of reduction in the profile of torque ripple with the cost of a slight reduction of 7.22% in the average torque. In addition, the initial and optimized design of 6/4 pole SRM is depicted in Figure 6a. The TO of material density was applied in [46] to minimize the torque ripple and the final design reach to the target torque value. The design space includes the half of the rotor pole as shown in Figure 6b, and after optimization, the torque reached the target value. The overview of TO applied to the reluctance machine for performance enhancement is shown in Table 1.
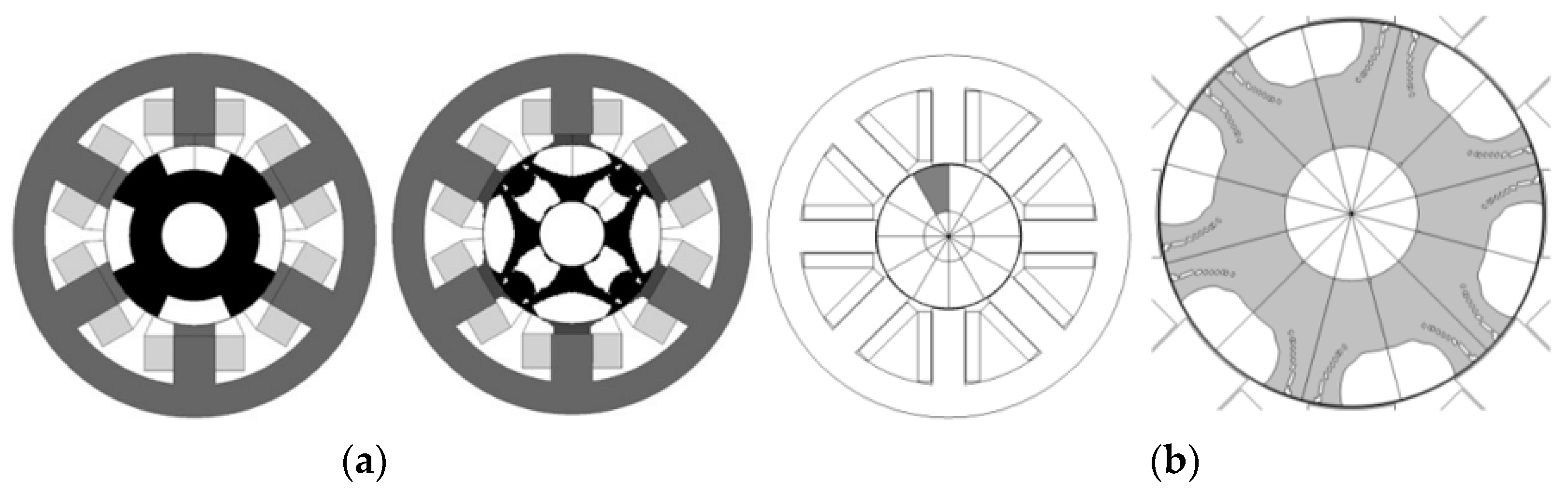
Figure 6. (a) Initial and optimized design of 6/4 SRM; (b) Initial design geometry and optimized design.
Table 1. Summary of TO used in reluctance machines for performance improvement.
| Machine Type | Optimization Method | Design Space | Objective Function | Prototype Fabrication |
Reference |
|---|---|---|---|---|---|
| SRM | Material density method | Stator teeth and rotor poles | Min. torque ripples | Yes | [44] |
| SRM | Level set method | Rotor poles | Max. average torque and min. torque ripples | No | [31] |
| SynRM | Level set method | The rotor | Max. average torque | No | [30] |
| SynRM | ON-OFF | The rotor | Max. torque | No | [4] |
| SRM | NGNet | Stator teeth | Min. iron losses | No | [27] |
| SRM | Gradient based ON-OFF | The rotor | Min. torque ripples | No | [42] |
| SRM | Material density + GCMMA | The rotor | Max. torque | No | [45] |
| SynRM | Material density + GCMMA | The rotor | Max. torque | No | [25] |
| SRM | ON-OFF NGNet | The rotor | Max. torque | No | [20] |
| SynRM | Using Gabor filter | The rotor | Min. torque ripples | No | [16] |
References
- Cavazzuti, M. Optimization Methods: From Theory to Design Scientific and Technological Aspects in Mechanics; Springer: Berlin/Heidelberg, Germany, 2012.
- Cupertino, F.; Pellegrino, G.; Gerada, C. Design of synchronous reluctance motors with multiobjective optimization algorithms. IEEE Trans. Ind. Appl. 2014, 50, 3617–3627.
- Barta, J.; Ondrusek, C. Rotor Design And Optimization Of Synchronous Reluctance Machine. MM Sci. J. 2015, 2015, 555–559.
- Pellegrino, G.; Cupertino, F.; Gerada, C. Barriers shapes and minimum set of rotor parameters in the automated design of Synchronous Reluctance machines. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1204–1210.
- Sato, S.; Sato, T.; Igarashi, H. Topology Optimization of Synchronous Reluctance Motor Using Normalized Gaussian Network. IEEE Trans. Magn. 2015, 51, 8200904.
- Kano, Y.; Terahai, T.; Kosaka, T.; Matsui, N.; Nakanishi, T. A new flux-barrier design of torque ripple reduction in saliency-based sensorless drive IPM motors for general industrial applications. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1939–1945.
- Fei, W.; Luk, P.C.K.; Shen, J.X.; Xia, B.; Wang, Y. Permanent-magnet flux-switching integrated starter generator with different rotor configurations for cogging torque and torque ripple mitigations. IEEE Trans. Ind. Appl. 2011, 47, 1247–1256.
- Valavi, M.; Nysveen, A.; Nilssen, R. Characterization of radial magnetic forces in low-speed permanent magnet wind generator with non-overlapping concentrated windings. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 2943–2948.
- Wang, B. Topology Optimization of Electric Machines: A Review. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–8.
- Credo, A.; Fabri, G.; Villani, M.; Popescu, M. Adopting the Topology Optimization in the Design of High-Speed Synchronous Reluctance Motors for Electric Vehicles. IEEE Trans. Ind. Appl. 2020, 56, 5429–5438.
- Guo, F.; Brown, I.P. Simultaneous Magnetic and Structural Topology Optimization of Synchronous Reluctance Machine Rotors. IEEE Trans. Magn. 2020, 56, 1–12.
- Korman, O.; Di Nardo, M.; Degano, M.; Gerada, C. On the Use of Topology Optimization for Synchronous Reluctance Machines Design. Energies 2022, 15, 3719.
- Cederlund, J.; Nategh, S.; Lennström, D. Topology Optimization of Electrical Machines for NVH Purposes in E-mobility Applications-Part 1. In Proceedings of the IECON 2021–47th Annual Conference of the IEEE Industrial Electronics Society, online, 13–16 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6.
- Choi, J.S.; Izui, K.; Nishiwaki, S.; Kawamoto, A.; Nomura, T. Topology Optimization of the Stator for Minimizing Cogging Torque of IPM Motors. IEEE Trans. Magn. 2011, 47, 3024–3027.
- Thabuis, A.; Ren, X.; Burnand, G.; Perriard, Y. Density-Based Topology Optimization of Conductor Paths for Windings in Slotted Electrical Machines. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6.
- Zhao, F.; Yan, R. Topology Optimization of Magnetic Actuator Using the Improved ON/OFF Method. In Proceedings of the 2012 Sixth International Conference on Electromagnetic Field Problems and Applications, Dalian, China, 19–21 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–4.
- Watanabe, K.; Suga, T.; Kitabatake, S. Topology Optimization Based on the ON/OFF Method for Synchronous Motor. IEEE Trans. Magn. 2017, 54, 1–4.
- Ishikawa, T.; Nakayama, K.; Kurita, N.; Dawson, F.P. Optimization of Rotor Topology in PM Synchronous Motors by Genetic Algorithm Considering Cluster of Materials and Cleaning Procedure. IEEE Trans. Magn. 2014, 50, 637–640.
- Takahashi, N.; Yamada, T.; Shimose, S.; Miyagi, D. Optimization of rotor of actual IPM motor using ON/OFF method. IEEE Trans. Magn. 2011, 47, 1262–1265.
- Choi, N.-S.; Kim, D.-H.; Lee, H.-B.; Byun, J.-K. Topology Optimization of Dielectric Resonator in 3-D Waveguide Structure Considering Higher Mode Incidence. IEEE Trans. Magn. 2012, 48, 559–562.
- Shiyang, F.; Watanabe, K. Topology optimization of rotor design in switched reluctance motor using immune algorithm. Int. J. Appl. Electromagn. Mech. 2020, 64, 413–420.
- Watanabe, K.; Campelo, F.; Igarashi, H. Topology optimization based on immune algorithm and multigrid method. IEEE Trans. Magn. 2007, 43, 1637–1640.
- Watanabe, K.; Campelo, F.; Iijima, Y.; Kawano, K.; Matsuo, T.; Mifune, T.; Igarashi, H. Optimization of Inductors Using Evolutionary Algorithms and Its Experimental Validation. IEEE Trans. Magn. 2010, 46, 3393–3396.
- Midha, C.; Mohammadi, M.H.; Silva, R.C.P.; Lowther, D.A. Selection of Spatial Filters for ON/OFF Based Topology Optimization of a C-Core Electromagnetic Actuator. IEEE Trans. Magn. 2019, 55, 1–4.
- Sato, T.; Watanabe, K.; Igarashi, H. Multimaterial Topology Optimization of Electric Machines Based on Normalized Gaussian Network. IEEE Trans. Magn. 2015, 51, 7202604.
- Otomo, Y.; Igarashi, H. Topology Optimization Using Gabor Filter: Application to Synchronous Reluctance Motor. IEEE Trans. Magn. 2021, 57, 1–4.
- Sasaki, H.; Igarashi, H. Topology Optimization Accelerated by Deep Learning. IEEE Trans. Magn. 2019, 55, 7401305.
- Sayed, E.; Bakr, M.H.; Bilgin, B.; Emadi, A. Gradient-Based Design Optimization of a Switched Reluctance Motor for an HVAC Application. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Detroit, MI, USA, 23–26 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1031–1037.
- Sethian, J.A.; Wiegmann, A. Structural Boundary Design via Level Set and Immersed Interface Methods. J. Comput. Phys. 2000, 163, 489–528.
- Osher, S.; Fedkiw, R.P. Level Set Methods: An Overview and Some Recent Results. J. Comput. Phys. 2001, 169, 463–502.
- Kim, Y.S.; Park, I.H. Topology Optimization of Rotor in Synchronous Reluctance Motor Using Level Set Method and Shape Design Sensitivity. IEEE Trans. Appl. Supercond. 2010, 20, 1093–1096.
- Zhang, H.; Wang, S. Topology Optimization of Rotor Pole in Switched Reluctance Motor for Minimum Torque Ripple. Electr. Power Components Syst. 2017, 45, 905–911.
- Yamashita, Y.; Okamoto, Y. Design Optimization of Synchronous Reluctance Motor for Reducing Iron Loss and Improving Torque Characteristics Using Topology Optimization Based on the Level-Set Method. IEEE Trans. Magn. 2020, 56, 1–4.
- Park, S.-I.; Min, S.; Yamasaki, S.; Nishiwaki, S.; Yoo, J. Magnetic Actuator Design Using Level Set Based Topology Optimization. IEEE Trans. Magn. 2008, 44, 4037–4040.
- Campelo, F.; Ramirez, J.; Igarashi, H. A survey of topology optimization in electromagnetics: Considerations and current trends. Academia 2010, 46, 2010.
- Midha, C. A Study of Topology Optimization Methods for the Design of Electromagnetic Devices; McGill University: Quebec City, QC, Canada, 2019.
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Multidiscip. Optim. 1989, 1, 193–202.
- Luo, J.; Luo, Z.; Chen, L.; Tong, L.; Wang, M.Y. A semi-implicit level set method for structural shape and topology optimization. J. Comput. Phys. 2008, 227, 5561–5581.
- Sanogo, S.; Messine, F.; Henaux, C.; Vilamot, R. Topology Optimization for Magnetic Circuits Dedicated to Electric Propulsion. IEEE Trans. Magn. 2014, 50, 1–13.
- Mohamodhosen, B.B.S.; Gillon, F.; Tounzi, M.; Chevallier, L. Topology optimisation using nonlinear behaviour of ferromagnetic materials. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 2211–2223.
- Gauthey, T.; Gangl, P.; Hassan, M.H. Multi-Material Topology Optimization with Continuous Magnetization Direction for Permanent Magnet Synchronous Reluctance Motors. arXiv 2021, arXiv:2107.04825.
- Rozvany, G.I.; Zhou, M.; Birker, T. Generalized shape optimization without homogenization. Struct. Optim. 1992, 4, 250–252.
- Manninen, A.; Keränen, J.; Pippuri-Mäkeläinen, J.; Metsä-Kortelainen, S.; Riipinen, T.; Lindroos, T. Topology Optimization for Additive Manufacturing of Switced Reluctance Machines. In Proceedings of the 18th Biennial IEEE Conference Electromagnetic Field Computation (CEFC), Hangzhou, China, 28–31 October 2018.
- Okamoto, Y.; Hoshino, R.; Wakao, S.; Tsuburaya, T. Improvement of Torque Characteristics For a Synchronous Reluctance Motor Using MMA-based Topology Optimization Method. IEEE Trans. Magn. 2017, 54, 1–4.
- Lee, J.; Seo, J.H.; Kikuchi, N. Topology optimization of switched reluctance motors for the desired torque profile. Struct. Multidiscip. Optim. 2010, 42, 783–796.
- Manninen, A.; Keränen, J.; Pippuri-Mäkeläinen, J.; Riipinen, T.; Metsä-Kortelainen, S.; Lindroos, T. Impact of topology optimization problem setup on switched reluctance machine design. In Proceedings of the 2019 22nd International Conference on the Computation of Electromagnetic Fields (COMPUMAG), Paris, France, 15–19 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4.
More
Information
Subjects:
Engineering, Electrical & Electronic
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
641
Revisions:
4 times
(View History)
Update Date:
18 May 2023
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




