Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Upaka Rathnayake
 -- 2141 2023-05-05 09:12:20 |
2 layout & references
Sirius Huang
 Meta information modification 2141 2023-05-06 03:03:21 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Jayathilake, T.; Gunathilake, M.B.; Wimalasiri, E.M.; Rathnayake, U. Wetland Water-Level Prediction. Encyclopedia. Available online: https://encyclopedia.pub/entry/43832 (accessed on 28 April 2024).
Jayathilake T, Gunathilake MB, Wimalasiri EM, Rathnayake U. Wetland Water-Level Prediction. Encyclopedia. Available at: https://encyclopedia.pub/entry/43832. Accessed April 28, 2024.
Jayathilake, Tharaka, Miyuru B. Gunathilake, Eranga M. Wimalasiri, Upaka Rathnayake. "Wetland Water-Level Prediction" Encyclopedia, https://encyclopedia.pub/entry/43832 (accessed April 28, 2024).
Jayathilake, T., Gunathilake, M.B., Wimalasiri, E.M., & Rathnayake, U. (2023, May 05). Wetland Water-Level Prediction. In Encyclopedia. https://encyclopedia.pub/entry/43832
Jayathilake, Tharaka, et al. "Wetland Water-Level Prediction." Encyclopedia. Web. 05 May, 2023.
Wetland Water-Level Prediction
Edit
This entry is adapted from the peer-reviewed paper 10.3390/environments10050075

Wetlands are simply areas that are fully or partially saturated with water. Wetlands have numerous hydrological, ecological, and social values. They play an important role in interactions among soil, water, plants, and animals. The rich biodiversity in the vicinity of wetlands makes them invaluable. Many anthropogenic activities damage wetlands. Climate change has adversely impacted wetlands and their biodiversity. The shrinking of wetland areas and reducing wetland water levels can therefore be frequently seen. However, the opposite can be seen during stormy seasons. Since wetlands have permissible water levels, the prediction of wetland water levels is important.

artificial neural network (ANN) anthropogenic activities climate change machine-learning techniques urbanization wetlands water-level prediction

1. Introduction

Wetlands are permanently or seasonally saturated with water. The Ramsar Convention defines wetlands as areas where water is the primary controlling factor in the environment and the plant and animal habitat of the wetland [1]. They play a crucial role in ecological systems. Wetlands are among the most productive ecosystems, also having multiple functions including flood attenuation, pollutant up-taking, recharge of the groundwater table, habitats for flora and fauna, water purification, stabilization of shorelines, water storage, carbon fixation, climate change mitigation, etc. Wetlands can trap sediment and heavy metals from surface runoff. Therefore, wetlands play an important role in nutrient retention and the purification of water while flowing through these ecosystems [2][3]. These ecosystems are more significant in ecological rejuvenation and contribute significantly to the conservation of biodiversity [4]. Therefore, it is a significant productive component of the environment [5]. Wetlands are important to mitigate climate-change impact [6]. They sometimes influence precipitation patterns and atmospheric temperatures [7]. The records showcase that the wetlands generally store 44 million tons of CO2 per year globally [8]. In addition, they provide recreational opportunities [9]. Furthermore, two thirds of the global fish harvest is associated with the conditions of coastal and inland wetlands. Significant income is generated from the fish industry in most developing countries. Therefore, wetlands will be more prominent in socio-economic aspects [10].
Wetlands are considered one of the world’s endangered ecosystems [11]. All over the world, wetland cover is being reduced due to urbanization and other human activities [12]. Wetlands significantly contribute to one of the land use types of the world, which takes around 6%. Therefore, their importance cannot be neglected in these sensitive areas. Nevertheless, threats and quality degradations of the wetland ecosystem can be observed due to environmental pollution and overexploitation [11]. Easy access to even conserved wetlands makes this degradation easier. Changes in the wetlands can be expected due to natural environmental fluctuations as well as human activities. Some of the anthropogenic activities are unintended due to poor knowledge and information. However, most anthropogenic activities that damage the wetland ecosystem are intended. A poor understanding of the importance of wetlands causes unintended damage, while negligence and less value given to wetlands cause intended damage [13]. Forming industrial zones is a significant anthropogenic contributor to the degradation of wetlands; therefore, many countries have now limited the use of these nearby areas of wetlands for industrial activities [14].
Maintaining the balance of the wetland ecosystem is highly important. The water level in a wetland is one of the important parameters to investigate, in addition to the quality of wetland water. The saturation of the wetland soil (hydrology) mainly determines how the soil, flora, and fauna develop. The richness of water within the ecosystem makes favorable conditions for the rapid growth of specially adapted plants (hydrophytes) and improves the quality of wetland (hydric) soil [15]. Therefore, wetland water-level prediction is important in several ways. Generally, wetlands have their own permissible water-level limits, whereas exceeding those limits can cause floods and other related environmental and hydrological issues [16]. Therefore, the wetland water levels reflect the general status of the wetland [17]. However, some countries still do not have a proper mechanism to map and monitor the water levels of the wetlands [18]. This could be due to the unavailability of measuring equipment as well as ignorance. However, some other countries have various ways to update their records on wetlands [19][20].

2. Importance of Wetland Water-Level Monitoring

Wetlands are usually found in low-energy domains, resulting in slow water flowing. This is because the land surface in these areas is relatively level [21]. Because wetlands are found in relatively leveled terrain, their surface area can be expanded and contracted as the water level changes, allowing a large quantity of water to be stored [15]. Fluctuations in wetland water levels are an important scenario as it improves the productivity and the biodiversity of the wetland areas [22]. Water level, hydro patterns, and residence time are the three key elements that can be used to identify the hydrologic behavior of wetlands [15]. Subtle changes in water levels can have a significant impact on vegetation patterns, characteristics, and ecological processes in wetland habitats. Therefore, the water level and the associated vegetation cover can be used to determine water levels during drought, flooding, and normal conditions [23].
Wetlands are responsible for 20–25% of methane emissions into the atmosphere; however, they absorb a significant amount of carbon dioxide. Wetland water levels play a vital role in controlling methane emissions by functioning as an interface between aerobic and anaerobic processes and determining the degree of carbon dioxide production [24][25]. In addition, wetland water levels reflect the dissolved oxygen conditions in the wetland’s soil–water system. The higher the wetland water level, the lower the dissolved oxygen concentration in the soil [15]. Anaerobic conditions are quickly developed in soils that are saturated rather than unsaturated soils, as the oxygen solubility in water is less. The amount and type of sediment–water nutrient exchange is affected by the frequency of water-level fluctuation, duration, and magnitude [26]. Therefore, the availability of water affects soil oxygen concentrations, which will adversely affect plant growth.
In addition, as a result of the water-level fluctuations, a direct impact on the plant and animal communities can be witnessed [27]. A case study done by Wilcox and Nichols [28] in the Lake Huron wetland has found that water-level fluctuations have an impact on the biodiversity and territory value of wetland plant communities. Therefore, water levels in wetlands are crucial to their survival and for the maintenance of the ecological balance of flora and fauna in wetlands. The species associated with wetlands have preferred water depths for their existence. Furthermore, some of the wetlands are situated along river basins and function as flood-detention basins. Those ecosystems generally fulfill a major task in managing flash floods that may happen due to extreme weather conditions. As such, water-level prediction and monitoring must be done to calculate the water-flowing depths downstream to prevent natural disasters such as floods [29]. Therefore, water-level measurement and forecasting will be more significant in wetland conservation and management [15][30]. It was observed that wetland water-level fluctuations are dependent on the seasonal and annual variation of climatic conditions. Therefore, evaluating water levels will be more applicable in forecasting varying climatic conditions from time to time [31]. For this purpose, models can be used to simulate and forecast wetland water levels when there will be a necessity to do so in decision-making relevant to wetlands or any other weather forecasting [32].

3. Available Machine-Learning Techniques to Predict Wetland Water Levels

Wetland water levels can be predicted in several ways, including physically based and data-driven approaches [33]. Physically based approaches can increase the level of complexity, are time-consuming to develop and require a high level of knowledge in the relevant field [16]. There are hydrologic and hydraulic models such as the Hydrologic Engineering Center’s River Analysis System (HEC-RAS), the Soil & Water Assessment Tool (SWAT), and MIKE, which can be used to simulate water levels [34]. Nevertheless, the major drawback with those methods is that they need a proper understanding of hydrological processes and the variety of data related to inflows and outflows, bathymetry data, meteorological data, etc. [35]. Moreover, model development and calibration are more challenging when limited data are available [36]. However, machine-learning techniques can overcome most of these difficulties in predicting water levels in wetlands [37].
The data-driven machine-learning approach is a very effective technique, as it can be applied in many nonlinear scenarios such as water-level forecasting, sediment transportation, water-quality prediction, groundwater modeling, etc. [38]. Change in the water level is a complex hydrological phenomenon, as there are many controlling factors [39]. In such cases, decision-making is challenging. In contrast, traditional prediction techniques are incapable of achieving the desired research purposes with the unavailability of large-scale data [40]. Therefore, machine-learning techniques possess many advantages that include implementation simplicity, rapid running speed and convergence, and strong adaptability [41]. Therefore, the machine-learning technique is one of the ideal tools for most complex situations [16].
Artificial neural networks (ANN), kernel methods, radial basis function (RBF), and support vector machines (SVM) have mainly been identified as commonly used machine-learning techniques in water-level predictions [16][42][43]. However, hydrological predictions using computer-based models can produce uncertainties and the results can differ from model to model [44]. Therefore, selecting a convenient machine-learning technique is a challenging task because the purpose of different techniques is not similar. Typically, the availability of the data can be taken into consideration as the key element to construct a learning algorithm in wetland water-level predictions [45].
Artificial neural network (ANN) models are very effective for hydrologic systems, as they can build up relationships from the given data [46]. McCulloch and Pitts [47] were considered the pioneers of the concept of the artificial neural network [48]. They imitated the functions of the human brain which connects several neurons [49]. With weighted connections, these neurons are organized into two or more layers [50]. Figure 1 shows a simple architecture of an artificial neural network for wetland water-level prediction. It consists of three layers including an input layer, a hidden layer, and an output layer. The network is initially trained using the known hydrological parameters and known water levels. Then, the trained network can be used to predict the unknown wetland water levels using the known hydrological parameters. The number of hidden layers may be increased depending on the problem.
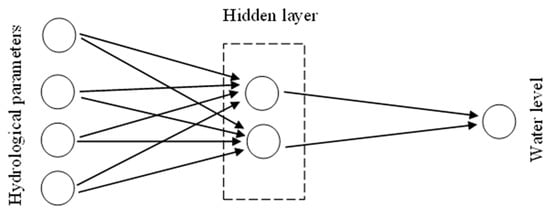
Environments 10 00075 g003 550
Figure 1. Layers in artificial neural networks.
The model runs to find the solution to the following mathematical function, which is time-dependent (refer to Equation (2)).
Y t = function   ( X i , t )
where YY is the dependent variable on time and Xi,Xi, is the independent variable based on the time domain. The nonlinear relationship is formulated as per Equation (2) in ANN. Many optimization algorithms, including the Levenberg–Marquardt algorithm (LM), the scaled conjugate gradient (SCG) algorithm, the Bayesian regularization (BR) algorithm, etc. are used in enhancing the performance of the developed ANN model [51][52].
Support vector machine (SVM) is another popular machine-learning technique that can be used to predict water levels, which is based on artificial intelligence that has been developed on statistical learning theory [41]. The SVM identifies support vector hyperplanes that can linearly group the vectors of various classes with a maximum distant margin between them [16]. SVM operation is carried out with the assistance of kernels. Although the accuracy in the neural networks depends on the number of nodes in the hidden layer, the accuracy of the support vector depends on kernel mapping. Polynomial, sigmoid, and radial basis functions can be used in this manner [16]. Nevertheless, the radial basis function (RBF) can be considered the best kernel function used in water-level predictions, and it gives a globally optimal solution while avoiding overturning [53]. Equations (3) and (4) present the mathematical formulation of SVM in generic forms. The regression function used in SVM can be formulated as Equation (3).
Y = ω T ∅ ( X ) + b
where ∅(X)∅(X) is a nonlinear function that is used to map the input vector to a high-dimensional space. ω is the weight vector and b is the bias. Minimizing the structural risk function (given in Equation (4)), the mapping function is estimated.
R = 1 2 ω T ω + C ∑ i = 1 N L ε ( Y i )
where N is the sample size and C finds the tradeoff between model complexity and empirical error. Lε is Vapnik’s ε intensive loss function.
Random forests are another machine-learning approach and consist of a collection of “m” number of tree predictors. They are produced by randomly selecting the variables from separate categories [54]. Nevertheless, when there is a huge number of trees in the model, issues can be raised due to overfitting. This issue can be overcome by selecting the number of trees that gives the lowest mean square [16]. Random forests can operate not only with nonlinear data but also with non-Gaussian data. Additionally, the relative importance of each variable can be measured in this technique, which utilizes variable selections [55]. Some other features of random-forest models are that they are less sensitive to outliers and noise, provide useful internal estimates of error, are faster than bagging, correlation, strength, and variable importance, and are simple and easily parallelized [54]. This method was also applicable to many water-related studies, including wetland water-level prediction [56]. The schematic diagram of a generic random-forest approach is given in Figure 2. As stated, there can be n number of trees for decision-making. After combining all decisions, the final decision or result is estimated.
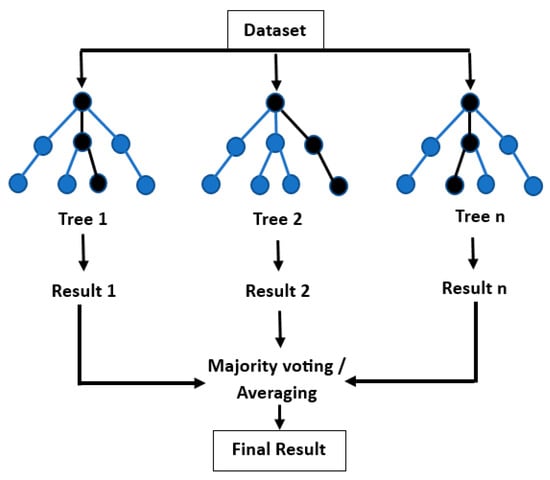
Environments 10 00075 g004 550
Figure 2. Schematic diagram of a generic Random-Forest approach.

References

  1. Gardner, R.C.; Davidson, N.C. The Ramsar Convention. In Wetlands; Springer: Dordrecht, The Netherlands, 2011; pp. 189–203.
  2. Janssen, R.; Goosen, H.; Verhoeven, M.L.; Verhoeven, J.T.A.; Omtzigt, A.Q.A.; Maltby, E. Decision support for integrated wetland management. Environ. Model. Softw. 2005, 20, 215–229.
  3. Savage, R.; Baker, V. The Importance of Headwater Wetlands and Water Quality in North Carolina; North Carolina Department of Environment and Natural Resources Diviion of Water Quality: Raleigh, NC, USA, 2007.
  4. Viaroli, P.; Bartoli, M.; Vymazal, J. Preface: Wetlands biodiversity and processes—Tools for conservation and management. Hydrobiologia 2016, 774, 1–5.
  5. Wu, H.; Zhang, J.; Ngo, H.H.; Guo, W.; Liang, S. Evaluating the sustainability of free water surface flow constructed wetlands: Methane and nitrous oxide emissions. J. Clean. Prod. 2017, 147, 152–156.
  6. Taillardat, P.; Thompson, B.S.; Garneau, M.; Trottier, K.; Friess, D.A. Climate change mitigation potential of wetlands and the cost-effectiveness of their restoration. Interface Focus 2020, 10, 20190129.
  7. Feher, L.C.; Osland, M.J.; Griffith, K.T.; Grace, J.B.; Howard, R.J.; Stagg, C.L.; Enwright, N.M.; Krauss, K.W.; Gabler, C.A.; Day, R.H.; et al. Linear and nonlinear effects of temperature and precipitation on ecosystem properties in tidal saline wetlands. Ecosphere 2017, 8, e01956.
  8. Stein, E.D.; Fetscher, A.E.; Clark, R.P.; Wiskind, A.; Grenier, J.L.; Sutula, M.; Collins, J.N.; Grosso, C. Validation of a wetland rapid assessment method: Use of EPA’s level 1-2-3 framework for method testing and refinement. Wetlands 2009, 29, 648–665.
  9. Noble, C.V.; Wakeley, J.S.; Roberts, T.H.; Henderson, C. Regional Guidebook for Applying the Hydrogeomorphic Approach to Assessing the Functions of Headwater Slope Wetlands on the Mississippi and Alabama Coastal Plains; Engineer Research and Development Center Vicksburg MS Environmental Lab: Vicksburg, MS, USA, 2007.
  10. Ringler, C.; Cai, X. Valuing fisheries and wetlands using integrated economic-hydrologic modeling—Mekong River Basin. J. Water Resour. Plan. Manag. 2006, 132, 480–487.
  11. Lefebvre, G.; Redmond, L.; Germain, C.; Palazzi, E.; Terzago, S.; Willm, L.; Poulin, B. Predicting the vulnerability of seasonally-flooded wetlands to climate change across the Mediterranean Basin. Sci. Total Environ. 2019, 692, 546–555.
  12. Kaleel, M.I.M. The Impact on Wetlands: A Study Based on Selected Areas in Ampara District of Sri Lanka. World News Nat. Sci. 2017, 7, 16–25.
  13. Chen, H.; Zhang, W.; Gao, H.; Nie, N. Climate Change and Anthropogenic Impacts on Wetland and Agriculture in the Songnen and Sanjiang Plain, Northeast China. Remote Sens. 2018, 10, 356.
  14. Chumaidiyah, E.; Dewantoro, M.D.R.; Kamil, A.A. Design of a Participatory Web-Based Geographic Information System for Determining Industrial Zones. Appl. Comput. Intell. Soft Comput. 2021, 2021, 6665959.
  15. USEPA. Methods for Evaluating Wetland Condition: Wetland Hydrology; EPA-822-R-08-024; Office of Water, U.S. Environmental Protection Agency: Washington, DC, USA, 2008.
  16. Choi, C.; Kim, J.; Kim, J.; Kim, H.S. Development of Combined Heavy Rain Damage Prediction Models with Machine Learning. Water 2019, 11, 2516.
  17. Jiang, X.; Wang, J.; Liu, X.; Dai, J. Landsat Observations of Two Decades of Wetland Changes in the Estuary of Poyang Lake during 2000–2019. Water 2021, 14, 8.
  18. Debanshi, S.; Pal, S. Wetland delineation simulation and prediction in deltaic landscape. Ecol. Indic. 2020, 108, 105757.
  19. Hossain, S.K.M.; Ema, S.A.; Sohn, H. Rule-Based Classification Based on Ant Colony Optimization: A Comprehensive Review. Appl. Comput. Intell. Soft Comput. 2022, 2022, 2232000.
  20. Li, J.; Chen, W. A rule-based method for mapping Canada’s wetlands using optical, radar and DEM data. Int. J. Remote Sens. 2005, 26, 5051–5069.
  21. Orme, A.R. Wetland Morphology, Hydrodynamics and Sedimentation. In Wetlands: A Threatened Landscape; Williams, M., Ed.; The Institute of British Geographers, The Alden Press Ltd.: Osney Mead, UK, 1990; pp. 42–94.
  22. Dai, X.; Wan, R.; Yang, G.; Wang, X.; Xu, L.; Li, Y.; Li, B. Impact of seasonal water-level fluctuations on autumn vegetation in Poyang Lake wetland, China. Front. Earth Sci. 2019, 13, 398–409.
  23. Liu, Q.; Liu, J.; Liu, H.; Liang, L.; Cai, Y.; Wang, X.; Li, C. Vegetation dynamics under water-level fluctuations: Implications for wetland restoration. J. Hydrol. 2020, 581, 124418.
  24. Kang, H.; Jang, I.; Kim, S. Key Processes in CH4 Dynamics in Wetlands and Possible Shifts with Climate Change. In Global Change and the Function and Distribution of Wetlands; Springer: Dordrecht, The Netherlands, 2012; pp. 99–114.
  25. Chimner, R.A.; Cooper, D.J. Influence of water table levels on CO2 emissions in a Colorado subalpine fen: An in situ microcosm study. Soil Biol. Biochem. 2003, 35, 345–351.
  26. Steinman, A.D.; Ogdahl, M.E.; Weinert, M.; Uzarski, D.G. Influence of water-level fluctuation duration and magnitude on sediment–water nutrient exchange in coastal wetlands. Aquat. Ecol. 2014, 48, 143–159.
  27. Van Der Valk, A.G.; Volin, J.C.; Wetzel, P.R. Predicted changes in interannual water-level fluctuations due to climate change and its implications for the vegetation of the Florida Everglades. Environ. Manag. 2015, 55, 799–806.
  28. Wilcox, D.A.; Nichols, S.J. The effects of water-level fluctuations on vegetation in a Lake Huron wetland. Wetlands 2008, 28, 487–501.
  29. Ramachandra, T.V.; Aithal, B.H.; Kumar, U. Conservation of wetlands to mitigate urban floods. J. Resour. Energy Dev. 2012, 9, 1–22.
  30. Kim, J.; Jung, J.; Han, D.; Kim, H.S. Prediction and Evaluation of Hydro-Ecology, Functions, and Sustainability of A Wetland Under Climate Change. Geophys. Res. Abstr. 2019, 21, EGU2019-6804-1.
  31. Mitsch, W.J.; Gosselink, J.G. Wetlands, E-Book. 2015. Available online: http://auburn.eblib.com/patron/FullRecord.aspx?p=1895927 (accessed on 29 January 2023).
  32. Dadaser-Celik, F.; Cengiz, E. A neural network model for simulation of water levels at the Sultan Marshes wetland in Turkey. Wetl. Ecol. Manag. 2013, 21, 297–306.
  33. Kusudo, T.; Yamamoto, A.; Kimura, M.; Matsuno, Y. Development and Assessment of Water-Level Prediction Models for Small Reservoirs Using a Deep Learning Algorithm. Water 2021, 14, 55.
  34. Andrei, A.; Robert, B.; Erika, B. Numerical Limitations of 1D Hydraulic Models Using MIKE11 or HEC-RAS software—Case study of Baraolt River, Romania. IOP Conf. Series: Mater. Sci. Eng. 2017, 245, 072010.
  35. Zhu, S.; Hrnjica, B.; Ptak, M.; Choiński, A.; Sivakumar, B. Forecasting of water level in multiple temperate lakes using machine learning models. J. Hydrol. 2020, 585, 124819.
  36. Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929.
  37. Truong, V.-H.; Ly, Q.V.; Le, V.-C.; Vu, T.-B.; Le, T.-T.; Tran, T.-T.; Goethals, P. Machine learning-based method for forecasting water levels in irrigation and drainage systems. Environ. Technol. Innov. 2021, 23, 101762.
  38. Yaseen, Z.M.; El-Shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844.
  39. Karimi, S.; Shiri, J.; Kisi, O.; Makarynskyy, O. Forecasting Water Level Fluctuations of Urmieh Lake Using Gene Expression Programming and Adaptive Neuro-Fuzzy Inference System. Int. J. Ocean Clim. Syst. 2012, 3, 109–125.
  40. Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A Review of the Artificial Neural Network Models for Water Quality Prediction. Appl. Sci. 2020, 10, 5776.
  41. Wang, H.; Song, L. Water Level Prediction of Rainwater Pipe Network Using an SVM-Based Machine Learning Method. Int. J. Pattern Recognit. Artif. Intell. 2019, 34, 2051002.
  42. Kisi, O.; Shiri, J.; Karimi, S.; Shamshirband, S.; Motamedi, S.; Petković, D.; Hashim, R. A survey of water level fluctuation predicting in Urmia Lake using support vector machine with firefly algorithm. Appl. Math. Comput. 2015, 270, 731–743.
  43. Yang, J.-H.; Cheng, C.-H.; Chan, C.P. A Time-Series Water Level Forecasting Model Based on Imputation and Variable Selection Method. Comput. Intell. Neurosci. 2017, 2017, 8734214.
  44. Altunkaynak, A. Forecasting Surface Water Level Fluctuations of Lake Van by Artificial Neural Networks. Water Resour. Manag. 2006, 21, 399–408.
  45. Najafabadi, M.M.; Villanustre, F.; Khoshgoftaar, T.M.; Seliya, N.; Wald, R.; Muharemagic, E. Deep learning applications and challenges in big data analytics. J. Big Data 2015, 2, 1.
  46. Nourani, V.; Mogaddam, A.A.; Nadiri, A.O. An ANN-based model for spatiotemporal groundwater level forecasting. Hydrol. Process. 2008, 22, 5054–5066.
  47. McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133.
  48. Govindaraju, R.S.; Rao, A.R. (Eds.) Artificial Neural Networks in Hydrology; Springer Science & Business Media: Dordrecht, The Netherlands, 2013; Volume 36.
  49. Sarker, I.H.; Kayes, A.S.M.; Watters, P. Effectiveness analysis of machine learning classification models for predicting personalized context-aware smartphone usage. J. Big Data 2019, 6, 57.
  50. Yin, C.; Rosendahl, L.; Luo, Z. Methods to improve prediction performance of ANN models. Simul. Model. Pract. Theory 2003, 11, 211–222.
  51. Gunathilake, M.B.; Karunanayake, C.; Gunathilake, A.S.; Marasingha, N.; Samarasinghe, J.T.; Bandara, I.M.; Rathnayake, U. Hydrological Models and Artificial Neural Networks (ANNs) to Simulate Streamflow in a Tropical Catchment of Sri Lanka. Appl. Comput. Intell. Soft Comput. 2021, 2021, 6683389.
  52. Perera, A.; Rathnayake, U. Rainfall and atmospheric temperature against the other climatic factors: A case study from Colombo, Sri Lanka. Math. Probl. Eng. 2019, 2019, 5692753.
  53. Bafitlhile, T.M.; Li, Z. Applicability of ε-Support Vector Machine and Artificial Neural Network for Flood Forecasting in Humid, Semi-Humid and Semi-Arid Basins in China. Water 2019, 11, 85.
  54. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32.
  55. Genuer, R.; Poggi, J.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236.
  56. Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Water Resources
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Tharaka Jayathilake
,
Miyuru B. Gunathilake
,
Eranga M. Wimalasiri
,
Upaka Rathnayake
View Times: 332
Revisions: 2 times (View History)
Update Date: 09 May 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback