Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 1 by Upaka Rathnayake and Version 2 by Sirius Huang.
Wetlands are simply areas that are fully or partially saturated with water. Wetlands have numerous hydrological, ecological, and social values. They play an important role in interactions among soil, water, plants, and animals. The rich biodiversity in the vicinity of wetlands makes them invaluable. Many anthropogenic activities damage wetlands. Climate change has adversely impacted wetlands and their biodiversity. The shrinking of wetland areas and reducing wetland water levels can therefore be frequently seen. However, the opposite can be seen during stormy seasons. Since wetlands have permissible water levels, the prediction of wetland water levels is important.
- artificial neural network (ANN)
- anthropogenic activities
- climate change
- machine-learning techniques
- urbanization
- wetlands
- water-level prediction
1. Introduction
Wetlands are permanently or seasonally saturated with water. The Ramsar Convention defines wetlands as areas where water is the primary controlling factor in the environment and the plant and animal habitat of the wetland [1]. They play a crucial role in ecological systems. Wetlands are among the most productive ecosystems, also having multiple functions including flood attenuation, pollutant up-taking, recharge of the groundwater table, habitats for flora and fauna, water purification, stabilization of shorelines, water storage, carbon fixation, climate change mitigation, etc. Wetlands can trap sediment and heavy metals from surface runoff. Therefore, wetlands play an important role in nutrient retention and the purification of water while flowing through these ecosystems [2][3][2,3]. These ecosystems are more significant in ecological rejuvenation and contribute significantly to the conservation of biodiversity [4]. Therefore, it is a significant productive component of the environment [5]. Wetlands are important to mitigate climate-change impact [6]. They sometimes influence precipitation patterns and atmospheric temperatures [7]. The records showcase that the wetlands generally store 44 million tons of CO2 per year globally [8]. In addition, they provide recreational opportunities [9]. Furthermore, two thirds of the global fish harvest is associated with the conditions of coastal and inland wetlands. Significant income is generated from the fish industry in most developing countries. Therefore, wetlands will be more prominent in socio-economic aspects [10].
Wetlands are considered one of the world’s endangered ecosystems [11]. All over the world, wetland cover is being reduced due to urbanization and other human activities [12]. Wetlands significantly contribute to one of the land use types of the world, which takes around 6%. Therefore, their importance cannot be neglected in these sensitive areas. Nevertheless, threats and quality degradations of the wetland ecosystem can be observed due to environmental pollution and overexploitation [11]. Easy access to even conserved wetlands makes this degradation easier. Changes in the wetlands can be expected due to natural environmental fluctuations as well as human activities. Some of the anthropogenic activities are unintended due to poor knowledge and information. However, most anthropogenic activities that damage the wetland ecosystem are intended. A poor understanding of the importance of wetlands causes unintended damage, while negligence and less value given to wetlands cause intended damage [13]. Forming industrial zones is a significant anthropogenic contributor to the degradation of wetlands; therefore, many countries have now limited the use of these nearby areas of wetlands for industrial activities [14].
Maintaining the balance of the wetland ecosystem is highly important. The water level in a wetland is one of the important parameters to investigate, in addition to the quality of wetland water. The saturation of the wetland soil (hydrology) mainly determines how the soil, flora, and fauna develop. The richness of water within the ecosystem makes favorable conditions for the rapid growth of specially adapted plants (hydrophytes) and improves the quality of wetland (hydric) soil [15]. Therefore, wetland water-level prediction is important in several ways. Generally, wetlands have their own permissible water-level limits, whereas exceeding those limits can cause floods and other related environmental and hydrological issues [16]. Therefore, the wetland water levels reflect the general status of the wetland [17]. However, some countries still do not have a proper mechanism to map and monitor the water levels of the wetlands [18]. This could be due to the unavailability of measuring equipment as well as ignorance. However, some other countries have various ways to update their records on wetlands [19][20][19,20].
2. Importance of Wetland Water-Level Monitoring
Wetlands are usually found in low-energy domains, resulting in slow water flowing. This is because the land surface in these areas is relatively level [21][47]. Because wetlands are found in relatively leveled terrain, their surface area can be expanded and contracted as the water level changes, allowing a large quantity of water to be stored [15]. Fluctuations in wetland water levels are an important scenario as it improves the productivity and the biodiversity of the wetland areas [22][48]. Water level, hydro patterns, and residence time are the three key elements that can be used to identify the hydrologic behavior of wetlands [15]. Subtle changes in water levels can have a significant impact on vegetation patterns, characteristics, and ecological processes in wetland habitats. Therefore, the water level and the associated vegetation cover can be used to determine water levels during drought, flooding, and normal conditions [23][49]. Wetlands are responsible for 20–25% of methane emissions into the atmosphere; however, they absorb a significant amount of carbon dioxide. Wetland water levels play a vital role in controlling methane emissions by functioning as an interface between aerobic and anaerobic processes and determining the degree of carbon dioxide production [24][25][50,51]. In addition, wetland water levels reflect the dissolved oxygen conditions in the wetland’s soil–water system. The higher the wetland water level, the lower the dissolved oxygen concentration in the soil [15]. Anaerobic conditions are quickly developed in soils that are saturated rather than unsaturated soils, as the oxygen solubility in water is less. The amount and type of sediment–water nutrient exchange is affected by the frequency of water-level fluctuation, duration, and magnitude [26][52]. Therefore, the availability of water affects soil oxygen concentrations, which will adversely affect plant growth. In addition, as a result of the water-level fluctuations, a direct impact on the plant and animal communities can be witnessed [27][53]. A case study done by Wilcox and Nichols [28][54] in the Lake Huron wetland has found that water-level fluctuations have an impact on the biodiversity and territory value of wetland plant communities. Therefore, water levels in wetlands are crucial to their survival and for the maintenance of the ecological balance of flora and fauna in wetlands. The species associated with wetlands have preferred water depths for their existence. Furthermore, some of the wetlands are situated along river basins and function as flood-detention basins. Those ecosystems generally fulfill a major task in managing flash floods that may happen due to extreme weather conditions. As such, water-level prediction and monitoring must be done to calculate the water-flowing depths downstream to prevent natural disasters such as floods [29][55]. Therefore, water-level measurement and forecasting will be more significant in wetland conservation and management [15][30][15,56]. It was observed that wetland water-level fluctuations are dependent on the seasonal and annual variation of climatic conditions. Therefore, evaluating water levels will be more applicable in forecasting varying climatic conditions from time to time [31][57]. For this purpose, models can be used to simulate and forecast wetland water levels when there will be a necessity to do so in decision-making relevant to wetlands or any other weather forecasting [32][36].3. Available Machine-Learning Techniques to Predict Wetland Water Levels
Wetland water levels can be predicted in several ways, including physically based and data-driven approaches [33][58]. Physically based approaches can increase the level of complexity, are time-consuming to develop and require a high level of knowledge in the relevant field [16]. There are hydrologic and hydraulic models such as the Hydrologic Engineering Center’s River Analysis System (HEC-RAS), the Soil & Water Assessment Tool (SWAT), and MIKE, which can be used to simulate water levels [34][59]. Nevertheless, the major drawback with those methods is that they need a proper understanding of hydrological processes and the variety of data related to inflows and outflows, bathymetry data, meteorological data, etc. [35][60]. Moreover, model development and calibration are more challenging when limited data are available [36][61]. However, machine-learning techniques can overcome most of these difficulties in predicting water levels in wetlands [37][62]. The data-driven machine-learning approach is a very effective technique, as it can be applied in many nonlinear scenarios such as water-level forecasting, sediment transportation, water-quality prediction, groundwater modeling, etc. [38][63]. Change in the water level is a complex hydrological phenomenon, as there are many controlling factors [39][64]. In such cases, decision-making is challenging. In contrast, traditional prediction techniques are incapable of achieving the desired research purposes with the unavailability of large-scale data [40][65]. Therefore, machine-learning techniques possess many advantages that include implementation simplicity, rapid running speed and convergence, and strong adaptability [41][66]. Therefore, the machine-learning technique is one of the ideal tools for most complex situations [16]. Artificial neural networks (ANN), kernel methods, radial basis function (RBF), and support vector machines (SVM) have mainly been identified as commonly used machine-learning techniques in water-level predictions [16][42][43][16,67,68]. However, hydrological predictions using computer-based models can produce uncertainties and the results can differ from model to model [44][69]. Therefore, selecting a convenient machine-learning technique is a challenging task because the purpose of different techniques is not similar. Typically, the availability of the data can be taken into consideration as the key element to construct a learning algorithm in wetland water-level predictions [45][70]. Artificial neural network (ANN) models are very effective for hydrologic systems, as they can build up relationships from the given data [46][71]. McCulloch and Pitts [47][72] were considered the pioneers of the concept of the artificial neural network [48][73]. They imitated the functions of the human brain which connects several neurons [49][74]. With weighted connections, these neurons are organized into two or more layers [50][75]. Figure 1 shows a simple architecture of an artificial neural network for wetland water-level prediction. It consists of three layers including an input layer, a hidden layer, and an output layer. The network is initially trained using the known hydrological parameters and known water levels. Then, the trained network can be used to predict the unknown wetland water levels using the known hydrological parameters. The number of hidden layers may be increased depending on the problem.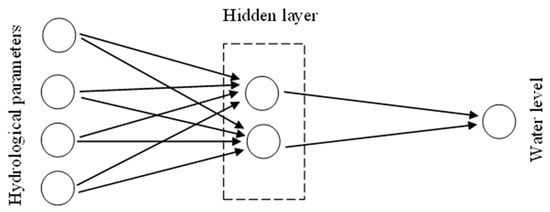
Figure 1.
Layers in artificial neural networks.
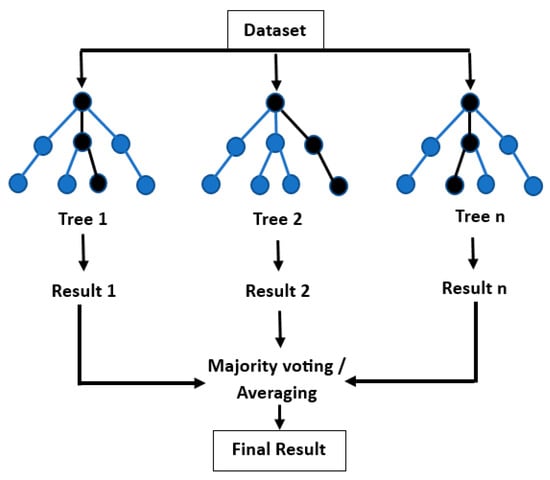
Figure 2.
Schematic diagram of a generic Random-Forest approach.
