Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Hongguang Lyu
 -- 6282 2023-04-18 11:32:33 |
2 add a table
Jason Zhu
 + 617 word(s) 6899 2023-04-19 04:29:08 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Lyu, H.; Hao, Z.; Li, J.; Li, G.; Sun, X.; Guoqing, Z.; Yin, Y.; Zhao, Y.; Zhang, L. Ship Autonomous Collision-Avoidance Strategies. Encyclopedia. Available online: https://encyclopedia.pub/entry/43169 (accessed on 07 May 2024).
Lyu H, Hao Z, Li J, Li G, Sun X, Guoqing Z, et al. Ship Autonomous Collision-Avoidance Strategies. Encyclopedia. Available at: https://encyclopedia.pub/entry/43169. Accessed May 07, 2024.
Lyu, Hongguang, Zengrui Hao, Jiawei Li, Guang Li, Xiaofeng Sun, Zhang Guoqing, Yong Yin, Yanjie Zhao, Lunping Zhang. "Ship Autonomous Collision-Avoidance Strategies" Encyclopedia, https://encyclopedia.pub/entry/43169 (accessed May 07, 2024).
Lyu, H., Hao, Z., Li, J., Li, G., Sun, X., Guoqing, Z., Yin, Y., Zhao, Y., & Zhang, L. (2023, April 18). Ship Autonomous Collision-Avoidance Strategies. In Encyclopedia. https://encyclopedia.pub/entry/43169
Lyu, Hongguang, et al. "Ship Autonomous Collision-Avoidance Strategies." Encyclopedia. Web. 18 April, 2023.
Ship Autonomous Collision-Avoidance Strategies
Edit
This entry is adapted from the peer-reviewed paper 10.3390/jmse11040830

Autonomous decision-making for ships to avoid collision is core to the autonomous navigation of intelligent ships. Related research has shown explosive growth. However, owing to the complex constraints of navigation environments, the Convention of the International Regulations for Preventing Collisions at Sea, 1972 (COLREGs), and the underactuated characteristics of ships, it is extremely challenging to design a decision-making algorithm for autonomous collision avoidance (CA) that is practically useful. Based on the investigation of many studies, decision-making algorithms can be attributed to three strategies: alteration of course alone, alteration of speed alone, and alteration of both course and speed. 

collision-avoidance strategy navigation path planning

1. Introduction

Owing to the advantages of large volume and low cost, waterway transportation accounts for approximately 90% of the global trade transportation volume. With the rapid development of the shipping industry and an increase in the number of ships, ships are being developed rapidly and intelligently. Compared with traditional manned ships, the decision-making and control technology of intelligent ships or Maritime Autonomous Surface Ships (MASS) has significant advantages in terms of economy, automation, and efficiency [1]. However, its decision-making mechanism is much more complicated than the former one since it needs to imitate a competent officer whose functionalities are experiential and intuitive [2] to perform CA decisions under all sorts of constraints [3][4], rather than to just provide instructions to the autopilot. These constraints include, but are not limited to, static obstacles, dynamic obstacles/ships [5], the COLREGs [6][7][8], limited ship’s maneuverability [2][9], accuracy of environment information [10], natural conditions, etc. [3][5][9][11][12]. Therefore, autonomous ship collision-avoidance (CA) decisions are challenging and worth studying in the field of marine navigation [9].
Autonomous ship CA decision is made from the perspective of safety, navigation practice, and regulations, using appropriate mathematical methods to determine CA measures, with the most dominant form being an optimal combination of altering course and changing speed simultaneously. In order to do this, the information of the navigation environment, the own ship, target ships, and other dynamic obstacles should firstly be collected, processed, and modeled to conduct a mathematical model of ship motion [5][13][14][15]. Additionally, according to the indicators of ship domain [16] and collision risk [17][18][19][20][21], and the identified complex ship encounter situations constrained by the COLREGs [22][23][24][25], sequential and proper CA actions are made to maintain a safe distance [26][27] between the own ship and target ships/obstacles to avoid collision.
The CA strategies chosen by an officer varies with the person’s condition, the ship‘s maneuverability, the navigation environment, and the application of the COLREGs. Due to the flexibility of the officer’s thinking, the underactuated characteristics of the ship, the complexity of the navigation environment, and the ambiguity of the COLREGs [28], a perfect CA decision is actually difficult to be completely simulated by mathematical or intelligent methods. Additionally, an autonomous CA decision-making mechanism and strategy selection principle followed by a machine should be framed and based on long-term accumulated human experience, maritime cases, and the requirements of the COLREGs [25][29][30][31].
At all times, ship collision avoidance at sea is typically achieved by altering the course, changing the speed, or a combination of both. In open waters, considering the response time of a vessel and the sailing habits of a crew, altering the course is the primary method of collision avoidance. In restricted waters, collision avoidance is often combined with speed changes [7]. Regardless of the type of CA action, according to the COLREGs, following the “early, large, wide, clear” principle is recommended. “Early” means taking large evasive action early and making such an action in ample time. “Large” means substantial action, that is, the action taken to avoid collision needs to be large enough to be easily observed visually by other vessels or by radar. If vessels are in sight of one another, it is common to alter by more than 30° at a time. In poor visibility, it is often necessary to alter by more than 30° and determine the timing of the turn. Regarding speed, it is usually advisable to slacken to half of the original speed or stop [25]. “Wide” means that a CA action should avoid the emergence of a close-quarters situation. Altering courses in open waters is the most effective way to avoid a close-quarters situation. In restricted waters, such as narrow waterways, ship CA actions should be conducted in a timely and substantial manner [7]. “Clear” means that a CA action should be effective and ensure that the other vessel is finally past and clear [30]. The original route should be resumed after complete collision avoidance is successful [32].
The COLREGs also require that vessels always sail at a safe speed at all times so that they can take proper and effective evasive actions to avoid collision and be stopped within a distance appropriate to the prevailing circumstances and conditions. Therefore, when the environment and the conditions of a ship change, it should be adjusted to sail at a safe speed [33].

2. Bibliometric Analysis and Thesis Research Factor

2.1. Development Trends and Source Analysis

The keyword used in the collection is “ship autonomous CA decisions”, which originates from the core collection of the Web of Science and is available exclusively in English. A brief bibliometric analysis of the literature was conducted to summarize the distribution and the scope of the literature from multiple perspectives. Figure 1 shows the publication dates of related papers over time. The number of papers published on autonomous CA decisions of ships is increasing annually, which is an important research issue in the current maritime field.
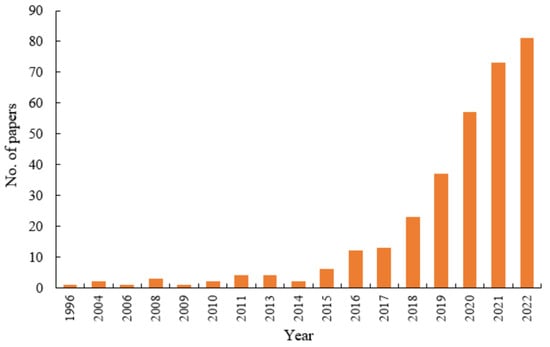
Jmse 11 00830 g002 550
Figure 1. Annual publication analysis of relevant papers.
The sources of publications for the collection of the literature are shown in Figure 2: papers related to ship CA research are published in “Ocean Engineering”, “Journal of Navigation”, “Journal of Marine Science and Engineering”, and other nautical journals, and, in recent years, research on autonomous ship CA has rapidly increased. Research on autonomous CA is not limited to open waters, but includes more complex waters, such as narrow waterways. For illustrative purposes, a journal title’s size indicates the relative number of papers published in that particular journal.
Jmse 11 00830 g003 550
Figure 2. Cloud map of publication sources.
According to navigation practices, there are four options for CA actions: (1) altering only the course; (2) altering only the speed; (3) altering the course and speed simultaneously; and (4) keeping the course and speed (the actions of stand-on vessels are not considered) [34]. Most early autonomous CA algorithms alter the course to avoid collisions. Many studies plan the trajectory first and then control the ship to sail along the track, without including the control of speed; there are a small number of studies on autonomous CA based on speed alteration. As shown in Figure 3, a statistical analysis of the selected papers shows that 64.4% of studies alter course for collision avoidance, 11.5% change speed for collision avoidance, and 24.1% combine alterations of course and speed for collision avoidance.
Jmse 11 00830 g004 550
Figure 3. Comparison of the number of CA papers.

2.2. Keywords

To better understand the development and the focus of automatic CA decision-making research in the literature, the abstracts of the selected papers were analyzed using the “VOSviewer” software, and the more popular research keywords are shown in Figure 4. The texts in assorted colors in the figure represent research hotspots in a chronological order. The size of the bubbles reflects the number of occurrences of the keywords in the literature, and the lines indicate their relevance to each other. These keywords indicate both the factors considered in the literature and the methodological or technical approach adopted, and they provide an overview of research on ship CA decisions in recent years. Early research has mainly focused on “own ship”, “COLREGs”, and “path planning”. Over time, many new buzzwords have emerged in CA research, such as “simulation”, “navigational safety”, “autonomous ships”, and “risk assessment”.
Jmse 11 00830 g005 550
Figure 4. Keyword clusters for ship CA decisions.
This indicates that research on ship CA decision-making is deepening and developing gradually; more real constraints, such as the environment under study, that can reflect the actual situation and new methods, such as deep learning (DL), are being used to obtain better solutions. From the perspective of time, researchers have begun to focus on autonomous CA. From the perspective of environmental interference, restricted waters and environments combined with wind, waves [35][36], and current interference have become the focus of research. From an analysis of the complexity of ship encounter situations, research on multi-ship encounter situations has become a hot topic in recent years. In addition, with the improvement in the accuracy and reliability of CA, an increasing number of factors related to CA are considered, such as “ship maneuverability” and “real-time performance.”

2.3. Research Factors

The first two sections were used to analyze and collect the titles and abstracts from the selected papers and combine them with the hot-cloud vocabulary. To further analyze the characteristics of research on CA decision-making in different waters, based on the literature analysis of Vagale et al. [32], ten performance factors were chosen for a comparative study. The choice of these ten factors was based on the most commonly available and relevant information on algorithm descriptions.
P1. Classification of research waters: open waters and congested waters. Generally, methods that can only avoid collision with dynamic target ships are suitable for open waters, and the others that can avoid collision with more than three dynamic ships and static obstacles simultaneously are suitable for congested waters.
P2. Depending on the complexity of the encounter situation, CA decision studies can be divided into two-ship and multi-ship encounters.
P3. Types of obstacles: static, dynamic, and mixed obstacles.
P4. Compliance with the COLREGs: consideration of compliance with the provisions of the COLREGs.
P5. Environmental disturbances: consideration of whether a ship is disturbed by wind, waves, and currents during a voyage.
P6. Real-time performance: the ability of an algorithm to react within a specified time. There are three levels: high (millisecond level, within 1 s), medium (second level, several seconds within 1 min), and low (more than 1 min).
P7. Ship maneuverability: this refers to the ability of a ship to maintain or change its motion state under control, that is, the ability of a ship to maintain or alter its course, speed, and position.
P8. The basis for judging the risk of collision is the consideration of the risk of collision, which is divided into distance to the closest point of approach (DCPA), time to the closest point of approach (TCPA), and ship domains (SDs).
P9. Altering the course/speed range: limited range of changing courses or speeds.
P10. Altering the course/speed laws: These are divided into objective function guide, heading/speed function, discrete variation, and gradual left/right-turn changes.

3. Automatic CA Strategy Based on Alteration of Course Alone

With the development of science and technology, the methods of these strategies have evolved from the earliest traditional mathematical methods to a stage where artificial intelligence techniques and various algorithms are integrated to solve problems, while considering the COLREGs and actual navigation situations. By summarizing the literature on ship autonomous CA algorithms, these research methods can be mainly classified into algorithms based on mathematical models, artificial intelligence, and soft computing.

3.1. Algorithms Based on Mathematical Models

Mathematical model-based algorithms represent environmental disturbances and ship-motion models more accurately and use quantifiable methods to solve CA decision-making problems, including geometric analysis, velocity obstacles (VO), and model predictive control (MPC).
(1)
Geometric analysis
Since the 1950s, the geometric analysis method has been used to solve the problem of automatic CA by establishing a geometric model of ship encounter to analyze the movement pattern in CA [37][38][39], including providing the DCPA, TCPA, and other CA parameters [21][40]. Lazarowska et al. [41] proposed a CA decision-making algorithm based on the path library method that considers the COLREGs, multi-ship encounters, and a few polygonal static obstacles. However, in this method, all target ships keep their course and speed so that the generated path is difficult to use in practice. Xu et al. [42] adopted a ship power-domain model based on the DCPA and TCPA to control ship course alteration and achieve ship CA. Tang et al. [43] proposed a CA algorithm by using a heading window, a set of unseaworthy heading angles as constraints, and a heading deviation angle as the optimization objective to determine the optimal navigation angle. This algorithm is less complex as only static obstacles are considered, and no dynamic obstacles are involved.
As the earliest research method for CA [44], the geometric analysis method mainly aims at the encounter between two ships, usually assuming that the ships keep their course and speed without considering each ship’s scale or maneuvering performance, resulting in deviations between the calculation results and reality.
(2)
VO
The velocity obstacle method is used to calculate the required heading or speed for CA by analyzing the spatial geometry between a ship and dynamic obstacles [17][22][23][24][27][45][46][47][48][49][50]. Tian et al. [47] proposed a method to avoid collisions by navigating a ship downstream to avoid static and dynamic obstacles based on the speed obstacle method. However, this method does not consider the requirements of the COLREGs. Zhang et al. [45] improved the speed obstacle method based on the dynamic vessel domain to avoid different obstacles according to an inland water environment, while considering the shallow-water effect. However, the resumption angle and the time were not calculated. Mou et al. [23] analyzed the relationship between the change in a ship’s velocity vector and the CA result after a nonlinear motion based on the ship’s domain and the speed-barrier method. They provided a collision-free-course-alteration range of the operating system, which can improve the efficiency of CA to a certain extent and is more in line with the requirements of the COLREGs and marine navigation habits. However, this method does not consider the maneuverability of a vessel and does not satisfy actual navigation conditions.
The VO method can avoid static and dynamic obstacles and can also consider the COLREGs, but it requires a good trajectory prediction of other vessels.
(3)
MPC
MPC solves the finite-time, open-loop optimization problem online at each sampling time, based on the current measurement information obtained, and applies the first element of the resulting control sequence to the controlled object. The process is repeated at the next sampling time, and the optimization problem is refreshed and solved again using new measurements as the initial conditions for predicting the future trajectories of the system at that point. The MPC algorithm consists of three steps: first, predicting the future output of the system based on historical information and future inputs from the ship, acting as a control via the course and speed; secondly, detecting the actual course and speed of the ship; and, thirdly, using this state to correct model-based prediction results before performing a new optimization. Abdelaal et al. [51] adopted a nonlinear MPC method combined with a ship-motion control model to achieve more accurate and fast ship CA decision-making and track control. However, their algorithm only considers CA between a single vessel and a point, such as a static obstacle, and only considers the alteration of the course to starboard. Based on the concept of optimal control, Chen et al. [52] established an optimal control model for multi-objective ship CA in open water, in which the ship’s heading is controlled by setting a rudder angle constraint. This can achieve multi-ship CA; however, the model takes a long time to compute, requires accurate initial conditions and constraints, and cannot handle environmental disturbances.
MPC has the advantages of a good control effect and strong robustness [8]. It can effectively overcome the uncertainty, nonlinearity, and correlation in the process, and it can easily deal with various constraints in the controlled and manipulated variables in the process. The influence of environmental factors on a ship can also be considered. However, the calculation time of the algorithm is affected by the complexity of the model. The more complex the model and the constraints, the calculation time of the algorithm will be longer.
(4)
Game Theory (GT)
Game theory describes the interaction of multiple decision-makers’ strategies, where the behavior of each decision-maker has an impact on other decision-makers in the game process. Game theory focuses on how the behavior of a decision-maker affects the behavior of other decision-makers. Wang et al. [53] developed a probabilistic model to solve the ship CA problem and designed a greedy algorithm to search for possible movement paths using a cost function to determine the evasive strategy of an unmanned surface vessel. However, this method does not consider the effects of the COLREGs or environmental disturbances.
Game theory can consider the requirements of the COLREGs and the parameters of vessel movement, and can avoid collisions with multiple vessels [10]; however, it cannot deal with static obstacles and has medium calculation time [54].
(5)
Artificial Potential Field (APF)
The APF method establishes a virtual force field containing both gravitational and repulsive fields and controls the direction of ship movement under the combined effect of these two forces [55]. Liu et al. [56] improves the APF functions for dynamic ships considering the COLREGs. However, the algorithm fails to adopt the speed change strategy and cannot deal with static lake obstacles. Xue et al. [57][58] proposed automatic trajectory planning based on the APF method and velocity vector by applying the alteration of heading angle as the main method to avoid collisions and considering the method of deceleration for emergencies. In the simulation experiment, only the course was changed to avoid collisions, whereas the speed was not altered, and there was a lack of experiments during emergencies. Zhang et al. [59] designed an APF-based intelligent navigation approach for a USV in a complex environment with a randomly moving target and multiple static or moving obstacles, yet the COLREG rules were not considered. Huang et al. [60] introduced a ship-maneuvering motion control model by combining a synergistic ship domain model with the APF method, and considering the effect of ship length on ship CA. In addition, the method investigates the situation when two vessels cross paths and the give-way vessel does not comply with the COLREGs. Lee et al. [61] used the velocity-potential field as the field function in the APF method. The algorithm is divided into course-alteration and track-keeping modes. This algorithm is simple, easy to implement, and suitable for real-time distributed CA systems. However, this method is only suitable for CA operations in open water and requires appropriate action by the crew on board. Lyu et al. [6][14][62] proposed a path-guided hybrid APF (PGHAPF) approach and the improved versions for restricted waters even in a practical environment [5][13]. The approach assumes that course alteration is the only strategy to avoid collisions and integrates the potential field and gradient methods, including potential field-based path planning for arbitrary static obstacles, gradient-based decision-making for dynamic obstacles, and optimization considering an a priori path and waypoint selection.
Although the APF method has fast calculation speed and strong adaptability, it has the disadvantage of a local minimum [63][64], which must be combined with other optimization algorithms to be solved [65].

3.2. Artificial Intelligence and Soft Computing-Based Algorithms

Neural networks, evolutionary algorithms, and swarm intelligence algorithms are the primary algorithms based on artificial intelligence and soft computing.
(1)
Knowledge-based systems
Knowledge-based systems can generate and utilize knowledge from various sources, data, and information for problem-solving procedures and support human learning, decision-making, and action [66]. He et al. [29] proposed a method for timing and selecting options for steering CA actions under three postures, first time-point of collision risk (FTCR), first time-point of the close situation (FTCS), and first time-point of immediate danger (FTID), to determine the ship avoidance action based on the COLREGs and ship maneuvering information.
The problems of knowledge-based systems are that they are difficult to develop a complete, accurate, and concise knowledge base, and they cannot deal with issues outside the knowledge base.
(2)
Neural Network (NN)
Neural networks, also known as artificial neural networks, are inspired by the human brain and mimic the way biological neurons transmit signals to each other [67]. Zhai et al. [68] used a multi-vessel automatic CA method based on deep neural networks using a double-depth Q-network and an empirical first-replay approach, which allows the model to converge faster, but the method cannot be used in actual navigation.
Neural networks can control ship movements without knowing the exact parameters of the ship; however, they must make full use of their methods and knowledge [69].
(3)
Evolutionary algorithms
Evolutionary algorithms are based on the Darwinian evolutionary theory, which consist of genetic algorithms (GA), genetic programming (GP), evolution strategies (ES), and evolutionary programming (EP). In the CA process, an optimal path is determined by selection, crossover, variation, and population control [70][71]. Tsou et al. [72] used a GA in conjunction with the COLREGs and the field of ship safety to find the optimal path from an economic point of view and to provide the best steering angle, resumption timing, and resumption angle. However, this optimal route produces an avoidance route that is not in line with navigation experience, and it may obfuscate target ships.
Evolutionary algorithms can be adapted to a wide range of problems in various environments and achieve satisfactory results. Evolutionary algorithms are widely applicable, highly nonlinear, easily modifiable, and parallelizable. However, the crossover and variation rates in these algorithms are difficult to determine, and most of these parameters have been chosen empirically [73].
(4)
Swarm intelligence algorithm (SIA)
An SIA is an optimization algorithm that imitates social biological groups, including bacterial foraging optimization (BFO), particle swarm optimization (PSO), and ant colony optimization (ACO). Liu et al. [74] used an optimization algorithm combining improved bacterial foraging and particle swarm algorithms, which has a strong global search capability and optimizes CA parameters, including CA angle and redirect angle, to generate CA routes for ships. Zheng et al. [75] proposed a hybrid path-planning algorithm that combines a simulated annealing algorithm and PSO, which can automatically give way and alter the course to avoid collisions. All of the above can only solve two-ship encounter situations or CA in a static environment [76] and cannot handle multi-ship encounter situations.
Lazarowska [77] used the ant colony algorithm to design an automatic CA decision algorithm considering the COLREGs, static obstacles, and multi-ship encounters. The algorithm assumes that all target ships keep their speed and course, and the calculation time of the algorithm is too long; therefore, real-time decision-making cannot be guaranteed. Zheng et al. [78] proposed an improved cultural particle swarm algorithm using the Kalman filter to smooth and predict a ship’s trajectory; this algorithm is based on the fuzzy distribution method, combined with the COLREGs, to determine the ship’s steering angle to achieve ship CA decisions. Zeng et al. [79] proposed a particle swarm genetic optimization CA decision algorithm that complies with the COLREGs, established a CA objective function based on the steering amplitude and sailing time, and obtained the optimal steering amplitude and required sailing time after steering. This method assumes that the evasive action information of the surrounding ships is obtained in real time between ships by using radar and AIS.
A swarm intelligence algorithm has the advantages of simple operation, fast convergence speed, and good global convergence, but the selection of parameters is important, and it is easy to fall into the local optimal solution.
(5)
Fuzzy logic (FL)
Fuzzy logic describes a system in a fuzzy language and is used to describe both the quantitative and qualitative models of the system. Hu et al. [80] proposed an automatic CA algorithm considering steering system, which searched for a new course from a knowledge base containing basic experts and used T-S fuzzy logic to solve uncertainties in heading control systems.
Fuzzy logic can be used for the control of complex objects. However, in practice, it is easier to implement a simple application control. The greater the number of input and output variables, the more difficult the reasoning of the fuzzy logic is [81].
(6)
Reinforcement learning (RL)
Reinforcement learning (RL) [82][83], deep reinforcement learning (DRL) [84][85][86], and other deep learning (DL) methods have been increasingly applied in the field of ship automatic CA [4][87]. For these methods, they consume significant time for training and their ability to deal with complex environments needs to be strengthened [88]. For example, target ships are set to keep their course and speed; otherwise, it is difficult to plan a feasible path [82]. Even the same input conditions may produce different CA decisions, and this uncertainty of the solution also limits their application in practice [89]. The reward function is mostly about the course and safety constraints. Even if multi-ship encounters can be handled, the interference of the environment still needs to be considered in the training of a CA decision-making model [83], and a cooperative multi-ship collision-avoidance scheme is also needed to be studied [86].

3.3. Summary and Comparison of Methods

Table 1 lists the considering factors in the automatic CA decision-making methods based on altering course. Because a CA action by changing course is easier to operate than a CA action by changing speed, and the former is easier to be found by target ships through vision, so ships often use steering avoidance in general navigation, especially in open waters. However, in restricted waters, it is difficult to ensure the safety of the ship only by steering avoidance due to the serious limitation of the steering range and operating space of the ship.
Table 1. Comparison of strategies based on altering course.
Method Refs. P1 P2 P3 P4 P5 P6 P7 P8 P9 P10 Limitations
Geometric analysis [41] CW TE/ME MO Y N H N SD Discrete solution space Trajectory base The target ships keep course and speed.
[42] OW TE DO Y N / Y CPA +0.1°/step Course alteration function Only one target ship, without wind, waves, currents, and consideration of other disturbances.
[43] CW / SO N N H Y / / Course alteration function Wind and current are not considered; only static obstacle avoidance.
VO [47] OW ME MO N N / Y CPA / Goal-directed behavior It does not consider the weather, sea conditions, and COLREGs constraints.
[45] OW TE/ME MO Y Y H Y CPA / Goal-directed behavior It does not consider the actual map, steering return angle, and time.
[23] OW ME DO Y N / N / −90°~90° Goal-directed behavior It can only be used in open waters, and studies in restricted waters and more complex environments are required.
MPC [51] OW TE MO Y N H Y SD / Discrete variation The algorithm only considers the CA between a single ship and point-like static obstacles.
Optimal control [52] OW ME DO N Y L Y CPA and SD −30°~30° Continuous change The calculation time is long, and precise initial conditions and constraints are required.
GT [53] OW TE/ME DO N N H Y / / Discrete variation It does not consider the impact of the COLREGs and environmental disturbances.
APF [56] OW TE/ME MO Y N H Y SD / Objective function guide Natural conditions and static obstacles are not considered.
[60] OW TE DO Y N M Y / −35°~35° Objective function guide The impact of wind, waves, and currents on the ship is not considered.
APF [61] OW TE/ME MO N Y / Y SD and CRI −90°~90° Objective function guide The influence of the shallow-water effect and shore-wall effect on ships is not considered.
[14] CW ME MO Y N H Y CPA and SD −180°~180° Objective function guide It does not re-plan to the original route, and route optimization is not considered.
[57][58] CW TE/ME MO Y Y / Y CPA Cubic spline smoothing Goal-guided behavior It does not consider weather conditions, extreme encounter cases, change of speed, or reversing in emergencies.
Knowledge-based system [29] OW TE DO Y N / Y FSCR, FTCS, and FTID / Course alteration function Only the avoidance actions of stand-on ships are studied, and further research is needed on give-way ships.
NN [68] OW ME MO Y N H N CPA −12°~12° Discrete variation It cannot be used for actual CA and does not consider restricted waters.
GA [72] CW TE/ME MO Y N M N CPA −30°~90° Course alteration function It will create an avoidance route that is not in line with nautical experience.
SIA [74] OW TE DO Y N / N CRI 30°~80° Objective function guide The impact of wind, waves, and currents on the ship is not considered.
[75] CW TE MO Y N / N CRI / Right turn change The impact of wind, waves, and currents on the ship is not considered.
[77] CW TE/ME MO Y N H N CRI / Objective function guide The shallow-water effect and the shore effect on ships are not considered.
[78] OW TE DO Y N / N CRI −35°~35° Objective function guide It plans path to the next waypoint after turning, without optimization.
SIA and EA [79] OW ME DO Y N H N CRI 30°~60° Right-turn change It assumes that all target ships (TSs) obey the COLREGs, and CA action information of TSs is obtained in real time.
FL [80] OW ME DO Y Y / Y CPA −35°~35° Course alteration function The accuracy of the results needs to be improved.
DRL [87] CW ME MO Y N / Y SD Action at∈{−Δψ, 0, Δψ}
Δψ > 0		 States, actions, and a reward function It considers simple restricted waters with an isolated square obstacle and 3 TSs’ reactive collision avoidance, rather than a smart action in the far range.
Autonomous CA algorithms by ship steering can be applied to all types of water. Early steering maneuvers are required in restricted and complex waters. Many studies have focused on single or multiple dynamic obstacles and have considered three main scenarios: ship maneuverability is considered in most cases, including ship dynamics, maneuvering models, dynamic models, and target ship motion constraints and limitations. However, certain problems remain:
(1)
Most verification algorithms assume that target ships keep their speed and comply with the COLREGs and do not consider the violations of the COLREGs by target ships.
(2)
A part of these algorithms does not consider the maneuverability of the ship, which makes them unsuitable for actual ship navigation.
(3)
Environmental disturbances, such as wind, waves, and currents, are not considered.

4. Automatic CA Strategy Based on Alteration of Speed Alone

In addition to the strategy based on altering course, an avoidance strategy based on altering speed is also an important optional strategy for ships to autonomously avoid collisions, particularly in restricted waters. Considering the maneuvering characteristics of ships and the habits of sailors, there are few studies on autonomous CA strategies based only on the alteration of speed. However, research on the optimization and strategy selection for avoidance based on altering speed should not be ignored.

4.1. Optimization of Strategy Selection for Changing Speed

For the CA strategy based on changing speed, the timing, amplitude, and rate of the speed alteration, and the maneuvering characteristics of a ship have a significant impact on the final CA result. Bi et al. [90] proposed a method to determine the best avoidance timing and action for a ship. Ma et al. [91] used a bacterial foraging algorithm in combination with the COLREGs and the field of ship safety to find CA strategies for altering speed from an economical perspective, including optimal shifting time, amplitude, and navigation recovery time. This assumed that a vessel’s speed can be immediately altered to a set value; however, in practice, speed alteration is gradual. Yu et al. [92] proposed a CA decision-making method for ship speed in narrow waters based on a mimic physics optimization algorithm. According to the requirements of the COLREGs on the speed-alteration action range and considering the influence of the deceleration stroke and the time required for deceleration on the CA effect, the collision risk and speed-alteration energy loss are used to evaluate the advantages and disadvantages of the CA decision, and the objective function of the ship’s speed-alteration CA is established.
According to different sailing situations, there are also some studies comparing the effects of different avoidance strategies through course and speed alterations and choosing the best one. Su et al. [93] studied a CA method for large ships in open waters. Considering the influence of difficult maneuvering ability and the large motion inertia of large ships, the slackening speed was prioritized, and geometric methods were used to calculate the speed. If the slackening speed cannot achieve the avoidance effect, collisions are avoided by ship steering.
Zhao et al. [46] improved the speed obstacle algorithm while considering ship maneuverability and the COLREGs and made decisions in two ways: altering course and altering speed. Hu et al. [94] established a multi-ship real-time collision risk analysis system with alteration course or speed based on the COLREGs and good ship skills, and they analyzed five factors affecting the collision risk of ships in real time.

4.2. Research on CA Law of Altering Speed

Altering speed avoidance includes increasing speed and slackening speed. In theory, increasing speed can also avoid collisions and conform to the safe speed requirement in the COLREGs. However, when sailing at sea, the feasibility of a ship to increase speed is weak. The acceleration of a ship causes the TCPA between two ships to decrease sharply, and the short reaction time for CA can easily appear as an illusion of target ships—altering speed only is difficult for target ships to visually see and not easily recognizable as course alteration—and increase the risk of collision [95]. However, there is sufficient reaction time for slackening speed [25]. When immediate danger occurs, it can also stop to avoid collision, which increases the safety of ship navigation [96]. In most cases, the CA strategy of a ship based on alteration of speed alone is slackening speed.
Automatic CA decision-making based on speed alteration also requires the right timing. An action that is too early does not conform to the CA psychology of a captain and officers, whereas too late an action will cause uncoordinated actions between ships and increase the risk of collision. In addition, under the influence of wind and waves [35][36], deceleration may lead to course changing of a ship. Therefore, to slacken speed or reverse it to avoid a collision, it is necessary to consider the ship’s course-keeping performance, the deflection effect of the bow when reversing, the forward stroke, the speed of the ship during the deceleration process, and the time required for the main engine to restart during an emergency. When a ship slackens speed, it should be noted that the speed cannot be less than the minimum value to maintain the rudder effect and avoid losing control of the ship. A CA action that only alters speed, whether for a conventional ship or an intelligent ship, is difficult for target ships to see visually and apparently, or it is not as easy to recognize as a course alteration. Therefore, it may appear as an obfuscate action to target ships, resulting in a collision.

5. Automatic CA Strategy Based on Altering Course and Speed

The autonomous CA strategy of a ship should be flexible and available at any time for course and speed alterations. Either one can be used alone or the two can be combined. However, the combination solution is technically difficult to implement because the CA effect of steering and the effect of speed alteration are not necessarily superimposed on each other, but may also be mutually offset [97].

5.1. Establishing Objective Function through Course and Speed

At present, research on a ship’s autonomous CA strategy combining altering course and speed is typically to construct the objective functions of speed and course, or their variation, to judge and select the optimal strategy [98].
According to the general requirements of the COLREGs, Zhang et al. [99] used a graphical method to analyze the CA performance of give-way and straight-way ships in typical encounter situations, calculated the collision probability, and used a linear expansion algorithm to alter the course and slacken speed. Szlapczynski [100] proposed a ship CA strategy based on an evolutionary algorithm by introducing a turning penalty mechanism and speed-reduction dynamic model that can minimize route detours while avoiding obstacles. Szlapczynski et al. [97][101] also used the ship domain to assess the collision risk of own ship using a ship dynamic model to estimate the moment and distance required to maneuver. A more applicable CA decision-making method is obtained by the improved modified Dijkstra’s algorithm to find the solution in a graph representing discrete solution space, which is tested in laboratory conditions and quasi-real conditions [9]. However, the CA maneuvers are limited to course alteration and those combing turns with speed reduction, and speed reduction is only conducted in the condition of keeping the course and natural deceleration owing to turns.
Huang et al. proposed a generalized velocity obstacle (GVO) algorithm, considering the COLREGs and ship dynamics in a certain extent. The feasible velocity is found by the UO set, i.e., a set collecting all the controls of the OS resulting in collisions to support the OOWs in decision-making. It should be noted that when the error between the predicted trajectory and the actual trajectory of the OS is large, the solution may be a failure [102].
Based on the idea of MPC, Johansen et al. [103][104][105] considered a ship-motion model with wind and flow interference, used a limited control sequence to divide the course and speed, chose different CA actions to predict ship-motion trajectories during a defined period, and subsequently made selections from these trajectories for an optimal CA maneuvering strategy. However, in this method, the accuracy of the mathematical model of ship motion determines the effectiveness of CA decision-making, and the simulation of the experimental method based on scene generation cannot predict the abnormal maneuvering of target ships. Eriksen et al. [106][107] proposed a branching-course MPC (BC-MPC) algorithm, which is included in a three-level integrated COLAV (CA) system and used for path planning, regular CA of dynamic ships, and emergency situations according to different scenarios. A full-trajectory generation mechanism consists of the numbers and duration of a series of course and speed maneuvers, at each level or trajectory of the system.
Hu et al. [108] proposed a multi-objective PSO algorithm that expresses the COLREGs as inequality constraints, integrates them into the algorithm, and sets an objective function that prioritizes the course/speed alteration preference over other objectives. Hirayama et al. [95] proposed a distributed stochastic search algorithm+ (DSSA+) to alter course and speed, considering the latest advances in ship maneuvering technology and the need to avoid collisions more effectively. However, there has been no analysis based on an actual situation for altering the course, speed, or a combination of course and speed alteration.
Tan et al. [109] proposed a fast-marching method (FMM) based on the path planning method for ship swarms, and a priority-based speed and heading-angle control algorithm considering the COLREGs, to design a CA strategy. This method fully considers the influence of environmental uncertainty, but it only considers the situation in which target ships keep their course and speed. Chen et al. [110] used a PSO algorithm to numerically optimize the CA criterion function and obtained the optimal path and corresponding operational decision for a ship to avoid collisions. However, the influence of ship motion characteristics has not been fully considered.

5.2. Safe-Speed and Limited-Speed Methods

Another method is to set a safe speed limit or to calculate the instant speed during steering and avoidance [65].
To solve the problem of ship CA in restricted waters, Zhang et al. [111] proposed a calculation method for ship CA time, distance, and position while considering multi-segment routes. This method considers the turning position, turning time, and safe speed of the ship. A safe speed can be used to avoid collisions near intersections in restricted waters. Zeng et al. [112] proposed a mathematical model for calculating DCPA and calculated the derivative of a ship’s course and speed. Thus, it is possible to quantitatively judge the effectiveness of changing course and speed to avoid collisions in different encounter situations.
It is difficult to achieve both safe speed and calculated speeds for ship maneuvering. In addition, these methods can only be used as auxiliary methods for CA, and they cannot deal with complex situations encountered by multiple ships in real time because these methods are not decision-making methods for the joint control of course and speed based on the risk of collision between ships.

5.3. Course and Speed Alteration Strategy Using Hybrid Algorithm

For steering avoidance, heading control can be achieved using only one algorithm. When combined with speed, it must be combined with methods such as speed vectors, collision cones, and deep reinforcement learning (DRL) [4].
Xu et al. [113] proposed a dynamic CA algorithm based on a layered artificial potential field with collision cone (LAPF-CC), using the relative distance and velocity as variables to determine the collision risk, and constructed a torque named “speed-torque”. The speed-torque, attraction, and repulsion work together to alter the course and speed of a USV. Song et al. [114] introduced a new predictive APF (PAPF) method to plan a smoother path with turning angle limit and velocity adjustment. However, this method does not consider the influence of environmental disturbances, such as wind, waves, and currents on ships. Guo et al. [115] combined the APF with DRL to propose an automatic path-planning method for unmanned ships. This method divides the action control strategy into heading and speed change control. It has the advantages of high precision and small navigation errors; however, it does not consider the influence of a ship’s dynamic properties and environmental disturbances. Xu et al. [116] proposed an intelligent hybrid CA algorithm based on DRL combined with collision cones, which can determine CA timing and corresponding CA actions according to different obstacles. However, this method only deals with the circumscribed circle of a static obstacle and cannot deal with dynamic obstacles, such as ships.
Shen et al. proposed an autonomous intelligent CA algorithm for unmanned ships based on a deep competitive Q-learning algorithm and A* algorithm. Using the A* algorithm and combining the ship’s maneuvering characteristics, a parallel dynamic CA decision-making scheme was proposed, which could avoid collision with 2–4 dynamic target ships and 1 static obstacle by altering the course alone or simultaneously altering the course and speed, assuming that all target ships comply with the COLREGs [117].

References

  1. Kim, T.; Schröder-Hinrichs, J. Research Developments and Debates Regarding Maritime Autonomous Surface Ship: Status, Challenges and Perspectives. In New Maritime Business; WMU Studies in Maritime Affairs: Cham, Switzerland, 2021; pp. 175–197.
  2. Öztürk, Ü.; Akdağ, M.; Ayabakan, T. A review of path planning algorithms in maritime autonomous surface ships: Navigation safety perspective. Ocean Eng. 2022, 251, 111010.
  3. Hinostroza, M.A.; Xu, H.; Guedes Soares, C. Cooperative operation of autonomous surface vehicles for maintaining formation in complex marine environment. Ocean Eng. 2019, 183, 132–154.
  4. Qiao, Y.; Yin, J.; Wang, W.; Duarte, F.; Yang, J.; Ratti, C. Survey of Deep Learning for Autonomous Surface Vehicles in Marine Environments. IEEE Trans. Intell. Transp. 2023, 24, 3678–3701.
  5. Zhu, Z.; Yin, Y.; Lyu, H. Automatic collision avoidance algorithm based on route-plan-guided artificial potential field method. Ocean Eng. 2023, 271, 113737.
  6. Lyu, H.G.; Yin, Y. COLREGS-Constrained Real-time Path Planning for Autonomous Ships Using Modified Artificial Potential Fields. J. Navig. 2019, 72, 588–608.
  7. Ohn, S.; Namgung, H. Requirements for Optimal Local Route Planning of Autonomous Ships. J. Mar. Sci. Eng. 2023, 11, 17.
  8. Sun, T.; Liu, C.; Xu, S.; Hu, Q.; Li, C. COLREGS-Complied Automatic Collision Avoidance for the Encounter Situations of Multiple Vessels. J. Mar. Sci. Eng. 2022, 10, 1688.
  9. Pietrzykowski, Z.; Wołejsza, P.; Nozdrzykowski, A.; Borkowski, P.; Banaś, P.; Magaj, J.; Chomski, J.; Mąka, M.; Mielniczuk, S.; Pańka, A.; et al. The autonomous navigation system of a sea-going vessel. Ocean Eng. 2022, 261, 112104.
  10. Lisowski, J. Sensitivity of Safe Trajectory in a Game Environment on Inaccuracy of Radar Data in Autonomous Navigation. Sensors 2019, 19, 1816.
  11. Campbell, S.; Naeem, W.; Irwin, G.W. A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres. Annu. Rev. Control 2012, 36, 267–283.
  12. Pietrzykowski, Z.; Wołejsza, P.; Borkowski, P. Decision Support in Collision Situations at Sea. J. Navig. 2017, 70, 447–464.
  13. Zhu, Z.; Lyu, H.; Zhang, J.; Yin, Y. An Efficient Ship Automatic Collision Avoidance Method Based on Modified Artificial Potential Field. J. Mar. Sci. Eng. 2022, 10, 3.
  14. Lyu, H.; Yin, Y. Fast Path Planning for Autonomous Ships in Restricted Waters. Appl. Sci. 2018, 8, 2592.
  15. Zhu, Z.; Lyu, H.; Zhang, J.; Yin, Y.; Fan, X. A practical environment potential field modelling method for complex geometric objects. J. Navig. 2022, 1–24.
  16. Deng, F.; Jin, L.; Hou, X.; Wang, L.; Li, B.; Yang, H. COLREGs: Compliant Dynamic Obstacle Avoidance of USVs Based on theDynamic Navigation Ship Domain. J. Mar. Sci. Eng. 2021, 9, 837.
  17. Chen, P.; Huang, Y.; Papadimitriou, E.; Mou, J.; van Gelder, P. Global path planning for autonomous ship: A hybrid approach of Fast Marching Square and velocity obstacles methods. Ocean Eng. 2020, 214, 107793.
  18. Gan, L.; Yan, Z.; Zhang, L.; Liu, K.; Zheng, Y.; Zhou, C.; Shu, Y. Ship path planning based on safety potential field in inland rivers. Ocean Eng. 2022, 260, 111928.
  19. Perera, L.P.; Guedes Soares, C. Collision risk detection and quantification in ship navigation with integrated bridge systems. Ocean Eng. 2015, 109, 344–354.
  20. Liu, K.; Yuan, Z.; Xin, X.; Zhang, J.; Wang, W. Conflict detection method based on dynamic ship domain model for visualization of collision risk Hot-Spots. Ocean Eng. 2021, 242, 110143.
  21. Szlapczynski, R. A Unified Measure of Collision Risk Derived from the Concept of a Ship Domain. J. Navig. 2006, 59, 477–490.
  22. Chen, P.; Huang, Y.; Papadimitriou, E.; Mou, J.; van Gelder, P.H.A.J. An improved time discretized non-linear velocity obstacle method for multi-ship encounter detection. Ocean Eng. 2020, 196, 106718.
  23. Mou, J.; Li, M.; Hu, W.; Zhang, X.; Gong, S.; Chen, P.; He, Y. Mechanism of dynamic automatic collision avoidance and the optimal route in multi-ship encounter situations. J. Mar. Sci. Technol. 2021, 26, 141–158.
  24. Du, L.; Goerlandt, F.; Valdez Banda, O.A.; Huang, Y.; Wen, Y.; Kujala, P. Improving stand-on ship’s situational awareness by estimating the intention of the give-way ship. Ocean Eng. 2020, 201, 107110.
  25. Woerner, K.; Benjamin, M.R.; Novitzky, M.; Leonard, J.J. Quantifying protocol evaluation for autonomous collision avoidance. Auton. Robot. 2019, 43, 967–991.
  26. Wang, T.; Wu, Q.; Zhang, J.; Wu, B.; Wang, Y. Autonomous decision-making scheme for multi-ship collision avoidance with iterative observation and inference. Ocean Eng. 2020, 197, 106873.
  27. Ni, S.; Wang, N.; Qin, Z.; Yang, X.; Liu, Z.; Li, H. A distributed coordinated path planning algorithm for maritime autonomous surface ship. Ocean Eng. 2023, 271, 113759.
  28. Perera, L.P. Deep Learning Toward Autonomous Ship Navigation and Possible COLREGs Failures. J. Offshore Mech. Arct. Eng. 2019, 142, 031102.
  29. He, Y.; Jin, Y.; Huang, L.; Xiong, Y.; Chen, P.; Mou, J. Quantitative analysis of COLREG rules and seamanship for autonomous collision avoidance at open sea. Ocean Eng. 2017, 140, 281–291.
  30. Woerner, K. Multi-Contact Protocol-Constrained Collision: Avoidance for Autonomous Marine Vehicles. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2016.
  31. Zaccone, R.; Martelli, M. A collision avoidance algorithm for ship guidance applications. J. Mar. Eng. Technol. 2019, 19, 62–75.
  32. Vagale, A.; Bye, R.T.; Oucheikh, R.; Osen, O.L.; Fossen, T.I. Path planning and collision avoidance for autonomous surface vehicles II: A comparative study of algorithms. J. Mar. Sci. Technol. 2021, 26, 1307–1323.
  33. Rutkowski, G. Determining Ship’s Safe Speed and Best Possible Speed for Sea Voyage Legs. Trans. Nav. Int. J. Mar. Navig. Saf. Sea Transp. 2016, 10, 425–430.
  34. Hong, S. Maritime Officers’ Strategies for Collision Avoidance in Crossing Situations. J. Ergon. Soc. Korea 2017, 36, 525–533.
  35. Gao, Q.; Song, L.; Yao, J. RANS Prediction of Wave-Induced Ship Motions, and Steady Wave Forces and Moments in Regular Waves. J. Mar. Sci. Eng. 2021, 9, 1459.
  36. Borkowski, P. Numerical Modeling of Wave Disturbances in the Process of Ship Movement Control. Algorithms 2018, 11, 130.
  37. Szlapczynski, R.; Szlapczynska, J. A Target Information Display for Visualising Collision Avoidance Manoeuvres in Various Visibility Conditions. J. Navig. 2015, 68, 1041–1055.
  38. Chang, K.; Jan, G.E.; Parberry, I. A Method for Searching Optimal Routes with Collision Avoidance on Raster Charts. J. Navig. 2003, 56, 371–384.
  39. Jones, K.D. Application of a Manœuvre Diagram to Multi-ship Encounters. J. Navig. 1974, 27, 19–27.
  40. Szlapczynski, R.; Szlapczynska, J. An analysis of domain-based ship collision risk parameters. Ocean Eng. 2016, 126, 47–56.
  41. Lazarowska, A. A new deterministic approach in a decision support system for ship’s trajectory planning. Expert Syst. Appl. 2017, 71, 469–478.
  42. Xu, W.; Yin, J.; Hu, J.; Li, K. Ship Automatic Collision Avoidance by Altering Course Based on Ship Dynamic Domain. In Proceedings of the 2016 IEEE Trustcom/BigDataSe/ISPA, Tianjin, China, 23–26 August 2016; pp. 2024–2030.
  43. Tang, P.; Zhang, R.; Liu, D.; Zou, Q.; Shi, C. Research on Near-Field Obstacle Avoidance for Unmanned Surface Vehicle Based on Heading Window. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC 2012), Taiyuan, China, 23–25 May 2012; pp. 1262–1267.
  44. Tam, C.; Bucknall, R.; Greig, A. Review of Collision Avoidance and Path Planning Methods for Ships in Close Range Encounters. J. Navig. 2009, 62, 455–476.
  45. Zhang, G.; Wang, Y.; Liu, J.; Cai, W.; Wang, H. Collision-Avoidance Decision System for Inland Ships Based on Velocity Obstacle Algorithms. J. Mar. Sci. Eng. 2022, 10, 814.
  46. Zhao, X.; He, Y.; Huang, L.; Mou, J.; Zhang, K.; Liu, X. Intelligent Collision Avoidance Method for Ships Based on COLRGEs and Improved Velocity Obstacle Algorithm. Appl. Sci. 2022, 12, 8926.
  47. Tian, Y.; Huang, L.; Xiong, Y.; Li, S. On the velocity obstacle based automatic collision avoidance with multiple target ships at sea. In Proceedings of the 2015 International Conference on Transportation Information and Safety (ICTIS 2015), Wuhan, China, 25–28 June 2015; pp. 468–472.
  48. Zhang, W.; Yan, C.; Lyu, H.; Wang, P.; Xue, Z.; Li, Z.; Xiao, B. COLREGS-based Path Planning for Ships at Sea Using Velocity Obstacles. IEEE Access 2021, 9, 32613–32626.
  49. Cho, Y.; Han, J.; Kim, J.; Lee, P.; Park, S. Experimental validation of a velocity obstacle based collision avoidance algorithm for unmanned surface vehicles. IFAC-Pap. 2019, 52, 329–334.
  50. Kuwata, Y.; Wolf, M.T.; Zarzhitsky, D.; L Huntsberger, T. Safe Maritime Autonomous Navigation With COLREGS, Using Velocity Obstacles. IEEE J. Ocean. Eng. 2014, 39, 110–119.
  51. Abdelaal, M.; Fränzle, M.; Hahn, A. Nonlinear Model Predictive Control for trajectory tracking and collision avoidance of underactuated vessels with disturbances. Ocean Eng. 2018, 160, 168–180.
  52. Chen, L.; Huang, L.; Xiong, Y. Collision avoidance control of multi-ships on sea based on optimal control. China Saf. Sci. J. (CSSG) 2014, 24, 15–21.
  53. Wang, J.; Wang, J.; Zhao, R.; Liang, X.; Wei, Q. Collision Avoidance Strategies for Unmanned Surface Vehicles Based on Probabilistic Game Theory Framework. In Proceedings of the OCEANS 2022-Chennai, Chennai, India, 21–24 February 2022; pp. 1–6.
  54. Lisowski, J.; Mohamed-Seghir, M. Comparison of Computational Intelligence Methods Based on Fuzzy Sets and Game Theory in the Synthesis of Safe Ship Control Based on Information from a Radar ARPA System. Remote Sens. 2019, 11, 82.
  55. Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. Int. J. Robot. Res. 1986, 5, 90–98.
  56. Liu, W.; Qiu, K.; Yang, X.; Wang, R.; Xiang, Z.; Wang, Y.; Xu, W. COLREGS-based collision avoidance algorithm for unmanned surface vehicles using modified artificial potential fields. Phys. Commun. 2023, 57, 101980.
  57. Xue, Y.; Lee, B.S.; Han, D. Automatic collision avoidance of ships. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2009, 1, 33–46.
  58. Xue, Y.; Clelland, D.; Lee, B.S.; Han, D. Automatic simulation of ship navigation. Ocean Eng. 2011, 38, 2290–2305.
  59. Zhang, G.; Han, J.; Li, J.; Zhang, X. APF-based intelligent navigation approach for USV in presence of mixed potential directions: Guidance and control design. Ocean Eng. 2022, 260, 111972.
  60. Huang, D.; Liu, Z.; Wang, X. Artificial potential field and ship maneuverability based collision avoidance path planning. In Proceedings of the 2020 Chinese Automation Congress (CAC 2020), Shanghai, China, 6–8 November 2020; Volume 1, pp. 2490–2495.
  61. Lee, M.; Nieh, C.; Kuo, H.; Huang, J. A collision avoidance method for multi-ship encounter situations. J. Mar. Sci. Technol. 2020, 25, 925–942.
  62. Lyu, H.G.; Yin, Y. Ship’s trajectory planning for collision avoidance at sea based on modified artificial potential field. In Proceedings of the 2017 2nd International Conference on Robotics and Automation Engineering (ICRAE 2017), Shanghai, China, 29–31 December 2017; pp. 351–357.
  63. Mohanan, M.G.; Salgoankar, A. A survey of robotic motion planning in dynamic environments. Robot. Auton. Syst. 2018, 100, 171–185.
  64. Ge, S.S.; Cui, Y.J. New potential functions for mobile robot path planning. IEEE Trans. Robot. Autom. 2000, 16, 615–620.
  65. Gao, P.; Zhou, L.; Zhao, X.; Shao, B. Research on ship collision avoidance path planning based on modified potential field ant colony algorithm. Ocean Coast. Manag. 2023, 235, 106482.
  66. Zhang, J.; Liu, J.; Hirdaris, S.; Zhang, M.; Tian, W. An interpretable knowledge-based decision support method for ship collision avoidance using AIS data. Reliab. Eng. Syst. Safe 2023, 230, 108919.
  67. Ahn, J.; Rhee, K.; You, Y. A study on the collision avoidance of a ship using neural networks and fuzzy logic. Appl. Ocean Res. 2012, 37, 162–173.
  68. Zhai, P.; Zhang, Y.; Shaobo, W. Intelligent Ship Collision Avoidance Algorithm Based on DDQN with Prioritized Experience Replay under COLREGs. J. Mar. Sci. Eng. 2022, 10, 585.
  69. Simsir, U.; Amasyal, M.F.; Bal, M.; Elebi, U.B.; Ertugrul, S. Decision support system for collision avoidance of vessels. Appl. Soft Comput. 2014, 25, 369–378.
  70. Tsou, M. Multi-target collision avoidance route planning under an ECDIS framework. Ocean Eng. 2016, 121, 268–278.
  71. Tam, C.; Bucknall, R. Path-planning algorithm for ships in close-range encounters. J. Mar. Sci. Technol. 2010, 15, 395–407.
  72. Tsou, M.; Kao, S.; Su, C. Decision Support from Genetic Algorithms for Ship Collision Avoidance Route Planning and Alerts. J. Navig. 2010, 63, 167–182.
  73. Kuczkowski, L.; Smierzchalski, R. Path planning algorithm for ship collisions avoidance in environment with changing strategy of dynamic obstacles. In Trends in Advanced Intelligent Control, Optimization and Automation; Springer: Cham, Switzerland, 2017; pp. 641–650.
  74. Liu, H.; Deng, R.; Zhang, L. The application research for ship collision avoidance with hybrid optimization algorithm. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA 2016), Ningbo, China, 1–3 August 2016; Volume 1, pp. 760–767.
  75. Zheng, J.; Wu, J.; Ma, Y.; Long, Y. A hybrid optimization algorithm of simulated annealing and particle swarm for unmanned surface vessel path planning. Period. Ocean. Univ. China 2016, 46, 116–122.
  76. Blindheim, S.; Rokseth, B.; Johansen, T.A. Autonomous machinery management for supervisory risk control using particle swarm optimization. J. Mar. Sci. Eng. 2023, 11, 327.
  77. Lazarowska, A. Ship’s trajectory planning for collision avoidance at sea based on ant colony optimisation. J. Navig. 2015, 68, 291–307.
  78. Zheng, Y.; Zhang, X.; Shang, Z.; Guo, S.; Du, Y. A decision-making method for ship collision avoidance based on improved cultural particle swarm. J. Adv. Transp. 2021, 2021, 1–31.
  79. Zeng, Y.; Zhang, J.; Zhang, M.; Zhang, D. Collision avoidance decision-making based on particle swarm optimization and genetic algorithm. J. Navig. China 2020, 43, 1–6+28.
  80. Hu, Y.; Meng, X.; Zhang, Q.; Park, G. A real-time collision avoidance system for autonomous surface vessel using fuzzy logic. IEEE Access 2020, 8, 108835–108846.
  81. Ahmed, Y.A.; Hannan, M.A.; Oraby, M.Y.; Maimun, A. COLREGs Compliant Fuzzy-Based Collision Avoidance System for Multiple Ship Encounters. J. Mar. Sci. Eng. 2021, 9, 790.
  82. Wang, C.; Zhang, X.; Yang, Z.; Bashir, M.; Lee, K. Collision Avoidance For Autonomous Ship Using Deep Reinforcement Learning And Prior-Knowledge-Based Approximate Representation. Front. Mar. Sci. 2023, 9, 1084763.
  83. Guan, W.; Zhao, M.; Zhang, C.; Xi, Z. Generalized Behavior Decision-Making Model for Ship Collision Avoidance via Reinforcement Learning Method. J. Mar. Sci. Eng. 2023, 11, 273.
  84. Jiang, L.; An, L.; Zhang, X.; Wang, C.; Wang, X. A human-like collision avoidance method for autonomous ship with attention-based deep reinforcement learning. Ocean Eng. 2022, 264, 112378.
  85. Guo, S.; Zhang, X.; Du, Y.; Zheng, Y.; Cao, Z. Path Planning of Coastal Ships Based on Optimized DQN Reward Function. J. Mar. Sci. Eng. 2021, 9, 210.
  86. Wang, W.; Huang, L.; Liu, K.; Wu, X.; Wang, J. A COLREGs-Compliant Collision Avoidance Decision Approach Based on Deep Reinforcement Learning. J. Mar. Sci. Eng. 2022, 10, 944.
  87. Shen, H.; Hashimoto, H.; Matsuda, A.; Taniguchi, Y.; Terada, D.; Guo, C. Automatic collision avoidance of multiple ships based on deep Q-learning. Appl. Ocean Res. 2019, 86, 268–288.
  88. Chen, C.; Chen, X.; Ma, F.; Zeng, X.; Wang, J. A knowledge-free path planning approach for smart ships based on reinforcement learning. Ocean Eng. 2019, 189, 106299.
  89. Xue, D.; Wu, D.; Yamashita, A.S.; Li, Z. Proximal policy optimization with reciprocal velocity obstacle based collision avoidance path planning for multi-unmanned surface vehicles. Ocean Eng. 2023, 273, 114005.
  90. Bi, X.; Jia, C.; Wu, Z. Opportunity and actions taken of ship’s changing speed collision-avoidance. J. Dalian Marit. Univ. 2004, 01, 26–28.
  91. Ma, W.Y.; Yang, J.X. Collision Avoidance Strategy Optimization of Ship’s Speed Alteration with Bacterial Foraging Algorithm. Appl. Mech. Mater. 2013, 278–280, 1318–1322.
  92. Yu, J.; Liu, Z.; Bu, R.; Gao, X.; Li, W. Artificial Physics Optimization Algorithm for Collision-avoidance Through Speed Alteration. Navig. China 2019, 42, 40–43.
  93. Su, L.; Qin, X.; Liu, Z.; Zhang, Z. Intelligent collision avoidance decision for single ship considering ship maneuverability. In Proceedings of the 2019 9th International Conference on Information Science and Technology (ICIST 2019), Hulunbuir, China, 2–5 August 2019; Volume 1, pp. 164–168.
  94. Hu, Y.; Zhang, A.; Tian, W.; Zhang, J.; Hou, Z. Multi-Ship Collision Avoidance Decision-Making Based on Collision Risk Index. J. Mar. Sci. Eng. 2020, 8, 640.
  95. Hirayama, K.; Miyake, R.; Shiota, T.; Okimoto, T. DSSA+: Distributed Collision Avoidance Algorithm in an Environment where Both Course and Speed Changes are Allowed. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13, 117–124.
  96. Perera, L.P.; Carvalho, J.P.; Soares, C.G. Fuzzy logic based decision making system for collision avoidance of ocean navigation under critical collision conditions. J. Mar. Sci. Technol. 2011, 16, 84–99.
  97. Szlapczynski, R.; Krata, P.; Szlapczynska, J. Ship domain applied to determining distances for collision avoidance manoeuvres in give-way situations. Ocean Eng. 2018, 165, 43–54.
  98. Kim, D.; Kim, J.; Kim, J.; Im, N. Development of ship collision avoidance system and sea trial test for autonomous ship. Ocean Eng. 2022, 266, 113120.
  99. Zhang, J.; Zhang, D.; Yan, X.; Haugen, S.; Guedes Soares, C. A distributed anti-collision decision support formulation in multi-ship encounter situations under COLREGs. Ocean Eng. 2015, 105, 336–348.
  100. Szlapczynski, R. A New Method of Ship Routing on Raster Grids, with Turn Penalties and Collision Avoidance. J. Navig. 2006, 59, 27–42.
  101. Szlapczynski, R.; Krata, P.; Szlapczynska, J. A Ship Domain-Based Method of Determining Action Distances for Evasive Manoeuvres in Stand-On Situations. J. Adv. Transp. 2018, 2018, 1–19.
  102. Huang, Y.; Chen, L.; van Gelder, P.H.A.J. Generalized velocity obstacle algorithm for preventing ship collisions at sea. Ocean Eng. 2019, 173, 142–156.
  103. Johansen, T.A.; Cristofaro, A.; Perez, T. Ship Collision Avoidance Using Scenario-Based Model Predictive Control. IFAC-Pap. 2016, 49, 14–21.
  104. Johansen, T.A.; Perez, T.; Cristofaro, A. Ship Collision Avoidance and COLREGS Compliance Using Simulation-Based Control Behavior Selection With Predictive Hazard Assessment. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3407–3422.
  105. Kufoalor, D.K.M.; Johansen, T.A.; Brekke, E.F.; Hepsø, A.; Trnka, K. Autonomous maritime collision avoidance: Field verification of autonomous surface vehicle behavior in challenging scenarios. J. Field Robot. 2020, 37, 387–403.
  106. Eriksen, B.; Bitar, G.; Breivik, M.; Lekkas, A. Hybrid Collision Avoidance for ASVs Compliant With COLREGs Rules 8 and 13–17. Front. Robot. AI 2020, 7, 11.
  107. Eriksen, B.H.; Breivik, M.; Wilthil, E.F.; Flåten, A.L.; Brekke, E.F. The branching-course model predictive control algorithm for maritime collision avoidance. J. Field Robot. 2019, 36, 1222–1249.
  108. Hu, L.; Naeem, W.; Rajabally, E.; Watson, G.; Mills, T.; Bhuiyan, Z.; Raeburn, C.; Salter, I.; Pekcan, C. A Multiobjective Optimization Approach for COLREGs-Compliant Path Planning of Autonomous Surface Vehicles Verified on Networked Bridge Simulators. IEEE Trans Intell. Transp. Syst. 2020, 21, 1167–1179.
  109. Tan, G.; Zou, J.; Zhuang, J.; Wan, L.; Sun, H.; Sun, Z. Fast marching square method based intelligent navigation of the unmanned surface vehicle swarm in restricted waters. Appl. Ocean Res. 2020, 95, 102018.
  110. Chen, L.; Huang, L. Ship Collision Avoidance Path Planning by PSO Based on Maneuvering Equation. In Future Wireless Networks and Information Systems; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2012; Volume 1, pp. 675–682.
  111. Zhang, Y.; Shi, G.; Liu, H.; Li, W. Decision supporting for ship collision avoidance in restricted waters. Int. J. Simul. Process Model. 2020, 15, 40–51.
  112. Zeng, Y.; Zhang, J.; Zhang, M.; Li, T. Anti-collision Decision Making by Course Alteration and Speed Change under COLREGs. In Proceedings of the 2019 5th International Conference on Transportation Information and Safety (ICTIS 2019), Liverpool, UK, 14–17 July 2019; pp. 25–31.
  113. Xu, X.; Pan, W.; Huang, Y.; Zhang, W. Dynamic Collision Avoidance Algorithm for Unmanned Surface Vehicles via Layered Artificial Potential Field with Collision Cone. J. Navig. 2020, 73, 1306–1325.
  114. Song, J.; Hao, C.; Su, J. Path planning for unmanned surface vehicle based on predictive artificial potential field. Int. J. Adv. Robot. Syst. 2020, 17, 1738075837.
  115. Guo, S.; Zhang, X.; Zheng, Y.; Du, Y. An Autonomous Path Planning Model for Unmanned Ships Based on Deep Reinforcement Learning. Sensors 2020, 20, 426.
  116. Xu, X.; Lu, Y.; Liu, G.; Cai, P.; Zhang, W. COLREGs-abiding hybrid collision avoidance algorithm based on deep reinforcement learning for USVs. Ocean Eng. 2022, 247, 110749.
  117. Shen, H. Collision Avoidance Navigation and Control for Unmanned Marine Vessels Based on Reinforcement Learning. Ph.D. Thesis, Dalian Maritime University, Dalian, China, 2018.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Transportation
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Hongguang Lyu
,
Zengrui Hao
,
Jiawei Li
,
Guang Li
,
Xiaofeng Sun
,
Zhang Guoqing
,
Yong YIN
,
Yanjie Zhao
,
Lunping Zhang
View Times: 299
Revisions: 2 times (View History)
Update Date: 19 Apr 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback