Wavefunction Collapse Broadens Molecular Spectrum

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Peter Lebedev-Stepanov	--	1663	2023-04-11 08:32:24	\|
2	formatted	Vicky Zhou	Meta information modification	1663	2023-04-11 08:44:21	\| \|
3	formatted	Vicky Zhou	Meta information modification	1663	2023-04-11 08:46:46	\| \|
4	formatted	Vicky Zhou	+ 3 word(s)	1694	2023-04-11 08:59:24	\| \|
5	formatted	Vicky Zhou	Meta information modification	1694	2023-04-11 08:59:53	\|

Peer Reviewed

This is a peer-reviewed entry published in Encyclopedia Journal, full entry can be found at 10.3390/encyclopedia3020029

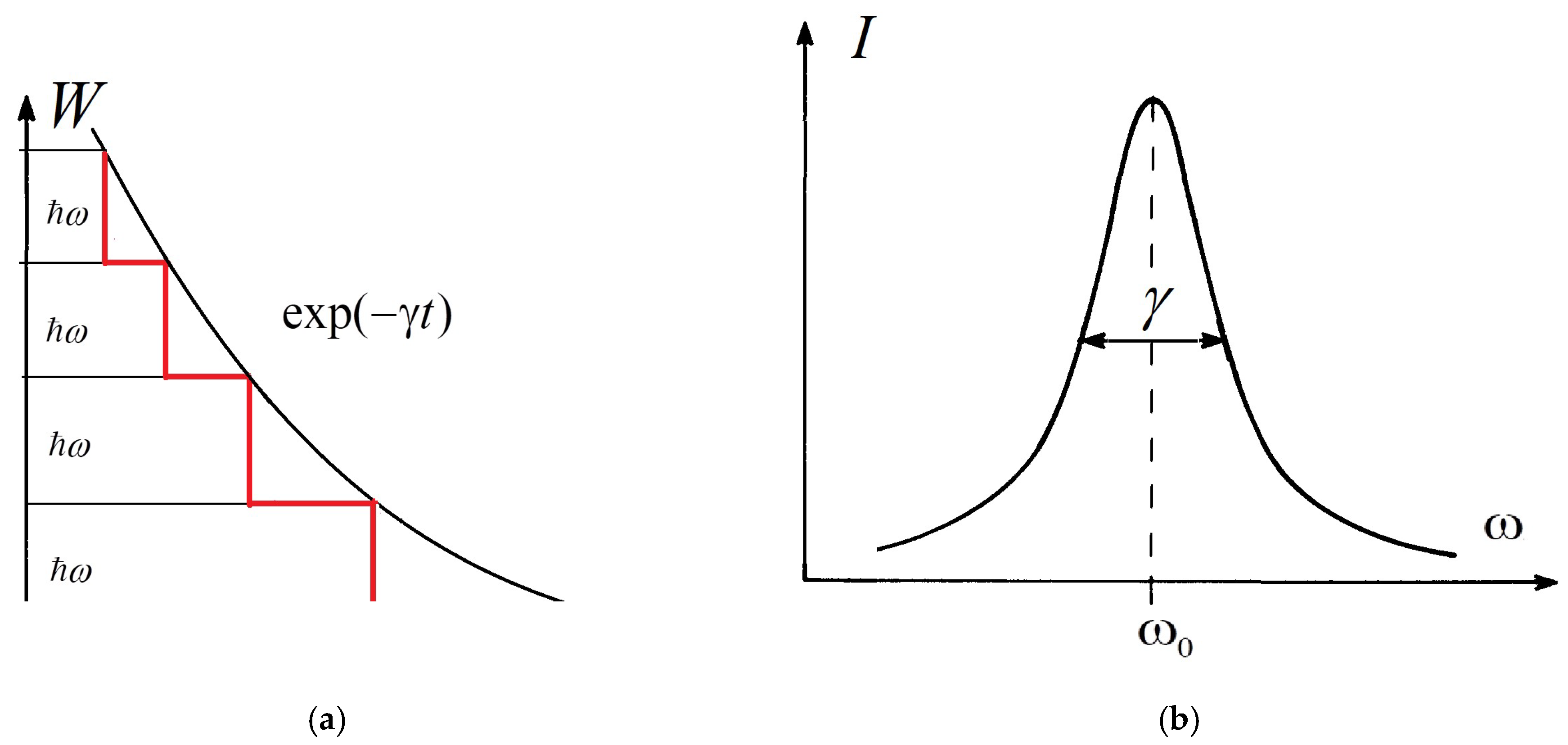
Spectral lines in the optical spectra of atoms, molecules, and other quantum systems are characterized by a range of frequencies $ω$ or a range of wavelengths $λ = 2 π c / ω$ , where c is the speed of light. Such a frequency or wavelength range is called the width of the spectral lines (linewidth). It is influenced by many specific factors. Thermal motion of the molecules results in broadening of the lines as a result of the Doppler effect (thermal broadening) and by their collisions (pressure broadening). The electric fields of neighboring molecules lead to Stark broadening. The linewidth to be considered here is the so-called parametric broadening (PB) of spectral lines in the optical spectrum. PB can be considered the fundamental type of broadening of the electronic vibrational–rotational (rovibronic) transitions in a molecule, which is the direct manifestation of the basic concept of the collapse of a wavefunction that is postulated by the Copenhagen interpretation of quantum mechanics. Thus, that concept appears to be not only valid but is also useful for predicting physically observable phenomena.

molecular spectrum electronic-vibrational level Franck–Condon principle collapse of wavefunction spectral line broadening adiabatic approximation polymethine dye linewidth

In the theory of atomic spectra, the important concept of natural linewidth is introduced. Electrons can occupy discrete energy states in the atom. If an electron is in an excited state, it can jump to an energetically lower state by radiating a photon. The result of this is that the lifetime of the excited state is not infinite. In classical theory, the energy of an electron in such a system decays exponentially with time due to it experiencing radiative friction.

A dipole emitter (linear harmonic oscillator) with a frequency

ω_{0}

is determined by the equation

\ddot{x} = - ω_{0}^{2} x - γ \dot{x}

with a radiative damping coefficient

$γ = \frac{2 ω_{0}^{2}}{3 c} r_{e},$

where $r_{e} = \frac{e^{2}}{4 π ε_{0} m_{e} c^{2}} \approx 2.818 \cdot 10^{- 15}$ m is the electron’s classical radius and $m_{e}$ and e are the mass and modulus of the electron’s charge, respectively. The solution of (1) is approximately ( $γ ≪ ω_{0}$ ).

$x = x_{0} \exp (- \frac{γ t}{2} - i ω_{0} t) .$

The energy of the oscillator, averaged over one period, decreases exponentially (Figure 1a, smooth black curve)

W = \frac{1}{2} m ({\dot{x}}^{2} + ω_{0}^{2} x^{2}) = W_{0} \exp (- γ t) .

Figure 1. Natural linewidth in the theory of atomic spectra: (a) in the classical picture, all atoms of an ensemble radiate continuously and simultaneously (black smooth exponential curve); quantum emission of light occurs in portions (red step curve); (b) radiation intensity spectral distribution of a classical dipole emitter described by a Lorentzian line; the damping coefficient

γ

determines the characteristic width of the line.

The radiation intensity distribution of this dipole emitter is described by the so-called Lorentzian line (Figure 1b).

I = \frac{I_{0}}{{(ω - ω_{0})}^{2} + γ^{2} / 4} .

The damping coefficient

γ

determines the characteristic width at half the height of the Lorentzian, i.e., the breadth at half the maximum intensity distribution. The linewidth introduced here is called the natural linewidth (Ref. ^[1], pp. 32–33). The atomic decay time (lifetime of excited state) is determined according to

τ_{0} = γ^{- 1}

. The condition

γ ≪ ω_{0}

expresses the fact that this time is very long compared with one period of the oscillator

2 π / ω_{0}

. For optical transitions, typical numerical values of

τ_{0}

are

10^{- 9} - 10^{- 8}

s, and thus

γ = 10^{8} - 10^{9} s^{- 1}

(Ref. ^[2], p. 308).

Experiments carried out by Wilhelm Wien (1919) confirmed the approximately exponential attenuation of the luminescence of atoms, as well as the order of magnitude of the characteristic value of the coefficient γ ^[3]. However, the frequency dependence of the coefficient γ given by Formula (2) has not been experimentally confirmed (Ref. ^[4], p. 348; Ref. ^[5], p. 644).

According to quantum theory, an excited atom emits a photon instantly upon transition to a lower energy state. The duration of the emission or absorption process does not appear in the theory and is considered to be negligible. This may seem to be in direct contradiction to Wien’s experiments. However, Wien’s experiments determined the time of emission not of a single atom but of a large number of atoms simultaneously. For a large number of atoms or molecules, classical and quantum theories lead to qualitatively similar results. According to quantum concepts, each excited atom or molecule has a dark pause, during which the atom is in an excited state but does not radiate. Suddenly, the atom emits a photon instantly.

A quantum picture of the change in the energy of an ensemble of excited atoms with time is shown in Figure 1a (red step curve). That picture differs sharply from the classical one (black smooth exponential curve in Figure 1a). The duration of any dark pause corresponds to the lifetime of the excited state of the individual atom concerned. The lifetimes of atoms even in the same state are different and distributed according to statistical law.

Quantum emission of light occurs in quants. First, one atom emits a photon, then another, and so on. Thus, the curve looks like a staircase. The height of all the steps is the same, but the width of the steps fluctuates chaotically. Each step corresponds to the radiation of an individual atom. However, in the presence of a large ensemble of excited atoms, in practice, it is possible to use an exponential instead of a step curve, as in the classical theory. Thus, if there is a large number of atoms, N₀, in the same excited state, then the change in the number of atoms in the excited state is given approximately by an exponential law with decrement γ:

N = N_{0} \exp (- γ t) .

The natural linewidth in quantum theory is explained by the uncertainty of the corresponding energy of excited levels of the atom. Heisenberg’s uncertainty relation can be written as

Δ E τ_{0} \geq ℏ

, where

τ_{0} = γ^{- 1}

. The ground state of the atom has an exact energy value, while the excited state has an energy uncertainty

Δ E \geq ℏ γ

. The typical magnitude of γ in conventional spectroscopic units is

10^{- 4} {cm}^{- 1}

(Ref. ^[2], p. 308), while the optical frequency is of the order of

10^{4} {cm}^{- 1}

. The general expression for γ (Ref. ^[1], p. 184) is defined as follows:

where

ρ_{W}

is the density of energy of the excited atomic states,

|H^{2}|

is the square of the matrix element of the interaction energy between electron and the electromagnetic field, and

\int d Ω

denotes integration over all directions of photon propagation.

Usually, two kinds of spectral-line broadening are considered ^[6]. Homogenous broadening is due to internal processes that broaden the optical lines in the spectrum of a single atom or molecule (e.g., radiative broadening that provides natural linewidth). Inhomogeneous broadening arises from the effects of the surroundings and external processes. For example, the stochastic electric fields of neighboring molecules lead to Stark broadening that manifests itself in fluctuations of the solvatochromic spectral shift ^[7]^[8], while Doppler broadening is due to thermal motion. It is generally accepted that all such broadenings are sufficiently small: many orders of magnitude smaller than the observed width of the optical absorption band of the molecule (10–10³ cm⁻¹).

There are complex internal processes in molecules that are not present in single atoms. Therefore, molecular spectra, which have the form of bands, do differ significantly from atomic ones. This difference is due to the fact that electronic transitions are influenced by the vibrational-rotational motions of groups of atoms within the molecule. Rovibronic transitions merge into absorption and emission bands corresponding to the energy spectrum of a molecule of this type ^[6].

An accurate description of quantum transitions in molecules can only be made on the basis of taking into account all the requirements of modern quantum mechanics. Let us recall the basic principles of the Copenhagen interpretation of quantum mechanics (CI), which is taken as a basis by most modern scientists ^[9]^[10]^[11]^[12]:

The wavefunction includes complete information about quantum objects and their states (completeness principle).
A quantum state represented by the linear superposition of the quantum states can be considered as an admissible quantum state (superposition principle).
Quantum objects have certain pairs of complementary properties that cannot all be observed or measured simultaneously (Bohr’s principle of complementarity).
Heisenberg’s uncertainty principle.
Max Born’s probability interpretation of squared wavefunction.
The quantum object under investigation is inseparable from the experimental device used to make the measurements. The interaction between the object and device forms an inseparable part of the quantum phenomena. The instantaneous collapse of the wavefunction (reduction of the wave packet) upon measurement is a manifestation of that inseparability principle.
Quantum and classical physics correspond to each other in the classical limit (Bohr’s correspondence principle).

Electronic-vibrational (vibronic) transitions in molecules are usually described on the basis of the Franck Condon (FC) principle. Historically, this principle was introduced in the early years of quantum mechanics (1925–1928) ^[13]^[14]^[15]^[16] before CI was finally formulated.

Therefore, the theory of molecular spectra based on the FC principle does not consistently take into account the postulates of the CI, and, in particular, the FC principle ignores the very important concept of wavefunction collapse. According to Don Howard ^[16], that is not surprising because the concept of wavefunction collapse was finally formulated only in the mid-1950s by W. Heisenberg: ‘Various other physicists and philosophers, including Bohm, Feyerabend, Hanson, and Popper, having further promoted the invention in the service of their own philosophical agendas.’

At the same time, the efficiency of the FC principle in the form in which it came into use in 1928 is proved by its satisfactory agreement with experiments on molecular spectroscopy ^[17]^[18]^[19]^[20]. However, a more consistent application of the postulates of the CI makes it possible to achieve a more detailed description in this area. In fact, the collapse of the wavefunction is manifested in so-called parametric broadening (PB) ^[21]^[22] that plays an important role in the formation of molecular vibronic spectra. Herein, consider the mechanism of PB using the example of a (0–0) vibronic transition in a series of polymethine dyes.

Although the electronic-vibrational (vibronic) terms of a molecule shall be considered, the same conclusions can be drawn in the general case of electronic-vibrational-rotational (rovibronic) transitions. Furthermore, although only the absorption spectra shall be considered, the broadening of emission spectra can be determined in a similar way.

The problem of calculating the vibronic transition in the adiabatic approximation was considered in general form in ^[21]^[22]. It is also shown there how the collapse of the wavefunction at the moment of absorption or emission of a phonon leads to parametric broadening of the vibronic line. Herein, consider this problem in the simplest one-dimensional case.

References

Heitler, W. The Quantum Theory of Radiation, 3rd ed.; Clarendon Press: Oxford, UK, 1954.
Haken, H.; Wolf, H.C. The Physics of Atoms and Quanta, 7th ed.; Springer-Verlag: Berlin, Germany, 2005.
Wien, W. Uber Messungen der Leuchtdauer der Atome und der Dampfung der Spektrallinien I. Ann. Phys. 1919, 60, 597–637.
Putilov, K.A.; Fabrikant, V.A. Course of Physics, 2nd ed.; Fizmatgiz: Moscow, Russia, 1963; Volume 3. (In Russian)
Mehra, J.; Rechenberg, H. The Historical Development of Quantum Theory: The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld: Its Foundation and the Rise of Its Difficulties 1900–1925; Springer: New York, NY, USA, 1982; Volume 1.
Frank-Kamenetskii, M.D.; Lukashin, A.V. Electron-vibrational interactions in polyatomic molecules. Sov. Phys. Usp. 1975, 18, 391–409.
Reichardt, C. Solvents and Solvent Effects in Organic Chemistry, 3rd ed.; WILEY-VCH: Weinheim, Germany, 2003.
Stepko, A.S.; Medvedeva, A.A.; Koshkin, A.V.; Lebedev-Stepanov, P.V. Specific Solvation of a 4-DASPI Dye in a Water-Ethylene Glycol Binary Solvent. Opt. Spectrosc. 2022, 130, 108–115.
Bohr, N. Atomic Theory and the Description of Nature; Cambridge University Press: Cambridge, UK, 1961.
Heisenberg, W. Physics and Philosophy: The Revolution in Modern Science; Harper Perennial Modern Classics: New York, NY, USA, 2007.
Heisenberg, W. The Development of the Interpretation of the Quantum Theory. In Niels Bohr and the Development of Physics; Pauli, W., Ed.; Pergamon: London, UK, 1955; pp. 12–29.
Hanson, N.R. Copenhagen Interpretation of Quantum Theory. Am. J. Phys. 1959, 27, 1–15.
Franck, J. Elementary processes of photochemical reactions. Trans. Faraday Soc. 1926, 21, 536–542.
Condon, E.U. Nuclear Motion Associated with Electron Transitions in Diatomic Molecules. Phys. Rev. 1928, 32, 858–872.
Condon, E.U. The Franck-Condon Principle and Related Topics. Am. J. Phys. 1947, 15, 365–374.
Howard, D. Who invented the Copenhagen Interpretation? A study in mythology. Philos. Sci. 2004, 71, 669–682.
Borrelli, A.R.; Capobianco, A.; Peluso, A. Generating Function Approach to the Calculation of Spectral Band Shapes of Free-Base Chlorin Including Duschinsky and Herzberg–Teller Effects. J. Phys. Chem. A 2012, 116, 9934–9940.
Baiardi, A.; Bloino, J.; Barone, V. General Time Dependent Approach to Vibronic Spectroscopy Including Franck–Condon, Herzberg–Teller, and Duschinsky Effects. J. Chem. Theory Comput. 2013, 9, 4097–4115.
Freidzon, A.Y.; Valiev, R.R.; Berezhnoy, A.A. Ab initio simulation of pyrene spectra in water matrices. RSC Adv. 2014, 4, 42054–42065.
Cerezo, J.; Aranda, D.; Ferrer, F.; Prampolini, G.; Santoro, F. Adiabatic-Molecular Dynamics Generalized Vertical Hessian Approach: A Mixed Quantum Classical Method To Compute Electronic Spectra of Flexible Molecules in the Condensed Phase. J. Chem. Theory Comput. 2020, 16, 1215–1231.
Lebedev-Stepanov, P. Parametric broadening of the molecular vibronic band due to zero-point oscillations and thermal fluctuations of interatomic bonds. AIP Adv. 2021, 11, 035115.
Lebedev-Stepanov, P.V. Parametric Broadening of the Electronic-Vibrational Spectrum of a Molecule Caused by Zero-Point Vibrations and Thermal Fluctuations of Interatomic Bonds. Dokl. Phys. 2021, 66, 277–284.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Quantum Science & Technology

Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Peter Lebedev-Stepanov

View Times: 759

Entry Collection: Applications of Quantum Mechanics

Online Date: 11 Apr 2023

Table of Contents

Video Upload Options

Confirm

References