Spectral lines in the optical spectra of atoms, molecules, and other quantum systems are characterized by a range of frequencies ω or a range of wavelengths λ=2πc/ω, where c is the speed of light. Such a frequency or wavelength range is called the width of the spectral lines (linewidth). It is influenced by many specific factors. Thermal motion of the molecules results in broadening of the lines as a result of the Doppler effect (thermal broadening) and by their collisions (pressure broadening). The electric fields of neighboring molecules lead to Stark broadening. The linewidth to be considered here is the so-called parametric broadening (PB) of spectral lines in the optical spectrum. PB can be considered the fundamental type of broadening of the electronic vibrational–rotational (rovibronic) transitions in a molecule, which is the direct manifestation of the basic concept of the collapse of a wavefunction that is postulated by the Copenhagen interpretation of quantum mechanics. Thus, that concept appears to be not only valid but is also useful for predicting physically observable phenomena.
- molecular spectrum
- electronic-vibrational level
- Franck–Condon principle
- collapse of wavefunction
- spectral line broadening
- adiabatic approximation
- polymethine dye
- linewidth
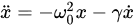
(1)
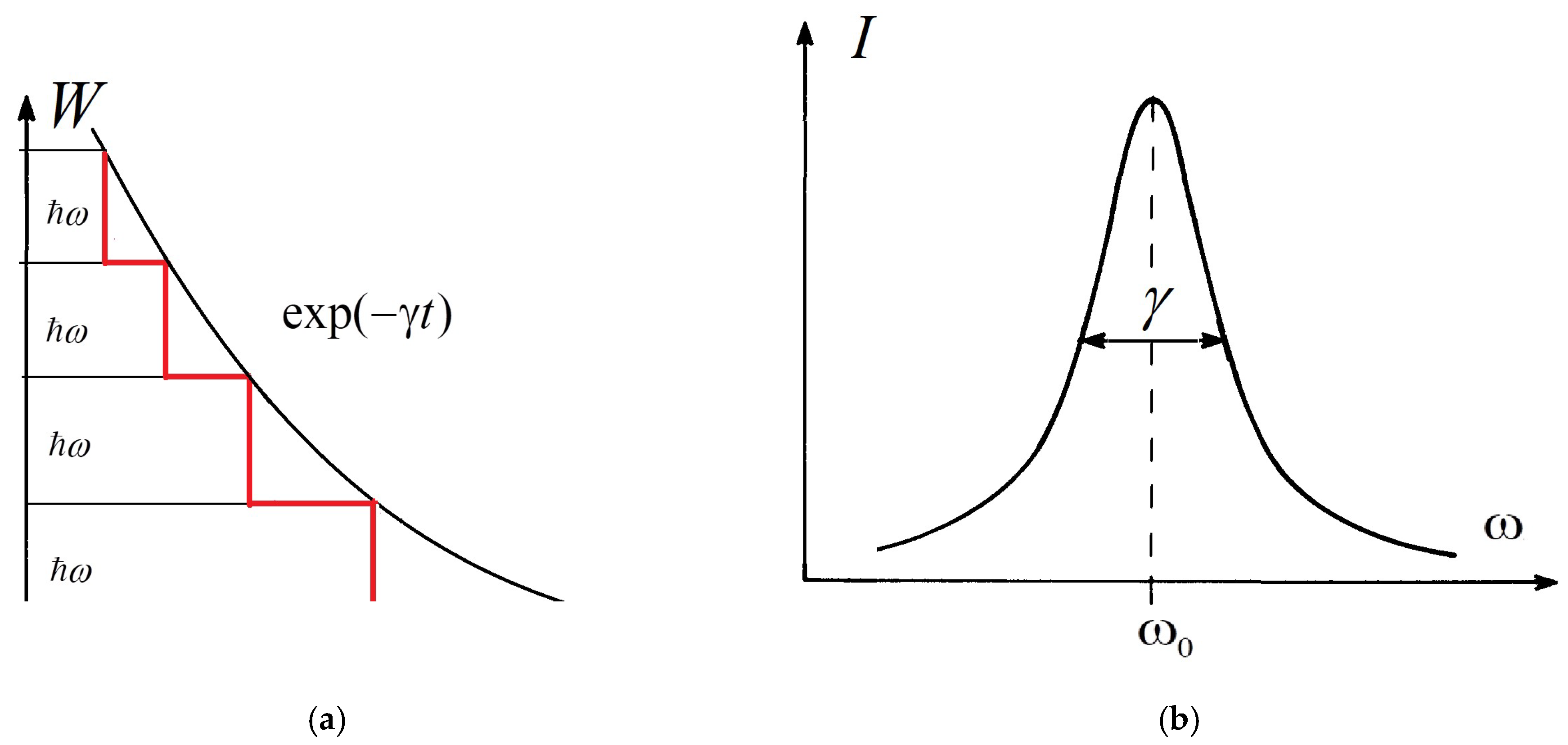
with a radiative damping coefficient
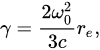
(2)
where 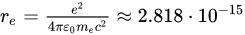 m is the electron’s classical radius and me and e are the mass and modulus of the electron’s charge, respectively. The solution of (1) is approximately (γ≪ω0).
m is the electron’s classical radius and me and e are the mass and modulus of the electron’s charge, respectively. The solution of (1) is approximately (γ≪ω0).
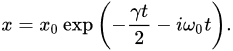


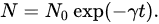
-
The wavefunction includes complete information about quantum objects and their states (completeness principle).
-
A quantum state represented by the linear superposition of the quantum states can be considered as an admissible quantum state (superposition principle).
-
Quantum objects have certain pairs of complementary properties that cannot all be observed or measured simultaneously (Bohr’s principle of complementarity).
-
Heisenberg’s uncertainty principle.
-
Max Born’s probability interpretation of squared wavefunction.
-
The quantum object under investigation is inseparable from the experimental device used to make the measurements. The interaction between the object and device forms an inseparable part of the quantum phenomena. The instantaneous collapse of the wavefunction (reduction of the wave packet) upon measurement is a manifestation of that inseparability principle.
-
Quantum and classical physics correspond to each other in the classical limit (Bohr’s correspondence principle).
References
- Heitler, W. The Quantum Theory of Radiation, 3rd ed.; Clarendon Press: Oxford, UK, 1954.
- Haken, H.; Wolf, H.C. The Physics of Atoms and Quanta, 7th ed.; Springer-Verlag: Berlin, Germany, 2005.
- Wien, W. Uber Messungen der Leuchtdauer der Atome und der Dampfung der Spektrallinien I. Ann. Phys. 1919, 60, 597–637.
- Putilov, K.A.; Fabrikant, V.A. Course of Physics, 2nd ed.; Fizmatgiz: Moscow, Russia, 1963; Volume 3. (In Russian)
- Mehra, J.; Rechenberg, H. The Historical Development of Quantum Theory: The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld: Its Foundation and the Rise of Its Difficulties 1900–1925; Springer: New York, NY, USA, 1982; Volume 1.
- Frank-Kamenetskii, M.D.; Lukashin, A.V. Electron-vibrational interactions in polyatomic molecules. Sov. Phys. Usp. 1975, 18, 391–409.
- Reichardt, C. Solvents and Solvent Effects in Organic Chemistry, 3rd ed.; WILEY-VCH: Weinheim, Germany, 2003.
- Stepko, A.S.; Medvedeva, A.A.; Koshkin, A.V.; Lebedev-Stepanov, P.V. Specific Solvation of a 4-DASPI Dye in a Water-Ethylene Glycol Binary Solvent. Opt. Spectrosc. 2022, 130, 108–115.
- Bohr, N. Atomic Theory and the Description of Nature; Cambridge University Press: Cambridge, UK, 1961.
- Heisenberg, W. Physics and Philosophy: The Revolution in Modern Science; Harper Perennial Modern Classics: New York, NY, USA, 2007.
- Heisenberg, W. The Development of the Interpretation of the Quantum Theory. In Niels Bohr and the Development of Physics; Pauli, W., Ed.; Pergamon: London, UK, 1955; pp. 12–29.
- Hanson, N.R. Copenhagen Interpretation of Quantum Theory. Am. J. Phys. 1959, 27, 1–15.
- Franck, J. Elementary processes of photochemical reactions. Trans. Faraday Soc. 1926, 21, 536–542.
- Condon, E.U. Nuclear Motion Associated with Electron Transitions in Diatomic Molecules. Phys. Rev. 1928, 32, 858–872.
- Condon, E.U. The Franck-Condon Principle and Related Topics. Am. J. Phys. 1947, 15, 365–374.
- Howard, D. Who invented the Copenhagen Interpretation? A study in mythology. Philos. Sci. 2004, 71, 669–682.
- Borrelli, A.R.; Capobianco, A.; Peluso, A. Generating Function Approach to the Calculation of Spectral Band Shapes of Free-Base Chlorin Including Duschinsky and Herzberg–Teller Effects. J. Phys. Chem. A 2012, 116, 9934–9940.
- Baiardi, A.; Bloino, J.; Barone, V. General Time Dependent Approach to Vibronic Spectroscopy Including Franck–Condon, Herzberg–Teller, and Duschinsky Effects. J. Chem. Theory Comput. 2013, 9, 4097–4115.
- Freidzon, A.Y.; Valiev, R.R.; Berezhnoy, A.A. Ab initio simulation of pyrene spectra in water matrices. RSC Adv. 2014, 4, 42054–42065.
- Cerezo, J.; Aranda, D.; Ferrer, F.; Prampolini, G.; Santoro, F. Adiabatic-Molecular Dynamics Generalized Vertical Hessian Approach: A Mixed Quantum Classical Method To Compute Electronic Spectra of Flexible Molecules in the Condensed Phase. J. Chem. Theory Comput. 2020, 16, 1215–1231.
- Lebedev-Stepanov, P. Parametric broadening of the molecular vibronic band due to zero-point oscillations and thermal fluctuations of interatomic bonds. AIP Adv. 2021, 11, 035115.
- Lebedev-Stepanov, P.V. Parametric Broadening of the Electronic-Vibrational Spectrum of a Molecule Caused by Zero-Point Vibrations and Thermal Fluctuations of Interatomic Bonds. Dokl. Phys. 2021, 66, 277–284.
